Introduction

Ever since the invention of mechanical testing machines, prediction of flow behavior of materials has captured the fascination of material scientists. This fascination has yielded many constitutive models over the years (Ref 1). A current review of literature indicates that even today, the subject is as captivating as it was in the 1980s (Ref 2,3,4). This may be attributed to the inability of a single model to connote the influence of all imposed parameters on material response, as well as the difficulty in depicting the flow behavior of different materials using a common model. In this scenario, researchers either modify the existing suitable models or propose new models to portray the behavior of new materials. Some of the popular models are Cheng–Zhang model (Ref 5), Kobayashi–Dodd model (Ref 6), Wang–Jiang model (Ref 7), SK-Paul model (Ref 8), KH model (Ref 9) and physically based models (Ref 10,11,12). In many cases, the new model is a modification or extension of an existing theory, as exemplified by modified Zerilli–Armstrong (MZA) (Ref 13,14,15,16), modified Johnson–Cook (MJC) (Ref 17,18,19,20,21), mechanical threshold stress (MTS) (Ref 22,23,24), etc. models.

An alternate approach to predict flow behavior over a very large domain is to combine several models with the help of computer codes as described by Lindgren et al. (Ref 25). This approach has been effective in modeling the flow response of SS 316L steel over a large range of temperatures and strain rates (Ref 25). However, this complex process may not appeal to the alloy designer who simply wishes to make minor variations in composition and then study the change in flow behavior. Such necessities frequently arise during optimization of element content in an alloy during its development stage. This is best exemplified by addition of interstitial elements to different grades of steels. One such example is addition of carbon to alloy D9, which improves creep properties and irradiation resistance by forming compound with Ti (Ref 26). Though the variation of carbon content is minor, it significantly alters the workability of the steel (Ref 13) (Ref 27). Another example is addition of nitrogen, which aims to improve creep strength and corrosion resistance of SS 316L (Ref 28, 29), yet it simultaneously influences the deformation characteristics by changing work hardening behavior and flow softening mechanisms. Therefore, the alloy designer tries to optimize the interstitial content by simultaneously monitoring workability and in-service properties of the alloy. In these situations, users may prefer mathematical or phenomenological models which are less complex and do not require a high level of programming skill. However, this composition-dependent facet of constitutive modeling is less explored and often gets neglected in popular discourse. Hitherto, ANN has often been recommended for such uses as it readily accommodates the composition in its input parameters (Ref 30,31,32).

This paper aims to highlight the different factors which must be considered before selecting a constitutive model to predict the flow behavior of alloy when minor alloying additions are varied. For this purpose, four grades of 316LN, an austenitic stainless steel, have been used to generate experimental data. Using the experimental result of two variants of the above-mentioned steel (i.e., with 0.07%N and 0.22% N), some frequently used phenomenological constitutive equations such as modified Johnson–Cook (MJC), strain compensated Arrhenius (SCA) and model D8A have been assessed in relation to an artificial neural network (ANN) model, taking into consideration the respective capabilities for flow prediction. Along with the usual statistical error analysis, five additional factors from the perspective of alloy development have also been used to assess the suitability of the model. The models which fulfill these six criteria have been amended to predict flow stress of other two variants of the steel (i.e., with 0.11%N and 0.14% N), and the predictions have been validated with the experimental data.

Materials and Method

Four grades of 316LN have been chosen as model alloys. The base alloy has nominal chemical composition (in wt.%) Fe-17.6Cr-12.3Ni-2.5Mo-1.7Mn-0.028C-xN, where x = 0.07, 0.11, 0.14 and 0.22 for the four grades designated as 7 N, 11 N, 14 N and 22 N, respectively. These grades were received in rolled plate form. In order to ensure similar grain size in 7 N, 11 N and 22 N steels, cylindrical bars machined from the plates were subjected to a common solution annealing treatment at 1373 K for 30 min. Subsequently, cylindrical specimens of 15 mm height and 10 mm diameter were machined from the solution annealed bars for compression testing. However, neither the bars machined from the 14 N plate nor the specimens fabricated thereof were subjected to any heat treatment. This was done consciously to determine the effect of small grain size variations on the capability of constitutive models. This is relevant because some degree of grain size variation across different heats is unavoidable during practical alloy development.

A servo-hydraulic, constant true strain rate compression testing machine with special quenching facility was used for the hot isothermal compression testing of the 7 N, 11 N and 22 N specimens. The uniaxial compression tests were performed in the temperature range of 1123-1423 K (at 100 K interval) and at constant true strain rates of 0.001, 0.01, 0.1, 1 and 10 s−1. Each specimen was deformed to a nominal strain of 50%.

However, the 14 N grade was tested using a Gleeble thermomechanical simulator in temperature domain 1123-1423 K at a strain rate of 0.1 s−1. All the tests were carried out in accordance with the ASTM E209 standard.

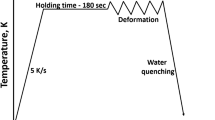
Before imparting the deformation, each specimen was heated at a rate of 5 K s−1 to the desired deformation temperature and soaked at that temperature for 2 min to achieve homogeneous temperature distribution throughout the specimen. The temperature of the specimen during the deformation was recorded using K-type thermocouples. To minimize the friction during deformation, graphite foils and Ni paste were used between specimens and the platens. As a result, no significant barreling of the specimen was observed after deformation. The load-stroke data recorded during the experiments were used to generate true stress–true plastic strain curves following the standard procedure recommended (Ref 33). The flow curves were corrected using the method suggested by (Ref 34), incorporating the adiabatic temperature rise measured during high strain rates, mostly at 1 and 10 s−1.

Experimental data obtained for 7 N and 22 N were used for the development of constitutive models describing the effect of nitrogen content on flow stress. Experimental data generated from the testing of 11 N and 14 N were used to verify the capability of various constitutive models. These two sets of data generated using two different machines (i.e., computer-controlled servo-hydraulic machine and Gleeble® 3500), have been chosen consciously for the purpose of validation, in order to study the effect of machine bias (if any) on predictability of the model. This is particularly important for application to industrial deformation practice. The utility of a constitutive model increases when the model is machine-independent.

Deformation Behavior of Different Variants of 316LN

The flow curves shown in Fig. 1 represent true stress-strain behaviour of 7 N, 11 N and 22 N grades of SS 316LN, respectively. These representative flow curves reveal the effects of strain and strain rate on flow stress of the three grades at 1223 K. The flow curves of these grades at the common deformation condition of 1123 K, 0.001 s−1 strain rate are compared in Fig. 1(d), which shows that nitrogen enrichment enhances the resistance to deformation. The effect of nitrogen on work hardening of the material, as shown in the inset image of Fig. 1(d), is in good agreement with the observations by other researchers (Ref 35,36,37,38), who, however, used different deformation modes and conditions. While nitrogen content enhances the strain hardening in the steel till the peak stress, no prominent effect on strain softening could be discerned beyond this point in the present study.

Fig. 1
figure 1

True stress–strain curves at 1223 K of (a) 7 N, (b) 11 N, (c) 22 N and (d) variation of flow stress at 1123 K, 0.001 s−1 for different variants

Full size image

Figure 1 also indicates that, at a given temperature and strain, increasing strain rate causes an increase in the flow stress up to the strain rate of 1 s−1. This effect of strain rate on flow behavior is known as ‘strain rate hardening’ or ‘positive strain rate sensitivity’. However, when the strain rate increases from 1 to 10 s−1, this behavior begins to reverse at higher strain levels, for example at true strain of 0.65. This softening behavior is known as ‘negative strain rate sensitivity’ and is often cited as a signature of flow instability. This behavior of 316LN has been reported and discussed in the literature (Ref 39,40,41). It is believed that the addition of nitrogen leads to increase in pinning of dislocation and multiplication of dislocation. These clusters of dislocations lead to flow localization. Adiabatic temperature rise causes combination of these localized regions to form shear bands and contribute to negative strain rate sensitivity (Ref 40).

The combined influence of strain rate and temperature on flow stress is demonstrated in Fig. 2. It is revealed that all the three grades exhibit negative strain rate sensitivity in the high strain rate (1-10 s−1) domain. However, this behavior also depends on temperature. The strain rate softening is more prominent at lower deformation temperatures. As the temperature increases, the rate sensitivity gradually reverses and the steels eventually show positive strain rate sensitivity. The temperature where the strain rate sensitivity transits from negative to positive depends on the chemical composition of the steel. The domain of negative strain rate sensitivity is marked as the ‘unstable’ domain in Fig. 2. In the stable domain, the phenomena of work hardening, flow saturation and eventual thermal softening have been seen in 7 N, 11 N and 22 N variants.

Fig. 2
figure 2

Variation of flow stress with temperature at (a) 7 N, (b) 11 N, (c) 22 N. Marked regions represent the unstable domain

Full size image

Prediction of Material Behavior

The flow behavior of the tested materials, as shown in Fig. 1 and 2, is governed by thermal softening, strain hardening/softening, strain rate hardening/softening and compositional strengthening. In order to predict or reproduce a stress–strain curve, a constitutive model therefore needs to represent the individual effects of all these phenomena, as well as the second-order interactions between them. Varied efforts to incorporate these phenomena have led to different types of models; however, a fundamental distinction may be drawn between two major types. The phenomenological type uses mathematical relationships to express the variation of physical parameters, notable examples being SCA (Ref 42,43,44,45,46,47), MJC (Ref 17,18,19,20,21), MZA (Ref 13,14,15,16), etc. Among these, the MJC and D8A models were specifically developed to depict the flow behavior of special grade steels (Ref 17, 48). The other type, namely the computational model, takes experimental data as input and uses algorithms of varying sophistication to identify trends and patterns between data points. These trends are used to predict flow behavior at the same or at different conditions, as is often done using ANN techniques (Ref 49, 50). A review of literature over the past 5 years reveals that both types of model continue to be actively use. Nearly 500 studies on SCA-based flow prediction alone have been published in the past 5 years, as collated by scientific databases such as Web of Science and ScienceDirect. The equivalent number for ANN-based flow prediction is approximately 160, with a rapid increase in the past 2 years.

It is also a fact that every constitutive model reported in the literature is suitable for one or the other material. Therefore, from the perspective of alloy development, the most suitable model can be chosen only by a critical comparison of different models using the same data base and common selection criteria. In this study, a comparison between three phenomenological models (SCA, MJC, D8A) and a computational model (ANN) is made so as to cover the broad categories of constitutive models. The same data sets are used to construct and assess all the models in order to eliminate any error due to imperfect sampling.

Strain Compensated Arrhenius Model (SCA)

The original form of the Arrhenius-type equation which is used for the flow stress prediction is as follows (Ref 51):

$$\sigma = \frac{1}{\alpha }\left[ {\sinh^{ - 1} \left( {\frac{{\exp \left( {{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q {RT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${RT}$}}} \right)}}{A}} \right)^{1/n} } \right]$$
(1)

The equation represents the combined effects of temperature (T) and strain rate (\(\dot{\varepsilon }\)) on the flow stress (σ) at a constant strain. R is universal gas constant (8.314 J/mol K). A, α, n and Q (kJ/mol) are the material constants represented by polynomial functions of strain (ε). Lin et al. (Ref 52) have used fifth-order polynomials for the 42CrMo steel. Peng et al. have used eighth-order polynomials for the titanium alloy (Ref 53). Trimble et al. have used second-order polynomials for the aluminum alloy (Ref 42). Samantaray et al. (Ref 54) have used third-order polynomial for representing α, Q and A, yet used zeroth-order polynomial to represent n. This survey suggests that the order of these polynomials depends on the choice of the user. The use of increasingly higher-order polynomials may result in lesser error in prediction. However, higher-order polynomials increase the complexity by introducing a greater number of experimental constants. Thus, the order of polynomials becomes a trade-off between the error in prediction and the number of experimental constants.

The constants n, α, Q and A, for 7 N and 22 N grades of the steel, are calculated at strain intervals of 0.05 following the iterative procedure described in Ref 41, 54. It has been found that the n and α constants can be reasonably fitted with a fourth-order polynomial fit for 7 N and fifth-order polynomial fit for 22 N, whereas the constants Q and ln A are satisfactorily fitted with a third-order polynomial. These functions are listed in Eq 2.

$$\begin{aligned} & \alpha = \alpha_{0} + \alpha_{1} \varepsilon + \alpha_{2} \varepsilon^{2} + \alpha_{3} \varepsilon^{3} + \alpha_{4} \varepsilon^{4} + \alpha_{5} \varepsilon^{5} \\ & n = n_{0} + n_{1} \varepsilon + n_{2} \varepsilon^{2} + n_{3} \varepsilon^{3} + n_{4} \varepsilon^{4} + n_{5} \varepsilon^{5} \\ & Q = Q_{0} + Q_{1} \varepsilon + Q_{2} \varepsilon^{2} + Q_{3} \varepsilon^{3} \\ & \ln A = A_{0} + A_{1} \varepsilon + A_{2} \varepsilon^{2} + A_{3} \varepsilon^{3} \\ \end{aligned}$$
(2)

The coefficients of these polynomial functions are given in Table 1. The flow curves predicted using these coefficients are shown in Fig. 3, along with the corresponding experimental flow curves for comparative purposes.

Table 1 Coefficient of the polynomial functions shown in Eq 2 for the grades 7 N and 22 N
Full size table
Fig. 3
figure 3

Experimentally obtained and SCA-predicted flow curves for 7 N and 22 N grades of 316LN in the temperature domain of 1123-1423 K at strain rate (a) 0.01 s−1 and (b) 1 s−1

Full size image

Modified Johnson–Cook Model (MJC)

One of the recent modifications to the original Johnson–Cook (JC) model by Lin et al. (Ref 17, 20) yield Eq 3:

$$\sigma = (A_{1} + A_{2} \varepsilon + A_{3} \varepsilon^{2} )(1 + A_{4} \ln \varepsilon^{\prime *} )\exp \left[ {\left( {\lambda_{1} + \lambda_{2} \ln \varepsilon^{\prime *} } \right)(T - T_{r} )} \right]$$
(3)

where A1, A2, A3, A4, λ1, λ2 are material constants, \(\varepsilon^{\prime *} = {{\varepsilon^{\prime } } \mathord{\left/ {\vphantom {{\varepsilon^{\prime } } {\varepsilon_{0}^{\prime } }}} \right. \kern-0pt} {\varepsilon_{0}^{\prime } }}\) is a dimensionless parameter with \(\varepsilon_{0}^{\prime }\) as the reference strain rate and \(\varepsilon^{\prime }\) as the current strain rate, and Tr is the reference temperature. The constants A1, A2 and A3 are obtained by fitting a second-order polynomial to the experimental stress–strain data at reference temperature (1123 K) and reference strain rate (1 s−1) (Ref 17).

All the calculated material constants of MJC model for the grades of 7 N and 22 N are given in Table 2. The flow curves predicted using these constants are compared with the experimentally obtained flow curves for the grades of 7 N and 22 N in Fig. 4.

Table 2 Material constants of MJC model for the grades 7 N and 22 N
Full size table
Fig. 4
figure 4

Experimentally obtained and MJC-predicted flow curves for 7 N and 22 N grades of 316LN in the temperature domain of 1123-1423 K at strain rate (a) 0.01 s−1 and (b) 1 s−1

Full size image

Model D8A

Model D8A mathematically expresses the flow stress as (Ref 48):

$$\sigma = (D_{1} + D_{2} (\varepsilon_{r} (1 - \exp ( - \varepsilon /\varepsilon_{r} )))^{n} )\exp \{ - (D{}_{3} + D_{4} \varepsilon )(T - T_{r} ) + (D_{5} + D_{6} (T - T_{r} ))\ln \dot{\varepsilon }^{*} \}$$
(4)

where D 1 represents the yield stress, D2 is the strain hardening coefficient, D3 represents the absolute effect of temperature, D4 represents the coupled effect of temperature and strain, D5 signifies the absolute effect of strain rate, D6 represents the coupled effect of temperature and strain rate, n is the strain hardening exponent, T r is the reference temperature, \(\dot{\varepsilon }\)* = \(\dot{\varepsilon }\)/\(\dot{\varepsilon }\) o , and ε r signifies the average critical strain for recovery.

The eight material constants D1, D2, D3, D4, D5, D6, n and ε r for three grades of 316LN have been obtained following the procedure described in (Ref 41). The calculated constants are listed in Table 3. The flow curves predicted using these constants are compared with the experimentally determined flow curves in Fig. 5.

Table 3 Material constants of Model D8A for the grades 7 N and 22 N
Full size table
Fig. 5
figure 5

Experimentally obtained and model D8A-predicted flow curves for 7 N and 22 N grades of 316LN in the temperature domain of 1123-1423 K at strain rate (a) 0.01 s−1 and (b) 1 s−1

Full size image

Artificial Neural Network (ANN)

ANN model uses multilayer perceptron (MLP)-based feed-forward network with back-propagation (BP) learning algorithm (Ref 55) for prediction of data sets, where the relationship between data elements varies frequently. This algorithm has been used to predict complex flow behaviors of materials on several occasions (Ref 30, 56, 57). Figure 6 illustrates the schematic of the model where process variables such as strain, strain rate, temperature and chemical composition are given as the inputs to the model, and flow stress is predicted as the output.

Fig. 6
figure 6

Artificial neural network architecture used in the present study

Full size image

For the present problem, one hidden layer with 10 neurons was chosen. The training process was optimized using Levenberg–Marquardt (L–M) algorithm as a back-propagation algorithm and sigmoidal function as an activation function (Ref 49, 58, 59). Data points comprising 60% of the experimentally generated data set were randomly selected. These data points were used to train the neural network. To evaluate the quality of the training, 10% of the data set was used. These 10% data were not included in the 60% previously used for training. Success of the training was verified by comparing the predicted data against the aforementioned 70% of the experimental data. Correlation coefficient of 0.99 was chosen as the criterion to ensure good quality of training. Upon successful completion of the training, the developed neural network was used to predict the flow curves in the entire tested regime for 7 N and 22 N grades. Figure 7 compares the predicted flow curves with the experimental data obtained for representative test conditions.

Fig. 7
figure 7

Experimentally obtained and ANN-predicted flow curves for 7 N and 22 N grades of 316LN in the temperature domain of 1123-1423 K at strain rate (a) 0.01 s−1 and (b) 1 s−1

Full size image

Discussions

It is evident from the available literature that the efficiency of a constitutive model is usually decided on the basis of statistical parameters associated with the error in prediction (Ref 54). However, this statistical analysis, while necessary, is not always sufficient when a constitutive model is evaluated from the perspective of alloy development. Therefore, five additional factors along with the usual statistical error analysis have been taken into account while assessing the efficiency of the models. These six factors are

Statistical Evaluation

This criterion appraises the error in the prediction of data as well as the ability to correctly reproduce the observed trends. A qualitative comparison of the predicted flow stress by different models with the experimental flow stress has already been showcased in Fig. 3, 4, 5 and 7. Though these figures provide a qualitative idea about the capability of a model to track the flow behavior with progress of deformation to certain strain level; from this pictorial presentation, it is difficult to zero-in on the optimal model. This difficulty invokes the necessity for quantifying the predictability of different models. In the field of statistical analysis, there exist many mathematical parameters which can quantify the proximity or difference between two sets of data. These parameters are described below.

For an ideal constitutive equation the difference between the predicted values and the experimentally obtained values is expected to be zero. However, this cannot be achieved in practice as no model can represent the physical behavior completely. Therefore, a constitutive model is considered a good model when the difference between experimentally obtained flow stress and predicted flow stress is close to zero. This difference is frequently quantified by the ‘Average Absolute Relative Error (AARE),’ which is mathematically defined as (Ref 41):

$${\text{AARE}} = \frac{1}{N}\sum\limits_{i = 1}^{i = N} {\left| {\frac{{\sigma_{\exp }^{i} - \sigma_{\text{pre}}^{i} }}{{\sigma_{\exp }^{i} }}} \right|} \times 100$$
(5)

where σpre is the predicted flow stress, σexp is the experimental flow stress, and N is the total number of experimental data points. In addition to minimizing AARE, the predicted stress–strain curve should bear geometrical similitude to the experimental stress–strain curve without scaling. This congruence can be verified by visual inspection and quantified by the ‘correlation coefficient (R),’ which is defined as:

$$R = \frac{{\sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\exp }^{i} - \overline{{\sigma_{\exp } }} } \right)\left( {\sigma_{\text{pre}}^{i} - \overline{{\sigma_{\text{pre}} }} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\exp }^{i} - \overline{{\sigma_{\exp } }} } \right)^{2} } \sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\text{pre}}^{i} - \overline{{\sigma_{\text{pre}} }} } \right)^{2} } } }}$$
(6)

where \(\overline{{\sigma_{\text{pre}} }}\) and \(\overline{{\sigma_{\exp } }}\) are the mean predicted stress and mean experimental stress values.

A value of R equal to 1 implies that there exists a perfect linear relationship between the experimental and predicted data, while a value of 0 implies that there is no linear correlation between the two sets of data. Therefore, a higher value of R often connotes better predictability of the model, yet is not the absolute parameter to measure it. The linear correlation between the experimental stress and predicted stress, if one exists, can be mathematically represented as

$$\sigma_{\text{pre}} = I + S\sigma_{\exp }$$
(7)

where I is the intercept and S is the slope of the correlation line. Ideally, the value of I should be 0 and the value of S should be 1. Either over-prediction or under-prediction is indicated by I ≠ 0 and S ≠ 1. In addition, standard deviation (SD) must also be considered as this quantifies the deviation of data points from the correlation line. A lower SD always connotes better predictability of a model compared to others. Considering these facts all the above described parameters have been monitored for different models and compared to identify the most suitable one among them. The values of the parameters are enlisted in Table 4. On the basis of the number of parameters for a model closer to their ideal values, a model can be recommended for the use. In order to represent this recommendation graphically, the four models have been assigned scores based on the parameters of Table 4. The plot shown in Fig. 8 represents these parameters in three dimensions; the standard deviation of the model, average of ARRE and intercept (I), and average of R and slope (S) of correlation line.

Table 4 Statistical parameters obtained for predictions by various models
Full size table
Fig. 8
figure 8

Statistical evaluation of different models using the same data set. Numbers on arrows indicate deviation from ideal model

Full size image

The scores of each model are assigned by normalizing each axis variable (for, e.g., standard deviation) with the maximum value of the variable (example highest standard deviation). Subsequently, these normalized values have been used to find the magnitude of the vector joining the ideal model and the concerned model; a higher magnitude indicating greater deviation from an ideal model. The significance of vector magnitude is described as follows. For an ideal model, correlation coefficient (R) associated with the prediction and slope (S) of the correlation line should be ≈ 1. AARE, intercept (I) and standard deviation should be ≈ 0. Considering the similar magnitude of the values, while R and S are represented by one axis, AARE and intercept (I) are represented by another axis of the three-dimensional space (Cube) represented in Fig. 8. For both the cases 50% weightage has been assigned to each value by taking average. The point with coordinate (R + S)/2 = 1, (AARE + I)/2 = 0 and SD = 0 is marked as ‘ideal condition’ in Fig. 8. With increasing deviations from ideality, the coordinate changes. The position vector beginning from the ideal point and ending at the coordinates of a specified model would be longer. Therefore, shorter is the vector, more accurate is the model. The scores indicated in Fig. 8 show that ANN is closer to the ideal model compared to all other models; hence, ANN is scored highest on statistical evaluation.

Ability to Correctly Represent Flow Instabilities in the Tested Domain

Instability of various forms can occur during hot deformation under certain conditions. In these cases, local variations in material flow are not representative of the bulk material flow characteristic. The manifestations of such instability could be strain rate softening rather than strain rate hardening, anomalous thermal softening, etc. In the tested grades of the material, flow instability is manifested by negative strain rate sensitivity and is confined to the domain of high strain rate and low temperatures, while in rest of the domain, the flow behavior shows positive strain rate sensitivity. The addition of alloying components can change material behavior and lead to flow instabilities through mechanisms like segregation, boundary decohesion, local strain variations, etc. (Ref 60). An optimal constitutive model should correctly represent the flow characteristic during the flow instability as well as stable flow conditions.

From Table 4, it can be noticed that the prediction capability of ANN model is better than SCA, MJC and D8A. The prediction by ANN shows SD and AARE almost half of the SD and AARE associated with the predictions by other models. From the analysis of the data obtained by prediction, it is observed that predictions by SCA, MJC and D8A largely fail in the domain of instability, which is shown in Fig. 2.

In constitutive models such as D8A, MJC and SCA, the absolute strain rate sensitivity is usually characterized by a material constant. This constant either carries a positive or negative numerical value, which mostly depends on the flow behavior of the material manifested over a larger part of the experimental domain. As example, in the present case, the material shows positive strain rate sensitivity over strain rate domain 0.001-1 s−1 at all temperatures. The data corresponding to this domain accounts for approximately 80% of the entire data population. Therefore, during optimization of the constant which represents strain rate sensitivity, the local characteristic of negative strain rate sensitivity gets suppressed. Consequently, when this constant is used for prediction, local behavior of the material is not perfectly depicted (which can be seen from Fig. 9), though the model predicts the global behavior satisfactorily.

Fig. 9
figure 9

Comparison of experimentally obtained and predicted flow curves by various models in unstable domain for (a) 7 N and (b) 22 N grades of 316LN

Full size image

In cases of ANN, 60% of the experimentally generated data set are chosen randomly for training, comprising data from both stable and unstable domains. Again, this algorithm does not use a logical constant or a specific equation to predict the flow behavior. As a result, the prediction in both stable and unstable domains remains equal, which is not possible with the models having constrained mathematical forms.

Provision for Easy Integration of Additional Variables

Hot deformation is a complex process which depends on several, often inter-related variables. With continuous improvements in alloying and processing methods, it is increasingly necessary to incorporate more variables and factors into the prediction of flow stress. It is desirable that these additional variables can be incorporated in a modular fashion, i.e., without changing the entire equation. Formulation of SCA model is a classic example of such a case. The effect of strain on flow behavior was not considered in the original form of Arrhenius-type equation. The equation was later modified to incorporate the effect of strain without compromising the original form of the equation. The modified model (SCA) is quite useful for flow prediction though the number of constants increases significantly. This provision in a model can greatly facilitate alloy development and related studies, if the number of constants can be kept limited. In the present case, the nitrogen content of the steel has been taken as a new variable since it significantly modifies the flow behavior.

It has been seen from Fig. 2 that the nitrogen significantly affects the yield stress and strain hardening behavior of the material; therefore, the effect of the nitrogen content can be expected on the parameters which represent these properties. A close examination of the constants given in Tables 1, 2 and 3 reveals that the material parameters which represent the effect of strain on deformation vary with change in nitrogen content.

In case of model SCA, all the coefficients of the polynomials, used to represent n, α, Q and ln A as functions of strain change with variation of nitrogen content. To incorporate the effect of nitrogen, all the coefficients have to be expressed as functions of nitrogen. While the coefficients of Q and ln A readily give scope for the incorporation of nitrogen content due to presence of similar number of coefficients for variants 7 N and 22 N (i.e., four coefficients), coefficients of n and α do not give any scope for it. This is because there are five coefficients each for Q and ln A for 7 N variant and six coefficients each for Q and ln A for 22 N variant. Therefore, it can be concluded that SCA is not a suitable model for further amendment. This observation implies that any model which includes a polynomial (of no fixed order) form is not suitable for further amendment. However, in cases where the coefficients are similar in number, there always is a chance of increase in the number of material constants after the amendment, which may not be always acceptable due to added complexity.

In D8A, the parameters D1 and n are found to vary with nitrogen content in the steel. Therefore, to incorporate the effect of nitrogen on flow stress these parameters are presented as linear functions of nitrogen.

$$\begin{aligned} & D_{1} = E_{1} + NE_{2} \\ & n = m_{1} + Nm_{2} \\ \end{aligned}$$
(8)

where N is the nitrogen content of the steel in wt.%. With the above modification Eq 4 can be rewritten as

$$\sigma = (E_{1} + NE_{2} + (E_{3} (\varepsilon_{r} (1 - \exp ( - \varepsilon /\varepsilon_{r} )))^{{(m_{1} + m_{2} N)}} )\exp \{ - (E{}_{4} + E_{5} \varepsilon )(T - T_{r} ) + (E_{6} + E_{7} (T - T_{r} ))\ln \dot{\varepsilon }^{*} \}$$
(9)

where E3, E4, E5, E6, E7 are average values of D2, D3, D4, D5 and D6, respectively, calculated at various nitrogen contents.

Similarly, in model MJC, the material constants A1, A2, A3 and λ1 show strong dependency on nitrogen content. Therefore, these constants have been modified as

$$\begin{aligned} & A_{1} = B_{1} + NB_{2} \\ & A_{2} = B_{3} + NB_{4} \\ & A_{3} = B_{5} + NB_{6} \\ & \lambda_{1} = \mu_{1} + N\mu_{2} \\ \end{aligned}$$
(10)

With the use of Eq 10, Eq 3 can be rewritten as ‘N-amended MJC’ as follows

$$\sigma = ((B_{1} + NB_{2} ) + (B_{3} + NB_{4} )\varepsilon + (B_{5} + NB_{6} )\varepsilon^{2} )(1 + B_{7} \ln \varepsilon '^{*} )\exp \left[ {\left( {(\mu_{1} + N\mu_{2} ) + \mu_{3} \ln \varepsilon '^{*} } \right)(T - T_{r} )} \right]$$
(11)

where B7, μ3 are the average values of A4 and λ2, respectively, calculated at various nitrogen contents. After modification, both the equations have equal number of material constants. The material constants of N-amended MJC and N-amended D8A are shown in Tables 5 and 6, respectively. There is no necessity for further modification to ANN model as material composition are given as input at the beginning.

Table 5 Material constants for N-amended D8A
Full size table
Table 6 Material constants for N-amended MJC model
Full size table

Possibility of Usage of the Model for Extrapolation

The need to modify an existing model frequently arises from the inability of the original model to predict the flow behavior in a domain much larger than the experimentally tested domain. The process of prediction of flow behavior at finer intervals in a domain where the applicability of model has been validated by experiments is called interpolation. The process of prediction of flow stress beyond the validated domain is called extrapolation. When minor changes in alloy composition are made, it may not be convenient to test each alloy variant at each deformation condition. The ability to extrapolate a model can greatly reduce time, material requirement and expenditure, which are crucial for industry. In the present study, this factor has been used to predict the flow stress behavior of two variants, i.e., 11 N and 14 N having different chemical composition.

The extrapolation of any trend beyond the experimental conditions is inherently risky since the actual material behavior may vary significantly outside the tested conditions. However, within allowable limits, the material behavior may be assumed to follow broadly similar trends. In such cases, a constitutive model should be able to extrapolate/interpolate the flow stress behavior with reasonable accuracy. This ability can be a factor to distinguish between different constitutive models. To verify the abilities of the constitutive models which have been developed using the experimental data of 7 N and 22 N grades, flow curves for 11 N and 14 N grades have been predicted. The prediction is validated against the experimental data generated for 11 N and 14 N. Comparison of the experimentally generated flow curves at some selected conditions and predicted flow curves by N-amended MJC, N-amended D8A and ANN are shown in Fig. 10. The statistical data for the prediction are given in Table 7. It can be noticed that both N-amended MJC and N-amended D8A are able to interpolate the flow behavior of 316LN successfully for the other grades of steel. However, the error associated with the prediction by ANN model is significantly higher than the error associated with the other two models. This finding contradicts the general belief in interpolation capability of ANN model. The large deviation can be attributed to the lack of training of the model at such conditions. This finding demonstrates that when the required ratio of data needed for training to the data needed for prediction (which is usually 7:3) reduces, the prediction capability of the model declines. Therefore, ANN model is not reliable when a large data set has to be predicted by using a smaller available data set.

Fig. 10
figure 10

Comparison of experimentally obtained and predicted flow curves by N-amended MJC, N-amended D8A and ANN model for (a) 11 N at 0.001 s−1 and (b) 11 N at 1 s−1 and (b) 14 N at 0.1 s−1

Full size image
Table 7 Statistical parameters obtained for predictions by various models
Full size table

Ease of Usage

The advent of high-performance computing has enabled the development of highly accurate and complex models in various fields. However, this complexity may often become a burden for production engineers in an industrial environment. For the constitutive model to be industrially relevant, the physical inputs should be few, there should be minimum requirement of special modeling/computational skills, and most importantly, the model should be robust. The robustness of the model is not only determined by the range of processing conditions which it can represent, but also by high repeatability and high reproducibility of the predicted results. The ease of usage of a model determines its acceptability in an environment where time and productivity is of essence. A model which is easy to use can be rapidly deployed for different alloy compositions, whereas a computation-intensive and knowledge-intensive model may be cumbersome to use.

A model which is system-specific or which produces different results in different runs can potentially complicate operations by introducing variations, whereas standardization and consistency are the demands of industrial production. Both N-amended MJC and N-amended D8A fully satisfy these criteria as these two models are presented in simple mathematical form and the calculation of flow stress is not system- or operator-dependent. On the contrary, ANN model demands some computational skill and the results are highly system- and operator-dependent.

Ability to Connote the Metallurgical Properties

During alloy development, it is often desired to interpret mechanical/metallurgical response in terms of properties such as strain rate sensitivity, strain hardening, yield stress, etc., while studying the deformation behavior of the alloy.

From the flow behavior analysis, it is observed that addition of nitrogen content significantly affects the yield point of the material and strain hardening behavior. This behavior should also be reflected in the constitutive model, in order to identify the effect of elements on yield point, strain hardening, thermal softening, etc. On account of this, the effect of nitrogen addition is clearly visible on these constants D1 and n of D8A which signify yield point and strain hardening of the material, respectively. Therefore, if required, N-amended D8A can directly be used to identify the influence of nitrogen on yield point and strain hardening at different temperatures and strain rates. However, in MJC and SCA, though the effect of nitrogen is visible on all the coefficients of strain, it is difficult to logically distinguish the influence of nitrogen on any specific material property. Therefore, N-amended MJC may not be as useful as N-amended D8A to study the influence of nitrogen on yield point and strain hardening at different temperatures and strain rates. In such cases, ANN too will not be very useful, as additional training is the prerequisite for any new prediction. However, additional calculations on predicted flow stress can give the required results.

A model whose constants can connote the physical properties is thus preferable to a ‘black-box’ model where the sum of parts is known, but the individual parts are hidden. Even if the individual parts are known, it may not always be possible to interpret them in terms of physical properties. Such a model is limited to flow stress prediction and cannot be readily used for material comparison or analysis of different responses at different deformation conditions. In such cases, the ANN model performs excellently, considering all the local variation. However, performance of ANN deteriorates as the fraction of data to be predicted slowly increases. In addition, the prediction is highly dependent on system and computational skill of the user. The model needs fresh training for every additional input. In light of the above, ANN is not recommended for interpolation and extrapolation, especially during alloy development. On such occasions modified mathematical models such as N-amended model D8A and N-amended MJC perform satisfactorily. These models give scope for addition of new parameters which account for the effect of element addition on the flow behavior, while also performing consistently during interpolation. Though these models cannot depict divergent behavior at specific deformation conditions, they effectively represent the aggregate, global behavior of the material, which is necessary knowledge for an alloy designer.

The above discussed points are schematically represented by the radar chart shown in Fig. 11. A similar approach has earlier been used by Holota et al. (Ref 61) for selection of material. The six ‘spokes’ of the chart each represent the six factors discussed a priori, on the basis of which relative performance of models can be assessed. Each model is represented by a closed loop. The six radii of this loop represent how well the model performs, with a higher radius indicating better performance and thus a better model. For instance, in Fig. 9, it is seen that ANN model performs well in instability prediction, but poorly in ease of implementation. On the contrary, MJC model performs well in ease of implementation but not as well in predicting instabilities. In view of the above discussed points and Fig. 11, it is clear that ANN model is a good choice when large fraction of data (70% of entire data set) is available for training and a comparatively small fraction of the data (30% of entire data set) has to be predicted. However, when all six criteria are considered, Model D8A is closest to the ideal model, and hence, it is an optimal choice from the perspective of alloy development.

Fig. 11
figure 11

Radar chart comparing performance of different models on the basis of six factors

Full size image

Conclusions

In this study, the utility of constitutive equations for prediction of flow behavior during alloy development stage has been analyzed using experimental results obtained from four grades of 316LN. For this study four commonly used models such as SCA, MJC, Model D8A and ANN model have been critically compared on the basis of six criteria. The key outcomes of this study are summarized below:

  1. 1.

    ANN model is a good choice when a large data set is available for training. If this condition is violated, the model is not suitable for interpolation/extrapolation. The prediction is operator and system-dependent. Therefore, it is not a very good choice for flow behavior study with varying alloying elements.

  2. 2.

    Models based on physical logic, such as SCA, D8A, MJC, are not system-dependent and have good reproducibility. However, these models do not represent local divergence in flow behavior (such as instability) as satisfactorily as a well-trained ANN model does.

  3. 3.

    SCA model contains four polynomial functions to represent the effect of strain. The orders of these polynomials are not fixed and vary randomly with change in chemical composition; therefore, the model does not give a scope for addition of new variables.

  4. 4.

    Both MJC and Model D8A are found suitable for their ease of use and scope for addition of new variables for alloy development. The modified versions of these two models, namely N-amended MJC and N-amended D8A, developed using experimental data of 7 N and 22 N grades satisfactorily predict the flow behavior of 11 N and 14 N grades of 316LN. N-amended D8A is preferred to N-amended MJC as constants of the former model can be directly used to represent the effect of nitrogen on yield stress and work hardening. The material constants can be suitably modified on the basis of experiments to extend the model for use in different alloy systems.