High Temperature Deformation Behavior and Constitutive Modeling for Flow Behavior of Alloy 718

Abstract

In the present work, hot deformation behavior of Alloy 718 was investigated over a temperature range of 1223–1373 K and strain rate range of 10⁻²–10 s⁻¹. The flow curves were corrected for adiabatic temperature rise, particularly at high strain rates. Arrhenius type constitutive equations were derived for Alloy 718 to model the peak flow stress from apparent and physically based approaches. A stress exponent of 5 was obtained from the power-law equation, indicating that the deformation is governed by the dislocation climb mechanism within the aforementioned processing domain. Further, to model the flow behavior, a generalized constitutive equation was derived in which the effect of strain on the flow stress was incorporated. In addition, artificial neural networks (ANN) method was also employed to model the flow behavior. Statistical parameters such as regression coefficient (R) and average absolute relative error (AARE) indicated that the ANN method was more accurate in predicting the flow behavior with R = 0.99 and AARE = 0.79% compared to the apparent-based constitutive equation with R = 0.99 and AARE = 4.5%. Accuracy of the derived constitutive equation as a material model in finite element (FE) simulation studies was also evaluated. Flow curve predictions obtained from the FE simulation were comparable to the experimental results. The microstructure and hardness at different locations in the deformed samples were consistent with the strain distribution map generated by the FE simulation.

Introduction

Alloy 718 is widely used in gas turbines, power generators, rocket engines, metal forming dies and containers. It possesses a combination of good mechanical properties and corrosion resistance up to 923 K. The main strengthening mechanism of this material is the precipitation of ordered-gamma double prime (γ″), which is coherent with the matrix and it acts as a strong barrier for the dislocation movement (Ref 1,2,3). In addition, the alloy also has other important phases such as delta phase and Laves phase (Ref 4,5,6). One of the major applications of Alloy 718 is turbine disks, which encounter both high stresses and temperatures (Ref 7). Several researchers investigated the flow behavior and microstructure evolution during deformation of different Ni-based alloys and developed processing maps (Ref 2, 8,9,10,11,12,13,14). Alloy 718 is very difficult to be formed due to its high resistance to deformation and shows a very narrow processing window to obtain the completely dynamic recrystallized structure.

It is known that the properties of manufactured products depend largely on the microstructure of the material. Understanding the material flow behavior is critical in identifying the processing parameters required to achieve the desired microstructure. Generally, hot deformation of materials involves several metallurgical mechanisms such as work hardening, dynamic recrystallization, dynamic recovery and flow instability. All these cause evolution of a complex microstructure during the processing. However, in order to achieve the required final microstructure and mechanical properties, the hot working parameters (temperature, strain rate and strain) have to be optimized (Ref 15, 16). Over the past decades, numerous efforts have been made to study the optimization of hot working parameters using mathematical and physical simulations.

Advanced numerical techniques such as finite element method, crystal plasticity method and artificial neural networks (ANN) are employed to optimize the thermo-mechanical processing parameters (Ref 17,18,19,20,21,22,23). Simulation studies also help to predict the evolution of microstructure of materials during hot working processes. In finite element simulations, the material flow behavior is modeled by a constitutive equation. A constitutive equation is a mathematical relation which is derived from experimental data relating the flow stress of materials and the hot working process parameters. The accuracy and reproducibility of finite element simulations depend largely on the constitutive equation used. Thus, it is important that a derived constitutive equation should be validated for its accuracy to be used as a generalized material model in finite element studies (Ref 24,25,26,27).

To control the evolution of microstructure during hot deformation, it is important to know the stress at which dynamic recrystallization initiates. Knowing this value of critical stress also helps in the modeling of hot working processes accurately. However, it is difficult to obtain the critical stress value directly from the flow curves. To calculate the flow curve characteristics (critical stress, peak stress, peak strain, steady state stress and saturated stress) a method has been proposed by Poliak and Jonas (Ref 28). According to that method, the occurrence of the inflection point in the plot between strain hardening rate $\left( {\theta = \left( {\frac{{{\text{d}}\sigma }}{{{\text{d}}\varepsilon }}} \right)_{{T, \dot{\varepsilon }}} } \right)$ and flow stress corresponds to the critical stress value, and the peak stress is obtained from the same plot at θ = 0. Here σ is flow stress (MPa), ε is strain, T is temperature (K) and $\dot{\varepsilon }$ is strain rate (s⁻¹).

The reported values of critical stress values normalized with respect to peak stress for 17-4 PH stainless steel, 304H austenitic stainless steel and medium carbon steel are 0.89, 0.875 and 0.879, respectively (Ref 29,30,31). Therefore, it is reasonable to consider that the peak stress is almost equal to the critical stress required to the onset of dynamic recrystallization (DRX) and it can be assumed that DRX begins at peak stress value.

Thomas et al. (Ref 2) investigated the hot deformation behavior of Alloy 718 over a range of temperatures (1173–1353 K) and strain rates (5 × 10⁻⁴-10^–1 s⁻¹). Before hot compression testing, the samples were annealed at 1353 K for 1 h in order to homogenize the microstructure. They reported that the homogenization temperature did not dissolve all precipitates and some second phase particles remained undissolved. These second phase particles promoted some hardening during deformation at 1173 K and influenced the deformation mechanism. Wang et al. (Ref 32) studied the hot deformation behavior of delta-processed Alloy 718 over a range of temperature (1223-1373 K) and strain rates (10⁻³-1 s⁻¹) mainly to understand the evolution of δ phase during hot deformation as well as the mechanisms of DRX. The main nucleation mechanisms of DRX for the delta-processed Alloy 718 reported by them are bulging of original grain boundaries and the δ phase stimulated DRX nucleation, which is dependent on the dissolution behavior of the δ phase. Tan et al. (Ref 11) conducted studies on the hot deformation behavior of fine grained Alloy 718 and proposed a constitutive equation. Recently, Pedro et al. (Ref 33) carried out the hot compression tests at two temperatures of 1233 K and 1293 K (below and above the δ-solvus temperature) on delta-processed Alloy 718. They reported partial dissolution and fracture of δ phase during the deformation resulting in fine and distributed δ particles near grain boundaries which were presumed to act as nucleation sites for DRX. Further, in that study they employed Estrin–Mecking–Bergstrom approach (Ref 34, 35) to model the flow behavior up to peak stress. Gujrati et al. (Ref 36) studied the relation between activation energy of hot deformation and deformation mechanisms in Alloy 718. Also, flow stress modeling was carried out using Schöcks–Seeger–Wolf, Kocks and Sellers models. Gupta et al. (Ref 37) correlated deformation parameters with microstructural evolution during hot deformation in Alloy 718. The processing parameters were optimized using processing map approach. Kumar et al. (Ref 38) studied the hot deformation of hot isostatically processed nickel-base superalloy and reported significant change in the flow stress due to adiabatic temperature rise, particularly at lower temperatures and high strain rates. However, most of the above reported studies have not considered the change in flow stress due to adiabatic temperature rise, nor the effect of strain on the flow stress. But in Ni-based alloys, it is observed that the flow stress varies with the strain. Hence, while modeling the flow curve, it is necessary to compensate the effect of strain in the constitutive equation.

In most of the above-mentioned research efforts, a constitutive equation was derived for Alloy 718, but there was no validation of the constitutive equation. Generally, a constitutive equation analysis involves linear regression of the experimental data. The derived constitutive equation might be confined to a limited processing domain where specific deformation mechanisms operate in the material. Therefore, the derived constitutive equation may not be accurate enough to predict the flow behavior when the flow stress exhibits nonlinear dependence on the processing parameters and also in experimental conditions which are different from the experimental conditions for which constitutive equation has been derived. In these conditions, ANN technique offers a more flexibility to describe the flow behavior over constitutive equation approach. Basically, ANN learns, memorizes and recognizes the data pattern during the training procedure without any prior assumption about their nature (Ref 39). Though ANN does not incorporate the physical knowledge about deformation behavior and restoration mechanisms, it is able to describe the flow behavior very accurately (Ref 39,40,41). In addition, studies on understanding the deformation mechanisms operating at the hot working temperatures are also scarce. It has been reported that the physically based approach can provide an insight of governing deformation mechanisms (Ref 42). Based on these inferences, the objective of present work is defined.

The main objective of the present work is to investigate the flow behavior and deformation mechanisms of Alloy 718 in a solution treated condition over a range of temperatures (1223–1373 K) and strain rates (10⁻²–10 s⁻¹) and to derive a constitutive equation by employing the apparent and physically based approaches. Also, an effort has been made to develop a generalized constitutive equation that considers the effect of strain on the flow stress and to validate the accuracy of the developed equation as a generalized material model by finite element simulation studies. In addition, the ANN method was also employed to study the flow behavior. Further, statistical parameters (regression coefficient and average absolute relative error) were employed to evaluate the performance of models. Finite element simulation was used to understand the strain distribution in samples after the deformation.

Experimental Procedure

The material used in this work is Alloy 718 and its nominal composition is listed in Table 1. The initial material, supplied in the extruded rod form, was solution treated for 4 h at 1373 K. The solution treatment temperature was selected based on the study by Wang et al. (Ref 32) in which the same temperature of 1373 K was used for solution treatment for superalloy 718. However, the treatment time used by them was 30 min. In an another study to investigate the effect of grain size of alloy 718 (unpublished work), the authors of the present paper varied the treatment duration from 10 min to 4 h at 1373 K. In the present work, 4 h solution treatment duration was chosen. After the heat treatment, cylindrical samples of dimensions 10 mm in diameter and 15 mm in length were cut using a wire cut electric discharge machine. Isothermal uniaxial compression tests were carried out in the Gleeble 3800 thermo-mechanical simulator at different temperatures of 1223, 1273, 1323 and 1373 K and different strain rates of 10⁻², 10⁻¹, 1 and 10 s⁻¹. During deformation, to reduce the friction between anvils and sample, a graphite sheet along with nickel paste was used as lubricant. The schematic shown in Fig. 1 explains the experimental procedure. Initially, the samples were heated to the testing temperature at a rate of 5 K/s and held at the testing temperature for 180 s and then compressed. Afterward, the deformed samples were water quenched in the testing chamber using two jets immediately after finishing the test. The total true strain given to the samples during deformation is 0.7. The true stress–true strain data were recorded using a data acquisition system.

Table 1 Chemical composition (in wt.%) of test material Alloy 718

Fig. 1

Schematic of experimental procedure

Results and Discussion

Initial Microstructure

The microstructure of Alloy 718, solution treated for 4 h at 1373 K, shows equi-axed grain structure with an average grain size of 120 μm.

Flow Curve Behavior

The true stress–true strain curves measured at different temperatures and strain rates are shown in Fig. 2. It is observed that for all test conditions flow stress is decreasing with increasing temperature and decreasing strain rate. In the initial stage of the flow curve, the flow stress is increasing with increasing strain due to strain hardening (increase in dislocation density), and once it reaches peak stress, flow softening (dynamic recovery) is observed. However, at lower strain rates (10⁻² and 10⁻¹ s⁻¹) steady state flow is observed after the peak stress with increasing strain, which occur when a balance between strain hardening and dynamic softening is attained. A similar type of flow behavior has been reported in Alloy 718 and other Ni-based alloys possessing low stacking fault energy, which indicates the DRX phenomenon during the deformation (Ref 9, 43, 44).

Fig. 2

True stress–true strain curves for Alloy 718 at different temperatures: (a) 1223 K, (b) 1273 K, (c) 1323 K and (d) 1373 K

It is worth to mention that, particularly at higher strain rates (1 and 10 s⁻¹) more flow softening is observed compared to that at the lower strain rates (10⁻² and 10⁻¹ s⁻¹) and this is attributed to adiabatic temperature rise (ATR) at higher strain rates. A thermocouple was welded on the periphery of the sample and the temperature rise in the sample was recorded online during the experiment. The variation in temperature rise for all strain rates at a temperature of 1223 K is shown in Fig. 3(a). The ATR (ΔT) at strain rates of 1 and 10 s⁻¹ at each temperature is shown in Fig. 3(b). Subsequently, change in the stress (Δσ) due to ATR is estimated by using an expression (Eq 1). The extent of ATR is decreasing with increasing the temperature and corrected flow stress due to ATR is also included in Fig. 2. As Ni exhibits poor thermal conductivity (~ 14.7 W/m K), the heat generated due to plastic deformation at higher strain rates has very less time to get dissipated from the sample and this causes the localized heating. The combination of large stored energy and adiabatic temperature rise enhances the dynamic recrystallization fraction at higher strain rates (Ref 11, 15, 45). The optical micrographs of samples deformed at 1373 K for different strain rates are presented in Fig. 4. It clearly seen that fraction of dynamic recrystallized grains increases with an increase in strain rate;

$$\Delta \sigma = \Delta T\left( {\frac{{{\text{d}}\sigma }}{{{\text{d}}T}}} \right)_{{\varepsilon , \dot{\varepsilon }}}$$

(1)

Fig. 3

(a) Variation of temperature with the strain during the tests conducted at 1223 K and different strain rates, (b) Adiabatic temperature rise (ΔT) for tests conducted at different temperatures and two different strain rates

Fig. 4

Optical micrographs of samples deformed at 1373 K and at different strain rates: (a) 10⁻¹ s⁻¹, (b) 1 s⁻¹ and 10 s⁻¹. Scale bar = 200 μm

Constitutive Equation Analysis

Apparent-Based Approach

In hot deformation, the flow stress highly depends on temperature and strain rate is described by an Arrhenius equation The effects of temperature and strain rate on deformation behavior are incorporated in the Zener–Hollomon parameter (Z), which is temperature compensated strain rate (Ref 46). In most of the previous studies, flow stress is modeled by an expression that relates the Zener–Hollomon parameter (Z) and flow stress (σ) as (Ref 47):

$$Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right) = f\left( \sigma \right)$$

(2)

where $\dot{\varepsilon }$ is strain rate (s⁻¹), Q is the activation energy (J/mol), R is the gas constant (J/mol K), T is the temperature (K).

Since both creep and hot working are considered as thermally activated processes, for hot deformation analysis, strain rate equations similar to those used in the creep studies are used. Generally, Arrhenius type equations are used to describe the relation among the flow stress, temperature and strain rate as:

$$\dot{\varepsilon } = A f\left( \sigma \right)\exp \left( {\frac{ - Q}{RT}} \right)$$

(3)

$$\dot{\varepsilon } = A_{1} \sigma^{n} \exp \left( {\frac{ - Q}{RT}} \right)$$

(4)

$$\dot{\varepsilon } = A_{2} \exp \left( {\beta \sigma } \right)\exp \left( {\frac{ - Q}{RT}} \right)$$

(5)

$$\dot{\varepsilon } = A_{3} \left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{{n_{1} }} \exp \left( {\frac{ - Q}{RT}} \right)$$

(6)

where $\dot{\varepsilon }$ is strain rate (s⁻¹), A, A₁, A₂, A₃, β, n and n₁ are the material constants, Q is the activation energy (J/mol), T is the temperature (K), σ is the flow stress (MPa), R is the gas constant (8.314 J/mol K) and α (≈ β/n MPa⁻¹) is the stress multiplier.

The power law (Eq 4) is preferred for lower stresses (ασ < 0.8), whereas for higher stresses, exponential law (Eq 5) (ασ > 1.2) is preferred. In addition to that, Sellers–Tegart (Ref 48, 49) hyperbolic sine law (Eq 6) suggested by Garofolo (Ref 50) (for all ασ) is used to cover a wide range of stresses.

From conventional Eq 4 and 6, the obtained values of n, n₁ and Q are referred to as apparent values, because internal microstructure state has not been taken into account. They are derived from the Arrhenius equation with linear regression analysis by assuming that the microstructure remains constant during deformation. Hence, this method is referred to as apparent-based approach. Consequently, from this approach, it is difficult to infer about deformation mechanisms operating in the material (Ref 42).

By applying the natural logarithm on both sides of Eq 4 and 5, the following expressions are obtained to evaluate the peak stress (σ_p).

$$\ln \dot{\varepsilon } + \frac{Q}{R}\left( {\frac{1}{T}} \right) = \ln A_{1} + n\ln \sigma_{\text{p}}$$

(7)

$$\ln \dot{\varepsilon } + \frac{Q}{R}\left( {\frac{1}{T}} \right) = \ln A_{2} + \beta \sigma_{\text{p}}$$

(8)

Assuming that the activation energy is constant at given temperature, the partial differentiation of Eq 7 and 8 with respect to σ_p, yields the following expressions:

$$n = \left[ {\frac{{\partial \ln \dot{\varepsilon }}}{{\partial \ln \sigma_{\text{p}} }}} \right]_{\text{T}}$$

(9)

$$\beta = \left[ {\frac{{\partial \ln \dot{\varepsilon }}}{{\partial \sigma_{\text{p}} }}} \right]_{\text{T}}$$

(10)

The values of n and β were obtained from the slope of the plot between $\ln \dot{\varepsilon }$ and ln σ_p and slope of the plot between $\ln \dot{\varepsilon }$ and σ_p, respectively. The corresponding plots are shown in Fig. 5(a) and (b). The linear regression analysis of the data points at each deformation temperature was performed. The value of slope varies with temperature. Therefore, the average values of n (= 6.06) and β (= 0.02281) were obtained from the average of all slopes, respectively. Eventually, the value of α (= 0.00376 MPa⁻¹) was obtained from the ratio of β/n.

Fig. 5

(a) Plot of $\ln \,\dot{\varepsilon }\,\,{\text{versus}}\,\,\ln \,\sigma_{\text{p}}$, (b) plot of $\ln \,\dot{\varepsilon }\,\,{\text{versus}}\,\, \sigma_{\text{p}}$

A similar value of α (= 0.0042 MPa⁻¹) was found by Gujrati et al. (Ref 36).

By applying the natural logarithm on both sides of Eq 6, we get the following expression:

$$\ln \dot{\varepsilon } + \frac{Q}{R}\left( {\frac{1}{T}} \right) = \ln A_{3} + n_{1} \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$$

(11)

At constant deformation temperature, the partial differentiation of Eq 11 with respect to σ_p, yields the following expression. The same is used to evaluate the value of n₁.

$$n_{1} = \left[ {\frac{{\partial \ln \dot{\varepsilon }}}{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}} \right]_{\text{T}}$$

(12)

The value of n₁ was obtained from the plot between $\ln \dot{\varepsilon }$ and $\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$ and the corresponding plot is shown in Fig. 6(a). The linear regression analysis of data points was performed at all deformation temperatures. The average value of n₁ (= 4.4) was obtained from the average of all slopes. A similar value of n₁ (= 4.57) was found by Gujrati et al. (Ref 36).

Fig. 6

(a) Plot of $\ln \,\dot{\varepsilon }\,\,{\text{versus}}\,\,\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$, (b) plot of $\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right] \,\,{\text{versus}}\,\,\frac{1000}{T}$

In order to calculate the deformation activation energy, partial differentiation of Eq 11 with respect to (1/T) at constant strain rate, yields the following expression

$$Q = Rn_{1} \left[ {\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}{{\partial \left( {1/T} \right)}}} \right]_{{\dot{\varepsilon }}}$$

(13)

The slopes obtained from the plot $\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$ against (1000/T) were used to calculate the Q value. The corresponding plot is shown in Fig. 6(b). The linear regression analysis of the data points was performed at all strain rates. The average value from all the slopes was considered to estimate the Q value. The Q value obtained from hyperbolic sine law is 478 kJ/mol. Earlier, similar Q values were reported by researchers in the literature for Alloy 718 subjected to hot deformation, e.g., Yuan and Liu (443 kJ/mol) (Ref 51), Weis (423 kJ/mol) (Ref 52), Garcia et al. (485 kJ/mol) (Ref 53), Tan et al. (406.5 kJ/mol) (Ref 11). However, in all these studies including the present study, the estimated Q value is quite higher than the self-diffusion activation energy (Q_sd) of nickel (285 kJ/mol) (Ref 54). The difference in the estimated Q and Q_sd of nickel is attributed to the complex alloy chemistry and microstructural characteristics (Ref 38, 55). Bi et al. (Ref 56) investigated the effect of concentration of alloying elements on the evolution of Q in nickel-based superalloys. It was found that the presence of different alloying elements like Cr, Ti, Mo, Nb and W invariably increases the Q value with increasing weight fraction. In addition to these factors, Tan et al. (Ref 11) reported that the Q value in Alloy 718 is dependent on the initial grain size and a decrease in grain size results in lower Q. Recently, Gujrati et al. (Ref 36) reported the Q value of 364 kJ/mol for Alloy 718 and the discrepancy in Q compared to Q_sd is attributed to occurrence of DRX during hot deformation.

Finally, the relation between the peak stress and Zener parameter was obtained by plotting ln [sinh (ασ_p)] against lnZ for hyperbolic sine law and the corresponding plot is shown in Fig. 7. The slope and intercept obtained from the plots are the final values of n₁ and A₃, respectively. The linear regression analysis of the data resulted in the following equation:

$$Z = \dot{\varepsilon } \exp \left( {\frac{477389}{RT}} \right) = 3.07 \times 10^{18} \times \left[ {\sinh \left( {0.00376 x \sigma_{\text{p}} } \right) } \right]^{4.4}$$

(14)

The values of experimental peak stresses are plotted against the predicted peak stresses calculated from the constitutive Eq 15 corresponding to hyperbolic sine law in Fig. 8. The predicted peak stress values are in good agreement with the experimental peak stress values.

$$\sigma_{\text{p}} = \frac{1}{\alpha } \sinh^{ - 1} \left( {\frac{Z}{{A_{3} }}} \right)^{{1/n_{1} }} = \frac{1}{0.00376} \sinh^{ - 1} \left( {\frac{{\dot{\varepsilon }\exp \left( {\frac{477389}{RT}} \right)}}{{3.07 \times 10^{18} }}} \right)^{1/4.4}$$

(15)

Fig. 7

Plot of $\ln \,Z\,\,v{\text{ersus}}\,\,\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]$

Fig. 8

Comparison of predicted peak stress and experimental peak stress

Physically Based Approach

The activation energy for hot deformation obtained from the apparent-based approach is 478 kJ/mol, which is quite distinct and higher than the activation energy for self-diffusion of pure Ni. Hence, it is difficult to infer about deformation mechanism from the apparent-based approach. Thomas et al. (Ref 2) have shown that if the deformation mechanism is controlled by dislocation climb, a constant stress exponent and activation energy for self-diffusion of a studied material can be used in the Sellers equation to describe the appropriate stress by incorporating the influence of temperature dependence of Young’s modulus and self-diffusion coefficient of the material. Hence, this method is referred to as physically based approach (Ref 42). Accordingly, the modified Sellers equation has been employed to describe the appropriate stress for materials like steels, aluminum alloy (Ref 57,58,59). The unified equation is expressed as follows:

$$\frac{{\dot{\varepsilon }}}{{D_{{\left( {\text{T}} \right)}} }} = B_{3} \left[ {\sinh \left( {\alpha^{{\prime }} \frac{\sigma }{{E_{{\left( {\text{T}} \right)}} }}} \right)} \right]^{{n^{\prime\prime}}}$$

(16)

where D_(T) is self-diffusion coefficient at a temperature, B₃ is material constant, n″ is stress exponent, α′ is stress multiplier, E_(T) is Young’s modulus at a temperature.

Therefore, physically based approach was employed to deduce the deformation mechanisms here and discussed in this section. In this approach, only two unknown parameters (α′ and B₃) have to be derived from Eq 16. To determine α′, similar approach discussed in Sect. 3.3.1 was employed. The power law and exponential law after including the D_(T) and E_(T) are expressed as

$$\frac{{\dot{\varepsilon }}}{{D_{{\left( {\text{T}} \right)}} }} = B_{1} \left[ {\frac{{\sigma_{\text{p}} }}{{E_{{\left( {\text{T}} \right)}} }}} \right]^{{n^{\prime}}}$$

(17)

$$\frac{{\dot{\varepsilon }}}{{D_{{\left( {\text{T}} \right)}} }} = B_{2} \exp \left( {\beta^{{\prime }} \frac{{\sigma_{\text{p}} }}{{E_{{\left( {\text{T}} \right)}} }}} \right)$$

(18)

where B₁, B₂ and β′ are material constants, n′ is true stress exponent.

The temperature dependent shear modulus (G_(T)) and self-diffusion coefficient (D_(T)) were calculated using Eq 19 and 20. The values of D_o = 1.6 × 10⁻⁴ m²/s, Q_sd = 285 kJ/mol and G_o (at 300 K) = 8.31 × 10⁴ MPa, corresponding to pure Ni were taken from Ashby tables (Ref 54). The Young’s modulus (E) was obtained by inserting the G values in the following relation (Ref 60) ($E = 2G\left( {1 + \nu } \right)$) (ν = 0.3).

$$D_{{\left( {\text{T}} \right)}} = D_{\text{o}} \exp \left( {\frac{{ - Q_{\text{sd}} }}{RT}} \right)$$

(19)

$$G_{{\left( {\text{T}} \right)}} = G_{\text{o}} \left( {1 - 0.5 \frac{{\left( {T - 300} \right)}}{{T_{\text{M}} }}} \right)$$

(20)

Here n′ and β′ were obtained from the slope of the plot between $\ln \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {D_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${D_{{\left( {\text{T}} \right)}} }$}}} \right)$ versus $\ln \left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right)$ and $\ln \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {D_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${D_{{\left( {\text{T}} \right)}} }$}}} \right)$ versus $\left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right)$, respectively, see Fig. 9(a) and (b). The α′(= 549) was calculated from the ratio of $\left( {{\raise0.7ex\hbox{${\beta^{{\prime }} }$} \!\mathord{\left/ {\vphantom {{\beta^{{\prime }} } {n^{{\prime }} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n^{{\prime }} }$}}} \right)$. The main advantage of this method is that all the data points lie on a single line, which means only a single regression is necessary to obtain α′. On the other hand, in the apparent-based approach, regression analysis has to be performed at each temperature.

Fig. 9

(a) Plot of ${\text{ln }}\left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right) \,\,{\text{versus}}\,\,\ln \left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } E}}\right.\kern-0pt} \!\lower0.7ex\hbox{$E$}}} \right)$, (b) plot of ${\text{ln }}\left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right) \,\,{\text{versus}}\,\, \left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } E}}\right.\kern-0pt} \!\lower0.7ex\hbox{$E$}}} \right)$

A linear fit of the plot between $\left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {D_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${D_{{\left( {\text{T}} \right)}} }$}}} \right)^{1/5}$ and $\sinh \left( {\alpha^{{\prime }} {\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right)$ with an intercept of zero (y = mx + 0) was done as shown in Fig. 10(a). The slope of the linear fit gives the value of (B₃)^(1/5) = 673 from Eq 6. The final resultant physically based constitutive equation can be expressed as:

$$Z = \dot{\varepsilon } \exp \left( {\frac{285000}{RT}} \right) = 2.2 \times 10^{10} \times \left[ {\sinh \left( {549 x {\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right) } \right]^{5}$$

(21)

The comparison between the values of the predicted peak stress calculated from the final Eq 21 corresponding to the physically based approach and the experimental peak stress values is shown in Fig. 10(b).

Fig. 10

(a) Plot used to determine B₃, (b) comparison between experimental peak stress and predicted peak stress

The interesting observations from the physically based approach are the true stress exponent (n′) obtained from the power law, i.e., the slope of the plot between $\ln \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {D_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${D_{{\left( {\text{T}} \right)}} }$}}} \right)$ versus $\ln \left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right)$ is ~ 5. In the present work, from the slope obtained from the plot shown in Fig. 9(a) it is deduced that the dislocation climb is the dominating deformation mechanism operating in the studied temperature and strain rate domain (Ref 54). However, power law is not capable to explain the flow behavior when ασ > 1.2. Hence, it is always suggested to employ sine hyperbolic law to represent the flow behavior in hot deformation studies since it covers a wide range of stresses.

Earlier, Thomas et al. (Ref 2) studied the effect of aging on the hot deformation of Alloy 718 by using the physically based approach and observed that experimental points obtained at different temperatures did not lie on a single line in the plot between $\ln \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {D_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${D_{{\left( {\text{T}} \right)}} }$}}} \right)$ versus $\ln \left( {{\raise0.7ex\hbox{${\sigma_{\text{p}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {E_{{\left( {\text{T}} \right)}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{{\left( {\text{T}} \right)}} }$}}} \right)$ like in the present work (particularly tests done at 1173 K and 1223 K). This was attributed to the high stress exponent observed due to the precipitates formed during the aging treatment in the material, further these precipitates hindered the dislocation movement and introduced a back stress.

Both Eq 15 and 21 derived based on the apparent and physically based approaches look almost similar to each other, but the nature of the material constant values are completely different after compensating the temperature effect by means of D_(T) and E_(T) in Eq 16.

Performance Evaluation of a Constitutive Equation

The prediction capability of a constitutive model is quantified by employing the statistical parameters such as correlating coefficient (R) and average absolute relative error (AARE) which are expressed as follows:

$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {e_{i} - \bar{e}} \right) \left( {P_{i} - \bar{P}} \right) }}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {e_{i} - \bar{e}} \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - \bar{P}} \right)^{2} } }}$$

(22)

$${\text{AARE}} \left( \% \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{e_{i} - p_{i} }}{{e_{i} }}} \right| \times 100$$

(23)

where e_i and e are experimentally measured value and mean value of all the experimental results, P_i and P are predicted value and mean value of all the predicted results calculated from the model, n is the total number of data points considered for the analysis. The correlation coefficient is frequently used to analyze the strength of the linear relationship between experimental and predicted values. When R is close to zero, it indicates that the regression line does not fit the data well and when R is close to 1, it indicates that the regression line fits the data well. However, higher R value always need not indicate the better performance of the model/equation because tendency of model/equation biased toward higher or lower values (Ref 61), whereas AARE is a measure of prediction accuracy of the model and it provides unbiased statistics by computing through term by term comparison of the relative errors (Ref 62).

The peak stress predicted from Eq 21 corresponding to physically based approach have shown a (R) = 0.96 and AARE (18%). On the other hand, in the apparent-based approach, a higher value of R = 0.99 and lower value of AARE = 6% were obtained. This indicates that the apparent-based approach is more reliable than the physically based approach for predicting the peak stress.

Effect of Strain on the Flow Stress

As mentioned earlier, the effect of strain on the flow stress is not considered in Eq 5 presuming that it has a negligible effect on the flow stress at the hot working temperatures. However, the effect of strain on the flow stress is significant at lower working temperatures. In order to model the entire flow curve, it is inappropriate to use the same material constants obtained at peak stress. This problem could be addressed by incorporating the influence of strain in the constitutive equation. This approach has been firstly described by Rao and Hawbolt (Ref 63) and then critically revised by Mirzadeh (Ref 64). It could be possible by establishing the relation between deformation strain and material constants (α, n₁, Q and A₃). The material parameters were derived using the above procedure (similar way to derived for peak stress) for a range of strains from 0.1 to 0.7 with an interval of 0.05. After deriving the material parameters for different strains, polynomial equations were used in order to attain a relationship between the deformation strain and material constants as shown in Fig. 11. A fourth-order polynomial Eq 24-27 reasonably fits the entire strain regime and the information about coefficients of polynomial equations is provided in Table 2. Therefore, the material constants can be calculated at any strain in the flow curve from polynomial equations. Subsequently, the flow stress can be predicted from a constitutive Eq 15 at any strain in the flow curve.

$$\alpha = \alpha_{0} + \alpha_{1} \varepsilon + \alpha_{2} \varepsilon^{2} + \alpha_{3} \varepsilon^{3}+ \alpha_{4} \varepsilon^{4}$$

(24)

$$n_{1} = n_{0} + n_{1} \varepsilon + n_{2} \varepsilon^{2} + n_{3} \varepsilon^{3} + n_{4} \varepsilon^{4}$$

(25)

$$Q = Q_{0} + Q_{1} \varepsilon + Q_{2} \varepsilon^{2} + Q_{3} \varepsilon^{3} + Q_{4} \varepsilon^{4}$$

(26)

$$\ln \,A_{3} = A_{0} + A_{1} \varepsilon + A_{2} \varepsilon^{2} + A_{3} \varepsilon^{3} + A_{4} \varepsilon^{4}$$

(27)

The predicted flow stress values obtained from the apparent-based approach is compared with the experimental flow stress at different temperatures and strain rates as shown in Fig. 12. The predicted flow stress results are comparable with the experimental results except the flow stress predicted at temperatures (1223 and 1273 K) and strain rates (1 and 10 s⁻¹). Initially, these curves had shown two stage strain hardening behavior [see Fig. 12(a) and (b)] and it can be noticed from the flow curves that, until strain of 0.25, flow stress at the strain rate of 10 s⁻¹ is lower than the flow stress measured at the strain rate of 1 s⁻¹. Therefore, during the evaluation of material constants, the flow stress measured at the strain rate of 10 s⁻¹ was not considered in the analysis till strain of 0.25. This might be a plausible reason for the deviation of predicted flow stress from experimental flow curves. The comparison of experimental stress and predicted stress is shown in Fig. 13. Most of the data points are close to the 45° line except a few data points corresponding to (1223 and 1273 K) and strain rates (1 and 10 s⁻¹). The values of R and AARE are 0.98 and 4.5%, respectively.

Fig. 11

Variation of material constants with true strain: (a) α, (b) n₁, (c) Q and (d) lnA₃

Table 2 Coefficients for the polynomial equations

Fig. 12

Comparison between predicted flow stress obtained from a constitutive equation and the experimental flow stress at different strain rates: (a) 1223 K, (b) 1273 K, (c) 1323 K and (d) 1373 K (line represents experimental curve and square symbol represents predicted value)

Fig. 13

Comparison between experimental flow stress and predicted flow stress calculated from apparent-based constitutive equation

Validation of a Constitutive Equation

To evaluate the prediction capability of a constitutive equation, two stress–strain curves randomly chosen corresponding to different temperatures 1323 and 1373 K and strain rates 10⁻² and 10⁻¹ s⁻¹ were eliminated during the calculation of material constants. Then the material constants obtained from the remaining stress–strain curves were employed to predict the flow behavior of the aforementioned stress–strain curves as shown in Fig. 14. The predicted values are reasonably close to the experimental values. This indicates that the derived constitutive equation is reasonably good enough to predict the flow curve behavior within the studied temperature and strain rate regime.

Fig. 14

Comparison of predicted stress with experimental stress

Flow Stress Modeling Using ANN

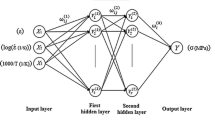
Typically ANN architecture consists of one input layer, one output layer and at least one intermediary hidden layer and these layers are connected by neurons. The input and output layers in an ANN model represent the independent and dependent variables, respectively. The neurons in the hidden layer are used solely for computational purposes. During training, the main aim is minimization of the target error, i.e., (ANN output—known target) by adjusting the weights and biases for the corresponding input data. The biases and weights are adjusted using back-propagation (BP) which is the most widely used learning algorithm for multilayer perception (Ref 65, 66). In the present work, to model the flow stress, a three layer network is employed and the schematic of the network is shown in Fig. 15. The inputs chosen for the model are temperature, strain rate and strain, respectively. The output of the model is flow stress. Levenberg–Marquardt (L–M) algorithm is the most time-efficient in terms of training the model and the same has been employed in this study.

Fig. 15

Schematic of ANN model

It is suggested that use of normalized data (both input and output) in the model allows the model to be more efficient. Therefore, before training of the network, input and output parameters are normalized to a range from 0.1 to 0.9. The most widely used equation for the normalization of the data is given below (Ref 67).

$$X^{{\prime }} = 0.1 + 0.8 x \left( {\frac{{X - X_{\hbox{min} } }}{{X_{\hbox{max} } - X_{\hbox{min} } }}} \right)$$

(28)

where X′ is the normalized data corresponding to X, X is the original data and X_max and X_min are the maximum and minimum values of X.

Eq 28 is used to normalize the temperature and flow stress data. The strain values are already within the 0.1-0.9, so, it need not be normalized further. It is not appropriate to use Eq 28 for normalizing the strain rate data directly or (as it is), because its value changes by several orders of magnitude and not uniformly distributed after normalization (Ref 68). Moreover, the normalized strain rate values obtained at lower strain rate is too small to be learned effectively by the ANN. Instead of strain rate, log (strain rate) is considered for the analysis, the equation employed for the normalization of strain rate is,

$$\dot{\varepsilon }^{{\prime }} = 0.1 + 0.8 x \left( {\frac{{\log \dot{\varepsilon } - \log \dot{\varepsilon }_{\hbox{min} } }}{{\log \dot{\varepsilon }_{\hbox{max} } - \log \dot{\varepsilon }_{\hbox{min} } }}} \right)$$

(29)

The reliability of an ANN model largely depends on the number of input–output data sets used to train the model. The total number of data points collected from the experimental flow curves is 960. In which 80% of the data was used for network training. This was accomplished by skipping the data points at regular intervals. The skipped data were used to test the prediction capability of the network. The parameters of the network used in the current work are listed in Table 3. During training, the model adjusts its weights through multiple passes of the provided input–output data. One complete pass of all input and output data is defined as an epoch. More the number of epochs, more accurate would be the results. The number of hidden neurons gives a measure of the complexity of the model. Too less a number would give inaccurate results. Thus for any ANN model to be efficient and accurate, the number of hidden neurons has to be optimized. The mean square error (MSE) was taken as a measure of the performance of the model. A target MSE of the order of 10⁻⁶ was set. MSE was calculated for varying number of hidden neurons. The iterations were stopped until the set target accuracy was achieved. Accordingly, in the present work the optimum number of hidden neurons was found to be 15, with an MSE of 2.64 e−06 after 570 epochs.

$${\text{MSE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {e_{i} - p_{i} } \right)^{2}$$

(30)

where n is the total number of data sets, e_i is the experimentally measured value and p_i is the predicted value from ANN model.

Table 3 The parameters of the ANN network used in the current work

The predicted flow stress obtained from ANN model showed very good agreement with the experimental results as shown in Fig. 16. The studied ANN model is able to predict the material flow behavior from 0.1 to 0.7 strain well, which including both stain hardening and flow softening. The calculated correlation coefficient of ANN model is almost close to 1 (0.999) which is higher than that of the apparent-based approach (0.98). In the flow stress values predicted by ANN model, most of the data points lie on the 45° line, which indicates that ANN model is more superior than the apparent-based approach. The AARE calculated from ANN model is 0.79% which is much smaller than that of the apparent-based approach (4.5%).

Fig. 16

Comparison between experimental flow stress and predicted flow stress calculated from artificial neural network model

From the above results, it is evident that both models are good in predicting the flow stress. The advantage of apparent-based approach is that it provides a simple mathematical relation which can be incorporated in finite element method for the simulation of the flow behavior of material in the studied temperature and strain rate domain, whereas from ANN model, no mathematical or empirical relation can be drawn. Nevertheless, the generated ANN model can be used to predict the flow behavior.

Finite Element Simulation

Finite element simulations were used to validate the constitutive equation generated by data obtained from the experiments conducted in Gleeble as a generalized material model. Finite element simulation package Simufact 14.0.1 was used for the simulation. A finite element model that replicates the Gleeble setup was used.

As the sample and process are axisymmetric, the problem was simplified into a 2-D axisymmetric one. Sample geometry was meshed with linear axisymmetric quadrilateral elements. An element edge length of 0.1 mm was used as shown in Fig. 17. Adaptive mesh refinement was also used to capture fine variations of the field variables. The adaptive mesh refinement algorithm automatically reduces mesh size where finer details are to be captured and uses coarser mesh wherever possible. This avoids errors due to mesh distortion without considerably increasing the computation time. A strain-based re-meshing algorithm was incorporated to avoid errors caused by excessive element distortion.

Fig. 17

Initial mesh generated for finite element simulation

Analogous to the Gleeble fixtures, the bottom plate was assumed to be fixed and the top plate moving such that a constant average plastic strain rate is maintained. Accordingly, top plate velocity was calculated based on the equations shown below.

$$\dot{\varepsilon } = \frac{v}{h}$$

(31)

$$v = \dot{\varepsilon } \times h$$

(32)

where $\dot{\varepsilon }$ is the average true strain rate, v is the velocity of top plate, h is the instantaneous height of the sample.

Temperature distribution was assumed to be uniform before deformation. Gleeble uses feedback-controlled resistance heating technique to compensate for the heat losses to the atmosphere. The measurements from the thermocouple during the experiment were found to be in reasonable agreement with the predicted temperatures at the same point in the simulation.

The material was assumed to be homogenous to start with and follow von-Mises yield criterion and an associated flow rule with isotropic strain and strain rate hardening. The empirical sine hyperbolic relation (Eq 15) predicts the flow stress as a function of strain rate and temperature.

In order to incorporate the effect of strain in the stress predictor, the above said plots were fitted with polynomial Eq 24-27, as shown in Table 2. These data were incorporated into Eq 15 and were used as the material model for simulation. The same was incorporated into the simulation using a user-defined material sub-routine code written in FORTRAN77. During the simulation, the sub-routine function was called at each time step with the strain, strain rate and temperature as the input arguments.

Shear friction condition was assumed. A friction factor of 0.15 was arrived up on by correlating the barreling width in simulation with experiments. The assumption of constant shear friction condition throughout the process is sufficient for accurate prediction of force versus stroke curve and the barreling of the sample. Depending on the process, friction conditions and material, one may choose a suitably different friction model as well for accurate prediction of material flow field (Ref 69). The thermal coefficient of expansion, heat conductivity and specific heat capacity of the material was incorporated from existing data library (Ref 70, 71). The variation of these properties with respect to temperature was also taken into account. Also, a fraction of the deformation work gets converted to heat. This generally varies with strain rate.

$${\text{Fraction}}\,{\text{of}}\,{\text{deformation}}\,{\text{work}}\,{\text{dissipated}}\,{\text{as}}\,{\text{heat}} = 0.95 \times \eta$$

(33)

where the heat generation efficiency factor (η) was calculated by the set of equations given below:

$$\eta = \left( {\begin{array}{*{20}l} {0 \quad {\text{when}}\quad \dot{\varepsilon } < 10^{ - 3} } \hfill \\ {0.316\,\log \left( {\dot{\varepsilon }} \right) + 0.95\quad {\text{when}}\quad 10^{ - 3} < \dot{\varepsilon } < 1} \hfill \\ {0.95\quad {\text{when}}\quad \dot{\varepsilon } > 1} \hfill \\ \end{array} } \right)$$

(34)

Simulation Results

In the experiment, the generated experimental stress–strain curves are average values. For a fair comparison, the average values of true stress versus true strain were calculated from the finite element simulation results. The data of force applied by the plate on the specimen and the plate displacement were made use of for the calculations. The true stress–true strain curves corresponding to hot compression at 0.1 s⁻¹ strain rate, at a temperature of 1223 K obtained from experiment and simulation are shown in Fig. 18. The strain distribution predicted by the FE simulation of the same experiment after deformation is shown in Fig. 19. Strain distribution is not uniform as can be seen from the figure, with 3 regions marked. Figure 20 shows the optical micrographs acquired from the corresponding regions. Region 1 labeled in the figure shows high strains, indicating high amount of deformation, reflected in the corresponding optical micrograph as can be seen in Fig. 20(a). Region 2 is the dead zone with negligible deformation, resulting in a nearly undeformed grain morphology as can be seen in Fig. 20(b). Region 3 lies between region 1 and the free surface of the sample and seems to have undergone lower strains compared to region 1. Figure 20(c) shows the corresponding grain morphology. Micro-Vickers hardness indentations with 1 kg load for a dwell time of 10 s were made at different locations on the sample before and after deformation. Before deformation, the sample showed a hardness value of 195 HV₁. Region 1 showed a hardness value of 270 HV₁, region 2, a hardness value of 215 HV₁ and region 3, a hardness value of 245 HV₁, which are consistent with the strain distribution map generated by FE simulation.

Fig. 18

Comparison of experimental curve at 1223 K, 10⁻¹ s⁻¹ with simulation data

Fig. 19

Strain distribution data in compression at 1223 K and 10⁻¹ s⁻¹

Fig. 20

Optical micrographs of a sample compressed at 1223 K and 10⁻¹ s⁻¹

Figure 21 shows the temperature distribution of a sample compressed at 1373 K and 10 s⁻¹ at a stroke position of 7.5 mm as predicted by the simulation. In accordance with strain distribution, the temperature is also the highest at the core and the lowest at the center of the contact surface. The adiabatic heat rise from the simulation (1406 K at periphery of the sample) is slightly higher than the experimental value [1400 K (see Fig. 3b)]. The slight difference could be due to the assumptions made in the simulation and material constants considered from the literature.

Fig. 21

Temperature distribution predicted by simulation at 7.5 mm stroke position

The sine hyperbolic equation is generally used for predicting the peak stress for any given temperature and strain rate. The use of the same as a material model, incorporating the effect of strain as well has been demonstrated. The true stress versus true strain curves predicted by the finite element simulations were found to match well with the actual experimental data. R and AARE values of the simulated data calculated with respect to the experimental values were 0.94 and 10.73%, respectively. These values are comparable to that of apparent-based approach. The above results confirm that the sine hyperbolic stress predictor can be used as a generalized material model in finite element simulation of Alloy 718 with reasonable accuracy.

Conclusions

• 1. Arrhenius type constitutive equations were derived to predict the peak flow stress by apparent and physically based approach:

  $$\begin{aligned} \sigma_{\text{p}} & = \frac{1}{0.00376} \sinh^{ - 1} \left( {\frac{{\dot{\varepsilon }\exp \left( {\frac{477389}{RT}} \right)}}{{3.07 \times 10^{18} }}} \right)^{1/4.4} \\ \sigma_{\text{p}} & = \frac{{E_{{\left( {\text{T}} \right)}} }}{549} \sinh^{ - 1} \left( {\frac{{\dot{\varepsilon }\exp \left( {\frac{285000}{RT}} \right)}}{{2.2 \times 10^{10} }}} \right)^{1/5} \\ \end{aligned}$$

• 2. Peak flow stress predicted from apparent-based approach showed better statistical performance (R = 0.99, AARE = 6%) compared to that of physically based approach (R = 0.96, AARE = 18%).

• 3. Dislocation climb was found to be the rate controlling mechanism operated in the studied range of temperature (1223-1373 K) and strain rate (10⁻² s⁻¹-10 s⁻¹).

• 4. Based on statistical analysis, it is found that ANN method is better than the derived constitutive equation to predict the flow stress.

• 5. Strain compensated constitutive equation was used as a material model for FE simulation. Flow stress values predicted by the simulation were comparable to the experimental results.

• 6. The equivalent plastic strain distribution of the deformed sample predicted by FE simulation showed a trend similar to the Vickers hardness measurements and the microstructure observed.