New Constitutive Model for Hot Deformation Behaviors of Ni-Based Superalloy Considering the Effects of Initial δ Phase

Abstract

The hot deformation behaviors of a typical Ni-based superalloy are investigated by uniaxial tensile tests over wide ranges of strain rate and deformation temperature. The experimental results show that the flow stress is sensitive to strain, strain rate, and deformation temperature. Especially, initial δ phase (Ni₃Nb) has a special effect on the flow stress. The initial δ phase can enhance the work-hardening behavior and result in the increased peak stress at relatively small strains. With the further straining, the initial δ phase can stimulate the dynamic recrystallization and promote the dynamic-softening behaviors. Considering the synthetical effects of deformation temperature, strain, strain rate, and initial δ phase on the hot deformation behaviors, a new phenomenological constitutive model is proposed. In the proposed model, the peak stress and material constant are expressed as functions of Zener-Hollomon parameter and the initial content of δ phase. A good agreement between the predicted and measured results shows that the proposed model can give an accurate and precise estimate of the hot deformation behaviors for the studied Ni-based superalloy.

Introduction

Generally, the hot deformation behaviors of metals or alloys during hot forming are very complex (Ref 1, 2). On the one hand, the hot deformation behaviors are significantly influenced by the thermo-mechanical parameters, such as strain rate, deformation temperature, and strain (Ref 3, 4). On the other hand, different metallurgical phenomena, including the work hardening (WH) (Ref 5, 6), dynamic recovery (DRV) (Ref 7, 8), and dynamic recrystallization (DRX) (Ref 9, 10), often occur in metals or alloys with low stacking fault energy during hot deformation. Additionally, for the multi-stage rolling or forging processes, the metadynamic recrystallization (MDRX) (Ref 11, 12) and static recrystallization (SRX) (Ref 13, 14) often appear. These metallurgical phenomena affect the final mechanical properties of materials and components. Therefore, understanding the hot deformation behaviors of metals or alloys has a great importance for designers to optimize the final microstructure and mechanical properties.

The constitutive models have been extensively and successfully used to numerically describe the hot deformation behaviors of metals or alloys. The numerical descriptions can be easily implemented into computer code to simulate the metal forming process. Recently, many constitutive models have been developed or improved to describe hot deformation behaviors of metals or alloys. Lin and Chen (Ref 1) presented a critical review on constitutive models for metals or alloys under hot working, and the constitutive models were divided into the phenomenological, physically based, and artificial neural network models. Arrhenius-type equation has been improved by some researchers to predict the hot deformation behaviors of different alloys. Considering the effects of strain on material parameters, Lin et al. (Ref 15) proposed an improved Arrhenius-type equation to describe the deformation behaviors of 42CrMo steel over wide ranges of strain rate and deformation temperature. Furthermore, this constitutive model has been successfully verified by some other alloys, such as magnesium alloys (Ref 16, 17), aluminum alloys (Ref 18-20), titanium alloys (Ref 21-23), and some other composite materials and pure metals (Ref 24, 25). Meanwhile, the Johnson-Cook (JC) constitutive model (Ref 26) is a most widely known as a forming temperature, stain and strain-rate-dependent phenomenological flow stress model. In recent years, some modified Johnson-Cook models were proposed to predict the hot deformation behaviors of Al-Zn-Mg-Cu alloys (Ref 27, 28), alloy steels (Ref 29-32), etc. Generally, physically based constitutive models can used to describe the intrinsic deformation mechanisms (Ref 33). Based on the classical stress-dislocation relation and the kinetics of dynamic recrystallization, He et al. (Ref 34), Lin et al. (Ref 35), Mejía et al. (Ref 36), Sajadifar and Yapici (Ref 37), and Liang et al. (Ref 38) developed the physically based constitutive equations for describing the work hardening-dynamic recovery and dynamic recrystallization behaviors of some typical alloys. In addition, some neural network models for alloys were established to predict hot deformation behaviors of some typical alloys, such as 42CrMo steel (Ref 39) and Al-Zn-Mg alloy (Ref 40).

Due to the excellent mechanical properties, good corrosion resistance under high temperature, Ni-based superalloys are widely used in the high-temperature parts of aviation and aerospace engines. Generally, Ni-based superalloy components are made through the complex thermo-mechanical processes, and the hot deformation behaviors are very sensitive to deformation parameters and initial δ phase (${\text{Ni}}_{3} {\text{Nb}}$) (Ref 41). Therefore, investigating the synthetical effects of the forming parameters and initial δ phase on the hot deformation behaviors and optimizing the forming processing are very important. Lin et al. (Ref 35), Liang et al. (Ref 38), Zhang et al. (Ref 42), Liu et al. (Ref 43), Ning et al. (Ref 44), Wu et al. (Ref 45), and Etaati et al. (Ref 46) developed the Arrhenius-type or physically based constitutive models to describe the hot deformation behaviors of typical superalloys.

Although the effects of δ phase on the hot deformation behaviors of Ni-based superalloys have been comprehensively discussed, the constitutive model considering the effects of initial δ phase is seldom reported. In this study, the hot deformation behaviors of a typical Ni-based superalloy with various initial contents of δ phase are investigated by uniaxial tensile tests over wide ranges of deformation temperature and strain rate. Based on the experimental results, a new phenomenological constitutive model is developed to describe the synthetical effects of deformation parameters and initial δ phase on the hot deformation behaviors of the studied Ni-based superalloy.

Material and Experiments

The material used in this study is a commercially Ni-based superalloy. The chemical compositions of the studied superalloy are shown in Table 1. The studied Ni-based superalloy is precipitation strengthen alloy, and the strengthening results from $\upgamma^{\prime\prime}$ phase (Ni₃Nb) and $\upgamma^{\prime}$ phase (Ni₃Al). The $\upgamma^{\prime\prime}$ phase is metastable in the thermal exposure and may transfer to δ phase (Ni₃Nb) in equilibrium. According to ISO 6892-2 (Ref 47), the specimens with the gage length of 30 mm and the diameter of 5 mm were machined (Fig. 1). The specimens were solution treated at 1040 °C for 45 min, and then cooled to room temperature in the air. In order to investigate the effects of initial δ phase on hot deformation behaviors of the studied superalloy, the solution-treated specimens were separately aged for 8, 12, and 24 h at 900 °C, and then cooled to room temperature in the air. Figure 2 shows the optical microstructures of the aged superalloy. From Fig. 2(a), it can be found that δ phases exist in two morphologies. i.e., when the aging time is 8 h, the short plate-like δ phase distributes at grain boundaries, while the spherical δ phase appears within grains. As the aging time is increased to 12 h, the plate-like δ phase grows from grain boundaries towards grain interior (Fig. 2b). When the aging time is continuously increased to 24 h, a large amount of long needle-like δ phases distribute throughout the whole grains, as shown in Fig. 2(c). It is obvious that the content of initial δ phase increases with increasing aging time. In order to quantitatively analyze the effects of initial δ phase on hot deformation behaviors, the Image-Pro Plus software, which is usually used by some international researchers, was used to evaluate the contents of initial δ phase, as shown in Fig. 3. In order to keep the accuracy of the evaluated contents of initial δ phase, ten different optical images for each specimen are evaluated, as shown in Table 2. Finally, the average volume fractions of initial δ phase in the specimens aged for 8, 12, and 24 h can be evaluated as 4.96%, 7.80%, and 12.09%, respectively.

Table 1 Chemical compositions of the studied Ni-based superalloy (wt.%)

Fig.1

Dimensions of tensile test specimen (unit: mm)

Fig. 2

Optical microstructures of the Ni-based superalloys aged for: (a) 8 h; (b) 12 h; (c) 24 h

Fig. 3

Optical microstructures used to measure volume fractions of δ phase by Image-Pro Plus software: (a) aged for 8 h; (b) aged for 12 h; (c) aged for 24 h (The red areas represent the delta-phase)

Table 2 Volume fractions (%) of δ phase in the specimens aged for 8, 12, and 24 h at different optical images

Uniaxial tensile tests were carried out on MTS-GWT2105 test machine at the deformation temperatures of 920, 950, 980, and 1010 °C. The constant tensile speeds of 0.3, 0.15, and 0.03 mm/s (i.e., initial strain rates of 0.01, 0.005, and 0.001 s⁻¹) were employed in tensile tests. Prior to loading, the specimens were heated to the deformation temperature with the heating rate of 10 °C/min, and held for 30 min to eliminate the thermal gradient. Here, a resistance furnace was used to heating specimen, and the fluctuation of temperature was controlled within 1 °C. A computer was used to control the experimental procedures and collect the experimental data automatically.

Results and Discussion

Correction of True Stress-True Strain Curves

Generally, constitutive models are established based on the true stress-true strain curves under constant strain rate. As mentioned in section 2, the uniaxial tensile tests were performed under constant tensile speed. Therefore, it is necessary to correct the experimental data to obtain true stress-true strain curves under constant strain rate.

Figure 4 shows a typical load-displacement curve of uniaxial tensile test and the morphology of fractured specimen. Obviously, the hot deformation behavior can be divided into three distinct stages, i.e., uniform deformation stage (I), diffusion necking stage (II), and localized necking stage (III), as shown in Fig. 4(a). In the early deformation, the load rapidly increases to the peak value, and the deformation of specimen is uniform. With the further straining, the local instability results in the strain localization. Due to the strain rate sensitivity of the material, the necking diffuses throughout the gage section of specimen. Therefore, the specimen shows the macroscopic uniform deformation and high uniform elongation, as shown in Fig. 5. Meanwhile, the load exhibits linear decrease characteristic roughly. At the final deformation stage, the onset of localized necking leads to the fracture of specimen. It is well known that the localized necking characteristic indicates the instability during tensile deformation. In this study, the investigation focuses on the hot deformation behavior before the localized necking.

Fig. 4

Hot tensile deformation characteristics: (a) typical load-displacement curve; (b) the morphology of fractured specimen

Fig. 5

Effects of deformation parameters on the strains corresponding to maximum uniform elongation (initial δ phase: 12.09%)

Generally, the true stress-true strain before the localized necking can be expressed as,

$$\upvarepsilon = \ln \left( {\frac{l}{{l_{0} }}} \right),$$

(1)

$$\upsigma = \frac{F}{{A_{0} }}\exp \left( \upvarepsilon \right),$$

(2)

where A ₀ is the initial cross-sectional area of specimen, l ₀ is the initial gage length of specimen, l is the instantaneous gage length of specimen, F is the deformation resistance, ε is the true strain, and σ is the true stress. From Eq 1 and 2, the true stress-true strain under constant tensile speed can be obtained.

In addition, the instantaneous strain rate can be usually evaluated by,

$$\dot{\upvarepsilon } = \frac{v}{l},$$

(3)

where $\dot{\upvarepsilon }$ is the strain rate and v is the tensile speed.

It is well known that the instantaneous gage length of specimen (l) gradually increases during the uniaxial tensile. According to Eq 3, the instantaneous strain rate decreases with the further deformation. In this study, a new method is proposed to obtain the true stress-true strain curves under constant strain rate. Taking the alloy with initial δ phase of 12.09% as an example, the followings introduce the correction procedure at the deformation temperature of 980 °C and strain of 0.1. According to Hollomon model, the flow stress can be expressed as (Ref 1, 48),

$$\upsigma = K\upvarepsilon^{n} \dot{\upvarepsilon }^{m} \exp \left( {\frac{Q}{{{\text{R}}T}}} \right),$$

(4)

where K is material constant, n is the strain hardening exponent, m is the strain rate sensitivity coefficient, T is the absolute temperature, R is the universal gas constant, Q is the apparent activation energy. Taking the logarithm of both sides of Eq 4, gives

$$\ln \upsigma = \ln K + n\ln \upvarepsilon + m\ln \dot{\upvarepsilon } + \frac{Q}{{{\text{R}}T}}.$$

(5)

Based on the experimental data, the true stress (Eq 2) and instantaneous strain rate (Eq 3) can be evaluated under the deformation temperature of 980 °C and strain of 0.1. Then, the relationship between the true stress and strain rate can be easily obtained from Eq 5, as shown in Fig. 6, and the value of m can be obtained as 0.1838 from the slop of the linear fitting line in$\ln \upsigma - \ln \dot{\upvarepsilon }$plot. Finally, the corrected true stresses at constant strain rates, i.e., 0.01, 0.005, 0.001 s⁻¹, can be evaluated, as shown in Table 3. Similarly, the correction of flow stress can be done for several strain levels, which are selected within 0.05-0.4 with the interval of 0.05 (within uniform elongation range). Therefore, the true stress-true strain curves under constant strain rate can be obtained, as shown in Fig. 7.

Fig. 6

Relationship between the true stress and strain rate (deformation temperature: 980 °C; strain: 0.1)

Table 3 The results of corrected true stresses under the deformation temperature of 980 °C and strain of 0.1

Fig. 7

True stress-true strain curves under constant tensile speed and constant strain rate (deformation temperature: 980 °C)

Hot Deformation Behaviors of the Studied Superalloy

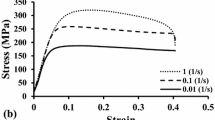
Firstly, the aged superalloy with initial δ phase of 12.09% is taken as an example to discuss the effects of deformation temperature, strain, and strain rate on the hot deformation behaviors. Figure 8 shows the typical true stress-true strain curves of the studied Ni-based superalloy before the localized necking. Obviously, the flow stresses are strongly dependent on the deformation temperature, strain and strain rate under all the tested conditions. The flow stress decreases with the increase of deformation temperature or the decrease of strain rate. Due to the work hardening-dynamic recovery, the true stress-true strain curves exhibit a peak stress at small strains. After the peak stress, the flow stresses decrease monotonically until large strains. Such features for the studied Ni-based superalloy with low stacking fault energy indicate the occurrence of dynamic recrystallization during hot deformation.

Fig. 8

True stress-true strain curves of the studied Ni-based superalloy with initial δ phase of 12.09% at: (a) $\dot{\upvarepsilon } = 0.001$ s⁻¹, (b) T = 980 °C

Figure 9 shows the effects of initial δ phase on the true stress-true strain curves of the studied Ni-based superalloy at deformation temperature of 950 °C and strain rate of 0.001 s⁻¹. As shown in Fig. 9, the peak stress increases with the increase of initial δ phase. It indicates that δ phase can enhance the work-hardening behavior at the beginning of hot deformation. After the peak stress, the flow stress drops monotonically, and dynamic-softening behaviors are more and more obvious with the increase of initial δ phase. The main reason for this phenomenon is that the existence of δ phase during hot deformation stimulates the dynamic recrystallization process.

Fig. 9

The true stress-true strain curves of the studied Ni-based superalloy with the initial δ phase contents of: (I) 4.96%; (II) 7.80%; (III) 12.09% (deformation temperature: 950 °C; strain rate: 0.001 s⁻¹)

Constitutive Model to Describe Hot Deformation Behaviors

Generally, the hot deformation behaviors of alloys can be described by (Ref 1, 49).

$$\frac{\upsigma }{{\upsigma_{\text{P}} }} = \left( {\frac{\upvarepsilon }{{\upvarepsilon_{\text{P}} }}\exp \left( {1 - \frac{\upvarepsilon }{{\upvarepsilon {}_{\text{P}}}}} \right)} \right)^{c} ,$$

(6)

where $\upsigma_{\text{P}}$ is the peak stress (MPa), $\upvarepsilon_{\text{P}}$ is the peak strain, c is the material constant.

Determination of Peak Stress $\upsigma_{\text{P}}$

Figure 10 shows the relationships between the peak stress $(\upsigma_{\text{P}}),$ deformation parameters and initial content of δ phase (V). It can be found that the deformation temperature, strain rate, and initial content of δ phase significantly influence the peak stress. Therefore, in order to accurately describe the hot deformation behaviors of the studied superalloy, the effects of initial δ phase on the peak stress should be considered when the constitutive model is developed.

Fig. 10

Relationships between the peak stress $(\upsigma_{\text{P}}),$deformation parameters, and initial content of δ phase (V)

Meanwhile, Fig. 10 indicates that the effects of initial δ phase on the hot deformation behaviors are relatively complex for the studied superalloy. So, in order to simplify the procedure to determine material constants, the effects of deformation temperature and strain rate on the peak stress are firstly considered. The superalloy with initial δ phase of 12.09% is taken as an example to show the method to establish the constitutive model. Generally, the peak stress can be evaluated through the following hyperbolic-sine Arrhenius equation (Ref 1, 50):

$$\dot{\upvarepsilon } = AF\left( {\upsigma_{\text{r}} } \right)\exp \left( { - \frac{Q}{{{\text{R}}T}}} \right),$$

(7)

where

$$F\left( {\upsigma_{\text{r}} } \right) = \left\{ {\begin{array}{*{20}c} {\upsigma_{\text{r}}^{{n^{\prime}}} } &\quad {\upalpha \upsigma < 0.8} \\ {\exp \left( {\upbeta \upsigma_{\text{r}} } \right)} &\quad {\upalpha \upsigma > 1.2} \\ {\left[ {\sinh \left( {\upalpha \upsigma_{\text{r}} } \right)} \right]^{n} } &\quad {{\text{for all }}\upsigma_{\text{r}} } \\ \end{array} } \right.$$

(8)

in which, $\upsigma_{\text{r}}$ is the peak stress (MPa), T is the absolute temperature (K), R is the universal gas constant (8.31 J/mol K). Q is the apparent hot deformation activation energy (kJ/mol). A, $n^{\prime}$, α, β, and n are material constants, $\upalpha = \upbeta/n^{\prime}$.

Generally, the effects of deformation temperature and strain rate on the deformation behaviors can be expressed by Zener-Hollomon (Z) parameter in the following exponent-type equation.

$$Z = \dot{\upvarepsilon }\exp \left( {\frac{Q}{{{\text{R}}T}}} \right).$$

(9)

Therefore, the flow stress can be written as a function of Z parameter, and the constitutive equation can be summarized as,

$$\upsigma_{\text{r}} = \frac{1}{\upalpha }\ln \left( {\left( \frac{Z}{A} \right)^{{{1 /n}}} + \left( {\left( \frac{Z}{A} \right)^{{{2/ n}}} + 1} \right)^{{{1/ 2}}} } \right).$$

(10)

For the low stress level (${\upalpha}\upsigma < 0.8$) and high stress level (${\upalpha}\upsigma > 1.2$), Eq 7 can be expressed as, respectively,

$$\dot{\upvarepsilon } = B\upsigma_{\text{r}}^{{n^{\prime}}} ,$$

(11)

$$\dot{\upvarepsilon } = B^{\prime}\exp \left( {\upbeta \upsigma_{\text{r}} } \right),$$

(12)

where B and $B^{\prime}$are material constants, which are independent on the deformation temperature. Taking the logarithm of both sides of Eq 11 and 12, respectively, gives

$$\ln \upsigma_{\text{r}} = - \ln B/n^{\prime} + \ln \dot{\upvarepsilon }/n^{\prime}$$

(13)

$$\upsigma_{\text{r}} = - \ln B^{\prime}/{\upbeta} + \ln \dot{\upvarepsilon }/{\upbeta}.$$

(14)

It can be easily obtained the relationships between the peak stress and strain rate, as shown in Fig. 11. Then, the values of $n^{\prime}$and β can be obtained from the slopes of the parallel straight lines in the $\ln \upsigma_{\text{r}} - \ln \dot{\upvarepsilon }$ and $\upsigma_{\text{r}} - \ln \dot{\upvarepsilon }$ plots, respectively. The averaged values of $n^{\prime}$ and β can be computed as 5.379 and 0.0289 MPa⁻¹, respectively. Then, ${\upalpha} = {\upbeta}/n^{\prime} = 0.00537$ MPa⁻¹.

Fig. 11

Relationships between: (a) $\ln \upsigma_{\text{r}}$ and $\ln \dot{\upvarepsilon }$; (b) $\upsigma_{\text{r}}$ and $\ln \dot{\upvarepsilon }$ (symbols for the experimental results; solid lines for the fitting line)

For all the stress level, Eq 7 can be represented as:

$$\dot{\upvarepsilon } = A\left[ {\sinh \left( {{\upalpha}\upsigma_{\text{r}} } \right)} \right]^{n} \exp \left( { - \frac{Q}{{{\text{R}}T}}} \right).$$

(15)

Taking the logarithm of both sides of Eq 15 gives

$$\ln \left[ {\sinh \left( {{\upalpha}\upsigma_{\text{r}} } \right)} \right] = \frac{{\ln \dot{\upvarepsilon }}}{n} + \frac{Q}{{{\text{R}}Tn}} - \frac{\ln A}{n}.$$

(16)

Substituting the values of deformation temperatures, strain rates, and peak stresses into Eq 16 gives the relationships of $\ln \left[ {\sinh \left( {{\upalpha}\upsigma_{\text{r}} } \right)} \right] - \ln \dot{\upvarepsilon }$ and $\ln \left[ {\sinh \left( {{\upalpha}\upsigma_{\text{r}} } \right)} \right] - 1000/T$, as shown in Fig. 12. Then, it is easy to evaluate the averaged values of material constants A, n and activation energy (Q) as $6.769 \times 10^{15}$ s⁻¹, 4.009 and 442.005 kJ/mol, respectively.

Fig. 12

Relationships between: (a) $\ln \left[ {\sinh \left( {\upalpha \upsigma_{\text{r}} } \right)} \right]$ and $\ln \dot{\upvarepsilon }$; (b) $\ln \left[ {\sinh \left( {\upalpha \upsigma_{\text{r}} } \right)} \right]$and 1000/T (symbols for the experimental results; solid lines for the fitting line)

Therefore, the peak stress can be described by the following equations when the initial content of δ phase is 12.09%.

$$\left\{ \begin{aligned} \upsigma_{\text{r}} = \frac{1}{0.00537}\ln \left[ {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{1/4.009} + \left( {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 {4.009}}} \right. \kern-0pt} {4.009}}}} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \hfill \\ Z = \dot{\upvarepsilon }{ \exp }\left( {\frac{ 4 42 0 0 5}{{{\text{R}}T}}} \right) \hfill \\ \end{aligned} \right..$$

(17)

In order to further investigate the effects of initial δ phase on the peak stress, the peak stress under the initial δ phase of 12.09% may be taken as the reference stress ($\upsigma_{\text{r}}$). Then, the relationships between $\ln \left( {\frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }}} \right)$ and V under various tested conditions can be obtained, as shown in Fig. 13. Obviously, there are good linear relationships between $\ln \left( {\frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }}} \right)$ and V. Therefore, the relationship between the peak stress and initial content of δ phase can be assumed as,

$$\frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }} = N\exp \left( {kV} \right),$$

(18)

where N and k are material constants, $\upsigma_{\text{r}}$ is reference peak stress when the initial content of δ phase is 12.09%. Taking the logarithm of both sides of Eq 18 gives,

$$\ln \left( {\frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }}} \right) = kV + \ln N.$$

(19)

Fig. 13

Relationships between $\ln \frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }}$ and V (fine lines are fitting lines; coarse line is the average fitting line)

By the linear fitting method, the average values of k and N can be evaluated as 0.0128 and 0.862 from the slop and intercept of the fitting line in $\ln \left( {\frac{{\upsigma_{\text{P}} }}{{\upsigma_{\text{r}} }}} \right) - V$ plot (Fig. 13), respectively. Therefore, the peak stress can be expressed as,

$$\upsigma_{\text{P}} = 0.862\exp \left( {0.0128V} \right)\upsigma_{\text{r}} .$$

(20)

Summarily, the peak stress for the studied Ni-based superalloy under all tested conditions can be summarized as,

$$\left\{ \begin{aligned} \upsigma_{\text{P}}& = 160.52\exp \left( {0.0128V} \right)\ln \left[ {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{1/4.009} + \left( {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 {4.009}}} \right. \kern-0pt} {4.009}}}} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \\ Z &= \dot{\upvarepsilon }{ \exp }\left( {\frac{ 4 4 2 0 0 5}{{{\text{R}}T}}} \right) \hfill \\ \end{aligned} \right..$$

(21)

Determination of Peak Strain $\upvarepsilon_{\text{P}}$

Generally, the dependence of peak strain on the deformation temperature and strain rate can be expressed as (Ref 51),

$$\upvarepsilon_{\text{P}} = k^{\prime}Z^{{n^{\prime}}} ,$$

(22)

where $k^{\prime}$and$n^{\prime}$are material constants. Taking the logarithm of both sides of Eq 22 gives

$$\ln \upvarepsilon_{\text{P}} = n^{\prime}\ln Z + \ln k^{\prime}.$$

(23)

For the superalloy with initial δ phase of 12.09%, the relationship between$\ln \upvarepsilon_{\text{P}}$ and$\ln Z$ can be obtained, as shown in Fig. 14. The values of $n^{\prime}$ and $k^{\prime}$can be obtained as 0.1382 and $3.064 \times 10^{ - 4}$ from the slope and intercept of the linear fitting line in $\ln \upvarepsilon_{\text{P}} - \ln Z$ plot, respectively. So,$\upvarepsilon_{\text{P}}$ can be written as,

$$\upvarepsilon_{\text{P}} = 3.064 \times 10^{ - 4} Z^{0.1382}$$

(24)

Fig. 14

Relationship between the peak strain $(\upvarepsilon_{\text{P}})$ and Z parameter

Additionally, Fig. 9 shows that the effects of initial δ phase on the peak strain are not obvious. In order to simplify the constitutive model, the effects of initial content of δ phase on the peak strain are ignored.

Determination of Material Constant c

Similarly, taking the superalloy with initial δ phase of 12.09% as an example, the procedure for determining material constant c is introduced at the deformation temperature of 950 °C and strain rate of 0.01 s⁻¹. In order to calculate the value of material constant c, taking the logarithm of both sides of Eq 6 gives

$$\ln \frac{\upsigma }{{\upsigma_{\text{P}} }} = c\left[ {\ln \left( {\frac{\upvarepsilon }{{\upvarepsilon_{\text{P}} }}} \right) + \left( {1 - \frac{\upvarepsilon }{{\upvarepsilon_{\text{P}} }}} \right)} \right].$$

(25)

In Eq 25, the peak stress ($\upsigma_{\text{P}}$) and peak strain ($\upvarepsilon_{\text{P}}$) can be obtained from Eq 21 and 24, respectively. Substituting the measured strains ($\upvarepsilon$) and the corresponding flow stresses ($\upsigma$) in the dynamic-softening stage into Eq 25. The relationship between $\ln \left( {{\upsigma \mathord{\left/ {\vphantom {\upsigma {\upsigma_{\text{P}} }}} \right. \kern-0pt} {\upsigma_{\text{P}} }}} \right)$ and $\left[ {\ln \left( {{\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right) + \left( {1 - {\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right)} \right]$ at the deformation temperature of 950 °C and strain rate of 0.01 s⁻¹ can be obtained, as shown in Fig. 15. Obviously, it can be found that there is a good linear relationship between $\ln \left( {{\upsigma \mathord{\left/ {\vphantom {\upsigma {\upsigma_{\text{P}} }}} \right. \kern-0pt} {\upsigma_{\text{P}} }}} \right)$ and $\left[ {\ln \left( {{\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right) + \left( {1 - {\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right)} \right]$. By the linear fitting method, the value of material constant c can be easily evaluated as 0.0998. Using the same method, the values of material constant c for the studied Ni-based superalloy under the other tested conditions can be evaluated, as shown in Tables 4, 5, and 6.

Fig. 15

Relationship between $\ln \left( {{\upsigma \mathord{\left/ {\vphantom {\upsigma {\upsigma_{\text{P}} }}} \right. \kern-0pt} {\upsigma_{\text{P}} }}} \right)$ and $\left[ {\ln \left( {{\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right) + \left( {1 - {\upvarepsilon \mathord{\left/ {\vphantom {\upvarepsilon {\upvarepsilon_{\text{P}} }}} \right. \kern-0pt} {\upvarepsilon_{\text{P}} }}} \right)} \right]$ at the deformation temperature of 950 °C and strain rate of 0.01 s⁻¹

Table 4 The values of material constant c under all the tested conditions (V = 4.96%)

Table 5 The values of material constant c under all the tested conditions (V = 7.80%)

Table 6 The values of material constant c under all the tested conditions (V = 12.09%)

Figure 16 shows the relationships between material constant c, deformation parameters, and initial content of δ phase. Obviously, the material constant c is sensitive to deformation temperature, strain rate, and initial content of δ phase. Therefore, the material constant c should be expressed as the functions of deformation parameters and initial content of δ phase.

Fig. 16

Relationships between material constant c, deformation parameters, and initial content of δ phase

In the following sections, the effects of deformation temperature and strain rate on material constant $c$ are firstly considered. Usually, the material constant c can be expressed as (Ref 52):

$$c_{\text{r}} = BZ^{\uplambda} ,$$

(26)

where B and $\uplambda$ are material constants. Taking the logarithm of both sides of Eq 26 gives

$$\ln c_{\text{r}} = \uplambda \ln Z + \ln B.$$

(27)

When the superalloy with initial δ phase of 12.09%, the values of λ and B can be obtained as 0.313 and $4.919 \times 10^{ - 7}$ from the slope and intercept of the linear fitting line in $\ln c_{\text{r}} - \ln Z$ plot (Fig. 17), respectively. Therefore, the effects of deformation temperature and strain rate on the material constant c can be expressed by.

$$c_{\text{r}} = 4.919 \times 10^{ - 7} \times Z^{0.313} .$$

(28)

Fig. 17

Relationship between the material constant (c) and Z parameter

If the material constant c under the initial δ phase of 12.09% is taken as the reference value, the relationships between $\ln \left( {\frac{c}{{c_{\text{r}} }}} \right)$ and V under various tested conditions can be obtained, as shown in Fig. 18. It can be found that there are good linear relationships between $\ln \left( {\frac{c}{{c_{\text{r}} }}} \right)$ and V. Therefore, the relationship between material constant c and initial content of δ phase can be assumed as,

$$\frac{c}{{c_{r} }} = M\exp \left( {KV} \right),$$

(29)

where M and K are material constants,$c_{\text{r}}$ is reference value under initial δ phase of 12.09%. Taking the logarithm of both sides of Eq 29 gives

$$\ln \left( {\frac{c}{{c_{r} }}} \right) = KV + \ln M.$$

(30)

Fig. 18

Relationships between $\ln \left( {\frac{c}{{c_{\text{r}} }}} \right)$ and V (fine lines are the fitting lines; coarse line is the average fitting line)

By the linear fitting method, the average values of K and M can be obtained as 0.1499 and 0.1828 from the slop and intercept of the fitting line in $\ln \left( {\frac{c}{{c_{\text{r}} }}} \right) - V$ plot (Fig. 18), respectively. Therefore, the peak stress can be expressed as,

$$c = 0.1828\exp \left( {0.1499V} \right)c_{\text{r}} .$$

(31)

Summarily, the material constant c with various initial contents of δ phase can be summarized as,

$$c = 0.899 \times 10^{ - 7} \exp \left( {0.1499V} \right)Z^{0.313} .$$

(32)

Verification of the Developed Constitutive Model

Based on the above analysis, the constitutive model to predict the hot deformation behaviors of the studied Ni-based superalloy can be summarized as,

$$\left\{ \begin{aligned} \frac{\upsigma }{{\upsigma_{\text{P}} }} &= \left( {\frac{\upvarepsilon }{{\upvarepsilon_{\text{P}} }}\exp \left( {1 - \frac{\upvarepsilon }{{\upvarepsilon {}_{\text{P}}}}} \right)} \right)^{c} \\ \upsigma_{\text{P}}& = 160.52\exp \left( {0.0128V} \right)\ln \left[ {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{1/4.009} + \left( {\left( {\frac{Z}{{6.769 \times 10^{15} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 {4.009}}} \right. \kern-0pt} {4.009}}}} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \\ \upvarepsilon_{\text{P}} &= 3.064 \times 10^{ - 4} Z^{0.1382} \\ c &= 0.899 \times 10^{ - 7} \exp \left( {0.1499V} \right)Z^{0.313} \\ Z &= \dot{\upvarepsilon }{ \exp }\left( {\frac{ 4 4 2 0 0 5}{{{\text{R}}T}}} \right) \hfill \\ \end{aligned} \right..$$

(33)

In order to verify the developed constitutive model, the comparisons between the measured and predicted results during hot deformation are carried out. Figure 19 shows the measured and predicted flow stress curves of the studied Ni-based superalloy under all the tested conditions. It can be seen that the predicted flow stresses well agree with the measured ones. In order to further confirm the high prediction accuracy of the developed constitutive model, the correlation coefficient (R) and average absolute relative error (AARE) between the predicted and measured flow stress are evaluated, respectively.

$$R = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {E_{i} - \bar{E}} \right)\left( {P_{i} - \bar{P}} \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{N} {\left( {E_{i} - \bar{E}} \right)^{2} \sum\limits_{i = 1}^{N} {\left( {P_{i} - \bar{P}} \right)^{2} } } } }},$$

(34)

$$ {\text{AARE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{E_{i} - P_{i} }}{{E_{i} }}} \right|} \times 100\% , $$

(35)

where E _i and P _i are the measured and predicted flow stress, respectively. $\bar{E}$ and $\bar{P}$ are the mean values of E _i and P _i , respectively. N is the total number of data used in this study. The correlation coefficient (R) is commonly employed as the statistical parameter and provides information regarding the strength of linear relationship between the measured and predicted values. The average absolute relative error (AARE) is computed through a term by term comparison of the relative error and therefore is an unbiased statistical parameter to further evaluate the predictability of model. Figure 20 shows the correlations between the measured and predicted flow stresses. It can be easily found that the correlation coefficient (R) and the average absolute relative error (AARE) are 0.9933 and 1.84%, respectively, which reflects an excellent capability of the established constitutive model to predict the hot deformation behaviors of the studied superalloy.

Fig. 19

Comparisons between the measured and predicted flow stress curves for all the tested conditions under the initial δ phase contents of: (a-c) 4.96%; (d-f) 7.80%; (g-i) 12.09%

Fig. 20

Correlation between the measured and predicted flow stresses

Conclusions

The hot deformation behaviors of a typical Ni-based superalloy are studied by uniaxial tensile tests. The initial δ phase can enhance work-hardening behavior at relatively small strains. With the further straining, the initial δ phase can promote dynamic-softening behavior. A new phenomenological constitutive model is proposed to describe the hot deformation behaviors of the studied Ni-based superalloy. In the proposed model, the synthetical effects of deformation temperature, strain, strain rate, and initial δ phase on the hot deformation behaviors are well considered. The good agreements between the measured and predicted results confirm that the developed model can present an accurate and precise estimation of the flow stress over wide ranges of deformation temperature, strain, strain rate, and initial content of δ phase.