Introduction

The flow behavior of metals and alloys at elevated temperatures is of great importance for industrial hot deformation processing. Recently, finite element (numerical) simulation as an efficient approach for the evaluation of the hot plastic deformability of metallic materials and the optimization of deformation conditions has been extensively applied to the study of metal plastic-forming processes (Ref 1-3). The numerical simulation can be reliable only when a proper constitutive equation is inserted into the finite element code as input data. These equations correlate thermomechanical processing parameters such as flow stress, strain, strain rate and temperature with each other.

So far, various models have been proposed by different researchers to predict the flow behavior during hot deformation for a wide variety of metals and alloys. As is well known, the exponential type equation has been widely adopted for establishing constitutive models (Ref 4, 5). However, this equation is inappropriate at low stresses. In another approach, Sellars and McTegart (Ref 6) proposed a hyperbolic-sine Arrhenius equation to describe the high temperature flow behavior of materials over a wide range of stresses. This kind of equation was used by other researchers for predicting the flow stress of various metals and alloys (Ref 7, 8). It should be noted that in the majority of previous studies on the constitutive analysis of hot flow behavior of materials, only the effect of deformation temperature and strain rate was taken into account. However, the influence of strain has not been considered for the development of the constitutive model. In order to incorporate the effect of strain on the constitutive model, Rao et al. (Ref 9) introduced a strain-dependent parameter into the hyperbolic-sine Arrhenius equation. Recently, a revised hyperbolic sine constitutive equation has been proposed to predict the high temperature flow behavior by considering strain compensation (Ref 4, 10-13). This model has been employed by various researchers to formulate the constitutive behaviors of 42CrMo steel (Ref 4), Cr20Ni25Mo4Cu superaustenitic stainless steel (Ref 12), Ti-modified austenitic stainless steel (Ref 13), AZ81 magnesium alloy (Ref 11) and Ti-6Al-4V alloy (Ref 10).

It is well known that work hardening and dynamic softening occur frequently during the hot deformation of metals and alloys. The two main restoration mechanisms are dynamic recovery (DRV) which leads to annihilation and rearrangement of dislocations, and DRX which results in the formation of new strain-free grains. In low stacking fault energy metals [such as the austenite phase in steels (Ref 14)], the ability of dislocations to climb and/or cross slip is hindered. Thus, in these materials DRV is suppressed and DRX acts as the major restoration mechanism during hot deformation processes (Ref 15-17). On the other hand, DRX dominates the microstructure and thus dictates the mechanical properties during hot deformation processing. Therefore, it can be concluded that the DRX behavior of austenite is of great importance during thermomechanical processing of steels.

During hot deformation, DRX can be initiated at a critical level of stress accumulation (Ref 18). The softening due to DRX causes the strain hardening rate to decrease, generating a peak on the flow curve at which the strain hardening rate equals zero. Although the existence of a peak on the flow curve indicates the formation of new grains, DRX actually starts at a critical strain (εc) which is lower than the strain at peak stress (εp) (Ref 19, 20). This critical strain is a function of initial microstructure and deformation conditions (Ref 21). So far, many studies have been conducted to study the typical behavior of DRX (Ref 22-24) as well as the kinetics of DRX (Ref 20, 25-27).

In this study, a strain dependent constitutive relationship for a medium carbon microalloyed steel was developed by utilizing the experimental data obtained from isothermal hot compression tests. The accuracy of the developed constitutive model was verified over the entire experimental range. Furthermore, the critical characteristics of DRX, including critical and peak strain, were determined using the work hardening rate versus true stress under different hot deformation conditions. Finally, the kinetics of DRX was analyzed by constructing the curve of recrystallized volume fraction based on the flow curves.

Experimental Procedure

The chemical composition (wt.%) of the investigated steel and its microstructure are shown in Table 1 and Fig. 1, respectively. The microstructure consists of relatively fine ferrite grains and pearlite colonies.

Table 1 Chemical composition (in wt.%) of the investigated steel
Full size table
Fig. 1
figure 1

The optical microstructure of the as-received material

Full size image

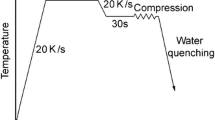
Cylindrical hot compression specimens, 12 mm in height and 8 mm in diameter [in accordance with ASTM E209 (Ref 28) were machined from a stock of material. In order to dissolve carbo-nitride precipitates (Ref 29), the specimens were heated up to 1200 °C in a separate resistance furnace and held isothermally for 5 min. After soaking, the specimens were moved immediately to the testing machine, a Zwick/Roell-250 machine equipped with a resistance furnace. To ensure that the temperature became homogeneous throughout the specimens during the hot compression test, they were held there for 5 min prior to straining. The hot compression tests were performed in the temperature range of 1000-1200 °C, at an interval of 50 °C, under constant strain rates of 0.01, 0.1 and 1 s−1, up to the true strain of 0.9. Upon completion of the hot compression test, the specimens were immediately quenched in tap water. The thermomechanical processing schedule is schematically shown in Fig. 2.

Fig. 2
figure 2

A schematic diagram of the thermomechanical processing schedule

Full size image

Results and Discussion

Analysis of Hot Flow Curves

The effect of strain rate and deformation temperature on the true stress-true strain curves of the investigated steel is shown in Fig. 3. It can be seen that these processing parameters (temperature and strain rate) have a remarkable impact on the flow curves. The flow stress level decreases with increasing compression temperature and/or decreasing strain rate. It is assumed that the formation of dislocations and their accumulation behind the barriers reduces the dislocation movements which, in turn, causes the flow stress to increase.

Fig. 3
figure 3

The true stress-true strain curves of microalloyed steel compressed at different temperatures under strain rates of (a) 0.01, (b) 0.1 and (c) 1 s−1

Full size image

Moreover, it can be clearly observed that almost all flow curves exhibit a peak followed by a gradual decline to a steady state stress which is indicative of the occurrence of DRX, except for the specimens deformed at 1000 and 1050 °C under the strain rate of 1 s−1. At the initial stage of straining, work hardening predominates and the flow stress exhibits a rapid increase up to a critical value with increasing strain. At the critical strain, where the driving force for DRX is attained, new grains start to nucleate which, in turn, results in a gradual decrease in the hardening rate. When the hardening rate becomes equal to the softening rate, the peak flow stress is reached. The flow softening beyond the peak stress, which is attributed to DRX (Ref 30), exceeds the hardening, thus, the stress drops gradually. Finally, the flow stress becomes steady when a new balance between softening rate and hardening rate is obtained.

For the case of the specimens deformed at 1000 and 1050 °C under the strain rate of 1 s−1, DRX conditions were apparently not achieved. Thus, one may conclude that the non-recrystallization temperature (T NR) for this microalloyed steel is below 1000 °C when compressed under a strain rate of 1 s−1. It has been reported (Ref 14, 31) that the dynamic strain induced precipitation occurs during deformation at temperatures lower than T NR in microalloyed steels. This precipitation is in turn responsible for the formation of pancaked austenite grains during deformation by hindering the occurrence of DRX (Ref 31). Furthermore, it can be concluded that the softening behavior during deformation at deformation temperatures close to T NR results from the counteracting effects of restoration mechanisms and work hardening of austenite (Ref 32).

In addition, at the deformation temperatures of 1100, 1150 and 1200 °C under the strain rate of 0.01 s−1 (Fig. 3a), multiple peak flow appears in contrast with single peak flow in other deformation conditions. It should be mentioned that such cyclic flow behavior is associated with grain coarsening during DRX (Ref 33). However, below the temperature of 1100 °C, only single peak behavior is recorded which is indicative of grain refining during DRX. It is well reported that increases in strain rate or reductions in the deformation temperature lead to the single peak behavior (Ref 33).

According to Fig. 3, at a constant strain rate, the peak stress and peak strain decrease with an increase in temperature. On the other hand, at a constant deformation temperature, the peak stress and peak strain decrease with a reduction of strain rate. It is well-known that higher temperatures and lower strain rates can promote the softening process by increasing the mobility of grain boundaries and providing longer time for dislocation annihilation and occurrence of DRX (Ref 12).

Evaluation of the Constitutive Model

The stress-strain data obtained from compression tests under different strain rates and temperature conditions can be used to determine the material constants of the constitutive equation. The hyperbolic sine-type equation Eq 1, which was proposed by Sellars and McTegart (Ref 6), has been widely adopted to characterize the relationship between deformation parameters and specimen response over a wide range of stresses:

$$ \dot{\upvarepsilon} = A\left[ {\sinh (\upalpha \upsigma )} \right]^{n} \exp \left( {\frac{ - Q}{RT}} \right) $$
(1)

where A (s−1), α (MPa−1) and n (stress exponent) are material constants, \( \dot{\upvarepsilon } \) is the strain rate (s−1), R is the universal gas constant (8.314 J/mol/K), σ is the flow stress (MPa), and Q is the activation energy for deformation (J/mol).

The value of the constant α is derived by the division of β and n 1 (Ref 13), which are material constants in the two limited conventional constitutive equations, i.e. the exponential law which is suitable at higher stresses Eq 2 and the power law which is applicable to lower stresses (Eq 3) (Ref 34):

$$ \dot{\upvarepsilon } = A_{2} \exp (\upbeta \upsigma ) $$
(2)
$$ \dot{\upvarepsilon } = A_{1} \upsigma^{{n_{1} }} $$
(3)

where A 1, n 1, β, and A 2 are material constants. Taking natural logarithm of both sides of Eqs 2 and 3 at a constant temperature respectively yields:

$$ \upsigma = \frac{1}{\upbeta }\ln \dot{\upvarepsilon } - \frac{1}{\upbeta }\ln A_{2} $$
(4)
$$ \ln \upsigma = \frac{1}{{n_{1} }}\ln \dot{\upvarepsilon } - \frac{1}{{n_{1} }}\ln A_{1} $$
(5)

Substituting the values of the flow stress and corresponding strain rate under the strain of 0.1 into the Eqs 4 and 5 gives the relationship between the flow stress and strain rate, as shown in Fig. 4. The value of β and n 1 are obtained as 0.19298 and 6.41922 from the slope of the lines in the \( \upsigma - \ln \dot{\upvarepsilon } \) and \( \ln \upsigma - \ln \dot{\upvarepsilon } \) plots, respectively. Hence, the value of the constant α at the strain of 0.1 is calculated to be 0.03006 MPa−1.

Fig. 4
figure 4

The relationship between flow stresses and strain rates at the true strain of 0.1 according to the (a) exponential law and (b) power law

Full size image

Taking natural logarithm from both sides of Eq 1 and rearranging them the following equation is derived:

$$ \ln \left[ {\sinh (\upalpha \upsigma )} \right] = \frac{{\ln \dot{\upvarepsilon }}}{n} + \frac{Q}{nRT} - \frac{\ln A}{n} $$
(6)

At the given true strain (ε = 0.1), substituting the value of flow stress and the corresponding strain rate into Eq 6, the value of n can be derived from the average slopes of the lines in \( \ln \left[ {\sinh (\upalpha \upsigma )} \right] - \ln \dot{\upvarepsilon } \) plots (Fig. 5) at all temperature levels. Assuming α = 0.03006, the value of n is calculated to be 6.42 at the true strain of 0.1.

Fig. 5
figure 5

The relationships between \( \ln \left[ {\sinh (\upalpha \upsigma )} \right] \) and \( \ln \dot{\upvarepsilon } \) at different temperatures, assuming α = 0.03006 MPa−1

Full size image

At a constant strain rate, the partial differentiation of Eq 1 with respect to 1/T, leads to the following equation:

$$ \frac{Q}{nRT} = \left[ {\frac{{\partial \ln \left[ {\sinh (\upalpha \upsigma )} \right]}}{{\partial \left( \frac{1}{T} \right)}}} \right]_{{\dot{\upvarepsilon }}} $$
(7)

According to Eq 7, the activation energy (Q) is determined from the slope of \( \ln \left[ {\sinh (\upalpha \upsigma )} \right] \) versus 1/T (Fig. 6), through averaging the slope values at different strain rates. Considering n = 6.42 and R = 8.314 J/mol/K, the Q value found at the true strain of 0.1 is obtained as 556.48 kJ/mol. This value for the activation energy deviates largely from the activation energy for self-diffusion in austenite [285 kJ/mol (Ref 35)], and is in agreement with other results on microalloyed steels (Ref 20, 30, 32, 36). Furthermore, comparing this value with the deformation activation energy of other microalloyed steels [305 kJ/mol (Ref 36), 393 kJ/mol (Ref 20), 375 kJ/mol (Ref 32) and 386 kJ/mol (Ref 30)] and C-Mn steels [338 kJ/mol (Ref 37) and 271.93 kJ/mol (Ref 38)] indicates that the activation energy significantly increases with the addition of niobium and vanadium. The existence of these elements and their carbo-nitride precipitation significantly affects the motion of dislocations and subgrain boundaries, leading to strong retardation in the process of DRV and the initiation of DRX (Ref 39). The calculated activation energy for the investigated material is comparable to the activation energy of 316 stainless steel (Ref 34).

Fig. 6
figure 6

The relationships between \( \ln \left[ {\sinh (\upalpha \upsigma )} \right] \) and 1/T at different strain rates, assuming α = 0.03006 MPa−1

Full size image

Furthermore, the value of ln A can be derived by substituting the obtained values of the stress exponent, stress multiplier and activation energy for all tested temperatures at the true strain of 0.1 into Eq 6. The value of ln A at the true strain of 0.1 is calculated to be 45.493.

This procedure has been executed to find the material parameters at various strains in the range of 0.1-0.9 with an interval of 0.05. Figure 7 shows the variations of the material constants (α, n, Q and ln A) with true strain. The material parameters display significant dependence on the amount of strain. The value of each material parameter drops gradually to a relatively steady amount as the deformation proceeds (i.e., as true strain increases). Hence, in order to predict the flow stress more precisely and accurately, the compensation of strain should be taken into account when evaluating the constitutive equation (Ref 5). To this end, the material parameters (α, n, Q and ln A) are represented as polynomial functions of strain (Ref 40). The calculated values for each material parameter in Fig. 7 suggest that the fourth order polynomial functions (given by Eqs 8-11) represent an appropriate correlation between each material parameter and true strain. The coefficients of the fourth order polynomial functions are shown in Table 2.

Fig. 7
figure 7

The variations of material constants (a) Q, (b) α, (c) n and (d) lnA as a function of true strain using a fourth order polynomial fit for the investigated microalloyed steel

Full size image
Table 2 The coefficients of the fourth order polynomial function for α, Q, n and ln A
Full size table
$$ \upalpha = \upalpha_{0} + \upalpha_{1} \upvarepsilon + \upalpha_{2} \upvarepsilon^{2} + \upalpha_{3} \upvarepsilon^{3} + \upalpha_{4} \upvarepsilon^{4} $$
(8)
$$ Q = Q_{0} + Q_{1} \upvarepsilon + Q_{2} \upvarepsilon^{2} + Q_{3} \upvarepsilon^{3} + Q_{4} \upvarepsilon^{4} $$
(9)
$$ n = n_{0} + n_{1} \upvarepsilon + n_{2} \upvarepsilon^{2} + n_{3} \upvarepsilon^{3} + n_{4} \upvarepsilon^{4} $$
(10)
$$ \ln A = A_{0} + A_{1} \upvarepsilon + A_{2} \upvarepsilon^{2} + A_{3} \upvarepsilon^{3} + A_{4} \upvarepsilon^{4} $$
(11)

Once the material parameters with the compensation of strain are evaluated, the flow stress in the temperature range of 1000-1200 °C and under strain rates of 0.01, 0.1 and 1 s−1 can be calculated at a particular strain, using the following equation (Ref 13):

$$ \upsigma = \frac{1}{\upalpha (\upvarepsilon )}\ln \left\{ {\left( {\frac{{Z_{{\left[ {Q(\upvarepsilon )} \right]}} }}{A(\upvarepsilon )}} \right)^{{\frac{1}{n(\upvarepsilon )}}} + \sqrt {\left( {\frac{{Z_{{\left[ {Q(\upvarepsilon )} \right]}} }}{A(\upvarepsilon )}} \right)^{{\frac{2}{n(\upvarepsilon )}}} + 1} } \right\} $$
(12)

where \( Z = \dot{\upvarepsilon }\exp \left( \frac{Q}{RT} \right) \) is the Zener-Hollomon parameter and all material parameters calculated from Eqs 8-11.

Verification of the Developed Constitutive Model

To provide a better impression of the accuracy of the developed constitutive model with the compensation of strain for high temperature flow behavior of the investigated microalloyed steel, a comparison of the predicted flow stresses with the experimental ones in a wide range of strain, temperature and strain rate is carried out. Figure 8 depicts these comparisons. It can be seen that the developed constitutive model can efficiently predict the flow stress of the investigated material over the entire range of deformation conditions.

Fig. 8
figure 8

Comparison between the experimental and predicted flow stresses at different temperatures under strain rates of (a) 0.01, (b) 0.1, (c) 1 s−1

Full size image

To provide better impression of the precision of the developed constitutive model, the predicted values of flow stress are plotted against the experimental ones in Fig. 9. It can be clearly observed that most of the data points lie fairly close to the best regression line and the square correlation coefficient (R 2) for the developed constitutive model is 0.988, which indicates that a good correlation between the predicted and experimental data has been achieved.

Fig. 9
figure 9

Correlation between experimental and predicted flow stresses at the chosen deformation conditions

Full size image

To further assess the reliability of the developed constitutive model, the average absolute relative error (Δ) between the calculated flow stress and the experimental flow stress is calculated. This statistical parameter is given by:

$$ \Delta (\% ) = \frac{1}{N}\sum\limits_{i = 1}^{N} {|\frac{{\upsigma_{ \exp }^{i} - \upsigma_{\rm p}^{i} }}{{\upsigma_{ \exp }^{i} }}| \times 100} $$
(13)

where σexp is the experimental flow stress, σp is the predicted flow stress and N is the total number of data points. The calculation result shows that the absolute average error in prediction for the entire range of deformation parameters is 6.08%, which also indicates that the developed constitutive model can effectively predict the high temperature flow behavior of the investigated microalloyed steel.

Analysis of DRX Behavior

Determination of Critical Characteristics of Dynamic Recrystallization

Using the true stress-true strain data, the values of the strain hardening rate (\( \uptheta = \frac{{\rm d}\upsigma }{{\rm d}\upvarepsilon} \)) for different deformation conditions are calculated and plotted against the true stress in Fig. 10. It can be seen that θ varies with σ due to the effect of both DRV and DRX. According to the approach of Poliak and Jonas (Ref 21, 41, 42), the point on the θ-σ curves at which the work hardening rate equals zero (θ = 0) represents the peak stress (σp) and the inflection point of the curves indicates the critical stress for the initiation of DRX (σc). The value of peak (εp) and critical strains (εc) can be defined by mapping the peak and critical stresses back onto the stress-strain curves (Ref 14).

Fig. 10
figure 10

θ-σ curves of the microalloyed steel under hot deformation conditions at different temperatures and strain rates of (a) 0.01 s−1, (b) 0.1 s−1 and (c) 1 s−1

Full size image

Najafizadeh and Jonas (Ref 24) have reported that the θ-σ curve up to the peak stress can be well described by a third order polynomial equation given by:

$$ \uptheta = a\upsigma^{3} + b\upsigma^{2} + c\upsigma + d $$
(14)

where a, b, c and d are constant parameters for each deformation condition.

If one differentiates Eq 14 twice with respect to σ, the following equation is obtained:

$$ \frac{{d^{2} \uptheta }}{{d\upsigma^{2} }} = 6a\upsigma + 2b $$
(15)

Therefore, the critical stress for initiation of DRX results by setting the Eq 15 equal to zero:

$$ \upsigma_{c} = \frac{ - b}{3a} $$
(16)

The results of peak and critical stresses and strains for the temperatures of 1000, 1100 and 1200 °C under different strain rates of 0.01, 0.1 and 1 s−1 are summarized in Table 3.

Table 3 Critical and peak stresses and strains at different deformation conditions
Full size table

According to Table 3, at a constant temperature, the critical and peak stresses and strains increase with an increase of the strain rate. However, at a constant strain rate, these parameters increase as the deformation temperature decreases. The average ratio of εc/εp and σc/σp are 0.37 and 0.81, respectively. Similar results have been reported by Xu et al. (Ref 20). Comparing these values with the values reported for stainless steel [εc/εp = 0.47 and σc/σp = 0.90 (Ref 19)] indicates that DRX is likely to occur in the present microalloyed steel. This may be attributed to the effect of microalloying elements on the motion of dislocation and subgrain boundaries.

Figure 11 illustrates the dependence of critical and peak stresses and their corresponding strains on the Zener-Hollomon parameter and, also, the linear regression results. It can be seen that the critical characteristics of DRX increase with increasing Z parameter. The relationship between these parameters and deformation conditions (Z) is expressed by a power law equation (AZ m, where A is a constant depending on the chemical composition and the initial grain size of material and m is a power law exponent) (Ref 32, 43). According to the linear regression results shown in Fig. 11, the following equations hold for the investigated steel:

$$ \upsigma_{\text{p}} = 0.1826Z^{0.1507} $$
(17)
$$ \upvarepsilon_{\text{p}} = 0.0017Z^{0.1324} $$
(18)
$$ \upsigma_{\text{c}} = 0.1362Z^{0.1528} $$
(19)
$$ \upvarepsilon_{\text{c}} = 3.041Z^{0.0903} $$
(20)
Fig. 11
figure 11

The relation between (a) σc, σp and (b) εc, εp with Z parameter, assuming Q = 459.33 kJ mol−1 (picking other values for Q entails a modification of the parameters A and n in Eqs 17-20)

Full size image

The dependence of these critical characteristics of DRX on temperature and strain rate lends support to the conclusion that the deformation is controlled by a thermally activated process (Ref 32).

The Kinetics of DRX

It has been reported that the volume fraction of dynamically recrystallized grains (X) can be derived from the flow curves (Ref 19, 25, 44). In this study, due to the relatively low stacking fault energy of austenite, the effect of DRV on flow softening was not considered (Ref 19, 25). Therefore, the flow softening was directly related to the volume fraction of DRX which is calculated from Eq 21 (Ref 19). In this equation, the σp-σ term indicates the flow softening from the peak stress to σ and the σp-σs term represents the maximum achievable softening (Ref 19). It should be mentioned that in this model the initiation of DRX was considered to occur at the peak stress (Ref 19). Moreover, the DRX time (t) from peak strain (εp) to strain of ε may be determined by Eq 22 (Ref 19).

$$ X = \frac{{\upsigma_{\text{p}} - \upsigma }}{{\upsigma_{\text{p}} - \upsigma_{\text{s}} }} $$
(21)
$$ t = \frac{{\upvarepsilon - \upvarepsilon_{\text{p}} }}{{\dot{\upvarepsilon }}} $$
(22)

Figure 12 shows the kinetics of DRX at different deformation conditions, using Eqs 21 and 22. These figures show that the DRX volume fraction (X) increases with strain and recrystallization time until a fully recrystallized microstructure is achieved by continuous nucleation and grain boundary migration (Ref 45). According to Fig. 12a, by increasing strain rate at the constant temperature of 1100 °C or decreasing deformation temperature under constant strain rate of 0.01 s−1, the recrystallization curve is shifted to the higher strains. Moreover, Fig. 12b illustrates this shift in terms of recrystallization times, which clearly demonstrates that the kinetics of DRX increases with increasing deformation temperature or strain rate.

Fig. 12
figure 12

Effect of deformation temperature and strain rate on the kinetics of DRX, (a) recrystallized volume fraction (X) versus strain, (b) X versus time

Full size image

Conclusions

In this study, the hot deformation behavior of a medium carbon microalloyed steel has been investigated using hot compression test in the temperature range of 1000-1200 °C and under different strain rates of 0.01, 0.1 and 1 s−1. The key results of this investigation are as follows:

  1. 1.

    The flow stress is strongly dependent on deformation temperature and strain rate and is seen to increase with decreasing temperature and increasing strain rate. Moreover, the investigated microalloyed steel shows cyclic flow behavior at the deformation temperatures of 1100, 1150 and 1200 °C under the strain rate of 0.01 s−1, associated with grain coarsening during DRX. Furthermore, DRX is found to be the main flow softening mechanism in almost all deformation conditions.

  2. 2.

    The material parameters in the hyperbolic sine constitutive equation (Q, n, A, and α) are found to be strain dependent and the functional relations between material constants and strain are identified by a fourth order polynomial fit.

  3. 3.

    The constitutive model incorporating the effect of strain achieves a good match to the experimentally recorded flow stress of the investigated alloy. The accuracy of the proposed model is evaluated by applying the absolute average error method with an error of 6.08%, indicating a good agreement between predicted and experimental flow stresses.

  4. 4.

    The critical characteristics of DRX (σp, εp, σc, εc) at different deformation conditions are extracted from the stress-strain curves, using the strain hardening parameter. Also, the relationships between these parameters and the Zener-Hollomon (Z) are expressed as power law equations.

  5. 5.

    By increasing the strain rate at a constant temperature or decreasing deformation temperature under a constant strain rate, the recrystallization curve shifts to higher strains. However, the kinetics of DRX increases with increasing deformation temperature or strain rate.