Clustering functional data via variational inference

Abstract

Among different functional data analyses, clustering analysis aims to determine underlying groups of curves in the dataset when there is no information on the group membership of each curve. In this work, we develop a novel variational Bayes (VB) algorithm for clustering and smoothing functional data simultaneously via a B-spline regression mixture model with random intercepts. We employ the deviance information criterion to select the best number of clusters. The proposed VB algorithm is evaluated and compared with other methods (k-means, functional k-means and two other model-based methods) via a simulation study under various scenarios. We apply our proposed methodology to two publicly available datasets. We demonstrate that the proposed VB algorithm achieves satisfactory clustering performance in both simulation and real data analyses.

1 Introduction

Functional data analysis (FDA), term first coined by Ramsay and Dalzell (1991), deals with the analysis of data that are defined on some continuum such as time. Theoretically, data are in the form of functions, but in practice they are observed as a series of discrete points representing an underlying curve. Ramsay and Silverman (2005) establish a foundation for FDA on topics including smoothing functional data, functional principal components analysis and functional linear models. Ramsay et al. (2009) provide a guide for analyzing functional data in R and Matlab using publicly available datasets. Wang et al. (2016) present a comprehensive review of FDA, in which clustering and classification methods for functional data are also discussed. Functional data analysis has been applied to various research areas such as energy consumption (Lenzi et al. 2017; De Souza et al. 2017; Franco et al. 2023), rainfall data visualization (Hael et al. 2020), income distribution (Hu et al. 2020), spectroscopy (Dias et al. 2015; Yang et al. 2021; Frizzarin et al. 2021), and Covid-19 pandemic (Boschi et al. 2021; Souza et al. 2023; Collazos et al. 2023), to mention a few.

Cluster analysis of functional data aims to determine underlying groups in a set of observed curves when there is no information on the group label of each curve. As described in Jacques and Preda (2014), there are three main types of methods used for functional data clustering: dimension reduction-based (or filtering) methods, distance-based methods, and model-based methods. Functional data generally belongs to the infinite-dimensional space, making those clustering methods for finite-dimensional data ineffective. Therefore, dimension reduction-based methods have been proposed to solve this problem. Before clustering, a dimension reduction step (also called filtering in James and Sugar, 2003) is carried out by the techniques including spline basis function expansion (Tarpey and Kinateder 2003) and functional principal component analysis (Jones and Rice 1992). Clustering is then performed using the basis expansion coefficients or the principal component scores, resulting in a two-stage clustering procedure. Distance-based methods are the most well-known and popular approaches for clustering functional data since no parametric assumptions are necessary for these algorithms. Nonparametric clustering techniques, including k-means clustering (Hartigan and Wong 1979) and hierarchical clustering (Ward 1963), are usually applied using specific distances or dissimilarities between curves (Delaigle et al. 2019; Martino et al. 2019; Zambom et al. 2019; Li and Ma 2020). It is important to note that distance-based methods are sometimes equivalent to dimension reduction-based methods if, for example, distances are computed using the basis expansion coefficients. Another widely-used approach is model-based clustering, where functional data are assumed to arise from a mixture of underlying probability distributions. For example, in Bayesian hierarchical clustering, a common methodology is to assume that the set of coefficients in the basis expansion representing functional data follow a mixture of Gaussian distributions (Wang et al. 2016).

Chamroukhi and Nguyen (2019) recently provided a comprehensive review for model-based clustering of functional data. A common model-based approach is to represent functional data as a linear combination of basis functions (e.g., B-splines) and consider a finite regression mixture model (Grün 2019) with the matrix of basis function evaluations as the design matrix and a set of basis expansion coefficients for each mixture component. The estimation and inference of the mixture parameters as well as the regression (or basis expansion) coefficients are usually conducted via the Expectation-Maximization (EM) algorithm (Samé et al. 2011; Jacques and Preda 2013; Giacofci et al. 2013; Chamroukhi 2016a; Grün 2019) or Markov Chain Monte Carlo (MCMC) sampling techniques (Ray and Mallick 2006; Fruhwirth-Schnatter et al. 2019). An alternative approach to EM and MCMC is the use of variational inference techniques.

Bayesian variational inference has found versatile applications within the field of FDA. Variational Bayes for fast approximate inference was applied in functional regression analysis by Goldsmith et al. (2011). Beyond functional regression, another pivotal facet of FDA lies in functional data registration, with a growing interest in the joint clustering and registration of functional data (Zhang and Telesca 2014). A novel adapted variational Bayes algorithm for smoothing and registration of functional data simultaneously via Gaussian processes was proposed by Earls and Hooker (2017). Nguyen and Gelfand (2011) considered a random allocation process, namely the Dirichlet labelling process, to cluster functional data and inferred model parameters by Gibbs sampling and variational Bayes. In a recent development, Rigon (2023) extended the work of Blei and Jordan (2006) and proposed an enriched Dirichlet mixture model for functional clustering via a variational Bayes algorithm. Rigon (2023) considered a Bayesian functional mixture model without random effects and introduced a functional Dirichlet multinomial process to allow the estimation of the number of clusters.

In this paper, we develop a novel variational Bayes algorithm for clustering functional data via a regression mixture model. In contrast to Rigon (2023), we consider a regression mixture model with random intercepts and take on a two-fold scheme for choosing the best number of clusters using the deviance information criterion (Spiegelhalter et al. 2002). We model the raw data, simultaneously obtaining clustering assignments and cluster-specific smooth mean curves. We compare the posterior estimation results from our proposed VB with the ones from MCMC. Our proposed method is implemented in R, and codes are available at https://github.com/chengqianxian/funclustVI.

The remainder of the paper is organized as follows. Section 2 presents an overview of variational inference, our two model settings and proposed algorithms. In Sect. 3, we conduct simulation studies to assess the performance of our methods under various scenarios. In Sect. 4, we apply our proposed methodology to real datasets. A conclusion of our study and a discussion on the proposed method are provided in Sect. 5.

2 Methodology

2.1 Overview of variational inference

Variational inference (VI) is a method from machine learning that approximates the posterior density in a Bayesian model through optimization (Jordan et al. 1999; Wainwright et al. 2008). Blei et al. (2017) provide an interesting review of VI from a statistical perspective, including some guidance on when to use MCMC or VI. For example, one may apply VI to large datasets and scenarios where the interest is to develop probabilistic models. In contrast, one may apply MCMC to small datasets for more precise samples but with a higher computational cost. In Bayesian inference, our goal is to find the posterior density, denoted by $p(\cdot \vert y)$, where y corresponds to the observed data. One can apply Bayes’ theorem to find the posterior, but this might not be easy if there are many parameters and non-conjugate prior distributions. Therefore, one can aim to find an approximation to the posterior. To be specific, one wants to find $q^*$ coming from a family of possible densities Q to approximate $p(\cdot \vert y)$, which can be solved in terms of an optimization problem with criterion f as follows:

$$\begin{aligned} q^* = \underset{q \in Q}{\textrm{argmin}}\,f(q(\cdot ), p(\cdot \vert y)). \end{aligned}$$

The criterion f measures the closeness between the possible densities q in the family Q and the exact posterior density p. When we consider the Kullback–Leibler (KL) divergence (Kullback and Leibler 1951) as criterion f, i.e.,

$$\begin{aligned} q^* = \underset{q \in Q}{\textrm{argmin}}\,\text{ KL }(q(\cdot ) \Vert p(\cdot \vert y)), \end{aligned}$$

(1)

this optimization-based technique to approximate the posterior density is called Variational Bayes (VB). Jordan et al. (1999) and Blei et al. (2017) show that minimizing the KL divergence is equivalent to maximizing the so-called evidence lower bound (ELBO). Let $\theta$ be a set of latent model variables, the KL divergence is defined as

$$\begin{aligned} \text{ KL }(q(\cdot ) \Vert p(\cdot \vert y)):= \int q(\theta )\log \frac{q(\theta )}{p(\theta \vert y)}d\theta , \end{aligned}$$

and it can be shown that

$$\begin{aligned} \int q(\theta )\log \frac{q(\theta )}{p(\theta \vert y)}d\theta =\log p(y)-\int q(\theta )\log \frac{p(\theta , y)}{q(\theta )}d\theta \end{aligned}$$

where the last term is the ELBO. Since $\log p(y)$ is a constant with respect to $q(\theta )$, this changes the problem in (1) to

$$\begin{aligned} q^* = \underset{q \in Q}{\textrm{argmax}}\,\text{ ELBO }(q). \end{aligned}$$

(2)

We, therefore, derive a VB algorithm for clustering functional data. We consider the mean-field variational family in which the latent variables are mutually independent, and a distinct factor governs each of them in the variational density. Finally, we apply the coordinate ascent variational inference algorithm (Bishop 2006) to solve the optimization problem in (2).

2.2 Assumptions and model settings

Let ${\textbf{Y}}_i$, $\{i=1,\ldots ,N\}$, denote the observed data from N curves, and for each curve i there are $n_i$ evaluation points, $t_{i1},..., t_{in_i}$, so that ${\textbf{Y}}_i =(Y_i(t_{i1}),\ldots ,Y_i(t_{in_i}))^T$. Let $Z_i$ be a hidden variable taking values in $\{ 1,\ldots ,K\}$ that determines which cluster ${\textbf{Y}}_i$ belongs to. We assume $Z_1,\ldots ,Z_N$ are independent and identically distributed with $P(Z_i=k) = \pi _k, \, k=1,...,K$, and $\sum _{k=1}^K \pi _k =1$. For the ith curve from cluster k, there is a smooth function $f_k$ evaluated at $\textbf{t}_i =(t_{i1},..., t_{in_i})^T$ so that $f_k(\textbf{t}_i) = (f_k(t_{i1}),\ldots ,f_k(t_{in_i}))^T$. Given that $Z_i=k$, we consider two different models for ${\textbf{Y}}_i$ based on the correlation structure of the errors. In Model 1, described in Sect. 2.2.1, we assume independent errors, and in Model 2, described in Sect. 2.2.2, we add a random intercept to induce a correlation between observations within each curve.

2.2.1 Model 1

Let us assume that

$$\begin{aligned} {\textbf{Y}}_i\, \vert \,(Z_i = k) = f_k(\textbf{t}_i) + \sigma _k{\varvec{\epsilon _i}} \end{aligned}$$

(3)

with conditionally independent errors ${\varvec{\epsilon }}_1,..., {\varvec{\epsilon }}_N,$ where ${\varvec{\epsilon }}_i=(\epsilon _{i1},..., \epsilon _{in_i})$ and ${\varvec{\epsilon _i}} \sim MVN (\textbf{0}, \mathrm{{I}}_{n_i}), i=1,...,N$, where $\mathrm{{I}}_{n_i}$ is an identity matrix of size $n_i$ and MVN represents the multivariate normal distribution. The functions $f_1,\ldots ,f_K$ can be written as a linear combination of M known B-spline basis functions, that is, $f_k(t_{ij}) = \sum _{m=1}^M B_m(t_{ij})\phi _{km}, \; j=1,..., n_i$, such that $f_k(\textbf{t}_i) = \textbf{B}_{i({n_i}\times M)}{\varvec{\phi }}_{k(M\times 1)}, i=1,..., N, k=1,...,K$, $\textbf{B}_i$ is an $n_i\times M$ matrix for the ith curve whose each entry (j, m) is the mth basis function evaluated at $t_{ij}$, $B_m(t_{ij})$, and ${\varvec{\phi }}_{k}$ is the basis coefficient vector for cluster k. Therefore,

$$\begin{aligned} {\textbf{Y}}_i \, \vert \,(Z_i =k) \sim MVN (\textbf{B}_i{\varvec{\phi }}_{k}, \sigma _k^2 \mathrm{{I}}_{n_i}), \; i=1,...,N, \;k=1,...,K. \end{aligned}$$

The proposed model is within the framework of a mixture of linear models, also known as the finite regression mixture model (Chamroukhi and Nguyen 2019). The finite regression mixture model offers a statistical framework for characterizing complex data from various unknown classes of conditional probability distributions (Peel and MacLahlan 2000; Melnykov and Maitra 2010; Chamroukhi 2016a; Grün 2019; Fruhwirth-Schnatter et al. 2019; McLachlan et al. 2019; Rigon 2023). In our model, we specifically consider Gaussian regression mixtures to deal with functional data that originate from a finite number of groups and are represented through a linear combination of B-spline basis functions plus some Gaussian random noise (Chamroukhi 2016b). Our model aligns with the classical finite Gaussian regression mixture model of order K, which can be expressed as follows:

$$\begin{aligned} f({\textbf{Y}}_i\vert \textbf{B}_i;{\varvec{\phi }}_{1},..., {\varvec{\phi }}_{K}, \sigma _{1}^2,..., \sigma _{K}^2)=\sum _{k=1}^K \pi _k \;g ({\textbf{Y}}_i; \textbf{B}_i{\varvec{\phi }}_{k}, \sigma _k^2 \mathrm{{I}}_{n_i}) \end{aligned}$$

where g is the density function of a $MVN(\textbf{B}_i{\varvec{\phi }}_{k}, \sigma _k^2 \mathrm{{I}}_{n_i})$.

In our proposed models, we employ B-spline basis functions to represent and smooth functional data. However, it is worth noting that alternative basis systems, such as the Fourier bases, wavelets, and polynomial bases can also be considered for this purpose (Ramsay and Silverman 2005). As discussed in Chamroukhi and Nguyen (2019), the B-spline basis system offers greater flexibility, allowing researchers to tailor their choice of B-spline order and the number of knots to suit their specific needs. For smoothing functional data, cubic B-splines, corresponding to an order of four, are sufficient and can provide satisfactory performance (Chamroukhi and Nguyen 2019). As in previous studies of functional data, we use cubic B-splines with equally spaced knots and assume that the number of basis functions M is predefined and known (Dias et al. 2009, 2015; Lenzi et al. 2017; Franco et al. 2023).

Let $\textbf{Z}=(Z_1,\ldots ,Z_N)^T$, ${\varvec{\phi }}=\{{\varvec{\phi }}_1,\ldots ,{\varvec{\phi }}_K\}$, ${\varvec{\pi }} = (\pi _1,\ldots ,\pi _K)^T$ and ${\varvec{\tau }} = (\tau _1,\ldots ,\tau _K)^T$, where $\tau _k = 1/\sigma ^2_k$ is the precision parameter. We take on a Bayesian approach to infer ${\varvec{Z}}$, ${\varvec{\phi }}$, ${\varvec{\pi }}$ and ${\varvec{\tau }}$, and assume the following marginal prior distributions for parameters in Model 1:

• ${\varvec{\pi }} \sim \text{ Dirichlet }(\textbf{d}^0)$ where $\textbf{d}^0$ is the parameter vector for a Dirichlet distribution;

• $Z_i\vert {\varvec{\pi }} \sim \text{ Categorical }({\varvec{\pi }})$;

• ${\varvec{\phi }}_k \sim MVN(\textbf{m}_k^0,s^0\textbf{I})$ with precision $v^0 = 1/s^0$ and $\textbf{I}$ an $M \times M$ identity matrix;

• $\tau _k = 1/\sigma ^2_k \sim \text{ Gamma }(a^0,r^0), \; k=1,...,K$.

We develop a novel VB algorithm which, for given data, approximates the posterior distribution by finding the variational distribution (VD), $q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }})$, with smallest KL divergence to the posterior distribution $p(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}\vert {\textbf{Y}})$. Minimizing the KL divergence is equivalent to maximizing the ELBO given by

$$\begin{aligned} \text{ ELBO }(q) = {{\mathbb {E}}}\left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] - {{\mathbb {E}}}\left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] . \end{aligned}$$

(4)

where $\log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }})$ is the complete data log-likelihood.

2.2.2 Model 2

We extend the model in Sect. 2.2.1 by adding a curve-specific random intercept $a_i$ which induces correlation among observations within each curve. The model now becomes:

$$\begin{aligned} Y_{ij}\, \vert \,(Z_i = k)=a_i+f_k(t_{ij})+\sigma _k\epsilon _{ij} \end{aligned}$$

(5)

where $\epsilon _{ij}\sim N(0, 1)$ and $a_i\sim N(0, \sigma _a^2)$ with $a_i$ and $\epsilon _{ij}$ independent for all i and j. We can write Model 2 in a vector form as

$$\begin{aligned} {\textbf{Y}}_i\, \vert \,(Z_i = k) = a_i\textbf{1}_{n_i} + f_k(\textbf{t}_i) + \sigma _k{\varvec{\epsilon _i}},\, i=1,2,...,N, \end{aligned}$$

in which $\textbf{1}_{n_i}$ is a column vector of length $n_i$ with all elements equal to 1, and further assume that ${\varvec{\epsilon _i}}\sim MVN(\textbf{0}, \mathrm{{I}}_{n_i})$ and $a_i\sim N(0, \sigma _a^2)$. This model can be rewritten as a two-step model:

$$\begin{aligned} {\textbf{Y}}_i\, \vert \,(Z_i = k, a_i)\sim MVN (\textbf{B}_i{\varvec{\phi }}_{k} + a_i\textbf{1}_{n_i}, \sigma _k^2 \mathrm{{I}}_{n_i}) \end{aligned}$$

and $a_i\sim N(0, \sigma _a^2), i=1,2,...,N$. Let $\textbf{a}=(a_1,\ldots ,a_N)^T$ and $\tau _a=1/\sigma ^2_a$. We assume the following marginal prior distributions for parameters in Model 2:

• ${\varvec{\pi }} \sim \text{ Dirichlet }(\textbf{d}^0)$;

• $Z_i\vert {\varvec{\pi }} \sim \text{ Categorical }({\varvec{\pi }})$;

• ${\varvec{\phi }}_k \sim MVN(\textbf{m}_k^0,s^0\textbf{I})$ with precision $v^0 = 1/s^0$;

• $\tau _k = 1/\sigma ^2_k \sim \text{ Gamma }(b^0,r^0), \; k=1,...,K$;

• $\tau _a = 1/\sigma ^2_a \sim \text{ Gamma }(\alpha ^0,\beta ^0)$;

• $a_i \vert \tau _a \sim N(0, \sigma _a^2)$ with $\tau _a=1/\sigma ^2_a$.

As in Model 1, we develop a VB algorithm to infer ${\varvec{Z}}$, ${\varvec{\phi }}$, ${\varvec{\pi }}$, ${\varvec{\tau }}$, $\textbf{a}$ and $\tau _a$. The ELBO under Model 2 is given by

$$\begin{aligned} \text{ ELBO }(q) = {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a},\tau _a)\right] - {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }},\textbf{a},\tau _a) \right] . \nonumber \end{aligned}$$

2.3 Steps of the VB algorithm

This section describes the main steps of the VB algorithm under Model 2 for inferring ${\varvec{Z}}$, ${\varvec{\phi }}$, ${\varvec{\pi }}$, ${\varvec{\tau }}$, $\textbf{a}$ and $\tau _a$. The proposed VB is summarized in Algorithm 1. The VB algorithm’s main steps and the ELBO calculation for Model 1 can be found in Appendix A.

First, we assume that the variational distribution belongs to the mean-field variational family, where ${\varvec{Z}}$, ${\varvec{\phi }}$, ${\varvec{\pi }}$ ${\varvec{\tau }}$, $\textbf{a}$ and $\tau _a$ are mutually independent and each governed by a distinct factor in the variational density, that is:

$$\begin{aligned} q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a)= & {} \prod _{i=1}^N q(Z_i) \times \prod _{k=1}^K q({\varvec{\phi }}_k) \times \prod _{k=1}^K q(\tau _k) \nonumber \\{} & {} \times q({\varvec{\pi }}) \times \prod _{i=1}^N q(a_i) \times q(\tau _a). \end{aligned}$$

(6)

We then derive a coordinate ascent algorithm to obtain the VD (Jordan et al. 1999; Blei et al. 2017). That is, we derive an update equation for each term in the factorization (6) by calculating the expectation of $\log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a)$ (the joint distribution of the observed data $\textbf{Y}$, hidden variables $\textbf{Z}$ and parameters ${\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a$, which is also called complete-data log-likelihood) over the VD of all random variables except the one of interest, where

$$\begin{aligned} \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a)= & {} \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}) \; + \; \log p(\textbf{Z} \vert {\varvec{\pi }}) \nonumber \\{} & {} +\log p({\varvec{\phi }}) + \log p({\varvec{\tau }}) \;+\; \log p({\varvec{\pi }}) \; \nonumber \\{} & {} +\log p(\textbf{a} \vert \tau _a) \; + \; \log p(\tau _a). \end{aligned}$$

(7)

So, for example, the optimal update equation for $q({\varvec{\pi }})$, $q^*({\varvec{\pi }})$, is given by calculating

$$\begin{aligned} \log q^*({\varvec{\pi }}) = {{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a) \right) \;+\; \text{ constant }, \end{aligned}$$

where $-{\varvec{\pi }}$ indicates that the expectation is taken with respect to the VD of all other latent variables but ${\varvec{\pi }}$, i.e., $\textbf{Z},{\varvec{\phi }}$, ${\varvec{\tau }}$, $\textbf{a}$ and $\tau _a$. In what follows we derive the update equation for each component in our model. For convenience, we use $\overset{\mathrm{\tiny {+}}}{\approx }$ to denote equality up to a constant additive factor.

2.3.1 VB update equations

(i) Update equation for $q({\varvec{\pi }})$

Since only the second term, $\log p(\textbf{Z} \vert {\varvec{\pi }})$, and the fifth term, $\log p({\varvec{\pi }})$, in (7) depend on ${\varvec{\pi }}$, the update equation $q^*({\varvec{\pi }})$ can be derived as follows.

$$\begin{aligned}{} & {} {\log q^*({\varvec{\pi }})} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a) \right) \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p(\textbf{Z}\vert {\varvec{\pi }}) \right) \; +\; {{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p({\varvec{\pi }})\right) \\{} & {} \quad = {{\mathbb {E}}}_{-{\varvec{\pi }}} \left[ \sum _{i=1}^N \sum _{k=1}^{K} \mathrm{{I}}(Z_i =k) \log \pi _k \right] + \log p({\varvec{\pi }}) \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^{K} \log \pi _k \left[ \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) \right] + \sum _{k=1}^{K} [d^0_k -1 ]\log \pi _k \\{} & {} \quad = \sum _{k=1}^{K} \log \pi _k \left[ \left( \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) + d^0_k \right) -1 \right] . \end{aligned}$$

Therefore, $q^*({\varvec{\pi }})$ is a Dirichlet distribution with parameters $\textbf{d}^*=(d_1^*,\ldots ,d_K^*)$, where

$$\begin{aligned} d^{*}_{k}= d^0_k + \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) . \end{aligned}$$

(8)

(ii) Update equation for $q(Z_i)$

$$\begin{aligned} \log q^*(Z_i){} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-Z_i} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a) \right) \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-Z_i} \left( \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})\right) \; +\; {{\mathbb {E}}}_{-Z_i} \left( \log p(\textbf{Z} \vert {\varvec{\pi }})\right) \end{aligned}$$

(9)

Note that we can write $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})$ and $\log p(\textbf{Z} \vert {\varvec{\pi }})$ into two parts, one that depends on $Z_i$ and one that does not, that is:

$$\begin{aligned} \log p(\textbf{Y}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})= & {} \sum _{k=1}^K \mathrm{{I}}(Z_i = k) \log p({\textbf{Y}}_i \vert Z_i =k, {\varvec{\phi }}_k,\tau _k, a_i) \nonumber \\{} & {} +\, \sum _{l:l\ne i} \sum _{k=1}^K \mathrm{{I}}(Z_l=k) \log p({\textbf{Y}}_l \vert Z_l=k,{\varvec{\phi }}_k,\tau _k, a_l) \nonumber \\ \log p(\textbf{Z} \vert {\varvec{\pi }})= & {} \sum _{k=1}^K \mathrm{{I}}(Z_i=k) \log \pi _k + \sum _{l:l\ne i} \sum _{k=1}^K \mathrm{{I}}(Z_l = k) \log \pi _k. \nonumber \end{aligned}$$

Now when taking the expectation in (9), the parts that do not depend on $Z_i$ in $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }},\textbf{a})$ and $\log p(\textbf{Z} \vert {\varvec{\pi }})$ will be added as a constant in the expectation. So, we obtain

$$\begin{aligned}{} & {} \log q^*(Z_i) \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^K \mathrm{{I}}(Z_i =k)\left\{ \frac{n_i}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k)\right. \nonumber \\{} & {} \qquad -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k){{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)\cdot q^*(a_i)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \nonumber \\{} & {} \qquad \left. \, + \,{{\mathbb {E}}}_{q^*({\varvec{\pi }})} (\log \pi _k) \right\} \nonumber \end{aligned}$$

Therefore, $q^*(Z_i)$ is a categorical distribution with parameters

$$\begin{aligned} p^*_{ik} = \frac{e^{\alpha _{ik}}}{\sum _{k=1}^Ke^{\alpha _{ik}}}, \end{aligned}$$

(10)

where

$$\begin{aligned} \alpha _{ik}= & {} \frac{n_i}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k) \nonumber \\{} & {} -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k){{\mathbb {E}}}_{q^*({\varvec{\phi }}_k) q^*(a_i)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \nonumber \\{} & {} +\, {{\mathbb {E}}}_{q^*({\varvec{\pi }})} (\log \pi _k). \nonumber \end{aligned}$$

Note that all expectations involved in the VB update equations are calculated in Sect. 2.3.2.

(iii) Update equation for $q({\varvec{\phi }}_k)$

Only the first term, $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})$, and the third term, $\log p({\varvec{\phi }})$, in (7) depend on ${\varvec{\phi }}_k$. In addition, similarly to the previous case for $q^*(Z_i)$, we can write $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})$ and $\log p({\varvec{\phi }})$ in two parts, one that depends on ${\varvec{\phi }}_k$ and the other that does not. Therefore, we obtain

$$\begin{aligned} \log q^*({\varvec{\phi }}_k){} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\phi }}_k} \left( \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})\right) +{{\mathbb {E}}}_{-{\varvec{\phi }}_k}\log p({\varvec{\phi }}) \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k) \sum _{i=1}^N \frac{n_i}{2}{{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] \nonumber \\{} & {} \quad \; - \; \frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N \left\{ {{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] \right. \nonumber \\{} & {} \quad \left. \times \,{{\mathbb {E}}}_{q^*(a_i)}[({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})]\right\} \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \quad + \frac{M}{2} \log v^0 \; - \;\frac{1}{2}v^0 ({\varvec{\phi }}_k -\textbf{m}_k^0)^T({\varvec{\phi }}_k -\textbf{m}_k^0) \end{aligned}$$

(12)

All expectations are defined in Sect. 2.3.2, but note that, for example, ${{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] = p^*_{ik}$ and

$$\begin{aligned}{} & {} {{{\mathbb {E}}}_{q^*(a_i)}[({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})]} \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k-\mu _{a_i}^*\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-\mu _{a_i}^*\textbf{1}_{n_i}) \nonumber \end{aligned}$$

where $\mu _{a_i}^*$ is the posterior mean of $q^*(a_i)$ which is derived later. We focus on the quadratic forms that appear in (11) and (12). Let ${\textbf{Y}}_i^*={\textbf{Y}}_i-\mu _{a_i}^*\textbf{1}_{n_i}$, we can write:

$$\begin{aligned}{} & {} \log q^*({\varvec{\phi }}_k) \overset{\mathrm{\tiny {+}}}{\approx }-\frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} ({\textbf{Y}}_i^* \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i^* - \textbf{B}_i{\varvec{\phi }}_k) \nonumber \\{} & {} \qquad - \;\frac{1}{2}v^0 ({\varvec{\phi }}_k -\textbf{m}_k^0)^T({\varvec{\phi }}_k -\textbf{m}_k^0) \nonumber \\{} & {} \quad = - \; \frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik}\left[ {\textbf{Y}}_i^{*T} {\textbf{Y}}_i^* - 2{\textbf{Y}}_i^{*T}\textbf{B}_i{\varvec{\phi }}_k + {\varvec{\phi }}_k^T\textbf{B}_i^T\textbf{B}_i{\varvec{\phi }}_k \right] \nonumber \\{} & {} \qquad \; -\frac{1}{2}v^0\left[ {\varvec{\phi }}^T_k{\varvec{\phi }}_k - 2(\textbf{m}_k^0)^T{\varvec{\phi }}_k + (\textbf{m}_k^0)^T\textbf{m}_k^0 \right] \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }-\frac{1}{2} {\varvec{\phi }}_k^T \left[ v^0\textbf{I} + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} \textbf{B}_i^T\textbf{B}_i \right] {\varvec{\phi }}_k \nonumber \\{} & {} \qquad + \left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^{*T} \textbf{B}_i \right] {\varvec{\phi }}_k. \end{aligned}$$

(13)

Now let

$$\begin{aligned} \mathbf {\Sigma }^*_k = \left[ v^0\textbf{I} + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} \textbf{B}_i^T\textbf{B}_i \right] ^{-1}. \end{aligned}$$

(14)

We can then rewrite (13) as

$$\begin{aligned} -\frac{1}{2} {\varvec{\phi }}_k^T \mathbf {\Sigma }^{*-1}_k {\varvec{\phi }}_k -\frac{1}{2}(-2)\left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^{*T} \textbf{B}_i \right] \mathbf {\Sigma }^*_k\mathbf {\Sigma }^{*-1}_k {\varvec{\phi }}_k. \end{aligned}$$

Therefore, $q^*({\varvec{\phi }}_k)$ is $MVN(\textbf{m}^*_k,\mathbf {\Sigma }^*_k)$ with $\mathbf {\Sigma }^*_k$ as in (14) and mean vector

$$\begin{aligned} \textbf{m}^*_k = \left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^{*T} \textbf{B}_i \right] \mathbf {\Sigma }^*_k. \end{aligned}$$

(15)

(iv) Update equation for $q(\tau _k)$

Similarly to the calculations in iii) we can write

$$\begin{aligned}{} & {} \log q^*(\tau _k) \overset{\mathrm{\tiny {+}}}{\approx }\log \tau _k \sum _{i=1}^N \frac{{n_i}}{2}p^*_{ik} \nonumber \\{} & {} \qquad -\frac{1}{2}\tau _k\sum _{i=1}^N p^*_{ik}{{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)\cdot q^*(a_i)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \nonumber \\{} & {} \qquad + \,(b^0 -1)\log \tau _k - r^0\tau _k \nonumber \end{aligned}$$

Therefore, $q^*(\tau _k)$ is a Gamma distribution with parameters

$$\begin{aligned} A^*_k = b^0 + \sum _{i=1}^N \frac{{n_i}}{2}p^*_{ik} \end{aligned}$$

(16)

and

$$\begin{aligned} R^*_{k}= & {} r^0 + \frac{1}{2} \sum _{i=1}^N\Big \{ p^*_{ik} {{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)\cdot q^*(a_i)}\Big [ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T\nonumber \\{} & {} \times ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \Big ]\Big \}. \end{aligned}$$

(17)

(v) Update equation for $q(a_i)$

$$\begin{aligned} \log q^*(a_i){} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-a_i} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}, \tau _a) \right) \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-a_i} \left( \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a})\right) \; +\; {{\mathbb {E}}}_{-a_i} \left( \log p(\textbf{a} \vert \tau _a)\right) \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-a_i}\left[ \sum _{k=1}^K \mathrm{{I}}(Z_i = k) \log p({\textbf{Y}}_i \vert Z_i =k, {\varvec{\phi }}_k,\tau _k, a_i)\right] \nonumber \\{} & {} \quad + \,{{\mathbb {E}}}_{-a_i}\left[ \sum _{k=1}^K \mathrm{{I}}(Z_i = k) \log p(a_i \vert \tau _a)\right] \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^K p^*_{ik} \left\{ \frac{{n_i}}{2}{{\mathbb {E}}}_{q^*(\tau _k)}\log \tau _k \right. \nonumber \\{} & {} \quad -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k {{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \nonumber \\{} & {} \quad \left. -\frac{1}{2}a_i^2{{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \right\} \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^K p^*_{ik} \left\{ -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k \left[ ({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i}) \right] \right. \nonumber \\{} & {} \quad \left. -\frac{1}{2}a_i^2{{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \right\} \nonumber \end{aligned}$$

Let ${\textbf{Y}}_{ik}^*={\textbf{Y}}_i-\textbf{B}_i\textbf{m}^*_k$, then

$$\begin{aligned}{} & {} \log q^*(a_i) \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^K p^*_{ik} \left\{ -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k \left[ ({\textbf{Y}}_{ik}^*-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_{ik}^*-a_i\textbf{1}_{n_i}) \right] -\frac{1}{2}a_i^2{{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \right\} \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }-\frac{{n_i}}{2} a_i^2 \sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k + a_i \sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k \textbf{1}_{n_i}^T{\textbf{Y}}_{ik}^* -\frac{1}{2}a_i^2 {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \nonumber \\{} & {} \quad = -\frac{1}{2}a_i^2 \left[ {n_i}\sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k + {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a\right] + a_i \sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k \textbf{1}_{n_i}^T{\textbf{Y}}_{ik}^* \nonumber \end{aligned}$$

Let

$$\begin{aligned} {\sigma }^{2*}_{a_i} = \left( {n_i}\sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k + {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a\right) ^{-1} \end{aligned}$$

(18)

and

$$\begin{aligned} {\mu }^{*}_{a_i} = {\sigma }^{2*}_{a_i}\sum _{k=1}^K p^*_{ik}{{\mathbb {E}}}_{q^*(\tau _k)}\tau _k \textbf{1}_{n_i}^T {\textbf{Y}}_{ik}^* \end{aligned}$$

(19)

Then $q^*(a_i)$ is $N({\mu }^{*}_{a_i},{\sigma }^{*2}_{a_i})$.

(vi) Update equation for $q(\tau _a)$

$$\begin{aligned}{} & {} \log q^*(\tau _a) \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-\tau _a} \left( \log p(\textbf{a} \vert \tau _a) + \log p(\tau _a)\right) \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-\tau _a}\left( \sum _{i=1}^N \log p(a_i \vert \tau _a)\right) + (\alpha ^0-1)\log \tau _a - \beta ^0 \tau _a \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }\frac{N}{2} \log \tau _a -\frac{1}{2}\tau _a \sum _{i=1}^N {{\mathbb {E}}}_{q^*(a_i)} a_i^2 + (\alpha ^0-1)\log \tau _a - \beta ^0 \tau _a \nonumber \\{} & {} \quad = \left( \alpha ^0+\frac{N}{2} -1\right) \log \tau _a -\left( \beta ^0 +\frac{1}{2} \sum _{i=1}^N {{\mathbb {E}}}_{q^*(a_i)} a_i^2 \right) \tau _a \nonumber \end{aligned}$$

Let

$$\begin{aligned} \alpha ^* = \alpha ^0+\frac{N}{2} \end{aligned}$$

and

$$\begin{aligned} \beta ^*=\beta ^0 +\frac{1}{2}\sum _{i=1}^N {{\mathbb {E}}}_{q^*(a_i)} a_i^2 \end{aligned}$$

(20)

$q^*(\tau _a)$ is Gamma($\alpha ^*, \beta ^*$).

2.3.2 Expectations

In this section, we calculate the expectations in the update equations derived in Sect. 2.3.1 for each component in the VD. Let ${\varvec{\Psi }}$ be the digamma function defined as

$$\begin{aligned} {\varvec{\Psi }}(x)=\frac{d}{dx}\log \Gamma (x), \end{aligned}$$

(21)

which can be easily calculated via numerical approximation. The values of the expectations taken with respect to the approximated distributions are given as follows.

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] = p^*_{ik} \end{aligned}$$

(22)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}) = \frac{A^{*}_{k}}{R^{*}_{k}} \end{aligned}$$

(23)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) = {\varvec{\Psi }}(A^{*}_k) - \log R^{*}_{k} \end{aligned}$$

(24)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _{k}) = {\varvec{\Psi }}(d^{*}_{k}) - {\varvec{\Psi }}\left( \sum _{k=1}^K d^{*}_{k}\right) \end{aligned}$$

(25)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _a)}(\tau _{a}) = \frac{ \alpha ^*}{\beta ^*} \end{aligned}$$

(26)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _a)}(\log \tau _{a}) = {\varvec{\Psi }}(\alpha ^{*}) - \log \beta ^{*} \end{aligned}$$

(27)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(a_i)} a_i^2 = \sigma _{a_i}^{*2} + \mu _{a_i}^{*2} \end{aligned}$$

(28)

In addition, using the fact that ${{\mathbb {E}}}({\textbf{X}}^T {\textbf{X}}) = \text{ trace }[\text{ Var }({\textbf{X}})] + {{\mathbb {E}}}({\textbf{X}})^T{{\mathbb {E}}}({\textbf{X}})$, we obtain

$$\begin{aligned}{} & {} {{{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] } \nonumber \\{} & {} \quad = \text{ trace }\left( \textbf{B}_i \mathbf {\Sigma }^*_k \textbf{B}_i^T \right) \nonumber \\{} & {} \qquad + \,({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i}), \end{aligned}$$

(29)

and

$$\begin{aligned}{} & {} {{{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)\cdot q^*(a_i)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] } \nonumber \\{} & {} \quad = {{\mathbb {E}}}_{q^*(a_i)}\left[ {{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \right] \nonumber \\{} & {} \quad = {{\mathbb {E}}}_{q^*(a_i)}\left[ \text{ trace }\left( \textbf{B}_i \mathbf {\Sigma }^*_k \textbf{B}_i^T \right) + ({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-a_i\textbf{1}_{n_i})\right] \nonumber \\{} & {} \quad = \text{ trace }\left( \textbf{B}_i \mathbf {\Sigma }^*_k \textbf{B}_i^T \right) + {n_i}\sigma _{a_i}^{*2} \nonumber \\{} & {} \qquad +\, ({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-\mu _{a_i}^*\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k-\mu _{a_i}^*\textbf{1}_{n_i}). \end{aligned}$$

(30)

2.4 ELBO calculation

In this section, we show how to calculate the ELBO under Model 2, which is the convergence criterion of our proposed VB algorithm and is updated at the end of each iteration until convergence. Equation (6) gives the ELBO:

$$\begin{aligned} \text{ ELBO }(q) = {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a},\tau _a)\right] - {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }},\textbf{a},\tau _a) \right] , \end{aligned}$$

where

$$\begin{aligned} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a},\tau _a) \right]= & {} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log p(\textbf{Z} \vert {\varvec{\pi }} \right) ] \nonumber \\{} & {} +\, {{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\phi }})\right] + {{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\tau }})\right] \nonumber \\{} & {} +\,{{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\phi }})] + {{\mathbb {E}}}_{q^*} \left[ \log p(\textbf{a} \vert \tau _a \right) \right] \nonumber \\{} & {} +\, {{\mathbb {E}}}_{q^*} \left[ \log p(\tau _a)\right] , \nonumber \end{aligned}$$

and

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a},\tau _a) \right] = {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\phi }}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\pi }}) \right] \nonumber \\{} & {} +\,{{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\tau }}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{a}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q(\tau _a) \right] .\nonumber \end{aligned}$$

Therefore, we can write the ELBO as the summation of 7 terms:

$$\begin{aligned} \text{ ELBO }(q)= & {} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}) \right] + diff_{\textbf{Z}} + diff_{{\varvec{\phi }}} \nonumber \\{} & {} + \,diff_{{\varvec{\tau }}} + diff_{{\varvec{\pi }}} + diff_{\textbf{a}} + diff_{\tau _a} \end{aligned}$$

(31)

where,

$$\begin{aligned} diff_{\textbf{Z}} = {{\mathbb {E}}}_{q^*}\left[ \log p (\textbf{Z} \vert {\varvec{\pi }})\right] -{{\mathbb {E}}}_{q^*}\left[ \log q(\textbf{Z})\right] . \end{aligned}$$

Specifically,

$$\begin{aligned} diff_{\textbf{Z}} = \sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik} {{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _k) - \sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik} \log p^{*}_{ik}. \end{aligned}$$

(32)

The other terms in (31) are calculated as follows:

$$\begin{aligned} diff_{{\varvec{\phi }}} = -\frac{1}{2}\sum _{k=1}^K v_k^0\{\text{ trace }\left( \mathbf {\Sigma }^*_k \right) + (\textbf{m}^*_k-\textbf{m}^0_k)^T(\textbf{m}^*_k-\textbf{m}^0_k)\} +\frac{1}{2}\sum _{k=1}^K \log \vert \mathbf {\Sigma }^*_k\vert , \end{aligned}$$

$$\begin{aligned} diff_{{\varvec{\tau }}}= & {} \sum _{k=1}^K \{(b^0-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k})-r^0{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k})\} \nonumber \\{} & {} - \, \sum _{k=1}^K\{A^*_k \log R_k^{*} - \log \Gamma (A^*_k)\nonumber \\{} & {} +\,(A^*_k-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) - R_k^{*}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}) \} , \end{aligned}$$

(33)

$$\begin{aligned} diff_{{\varvec{\pi }}}{} & {} \equiv \sum _{k=1}^K (d_k^0-d_k^{*}){{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _{k}),\\ diff_{\textbf{a}}{} & {} =-\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \sum _{i=1}^{N}{{\mathbb {E}}}_{q^*(a_i)} a_i^2+\sum _{i=1}^{N}\log \sigma _{a_i}^*, \\ diff_{\tau _a}{} & {} =(\alpha ^0-1){{\mathbb {E}}}_{q^*(\tau _a)}(\log \tau _{a})-\beta ^0 {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \\{} & {} \quad - \alpha ^*\log \beta ^*-(\alpha ^*-1){{\mathbb {E}}}_{q^*(\tau _a)}(\log \tau _{a})+\beta ^* {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a \\{} & {} = (\alpha ^0-\alpha ^*){{\mathbb {E}}}_{q^*(\tau _a)}(\log \tau _{a}) - (\beta ^0 -\beta ^*) {{\mathbb {E}}}_{q^*(\tau _a)}\tau _a -\alpha ^*\log \beta ^* \end{aligned}$$

and

$$\begin{aligned}{} & {} {{{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}, \textbf{a}) \right] } \\{} & {} \quad =\sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik}\left\{ \frac{{n_i}}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) \right. \\{} & {} \left. \qquad -\frac{1}{2}\frac{A_k^{*}}{R_k^{*}}{{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)\cdot q^*(a_i)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i})^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k-a_i\textbf{1}_{n_i}) \right] \right\} . \end{aligned}$$

Therefore, at iteration c, we calculate $\text{ ELBO}^{(c)}$ using all parameters obtained at the end of iteration c. Convergence of the algorithm is achieved if $\text{ ELBO}^{(c)}-\text{ ELBO}^{(c-1)}$ is smaller than a given threshold. It is important to note that we use the fact that $\displaystyle \lim \nolimits _{p^{*}_{ik} \rightarrow 0} p^{*}_{ik}\log p^{*}_{ik}=0$ to avoid numerical issues when calculating (32). Numerical issues also exist in calculating the term $\{A^*_k \log R_k^{*} - \log \Gamma (A^*_k) +(A^*_k-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) - R_k^{*}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}) \}$ in (33), so we will approximate it by the following digamma and log-gamma approximations. Note that we use (23) and (24) for ${{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k})$ and ${{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k})$, respectively.

• (1) digamma approximation based on asymptotic expansion:

  $$\begin{aligned} {\varvec{\Psi }}(A_k^{*})\approx \log A_k^{*} - 1/(2A_k^{*}). \end{aligned}$$

• (2) log-gamma Stirling’s series approximation:

  $$\begin{aligned} \log \Gamma (A_k^{*})\approx A_k^{*}\log (A_k^{*}) - A_k^{*} - \frac{1}{2}\log (A_k^{*}). \end{aligned}$$

Therefore, plugging in these two approximations, we obtain

$$\begin{aligned}{} & {} A^*_k \log R_k^{*} - \log \Gamma (A^*_k) +(A^*_k-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) - R_k^{*}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}) \nonumber \\{} & {} \quad = A^*_k \log R_k^{*} - \log \Gamma (A^*_k) +(A^*_k-1)({\varvec{\Psi }}(A^{*}_k) - \log R^{*}_{k}) - R_k^{*}\frac{A^{*}_{k}}{R^{*}_{k}} \nonumber \\{} & {} \quad \approx \frac{1}{2}\log A_k^{*} +\frac{1}{2A^*_k}-\frac{1}{2}\nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }\frac{1}{2}\log A_k^{*} +\frac{1}{2A^*_k} = \frac{1}{2}\left( \log A_k^{*} + \frac{1}{A^*_k}\right) \nonumber \end{aligned}$$

Algorithm 1

Clustering functional data via variational inference with random intercepts

3 Simulation studies

In Sect. 3.1, we present the metrics used to evaluate the performance our proposed methodology. Sections 3.2 and 3.3 present the simulation scenarios and results for Model 1 and Model 2, respectively.

3.1 Performance metrics

We evaluate the clustering performance of our proposed algorithm by two metrics: mismatches (Zambom et al. 2019) and V-measure (Rosenberg and Hirschberg 2007). Mismatch rate is the proportion of subjects misclassified by the clustering procedure. In our case, each subject corresponds to a curve in our functional dataset. V-measure, a score between zero and one, evaluates the subject-to-cluster assignments and indicates the homogeneity and completeness of a clustering procedure result. Homogeneity is satisfied if the clustering procedure assigns only those subjects that are members of a single group to a single cluster. Completeness is symmetrical to homogeneity, and it is satisfied if all those subjects that are members of a single group are assigned to a single cluster. The V-measure is one when all subjects are assigned to their correct groups by the clustering procedure. One may also consider alternative metrics to evaluate clustering performance, such as the Rand index (Rand 1971) and the mutual information (Cover 1999). The Rand index measures the similarity between two data partitions by counting the number of pairs of observations that are either correctly grouped together (i.e., true positives) or correctly separated (i.e., true negatives) in both partitions. Mutual information, on the other hand, quantifies the information shared between two data partitions. Along with the V-measure, these metrics are commonly used for clustering and partition evaluation, but they each have different mathematical formulations and emphasize different aspects of clustering performance.

For comparison purposes, we also investigate the performance, in terms of mismatch and V-measure, of the classical clustering algorithms including k-means for raw data (discrete observed points), and k-means for functional data (referred to as functional k-means, Febrero-Bande and de la Fuente (2012)), and two other model-based algorithms: funFEM (Bouveyron et al. 2015) and SaS-Funclust (Centofanti et al. 2023). The funFEM method was proposed for the inference of the discriminative functional mixture model to cluster functional data via the EM algorithm. The SaS-Funclust method, short for sparse and smooth functional clustering, was developed to facilitate sparse clustering for functional data via a functional Gaussian mixture model and penalized maximum likelihood estimation.

To further evaluate the performance of the proposed VB algorithm in terms of the estimated mean curves, we calculate the empirical mean integrated squared error (EMISE) for each cluster in each simulation scenario. For simplicity, we generate curves with equal number of observed values, that is n, in our simulation study. The EMISE is obtained as follows:

$$\begin{aligned} \text {EMISE}_k=\frac{T}{n}\sum _{j=1}^{n}\text {EMSE}_k(t_j), \end{aligned}$$

(34)

where T is the curve evaluation interval length, n is total number of observed evaluation points, and the empirical mean squared error (EMSE) at point $t_j$ for cluster k, $\text {EMSE}_k(t_j)$, is given by

$$\begin{aligned} \text {EMSE}_k(t_j)=\frac{1}{S}\sum _{s=1}^{S}\left[ f_k(t_j)-{\hat{f}}_k^s(t_j)\right] ^2, \end{aligned}$$

in which s corresponds to the sth simulated dataset among S datasets in total, $f_k(t_j)$ is the value of the true mean function in cluster k evaluated at point $t_j$ and ${\hat{f}}_k^s(t_j)$ is its corresponding estimated value for the sth simulated dataset. The estimated value ${\hat{f}}_k^s(t_j)$ is calculated using the B-spline basis expansion with coefficients corresponding the to posterior mean (15) obtained at the convergence of the VB algorithm.

3.2 Simulation study on Model 1

In Sects. 3.2.1 and 3.2.2, we first conduct simulation studies for Model 1 which comprises six different scenarios, five of which have three clusters ($K=3$) while the last scenario has four clusters ($K=4$). For each simulation scenario, we generate 50 datasets and apply the proposed VB algorithm to each dataset, considering the number of basis functions to be six except for Scenario 5, which uses 12 basis functions. The ELBO convergence threshold is 0.01, with a maximum of 100 iterations. We use the clustering results of k-means to initialize $p^{*}_{ik}$ in our VB algorithm.

We further conduct simulation studies on Model 1 to investigate the performance of the VB algorithm, including a prior sensitivity analysis in Sect. 3.2.3, choice of the number of clusters in Sect. 3.2.4 and misspecification of the type of basis functions in Sect. 3.2.5. We compare the posterior estimation results from VB to the ones from MCMC in Sect. 3.2.6.

3.2.1 Simulation scenarios

Scenarios 1 and 2 are adopted from Zambom et al. (2019). Each dataset is generated from 3 possible clusters ($k=1,2,3$) with $N=50$ curves per cluster. For each curve, we assume there are $n=100$ observed values across a grid of equally spaced points in the interval $[0, \pi /3]$.

Scenario 1, $K = 3$:

$$\begin{aligned} Y_{ik}(t_j)=a_i+b_k+c_k \sin (1.3t_j)+t_j^3+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_i\sim U(-1/4,1/4)$, $\delta _{ij}\sim N(0, 0.4^2)$, $b_1=0.3$, $b_2=1$, $b_3=0.2$, $c_1=1/1.3$, $c_2=1/1.2$, and $c_3=1/4$.

Scenario 2, $K = 3$:

$$\begin{aligned} Y_{ik}(t_j)=a_i+b_k \exp (c_kt_j)-t_j^3+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_i\sim U(-1/4,1/4)$, $\delta _{ij}\sim N(0, 0.3^2)$, $b_1=1/1.8$, $b_2=1/1.7$, $b_3=1/1.5$, $c_1=1.1$, $c_2=1.4$, and $c_3=1.5$.

In Scenarios 3 and 4, each dataset is also generated considering three clusters ($k=1,2,3$) with 50 curves each. The mean curve of the functional data in each cluster is generated from a pre-specified linear combination of B-spline basis functions. The number of basis functions is the same across clusters but the coefficients of the linear combination are different, one set per cluster (see Table 1). We apply the function create.bspline.basis in the R package fda to generate six B-spline basis functions of order 4, $B_l(\cdot )$, $l=1,...,6,$ evaluated on equally spaced points, $t_j$, $j=1,...,100$, in the interval [0, 1].

Scenarios 3 and 4, $K = 3$:

$$\begin{aligned} Y_{ik}(t_j)=\sum _{l=1}^{6}B_l(t_j)\phi _{kl}+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k and $\delta _{ij}\sim N(0, 0.4^2)$. Table 1 presents the vector of coefficients for each cluster k, ${\varvec{\phi }}_k = (\phi _{k1},\ldots ,\phi _{k6})^T$, used in Scenarios 3 and 4. Figure 1 illustrates the true mean curves for the three clusters and their corresponding basis functions for Scenarios 3 and 4.

Table 1 Coefficient vectors of six B-spline basis functions for each cluster in Scenarios 3 and 4

Scenario 5 ($K=3$) is based on one of the simulation scenarios used in Dias et al. (2009) in which the curves mimic the energy consumption of different types of consumers in Brazil. There are 50 curves per cluster and for each curve we generate 96 points based on equally spaced time points, $t_j, \; j=1,...,96$ in the interval [0, 24] (corresponding to one observation every 15 min over a 24-hour period).

Scenario 5, $K = 3$:

$$\begin{aligned} Y_{i1}(t_j)= & {} 0.1(0.4 + \exp (-(t_j-6)^2/3) +\, 0.2 \exp (-(t_j-12)^2/25) \\{} & {} +\,0.5 \exp (-(t_j-19)^2/4))+\delta _{ij} \\ Y_{i2}(t_j)= & {} 0.1(0.2 + \exp (-(t_j-5)^2/4) \\{} & {} +\, 0.25 \exp (-(t_j-18)^2/5))+\delta _{ij} \\ Y_{i3}(t_j)= & {} 0.1(0.2 + \exp (-(t_j-3)^2/4) \\{} & {} +\, 0.25 \exp (-(t_j-16)^2/5))+\delta _{ij} \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at time $t_j$ of the ith curve from cluster k, $i=1,...,50$, $j=1,...,96$, $k=1,2,3$, and $\delta _{ij}\sim N(0, 0.012^2)$.

Scenario 6 also corresponds to one of the simulation scenarios considered by Zambom et al. (2019), where there are $K=4$ clusters with 50 curves each. Each curve has 100 observed values based on equally spaced points, $t_j$, $j=1,...,100$, in the interval $[0, \pi /3]$.

Scenario 6, $K = 4$:

$$\begin{aligned} Y_{ik}(t_j)=a_i+b_k - \sin (c_k\pi t_j) + t_j^3+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3,4, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_i\sim U(-1/3,1/3)$, $\delta _{ij}\sim N(0, 0.4^2)$, $b_1=0.2$, $b_2=0.5$, $b_3=0.7$, $b_4=1.3$, $c_1=1.1$, $c_2=1.4$, $c_3=1.6$ and $c_4=1.8$.

Fig. 1

Cluster true mean curves (solid curves) and their corresponding six B-splines basis functions (dashed curves) for simulation scenarios 3 (left) and 4 (right)

3.2.2 Simulation results for Model 1

Figure 2 shows the raw curves (color-coded by cluster) from one of the 50 generated datasets for each simulation scenario. In addition, the true mean curves ($f_k(\textbf{t})$, $k=1,\ldots ,K$) and the estimated smoothed mean curves (${\hat{f}}_k(\textbf{t})=\textbf{B}\textbf{m}^*_k$, $k=1,\ldots ,K$) are shown in black and red, respectively. We can observe that the true and estimated mean curves almost coincide within each cluster in all scenarios.

Table 2 Simulation results for Model 1 Mismatches rate and V-measure values for each simulation scenarios

Table 2 displays the mean and standard deviation of mismatch rates (M) and V-measure values (V) across 50 simulated datasets for each scenario. For the sake of completeness, we have included the results from Scenario 7 in Sect. 3.2.4 and Scenario 8 in Sect. 3.2.5 in Table 2 as they pertain to the study of Model 1. The proposed VB algorithm performs the best in all scenarios except for Scenario 5 where we simulate the curves that mimic daily energy consumption. Across Scenarios 1 to 6, VB demonstrates impressive results with a mean mismatch rate of 5.13% and a mean V-measure of 88.06%. Notably, the mean mismatch rate achieved by VB is 55.71%, 83.6%, 85.86%, and 73.41% lower than that of classical k-means, functional k-means, funFEM, and SaS-Funclust, respectively. Meanwhile, VB’s mean V-measure surpasses the compared methods by 5.36%, 38.75%, 85.9%, and 8.46%, respectively. In Scenarios 3 and 4, where data is simulated through a linear combination of six predefined basis functions, VB exhibits perfect classification, with $M=0$ and $V=1$, which aligns with expectations since the raw data in these scenarios share the same structure as the proposed model. Comparatively, classical k-means generally outperforms functional k-means, funFEM, and SaS-Funclust in Scenarios 1, 2, 3, and 6, as similarly found in Zambom et al. (2019). The SaS-Funclust method excels in Scenario 5, with a slightly (0.0067) lower mismatch rate and a marginally (0.0053) higher V-measure than VB. Functional k-means also demonstrates competitive performance in Scenario 5, comparable to VB and SaS-Funclust.

In terms of computational efficiency, the run times for the proposed VB algorithm of Model 1 across the 50 simulated datasets from Scenarios 1 to 6 are as follows: 1.97 min, 5.41 min, 1.41 min, 1.61 min, 3.60 min, and 5.32 min. For comparison, SaS-Funclust required significantly longer computation times: 60.16 min, 68.94 min, 65.04 min, 68.19 min, 72.26 min, and 129.47 min for the respective scenarios. On average, the proposed VB algorithm demonstrates exceptional speed, being approximately 20 times faster than SaS-Funclust. The algorithm was implemented in R version 3.6.3 on a computer using the Mac OS X operating system with a 1.6 GHz processor and 8 GBytes of random access memory, same for the simulation study for Model 2 in Sect. 3.3.

Fig. 2

Simulation results for Model 1. Example of simulated data under each proposed scenario. Raw curves (different colors correspond to different clusters), cluster-specific true mean curves (in black) and corresponding estimated mean curves (in red) (color figure online)

Table 3 presents the EMISE for each cluster in each Scenario. We can observe small EMISE values, which are consistent with the results shown in Fig. 2, where there is a small difference between the red curves (i.e., the estimated mean functions) and the black curves (i.e., the true mean functions). A plot of EMSE values versus observed points for each cluster in Scenario 1 is presented in Fig. 3 while plots of EMSE values for Scenarios 2, 3, 4, 5 and 6 are provided in Fig. 11 in Appendix B.

Table 3 Simulation results for Model 1. The empirical mean integrated squared error (EMISE) for the estimated mean curve in each cluster in each scenario

Fig. 3

Simulation results for Model 1. Empirical mean squared error (EMSE) versus each evaluation point x for each cluster in Scenario 1

3.2.3 Prior sensitivity analysis

In Bayesian analysis, it is important to assess the effects of different prior settings in the posterior estimation. In this section, we carry out a sensitivity analysis on how different prior settings may affect the results of our proposed VB algorithm. Our sensitivity analysis focuses on the prior distribution of the coefficients ${\varvec{\phi }}_k$ of the B-spline basis expansion of each cluster-specific mean curve. We assume ${\varvec{\phi }}_k$ follows a multivariate normal prior distribution with a mean vector $\textbf{m}_k^0$ and $s^0\textbf{I}$ as the covariance matrix. We simulated data according to Scenario 3 in Sect. 3.2.1 and four different prior settings as follows:

• Setting 1: use the true coefficients as the prior mean vector and consider a small variance ($s^0=0.01$).

• Setting 2: use the true coefficients as the prior mean vector but consider a larger variance than in Setting 1 ($s^0=1$).

• Setting 3: use a prior mean vector that is different than the true vector of coefficients with a small variance ($s^0=0.01$).

• Setting 4: set the prior mean vector of coefficients to a vector of zeros with a small variance ($s^0=0.01$).

Setting 1 has the strongest prior information among these four prior settings, while setting 4 is the most non-informative prior case. In setting 3, the prior mean vector of coefficients is generated from sampling from a multivariate normal distribution with a mean vector corresponding to the true coefficients and covariance matrix $\sigma ^2\textbf{I}$, with $\sigma ^2 =0.5$. For each prior setting, we simulate 50 datasets as in Scenario 3, obtaining the average mismatch rate and V-measure, which are displayed in Table 4. First, we can observe that all the curves are correctly clustered under Setting 1, which has the strongest prior information. Then, as we relax the prior assumptions in two possible directions (i.e., more considerable variance or less informative mean vector), the mismatch rate increases, and the V-measure decreases. However, the clustering performance does not decrease much, only 4.67% higher in mismatches and 3.73% lower in V-measure.

Table 4 Simulation results for Model 1. Mean mismatch rate and V-measure value from prior sensitivity analysis in Scenario 3

3.2.4 Choosing the number of clusters

Choosing an appropriate number of clusters, denoted as K, holds paramount importance within clustering procedures. This decision aligns with determining the number of mixture components in a regression mixture model. One of the most widely applied methodologies to deal with uncertainty in the cluster numbers is the two-fold scheme that one first fits the mixture model with different predefined numbers of mixtures and then use some information criteria to select the best one (Chen et al. 2012; Nieto-Barajas and Contreras-Cristán 2014; Wang and Lin 2022). Alternatively, one can explore concurrent approaches for optimal cluster number selection, including techniques such as overfitted Bayesian mixtures, tailored to address scenarios with large unknown K (Rousseau and Mengersen 2011), selection through penalized maximum likelihood (Chamroukhi 2016b), and the application of infinite mixture models such as Dirichlet process mixture models (Escobar and West 1995; Ray and Mallick 2006; Petrone et al. 2009; Rodríguez et al. 2009; Angelini et al. 2012; Heinzl and Tutz 2013; Rigon 2023).

In our study, we employ the afterward model selection (i.e., two-fold) scheme to determine the most suitable number of clusters. Assuming some prior knowledge of K, we establish a clustering model for a range of integers based on this prior information, employing the VB algorithm for each K. For model comparison, we utilize the deviance information criterion (DIC) (Spiegelhalter et al. 2002), which can be applied to select the optimal number of clusters within a comparable Bayesian clustering framework (Gao et al. 2011; Anderson et al. 2014; Komárek 2009). DIC is built to balance the model fitness and complexity under a Bayesian framework, and a lower DIC indicates a better model. Nonetheless, the DIC is not an integral component of the core methodology and can be substituted with alternative model selection criteria such as the WAIC (Watanabe and Opper 2010) and LPML (Geisser and Eddy 1979) when someone’s concern is predictive goodness-of-fit. In our Model 1 setting, the DIC can be obtained as follows:

$$\begin{aligned} DIC=-4{{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] + 2{\overline{D}}, \end{aligned}$$

where ${{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right]$ can be computed after the convergence of our proposed VB algorithm based on the ELBO. The term ${\overline{D}}$ corresponds to the log-likelihood $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }})$ evaluated at the expected value of each parameter posterior. For example, when we calculate the term $\log \tau _{k}$ in $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }})$, we replace it by $\log \,({{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}))$.

Fig. 4

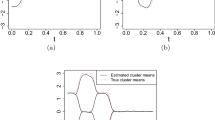
Simulation results for Model 1, Scenario 7, $K=6$. Left: boxplots of DIC values under different $K \in \{1, 2,..., 10\}$. The best number of clusters is six which has the smallest DIC. Right: the clustering results for $K=6$ for one of the simulated data sets. Raw curves (different colors correspond to different clusters), cluster-specific true mean curves (in black) and corresponding VB estimated mean curves (in red) (color figure online)

We consider a more complex scenario, namely Scenario 7, where $K=6$ in this simulation study which was also analyzed in Zambom et al. (2019). The data are generated as follows:

Scenario 7, $K = 6$:

$$\begin{aligned} Y_{ik}(t_j)=a_i + \cos (b_k\pi t_j) - t_j^2+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,..., 6, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_i\sim U(-1/4,1/4)$, $\delta _{ij}\sim N(0, 0.3^2)$, $b_1=1$, $b_2=1.2$, $b_3=1.4$, $b_4=1.6$, $b_5=1.8$ and $b_6=2$.

We assume a prior information of the number of clusters that K is around 6. Accordingly, we evaluate a range of potential K values, specifically $\{2, 3,..., 10\}$. For each K, we apply the VB algorithm to cluster the observed functional data and calculate the resulting DIC. Within this scope, for each $K \in \{2, 3,..., 10\}$, we repeat the simulation analysis for 50 times utilizing different random seeds to generate data. The left plot in Fig. 4 displays a boxplot representation of the DIC values for each K. It is evident that our DIC-based approach adeptly identifies the correct K (in this case, $K=6$), yielding the lowest DIC. The accompanying right plot in Fig. 4 showcases the clustering results for one of the simulated data sets under Scenario 7, demonstrating a highly satisfactory estimation of the true mean curves.

The quantitative evaluation of VB clustering performance in Scenario 7, along with a comparison to the other methods, is presented in Table 2. The VB algorithm performs the best among the others with a mean mismatch rate of 0.3001 and a mean V-measure of 0.7528. The mean mismatch rate of VB is 0.03%, 61.33%, 63.33%, and 58.13% lower than that of the classical k-means, functional k-means, funFEM and SaS-Funclust methods, while the mean V-measure is 0.41%, 36.25%, 1393.65%, and 21.83% higher, respectively. It is important to note that Scenario 7, characterized by a more complex structure with multiple groups of curves and overlapping patterns, poses a greater challenge for all methods, leading to overall reduced performance compared to other scenarios. FunFEM, in particular, encounters significant difficulties, with a V-measure approaching 0 due to the misclassification of more than 80% of curves.

3.2.5 Misspecification of the type of basis functions

This section illustrates the performance of the VB algorithm in case of misspecification of the type of basis functions via a simulation study, namely Scenario 8. We generate seven Fourier basis functions with equally spaced points on the interval [0, 1], which are shown in Fig. 5b, and simulate the data for three clusters $(k=1, 2, 3)$ with 50 curves ($i=1, 2,..., 50$) and 100 values $(t_j, j=1, 2,..., 100)$ on each curve in each cluster using a linear combination of these Fourier basis functions as follows:

Scenario 8, $K = 3$:

$$\begin{aligned} Y_{ik}(t_j)=\sum _{l=1}^{7}G_l(t_j)\phi _{kl}+\delta _{ij}; i=1,\ldots ,50; j=1,\ldots ,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ for the ith curve from cluster k, $G_l(t_j)$ is the lth Fourier basis function evaluated at point $t_j$, $\phi _{kl}$ is the corresponding basis function coefficient, and $\delta _{ij}\sim N(0, 4)$. In this simulation study, the vectors of basis function coefficients for each cluster are:

$$\begin{aligned} {\varvec{\phi }}_{1}= & {} (\phi _{11}, \phi _{12},\ldots , \phi _{17})^T=(0.75, 0.50, 0.90, 1.25, 0.90, 0.50, 0.40)^T,\\ {\varvec{\phi }}_{2}= & {} (\phi _{21}, \phi _{22},\ldots , \phi _{27})^T=(0.40, 0.70, 0.90, 0.25, 0.75, 1.25, 1.50)^T\hbox {, and}\\ {\varvec{\phi }}_{3}= & {} (\phi _{31}, \phi _{32},\ldots , \phi _{37})^T=(0.10, 0.30, 1.20, 1.30, 0.05, -0.20, -0.30)^T. \end{aligned}$$

Figure 5c presents the raw curves with each cluster distinguished by a unique color. Notably, when compared to the B-spline bases, the Fourier bases exhibit a more intricate curve structure, suggesting the potential need for an increased number of B-spline basis functions to adequately represent these functional curves, as observed in Souza et al. (2023). Consequently, we have generated 15 B-spline bases from the interval [0, 1], as illustrated in Fig. 5a, to cluster the curves derived from a linear combination of the Fourier bases. The resulting VB estimated mean curves (solid lines) are juxtaposed with the true mean curves (dashed lines) in Fig. 5d from one of the simulated data sets.

While a minor discrepancy is observable between the true and estimated mean curves at the left boundary for the red and green groups, it is evident that the VB algorithm achieves highly accurate estimations of the true mean curves across all clusters. As shown in Table 2, the computed mean mismatch rate (sd) and mean V-measure (sd) from clustering 50 different simulated datasets are 0.067 (0.135) and 0.947 (0.108), respectively. In comparison to classical k-means, functional k-means, and funFEM, the mean mismatch rate from VB is 30.52%, 71.26%, and 87.65% lower, while the mean V-measure is 2%, 49.72%, and 711.92% higher. Unfortunately, SaS-Funclust struggles to cluster the curves, resulting in a V-measure of zero. This simulation illustrates the robustness of the VB algorithm in clustering functional data, even when confronted with the misspecification of basis function types.

Fig. 5

Simulation results for Model 1, Scenario 8, $K=3$. a B-spline basis functions for model fit. b Fourier basis functions for data generation. c Raw curves from three clusters (distinct colors for each cluster). d Cluster-specific true mean curves (dashed) and corresponding VB estimated mean curves (solid) (color figure online)

Fig. 6

Simulation results for Model 1, Scenario 1, $K=3$. Posterior distributions of the B-spline basis coefficients and the precision parameter for each cluster (one column for each cluster). In each plot, the dashed red line is from the VB algorithm and the solid blue line from MCMC

3.2.6 Comparison with MCMC posterior estimation

In our simulation study on Model 1, VB is shown to yield accurate mean curve estimates and satisfactory outcomes in clustering functional data. Although mean-field VB, as an alternative to MCMC, boasts a lower computational cost, it may potentially underestimate the posterior variance (Wang and Titterington 2005). To investigate this concern in the context of clustering functional data through a B-spline regression mixture model, we employ the MCMC-based Gibbs sampling algorithm for simulated data under Scenario 1. The resulting posterior distribution from Gibbs is based on 9000 MCMC samples following a 1000-sample burn-in and with a thinning of 1 from one chain. The convergence of the MCMC algorithm was well assessed and checked by the trace plot. Figure 6 illustrates the marginal posterior density of each basis coefficient $\phi _{km}$, $k=1, 2, 3$, $m = 1, \ldots , 6$, and the precision parameter $\tau _k$, $k=1, 2, 3$, for each cluster, organized by columns. In each plot, the dashed red line represents the corresponding posterior density from VB, while the solid blue line is derived from MCMC. We observe a robust consistency in the estimated posterior distributions between MCMC and VB. A similar consistency between VB and MCMC in posterior estimation under a regression setting was found by Faes et al. (2011), Luts and Wand (2015), Xian et al. (2024).

To elucidate the uncertainty from the estimated mean curves, we utilize Scenarios 1 and 3 as illustrative examples. We construct 95% credible bands, both from MCMC and VB, for the true mean curves based on the posterior distribution of the B-spline coefficients. Figure 7 presents the results, with the first row corresponding to Scenario 1 and the second row to Scenario 3. In each plot, the solid colored lines depict the estimated mean curves from VB or MCMC, while the black solid lines represent the true mean curves. The 95% credible bands are shown as dashed lines, with different colors for different clusters. In Scenario 1, VB provides comparable point and interval estimation results with MCMC. In contrast, in Scenario 3, VB provides more accurate estimated mean curves, particularly at the left tails. Importantly, we observed no substantial differences in the resulting credible bands between VB and MCMC. In terms of computational cost for one simulation, VB took 5.5 s to produce the results, while the Gibbs sampler took 2.9 min for Scenario 1. In Scenario 3, VB took 5.8 s, while MCMC took 2.6 min. Overall, VB was more than 20 times faster than MCMC.

Fig. 7

Simulation results for Model 1, Scenarios 1 and 3. The 95% credible bands for the true mean curves from VB (the left column) and MCMC (the right column). The solid colored lines represent the estimated mean curves, with the true mean curves depicted by black solid lines. The 95% credible bands are illustrated by the corresponding dashed lines (color figure online)

3.3 Simulation study on Model 2

3.3.1 Simulation scenarios

We also investigate the performance of our proposed VB algorithm under Model 2 using simulated data. We consider the simulation schemes of Scenario 1 and Scenario 3 in Sect. 3.2.1, but add a random intercept to each curve, to construct four different scenarios namely Scenario 9, Scenario 10, Scenario 11, and Scenario 12.

Scenario 9, $K = 3$:

Scenario 9 is constructed based on Scenario 1. The data are simulated as follows.

$$\begin{aligned} Y_{ik}(t_j)=a_{ik}+b_k+c_k \sin (1.3t_j)+t_j^3+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_{ik}\sim N(0, 0.4^2)$, $\delta _{ij}\sim N(0, 0.2^2)$, $b_1=-0.25$, $b_2=1.25$, $b_3=2.50$, $c_1=1/1.3$, $c_2=1/1.2$, and $c_3=1/4$.

Scenario 10, $K = 3$:

Scenario 10 is developed based on Scenario 3. In this scenario, we consider a very small variance for the random intercept which almost resembles the case without a random intercept. Data are generated as follows.

$$\begin{aligned} Y_{ik}(t_j)=a_{ik} + \sum _{l=1}^{6}B_l(t_j)\phi _{kl}+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_{ik}\sim N(0, 0.05^2)$, $\delta _{ij}\sim N(0, 0.4^2)$. The B-spline coefficients, $\phi _{kl}$, remain the same and are presented in Table 1, which are also used in Scenarios 9 and 10.

Scenario 11, $K = 3$:

Scenario 11 is similar to Scenario 10, but with larger variance for the random intercept but smaller variance for the random error. Data are generated as follows.

$$\begin{aligned} Y_{ik}(t_j)=a_{ik} + \sum _{l=1}^{6}B_l(t_j)\phi _{kl}+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_{ik}\sim N(0, 0.3^2)$, $\delta _{ij}\sim N(0, 0.15^2)$.

Scenario 12, $K = 3$:

Scenario 12 is similar to Scenario 10, but with larger variance for the random intercept. In this scenario, we use larger variance for the random error compared with that in Scenario 11, indicating a more complex case. Data are generated as follows.

$$\begin{aligned} Y_{ik}(t_j)=a_{ik} + \sum _{l=1}^{6}B_l(t_j)\phi _{kl}+\delta _{ij}; i=1,...,50; j=1,...,100; k=1,2,3, \end{aligned}$$

where $Y_{ik}(t_j)$ denotes the value at point $t_j$ of the ith curve from cluster k, $a_{ik}\sim N(0, 0.6^2)$, $\delta _{ij}\sim N(0, 0.4^2)$.

3.3.2 Simulation results for Model 2

Figure 8 shows the curves from one of the 50 simulated datasets for Scenarios 9 and 11. Due to the similarity among Scenarios 10, 11 and 12, the curves for Scenarios 10 and 12 are presented in Fig. 12 of Appendix B. In Fig. 8, we can observe a slight difference between each cluster’s true mean curve and the estimated mean curve. Furthermore, more variation occurs after adding the random intercept. Especially in Scenario 12, with large variances, there is a more substantial overlap among curves from different clusters, resulting in a more complex scenario for clustering than the corresponding Scenario 3 in Sect. 3.2.

Table 5 Simulation results for Model 2. Mismatch rate and V-measure values for each simulation scenario

Table 5 presents the numerical results, including the mean mismatch rate and the mean V-measure with their corresponding standard deviations from the 50 different simulated datasets under each scenario considered. In Scenario 9, where the true mean curves exhibit relative parallelism, we do not observe a significant difference in the mean mismatch rate (approximately 10%) and the mean V-measure (approximately 0.7) among our VB model, the classical k-means, and SaS-Funclust. In contrast, in Scenario 9, the functional k-means and funFEM methods exhibit a larger mean mismatch rate and an 18.78% lower mean V-measure than VB. In Scenario 10, where the true mean curves intersect, our proposed model achieves a significantly lower mean mismatch rate of 0.0299, in contrast to the other methods: 0.1404 for classical k-means, 0.2799 for functional k-means, 0.1845 for funFEM, and 0.3333 for SaS-Funclust. Moreover, the mean V-measure obtained from VB is 0.9767, which is 9.28%, 69.33%, 34.09%, and 33.12% higher than the results from the aforementioned methods, respectively.

Fig. 8

Simulation results for Model 2. Example of simulated data under Scenario 9 (left) and Scenario 11 (right). Raw curves (different colors correspond to different clusters), cluster-specific true mean curves (in black) and corresponding estimated mean curves (in red) (color figure online)

When the random intercept variance becomes larger in Scenario 11, even with a smaller random error variance, clustering curves via our proposed model becomes more challenging. The mean mismatch rate increases to 0.1453 from 0.0299, while the mean V-measure drops to 0.7923 from 0.9767 in Scenario 10. Nonetheless, our model continues to outperform the other considered methods, with differences in mismatch rates of 0.0118 for classical k-means, 0.1974 for functional k-means, 0.0576 for funFEM, and 0.0519 for SaS-Funclust. In Scenario 12, where there is a further increase in variance in the random intercept, we observe that the clustering performance of all methods deteriorates, leading to higher mismatch rates and lower V-measure values. Nevertheless, the VB algorithm still stands out by achieving the lowest mean mismatch rate and the highest mean V-measure compared to the other methods. The larger standard deviation of mismatch rates and V-measure of VB compared to other methods happen because, among the 50 different runs, there are 11 runs where our method can 100% correctly assign each curve to the cluster it belongs to, resulting in a mismatch rate of zero and a V-measure of one. At the same time, using the classical k-means as an example, there is no run where the classical k-means provides such perfect clustering results. Besides, among the 50 different runs, there are 41 runs where our method provides lower mismatch rates and higher V-measures than the classical k-means.

Table 6 shows the EMISE for each cluster in Scenarios 9, 10, 11 and 12 based on Model 2. Small EMISE values once again indicate that the true mean curves and the corresponding curves have a small difference. We also find that compared with Table 3 based on Model 1, the EMISE values based on Model 2 are larger. This is in our expectation since adding a random intercept to each curve will bring more variation to the curves, and as a result, more variation in the estimated mean curves, in Scenario 12 especially when we have a larger variance for generating random intercepts. Plots of EMSE values in Scenarios 7, 8, 9, and 10 based on Model 2 are provided in Fig. 13 in Appendix B.

For the computational cost, the run times of the proposed VB algorithm of Model 2 for 50 simulated datasets from Scenarios 9, 10, 11 and 12 are 40.96 min, 1.52 min, 10.46 min, and 11.52 min, respectively. For comparison, SaS-Funclust takes longer computation times: 45.06 min, 65.17 min, 64.35 min and 64.2 min for the respective scenarios.

Table 6 Simulations results for Model 2. The empirical mean integrated squared error (EMISE) for the estimated mean curve in each cluster in each scenario

4 Application to real data

In this section, we apply our proposed method in Sect. 2 to the growth and the Canadian weather datasets, which are both publicly available in the R package fda.

The Growth data (Tuddenham and Snyder 1954) includes heights (in cm) of the 93 children over 31 unevenly spaced time points from the age of one to eighteen. Raw curves without any smoothing are shown in Fig. 9, where the green curves correspond to boys and blue curves to girls. In this case, we apply our proposed method to the growth curves considering two clusters and compare the inferred cluster assignments (boys or girls) to the true ones.

The Canadian weather data (raw data are presented in Fig. 14 in Appendix B) contains the daily temperature at 35 different weather stations (cities) in Canada, averaged out from the year of 1960 to 1994. However, unlike the growth data, we do not know the true number of clusters in the weather data. Therefore, in order to find the best number of clusters, we apply the DIC for model comparison.

The number of B-spline basis functions is fixed and known within the VB algorithm. As discussed in Rossi et al. (2004), a low number of basis functions can be applied to get rid of the measurement noise. Another feature of the B-spline basis system is that increasing the number of B-spline bases does not always improve certain aspects of the fit to the data (Ramsay and Silverman 2005). Based on Liu and Yang (2009), ten B-spline basis functions are relatively reasonable for clustering the Growth data with two clusters. The Canadian weather data presents a higher variation (larger noise) than the Growth data. Therefore, curves with a moderate smoothing, rather than with more roughness, may more accurately reflect the underlying functional structures, and the underlying clusters. So, we use six B-spline basis functions to represent the weather data within the VB algorithm. It is important to note that we do not have a strong prior knowledge of these real datasets but still need to provide appropriate prior hyperparameters for the VB algorithm. As a solution, we randomly select one underlying curve in each dataset and fit a B-spline regression to obtain a vector of coefficients which is then modified across different clusters resulting in the prior mean vectors $\textbf{m}_k^0$ for $k=1,...,K$. We set $s^0=0.1$, corresponding to a precision of 10, as the prior variance of these coefficients which provides a useful information as assumed in real world. For the Dirichlet prior distribution of ${\varvec{\pi }}$, we use $\textbf{d}^0=(1/K,...,1/K)$, indicating that for each curve, the probability of assignment to each cluster is a priori equal across clusters. For the Gamma prior distribution of the precision, $\tau _k=1/\sigma _k^2$, we prefer a large prior mean (e.g., 10) and a small prior variance (e.g., 0.1) which serve as informative prior knowledge, and therefore, we set $a^0 = 2000$ and $r^0 = 100$ for the growth data, and $a^0 = 1000$ and $r^0 = 800$ for the weather data. The ELBO convergence threshold is 0.001.

Since we know there are two clusters (boys and girls) in the growth dataset, $K=2$ is preset for the clustering procedure. We apply the proposed VB algorithms under Models 1 and 2 to cluster the growth curves with 50 runs corresponding to 50 different initializations. The classical k-means method is also applied to the raw curves for performance comparison purposes. Figure 9 presents the estimated mean curves for each cluster corresponding to the the best VB run (the one with maximum ELBO after convergence) along with the empirical mean curves from both models (left graph for Model 1 while right for Model 2). The empirical mean curves are calculated by considering the true clusters and calculating their corresponding point-wise mean at each time point. Some difference between the estimated and the empirical curves can be observed for the girls due to a potential outlier. Regarding clustering performance, the mean mismatch rates for the VB algorithms under Model 1 and Model 2, and k-means are 33.33%, 20.47% and 34.41%, respectively. V-measure is more sensitive to misclassification than mismatch rate and, therefore, we obtain low mean V-measure values of 7.75% for VB under Model 1, 33.75% for VB under Model 2, and 6.37% for k-means. We can see the clustering performance significantly improved after adding a random intercept to each curve. Compared with Model 1, the mean mismatch rate from Model 2 is lower by 12.86%, and the mean V-measure is higher by 26%.

For the Canadian weather dataset analysis, we considered temperature data from all stations except those located in Vancouver and Victoria because they present relatively flat temperature curves compared to other locations. We applied the proposed VB algorithm under Model 1 to the weather data. The left plot in Fig. 10 shows the DIC values for different possible numbers of clusters ($K=2,3,4,5$). We can observe that the best number of clusters for separating the Canadian weather data is three, which corresponds to the smallest DIC. Finally, we present the clustering results with $K=3$ on a map of Canada in the right plot in Fig. 10. As can be seen, when $K=3$, we have three resulting groups in three different colors. In general, most of the weather stations in purple are located in northern Canada. In contrast, stations in southern Canada are separated into two groups color-coded in blue and red on the map of Canada. Although some stations may be incorrectly clustered, we can still see a potential pattern that makes sense geographically.

Fig. 9

Raw curves (dashed curves) from the Growth dataset where green curves refer to the boys’ heights while the blue ones are for the girls’, with empirical mean curves (in solid black) and our VB estimated mean curves (in solid red). The left graph is resulted from Model 1 while the right is from Model 2 (color figure online)

Fig. 10

Left: DIC values for different clusters ($K=2,3,4,5$) in Canadian weather data. The best number of clusters is three which has the smallest DIC. Right: Clustering results under Model 1 (cities with same color are predicted in the same cluster) for Canadian weather data with preset three clusters ($K=3$) (color figure online)

5 Conclusion and discussion

This paper develops a new model-based algorithm to cluster functional data via Bayesian variational inference. We first provide an overview of variational inference, a method used to approximate the posterior distribution under the Bayesian framework through optimization. We then derive a mean-field Variational Bayes (VB) algorithm. Next, the coordinate ascent variational inference is applied to update each term in the variational distribution factorization until convergence of the evidence lower bound. Finally, each observed curve is assigned to the cluster with the largest posterior probability.

We build our proposed VB algorithm under two different models. In Model 1, we assume the errors are independent, which may be a strong assumption. Motivated by the Growth data for the children’s heights, which show a parallel structure indicating a shift among curves, we extended our approach to Model 2, which includes more complex variance-covariance structures by adding a random intercept for each curve.

The performance of our proposed VB algorithm in clustering functional data is supported by simulations and real data analyses. In simulation studies, VB accurately estimates mean curves, closely aligning with true curves, resulting in minimal empirical mean integrated squared errors and demonstrating a good fit. In most scenarios, VB consistently outperforms other considered methods (classical k-means, functional k-means, funFEM, and SaS-Funclust) with the highest V-measure and the lowest mismatch rate. We provide insight into the selection of the number of clusters (mixture components) through a two-fold scheme based on DIC. Robustness is assessed via a sensitivity analysis across different prior settings and a study involving a misspecified type of basis functions. In our simulations, the proposed VB algorithm demonstrated computational efficiency, averaging 4 s to cluster each simulated dataset. In particular, for simulated data under Scenarios 1 and 3, VB is over 20 times faster than MCMC (Gibbs sampler). Moreover, VB demonstrates strong consistency with MCMC in estimating the marginal posterior distribution of B-spline basis coefficients and precision parameters. In addition to simulation studies, applying the VB algorithm to the Growth data reveals that Model 2 with a random intercept surpasses Model 1 in both mean curve estimation and clustering performance when the curves from the same cluster show a parallel structure.

The main advantage of our proposed VB algorithm is that we model the raw data and obtain clustering assignments and cluster-specific smooth mean curves simultaneously. In other words, compared to some previous methods where researchers first smooth the data and then cluster the data using only the information after smoothing (e.g., the coefficients of B-spline basis functions); our model, as a regression mixture model, directly uses the raw data as input, performing smoothing and clustering simultaneously. In addition, as we take a Bayesian inference approach, we can measure the uncertainty of our proposed clustering using the obtained cluster assignment posterior probabilities.

While our study has introduced the VB algorithm to cluster functional data using a B-spline regression mixture model, it is important to recognize its limitations. Although our Model 2, which includes a random intercept, provides a more flexible dependence structure, one could explore more intricate Gaussian processes for modeling the random errors. Additionally, it is worth noting that VB is not the sole method for clustering functional data with regression mixtures; alternatives like Gibbs sampler (as used for comparison here) or other MCMC-based algorithms can also be considered. In this work, we focus on the case where, for each curve, the number of basis functions is smaller than the number of evaluation points ($M < n$). So, future work may include investigation and further extension of the proposed VB under high-dimensional settings ($M>>n$), paying special attention to the issue of underestimation of the variability of the posterior estimates (Mukherjee and Sen 2022; Devijver 2017). For large datasets (large number of curves, N), the coordinate ascent variational inference algorithm, which considers all data points, may result in a high computational cost. Therefore, one may consider scalable algorithms such as the stochastic variational inference (Hoffman et al. 2013) for approximating the posterior distributions.

Furthermore, our approach relies on the assumption that the number of B-spline basis functions (M) is known prior to applying the VB algorithm. This assumption aligns with practical scenarios where researchers may subjectively determine M based on their expertise and/or visual inspection of the curves (Franco et al. 2023; Günther et al. 2021; Lenzi et al. 2017). However, to enhance the model’s adaptability and automate the selection process, future investigations could explore the integration of a mechanism for selecting the number of B-spline bases directly within the VB algorithm itself. Relevant approaches and references for the selection of the number of basis functions include Souza et al. (2023); Devijver et al. (2020); Gálvez et al. (2015); Yuan et al. (2013); Dias and Garcia (2007), and DeVore et al. (2003).

Appendices

VB algorithm for Model 1

1.1 Main steps

This section describes the main steps of the VB algorithm for inferring ${\varvec{Z}}$, ${\varvec{\phi }}$, ${\varvec{\pi }}$ and ${\varvec{\tau }}$ in Model 1 in Sect. 2.2.1, which is summarized in Algorithm 2.

• 1. VD factorization

  $$\begin{aligned} q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) = \prod _{i=1}^N q(Z_i) \times \prod _{k=1}^K q({\varvec{\phi }}_k) \times \prod _{k=1}^K q(\tau _k) \times q({\varvec{\pi }}) \end{aligned}$$

  (A1)

• 2. Complete data log-likelihood

  $$\begin{aligned} \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }})= & {} \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }}) \; + \; \log p(\textbf{Z} \vert {\varvec{\pi }}) \nonumber \\{} & {} + \log p({\varvec{\phi }}) \;+\; \log p({\varvec{\tau }}) \;+\; \log p({\varvec{\pi }}). \end{aligned}$$

  (A2)

• 3. Update equations

(i)Update equation for $q({\varvec{\pi }})$

Since only the second term, $\log p(\textbf{Z} \vert {\varvec{\pi }})$, and the last term, $\log p({\varvec{\pi }})$, in (A2) depend on ${\varvec{\pi }}$, the update equation $q^*({\varvec{\pi }})$ can be derived as follows.

$$\begin{aligned}{} & {} {\log q^*({\varvec{\pi }})} \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right) \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p(\textbf{Z}\vert {\varvec{\pi }}) \right) \; +\; {{\mathbb {E}}}_{-{\varvec{\pi }}} \left( \log p({\varvec{\pi }})\right) \nonumber \\{} & {} \quad = {{\mathbb {E}}}_{-{\varvec{\pi }}} \left[ \sum _{i=1}^N \sum _{k=1}^{K} \mathrm{{I}}(Z_i =k) \log \pi _k \right] + \log p({\varvec{\pi }}) \nonumber \\{} & {} \quad \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^{K} \log \pi _k \left[ \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) \right] + \sum _{k=1}^{K} [d^0_k -1 ]\log \pi _k\nonumber \\{} & {} \quad = \sum _{k=1}^{K} \log \pi _k \left[ \left( \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) + d^0_k \right) -1 \right] .\nonumber \end{aligned}$$

Therefore, $q^*({\varvec{\pi }})$ is a Dirichlet distribution with parameters $\textbf{d}^*=(d_1^*,\ldots ,d_K^*)$, where

$$\begin{aligned} d^{*}_{k}= d^0_k + \sum _{i=1}^N {{\mathbb {E}}}_{q^{*}(Z_i)}\left( \mathrm{{I}}(Z_i=k)\right) . \end{aligned}$$

(3)

(ii) Update equation for $q(Z_i)$

$$\begin{aligned} \log q^*(Z_i) \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-Z_i} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right) \end{aligned}$$

(4)

When taking the expectation above we just need to consider the first term, $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})$, and the second term, $\log p(\textbf{Z} \vert {\varvec{\pi }})$, in (A2). Note that we can write $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})$ and $\log p(\textbf{Z} \vert {\varvec{\pi }})$ into two parts, one that depends on $Z_i$ and one that does not.

$$\begin{aligned} \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})= & {} \sum _{k=1}^K \mathrm{{I}}(Z_i = k) \log p({\textbf{Y}}_i \vert Z_i =k, {\varvec{\phi }}_k,\tau _k) \nonumber \\{} & {} +\,\sum _{l:l\ne i} \sum _{k=1}^K \mathrm{{I}}(Z_l=k) \log p({\textbf{Y}}_l \vert Z_l=k,{\varvec{\phi }}_k,\tau _k) \nonumber \\ \log p(\textbf{Z} \vert {\varvec{\pi }})= & {} \sum _{k=1}^K \mathrm{{I}}(Z_i=k) \log \pi _k + \sum _{l:l\ne i} \sum _{k=1}^K \mathrm{{I}}(Z_l = k) \log \pi _k \nonumber \end{aligned}$$

Now when taking the expectation in (4) the parts that do not depend on $Z_i$ in $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})$ and $\log p(\textbf{Z} \vert {\varvec{\pi }})$ in (A2) will be added as a constant in the expectation. So, we obtain

$$\begin{aligned} \log q^*(Z_i){} & {} \overset{\mathrm{\tiny {+}}}{\approx }\sum _{k=1}^K I(Z_i =k)\left\{ \frac{n_i}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k) \right. \nonumber \\{} & {} \quad -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k){{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k) \right] \nonumber \\{} & {} \quad \left. + \,{{\mathbb {E}}}_{q^*({\varvec{\pi }})} (\log \pi _k) \right\} \nonumber \end{aligned}$$

Therefore, $q^*(Z_i)$ is a categorical distribution with parameters

$$\begin{aligned} p^*_{ik} = \frac{e^{\alpha _{ik}}}{\sum _{k=1}^Ke^{\alpha _{ik}}}, \end{aligned}$$

(5)

where

$$\begin{aligned} \alpha _{ik}= & {} \frac{n_i}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k) -\frac{1}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k){{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k) \right] \nonumber \\{} & {} + \,{{\mathbb {E}}}_{q^*({\varvec{\pi }})} (\log \pi _k). \nonumber \end{aligned}$$

(iii)Update equation for $q({\varvec{\phi }}_k)$

Note that only the first term, $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})$, and the third term, $\log p({\varvec{\phi }})$, in (A2) depend on ${\varvec{\phi }}_k$. Similarly to the previous case for $q^*(Z_i)$, we can write $\log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\phi }},{\varvec{\tau }})$ and $\log p({\varvec{\phi }})$ in two parts, one that depends on ${\varvec{\phi }}_k$ and the other that does not. Therefore, we obtain

$$\begin{aligned} \log q^*({\varvec{\phi }}_k){} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{-{\varvec{\phi }}_k} \left( \log p(\textbf{Y},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right) \nonumber \\{} & {} \overset{\mathrm{\tiny {+}}}{\approx }{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _k) \sum _{i=1}^N \frac{n_i}{2}{{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] \nonumber \\{} & {} \quad \; - \; \frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k)\sum _{i=1}^N \nonumber \\{} & {} \quad \left\{ {{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)\right\} \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \quad -\frac{M}{2} \log v^0 \; - \;\frac{1}{2}v^0 ({\varvec{\phi }}_k -\textbf{m}_k^0)^T({\varvec{\phi }}_k -\textbf{m}_k^0) \end{aligned}$$

(7)

All expectations will be later defined, but note that, for example, ${{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] = p^*_{ik}$. First, we will focus on the quadratic forms that appear in (6) and (7).

$$\begin{aligned}{} & {} -\frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k) \nonumber \\{} & {} \quad - \;\frac{1}{2}v^0 ({\varvec{\phi }}_k -\textbf{m}_k^0)^T({\varvec{\phi }}_k -\textbf{m}_k^0) = \nonumber \\{} & {} \quad - \; \frac{1}{2} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik}\left[ {\textbf{Y}}_i^T {\textbf{Y}}_i - 2{\textbf{Y}}_i^T\textbf{B}_i{\varvec{\phi }}_k + {\varvec{\phi }}_k^T\textbf{B}_i^T\textbf{B}_i{\varvec{\phi }}_k \right] \nonumber \\{} & {} \quad -\frac{1}{2}v^0\left[ {\varvec{\phi }}^T_k{\varvec{\phi }}_k - 2(\textbf{m}_k^0)^T{\varvec{\phi }}_k + (\textbf{m}_k^0)^T\textbf{m}_k^0 \right] \overset{\mathrm{\tiny {+}}}{\approx }\nonumber \\{} & {} \quad -\frac{1}{2} {\varvec{\phi }}_k^T \left[ v^0\textbf{I} + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} \textbf{B}_i^T\textbf{B}_i \right] {\varvec{\phi }}_k \nonumber \\{} & {} \quad -\,\frac{1}{2}(-2)\left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^T \textbf{B}_i \right] {\varvec{\phi }}_k \end{aligned}$$

(8)

Now let

$$\begin{aligned} \mathbf {\Sigma }^*_k = \left[ v^0\textbf{I} + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} \textbf{B}_i^T\textbf{B}_i \right] ^{-1}. \end{aligned}$$

(9)

We can then rewrite (8) as

$$\begin{aligned} -\frac{1}{2} {\varvec{\phi }}_k^T \mathbf {\Sigma }^{*-1}_k {\varvec{\phi }}_k -\frac{1}{2}(-2)\left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^T\textbf{B}_i \right] \mathbf {\Sigma }^*_k\mathbf {\Sigma }^{*-1}_k {\varvec{\phi }}_k. \end{aligned}$$

Therefore, $q^*({\varvec{\phi }}_k)$ is $MVN(\textbf{m}^*_k,\mathbf {\Sigma }^*_k)$ with $\mathbf {\Sigma }^*_k$ as in (9) and mean vector

$$\begin{aligned} \textbf{m}^*_k = \left[ v^0(\textbf{m}_k^0)^T + {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _k) \sum _{i=1}^N p^*_{ik} {\textbf{Y}}_i^T \textbf{B}_i \right] \mathbf {\Sigma }^*_k. \end{aligned}$$

(10)

(iv) Update equation for $q(\tau _k)$

Similarly to the calculations in i) and ii) we can write

$$\begin{aligned}{} & {} \log q^*(\tau _k) \overset{\mathrm{\tiny {+}}}{\approx }\log \tau _k \sum _{i=1}^N \frac{n_i}{2}p^*_{ik} -\frac{1}{2}\tau _k\sum _{i=1}^N p^*_{ik}{{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)\right] \nonumber \\{} & {} \qquad + \; (a^0 -1)\log \tau _k - r^0\tau _k \nonumber \end{aligned}$$

Therefore, $q^*(\tau _k)$ is a Gamma distribution with parameters

$$\begin{aligned} A^*_k = a^0 + \sum _{i=1}^N \frac{n_i}{2}p^*_{ik} \end{aligned}$$

(11)

and

$$\begin{aligned} R^*_{k} = \left( r^0 + \frac{1}{2} \sum _{i=1}^N p^*_{ik} {{\mathbb {E}}}_{q^*({\varvec{\phi }}_k)}\left[ ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)\right] \right) . \end{aligned}$$

(12)

4. Expectations

Next, we calculate the expectations in the update equations for each component in the VD. Let ${\varvec{\Psi }}$ be the digamma function defined as

$$\begin{aligned} {\varvec{\Psi }}(x)=\frac{d}{dx}\log \Gamma (x), \end{aligned}$$

(13)

which can be easily calculated via numerical approximation. The values of the expectations taken with respect to the approximated distributions are given as follows.

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(Z_i)}[ \mathrm{{I}}(Z_i=k)] = p^*_{ik} \end{aligned}$$

(14)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k}) = \frac{A^{*}_{k}}{R^{*}_{k}} \end{aligned}$$

(15)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) = {\varvec{\Psi }}(A^{*}_k) - \log R^{*}_{k} \end{aligned}$$

(16)

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _{k}) = {\varvec{\Psi }}(d^{*}_{k}) - {\varvec{\Psi }}\left( \sum _{k=1}^K d^{*}_{k}\right) \end{aligned}$$

(17)

In addition, using the fact that ${{\mathbb {E}}}({\textbf{X}}^T {\textbf{X}}) = \text{ trace }[\text{ Var }({\textbf{X}})] + {{\mathbb {E}}}({\textbf{X}})^T{{\mathbb {E}}}({\textbf{X}})$, we obtain

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*({\varvec{\phi }})}\left[ ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)\right] \nonumber \\{} & {} \quad = \text{ trace }\left( \textbf{B}_i \mathbf {\Sigma }^*_k \textbf{B}_i^T \right) +\, ({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k)^T({\textbf{Y}}_i - \textbf{B}_i\textbf{m}^*_k). \end{aligned}$$

(18)

1.2 ELBO calculation

In this section, we show how to calculate the ELBO, which is the convergence criterion of our proposed VB algorithm and will be updated at the end of each iteration until it converges. Equation (4) gives the ELBO:

$$\begin{aligned} \text{ ELBO }(q) = {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] - {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] , \end{aligned}$$

where

$$\begin{aligned}{} & {} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}},\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] = {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] +{{\mathbb {E}}}_{q^*} \left[ \log p\left( \textbf{Z} \vert {\varvec{\pi }} \right) \right] \nonumber \\{} & {} \quad +{{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\phi }})\right] + {{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\tau }})\right] + {{\mathbb {E}}}_{q^*} \left[ \log p({\varvec{\phi }})\right] , \nonumber \end{aligned}$$

and

$$\begin{aligned} {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right]= & {} {{\mathbb {E}}}_{q^*} \left[ \log q(\textbf{Z}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\phi }}) \right] \nonumber \\{} & {} +\, {{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\pi }}) \right] + {{\mathbb {E}}}_{q^*} \left[ \log q({\varvec{\tau }}) \right] \nonumber \end{aligned}$$

Therefore, we can write the ELBO as the summation of 5 terms:

$$\begin{aligned} \text{ ELBO }(q)= & {} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right] + diff_{\textbf{Z}} + diff_{{\varvec{\phi }}} \nonumber \\{} & {} + \,diff_{{\varvec{\tau }}} + diff_{{\varvec{\pi }}} \end{aligned}$$

(19)

where,

$$\begin{aligned} diff_{\textbf{Z}} = {{\mathbb {E}}}_{q^*}\left[ \log p (\textbf{Z} \vert {\varvec{\pi }})\right] -{{\mathbb {E}}}_{q^*}\left[ \log q(\textbf{Z})\right] . \end{aligned}$$

Specifically,

$$\begin{aligned} diff_{\textbf{Z}} \equiv \sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik} {{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _k) - \sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik} \log p^{*}_{ik}. \end{aligned}$$

(20)

The other terms in (19) are calculated as follows:

$$\begin{aligned} diff_{{\varvec{\phi }}}\equiv & {} -\frac{1}{2}\sum _{k=1}^K v_k^0\{\text{ trace }\left( \mathbf {\Sigma }^*_k \right) + (\textbf{m}^*_k-\textbf{m}^0_k)^T(\textbf{m}^*_k-\textbf{m}^0_k)\} +\frac{1}{2}\sum _{k=1}^K \log \vert \mathbf {\Sigma }^*_k\vert ,\nonumber \\ diff_{{\varvec{\tau }}}\equiv & {} \sum _{k=1}^K \{(a^0-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k})-r^0{{\mathbb {E}}}_{q^*(\tau _k)}(\tau _{k})\} \nonumber \\{} & {} -\, \sum _{k=1}^K\{A^*_k(\log R_k^{*}-1) - \log \Gamma (A^*_k) +\,(A^*_k-1){{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k})\}, \nonumber \\ diff_{{\varvec{\pi }}}\equiv & {} \sum _{k=1}^K (d_k^0-d_k^{*}){{\mathbb {E}}}_{q^*({\varvec{\pi }})}(\log \pi _{k}), \end{aligned}$$

(21)

and

$$\begin{aligned} {{\mathbb {E}}}_{q^*} \left[ \log p({\textbf{Y}}\vert \textbf{Z},{\varvec{\pi }},{\varvec{\phi }},{\varvec{\tau }}) \right]= & {} \sum _{i=1}^{N}\sum _{k=1}^K p^{*}_{ik}\left\{ \frac{n_i}{2}{{\mathbb {E}}}_{q^*(\tau _k)}(\log \tau _{k}) -\frac{1}{2}\frac{A_k^{*}}{R_k^{*}} \right. \nonumber \\{} & {} \left. {{\mathbb {E}}}_{q^*({\varvec{\phi }})}\left[ ({\textbf{Y}}_i \; - \, \textbf{B}_i{\varvec{\phi }}_k)^T({\textbf{Y}}_i - \textbf{B}_i{\varvec{\phi }}_k)\right] \right\} . \end{aligned}$$

(22)

Therefore, at iteration c, we calculate $\text{ ELBO}^{(c)}$ using all parameters obtained at the end of iteration c. Convergence of the algorithm is achieved if $\text{ ELBO}^{(c)}-\text{ ELBO}^{(c-1)}$ is smaller than a given threshold. It is important to note that we use the fact that $\displaystyle \lim \nolimits _{p^{*}_{ik} \rightarrow 0} p^{*}_{ik}\log p^{*}_{ik}=0$ to avoid numerical issues when calculating (20).

Algorithm 2

Clustering functional data via variational inference

Plots

See Figs. 11, 12, 13, 14.

Fig. 11

EMSE versus the observed evaluation point for each cluster in Scenarios 2, 3, 4, 5 and 6. In Scenario 5, the straight line in cluster one does not mean there is no EMSE. This is because compared to cluster two and three, the EMSE in cluster one is very small (the median is $1.41\times 10^{-11}$)

Fig. 12

Example of simulated data under Scenario 10 (left) and Scenario 12 (right) for Model 2. Raw curves (different colors correspond to different clusters), cluster-specific true mean curves (in black) and corresponding estimated mean curves (in red) (color figure online)

Fig. 13

EMSE versus the observed evaluation point for each cluster in Scenarios 9, 10, 11 and 12

Fig. 14

Raw curves of the Canadian weather data. Different curves have different colors