1 Introduction

Owing to the increasing availability of high-dimensional datasets, regression models for multivariate response and high-dimensional predictors have become important tools.

In this article, we describe two procedures where a random target variable \(\varvec{Y} \in \mathbb {R}^q\) depends on explanatory variables within a cluster-specific regression model. Each cluster is represented by a parametric distribution, the entire dataset being modeled by a mixture of these distributions. The model assumes that each observation \(i \in \{1,\ldots ,n\}\) originates from one of K disjoint classes and that the data \((\varvec{Y}_i,\varvec{x}_i) \in \mathbb {R}^q \times \mathbb {R}^p\) are independent and identically distributed such that if i belongs to class \(k \in \{1,\ldots ,K\}\), the target variable \(\varvec{Y}_i\) results from a regression model

$$\begin{aligned} \varvec{Y}_i=\mathbf {B}_k \varvec{x}_i + \varvec{\varepsilon }_i \end{aligned}$$
(1)

with an unknown matrix of coefficients \(\mathbf {B}_k\in \mathbb {R}^{q\times p}\) and independent errors \(\varvec{\varepsilon }_i \sim \mathcal {N}_q(0,\Sigma _k)\) with an unknown diagonal covariance matrix \(\Sigma _k\) of size \(q \times q\). Each observation \(i \in \{1,\ldots ,n\}\) has a probability \(\pi _k\) to belong to the cluster \(k\in \{1,\ldots ,K\}\).

We work with high-dimensional data, in other words the number of parameters to estimate \( K(qp+q+1)-1\) is larger than the number of observed target values \(q \times n\). Two ways are considered in this paper, coefficients sparsity and ranks sparsity. The first approach consists in estimating the matrix \(\mathbf {B}_k\) by a matrix with few nonzero coefficients. The well-known Lasso estimator, introduced by Tibshirani (1996) for linear models, is the solution chosen here. We refer to Bühlmann and van de Geer (2011) for an overview of the Lasso estimator and to Meinshausen and Bühlmann (2010) for stability selection results. In the second approach, we consider the rank sparsity in \(\mathbf {B}_k\). This idea dates back to the 1950’s and was initiated by Anderson (1951) for the linear model. Izenman (1975) introduced the term of reduced-rank regression for this class of models. For more recent works, we refer to Giraud (2011) and to Bunea et al. (2012). Nevertheless, the linear model is appropriate for homogeneous observations, which is a strong assumption. We extend in this paper those methods to mixture regression models.

Remark that we estimate the number of components, model parameters and cluster proportions. In the case of a large number of regressor variables, we use variable selection tools in order to detect relevant regressors. Since the structure of interest may often be contained into a subset of available variables and many attributes may be useless or even harmful to detect a reasonable clustering structure, it is important to select the relevant indices. Moreover, removing irrelevant indices enables us to get an easier model and largely enhance comprehension.

An important extension of a high-dimensional dataset is a functional dataset. We refer to Ramsay and Silverman (2005) for an overview. Moreover, a lot of recent works have been done on regression models for functional data: for example, we refer to Ciarleglio and Ogden (2014) for a study with scalar response and functional regressors. In this paper, we focus on the projection of functions onto a well-suited wavelet basis. Indeed, wavelets handle many types of functional data, because they represent global and local attributes of functions and can deal for example with discontinuities. Moreover, a large class of functions is well represented with few nonzero coefficients for a suitable wavelet, which leads to a sparse matrix of coefficients and then to a sparse regression matrix.

We propose here two procedures for clustering high-dimensional or functional data, where the high-dimensional or functional random target variable \(\varvec{Y} \in \mathbb {R}^q\) depends on high-dimensional or functional predictors \(\varvec{x} \in \mathbb {R}^p\) with a cluster-specific regression model.

Our two procedures are mainly based on three recent works. Firstly, we refer to the article of Städler et al. (2010), which studies a finite mixture regression model. Even if we work on a multivariate version of it, the model considered in the article of Städler et al. (2010) is adopted here. The second, the article of Meynet and Maugis-Rabusseau (2012), deals with model-based clustering in density estimation. They propose a procedure, called the Lasso-MLE procedure, which determines the number of clusters, the set of relevant indices for the clustering and a clustering of the observations, with high-dimensional data. We extend this procedure to regression models. Finally, Giraud (2011) suggests a low rank estimator for the linear model. To consider the matrix structure, we extend this last approach to mixture models.

We consider a finite mixture of Gaussian regression models. The two procedures we propose follow the same steps. Firstly, a penalized likelihood approach is considered to determine potential sets of relevant indices. Varying the regularization parameter, a data-driven collection of models is constructed where each model has a reasonable complexity. The second step of the procedures consists in refitting parameters by a less biased estimator, restricting the model on selected indices. Then, we select a model among the collection using the slope heuristic, which was introduced by Birgé and Massart (2007). The difference between the two procedures is in the refitting step. In the first procedure, later called Lasso-MLE procedure, the maximum likelihood estimator is used. The second procedure, called Lasso-Rank procedure, deals with low rank estimation. For each model in the collection, a subcollection of models with means estimated by various low rank matrices is constructed. It leads to sparsity for the coefficients and for the rank, and it considers the mean within its matrix structure.

The article is organized as follows. Section 2 deals with Gaussian mixture regression models and the considered collection of models is described. In Sect. 3, the two procedures that we propose to solve the problem of high-dimensional regression data clustering are described. Section 4 presents an illustrative example, to highlight each choice done in the two procedures. Section 5 states the functional data case, with a description of the projection proposed to convert these functions into coefficients data. We end this section by studying simulated and benchmark data. Finally, a conclusion section ends this article.

2 Finite mixture of Gaussian regression models

The model used is a finite Gaussian mixture regression model. Städler et al. (2010) describe this model when the deterministic predictors \(\varvec{x} \in \mathbb {R}^p\) are multivariate and the target variable \(\varvec{Y} \in \mathbb {R}\) is a scalar. In this section, it is generalized to multivariate response. Let us mention that this model has already been introduced, we refer for example to Jones and McLachlan (1992). In this paper, we deal with high-dimensional data.

2.1 The model

We observe n independent couples \(((\varvec{y}_{1}, \varvec{x}_{1}), \ldots , (\varvec{y}_{n}, \varvec{x}_{n}))\), where \(\varvec{x}_i \in \mathbb {R}^p\) are deterministic predictors and \(\varvec{y}_i \in \mathbb {R}^q\) is a realization of a random variable \(\varvec{Y}_i\in \mathbb {R}^q\) of unknown density \(s^*(.|\varvec{x}_i)\), for all \(i \in \{1,\ldots ,n\}\). The random response variable \(\varvec{Y}_i \in \mathbb {R}^q\) depends on a set of explanatory variables, written \(\varvec{x}_i \in \mathbb {R}^p\), through a regression-type model. If \((\varvec{Y}_i,\varvec{x}_i)\) originates from an individual i in class k, we assume that

$$\begin{aligned} \varvec{Y}_i = \mathbf {B}_k \varvec{x}_i + \varvec{\varepsilon }_i ; \end{aligned}$$

where \(\varvec{\varepsilon }_i \sim \mathcal {N}_q(0, \varvec{\Sigma }_k)\), \(\mathbf {B}_k \in \mathbb {R}^{q \times p}\) is the matrix of class-specific regression coefficients and \(\varvec{\Sigma }_k\) is \(q\times q\) diagonal positive-definite matrix.

We assume the following Gaussian regression mixture model:

  • \((\varvec{Y}_1,\ldots , \varvec{Y}_n)\) are independent,

  • \(\varvec{Y}_i\) has the density \(s_{\varvec{\xi }}^K(.|\varvec{x}_i)\), with

    $$\begin{aligned} s_{\varvec{\xi }}^K(\varvec{y}|\varvec{x})&=\sum _{k=1}^{K} \frac{\pi _{k}}{(2 \pi )^{q/2} \text {det}(\varvec{\Sigma }_k)^{1/2}} \exp \left( -\frac{(\varvec{y}-\mathbf {B}_{k} \varvec{x})^t \varvec{\Sigma }_{k}^{-1}(\varvec{y}-\mathbf {B}_{k} \varvec{x})}{2} \right) ;\\ \varvec{\xi }&=(\pi _{1},\ldots , \pi _{K},\mathbf {B}_{1},\ldots ,\mathbf {B}_{K},\varvec{\Sigma }_{1},\ldots ,\varvec{\Sigma }_{K}) \in \Xi _{K}\\ \Xi _K&= \left( \Pi _{K} \times (\mathbb {R}^{q\times p})^K \times (\mathbb {D}_q^{++})^K \right) ; \\ \Pi _{K}&= \left\{ (\pi _{1}, \ldots , \pi _{K}) ; \pi _{k} >0 \text { for } k \in \{1,\ldots , K\} \text { and } \sum _{k=1}^{K} \pi _{k} = 1 \right\} ; \\ \mathbb {D}_q^{++}&\text { is the set of } q \times q \text { diagonal and positive-definite matrices} . \end{aligned}$$

We have denoted by \(\pi _k\) the proportion of the class k. For all \(k \in \{1,\ldots ,K\}\), for all \(m \in \{1,\ldots ,q\}\), for \(\varvec{x} = (\xi _1,\ldots , \xi _p) \in \mathbb {R}^p\), \([\mathbf {B}_k \varvec{x}]_m= \sum _{j=1}^{p} [\mathbf {B}_{k}]_{m,j} \xi _{j}\) is the mth component of the mean of the kth mixture component.

We prefer to work with a reparametrized version of this model whose penalized maximum likelihood estimator is scale-invariant and easier to compute. Indeed, it is not equivariant under scaling of the response. More precisely, consider the transformation

$$\begin{aligned} \check{\varvec{Y}} = b\varvec{Y}, \check{\varvec{B}}=b\varvec{B}, \check{\varvec{\Sigma }} = b^2 \varvec{\Sigma }, \end{aligned}$$

for \(b>0\) which leaves the model invariant. A reasonable estimator based on transformed data \(\check{\varvec{Y}}\) should lead to an estimator which is related to the first one up to the homothetic transformation. This is not the case for the maximum likelihood estimator of \(\varvec{B}\) and \(\varvec{\Sigma }\). Secondly, the optimization of the log-likelihood is non-convex and hence, it leads to computational issues. Then, we reparametrize the model described above by generalizing the reparametrization described by Städler et al. (2010).

For all \(k \in \{1,\ldots ,K\}\), we define the new parameters by

$$\begin{aligned} \varvec{P}_k ^t\varvec{P}_k = \varvec{\Sigma }_k^{-1};\\ \varvec{\Phi }_k=\varvec{P}_k \mathbf {B}_k; \end{aligned}$$

where \(\varvec{\Phi }_k \in \mathbb {R}^{q \times p}\), \(\varvec{P}_k\) is the Cholesky decomposition of the positive-definite matrix \(\varvec{\Sigma }_k^{-1}\). Remark that \(\varvec{P}_k\) is a diagonal matrix of size \(q \times q\).

The model within its reparametrized form is then

  • \((\varvec{Y}_1,\ldots , \varvec{Y}_n)\) are independent,

  • \(\varvec{Y}_i\) has the density \(h_\theta ^K(.|\varvec{x}_i)\), with

    $$\begin{aligned}&h_\theta ^K(\varvec{y}|\varvec{x})=\sum _{k=1}^{K} \frac{\pi _{k} \det (\varvec{P}_k)}{(2 \pi )^{q/2}} \exp \left( -\frac{(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k \varvec{x} )^t(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k \varvec{x} )}{2} \right) \\ \theta&=(\pi _{1},\ldots , \pi _{K},\varvec{\Phi }_{1},\ldots ,\varvec{\Phi }_{K},\varvec{P}_{1},\ldots ,\varvec{P}_{K}) \in \Theta _K\\&= \left( \Pi _{K} \times (\mathbb {R}^{p \times q})^K\times (\mathbb {D}_q^{++})^K \right) \\&\Pi _{K} = \left\{ (\pi _{1}, \ldots , \pi _{K}) ; \pi _{k} >0 \text { for } k \in \{1,\ldots , K\} \text { and } \sum _{k=1}^{K} \pi _{k} = 1 \right\} \\&\mathbb {D}_q^{++} \text { is the set of diagonal and positive-definite matrices in } \mathbb {R}^q . \end{aligned}$$

For the sample \(((\varvec{y}_1,\varvec{x}_1),\ldots , (\varvec{y}_n,\varvec{x}_n))\), the log-likelihood of this model equals

$$\begin{aligned}&l(\theta ,\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n)\\&\quad =\sum _{i=1}^n \log \left( \sum _{k=1}^{K} \frac{\pi _{k} \det (\varvec{P}_k)}{(2 \pi )^{q/2}} \exp \left( -\frac{(\varvec{P}_k\varvec{y}_i-\varvec{\Phi }_k\varvec{x}_i)^t(\varvec{P}_k\varvec{y}_i-\varvec{\Phi }_k\varvec{x}_i)}{2} \right) \right) ; \end{aligned}$$

and the maximum likelihood estimator (MLE) is

$$\begin{aligned} {\hat{\theta }}^{MLE} := \underset{\theta \in \Theta _K}{\mathrm{argmin}} \left\{ -\frac{1}{n} l (\theta , \varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) \right\} . \end{aligned}$$

Since we deal with the high-dimension case, this estimator has to be regularized to get stable estimates. Therefore, we propose the \(\ell _1\)-norm penalized MLE

$$\begin{aligned} \hat{\theta }^{\text {Lasso}}(\lambda ) := \underset{\theta \in \Theta _K}{\mathrm{argmin}} \left\{ -\frac{1}{n} l_{\lambda }(\theta , \varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) \right\} ; \end{aligned}$$
(2)

where

$$\begin{aligned} - \frac{1}{n} l_\lambda (\theta , \varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) = -\frac{1}{n} l(\theta , \varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) + \lambda \sum _{k=1}^{K} \pi _k ||\varvec{\Phi }_k||_1 ; \end{aligned}$$

where \(||\varvec{\Phi }_k||_1 = \sum _{j=1}^p \sum _{m=1}^q |[\varvec{\Phi }_k]_{m,j}|\) and where \(\lambda > 0\) has to be specified. Remark that this estimator is not the usual \(\ell _1\)-estimator, called the Lasso estimator, introduced by Tibshirani (1996). Indeed, the \(\ell _1\)-norm of the coefficients matrices \(\varvec{\Phi }_k\) and small variances are penalized simultaneously, which has some close relations to the Bayesian Lasso (see Park and Casella (2008)). Moreover, the reparametrization allows us to consider non-standardized data.

Notice that we restrict ourselves in this article to diagonal covariance matrices which are dependent of the clusters. We assume that the coordinates of the \(\varvec{Y}_i\) are independent, which is a strong assumption, but it allows us to reduce easily the dimension. We refer to Celeux and Govaert (1995) for different parametrizations of the covariance matrix. Nevertheless, because we work with high-dimensional data (p and q are high and n is small) we prefer a parsimonious model from the diagonal family. We allow different volume clusters because it leads to detect many clustering structures, as explained in Celeux and Govaert (1995).

2.2 Clustering with finite mixture of Gaussian regression models

Suppose that there is a known number of clusters K and assume that we get, from the observations, an estimator \(\hat{\theta }\) such that \(h_{\hat{\theta }}^K\) well approximates the unknown density \(s^{*}(.|\varvec{x}_i)\). We look at this problem as a missing data problem: if we denote by \(\varvec{Z}=(\varvec{Z}_{1}, \ldots , \varvec{Z}_{n})\) the component membership, where \(\varvec{Z}_{i}=([\varvec{Z}_{i}]_1,\ldots , [\varvec{Z}_{i}]_K)\) for \(i \in \{1,\ldots ,n\}\) is defined by

$$\begin{aligned} \, [\varvec{Z}_{i}]_k= \left\{ \begin{array}{ll} 1 &{} \text { if } i \text { originates from mixture component } k; \\ 0 &{} \text { otherwise;} \end{array} \right. \end{aligned}$$

the complete data are \(((\varvec{y}_{1},\varvec{x}_{1},\varvec{z}_{1}), \ldots , (\varvec{y}_{n}, \varvec{x}_{n},\varvec{z}_{n}))\). Remark that \(\varvec{Z}_i\) follows a multinomial distribution with parameters 1 and \((\pi _1,\ldots , \pi _K)\).

Thanks to the estimator \(\hat{\theta }\), the Maximum A Posteriori principle (MAP principle) is used to cluster data. Specifically, for all \(i \in \{1,\ldots ,n\}\), for all \(k \in \{1,\ldots , K\}\), consider

$$\begin{aligned} \hat{\varvec{\tau }}_{i,k} (\hat{\theta }) =\frac{\hat{\pi }_{k} \det (\hat{\varvec{P}}_k) \exp \left( - \frac{1}{2} (\hat{\varvec{P}}_k \varvec{y}_i - \hat{\varvec{\Phi }}_k\varvec{x}_i)^t (\hat{\varvec{P}}_k \varvec{y}_i - \hat{\varvec{\Phi }}_k\varvec{x}_i) \right) }{\sum _{r=1}^{K} \hat{\pi }_r \det (\hat{\varvec{P}}_r) \exp \left( - \frac{1}{2} ( \hat{\varvec{P}}_r \varvec{y}_i - \hat{\varvec{\Phi }}_r\varvec{x}_i)^t ( \hat{\varvec{P}}_r \varvec{y}_i - \hat{\varvec{\Phi }}_r\varvec{x}_i)\right) } \end{aligned}$$

the posterior probability of \(\varvec{y}_i\) with i coming from the component k, where \(\theta = (\pi ,\varvec{\Phi },\varvec{P})\). Then, data are partitioned by the following rule:

$$\begin{aligned} \, [\hat{\varvec{Z}}_{i}]_k= \left\{ \begin{array}{ll} 1 &{} \text { if } \hat{\varvec{\tau }}_{i,k}(\hat{\theta }) > \hat{\varvec{\tau }}_{i,l}(\hat{\theta }) \text { for all } l\ne k \text { ;}\\ 0 &{} \text { otherwise.} \end{array} \right. \end{aligned}$$

2.3 Numerical optimization

First, we introduce a generalized EM algorithm to approximate \( \hat{\theta }^{\text {Lasso}}(\lambda )\) defined in (2) for \(\lambda >0\). Then, we discuss initialization and stopping rules in practice, before studying theoretically the convergence of this algorithm.

2.3.1 Generalized EM algorithm for approximating the Lasso estimator

From an algorithmic point of view, we use a generalized EM algorithm to compute the MLE and the \(\ell _1\)-norm penalized MLE. The EM algorithm was introduced by Dempster et al. (1977) to approximate the MLE of mixture model parameters. It is an iterative procedure based on the maximization of the expected value of the log-likelihood function with respect to the conditional distribution of \(\varvec{Z}\) given the observations, under the current estimation of the parameters. Using the Karush–Kuhn–Tucker conditions, we extend the second step to compute the MLE, penalized or not, under rank constraint or not, as it was done in the scalar case in Städler et al. (2010). All those computations are available in Appendix “EM algorithms”. The next updating formulae for the Lasso estimator defined by (2) are then obtained. Remark that it includes MLE. In the following, we consider the real n-space \(\mathbb {R}^n\) with the dot product denoted by \(<.,.>\), and with the associated norm denoted by \(||.||_2\). For all \(j \in \{1,\ldots ,p\}\), for all \(k \in \{1,\ldots , K\}\), for all \(m\in \{1,\ldots ,q\}\), for all \(i\in \{1,\ldots ,n\}\), we denote

$$\begin{aligned}{}[\varvec{\widetilde{y}}^{(\text {ite})}_i]_{k,m}&= \sqrt{\varvec{\tau }^{(\text {ite})}_{i,k}} [\varvec{y}_i]_m;\nonumber \\ [\varvec{\widetilde{x}}^{(\text {ite})}_i]_{k,j}&= \sqrt{\varvec{\tau }^{(\text {ite})}_{i,k}} [\varvec{x}_i]_j ;\nonumber \\ \Delta _{k,m}&= \left( -n_k^{(\text {ite})} \langle [{\varvec{\widetilde{y}}}^{(\text {ite})}_.]_{k,m},[\varvec{\Phi }_k]^{(\text {ite})}_{m,.} [{\varvec{\widetilde{x}}^{(\text {ite})}}_.]_{k,.} \rangle \right) ^2 - 4 ||[{\varvec{\widetilde{y}}}^{(\text {ite})}_.]_{k,m}||_ 2^2 ; \end{aligned}$$
(3)
$$\begin{aligned}{}[\varvec{S}_{k}]_{j,m}^{(\text {ite})}&=-\sum _{i=1}^{n} [\varvec{\widetilde{x}}^{(\text {ite})}_i]_{k,j} [\varvec{P}_k]^{(\text {ite})}_{m,m} [\varvec{\widetilde{y}}^{(\text {ite})}_i]_{k,m} + \sum _{\genfrac{}{}{0.0pt}{}{j_2=1 }{ j_2\ne j}}^{p} [\varvec{\widetilde{x}}^{(\text {ite})}_i]_{k,j} [\varvec{\widetilde{x}}^{(\text {ite})}_i]_{k,j_2} [\varvec{\Phi }_k]^{(\text {ite})}_{m,j_2} ;\nonumber \\ n_{k}&= \sum _{i=1}^{n} \varvec{\tau }_{i,k}^{(\text {ite})}. \end{aligned}$$
(4)

Moreover, we consider \(t^{(\text {ite})} \in (0,1]\) the largest value in \(\{0.1^l, l\in \mathbb {N} \}\) such that the update of \(\pi \) defined in (7) leads to improving the expected complete penalized log-likelihood function. Then, we update the parameters by

$$\begin{aligned} g^{(\text {ite})}_{i,k}= & {} \exp \left( -\frac{1}{2}\left( \varvec{P}^{(\text {ite})}_k \varvec{y}_i-\varvec{\Phi }_k^{(\text {ite})} \varvec{x}_i\right) ^t\left( \varvec{P}^{(\text {ite})}_k \varvec{y}_i-\varvec{\Phi }_k^{(\text {ite})} \varvec{x}_i\right) \right) \end{aligned}$$
(5)
$$\begin{aligned} \varvec{\tau }^{(\text {ite})}_{i,k}= & {} \frac{\pi _{k}^{(\text {ite})}\det \varvec{P}_k^{(\text {ite})} g^{(\text {ite})}_{i,k}}{\sum _{r=1}^K \pi _{r}^{(\text {ite})}\det \varvec{P}_r^{(\text {ite})} g^{(\text {ite})}_{i,r}} ; \end{aligned}$$
(6)
$$\begin{aligned} \pi _{k}^{\text {(ite+1)}}= & {} \pi _{k}^{(\text {ite})}+t^{(\text {ite})} \left( \frac{n_k^{(\text {ite})}}{n} - \pi _{k}^{(\text {ite})}\right) ;\end{aligned}$$
(7)
$$\begin{aligned} \, [\varvec{P}_k]_{m_1,m_2}^{\text {(ite+1)}}= & {} \left\{ \begin{array}{lll} &{}\frac{n_k^{(\text {ite})} \langle [{\varvec{\widetilde{y}}}^{(\text {ite})}_.]_{k,m}, [\varvec{\Phi }_k]_{m,.}^{(\text {ite})} [{\varvec{\widetilde{x}}^{(\text {ite})}}_.]_{k,.} \rangle + \sqrt{\Delta _{k,m}}}{2 n_k^{(\text {ite})} ||[{\varvec{\widetilde{y}}}^{(\text {ite})}_.]_{k,m}||_2^2}&{} \text { if } m_1=m_2=m;\\ &{}0 &{}\text { elsewhere;}\\ \end{array} \right. \end{aligned}$$
(8)
$$\begin{aligned} \, [\varvec{\Phi }_k]_{m,j}^{\text {(ite+1)}}= & {} \left\{ \begin{array}{lll} &{}\frac{-[\varvec{S}_{k}]^{(\text {ite})}_{j,m}+ n\lambda \pi ^{(\text {ite})}_{k} }{||[{\varvec{\widetilde{x}}^{(\text {ite})}}_.]_{k,j}||_{2}^2} &{} \text { if } [\varvec{S}_{k}]^{(\text {ite})}_{j,m}>n \lambda \pi ^{(\text {ite})}_{k} ;\\ &{}-\frac{[\varvec{S}_{k}]^{(\text {ite})}_{j,m}+ n\lambda \pi ^{(\text {ite})}_{k} }{||[{\varvec{\widetilde{x}}^{(\text {ite})}}_.]_{k,j}||_{2}^2} &{} \text { if } [\varvec{S}_{k}]^{(\text {ite})}_{j,m} < -n \lambda \pi _{k}^{(\text {ite})} ; \\ &{} 0 &{}\text { else ;} \end{array} \right. \end{aligned}$$
(9)

In this case, the EM algorithm corresponds to alternating between the E-step [computation of (6)] and the M-step [computation of (7), (8) and (9)].

Remark that to approximate the MLE under rank constraint, we use an easier EM algorithm which is described in details in the Appendix. In the E-step, we compute the a posteriori probability of each observation to belong to each cluster according to the current estimations. In the M-step, we consider each observation within its estimated cluster, and we consider the linear regression estimators under rank constraint by keeping the biggest singular values.

2.3.2 Initialization and stopping rules

We initialize the clustering process with the k-means algorithm on couples \((\varvec{y}_i,\varvec{x}_i) \in \mathbb {R}^{q}\times \mathbb {R}^p\), for all \(i \in \{1,\ldots ,n\}\). According to this clustering, we compute the linear regression estimators in each class. Then, we run a small number of times the EM-algorithm, repeat this initialization many times and keep the one which corresponds to the highest log-likelihood.

To stop the algorithm, we propose to run it a minimum number of times, and to specify a maximum number of iterations to make sure that it will stop. Between these two bounds, we stop the running if a relative criteria on the log-likelihood is small enough and if a relative criteria on the parameters is small enough too. Those criteria are adapted from Städler et al. (2010).

By those rules, we are trying to attain a local optimum as close as possible to a global optimum of the likelihood function.

2.3.3 Numerical convergence of this algorithm

We address here the convergence properties of the generalized EM algorithm described in Sect. 2.3.1. Although convergence to stationary points has been established for the EM algorithm (see Wu 1983), it is not true without conditions which are hard to verify for a generalized EM algorithm.

The results that we prove are quite similar to those provided by Städler et al. (2010), because the algorithms are similar. We refer the interested reader to this article for proofs of the following results when \(q=1\). The same ideas of proof are working for any values of q.

Proposition 1

The algorithm described in Sect. 2.3.1 has the descent property: for \(\text {ite} \in \mathbb {N}^*\),

$$\begin{aligned} -\frac{1}{n} l_{\lambda } (\theta ^{(\text {ite}+1)},\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) \le -\frac{1}{n} l_{\lambda } (\theta ^{(\text {ite})},\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) \end{aligned}$$

Proposition 1 is clear by construction of \(\theta ^{(\text {ite}+1)}\), the M-step of the algorithm being a coordinate-wise minimization.

Proposition 2

Assume that \(\varvec{y}_i \ne 0\) for all \(i \in \{1,\ldots ,n\}\). Then, for \(\lambda >0\), the function \(\theta \mapsto l_{\lambda } (\theta ,\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n)\) defined in (2) is bounded from above for all values \(\theta \in \Theta _K\).

This is true because we penalize the log-likelihood by \(\varvec{\Phi }=(\varvec{\Phi }_1,\ldots , \varvec{\Phi }_K)\), where \(\varvec{\Phi }_k =\varvec{P}_k {B}_k\), and then small variances are penalized also. This is not the case for the unpenalized criteria, which is unbounded if the variance of a coordinate of a variable tends to 0 (see McLachlan and Peel 2004 for more details).

Corollary 1

For the algorithm described in Sect. 2.3.1,

$$\begin{aligned} - \frac{1}{n} l_{\lambda } (\theta ^{(\text {ite})},\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n) \end{aligned}$$

decreases monotonically to some value \(\bar{l}> -\infty \).

According to this corollary, we know that the algorithm converges to some finite value, depending on initial values.

Theorem 1

For the algorithm described in Sect. 2.3.1, every cluster point \(\bar{\theta } \in \Theta _K\) of the sequence \(\left\{ \theta ^{(\text {ite})}, \text {ite}=0,1,\ldots \right\} \) generated by the algorithm is a stationary point of the function

$$\begin{aligned} \theta \mapsto l_\lambda (\theta ,\varvec{y}_1,\varvec{x}_1,\ldots , \varvec{y}_n,\varvec{x}_n). \end{aligned}$$

This theorem proves that the algorithm converges to a stationary point. We refer to Tseng (2001) for the definition of a stationary point for non-differentiable functions.

Corollary 1 is deduced from Proposition 1 and Proposition 2. Theorem 1 is more difficult to prove, and we refer to Städler et al. (2010) for a proof when \(q=1\).

2.4 Variable selection and model collection

We deal with high-dimensional data where we observe a small number of target values and we have to estimate many coefficients. Then, we have to focus on indices that are relevant for the clustering. The notion of irrelevant indices has to be defined.

Definition 1

A couple \((\varvec{y}_m,\varvec{x}_j)\) is said to be irrelevant for the clustering if \([\varvec{\Phi }_{1}]_{m,j} = \ldots = [\varvec{\Phi }_{K}]_{m,j}=0\), which means that the variable \(\varvec{x}_j\) does not explain the variable \(\varvec{y}_m\) for the clustering process. We also say that the indices (m, j) are irrelevant if the couple \((\varvec{y}_m,\varvec{x}_j)\) is irrelevant. A relevant couple is a couple which is not irrelevant: at least in one cluster k, the coefficient \([\varvec{\Phi }_k]_{m,j}\) is not equal to zero. We denote by J the set of indices (m, j) of relevant couples \((\varvec{y}_m,\varvec{x}_j)\).

Remark that \(J \subset \{1,\ldots ,q\}\times \{1,\ldots ,p\}\). We denote by \(^c J\) the complement of J in \(\{1,\ldots ,q\} \times \{ 1,\ldots ,p\}\). For all \(k \in \{1,\ldots ,K\}\), we denote by \(\varvec{\Phi }_k^{[J]}\) the matrix of size \(q\times p\) with 0 on the set \(^c J\). We also define by \(\mathcal {H}_{(K,J)}\) the model with K components and where J is the set of relevant indices:

$$\begin{aligned} \mathcal {H}_{(K,J)}&= \left\{ h_{\theta }^{(K,J)}(\varvec{y}|\varvec{x}) = \sum _{k=1}^{K} \frac{\pi _{k} \det (\varvec{P}_k)}{(2 \pi )^{q/2}} \exp \left( -\frac{(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k^{[J]} \varvec{x} )^t(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k^{[J]} \varvec{x} )}{2} \right) , \right. \nonumber \\&\qquad \quad \theta =(\pi _1,\ldots , \pi _K,\varvec{\Phi }_1^{[J]},\ldots , \varvec{\Phi }_K^{[J]}, \varvec{P}_1,\ldots ,\varvec{P}_K) \in \Theta _{(K,J)}\nonumber \\&\qquad \left. \phantom {\left\{ h_{\theta }^{(K,J)}(\varvec{y}|\varvec{x}) = \sum _{k=1}^{K} \frac{\pi _{k} \det (\varvec{P}_k)}{(2 \pi )^{q/2}} \exp \left( -\frac{(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k^{[J]} \varvec{x} )^t(\varvec{P}_k\varvec{y}-\varvec{\Phi }_k^{[J]} \varvec{x} )}{2} \right) , \right. }= \Pi _K \times \left( \mathbb {R}^{q \times p} \right) ^K \times \left( \mathbb {D}_q^{++} \right) ^K \right\} . \end{aligned}$$
(10)

We construct a collection of models by varying the number of components K and the indices set of relevant couples J.

The subset J is constructed with the Lasso estimator defined in (2). Nevertheless, to be consistent with the definition of relevant couples, the Group-Lasso estimator could be preferred, where coefficients \(\{[\varvec{\Phi }_{1}]_{m,j},\ldots ,[\varvec{\Phi }_{K}]_{m,j}\}\) are grouped. We focus here on the Lasso estimator, but the Group-Lasso approach is described in the Appendix. It gives mainly the same results, but the Lasso estimator permits to consider also isolated irrelevant indices.

3 Two procedures

The goal of our procedures is, given a sample \(((\varvec{y}_1,\varvec{x}_1),\ldots ,(\varvec{y}_n,\varvec{x}_n)) \in (\mathbb {R}^q \times \mathbb {R}^p)^n\), to cluster individuals. Thus, we have to estimate, according to \(\mathcal {H}_{(K,J)}\) defined in (10), the number of clusters K, the relevant indices set J, and the parameter \(\theta \). We want to take advantage of the sparsity property of the \(\ell _1\)-penalization to perform automatic index selection and to deduce J. Then, we compute another estimator restricted on coordinates with relevant indices, which will work better because it is no longer an high-dimensional issue. Thus, we avoid shrinkage problems due to the Lasso estimator. The first procedure takes advantage of the MLE, whereas the second one takes into account the matrix structure of \(\varvec{\Phi }\) through a low rank estimation.

3.1 Lasso-MLE procedure

This procedure is decomposed into three main steps: we construct a collection of models, then in each model we compute the MLE and finally we select the best model among the collection of models.

The first step consists in constructing a collection of models \(\{\mathcal {H}_{(K,J)}\}_{(K,J) \in \mathcal {M}}\) in which \(\mathcal {H}_{(K,J)}\) is defined by Eq. (10), and the collection of models is indexed by \( \mathcal {M}= \mathcal {K} \times \mathcal {J}\). We denote by \(\mathcal {K}\subset \mathbb {N}^*\) the admitted number of clusters. We assume that we could bound \(\mathcal {K}\) without loss of generality. We also denote \(\mathcal {J} \subset \mathcal {P} (\{1,\ldots ,q\} \times \{1,\ldots ,p\})\) the set of admitted relevant indices set.

Fix \(K \in \mathcal {K}\). To detect the relevant indices and construct the set \(J \in \mathcal {J}\), we penalize the log-likelihood by an \(\ell _1\)-penalty on the mean parameters proportional to \(||\varvec{\Phi }_k||_1 = \sum _{j=1}^p \sum _{m=1}^q |[\varvec{\Phi }_k]_{m,j}|\). In \(\ell _1\)-procedures, the choice of the regularization parameter is often difficult: fixing the number of components \(K \in \mathcal {K}\), we propose to construct a data-driven grid \(G_K\) of regularization parameters by using the updating formulae [(6), (7), (8) and (9)] of the parameters in the EM algorithm. We give a formula for \(\lambda \), the regularization parameter, depending on which coefficients we want to estimate by zero, for all \(k \in \{1,\ldots ,K\}, j\in \{1,\ldots ,p\}, z\in \{1,\ldots ,q\}\):

$$\begin{aligned}{}[\varvec{\Phi }_k]_{m,j} = 0 \Leftrightarrow&\,\, [\varvec{\lambda }_{k}]_{j,m}= \frac{|[\varvec{S}_{k}]_{j,m}|}{n \pi _{k}}; \end{aligned}$$

where \([\varvec{S}_{k}]_{j,m}\) is defined by (4). Then, we define the data-driven grid for the regularization parameter by

$$\begin{aligned} G_K = \left\{ [\varvec{\lambda }_{k}]_{j,m}, k\in \{1,\ldots ,K\}, j \in \{1,\ldots ,p\}, m \in \{1,\ldots ,q\}\right\} . \end{aligned}$$
(11)

We approximate it by MLE.

Then, for each \(\lambda \in G_K\), we compute the Lasso estimator defined by

$$\begin{aligned} \hat{\theta }^{\text {Lasso}}(\lambda ) = \underset{\theta \in \Theta _{K}}{ \mathrm{argmin}} \left\{ -\frac{1}{n} \sum _{i=1}^n \log (h_{\theta }^{K}(\varvec{y}_i|\varvec{x}_i)) + \lambda \sum _{k=1}^K \pi _k ||\varvec{\Phi }_k||_1 \right\} . \end{aligned}$$

For a fixed number of mixture components \(K \in \mathcal {K}\) and a regularization parameter \(\lambda \in G_K\), we use an EM algorithm to approximate this estimator. Then, for each \(K \in \mathcal {K}\) and for each \(\lambda \in G_K\), we construct the relevant indices set \(J_{K,\lambda }\). We denote by \(\mathcal {J}\) the collection of the relevant indices set \(J_{K,\lambda }\) by varying \(\lambda \in G_K\) and \(K \in \mathcal {K}\):

$$\begin{aligned} \mathcal {J} = \cup _{K \in \mathcal {K}} \cup _{\lambda \in G_K} J_{K,\lambda }. \end{aligned}$$

The second step consists in approximating the MLE

$$\begin{aligned} \hat{h}^{(K,J)}= \underset{h \in \mathcal {H}_{(K,J)}}{ \mathrm{argmin}} \left\{ -\frac{1}{n} \sum _{i=1}^n \log (h(\varvec{y}_i|\varvec{x}_i)) \right\} ; \end{aligned}$$

using the EM algorithm for each model \((K,J)\in \mathcal {M}\).

The third step is devoted to model selection. Rather than selecting the regularization parameter, we select the refitted model. Instead of using an asymptotic criterion, as BIC or AIC, we use the slope heuristic introduced by Birgé and Massart (2007), which is a non-asymptotic criterion for selecting a model among a collection of models. Let us explain briefly how it works. Firstly, models are grouped according to their dimension D, to obtain a collection of models \(\{\mathcal {H}_{D} \}_{D \in \mathcal {D}} \). The model dimension is the number of parameters estimated in this model. For each dimension D, let \(\hat{h}_{D}\) be the estimator which maximizes the likelihood function among the estimators associated to a model of dimension D. Also, the function \(D/n \mapsto 1/n \sum _{i=1}^n \log (\hat{h}_{D}(\varvec{y}_i|\varvec{x}_i))\) has a linear behavior for large dimensions. We estimate the slope, denoted by \(\hat{\kappa }\), which will be used to calibrate the penalty. The minimizer \(\hat{D}\) of the penalized criterion \(-1/n \sum _{i=1}^n \log (\hat{h}_{D}(\varvec{y}_i|\varvec{x}_i)) + 2 \hat{\kappa } D/n\) is determined, and the model selected is \((K_{\hat{D}},J_{\hat{D}})\). Remark that \(D_{K,J} = K(|J|+q+1)-1\) is the dimension associated to the model \(\mathcal {H}_{(K,J)}\).

Note that the model is selected after refitting, which avoids issue of regularization parameter selection. For an oracle inequality to justify the slope heuristic used here, see Devijver (2015).

3.2 Lasso-Rank procedure

The previous procedure does not take into account the multivariate structure, and therefore we propose a second procedure that takes into account this structure. For each model belonging to the collection \(\mathcal {H}_{(K,J)}\), a subcollection is constructed, varying the rank of \(\varvec{\Phi }\). Let us describe this procedure.

As in the Lasso-MLE procedure, we first construct a collection of models through varying the sparsity by varying the regularization parameter of the Lasso estimator. Remark that we focus here on column sparsity to keep the matrix structure.

The second step consists in constructing a subcollection of models with rank sparsity, denoted by

$$\begin{aligned} \{\check{\mathcal {H}}_{(K,J,R)}\}_{(K,J,R) \in \check{\mathcal {M}}}. \end{aligned}$$

The model \(\check{\mathcal {H}}_{(K,J,R)}\) has K components, J is the set of relevant indices and R is the vector of the ranks of regression coefficients in each group:

$$\begin{aligned} \check{\mathcal {H}}_{(K,J,R)}= \left\{ \varvec{h}_{\theta }^{(K,J,R)}(\varvec{y}|\varvec{x}) \right\} \end{aligned}$$
(12)

where

$$\begin{aligned} h_{\theta }^{(K,J,R)}(\varvec{y}|\varvec{x})&= \sum _{k=1}^{K} \frac{\pi _{k} \det (\varvec{P}_k)}{(2 \pi )^{q/2}} \exp \left( -\frac{(\varvec{P}_k\varvec{y}-(\varvec{\Phi }_k^{R_k})^{[J]} \varvec{x} )^t(\varvec{P}_k\varvec{y}-(\varvec{\Phi }_k^{R_k})^{[J]} \varvec{x} )}{2} \right) ; \nonumber \\ \theta&=(\pi _1,\ldots , \pi _K,(\varvec{\Phi }_1^{R_1})^{[J]},\ldots , (\varvec{\Phi }_K^{R_K})^{[J]}, \varvec{P}_1,\ldots ,\varvec{P}_K) \in \Theta _{(K,J,R)} \nonumber \\ \Theta _{(K,J,R)}&= \Pi _K \times \Psi _{(K,J,R)} \times \left( \mathbb {R}_+^{q} \right) ^K ; \nonumber \\ \Psi _{(K,J,R)}&= \left\{ \left. \left( (\varvec{\Phi }_1^{R_1})^{[J]},\ldots , (\varvec{\Phi }_K^{R_K})^{[J]}\right) \in \left( \mathbb {R}^{q \times p} \right) ^K \right| \text {Rank}(\varvec{\Phi }_k)\right. \\&\quad \;\;\left. =R_k \text { for all } k \in \{1,\ldots ,K\} \right\} ; \end{aligned}$$

and \(\check{\mathcal {M}}= \mathcal {K} \times \mathcal {J} \times \mathcal {R}\). We denote by \(\mathcal {K} \subset \mathbb {N}^*\) the admitted number of clusters, \(\mathcal {J}\) a random collection of subsets of \(\{1,\ldots ,p\}\) constructed by the Lasso estimator and \(\mathcal {R}\) the set of vectors of size \(K \in \mathcal {K}\) with rank values for each regression matrix. We compute the MLE under the rank constraint with an EM algorithm. Indeed, the estimator of \(\varvec{\Phi }_k\), for the cluster k, is constrained to have a rank equals to \(R_k\), by keeping only the \(R_k\) largest singular values. More details are given in the Appendix. It leads to an estimator of the mean with row sparsity and low rank for each model. Then, a model is selected using the slope heuristic. This step is justified theoretically in Devijver (2015).

3.3 Some comments

Those two procedures have been implemented in Matlab, with Benjamin Auder and the Matlab code is available. Note that we run the EM algorithm several times: once to construct the regularization grid, twice for each regularization parameter for the Lasso-MLE procedure (once to approximate the Lasso estimator, and once to refit it with the MLE) and more times for the Lasso-Rank procedure (the ranks vector varies also). If we look at every regularization parameter in the grid defined in (11), there are \(K\times p \times q\) values and then we compute the EM algorithm \(2\times K\times p\times q +1\) times, which could be large. Even if each EM algorithm is fast (implemented in C), it should be repeated a lot of time, which is time-consuming. We propose to the user to select relevant regularization parameters: either a regular subcollection of \(G_K\), to get various sparsities, or focusing on the large values of regularization parameters, to get sparse solutions.

4 Illustrative example

We illustrate our procedures on five different simulated datasets, adapted from Städler et al. (2010). Firstly, we present the models used in these simulations. Then, we validate numerically each step and we finally compare the results of our procedures with other methods. Remark that we consider here some examples to illustrate our methods, but not a complete analysis. We highlight some issues which seem to be important. Moreover, we do not illustrate the one-component case, as we are focusing on clustering. If, on some dataset, we are not convinced by the clustering, we add to the collection of models some models with one component, more or less sparse, using the same pattern (computing the Lasso estimator to get the relevant indices for various regularization parameters and refitting parameters with the MLE, under rank constraint or not) and then we select a model among this collection of linear and mixture models.

4.1 The model

Let \(\varvec{x}\in (\mathbb {R}^p)^n\) be a sample of size n distributed according to p-multivariate standard Gaussian with \(p=10\) or \(p=30\). We consider a mixture of two components. Besides, we fix the number of relevant indices to be 4 in each cluster. More precisely, the first four variables of \(\varvec{Y}\) are explained respectively by the first four variables of \(\varvec{x}\). Fix \(\pi = \left( \frac{1}{2},\frac{1}{2}\right) \) and \(\varvec{P}_k=\sigma I_q\) for all \(k \in \{1,2\}\), where \(I_q\) denotes the identity matrix of dimension q. Take a sample of \(\varvec{Y}\) according to a q multivariate Gaussian mixture with \(q=5\) or \(q=10\), with mean \(\mathbf {B}_k \mathbf {x}\) and with covariance matrix \(\varvec{\Sigma }_k= (\varvec{P}_k^t \varvec{P}_k)^{-1}=\sigma ^2 I_q\), for the cluster k.

The difficulty of the clustering is partially controlled by the signal-to-noise ratio (denoted SNR). In this context, we extend the natural idea of the SNR with the following definition, where \(\text {Tr}(A)\) denotes the trace of the matrix A,

$$\begin{aligned} \text {SNR}= \frac{\text {Tr}(\text {Var}(\varvec{Y}))}{\text {Tr}(\text {Var}(\varvec{Y}|\mathbf {B}_k=0 \text { for all } k \in \{1,\ldots ,K\}))}. \end{aligned}$$

Remark that it only controls the distance between the signal with or without the noise and not the distance between signals across clusters.

We consider five different models, varying n, the SNR and the distance between the clusters. Details are available in Table 1.

Table 1 Description of the different models for \(K=2\) classes
Full size table

We run our procedures with the number of components varying in \(\mathcal {K} = \{2,\ldots ,5 \}\).

Model 1 serves for illustrating our procedures in low dimensional models. Moreover, it is chosen in the next section to illustrate each step of the procedure (variable selection, construction of models and model selection). Model 5 is considered because it is high-dimensional. Model 2 is easier than the others, because clusters are not so close to each other according to the noise. Model 3 is similar to Models 1 and 2, but n is small and the noise is more important. We will see that the clustering is more difficult in this case. Model 4 has a larger SNR, nevertheless, the problem of clustering is difficult, because \(\mathbf {B}_k\)’s are close to each other.

Our procedures are run 20 times and we compute statistics over those 20 simulations. It is a small number of simulations, but the whole procedure is time-consuming and results are convincing enough.

For the initialization step, we repeat 50 times the initialization and keep the one which maximizes the log-likelihood function after 10 iterations. Those choices are size-dependent. We have done a numerical study which is not reported here to fit them.

4.2 Sparsity and model selection

To illustrate both procedures, all analyses made in this section are done from Model 1, since the choice of each step is clear.

Firstly, we compute the grid of regularization parameters. More precisely, each regularization parameter is computed from maximum likelihood estimations (using EM algorithm) and gives an associated sparsity (computed by the Lasso estimator, using again the EM algorithm). In Figs. 1 and 2, the collection of relevant indices selected by this grid is plotted.

Fig. 1
figure 1

For one simulation, the number of false relevant (in red color) and true relevant (in blue color) indices generated by the Lasso, by varying the regularization parameter \(\lambda \) in the grid \(G_2\)

Full size image
Fig. 2
figure 2

For one simulation, zoom in on the number of false relevant (in red color) and true relevant (in blue color) indices generated by the Lasso, by varying the regularization parameter \(\lambda \) around the interesting values

Full size image

Firstly, note that the number of relevant indices selected by the Lasso decreases when the regularization parameter increases. Moreover, we analyze which indices are selected, that is to say if we select true relevant or false relevant indices. If the regularization parameter is not too large, the true relevant indices are selected. Even more, if the regularization parameter is well-chosen, we select only the true relevant indices. In our example, we remark that if \(\lambda =0.09\), we have selected exactly the true relevant indices. This grid construction seems to be well-chosen according to our simulations.

From this variable selection, each procedure (Lasso-MLE or Lasso-Rank) leads to a collection of models, by varying the sparsity thanks to the grid of regularization parameters and the number of components.

Within this collection of models, we select a model using the slope heuristic criterion.

We want to select the best model by optimizing a penalized criterion. This penalty is computed by performing a linear regression on the couples of points \(\{ (D/n ; -1/n\sum _{i=1}^n \log (\hat{h}_{D}(\varvec{y}_i|\varvec{x}_i))) \}\). The slope \(\hat{\kappa }\) allows us to have access to the best model, the one with dimension \(\hat{D}\) minimizing

$$\begin{aligned} -\frac{1}{n} \sum _{i=1}^n \log (\hat{h}_{D}(\varvec{y}_i|\varvec{x}_i))+2 \hat{\kappa } \frac{D}{n}. \end{aligned}$$

In practice, we have to look if couples of points have a linear behavior. For each procedure, we construct a different collection of models and we have to justify this behavior. Figures 3 and 4 represent the log-likelihood in function of the dimension of the models, for collections of models constructed respectively by the Lasso-MLE procedure and by the Lasso-Rank procedure.

Fig. 3
figure 3

For one simulation, slope graph get by our Lasso-Rank procedure. For large dimensions, we observe a linear part

Full size image
Fig. 4
figure 4

For one simulation, slope graph get by our Lasso-MLE procedure. For large dimensions, we observe a linear part

Full size image

The couples are plotted by points, whereas the estimated slope is specified by a dotted line. We observe more than a line (4 for the Lasso-MLE procedure, more for the Lasso-Rank procedure). This phenomenon is explained by a linear behavior for each model subcollection, when we fix the number of classes and the rank. However, the linear behavior is almost the same and leads to select the same penalty coefficient. Nevertheless, slopes are almost the same and select the same model. In practice, we estimate the slope with the Capushe package described in Baudry et al. (2012).

4.3 Assessment

We compare our procedures to three other procedures on the simulated models.

Firstly, let us give some remarks about Model 1. For each procedure, we get a good clustering and a very low Kullback–Leibler divergence. Indeed, the sample size is large and estimations are good. That is the reason why, in this subsection, we focus on Models 2, 3 and 4.

To compare our procedures with others, the Kullback–Leibler divergence of the density selected from the true density and the ARI (the Adjusted Rand Index, measuring the similarity between two data clusterings, knowing that the closer the ARI to 1, the more similar the two partitions) are computed, and we note which indices are selected and how many clusters are selected. For more details on the ARI, see Hubert and Arabie (1985).

From the Lasso-MLE collection of models, we consider two models, to compare our procedures with. We compute the oracle model (the model which minimizes the Kullback–Leibler divergence of it from the true density) and the model which is selected by the BIC criterion instead of the slope heuristic. According to the oracle model, we know how good we could get for this collection of models for the Kullback–Leibler divergence and how this model, is good for clustering data.

The third procedure we compare with is the MLE, assuming that we know how many clusters there are, fixed to 2. We use this procedure to show that variable selection is needed.

In each case, we use the MAP principle to get the clustering.

We do not plot the Kullback–Leibler divergence for the MLE procedure, because values are too high and make the boxplots unreadable.

Fig. 5
figure 5

Boxplots of the Kullback–Leibler divergence of the density selected from the true density over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) for Model 2

Full size image
Fig. 6
figure 6

Boxplots of the ARI over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) and the MLE (MLE) for Model 2

Full size image
Fig. 7
figure 7

Boxplots of the Kullback–Leibler divergence of the density selected from the true density over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) for Model 3

Full size image
Fig. 8
figure 8

Boxplots of the ARI over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) and the MLE (MLE) for Model 3

Full size image
Fig. 9
figure 9

Boxplots of the Kullback–Leibler divergence of the density selected from the true density over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) for Model 4

Full size image
Fig. 10
figure 10

Boxplots of the ARI over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) and the MLE (MLE) for Model 4

Full size image
Fig. 11
figure 11

Boxplots of the Kullback–Leibler divergence of the density selected from the true density over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) for Model 5

Full size image
Fig. 12
figure 12

Boxplots of the ARI over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (BIC) and the MLE (MLE) for Model 5

Full size image

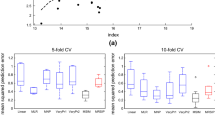
From Figs. 5 and 6 we see that, for Model 2, the Kullback–Leibler divergence is small and the ARI is close to 1, except for the MLE procedure. Boxplots are still readable with those values, but it is important to highlight that variable selection is needed, even in a model with reasonable dimension. The collections of models are then well constructed. Model 3 is more difficult, because the noise is higher. That is why results, summarized in Figs. 7 and 8, are not as good as for Model 2. Nevertheless, our procedures lead to the best ARI and the Kullback–Leibler divergences are close to the one of the oracle. Similar remarks are made for the results for Model 4. In this study, means are closer, according to the noise. Results are summarized in Figs. 9 and 10. Model 5 is a high-dimensional model. Models selected by the BIC criterion are bad, in comparison with models selected by our procedures, or in comparison with the oracle models. They are bad for estimation, according to the Kullback–Leibler divergence boxplots in Fig. 11, but also for clustering, according to Fig. 12. Our models are not as well as constructed previously, due to the high-dimensional context. It explains the high Kullback–Leibler divergence. However, our performances in clustering are good.

Note that the Kullback–Leibler divergence is smaller for the Lasso-MLE procedure, thanks to the maximum likelihood refitting. Moreover, the true model has no matrix structure. If we compare with the MLE, where we do not use the sparsity hypothesis, we conclude that estimations are not satisfactory, due to the high-dimensional context. The Lasso-MLE procedure, the Lasso-Rank procedure and the BIC model work almost as well as the oracle, which means that models are well selected.

Table 2 Mean number {TR, FR} of true relevant and false relevant indices over the 20 simulations for each procedure, for models 2, 3 and 4
Full size table

In Table 2, we summarize results about indices selection. For each model and for each procedure, we compute how many true relevant and false relevant indices are selected.

The true model has 4 relevant indices, which are always recognized. The Lasso-MLE has less false relevant indices than the others, which means that the true structure was found. The Lasso-Rank has 24 false relevant indices, because of the matrix structure: the true rank in each component was 4, then the estimator restricted on relevant indices is a \(4 \times 4\) matrix and we get 12 false relevant indices in each component. Nevertheless, it is the smallest matrix if select every relevant indices. The BIC estimator and the oracle have a large variability for the false relevant indices.

Remark that all procedures have selected the true number of components.

Thanks to the MLE, the first procedure has good performance in estimation (better than the second one). However, depending on the data, the second procedure could be more attractive. If there is a matrix structure, for example if most of the variation of the response \(\varvec{Y}\) is caught by a small number of linear combinations of the predictors, the second procedure will work better.

5 Functional data

A main aspect of our methods is the fact that they can be applied to functional data as well. Indeed, in different fields of applications, the considered data are functions. The functional data analysis has been popularized first by Ramsay and Silverman (2005). This book gives a description of the main tools to analyze functional data. We also refer to Ferraty and Vieu (2006). In a density estimation framework, we refer to Gareth and Sugar (2003), who used a model-based approach for clustering functional data. About functional regression, however, the main part of the existing literature is focused on \(\varvec{Y}\) scalar and \(\varvec{x}\) functional. For example, we refer to Zhao et al. (2012) for using wavelet basis in linear model, Yao et al. (2011) for functional mixture regression, or Ciarleglio and Ogden (2014) for using wavelet basis in functional mixture regression. In this section, we focus on \(\varvec{Y}\) and \(\varvec{x}\) both functional. In this regression context, we are interested in clustering: it leads to identifying individuals involved in the same relation between \(\varvec{Y}\) and \(\varvec{x}\). Denote that, with functional data, we have to denoise and to smooth signals to remove the noise and capture only the important patterns in the data. Here, we explain how our procedures are applied in this context. Note that we could apply our procedures with scalar response and functional regressor, or, on the contrary, with functional response and scalar regressor. We explain how our procedures work in the more general case. Remark that we focus here on the wavelet basis, to take advantage of the time-scale decomposition, but the same analysis is available on Fourier basis or splines.

5.1 Functional regression model

We observe deterministic functional predictors \(({f}_i)_{1\le i \le n}\) defined on \(I_F\) and a sample \(({g}_i)_{1 \le i \le n}\) of functional response associated with the random variables \({G}_i\) defined on \(I_G\). If the observation \(i \in \{1,\ldots ,n\}\) originates from the cluster k, the model assumes that there exists a function \(\varvec{B}_k : I_F \times I_G \rightarrow \mathbb {R}\) such that, for \(t \in I_G\),

$$\begin{aligned} {G}_i(t)= \int _{I_F} {f}_i(u) \mathbf {B}_k(u,t) du + {\varepsilon }_i(t), \end{aligned}$$
(13)

where \({\varepsilon }_i\) is a residual function. This linear model, restricted on each cluster, is introduced in Ramsay and Silverman (2005).

Unfortunately, we observe data on discretized time, and we have access to \((({f}_i(t_j))_{1\le j \le p})_{1\le i \le n}\) and \((({g}_i(t_m))_{1\le m \le q})_{1\le i \le n}\).

If we assume that, for all \((t_m)_{1\le m \le q}\), for all \(i \in \{1,\ldots ,n\}\), \(\varvec{\varepsilon }_i(t_m) \sim \mathcal {N}(0,\varvec{\Sigma }_k)\), Model (13) is an integrated version of Model (1). Depending on the cluster k, the linear relation of \(\varvec{G}_i\) with respect to \(\varvec{f}_i\) is described by the function \(\mathbf {B}_k\).

5.2 Two procedures to deal with functional data

5.2.1 Projection onto a wavelet basis

We project the functional data onto some basis, to get data as described in the Gaussian mixture regression model (1). In this article, we deal with wavelet basis, because they represent localized features of functions in a sparse way. If the coefficient matrices \({\varvec{x}}_i\) and \({\varvec{y}}_i\) associated to function \(f_i\) and \(g_i\) are sparse, the regression matrix \(\mathbf {B}\) has more chance to be sparse. Moreover, if the basis is well-suited, we are able to represent a signal with few coefficients, which reduces the dimension. For details about the wavelet theory, see Mallat (1999).

We begin with an overview of some important aspects of wavelet basis.

Let \(\psi \) be a real wavelet function, satisfying for \(t\in \mathbb {R}\),

$$\begin{aligned} \psi \in L^1 \cap L^2, t \psi \in L^1, \text { and } \int _{\mathbb {R}} \psi (t) dt =0. \end{aligned}$$

We denote for \((l,h)\in \mathbb {Z}^2\) by \(\psi _{l,h}\) the function defined from \(\psi \) by dyadic dilation and translation:

$$\begin{aligned} \psi _{l,h}(t)=2^{l/2} \psi (2^l t-h) \text { for } (l,h) \in \mathbb {Z}^2, \text { for } t \in \mathbb {R}. \end{aligned}$$

We define the wavelet coefficients of a signal f by

$$\begin{aligned} d_{l,h}(f) =\int _{\mathbb {R}} f(t) \psi _{l,h}(t)dt \text { for } (l,h) \in \mathbb {Z}^2. \end{aligned}$$

Let \(\varphi \) be a scaling function, related to \(\psi \), and let \(\varphi _{l,h}\) be the dilatation and translation of \(\varphi \) for \((l,h) \in \mathbb {Z}^2\). We also define, for \((l,h) \in \mathbb {Z}^2\), \(\mathbf {B}_{l,h}(f) = \int _{\mathbb {R}} f(t) \varphi _{l,h}(t)dt\).

Note that scaling functions serve to construct approximations of the function of interest, while the wavelet functions serve to provide the details not captured by successive approximations.

We denote by \(V_l\) the space generated by \(\{\varphi _{l,h}\}_{h \in \mathbb {Z}}\) and by \(W_l\) the space generated by \(\{ \psi _{l,h}\}_{h \in \mathbb {Z}}\) for all \(l \in \mathbb {Z}\). Remark that

$$\begin{aligned} V_{l-1}&= V_l \oplus W_l \text { for all } l \in \mathbb {Z} ;\\ \text {L}^2&= \oplus _{l \in \mathbb {Z}} W_l. \end{aligned}$$

Let \(L \in \mathbb {N}^*\). A signal f is decomposed by the approximation at the level L \(A_L(f)\) and by the details \((d_{l,h})_{l <L}\), where

$$\begin{aligned} A_L(f) = \sum _{l >L} \sum _{h \in \mathbb {Z}} d_{l,h} (f) \psi _{l,h} = \sum _{h \in \mathbb {Z}} \varvec{B}_{L,h}(f) \varphi _{L,h}. \end{aligned}$$

This decomposition emphasizes the local nature of the wavelets, which, through the variable selection, highlights useful patterns for the clustering analysis.

We consider the sample \(({f}_i,{g}_i)_{1\le i \le n}\) and introduce the wavelet expansion of \({f}_i\) onto the basis \(\mathcal {B}= ((\varphi _{L,h})_{h \in \mathbb {Z}},(\psi _{l,h})_{l\le L, h \in \mathbb {Z}})\): for all \(t \in [0,1] \),

$$\begin{aligned} {f}_i(t)= \underbrace{\sum _{h \in \mathbb {Z}} \mathbf {B}_{L,h} ({f}_i) \varphi _{L,h}(t)}_{A_L(f)(t)} + \sum _{l\le L} \sum _{h\in \mathbb {Z}}d_{l,h}({f}_i) \psi _{l,h}(t). \end{aligned}$$

The collection \(\{\mathbf {B}_{L,h}({f}_i),d_{l,h}({f}_i) \}_{l \le L,h \in \mathbb {Z}}\) is the Discrete Wavelet Transform (DWT) of \(f_i\) in the basis \(\mathcal {B}\).

We denote by \((\varvec{x}_1,\ldots ,\varvec{x}_n)\) the wavelet coefficient decomposition vectors, and the orthonormal characterization leads to

$$\begin{aligned} (({f}_i(t_j))_{1\le j \le p})=\varvec{W} \varvec{x}_i ; \end{aligned}$$

where \(\varvec{x}_i\) the matrix of coefficients in the basis \(\mathcal {B}\), and \(\varvec{W}\) a matrix defined by \(\varphi \) and \(\psi \). The DWT is performed by a computationally fast pyramid algorithm (see Mallat 1989). In the same way, there exists \(\varvec{W}^{'}\) such that \((({g}_i(t_m))_{1\le m \le q})=\varvec{W}^{'} \varvec{y}_i\), with \((\varvec{y}_1,\ldots ,\varvec{y}_n)\) a sample of wavelet coefficient decomposition vectors. As the matrices \(\varvec{W}\) and \(\varvec{W}^{'}\) are orthogonal, the mixture structure and Gaussian noise are kept. We consider the wavelet coefficient dataset \(((\varvec{y}_1,\varvec{x}_1),\ldots ,(\varvec{y}_n,\varvec{x}_n))\), which defines n observations whose probability distribution is modeled by the finite Gaussian mixture regression model (1).

5.2.2 Our procedures

We apply our both procedures to wavelet coefficient and obtain a clustering of the data. Rather than considering discretized functions \((({g}_i(t_m))_{1\le m \le q}, (({f}_i(t_j))_{1\le j \le p}))_{1\le i \le n}\), we run our procedures on the wavelet coefficients sample \((\varvec{y}_i,\varvec{x}_i)_{1\le i \le n}\). The notion of relevant indices is quiet natural in this context: we are looking for patterns which explain the response variable, to focus on those who discriminate for the clustering.

5.3 Numerical experiments

We illustrate our procedures on functional data by using the Matlab wavelet toolbox (see Misiti et al. 2004 for details). Firstly, we simulate functional datasets, where the true model belongs to the collection of models. Then, we run our procedure on an electricity dataset, to cluster successive days. We have access to time series on load consumption measured every half-hour during 70 days. We extract the signal of each day and construct couples by each day and its eve and we aim at clustering these couples. To finish, we test our procedures on the well-known Tecator dataset. For each meat sample the data consists of a 100 channel spectrum of absorbances and the fat contents. These experiments illustrate different aspects of our procedures. Indeed, the simulated example illustrates that our procedures work in a functional context. The second example demonstrates the use of them for classification of real data already studied and in which we clearly understand the clusters. The last example also illustrates the use of the clustering to perform prediction.

5.3.1 Simulated functional data

Firstly, we simulate a mixture regression model. Let f be a sample of a noised cosine function, discretized on a 15 points grid. Let g be, depending on the cluster, either f or \(-{f}\), computed by a white-noise. Then, there are two clusters.

We use the Daubechies-2 basis at level 2 to decompose the signal.

Our procedures are run 20 times. The number of clusters is known, \(\mathcal {K} = K =2\). We compare the models we get by our procedures with the oracle model among the collection constructed by the Lasso-MLE procedure and with the model selected by the BIC criterion among this collection (Fig. 13).

Fig. 13
figure 13

Boxplots of the ARI over the 20 simulations, for the Lasso-MLE procedure (LMLE), the Lasso-Rank procedure (LR), the oracle (Oracle), the BIC estimator (Bic) and the MLE (MLE)

Full size image

The ARIs are lower for models constructed by our procedures. This simulated dataset shows that our procedures also perform clustering of functional data, considering the projection of the data onto a suitable wavelet basis.

5.3.2 Electricity dataset

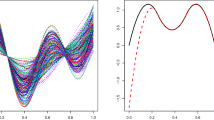
We study the clustering of the electricity dataset. This example is studied in Misiti et al. (2007). We work on a sample of size \(n=70\) of couples of days, which is plotted in Fig. 14. For each couple, we have access to the half-hour load consumption.

Fig. 14
figure 14

Plot of the 70-sample of half-hour load consumption, on 2 days

Full size image
Fig. 15
figure 15

Plot of a week of load consumption

Full size image

We want to cluster the relationship between two successive days. In Fig. 15, we plot a week of load consumption.

In each couple, the first day corresponds to regressors and the second day corresponds to the response. In our opinion, a linear model is not appropriate, as the behavior from the eve to the day depends on which day we consider: there is a difference between working days and weekend days, which are both involved in Fig. 15.

To apply our procedures, we project the functions onto a wavelet basis. The symmlet-4 basis, at level 5, is used.

We run our procedures with the number of clusters varying from 2 to 6. Both our procedures select a model with 4 components. The first one considers couples of weekdays, the second Friday–Saturday, the third component is Saturday–Sunday and the fourth considers Sunday–Monday. This result is faithful with the knowledge we have about these data. Indeed, working days are similar, depending on the eve, whereas days off are different from their eve. Moreover, Misiti et al. (2007) obtained the same classification for this example.

5.3.3 Tecator dataset

This example deals with spectrometric data. More precisely, a food sample has been considered, which contained finely chopped pure meat with different fat contents. The data consist in a 100-channel spectrum of absorbances in the wavelength range \(850-1050\) nm and of the fat percentage. We observe a sample of size \(n=215\). These data have been studied in a lot of articles, we refer for example to Ferraty and Vieu (2006). They test prediction and classification, supervised (where the fat content becomes a class, determined by whether the content is larger or smaller than \(20~\%\)), or not (ignoring the response variable). In this work, we take a different approach: we cluster data according to the relation between the fat content and the absorbance spectrum. We do not predict the response variable, because we do not know the class of a new observation. Estimate the class of a new observation is a difficult problem, in which we are not involved in this article.

One advantage of our procedures is that we know which coefficients, in the wavelet basis decomposition of the spectrum, are useful to describe the fat content.

Fig. 16
figure 16

Summarized results for Model 1. The graph on the left is a candidate for representing each cluster, constructed by the mean of reconstructed spectrum over an a posteriori probability greater than 0.6. On the right side, we present the boxplot of the fat values in each class, for observations with an a posteriori probability greater than 0.6

Full size image
Fig. 17
figure 17

Summarized results for Model 2. The graph on the left is a candidate for representing each cluster, constructed by the mean of reconstructed spectrum over an a posteriori probability greater than 0.6. On the right side, we present the boxplot of the fat values in each class, for observations with an a posteriori probability greater than 0.6

Full size image

The sample will be split into two subsamples, 165 observations for the learning set and 50 observations for the test set. This split is such that there is the same marginal distribution for the response in each sample.

The spectrum is a function, and we decompose it onto the Haar basis, at level 6. Our model does not take into account a constant coefficient to describe the response. Thereby, before running our procedure, we center the response according to the learning sample and each function \(\varvec{x}_i\) for every observation in the whole sample. Then, we estimate the mean of the response by the mean \(\hat{\mu }\) over the learning sample.

We construct models on the training set using our procedure Lasso-MLE. Thanks to the estimations, we have access to relevant indices and we reconstruct signals by keeping only relevant indices. We also have access to the estimated a posteriori probability, and hence know the estimated probability for every observation to belong to each cluster. The procedure selects two models that we describe here. In Figs. 16 and 17, clusters performed on the training set are represented for the different models. The graph on the left is a candidate for representing each cluster, constructed by the mean of the spectra with an a posteriori probability greater than 0.6. We plot the reconstruction of the curve by keeping only variables corresponding to relevant indices in the wavelet decomposition. On the right side, we present the boxplot of the fat contents in each class, for observations with an a posteriori probability greater than 0.6.

The first model has two classes, which are distinguished in the absorbance spectrum by the bump on wavelength around 940 nm. The first cluster is dominating, with \(\hat{\pi }_1=0.95\). The fat content is smaller in the first cluster than in the second cluster. According to the signal reconstruction, we see that almost all indices have been selected. This model seems consistent with the classification goal.

The second model has 3 classes and we remark several important wavelengths. Around 940 nm, there is a difference between classes, corresponding to the bump in Model 1. Around 970 nm, there is also a difference between classes, with higher or smaller values. The first class is dominating, with \(\hat{\pi }_1=0.89\). Just a few number of indices have been selected and we are able to understand which coefficients are discriminating.

The first model selects only two classes, but almost all indices, whereas the second model has more classes and less indices: there is a trade-off between clusters and variable selection for the dimension reduction.

Based on these classifications, we compute the response according to the linear model. We use two ways to compute the fitted response \(\hat{\varvec{y}}\): either considering the linear model in the cluster selected by the MAP principle, or mixing estimations in each cluster thanks to the a posteriori probabilities. We summarize the results via the Mean Absolute Percentage Error, \(\text {MAPE}=\frac{1}{n} \sum _{i=1}^n |(\hat{\varvec{y}}_i-\varvec{y}_i) / \varvec{y}_i|\), presented in Table 3.

Table 3 Mean absolute percentage of error of the predicted value, for each model, for the learning sample
Full size table

We next work with the test sample. We use the response and the regressors to know the a posteriori of each observation. Then, using our models, we compute the predicted fat values from the spectrometric curve, as before according to two ways, mixing or choosing the classes (Table 4).

Table 4 Mean absolute percentage of error of the predicted value, for each model, for the test sample
Full size table

Because the models are constructed on the learning sample, the MAPE for this sample are lower than for the test sample. Nevertheless, results are similar, saying that models are well constructed. This is particularly the case for Model 1, which is more consistent over a new test sample.

To conclude this study, we highlight the advantages of our Lasso-MLE procedure on these data. It provides a clustering of data, similar to the one done with supervised clustering in Ferraty and Vieu (2006), but we explain how this clustering is done.

This work has been done with the Lasso-MLE procedure. However, the same kind of results were obtained with the Lasso-Rank procedure.

6 Conclusion

In this article, two procedures are proposed to cluster regression data. Detecting the relevant clustering indices, the procedures are especially designed for high-dimensional data. We use an \(\ell _1\)-regularization procedure to select indices and then deduce a reasonable random collection of models. Thus, we recast estimations of parameters of these models into a general model selection problem. These procedures are compared with commonly-used criteria on simulated data: the BIC criterion used to select a model, the maximum-likelihood estimator and the oracle model. In addition, we compare our procedures to other methods on benchmark data. Our procedures are applicable to functional data through projecting coefficients onto a wavelet basis.