1 Introduction

Studies of solutions to the Navier–Stokes–Voigt equations and very similar models have occupied much attention in the mathematical literature, see e.g. Oskolkov [1,2,3,4,5,6], Oskolkov and Shadiev [7], Ladyzhenskaya [8, 9], Badday and Harfash [10], Baranovskii [11], Berselli and Bisconti [12], Bisconti and Mariano [13], Celebi et al. [14], Damázio et al. [15], Di Plinio et al. [16], Kalantarov and Titi [17, 18], Kalantarov et al. [19], Krasnoschok et al. [20], Layton and Rebholz [21], Niche [22], Pavlovskii [23], Sviridyuk and Sukacheva [24], Sukacheva and Kondyukov [25], Sukacheva and Matveeva [26], Sukacheva and Sviridyuk [27], Zvyagin [28, 29]. Much of this work has been related to existence and regularity of a solution and a great deal of this is to be found in the Russian mathematical literature. For example, a recent interesting article of Sukacheva [30] contains pertinent references to much of this work.

In particular, thermal effects have been analysed in conjunction with Navier–Stokes–Voigt theory, see e.g. Oskolkov [3, 4], Sukacheva and Matveeva [26]. Hydrodynamical stability analyses of thermal convection with a Navier–Stokes–Voigt fluid may be found in Straughan [31, 32].

The Navier–Stokes–Voigt system of equations modifies the Navier - Stokes equations by addition of a term of form \({{\hat{\lambda }}}\Delta \partial v_i/\partial t\), where \(v_i\) is the velocity field, \({{\hat{\lambda }}}>0\) is the Kelvin–Voigt coefficient, and \(\Delta \) is the Laplacian.

Damázio et al. [15] analyse solution properties to the Navier–Stokes–Voigt equations but they point out that it is not correct to think of the additional term \({{\hat{\lambda }}}\Delta \partial v_i/\partial t\) as being part of the Cauchy stress tensor, and one should treat it as a regularizing term, cf. Oskolkov [2], Ladyzhenskaya [9]. The reason for this is that the derivative in the additional term is not an objective derivative. Straughan [33] also comments on this and he observes that one could modify the offending term by replacing it with an objective corotational derivative, which in turn leads to a Walters’ B fluid, Beard and Walters [34]. This derivative is also incorporated in the analysis of Frolovskaya and Pukhnachev [35], Pukhnachev and Frolovskaya [36].

In the stability analysis of higher gradient theories of Navier–Stokes equations by Straughan [37], there are two models which are derived by continuum mechanics principles which include naturally the Kelvin–Voigt term in the Navier–Stokes–Voigt equations, these being the theory for a dipolar fluid, Bleustein and Green [38], Green and Naghdi [39], Jordan and Puri [40, 41], and the theory for the gradient kinetic energy model of Fried and Gurtin [42].

The object of this article is to examine some stability problems primarily with the model of Fried and Gurtin [42] and draw attention to some issues which arise due to nonlinear terms not present in classical Navier–Stokes–Voigt theory. We also comment on two models of Oskolkov [3, 4], which are closely related to the Navier–Stokes–Voigt equations.

2 Governing equations

In the interests of clarity we present the Navier–Stokes equations, the Navier–Stokes–Voigt equations, and their counterparts incorporating temperature, employing a Boussinesq approximation, Barletta [43, 44]. Throughout, we employ standard indicial notation together with the Einstein summation convention. For example,

$$\begin{aligned} v_{i,i}=\sum _{i=1}^3\frac{\partial v_i}{\partial x_i}= \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y} +\frac{\partial w}{\partial z}, \end{aligned}$$

where \(\textbf{v}=(u,v,w)\equiv (v_1,v_2,v_3).\) Also,

$$\begin{aligned} v_jv_{i,j}=\sum _{j=1}^3v_j\frac{\partial v_i}{\partial x_j}= u\frac{\partial v_i}{\partial x} +v\frac{\partial v_i}{\partial y} +w\frac{\partial v_i}{\partial z},\quad i=1,2,3, \end{aligned}$$

and

$$\begin{aligned} v_{i,jj}=\Delta v_i= \frac{\partial ^2 v_i}{\partial x^2} +\frac{\partial ^2 v_i}{\partial y^2} +\frac{\partial ^2 v_i}{\partial z^2},\quad i=1,2,3. \end{aligned}$$

Let \(v_i(\textbf{x},t)\) denote the fluid velocity at a point \(\textbf{x}\) at time t and let \(\nu >0\) be the constant kinematic viscosity. The Navier–Stokes equations for an incompressible fluid are

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t} +v_j\frac{\partial v_i}{\partial x_j}=-\frac{1}{\rho }\,\frac{\partial p}{\partial x_i}+\nu \Delta v_i+f_i,\\&\frac{\partial v_i}{\partial x_i}=0, \end{aligned} \end{aligned}$$
(1)

where \(p(\textbf{x},t)\) is the pressure, \(\rho \) is the constant density, and \(f_i\) is an external body force. If \({\hat{\lambda }}>0\) denotes the Kelvin–Voigt coefficient then the Navier–Stokes–Voigt equations are

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t} +v_j\frac{\partial v_i}{\partial x_j}-{{\hat{\lambda }}}\Delta \frac{\partial v_i}{\partial t}&=-\frac{1}{\rho }\,\frac{\partial p}{\partial x_i}+\nu \Delta v_i+f_i,\\&\frac{\partial v_i}{\partial x_i}=0. \end{aligned} \end{aligned}$$
(2)

In this article we shall be concerned with thermal convection and then employing a Boussinesq approximation, Barletta [43, 44], the equations corresponding to (1) are

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t} +v_j\frac{\partial v_i}{\partial x_j}=-\frac{1}{\rho }\,\frac{\partial p}{\partial x_i}+\nu \Delta v_i+\alpha gTk_i,\\&\frac{\partial v_i}{\partial x_i}=0,\\&\frac{\partial T}{\partial t}+v_i\frac{\partial T}{\partial x_i}=\kappa \Delta T, \end{aligned} \end{aligned}$$
(3)

where \(T(\textbf{x},t)\) is the temperature of the fluid at position \(\textbf{x}\) and time t, \(\alpha \) is the thermal expansion coefficient of the fluid, g is gravity which is assumed acting in the downward direction, \(\kappa \) is the thermal diffusivity of the fluid, and \(\textbf{k}=(0,0,1)\). The analogous equations for a Navier–Stokes–Voigt fluid are

$$\begin{aligned} \begin{aligned}&\frac{\partial v_i}{\partial t} +v_j\frac{\partial v_i}{\partial x_j}-{{\hat{\lambda }}}\Delta \frac{\partial v_i}{\partial t} =-\frac{1}{\rho }\,\frac{\partial p}{\partial x_i}+\nu \Delta v_i+\alpha gTk_i,\\&\frac{\partial v_i}{\partial x_i}=0,\\&\frac{\partial T}{\partial t}+v_i\frac{\partial T}{\partial x_i}=\kappa \Delta T. \end{aligned} \end{aligned}$$
(4)

As pointed out by Damázio et al. [15], it is sometimes argued that the momentum equation (4)\(_1\) arises from the equation

$$\begin{aligned} {\dot{v}}_i=\frac{1}{\rho }\,\sigma _{ji,j}+\alpha gTk_i, \end{aligned}$$

where a superposed dot denotes the material derivative, and \(\sigma _{ij}\) is the Cauchy stress tensor. This would mean

$$\begin{aligned} \sigma _{ij}=-p\delta _{ij}+2\mu d_{ij}+2{{\hat{\lambda }}}d_{ij,t}, \end{aligned}$$
(5)

where \(\mu =\rho \nu \) is the dynamic viscosity of the fluid, and \(d_{ij}\) is the symmetric part of the velocity gradient, \(v_{i,j}\), i.e.

$$\begin{aligned} d_{ij}=\frac{1}{2}(v_{i,j}+v_{j,i}). \end{aligned}$$
(6)

We also require the skew-symmetric part of the velocity gradient, \(\omega _{ij}\), and this is,

$$\begin{aligned} \omega _{ij}=\frac{1}{2}(v_{i,j}-v_{j,i}). \end{aligned}$$
(7)

In direct tensor notation we write these as D and W, i.e. \(D\equiv d_{ij}\) and \(W\equiv \omega _{ij}\), and \(\Sigma \) denotes \(\sigma _{ij}\). Damázio et al. [15] argues that (5) is not correct because \(d_{ij,t}\) is not an objective derivative. Straughan [33] argues that one could employ a corotational derivative to write instead

$$\begin{aligned} \Sigma =-pI+2\mu D+2\lambda ({\dot{D}}-WD-DW^T). \end{aligned}$$
(8)

The corotational derivative is objective, see e.g. Morro [45], and (8) leads to what is known as a Walters B fluid, see e.g. Straughan [33]. However, the corotational derivative is not the only objective derivative, there are many, see Morro [45], e.g. \(d_{ij,t}\) could be replaced by a Cotter–Rivlin derivative

$$\begin{aligned} {\buildrel \triangle \over D}={\dot{D}}-WD-DW^T+2D^2, \end{aligned}$$

or by an Oldroyd derivative

$$\begin{aligned} {\buildrel \diamondsuit \over D}={\dot{D}}-LD-DL^T, \end{aligned}$$

where \(L\equiv v_{i,j}\). These are only some of the possible objective derivatives one may use. The use of objective derivatives to obtain rate type theories in porous media or in viscoelastic fluids is succinctly explained in Morro [46] and in Giorgi and Morro [47].

This clearly leads to a problem in designing a nonlinear variant of the Navier–Stokes–Voigt equations (4). What derivative should one employ instead of \(d_{ij,t}\)? A not dissimilar problem arises in the Navier–Stokes theory of thermal convection when one employs a Cattaneo theory of heat transport rather than a Fourier one, see Gentile and Straughan [48]. Perhaps the appropriate model could be assessed as suggested by Ladyzhenskaya [49] in another fluid dynamical context, when she wrote that... “which of these systems will be most appropriate for the description of viscous incompressible flow will be shown by future comprehensive mathematical and physical analysis". While these remarks were not presented directly at Navier–Stokes–Voigt theory they are certainly very pertinent in this case.

In this work we firstly examine thermal convection in a Navier–Stokes–Voigt like theory using three models. One is the Fried and Gurtin [42] model, the second is the dipolar fluid model, Bleustein and Green [38], Green and Naghdi [39], and the third is to employ a corotational derivative as in (8).

3 Thermal convection

Here we analyse the problem of thermal convection in a horizontal layer of fluid contained between the planes \(z=0\) and \(z=d\). The boundaries are maintained at constant temperatures \(T_L\) when \(z=0\) and \(T_U\) when \(z=d\). The steady state for all three classes of fluid considered here is

$$\begin{aligned} {\bar{\textbf{v}}}\equiv 0,\qquad {{\bar{T}}}=-\beta z+T_L, \end{aligned}$$

where \(\beta =(T_L-T_U)/d\) is positive. The perturbation equations are derived and non-dimensionalized in Straughan [37] for the Fried and Gurtin [42] model and for the dipolar fluid. With \(u_i,\theta ,\pi \) being the perurbations to \({{\bar{v}}}_i,{{\bar{T}}}, {{\bar{p}}}\) the non-dimensional perturbation equations are

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda (\Delta u_{i,t}+u_{j,k}u_{i,jk}+u_j\Delta u_{i,j})=-\pi _{,i}+R\theta k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(9)

for the Fried-Gurtin model. The coefficient of \(\lambda \) is written differently in Fried and Gurtin [42,  Eq. (160)]. They write it as

$$\begin{aligned} \Delta {\dot{u}}_i-u_{i,k}\Delta u_k-u_{i,kj}u_{k,j}. \end{aligned}$$
(10)

However, when one recalls the dot means material derivative, the expression in (10) is equivalent to the one in Eq. (9)\(_1\). The perturbation equations for the dipolar fluid are

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda (\Delta u_{i,t}+u_j\Delta u_{i,j}+u_{j,i}\Delta u_j)=-\pi _{,i}+R\theta k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta . \end{aligned} \end{aligned}$$
(11)

The nonlinear terms in (11) involving \(\lambda \) arise because Green and Naghdi [39] derive an inertia term which corresponds to a kinetic energy which contains in addition to the usual velocity squared piece a term of form \(m_{ka}u_{i,k}u_{i,a}\). They show that their inertia term transforms correctly as in their Eq. (15). Sometimes the isothermal equivalent of (9) are referred to as the Navier–Stokes—\(\alpha \beta \) equations, see Kim et al. [50], Capriz and Fried [51]. In that case \(\alpha ^2\) identifies with \(\lambda \) while \(\beta ^2\) identifies with \(\xi \). In the case of the corotational derivative the non-dimensional perturbation equations can be shown to be

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda \Delta u_{i,t} -2\lambda \bigl [(u_kd_{ij})_{,kj}-(\omega _{ik}d_{kj})_{,j}-(d_{ik}\omega _{jk})_{,j}\bigr ]\\&\quad =-\pi _{,i}+R\theta k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta . \end{aligned} \end{aligned}$$
(12)

Each of the sets of Eqs. (9), (11), (12) holds on \(\{(x,y)\in \mathbb {R}^2\}\times \{z\in (0,1)\}\) for \(t>0\). The boundary conditions are

$$\begin{aligned} u_i=0,\qquad \theta =0,\qquad z=0,1, \end{aligned}$$
(13)

with \(u_i,\theta \) and \(\pi \) satisfying a periodic pattern in x, y which tiles the plane. Since the Fried-Gurtin and dipolar fluid models arise from assuming the second gradients of velocity are present in the constitutive theory these equations contain the term \(-\xi \Delta ^2u_i\). One may also analyse the equivalent problem with a corotational derivative. If one is interested only in Navier–Stokes–Voigt theory then one may take \(\xi =0\). However, when \(\xi >0\) we require an extra boundary condition and we here assume

$$\begin{aligned} \frac{\partial u_i}{\partial n}=0,\qquad \textrm{on}\,\,z=0,1, \end{aligned}$$
(14)

where the derivative indicates that in the direction of the unit outward normal. With this choice existence of a solution follows from Degiovanni et al. [52]. There are other boundary conditions one may employ, cf. Straughan [37], but one has to be very careful to employ meaningful boundary conditions, cf. Ladyzhenskaya [53].

To analyse linear instability with equations (9), (11) or (12) one discards the nonlinear terms and one assumes a time dependence like \(e^{\sigma t}\), i.e. one chooses \(u_i=u_i(\textbf{x})e^{\sigma t},\) \(\theta =\theta (\textbf{x})e^{\sigma t},\) \(\pi =\pi (\textbf{x})e^{\sigma t}.\) Then the resulting set of equations is the same for each of the three systems and is

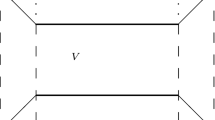
$$\begin{aligned} \begin{aligned}&\sigma u_i-\sigma \lambda \Delta u_i =-\pi _{,i}+R\theta k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr\sigma \theta =Rw+\Delta \theta . \end{aligned} \end{aligned}$$
(15)

The boundary conditions are (13) and (14), and \(u_i,\theta ,\pi \) are periodic in x, y. Let V be a period cell for the solution. Since \(\sigma \) is at the outset possibly complex we suppose \(u_i,\theta ,\pi \) are complex. Multiply (15)\(_1\) by \(u_i^*\), where the \(*\) denotes complex conjugate, and integrate over V. Likewise, multiply (15)\(_3\) by \(\theta ^*\) and integrate over V. With \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert \) denoting the inner product and norm on \(L^2(V)\), we add the results after integration by parts to obtain

$$\begin{aligned} \begin{aligned}&\sigma (\Vert \textbf{u}\Vert ^2+\lambda \Vert \nabla \textbf{u}\Vert ^2+Pr\Vert \theta \Vert ^2)\\&\quad = -\Vert \nabla \textbf{u}\Vert ^2-\xi \Vert \Delta \textbf{u}\Vert ^2-\Vert \nabla \theta \Vert ^2 +2R\bigl [(\theta ,w^*)+(w,\theta ^*)\bigr ]. \end{aligned} \end{aligned}$$
(16)

Let \(\sigma =\sigma _r+i\sigma _1\) and take the real and imaginary part of (16) to find

$$\begin{aligned} \sigma _1(\Vert \textbf{u}\Vert ^2+\lambda \Vert \nabla \textbf{u}\Vert ^2+Pr\Vert \theta \Vert ^2)=0. \end{aligned}$$

Thus, for a non-zero solution we must have \(\sigma _1=0\). Hence, the strong principle of exchange of stabilties holds and the transition to instability is by stationary convection.

To analyse nonlinear stability we return to (9), (11) or (12) and multiply the momentum equation by \(u_i\), the temperature equation by \(\theta \), we integrate each over V and add the results. After some integrations by parts one finds

$$\begin{aligned} \frac{dE}{dt}=RI-D, \end{aligned}$$
(17)

where

$$\begin{aligned} E=\frac{1}{2}\Vert \textbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \textbf{u}\Vert ^2+\frac{Pr}{2}\Vert \theta \vert ^2, \end{aligned}$$

and

$$\begin{aligned} I=2(\theta ,w), \end{aligned}$$

together with

$$\begin{aligned} D=\Vert \nabla \textbf{u}\Vert ^2+\xi \Vert \Delta \textbf{u}\Vert ^2+\Vert \nabla \theta \vert ^2. \end{aligned}$$

Define now \(R_E\) by

$$\begin{aligned} \frac{1}{R_E}=\max _H\,\frac{I}{D} \end{aligned}$$

where H consists of \(u_i\in W^{2,2}(V)\), \(\theta \in W^{1,2}(V)\), together with periodic boundary conditions in x, y and (13) and (14). This maximum problem is analysed in Straughan [37] where it is shown that the Euler–Lagrange equations are the same as those for linear instability. Thus, one has the optimum result that the linear instability boundary is the same as the nonlinear stability one and subcritical instabilities cannot arise.

Straughan [37] shows the nonlinear terms in (9) and (11) vanish in the energy stability analysis. To show the nonlinear terms arising from (12) also do not contribute we observe that they are

$$\begin{aligned}&(u_iu_j,u_{i,j})+(u_i,\theta \theta _{,i})\\&\qquad +2\lambda (u_i,[u_kd_{ij}]_{,kj}-[\omega _{ik}d_{kj}]_{,j}-[d_{ik}\omega _{jk}]_{,j}), \end{aligned}$$

where

$$\begin{aligned} d_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}),\qquad \omega _{ij}=\frac{1}{2}(u_{i,j}-u_{j,i}). \end{aligned}$$

The first two terms vanish by standard calculations. For the remaining terms, observe that

$$\begin{aligned} 2\lambda (u_i,[u_kd_{ij}]_{,kj})=&-2\lambda \int _Vu_{i,j}u_kd_{ij,k}dx\\ =&-\lambda \int _Vu_ku_{i,j}u_{i,jk}dx-\lambda \int _Vu_ku_{i,j}u_{j,ik}dx\\ =&-\frac{\lambda }{2}\int _Vu_k(u_{i,j}u_{i,j})_{,k}dx-\lambda \int _Vu_ku_{i,j}u_{j,ik}dx. \end{aligned}$$

The first term on the right vanishes after integration by parts, since \(u_{k,k}=0\). Then,

$$\begin{aligned} -\lambda \int _Vu_ku_{i,j}u_{j,ik}dx=&\lambda \int _Vu_ku_{i,jk}u_{j,i}dx\\ =&\lambda \int _Vu_ku_{j,ik}u_{i,k}dx, \end{aligned}$$

where we integrated by parts with respect to \(x_k\) and then i and j have been reversed. Hence,

$$\begin{aligned} \int _Vu_ku_{i,j}u_{j,ik}dx=0. \end{aligned}$$

For the remaining two terms write as

$$\begin{aligned} 2\lambda \int _V(u_{i,j}\omega _{ik}d_{kj}+u_{i,j}d_{ik}\omega _{jk})dx. \end{aligned}$$
(18)

In the second of these switch i, j so it becomes

$$\begin{aligned} \int _Vu_{j,i}d_{jk}\omega _{ik}dx=\int _Vu_{j,i}d_{kj}\omega _{ik}dx, \end{aligned}$$

since \(d_{jk}=d_{kj}\). Then (18) becomes

$$\begin{aligned} 4\lambda \int _Vd_{ij}d_{kj}\omega _{ik}dx. \end{aligned}$$

Next, switch i, k so this becomes

$$\begin{aligned} 4\lambda \int _Vd_{kj}d_{ij}\omega _{ki}dx=-4\lambda \int _Vd_{kj}d_{ij}\omega _{ik}dx, \end{aligned}$$

since \(\omega _{ij}=-\omega _{ji}\). Thus, the sum in (18) vanishes and this establishes (17) in the case of the corotational derivative.

Numerical results for the linear instability problem (15) are given in Straughan [37] where the equivalent problem with \(\lambda =0\) is analysed. The fact that exchange of stabilities holds and the linear instability threshold is the same as the global nonlinear stability one is due to the fact that the linear operator is symmetric and the nonlinear terms satisfy \((U,N(U))=0\) where \(U=(u,v,w,\theta )\), the inner product is in \((L^2(V))^4\), and N represents all the nonlinear terms in (9), (11) or (12), and thus the conditions of the theorem of Galdi and Straughan [54] are satisfied.

For the thermal convection problem (Bénard problem) with a (generalized) Navier–Stokes–Voigt fluid the equivalence of the linear and nonlinear stability boundaries is special, and will not hold in general for other problems with this class of fluid. We now examine another convection problem for Navier–Stokes–Voigt theory where this is not true, even though the nonlinear terms satisfy \((U,N(U))=0\).

4 Thermosolutal convection

We now examine the problem of thermal convection with a generalized Navier–Stokes–Voigt fluid but when there is a salt field present. We could work with the analogue of any of the systems (9), (11) or (12), the results for linear instability and nonlinear energy stability turn out to be the same for each model. Hence, we restrict attention to the Fried–Gurtin model.

The fluid is assumed to be contained in the horizontal layer \(z\in (0,d)\) with the boundary conditions

$$\begin{aligned}&v_i=0,\quad T=T_L,\quad C=C_L,\qquad z=0;\\&v_i=0,\quad T=T_U,\quad C=C_U,\qquad z=d, \end{aligned}$$

where \(C(\textbf{x},t)\) is the concentration of solute, \(T_L,T_U,C_L,C_U\) are constants with \(C_L>C_U\) and \(T_L>T_U\). Hence, the layer is heated below and simultaneously salted below. This problem without the bi-Laplacian term and for Navier–Stokes–Voigt theory is handled in Straughan [31]. For the Fried–Gurtin theory the non-dimensional perturbation equations which arise become, cf. (9),

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda (\Delta u_{i,t}+u_{j,k}u_{i,jk}+u_j\Delta u_{i,j})\\&\qquad \qquad \qquad =-\pi _{,i}+R\theta k_i-\mathcal {C}\phi k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta ,\\&Ps(\phi _{,t}+u_i\phi _{,i})=\mathcal {C}w+\Delta \phi , \end{aligned} \end{aligned}$$
(19)

where \(\phi (\textbf{x},t)\) is the perturbation to C and Ps is the salt Prandtl number. The boundary conditions are

$$\begin{aligned} u_i=0,\quad \theta =0,\quad \phi =0,\qquad z=0,1, \end{aligned}$$

together with \(u_i,\theta ,\phi ,\pi \) being periodic in x, y.

Exchange of stabilities does not hold for a solution to this problem. The linear instability equations are

$$\begin{aligned} \begin{aligned}&\sigma u_i-\sigma \lambda \Delta u_i=-\pi _{,i}+R\theta k_i-\mathcal {C}\phi k_i+\Delta u_i-\xi \Delta ^2u_i,\\&u_{i,i}=0,\\&Pr\sigma \theta =Rw+\Delta \theta ,\\&Ps\sigma \phi =\mathcal {C}w+\Delta \phi . \end{aligned} \end{aligned}$$
(20)

To solve this system of equations one removes \(\pi \) and finds that w satisfies the equation

$$\begin{aligned} -\sigma \Delta w+\lambda \sigma \Delta ^2w=-R\Delta ^*\theta +\mathcal {C}\Delta ^*\phi -\Delta ^2w+\xi \Delta ^3w. \end{aligned}$$
(21)

To solve the linear instability problem one now needs to find a numerical solution to (21) and (20)\(_{3,4}\) with the boundary conditions

$$\begin{aligned} w=w^{\prime }=w^{\prime \prime }=0,\quad \theta =0,\quad \phi =0,\qquad z=0,1. \end{aligned}$$

To obtain a nonlinear energy stability threshold one multiplies (19)\(_1\) by \(u_i\), (19)\(_3\) by \(\theta \) and (19)\(_4\) by \(\phi \) and one integrates each over V. Upon addition of the resulting equations one may obtain

$$\begin{aligned}&\frac{d}{dt}\Bigl (\frac{1}{2}\Vert \textbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \textbf{u}\Vert ^2 +\frac{Pr}{2}\Vert \theta \Vert ^2+\frac{Ps}{2}\Vert \phi \Vert ^2\Bigr )\\&\quad =2R(w,\theta )-\Vert \nabla \textbf{u}\Vert ^2-\xi \Vert \Delta \textbf{u}\Vert ^2-\Vert \nabla \theta \Vert ^2-\Vert \nabla \phi \Vert ^2. \end{aligned}$$

One may develop a global nonlinear energy stability analysis as seen in Sect. 4 and one then finds the same stability threshold as in that section. This is due to the fact that the production term \(2R(\theta ,w)\) does not contain \(\phi \).

We do not present numerical results for the linear instability problem here but we observe that they will feature stationary convection and oscillatory convection thresholds, the latter depending on the Kelvin–Voigt parameter \(\lambda \).

In this section we encountered an example where the linear instability threshold is not the same as the nonlinear energy stability one. However, the basic state still has \({{\bar{v}}}_i\equiv 0\) and so there is no contribution from the nonlinear terms to the linear instability theory. We now briefly examine parallel shear flow in a generalized Navier–Stokes–Voigt theory where the nonlinear terms do introduce a contribution into the linear instability problem, and this will in turn, generally, change the instability thresholds.

5 Parallel shear flow

In this section we consider parallel shear flow in an isothermal situation. Thermal effects may be incorporated as is done for Navier-Stokes theory by Gage and Reid [55], but we presently omit these to concentrate on the novelties already present in the isothermal case.

We here consider the Fried–Gurtin model, but we stress that now each different model for a generalized Navier–Stokes–Voigt fluid will potentially lead to a different Orr–Sommerfeld equation for the linear instability thresholds and hence it is vital to recognize this. Since we are interested in Navier–Stokes–Voigt theory we do not consider the bi-Laplacian term in the momentum equation. In this case the equations for the Fried–Gurtin model may be written

$$\begin{aligned} \begin{aligned}&v_{i,t}+v_jv_{i,j}-\lambda (\Delta v_{i,t}+v_{j,k}v_{i,jk}+v_j\Delta v_{i,j})=-p_{,i}+\frac{1}{R}\,\Delta v_i,\\&v_{i,i}=0, \end{aligned} \end{aligned}$$
(22)

where we have non-dimensionalized and R is the Reynolds number.

The Navier–Stokes equations are derived from (22) by taking \(\lambda =0\), while the usual Navier–Stokes–Voigt equations follow from (22) by omitting the \(v_{j,k}v_{i,jk}\) and \(v_j\Delta v_{i,j}\) terms.

We consider the fluid in the horizontal layer \(\{z\in (0,1)\}\) and restrict attention to two-dimensional flow, a scenario which usually involves Squire’s theorem. Then, the basic flow consists of \(\textbf{v}=(U(y),0).\) For example, with a constant pressure gradient \(p_x\) one has Poiseuille flow where \(U=1-y^2\). A perturbation solution is sought where \(\textbf{u}=(u(x,y,t),v(x,y,t))\). One derives the linearized perturbation equations from (22) yielding partial differential equations for u and v. A stream function \(\psi (x,y,t)\) is introduced with \(u=\psi _y,\) \(v=-\psi _x,\) and the solution is then written as

$$\begin{aligned} \psi =\phi (y)e^{ia(x-ct)},\qquad p=p(y)e^{ia(x-ct)}. \end{aligned}$$

The pressure is eliminated and one derives the Orr–Sommerfeld equation governing the Reynolds number threshold. This threshold depends on U(y). For Navier–Stokes theory the Orr–Sommerfeld equation is

$$\begin{aligned} (U-c)(D^2-a^2)\phi -U^{\prime \prime }\phi =\frac{1}{iaR}\,(D^2-a^2)^2\phi , \end{aligned}$$

where \(D=d/dy\), see e.g. Dongarra et al. [56]. For Navier–Stokes–Voigt theory the Orr–Sommerfeld equation is

$$\begin{aligned} (U-c)(D^2-a^2)\phi -U^{\prime \prime }\phi =\Bigl (\frac{1}{iaR}+c\lambda \Bigr )\,(D^2-a^2)^2\phi , \end{aligned}$$

see Shankar and Shivakumara [57]. For the Fried–Gurtin model (22) I calculate the Orr–Sommerfeld equation to be

$$\begin{aligned} \begin{aligned}&(U-c)(D^2-a^2)\phi -U^{\prime \prime }\phi \\&\quad +\lambda \bigl [2U^{\prime }D(D^2-a^2)\phi +U(D^2-a^2)\phi -2U^{\prime \prime \prime }D\phi -2U^{IV}\phi \bigr ]\\&\quad \quad =\Bigl (\frac{1}{iaR}+c\lambda \Bigr )\,(D^2-a^2)^2\phi . \end{aligned} \end{aligned}$$
(23)

Equation (23) shows how a different model of Navier–Stokes–Voigt theory will have a very different spectrum of eigenvalues of linear instability theory. It is important to realize that (23) is only for the Fried–Gurtin model. In general, one expects a different Orr–Sommerfeld equation for a dipolar fluid, or when an appropriate objective derivative is employed.

Nonlinear energy stability analyses of Poiseuille and Couette flows for the classical Navier–Stokes–Voigt fluid may be found in Mulone [58].

6 Magnetohydrodynamics

The Navier–Stokes–Voigt equations coupled with magnetohydrodynamics are analysed by Kuberry et al. [59] and by Sukacheva [30] who also refers to several other papers on the subject. These works do not specifically cover the stability problem.

We here briefly consider the thermal convection problem with a magnetic field in the Fried–Gurtin model introduced in Sect. 4. The classical problem with Navier–Stokes theory is covered in depth by Chandrasekhar [60, Chapter 3], who shows how the relevant equations may be derived from appropriate forms of Ampère’s law, Faraday’s law and Ohm’s law. This approach may be employed with a Fried–Gurtin model, a dipolar fluid, employing the Kelvin–Voigt term as a regularizing agent or by introducing a generalized Navier–Stokes–Voigt theory with an objective derivative. With a vertical magnetic field the basic equations may be derived as in Chandrasekhar [60] with the same steady state as given there. For the Fried–Gurtin model the nonlinear perturbation equations may be shown to be

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda (\Delta u_{i,t}+u_{j,k}u_{i,jk}+u_j\Delta u_{i,j})-Pmh_jh_{i,j}\\&\quad =-\pi _{,i}+R\theta k_i+\Delta u_i+\mathcal {Q}h_{i,z}-\xi \Delta ^2 u_i,\\&u_{i,i}=0,\\&Pm(h_{i,t}+u_jh_{i,j}-h_ju_{i,j})=\mathcal {Q}u_{i,z}+\Delta h_i,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(24)

holding in \(\mathbb {R}^2\times \{z\in (0,1)\}\) for \(t>0\). In these equations \(h_i\) is the perturbation magnetic field, Pm is the magnetic Prandtl number, and \(Q={\mathcal {Q}}^2\) is the Chandrasekhar number measuring the size of the magnetic field. The boundary conditions are as given in Chandrasekhar [60] except when the bi-Laplacian is present we also require \(\partial u_i/\partial n=0\) on \(z=0,1\).

Employing a time dependence like \(e^{\sigma t}\), the linearized system of equations is

$$\begin{aligned} \begin{aligned}&\sigma u_i-\lambda \sigma \Delta u_i =-\pi _{,i}+R\theta k_i+\Delta u_i+\mathcal {Q}h_{i,z}-\xi \Delta ^2 u_i,\\&u_{i,i}=0,\\&Pm\sigma h_i=\mathcal {Q}u_{i,z}+\Delta h_i,\\&Pr\sigma \theta =Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(25)

and the pressure is removed to arrive at the following system of equations in \(w,h_3\) and \(\theta \),

$$\begin{aligned} \begin{aligned}&-\sigma \Delta w+\lambda \sigma \Delta ^2w =-R\Delta ^*\theta -\Delta ^2w+\xi \Delta ^3w-\mathcal {Q}\Delta h_{3,z},\\&Pm\sigma h_3=\mathcal {Q}w_{,z}+\Delta h_3,\\&Pr\sigma \theta =Rw+\Delta \theta . \end{aligned} \end{aligned}$$
(26)

This system of equations should be solved numerically to find the stationary convection boundary and also the oscillatory convection thresholds.

When \(\xi =0\), the stationary convection threshold is the same as that in Chandrasekhar [60, pp. 165–172]. However, when \(\xi =0\) the oscillatory convection boundary will only coincide with that of Chandrasekhar [60] when \(\lambda =0\), otherwise it is different.

7 Rotation

The problem of thermal convection in a horizontal layer of fluid which is rotating with a constant angular velocity about a vertical axis, known as the rotating Bénard problem, is one with many real life applications in industry, in geophysics and in other areas.

We wish to consider the analogous problem but now for a Navier–Stokes–Voigt fluid. Chandrasekhar [60, pp. 80–83] shows how to modify the Navier–Stokes equations to account for the layer rotating with constant angular velocity. He lets a point \((\xi ,\eta ,\zeta )\) in a fixed inertial frame be transformed to a point (x, y, z) in a frame rotating with the fluid via the rotation matrix

$$\begin{aligned} Q= \begin{pmatrix} cos\,\Omega t &{}\quad \sin \,\Omega t &{}\quad 0 \\ -sin\,\Omega t &{}\quad \cos \,\Omega t &{}\quad 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \end{aligned}$$

where \(\Omega \) is the constant angular velocity. He differentiates x and y with respect to t and obtains expressions for the velocity and acceleration in the rotating frame. If superscript (0) denotes the quantity in the inertial frame then Chandrasekhar [60] shows that

$$\begin{aligned} \textbf{u}=\textbf{u}^{(0)}-\varvec{\Omega }\times \textbf{r} \end{aligned}$$
(27)

and

$$\begin{aligned} \Bigl (\frac{d\textbf{u}^{(0)}}{dt}\Bigr )^{(0)}=\frac{d\textbf{u}}{dt}+2\varvec{\Omega }\times \textbf{u} -\frac{1}{2}\,\textrm{grad}\bigl (\vert \varvec{\Omega }\times \textbf{r}\vert ^2\Bigr ). \end{aligned}$$
(28)

For the Navier–Stokes equations he shows that (28) leads to the momentum equation referred to an observer in the rotating frame of form

$$\begin{aligned} u_{i,t}+u_ju_{i,j}=\alpha g\theta k_i-\pi _{,i}+\nu \Delta u_i+2(\textbf{u}\times \varvec{\Omega })_i, \end{aligned}$$
(29)

where the grad term in (28) is absorbed into the pressure \(\pi \). Thus, (29) together with the temperature equation corresponds to equations (3) for the rotating layer.

What should the generalization of the Navier–Stokes–Voigt equations (4) be to incorporate a rotating layer? One could simply add \(-{{\hat{\lambda }}}\Delta \partial u_i/\partial t\) to the momentum equation (29) and be honest that one is adding this term purely for regularity reasons. Using the chain rule the Laplacian is invariant in the \((\xi ,\eta ,\zeta )\) frame or the (x, y, z) frame. However, \(\Delta \partial u_i/\partial t\) is the Laplacian of a local acceleration and one may argue that this must be accounted for in order to derive the correct analogue for Navier–Stokes–Voigt theory. Given the remarks of Damázio et al. [15] one could replace \(-{{\hat{\lambda }}}\Delta \partial u_i/\partial t\) by an objective derivative in the expression for the extra stress, i.e. if

$$\begin{aligned} \sigma _{ij}=-p\delta _{ij}+S_{ij}, \end{aligned}$$

then instead of writing

$$\begin{aligned} S_{ij}=2\mu d_{ij}+2\rho {{\hat{\lambda }}}d_{ij,t}, \end{aligned}$$

one writes

$$\begin{aligned} S_{ij}=2\mu d_{ij}+2\rho {{\hat{\lambda }}}d_{ij}^{\,O}, \end{aligned}$$

where \(d_{ij}^{\,O}\) is an objective derivative. For example, with a corotational derivative one would have

$$\begin{aligned} S_{ij}&=2\mu d_{ij}+2\rho {{\hat{\lambda }}}({\dot{\overline{d_{ij}}}}-\omega _{ik}d_{kj}-d_{ik}\omega _{jk})\\&=2\mu d_{ij}+\rho {{\hat{\lambda }}}\Delta u_{i,t}+2\rho {{\hat{\lambda }}}(u_kd_{ij,k}-\omega _{ik}d_{kj}-d_{ik}\omega _{jk}). \end{aligned}$$

Given the work of Chandrasekhar [60] leading to (29) this would lead to non-dimensional perturbation equations for rotating convection in a Navier–Stokes–Voigt fluid of form

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda \Delta u_{i,t}=R\theta k_i-\pi _{,i}+\Delta u_i\\&\qquad \qquad +T(\textbf{u}\times \textbf{k})_i+\lambda (u_kd_{ij,k}-\omega _{ik}d_{kj}-d_{ik}\omega _{jk}),\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(30)

where T is the Taylor number which is a measure of the angular rotation speed.

If one were to develop a linear instability analysis from (30) then because the basic state is zero velocity (apart from a rigid rotation) the nonlinear terms are not present and (30) are formally equivalent to what one would obtain with an ad hoc procedure of adding \(-\lambda \Delta u_{i,t}\) at the outset. Nevertheless, it is very important to realize that things are different for any nonlinear analysis, whether it be by weakly nonlinear theory, energy stability theory, or otherwise. In that case the nonlinear contributions from \(u_ju_{i,j}\), \(u_i\theta _{,i}\) must be taken into account but so too must the nonlinear terms from the objective derivative, in this case the terms \(u_kd_{ij,k}-\omega _{ik}d_{kj}-d_{ik}\omega _{jk}.\)

We only deal with the basic rotating Bénard problem. But, if one includes more complicated effects which involve a basic state where the velocity is non zero then this would need to be accounted for even in the linear instability theory.

8 Oskolkov models

In this section we investigate two models proposed by Oskolkov [3, 4] which are very much inspired by Navier–Stokes–Voigt theory. Oskolkov mainly works with isothermal theory but he does in both papers also work with the analogous models involving a temperature field. We focus on these.

Oskolkov [4] begins with a highly nonlinear system of equations and works primarily with what he calls the “essential linearized invariant". For a system involving temperature and employing a Boussinesq approximation the system of Oskolkov [4] may be written

$$\begin{aligned} \begin{aligned}&v_{i,t}+v_jv_{i,j}-\nu \Delta v_i-{{\hat{\lambda }}}\frac{\partial }{\partial t}\,\Delta v_i -{{\hat{\lambda }}}\bigl [v_k(v_{i,j}+v_{j,i})_{,k}\bigr ]_{,j} =-\frac{1}{\rho }p_{,i}+\alpha gTk_i,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \Delta T. \end{aligned} \end{aligned}$$
(31)

If one studies thermal convection (Bénard problem) with (31) then it is straightforward to show exchange of stabilities holds for the linearized problem and also to show that the linear instability threshold is the same as the global nonlinear energy stability one. However, our interest here is in a variant model Oskolkov [4] proposes in Section 4 of his paper, see also Eqs. (3.47)–(3.49). This variant model changes the \(v_k\) in the last term on the left of (31) and replaces \(v_k\) by a function \(V_k\) which is known. The function \(V_k\) is divergence free and its second spatial derivatives are bounded by a constant, i.e.

$$\begin{aligned} V_{m,m}=0,\qquad \max \vert V_{k,jm}\vert \le K<\infty , \end{aligned}$$

for some constant K. This leads to the system of equations

$$\begin{aligned} \begin{aligned}&v_{i,t}+v_jv_{i,j}-\nu \Delta v_i-{{\hat{\lambda }}}\frac{\partial }{\partial t}\,\Delta v_i -{{\hat{\lambda }}}[v_kv_{i,jk}]_{,j}-{{\hat{\lambda }}}[V_kv_{j,ik}]_{,j} =-\frac{1}{\rho }p_{,i}+\alpha gTk_i,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \Delta T. \end{aligned} \end{aligned}$$
(32)

We also analyse a second variant model proposed by Oskolkov [3] where \(v_k\) in both terms 5 and 6 on the right of (31) is replaced with a known field \(\textbf{V}\). Thus, the second system of Oskolkov we consider is

$$\begin{aligned} \begin{aligned}&v_{i,t}+v_jv_{i,j}-\nu \Delta v_i-{{\hat{\lambda }}}\frac{\partial }{\partial t}\,\Delta v_i -{{\hat{\lambda }}}\bigl [V_k(v_{i,j}+v_{j,i})_{,k}\bigr ]_{,j} =-\frac{1}{\rho }p_{,i}+\alpha gTk_i,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \Delta T. \end{aligned} \end{aligned}$$
(33)

We assume \(\textbf{V}\) satisfies the same conditions as before.

For both systems (32) and (33) one may study thermal convection in a horizontal layer as is done in section 4. The non-dimensional equations which arise in each case are

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda \Delta u_{i,t}=\pi _{,i}+R\theta k_i+\Delta u_i+\lambda (u_ku_{i,jk})_{,j}+\lambda (V_ku_{j,ik})_{,j},\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(34)

arising from (32) and

$$\begin{aligned} \begin{aligned}&u_{i,t}+u_ju_{i,j}-\lambda \Delta u_{i,t}=\pi _{,i}+R\theta k_i+\Delta u_i +\lambda \bigl [V_k(u_{i,j}+u_{j,i})_{,k}\bigr ]_{,j},\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw+\Delta \theta , \end{aligned} \end{aligned}$$
(35)

which follows from (33). We suppose the solution is periodic in x, y and satisfies the boundary conditions

$$\begin{aligned} u_i=0,\quad \theta =0,\qquad \textrm{on}\,\,z=0,1. \end{aligned}$$

To analyse energy stability of a solution to (34) we suppose \(\textbf{V}\) is also zero on \(z=0,1\) and then we multiply (34)\(_1\) by \(u_i\), (34)\(_3\) by \(\theta \), we integrate each resulting equation over V and add the results to find

$$\begin{aligned} \frac{d}{dt}\Bigl (\frac{1}{2}\Vert \textbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \textbf{u}\Vert ^2+\frac{Pr}{2}\Vert \theta \Vert ^2\Bigr ) =2R(\theta ,w)-\Vert \nabla \textbf{u}\Vert ^2-\Vert \nabla \theta \Vert ^2. \end{aligned}$$
(36)

The nonlinear terms on the right of (34) disappear because

$$\begin{aligned} \lambda \bigl (u_i,(u_ku_{i,jk})_{,j}\bigr )=&-\lambda (u_k,u_{i,j}u_{i,jk})\\ =&-\frac{\lambda }{2}\bigl (u_k,(u_{i,j}u_{i,j})_{,k}\bigr )\\ =&0. \end{aligned}$$

Also

$$\begin{aligned} \lambda \bigl (u_i,(V_ku_{j,ik})_{,j}\bigr )=&-\lambda (V_ku_{i,j},u_{j,ik})\\ =&\lambda (V_ku_{i,jk},u_{j,i})\\ =&\lambda (V_ku_{j,ik},u_{i,j})\\ =&0. \end{aligned}$$

A similar calculation establishes the same outcome from (35). Thus, one obtains from (36), the global nonlinear energy stability threshold is the same as the one for thermal convection with Navier–Stokes theory. Details are similar to Straughan [61]. However, the linear instability problem for either (34) or (35) will be different and will, in general, not lead to coincidence of linear instability and nonlinear stability. Indeed, depending on the choice of \(V_i\) the linear instability equations will not simply reduce to a simple system in w and \(\theta \). In some ways \(V_i\) may be thought of as a control variable which could lead to interesting behaviour.

The two models of Oskolkov just discussed are interesting from a mathematical viewpoint. It remains to be seen whether they are useful in physical problems.

9 Conclusions

This article examines various variants of what might be called Navier–Stokes–Voigt equations. One approach is to add a Kelvin–Voigt term as a regularization function. One may also attempt to set the Navier–Stokes–Voigt equations on a firmer physical basis by incorporating other terms such as objective derivatives. Given the interest in Navier–Stokes–Voigt theories we believe such a discussion is appropriate.