Stability of plane Poiseuille and Couette flows of Navier–Stokes–Voigt fluid

Abstract

The temporal stability of plane Poiseuille and Couette flows for a Navier–Stokes–Voigt type of viscoelastic fluid is examined. The primary unidirectional flow is between two infinite rigid parallel plates, which are either fixed or in relative motion. To investigate the instability of the basic flow, a numerical solution of the resulting eigenvalue problem is performed. Despite the base flow remains to be unaltered, the stability properties differ from those of a Newtonian fluid. In the case of plane Poiseuille flow, two values of the Reynolds number are found to be needed to specify the linear instability criteria owing to the existence of closed neutral stability curves and also the instability emerges only in a certain range of the Kelvin–Voigt parameter $\Lambda$. To the contrary, instability occurs for all nonzero values of $\Lambda$ in the case of plane Couette flow and a single critical value of the Reynolds number is adequate to discuss the stability/instability of fluid flow due to the parabolic nature of the neutral stability curves. The sensitivity of the Kelvin–Voigt parameter is clearly discerned on the stability of both types of flows. The variations of streamlines at the dominant mode of instability are analyzed in comprehending the underlying instability mechanism and shedding light on the secondary flow pattern.

1 Introduction

The study of stability/instability of the classical laminar flows of an incompressible fluid has attracted considerable attention of researchers both theoretically and experimentally because of its applications in many physical situations, for example, in astrophysics, meteorology, oceanography, geophysics, and engineering (Drazin and Reid [1]). This topic is still continued to be an object of extensive study because the transition from laminar flows to instability, turbulence and chaos are not completely understood. The work of Reynolds stimulated the theoretical investigation of Orr [2] and Sommerfeld [3], where they independently considered small traveling-wave disturbances of an otherwise steady, parallel flow and derived the Orr–Sommerfeld equation. The Orr–Sommerfeld equation for the flow associated with plane Poiseuille flow (PPF) yields instability, while the basic flow remains to be stable for plane Couette flow (PCF). The work on the stability of PPF/PCF has also been extended to account for the effects of transverse magnetic field (Lock [4]/Kakutani [5]), throughflow (Fransson and Alfredsson [6]/Shankar and Shivakumara [7]), and the global nonlinear stability (Falsaperla et al. [8]), whereas Nield [9]/Shankar et al. [10] reported the results on the linear stability of PPF/PCF in a porous domain and contrary to the clear fluid layer case, it is shown that PCF displays a linear instability.

Majority of the investigations on the stability of channel fluid flows are dealt with Newtonian fluids. In many industrial processes, however, non-Newtonian liquids are used as working fluids. Viscoelasticity, shear thinning/thickening and couple stresses are few of the many characteristics of most non-Newtonian fluids. Among them, viscoelastic fluid models, which account for elastic and memory effects, have occupied a distinctive place in the literature over the last few decades. The field of viscoelastic fluids is vast and as such there exists a variety of constitutive equations describing the behavior of such fluids. A large number of works have been done on the investigation of the stability of parallel shear flows that include PPF and PCF of viscoelastic fluids. The effect of slight viscoelasticity on the stability of PPF was scrutinized by Chun and Schwarz [11] considering the second-order rheological model and observed that the critical Reynolds number decreases with increasing non-Newtonian parameter. Porteous and Denn [12] examined the stability of PPF of Maxwell fluid, while Kundu [13] analyzed the stability of PPF for an Oldroyd-B fluid subject to small disturbances and both studies revealed that the influence of elasticity is to destabilize the flow. The hydrodynamic stability of PPF for a couple stress fluid was explored by Jain and Stokes [14] and showed both stabilizing and destabilizing impacts on the fluid flow. The classical energy method of Orr was employed by Kundu [15] to scrutinize the stability of PCF of a second-order fluid and noted that the presence of elasticity is to affect the stability either way depending on the governing parameters. In the creeping flow limit (Reynolds number $R \to 0$), Ho and Denn [16] demonstrated that the Poiseuille flow in a channel for the upper convected Maxwell (UCM) fluid is linearly stable. Lee and Finlayson [17] looked at the stability of fully developed Poiseuille and Couette flows of Maxwell fluid between two flat plates and no unstable eigenvalues were established. By discussing the linear stability of PCF for UCM fluid, Renardy and Renardy [18] ruled out the possibility of the occurrence of any instability. A comparison of the linear stability characteristics between the Oldroyd-B and the UCM fluid models can be found in the work of Sureshkumar and Beris [19] wherein they showed the presence of a nonzero solvent viscosity has a pronounced stabilizing effect on the flow. Subsequently, Sadanandan and Sureshkumar [20] carried out a modal stability analysis to explore the impact of fluid elasticity on the Tollmien–Schlichting mode at different values of the ratio of solvent to solution viscosity and disclosed a non-monotonic dependence of the critical Reynolds number on the elasticity number, similar to the UCM limit. In examining PPF for shear-thinning fluids modeled through the Carreau rheological law with viscosity perturbations ignored, Chikkadi et al. [21] displayed the transient growth is slightly decreased. The stability of PPF and PCF of an Oldroyd-B fluid in the presence of a transverse magnetic field was considered by Eldabe et al. [22]. It is observed that the magnetic field has a stabilizing effect on the Poiseuille flow, while it has both destabilizing and stabilizing influence on the Couette flow. With viscosity perturbations obtained approximately by the Carreau fluid in a channel bounded by two parallel plates, it is noted that the transient growth is slightly increased (Nouar et al. [23]), whereas in the Couette flow, it is increased substantially in a shear-thinning fluid flow (Liu and Liu [24]). A comprehensive overview of earlier research on the outcomes of linear stability pertaining to viscoelastic channel flow is presented by Chaudhary et al. [25]. Of late, Ortín [26] studied the oscillatory flows of UCM for low Reynolds number between parallel plates and concluded that the onset of instability is triggered by the divergence of stresses in the direction of the flow. By employing a modal analysis, Khalid et al. [27] disclosed that PPF of an Oldroyd-B fluid becomes unstable to a center mode with phase speed close to the maximum base flow velocity.

Another significant class of viscoelastic fluids exists and is known by the names of Kelvin and Voigt (Berselli and Bisconti [28], Layton and Rebholz [29], Chiriţă and Zampoli [30]), called the Kelvin–Voigt fluids. Interest in these fluids was sparked by the work of Russian researchers. Oskolkov [31, 32] provided a number of intriguing models for the Kelvin–Voigt fluids. The equations of motion for viscoelastic fluids of Maxwell, Oldroyd and Kelvin–Voigt types are succinctly summarized in the article of Oskolkov and Shadiev [33]. In a separate development, Straughan [34,35,36] studied thermal and thermosolutal convection in a horizontal layer of Kelvin–Voigt fluids of different orders for the first time in the literature. The condition for the onset of convection and also the nonlinear stability aspects of the problem are discussed, in general. Recently, Shankar and Shivakumara [37] investigated numerically the stability of natural convection in a vertical layer of Navier–Stokes–Voigt fluid. The Kelvin–Voigt fluids are increasingly used in practical applications, particularly in industrial and engineering fields (Greco and Marano [38], Lewandowski and Chorążyczewski [39], Jakeman and Hurle [40]).

Although instabilities associated with the Kelvin–Voigt fluid of different orders have been studied extensively in a horizontal geometry of the Bénard type (free convection), the hydrodynamic stability (forced convection) of such fluid flows has not received any attention in the literature to the best of our knowledge. Understanding the combined effects of inertia and viscoelasticity in parallel shear flows is important because of their significance in the phenomenon of turbulent drag reduction (Larson [41]). The purpose of the present investigation is to discuss the stability of PPF and PCF of the Navier–Stokes–Voigt fluid or the Kelvin–Voigt fluid of order zero. The neutral stability condition and the critical Reynolds number are obtained for different values of the characteristic governing parameters of viscoelasticity. Some novel results not found in Newtonian and other types of viscoelastic fluid flows are uncovered.

The layout of the remaining paper is organized as follows: the mathematical formulation of the Navier–Stokes–Voigt fluid and the corresponding governing equations are given in Sect. 2. The solution of the basic state is obtained in Sect. 3, while Sect. 4 provides the linear perturbed equations, which leads to a modified Orr–Sommerfeld equation. In Sect. 5, the integral method which provides a qualitative behavior of flow stability is discussed. A detailed computational procedure using the Chebyshev collocation method and the code validation are given in Sect. 6. Section 7 presents different eigenspectra for various values of the Kelvin–Voigt parameter for both PPF and PCF, followed by a growth rate analysis and neutral stability curves. Significant findings of this study are concluded in Sect. 8.

2 Mathematical formulation

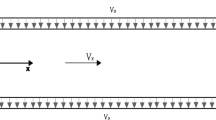
Let us consider a layer of an incompressible Navier–Stokes–Voigt fluid between two rigid parallel plates of infinite length, separated by a distance of $2h$ as shown in Fig. 1. We employ a Cartesian coordinate system midway between the plates to describe the flow where the $x$-axis is horizontal and parallel to the slab, the $y$-axis is also horizontal and the $z$-axis is vertical. The constitutive equation for the Navier–Stokes–Voigt fluid or the Kelvin–Voigt fluid of order zero is (Oskolkov [32], Straughan [36] and references therein)

$${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{T} }} = - p{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{I} }} + \rho \hat{\lambda }\frac{\partial }{\partial t}\left( {\nabla {\mathbf{V}} + \nabla {\mathbf{V}}^{{{\text{tr}}}} } \right) + \mu \left( {\nabla {\mathbf{V}} + \nabla {\mathbf{V}}^{{{\text{tr}}}} } \right),$$

(1)

where ${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{T} }}$ is the stress tensor, $p$ is the pressure, ${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{I} }}$ is the identity tensor, $\rho$ is the fluid density, $\hat{\lambda }$ is the Kelvin–Voigt coefficient, $t$ is the time, ${\mathbf{V}} = (u,v,w)$ is the velocity, $\mu$ is the fluid viscosity and the superscript tr represents the transpose. When $\hat{\lambda } = 0$, Eq. (1) reduces to the standard Stokes’ law. Since ${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{T} }}^{{{\text{tr}}}} = {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{T} }}$, the conservation of linear momentum equation is

$$\rho \left[ {\frac{{\partial {\mathbf{V}}}}{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right){\mathbf{V}}} \right] = \nabla \cdot {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{T} }}.$$

(2)

Fig. 1

a Physical configuration of the horizontal channel for PPF. b Physical configuration of the horizontal channel for PCF

Also,

$$\nabla \cdot {\mathbf{V}} = 0,$$

(3)

as the fluid is incompressible and note that $\nabla (\nabla \cdot {\mathbf{V}}^{{{\text{tr}}}} ) = 0$. With these, Eq. (2) now takes the form

$$\left( {1 - \hat{\lambda }\nabla^{2} } \right)\frac{{\partial {\mathbf{V}}}}{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right){\mathbf{V}} = - \frac{1}{\rho }\nabla P + \frac{\mu }{\rho }\,\nabla^{2} {\mathbf{V}},$$

(4)

where $P$ is the total pressure.

Case (i): Plane Poiseuille flow (PPF)

In this case, both the plates are at rest and the flow is driven due to a uniform pressure gradient in the flow direction. The variables are written in a dimensionless form such that the coordinates $(x,y,z)$ by the half-width of the channel $h$, the fluid velocity ${\mathbf{V}}$ by the velocity at the center line of the channel $U_{0}$, the pressure $P$ by $\rho U_{0}^{2}$ and the time $t$ by $h/U_{0}$, with the dimensionless parameters, $R = U_{0} h\rho /\mu$ and $\Lambda = \hat{\lambda }/h^{2}$. Here, $R$ is the Reynolds number and $\Lambda$ is the Kelvin–Voigt parameter. Equations (3) and (4) in the dimensionless form are

$$\nabla \cdot {\mathbf{V}} = 0,$$

(5a)

$$\left( {1 - \Lambda \nabla^{2} } \right)\frac{{\partial {\mathbf{V}}}}{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right){\mathbf{V}} = - \nabla P + \frac{1}{R}\nabla^{2} {\mathbf{V}}.$$

(5b)

The no-slip boundary condition suggests that

$${\mathbf{V}} = 0\;\;{\text{at}}\;\;z = \pm 1.$$

(6)

Case (ii): Plane Couette flow (PCF)

Here, both the plates are considered to be moving in the opposite directions with a uniform speed $U_{0}$, and there is no pressure gradient in the fluid. Equation (5) holds for this case as well but the definition of $R$ and the boundary conditions differ.

The boundary conditions to this case are

$${\mathbf{V}} = \pm 1\;\;{\text{at}}\;\;z = \pm 1.$$

(7)

3 Base flow

The base flow is fully developed, unidirectional, steady and laminar, i.e., ${\mathbf{V}} = {\mathbf{V}}_{b} = [u_{b} (z),0,0]$, where the suffix b serves to denote the basic flow. Under these circumstances, Eq. (5) reduces to the ordinary differential equation

$$\frac{{{\text{d}}^{2} u_{b} }}{{{\text{d}}z^{2} }} = - R\frac{{{\text{d}}P_{b} }}{{{\text{d}}x}}.$$

(8)

The boundary conditions for case (i) and case (ii) are, respectively, given by

$$u_{b} = 0\,\,\,{\text{at}}\,\,z = \pm 1,$$

(9a)

and

$$u_{b} = \pm 1\,\,\,{\text{at}}\,\,z = \pm 1.$$

(9b)

The solution of Eq. (8) corresponding to Eqs. (9a) and (9b) is, respectively,

$$u_{b} = 1 - z^{2} ,$$

(10a)

and

$$u_{b} = z.$$

(10b)

The above solutions are exactly the same as that of Newtonian fluid (Drazin and Reid [1]). That is, the stationary solution of these flows is parallel, where the velocity only depends on the distance from the wall. For PCF, the velocity profile varies linearly between the two moving plates, whereas the velocity profile is parabolic in the direction of the negative pressure gradient in the case of PPF.

4 Stability analysis

To study the hydrodynamic stability of the problems, the instantaneous flow velocity and the pressure are taken as the sum of basic state and disturbed state quantities as

$$u = u_{b} + u^{\prime},\,v = v^{\prime},\,w = w^{\prime},\,P = P_{b} + P^{\prime},$$

(11)

where the primes identify the perturbation contributions. Substituting Eq. (11) into Eq. (5) and neglecting the nonlinear terms yields (in components)

$$\frac{{\partial u^{\prime}}}{\partial x} + \frac{{\partial v^{\prime}}}{\partial y} + \frac{{\partial w^{\prime}}}{\partial z} = 0,$$

(12)

$$\left( {1 - \Lambda \nabla^{2} } \right)\frac{{\partial u^{\prime}}}{\partial t} + \left( {u_{b} \frac{{\partial u^{\prime}}}{\partial x} + Du_{b} w^{\prime}} \right) = - \frac{{\partial P^{\prime}}}{\partial x} + \frac{1}{R}\nabla^{2} u^{\prime},$$

(13)

$$\left( {1 - \Lambda \nabla^{2} } \right)\frac{{\partial v^{\prime}}}{\partial t} + u_{b} \frac{{\partial v^{\prime}}}{\partial x} = - \frac{{\partial P^{\prime}}}{\partial y} + \frac{1}{R}\nabla^{2} v^{\prime},$$

(14)

$$\left( {1 - \Lambda \nabla^{2} } \right)\frac{{\partial w^{\prime}}}{\partial t} + u_{b} \frac{{\partial w^{\prime}}}{\partial x} = - \frac{{\partial P^{\prime}}}{\partial z} + \frac{1}{R}\nabla^{2} w^{\prime}.$$

(15)

The relevant boundary conditions are

$$u^{\prime} = v^{\prime} = w^{\prime} = 0\;\;{\text{at}}\;\;z = \pm 1.$$

(16)

The linear stability analysis consists of presuming the existence of sinusoidal disturbances to the basic state, which is the flow whose stability is being investigated. On this background flow, we superpose a spatially extended disturbance of the form

$$\left\{ {u^{\prime},v^{\prime},w^{\prime},P^{\prime}} \right\} = \left\{ {\hat{u},\hat{v},\hat{w},\hat{P}} \right\}(z){\text{e}}^{{i\left( {ax + by - act} \right)}} ,$$

(17)

where $a$ and $b$ are the wave numbers in the $x$- and $y$-direction, respectively, and $c( = c_{r} + ic_{i} )$ is the complex wave speed. The phase velocity is the real part of $c$, while the temporal growth rate is the imaginary part of $c$. The beauty of normal modes lies in their ability to offer a complete description for the evolution of any arbitrary disturbance in most cases. By introducing the notion of normal modes, the advent of harmonic analysis facilitated the study of the stability of mechanical systems. A normal mode is a pattern of oscillations in which the entire system oscillates in space/time with the same wavelength/frequency. Substitution of Eq. (17) into Eqs. (12)–(16) yields

$$ia\hat{u} + ib\hat{v} + D\hat{w} = 0,$$

(18)

$$ia\left\{ {u_{b} - \left[ {1 - \Lambda \left( {D^{2} - a^{2} - b^{2} } \right)} \right]c} \right\}\hat{u} + Du_{b} \hat{w} = - ia\hat{P} + \frac{1}{R}\left( {D^{2} - a^{2} - b^{2} } \right)\hat{u},$$

(19)

$$ia\left\{ {u_{b} - \left[ {1 - \Lambda \left( {D^{2} - a^{2} - b^{2} } \right)} \right]c} \right\}\hat{v} = - ib\hat{P} + \frac{1}{R}\left( {D^{2} - a^{2} - b^{2} } \right)\hat{v},$$

(20)

$$ia\left\{ {u_{b} - \left[ {1 - \Lambda \left( {D^{2} - a^{2} - b^{2} } \right)} \right]c} \right\}\hat{w} = - D\hat{P} + \frac{1}{R}\left( {D^{2} - a^{2} - b^{2} } \right)\hat{w},$$

(21)

$$\hat{u} = \hat{v} = \hat{w} = 0\;\;{\text{at}}\;\;z = \pm 1.$$

(22)

Testing the validity of Squire's [42] theorem would be beneficial at this point, and to do so, the following transformations are employed

$$\tilde{a} = \sqrt {a^{2} + b^{2} } ,\,\tilde{u} = \frac{{\left( {a\hat{u} + b\hat{v}} \right)}}{{\tilde{a}}}\,,\,\tilde{w} = \hat{w},\,\tilde{P} = \frac{{\tilde{a}}}{a}\hat{P},\,\tilde{R} = \frac{a}{{\tilde{a}}}R,\,\,\,\tilde{\Lambda } = \Lambda .$$

(23)

We can easily check that Squire's theorem continues to hold for the present problem under the above transformations indicating the sufficiency of considering only two-dimensional disturbances and enforce $b = v = 0$. Elimination of the pressure term from Eqs. (19) and (21), leads to the stability equation (after ignoring tildes)

$$\left( {u_{b} - c\left[ {1 - \Lambda \left( {D^{2} - a^{2} } \right)} \right]} \right)\left( {D^{2} - a^{2} } \right)w - D^{2} u_{b} \,w = \frac{1}{iaR}\left( {D^{2} - a^{2} } \right)^{2} w.$$

(24)

The boundary conditions are on $w$ only

$$w = Dw = 0\,\,{\text{at}}\,\,z = \pm 1.$$

(25)

Equations (24) and (25) form a fourth order homogeneous ordinary differential equation with homogeneous boundary conditions of the Orr–Sommerfeld type. The above formulation holds for both the flow problems but the basic velocity differs. For the case of $\Lambda = 0$, Eq. (24) reduces to the well celebrated Orr–Sommerfeld equation. The resulting eigenvalue problem satisfies the dispersion relation with the following functional form and has a nonzero solution only when

$$f\left( {R,\Lambda ,a,c_{r} ,c_{i} } \right) = 0,$$

(26)

is singular.

5 Integral method: sufficient condition for stability

The sign of the parameter $c_{i}$ yields the most important information as it allows one to detect the linear stability ($c_{i} < 0$) or instability ($c_{i} > 0$) of the base flow. A simple method for obtaining a sufficient condition for the stability of fluid flow has been given in the book by Drazin and Reid [1]. Accordingly, we first multiply the resulting stability equation by $\overline{w}$, the complex conjugate of $w$, and integrate over the channel width to get

$$\begin{aligned} I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} & = - iaR\left\{ {\int\limits_{ - 1}^{1} {\left[ {u_{b} \left| {w^{\prime}} \right|^{2} + \left( {a^{2} u_{b} + u^{\prime\prime}_{b} } \right)\left| w \right|^{2} } \right]} {\textit{d}}z + \int\limits_{ - 1}^{1} {u^{\prime}_{b} w^{\prime}\overline{w}\,{\textit{d}}z} } \right\} \\ & \quad + iaRc\left[ {\left( {I_{1}^{2} + a^{2} I_{0}^{2} } \right) + \Lambda \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)} \right], \\ \end{aligned}$$

(27)

where

$$I_{n}^{2} = \int\limits_{ - 1}^{1} {\left| {D^{n} w} \right|^{2} {\textit{d}}z} ,\,\, n = 0,1,2.$$

(28)

Equating the imaginary and real parts on both sides of Eq. (27), we obtain, respectively,

$$c_{r} \left[ {I_{1}^{2} + a^{2} I_{0}^{2} + \Lambda \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)} \right] = \int\limits_{ - 1}^{1} {\left[ {u_{b} \left| {w^{\prime}} \right|^{2} + \left( {a^{2} u_{b} + \frac{1}{2}u^{\prime\prime}_{b} } \right)\left| w \right|^{2} } \right]} {\textit{d}}z,$$

(29)

and

$$aRc_{i} \left[ {I_{1}^{2} + a^{2} I_{0}^{2} + \Lambda \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)} \right] = - \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right) - \frac{1}{2}iaR\int\limits_{ - 1}^{1} {u^{\prime}_{b} \left( {w^{\prime}\overline{w} - w\overline{w}^{\prime}} \right)} \,{\textit{d}}z.$$

(30)

Equation (30) is simply the energy equation for the two-dimensional disturbances propagating in the direction of the basic flow. The terms on the left-hand side represent the rate of increase of the kinetic energy of the perturbation and there is a contribution from the viscoelasticity of the fluid as well. The first and the second terms on the right-hand side signify the rate of dissipation of the perturbation due to viscosity and the energy transfer from the base flow to the perturbation, respectively. Moreover, the base flow is stable provided $\,ac_{i} < 0$ for all functions $w(z)$ satisfying Eqs. (25) and (30) which requires that

$$\begin{aligned} 0 & > aRc_{i} \left[ {I_{1}^{2} + a^{2} I_{0}^{2} + \Lambda \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)} \right] \\ & = - \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right) - \frac{1}{2}iaR\int\limits_{ - 1}^{1} {u^{\prime}_{b} \left( {w^{\prime}\overline{w} - \overline{w}^{\prime}w} \right)} \,{\textit{d}}z. \\ \end{aligned}$$

(31)

We define $q =\underset{-1 \le z \le 1}{\,\,\text{max}} \left| {u^{\prime}_{b} } \right|$ and note that

$$\left| {\frac{1}{2}i\int\limits_{ - 1}^{1} {u^{\prime}_{b} \left( {w^{\prime}\overline{w} - \overline{w}^{\prime}w} \right){\textit{d}}z} } \right| \le q\int\limits_{ - 1}^{1} {\left| w \right|\left| {w^{\prime}} \right|\,} {\text{d}}z \le qI_{0} I_{1} ,$$

(32)

by the Schwarz's inequality. This gives an upper bound for $c_{i}$ as

$$c_{i} \le \frac{{qI_{0} I_{1} - \frac{1}{aR}\left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)}}{{\left[ {I_{1}^{2} + a^{2} I_{0}^{2} + \Lambda \left( {I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} } \right)} \right]}}.$$

(33)

From Eq. (33), it is evident that the upper bound on the growth rate of unstable mode decreases with increasing $\Lambda$ and the sufficient condition for the stability of fluid flow is

$$I_{2}^{2} + 2a^{2} I_{1}^{2} + a^{4} I_{0}^{2} > aRqI_{0} I_{1} ,$$

(34)

which concurs with that of a Newtonian fluid (Drazin and Reid [1]). Since the growth rate $c_{i}$ depends on the Kelvin–Voigt parameter $\Lambda$, it is pertinent to compute the growth rate $c_{i}$ numerically for various values of governing parameters to assess the possibility of the existence of instability. This can be achieved by imposing $c_{i}$ = 0, namely the neutral stability condition, delimiting the boundary between the regions of parametric stability and instability.

6 Numerical method

The Chebyshev collocation method is adopted to solve the eigenvalue problem of both the flows.

Case (i) Plane Poiseuille flow

Since $u_{b}$ is an even function of $z$, let us consider the even solution $w = w^{e}$ in terms of the truncated modified Chebyshev series as

$$w = w^{e} = \sum\limits_{i = 1}^{N} {\xi_{i} w_{i}^{e} \left( z \right)} ,$$

(35)

where $\xi_{i}$ are the unknown coefficients, $w_{i}^{e} (z)$ are chosen satisfying the boundary conditions in the form

$$w_{i}^{e} (z) = \left( {1 - z^{2} } \right)^{2} T_{2i - 2} (z),$$

(36)

and $T_{i} (z)$ denotes the ith degree Chebyshev polynomial of first kind which are defined by a three-term recurrence relation

$$T_{0} (z) = 1;\,\,T_{1} (z) = z;\,\,T_{n + 1} (z) - 2zT_{n} (z) + T_{n - 1} (z) = 0\,\,(n \ge 1).$$

(37)

Substituting Eq. (35) into Eq. (24) and requiring that Eq. (24) be satisfied at $N$ collocation points $z_{1} ,z_{2} , \ldots ,z_{N}$, where

$$z_{n} = \cos \left[ {\left( {n - 1} \right)\pi /\left( {2N - 1} \right)} \right],\,\,n = 1,2, \ldots ,N.$$

(38)

Case (ii) Plane Couette flow

Since u_b is an odd function of z, the odd solution $w = w^{o}$ may be expressed as

$$w = w^{o} = \sum\limits_{i = 1}^{N} {\xi_{i} w_{i}^{o} \left( z \right)} ,$$

(39)

where

$$w_{i}^{o} (z) = \left( {1 - z^{2} } \right)^{2} T_{i - 1} (z).$$

(40)

Let $z_{n}$ denote the collocation points defined as

$$z_{n} = \cos \left[ {n\pi /\left( {N + 1} \right)} \right],\,\, n = 1,2, \ldots ,N.$$

(41)

In both the cases, we obtain $N$ algebraic equations for $N$ unknowns $\xi_{1} ,\xi_{2} , \ldots ,\xi_{N}$ which can be written in the form

$$AX = cBX,$$

(42)

where $X = \left( {\xi_{1} ,\xi_{2} , \ldots ,\xi_{N} } \right)^{{\text{T}}}$, $A$ and $B$ are the coefficient matrices of dimension $N \times N$ given by

$$A(n,i) = u_{b} \left( {z_{n} } \right)\left( {D^{2} - a^{2} } \right)w_{i} \left( {z_{n} } \right) - D^{2} u_{b} \left( {z_{n} } \right)\,w_{i} \left( {z_{n} } \right) - \frac{1}{iaR}\left( {D^{2} - a^{2} } \right)^{2} w_{i} \left( {z_{n} } \right),$$

(43)

$$B\left( {n,i} \right) = \left[ {1 - \Lambda \left( {D^{2} - a^{2} } \right)} \right]\left( {D^{2} - a^{2} } \right)w_{i} \left( {z_{n} } \right).$$

(44)

We note that $A$ is complex and $B$ is real. For fixed values of $R,\,\,\Lambda$ and $a$, a nontrivial solution to the above generalized eigenvalue problem is possible when the wave speed $c$ satisfies the dispersion relation given by Eq. (26). From the $N$ eigenvalues one having the largest imaginary part of, say $c_{1} = c_{r1} + ic_{i1}$ is selected. We then employ the secant method iteration either to $R$, with $a$ fixed, or to $a$, with $R$ fixed, until the imaginary part of $c_{i1}$ ceases to zero, to obtain the neutral stability point. The infimum of $R$ as a function of $a$ or vice versa gives the critical Reynolds number $R_{c}$ and the critical wave number $a_{c}$. The real part of $c_{1}$, i.e., $c_{r1}$, gives the critical wave speed. This procedure is repeated for various values of $\Lambda$.

The convergence of the results is tested by computing the triplets $\left( {R_{Dc} ,\,a_{c} ,c_{c} } \right)$ by varying the collocation points $N$ for different values of $\Lambda$ (see Tables 1 and 2). Based on various numerical experiments, to preserve the accuracy of the numerical results, the maximum order of the Chebyshev polynomial in the approximation of the different field variables is set to 30 in the case of PPF (Table 1). For a Newtonian fluid, PPF is linearly unstable for the Reynolds number exceeding 5772.22 which was given by Orszag [43] and our result has also predicted the same value of the Reynolds number when $\Lambda = 0$. In the case of PCF, it is seen that more collocation points are required to achieve satisfactory convergence in the results for smaller values of $\Lambda$ (Table 2). The numerical data quoted here are accurate to six decimal places.

Table 1 Process of convergence of the Chebyshev collocation method for different values of $\Lambda$ (PPF)

Table 2 Process of convergence of the Chebyshev collocation method for different values of $\Lambda$ (PCF)

7 Discussion of the results

The stability of PPF and PCF is analyzed for the Navier–Stokes–Voigt type of viscoelastic fluid. Equations (24) an (25) define the eigenvalue problem, and it forms the cornerstone of the stability analysis. We believe that the present findings are worthy and ought to be brought to the attention of workers dealing with practical hydrodynamical stability problems.

7.1 Eigenspectrum

We first discuss the key differences in the eigenspectrum of Navier–Stokes–Voigt and the Newtonian fluids. The results of Navier–Stokes–Voigt fluid reduce to the Newtonian one when $\Lambda = 0$. Figure 2a–d displays the eigenspectra for the plane Poiseuille flow for different values of $N$ when $\Lambda = 0$, $R = 10^{4}$ and $a = 1$ as they provide information about the scattering of complex eigenvalues with an increase in the order of polynomial. The eigenspectrum shows a characteristic ‘Y-shaped’ structure in the $(c_{r} ,c_{i} )$-plane which has basically three different branches. In the figures, the A branch is the upper left one, the P branch is the upper right one, and the S branch is the lower one. The phase speeds $c_{r}$ of A, P, and S modes approach 0 (wall mode), 1 (center mode), and 2/3 (damped mode), respectively. Figure 2a demonstrates the inaccuracy caused by having insufficient polynomials, especially on the S-mode and the eigenvalues at the intersection when $N$ = 80. The splitting in the damped mode is symptomatic of insufficient polynomials and by increasing the number of polynomials we are able to overcome the splitting problem as in Fig. 2b–d. Indeed, Y-like structure with noted APS branches is observed in Fig. 2d with $N = 120$. It is clear from these figures that A branch becomes unstable (Schmid and Henningson [44]), this being the ‘Tollmien–Schlichting’ instability. The most unstable mode, which is responsible for the instability to occur in this wall mode, is 0.23752648 + i0.00373967 and a similar kind of finding is reported by Dongarra et al. [45]. The eigenspectra presented in Fig. 3a–d for $\Lambda = 10^{ - 5}$ show similar structures with APS branches as viewed in the case of $\Lambda = 0$. It is seen that the presence of Kelvin–Voigt parameter does not affect much either the eigenvalues near the center of the Y-structure or the value of N. But the S-mode whose phase speed approaches 2/3 now shifts toward the left side. The most unstable modes of PPF for different values of $\Lambda$ with varying N are given in Table 3 for the benefit of others who might use this calculation as a yardstick. It is noticed from the table that there is a rapid convergence of the eigenvalue with increasing $N$ which is independent of $\Lambda$. Besides, a change in the most unstable mode is evident with increasing $\Lambda$.

Fig. 2

Eigenspectra for PPF with a $N = 80$, b $N = 90$, c $N = 100$ and d $N = 120$ when $R = 10^{4} ,a = 1$ and $\Lambda = 0$. Star (red color) denotes the most unstable mode and its eigenvalue is $c_{r} + ic_{i} = {0}{\text{.23752648 + }}i{ 0}{\text{.00373967}}$. (color figure online)

Fig. 3

Eigenspectra for PPF with a $N = 80$, b $N = 90$, c $N = 100$ and d $N = 120$ when $R = 10^{4} ,a = 1$ and $\Lambda = 10^{ - 5}$. Star (red color) denotes the most unstable mode and its eigenvalue is $c_{r} + ic_{i} = {0}{\text{.23746673 + }}i\,{0}{\text{.00274110}}$. (color figure online)

Table 3 Chebyshev approximation to the most unstable mode of PPF for different values of $\Lambda$ when $R = 10^{4}$ and $a = 1$

Figure 4a–d displays the eigenspectra for PCF when $R = 25000$ and $a = 1$ for $\Lambda \ne 0$ with $N$ = 150. The computed spectrum for PCF is very different from PPF. Contrary to the PCF for a Newtonian fluid, unstable mode exists in the case of the Navier–Stokes–Voigt fluid. The structure of the eigenspectra changes to ‘X-shaped’ from a unique structure with increasing $\Lambda$. The results of the most unstable mode for PCF when $R = 25000$ and $a = 1$ are given in Table 4 for different values of $\Lambda$ and note that the lower values of $N$ are sufficient to get accurate results as $\Lambda$ increases.

Fig. 4

Eigenspectra for PCF with a $\Lambda = 10^{ - 3}$, b $\Lambda = 10^{ - 2}$, c $\Lambda = 10^{ - 1}$ and d $\Lambda = 10^{0}$ when $R = 25000,\,a = 1$ and N = 150

Table 4 Chebyshev approximation to the most unstable mode of PCF for different values of $\Lambda$ when $R = 2.5 \times 10^{4}$ and $a = 1$

7.2 Growth rate analysis

The temporal growth rate $c_{i}$ is computed as a function of $a$ for different values of $\Lambda$ and $R$ in order to determine when the unstable conditions may start to emerge in the parametric plane $(a,c_{i} )$. The growth rate plots are illustrated in Figs. 5 and 6 for PPF and PCF, respectively. The main characteristics of these figures are that the growth rate starts from a negative value and remains to be negative for some values of the governing parameters signifying that the base flow is always linearly stable, while for some other choice of parametric values, it gradually increases and becomes positive with increasing $a$, which entails the onset of instability. Figure 5 shows the possibility of flow becoming unstable as $c_{i}$ undergoes a transition from negative to positive in a certain parametric space of $\Lambda ( \le 10^{ - 5} )$ but the flow remains to be stable with increasing $\Lambda ( \ge 10^{ - 4} )$ as the value of c_i remains to be always negative. The same scenario is observed at higher values of the Reynolds number too (figures are not shown). This feature is completely surprising as PPF exhibits a stable behavior after certain values of $\Lambda$. As depicted in Fig. 6a, the value of c_i is always negative for all values of the Reynolds number when $\Lambda = 0$, indicating that no instability is possible for PCF, and this behavior was pointed out previously by Drazin and Reid [1]. Figure 6b demonstrates the occurrence of transition from stability to instability for all the considered values of $\Lambda \ne 0$, a complete contrast result observed in an ordinary viscous fluid. Thus, the presence of viscoelasticity turns out to mean a significant difference in both the cases of fluid flows compared to that of a Newtonian fluid.

Fig. 5

Plots of growth rate $c_{i}$ versus $a$ for different values of $\Lambda$ with $R = 5 \times 10^{4}$ for PPF

Fig. 6

Plots of growth rate $c_{i}$ versus $a$ for different values of a $R$ with $\Lambda = 0$ and b $\Lambda$ with $R = 5 \times 10^{5}$ for PCF

7.3 Neutral stability curves

The neutral stability condition $c_{i}$ is the bulk of a linear stability analysis as it provides the threshold between linear stability and instability. The graphical way to convey this information is by drawing a curve in the parametric plane $\left( {a,R} \right)$ and the lowest neutral stability curve in this plane captures the parametric condition for the initiation of the instability. As this curve usually features an absolute minimum of $R$ for a given $a$, this minimum yields the onset for the linear instability. The values of $a$ and $R$ for such a minimum are called the critical values and are denoted by $a_{c}$ and $R_{c}$, respectively. The physical meaning of the critical conditions is that no modal linear instability is possible for $R < R_{c}$. The adjective “modal” employed here is important as, generally speaking, it has been reported the possibility of non-modal linear instability occurring at the subcritical condition $R < R_{c}$.

In the case of PPF, it is curious to visualize how the neutral stability curves behave as the switching over of flow from instability to stability ensues depending on the intensity of the elasticity of the fluid. Figure 7 displays the evolution of neutral stability curves for different values of $\Lambda$. Some novel consequences not perceived either in the Newtonian fluid or any other types of viscoelastic fluids are found in a certain range of values of $\Lambda$. It is seen that the neutral curves appear to be parabolic type and the instability arises within the region entrapped by the these curves for $\Lambda = 10^{ - 10}$. Also, the instability region becomes unbounded so that there exists $R_{\min }$, but not $R_{\max }$. Nonetheless, with increasing $\Lambda ( = 10^{ - 5} )$ the neutral stability curves form closed loops with the region of instability confined to the interior of the loop which indicates the requirement of two critical values of the Reynolds number to specify the linear instability criteria. The region inside the loop corresponds to instability ($c_{i} > 0$) and the outside defines the parametric conditions of linear stability ($c_{i} < 0$). Though the region of instability shrinks toward the lower wave number side with further increase in $\Lambda$, it shows a stabilizing effect as the minimum value of R increases. However, the instability region eventually disappears and the flow becomes stable for $\Lambda \ge 0.0000764$. Thus, it is possible to control the instability of fluid flow by tuning the viscoelasticity of the fluid.

Fig. 7

Neutral stability curves in the $(a,R)$-plane for different values of $\Lambda$ for PPF

Figure 8 demonstrates the neutral stability curves for different values of $\Lambda$ for PCF. The flow becoming unstable is evident due to the viscoelasticity of the fluid, but otherwise, the flow is found to be stable always. The closed type of neutral curve is not visualized in this case. The neutral curves show an upward concave shape and exhibit only single but different minimum for each value of $\Lambda$ which indicates that the system possesses only one upper cut off R with respect to a band of wave number. The figure reveals that the instability activates first at a higher value of $\Lambda$ that too in the lower wave number range and also there is a steep variation in the neutral stability curve as $\Lambda$ assumes lesser and lesser values.

Fig. 8

Neutral stability curves in the $(a,R)$-plane for different values of $\Lambda$ for PCF

7.4 Critical conditions for the instability

Figure 9a–c represents the variation of $R_{c} ,a_{c}$ and $c_{c}$, respectively, with $\Lambda$, and it clearly establishes the feature suggested in Figs. 7 and 8. According to the linear stability analysis, the basic state is asymptotically stable below the $R_{c}$ curves, where the value of $c_{i}$ is always negative. In the region above these curves, there is at least one positive value of $c_{i}$ for which the flow is unstable. In the case of PPF, it is seen that the curve of $R_{c}$ remains almost unchanged with $\Lambda$ initially and then it increases suddenly with further increase in $\Lambda$ and stops (Fig. 9a). Thus, there exists a threshold value of $\Lambda ( \ge 0.0000764)$ after which the base flow is always stable because the perturbations display a negative growth rate. This suggests that instability exists only in a particular parametric space of $\Lambda \in \left[ {0,0.0000763} \right]$. In this range, the system shows a stabilizing effect on the basic flow. In the case of PCF, it is observed that $R_{c}$ decreases steadily with increasing $\Lambda$ and tends to a constant value as $\Lambda$ approaches a higher value. Thus, increasing $\Lambda$ instills destabilizing effect on the base flow. This is contrary to the conclusion drawn in the literature for an ordinary viscous fluid (Drazin and Reid [1]) and also for some other types of viscoelastic fluids (Chaudhary et al. [25]) in the case of PCF where the base flow remains to be stable to disturbances of all wave numbers at all values of the Reynolds number. This can be witnessed in the limit $\Lambda \to 0$. The behavior reported in Fig. 8, suggesting an abrupt increase in the critical value of $R$ with decreasing $\Lambda$, is confirmed quite clearly by the curves displayed in Fig. 9a. In fact, it is quite evident that the critical value of $R$ tends to infinity as $\Lambda \to 0$. It is also perceived from the figure that the critical Reynolds number of PPF lies well below that of PCF till $\Lambda = 4 \times 10^{ - 5}$ after which an opposite behavior is noticed as the curves of $R_{c}$ crossover. This indicates that PCF has a more stabilizing effect than PPF for $\Lambda < 4 \times 10^{ - 5}$ and the trend gets reversed for $\Lambda \ge 4 \times 10^{ - 5}$.

Fig. 9

Variation of critical values of a $R$, b $a_{{}}$ and c $c$ versus $\Lambda$

Figure 9b points out that the onset of instability involves smaller and smaller wave numbers as $a_{c}$ is a decreasing function of $\Lambda$ for both PPF and PCF. Thus, the size of the convection cell increases with increasing $\Lambda$. Moreover, the cell size of PCF is smaller than PPF. These feature are perfectly coherent with the plots of the neutral stability curves represented in Figs. 7 and 8. The critical wave speed $c_{c}$ also decreases with $\Lambda$ in both cases (Fig. 9c)). In the case of PPF, only positive $c_{c}$ exists implying that cells move only in the rightward direction and this is due to the symmetry in the basic flow which has resulted in the non-existence of different set of onset modes, whereas both positive and negative values of $c_{c}$ exist for the PCF. This is because if $c = c_{1} + ic_{2}$ is an eigenvalue of $B^{ - 1} A$ for a fixed value of $\Lambda$, then $c = - c_{1} + ic_{2}$ is also its eigenvalue as $u_{b}$ is an odd function of $z$. Therefore, if traveling-wave disturbances with the critical wave speed $c_{c}$ exist, then those with $- c_{c}$ also exist. Thus, unstable modes travel in both the positive $x$-direction ($c_{c} > 0$) and the negative $x$-direction ($c_{c} < 0$) with the same speed.

7.5 Secondary flow pattern

In order to validate the dominant mode of instability and understand the flow dynamics, the stream function contour at the critical level is analyzed. These secondary flow patterns are the dominant mode of instability at the critical point and are quite important as they define the initiation of the instability. In fact, even if the flow patterns of convection are evaluated according to the linear stability theory, it is generally retained that such patterns are the starting point for the development of the nonlinear analysis of convection. In the present case, forced flow is only the factor that decides the flow pattern. For the purpose of drawing the streamlines, a suitable stream function $\psi (x,z,t)$ is defined such that $u = {{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial z}}} \right. \kern-0pt} {\partial z}}$ and $w = {{ - \partial \psi } \mathord{\left/ {\vphantom {{ - \partial \psi } {\partial x}}} \right. \kern-0pt} {\partial x}}$. The distribution of the stream function consists of alternatively clockwise (positive streamline) and counter clockwise (negative streamline) rotating convective cells. The plots of streamlines for PPF and PCF are shown in Figs. 10a–d and 11a–d, respectively, at the critical level in the $xz$-plane, where the x-direction in the figures is considered for a single period ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } {a_{c} }}} \right. \kern-0pt} {a_{c} }}$. The effect of Kelvin–Voigt parameter on the shape of the cellular pattern for PPF is tested by increasing $\Lambda$ gradually from 0 to 0.00007. It is seen that the perturbation patterns are centro-symmetric with respect to the horizontal mid-plane for PPF and a single cell covers the entire domain for all values of $\Lambda$ (Fig. 10a–d). Even though the shape of the disturbances does not depend on the values of $\Lambda$, the cell width and also the magnitude of $\psi$ change with $\Lambda$. In the case of PCF, the asymmetric form of the cells is clearly perceivable. The streamlines concentrate in the vicinity of the lower region of the domain when $\Lambda = 0.001$ (Fig. 11a) and shift to the upper region with increasing $\Lambda$ to 0.01 (Fig. 11b). Moreover, the cells start to move toward the center of the channel with a further increase in $\Lambda$ (Fig. 11c, d). In general, there is a tendency for the cells to acquire a boundary layer structure (either upper or lower) with decreasing $\Lambda$.

Fig. 10

Perturbation streamlines for PPF: a $\Lambda = 0$, b $\Lambda = 0.00001$, c $\Lambda = 0.00003$ and d $\Lambda = 0.00007$

Fig. 11

Perturbation streamlines for PCF: a $\Lambda = 0.001$, b $\Lambda = 0.01$, c $\Lambda = 0.1$ and d $\Lambda = 1$

8 Conclusions

The effect of viscoelasticity on the hydrodynamic stability of plane Poiseuille and Couette flows has been analyzed using the Navier–Stokes–Voigt fluid model. The linear perturbations of the base flow have been studied by employing a modal analysis. The validity of Squire's theorem has been established. Although the employed integral method offers insight into the qualitative behavior of the fluid flow, it does not provide any quantitative information about the influence of the Kelvin–Voigt parameter $\Lambda$ on the growth rate. As a result, numerical experiments have been conducted to investigate how the spurious eigenvalues form when $\Lambda$ is present. In the case of PPF, most of the general features of the eigenspectrum for the Navier–Stokes–Voigt fluid are, in fact, similar to that of Newtonian fluid flow with only one unstable mode on the A branch. In addition, it has been observed that the majority of the damped eigenmodes (S-mode) of regular Y-like structures shift toward the left with increasing $\Lambda$. In the case of PCF, a unique structure is found at initial values of $\Lambda$ and then it turns to X-like structure with increasing $\Lambda$. The neutral stability curves are exhibited in the ($a,R$)-plane, where $a$ is the wave number and the impact of $\Lambda$ on the critical conditions is evaluated. The stream function contours are analyzed to validate the least stable mode obtained from the linearized stability theory, which may be the starting point for analyzing the phenomenon of nonlinear saturation expected to happen at moderately supercritical Reynolds numbers. The similarities and differences between the linear instability characteristics of PCF and PPF are also presented. Some interesting and unexpected results on the stability characteristics of the fluid flow are established.

• The PPF is unstable for values of $\Lambda \le 0.0000763$ and within this range the flow gets stabilized with increasing $\Lambda$. For $\Lambda > 0.0000763$, however, the flow remains to be stable always. One of the striking features that do not carry over from the other types of viscoelastic, inelastic couple stress and Newtonian fluids is the occurrence of closed neutral curves, indicating the requirement of two critical Reynolds numbers to specify the linear instability criteria instead of the usual single critical value.

• Although PCF in a channel of Newtonian fluid is stable to small disturbances for all values of the Reynolds number, the flow becomes unstable for the Navier–Stokes–Voigt fluid. In fact, the onset of instability is speeded up with increasing $\Lambda$.

• The PPF has a more stabilizing effect than PCF for values of $\Lambda \ge 4 \times 10^{ - 5}$ and prior to which an opposite trend prevails.

• The secondary flow patterns remain similar for all values of $\Lambda$ in the case of PPF, while in PCF streamlines change drastically. The size of the convection cells is larger in PPF compared to PCF, and also it increases with $\Lambda$ both in PPF and PCF. The cells move only in the positive x-direction in PPF, whereas in PCF it moves both in positive and negative x-directions with the same speed.

An attempt toward the global nonlinear stability analysis for such systems can be of great interest to gain possible clues regarding the transition to turbulence in terms of bifurcation. Another important aspect is the possible existence of a subcritical instability, and it can happen under parametric conditions incompatible with the onset of linear instability, viz. a Reynolds number smaller than its critical value. The existence of such a phenomenon can hardly be detected in a framework based on the linearized governing equations. These analyses are left for our future studies.