Statistically consistent and computationally efficient inference of ancestral DNA sequences in the TKF91 model under dense taxon sampling

Abstract

In evolutionary biology, the speciation history of living organisms is represented graphically by a phylogeny, that is, a rooted tree whose leaves correspond to current species and whose branchings indicate past speciation events. Phylogenetic analyses often rely on molecular sequences, such as DNA sequences, collected from the species of interest, and it is common in this context to employ statistical approaches based on stochastic models of sequence evolution on a tree. For tractability, such models necessarily make simplifying assumptions about the evolutionary mechanisms involved. In particular, commonly omitted are insertions and deletions of nucleotides—also known as indels. Properly accounting for indels in statistical phylogenetic analyses remains a major challenge in computational evolutionary biology. Here, we consider the problem of reconstructing ancestral sequences on a known phylogeny in a model of sequence evolution incorporating nucleotide substitutions, insertions and deletions, specifically the classical TKF91 process. We focus on the case of dense phylogenies of bounded height, which we refer to as the taxon-rich setting, where statistical consistency is achievable. We give the first explicit reconstruction algorithm with provable guarantees under constant rates of mutation. Our algorithm succeeds when the phylogeny satisfies the “big bang” condition, a necessary and sufficient condition for statistical consistency in this setting.

1 Introduction

Background In evolutionary biology, the speciation history of living organisms is represented graphically by a phylogeny, that is, a rooted tree whose leaves correspond to current species and branchings indicate past speciation events. Phylogenies are commonly estimated from molecular sequences, such as DNA sequences, collected from the species of interest. At a high level, the idea behind this inference is simple: The further apart in the tree of life are two species, the greater is the number of mutations to have accumulated in their genomes since their most recent common ancestor. In order to obtain accurate estimates in phylogenetic analyses, it is a standard practice to employ statistical approaches based on stochastic models of sequence evolution on a tree. For tractability, such models necessarily make simplifying assumptions about the evolutionary mechanisms involved. In particular, commonly omitted are insertions and deletions of nucleotides—also known as indels. Properly accounting for indels in statistical phylogenetic analyses remains a major challenge in computational evolutionary biology.

Here, we consider the related problem of reconstructing ancestral sequences on a known phylogeny in a model of sequence evolution incorporating nucleotide substitutions as well as indels. The model we consider, often referred to as the TKF91 process, was introduced in the seminal work of Thorne et al. (1991) on the multiple sequence alignment problem. (See also Thorne et al. 1992.) Much is known about ancestral sequence reconstruction (ASR) in substitution-only models. See, e.g., Evans et al. (2000), Mossel (2001), Sly (2009) and references therein, as well as Liberles (2007) for applications in biology. In the presence of indels, however, the only previous ASR result was obtained in Andoni et al. (2012) for vanishingly small indel rates in a simplified version of the TKF91 process. The results in Andoni et al. (2012) concern what is known as “solvability”; roughly, a sequence is inferred that exhibits a correlation with the true root sequence bounded away from 0 uniformly in the depth of the tree. The ASR problem in the presence of indels is also related to the trace reconstruction problem. See, e.g., the survey Mitzenmacher (2009) and references therein.

A desirable property of a reconstruction method is statistical consistency, which roughly says that the reconstruction is correct with probability tending to one as the amount of data increases. It is known (Evans et al. 2000) that this is typically not information-theoretically achievable in the standard setting of the ASR problem. Here, however, we consider the taxon-rich setting, in which we have a sequence of trees with uniformly bounded heights and growing number of leaves. Building on the work of Gascuel and Steel (2010), a necessary and sufficient condition for consistent ancestral reconstruction was derived in Fan and Roch (2018, Theorem 1) in this context.

Our results In the current paper, our interest is in statistically consistent estimators for the ASR problem under the TKF91 process in the taxon-rich setting, which differs from the “solvability” results in Andoni et al. (2012). In fact, an ASR statistical consistency result in this context is already implied by the general results of Fan and Roch (2018). However, the estimator in Fan and Roch (2018) has drawbacks from a computational point of view. Indeed, it relies on the computation of total variation distances between leaf distributions for different root states—and we are not aware of a tractable way to do these computations in TKF models. The main contribution here is the design of an estimator which is not only consistent but also constructive and computationally tractable. We obtain this estimator by first estimating the length of the ancestral sequence and then estimating the sequence itself conditioned on the sequence length. The latter is achieved by deriving explicit formulas to invert the mapping from the root sequence to the distribution of the leaf sequences. (In statistical terms, we establish an identifiability result.)

Further related results For tree reconstruction problems in the presence of indels, Daskalakis and Roch (2013) devised the first polynomial-time phylogenetic tree reconstruction algorithm. In subsequent work, Ganesh and Zhang (2019) obtained a significantly improved sequence-length requirement in a certain regime of parameters. There is also a large computational biology literature on methods for the co-estimation of phylogenetic trees and multiple sequence alignment, typically without much theoretical guarantees. See, e.g., Warnow (2013) and references therein. Note that our approach to ASR does not require multiple sequence alignment.

Outline In Sect. 2, we first recall the definition of the TKF91 process and our key assumptions on the sequence of trees. We then describe our new estimator and state the main results. In Sect. 3, we give some intuition behind the definition of our estimator by giving a constructive proof of root-state identifiability for the TKF91 model. The proofs of the main results are given in Sect. 4. A summary discussion is given in Sect. 5. Some basic properties of the TKF91 process are derived in Sect. A. A table of notations that are frequently used in this paper is provided in Sect. B for convenience of the reader.

2 Definitions and main results

Before stating our main results, we begin by describing the TKF91 model of Thorne et al. (1991), which incorporates both substitutions and insertions/deletions (or indels for short) in the evolution of a DNA sequence on a phylogeny. For simplicity, we follow Thorne et al. and use the F81 model (Felsenstein 1981) for the substitution component of the model, although our results can be extended beyond this simple model. For ease of reference, a number of useful properties of the TKF91 model are derived in Sect. A.

2.1 TKF91 process

We first describe the Markovian dynamics on a single edge of the phylogeny. Conforming with the original definition of the model (Thorne et al. 1991), we use an “immortal link” as a stand-in for the empty sequence.

Definition 1

(TKF91 sequence evolution model on an edge) The TKF91 edge process is a Markov process ${\mathcal {I}}=({\mathcal {I}}_t)_{t\ge 0}$ on the space ${\mathcal {S}}$ of DNA sequences together with an immortal link “$\bullet$”, that is,

$$\begin{aligned} {\mathcal {S}} := ``\bullet \text {''} \otimes \bigcup _{M\ge 0} \{A,T,C,G\}^M, \end{aligned}$$

(1)

where the notation above indicates that all sequences begin with the immortal link (and can otherwise be empty). We also refer to the positions of a sequence (including nucleotides and the immortal link) as sites. Let $(\nu ,\lambda ,\mu )\in (0,\infty )^3$ and $(\pi _A,\pi _T,\pi _C,\pi _G)\in [0,\infty )^4$ with $\pi _A +\pi _T + \pi _C + \pi _G = 1$ be given parameters. The continuous-time Markovian dynamic is described as follows: If the current state is the sequence $\vec {x}$, then the following events occur independently:

• (Substitution) Each nucleotide (but not the immortal link) is substituted independently at rate $\nu >0$. When a substitution occurs, the corresponding nucleotide is replaced by A, T, C and G with probabilities $\pi _A,\pi _T,\pi _C$ and $\pi _G$, respectively.

• (Deletion) Each nucleotide (but not the immortal link) is removed independently at rate $\mu >0$.

• (Insertion) Each site gives birth to a new nucleotide independently at rate $\lambda >0$. When a birth occurs, a nucleotide is added immediately to the right of its parent site. The newborn site has nucleotides A, T, C and G with probabilities $\pi _A,\pi _T,\pi _C$ and $\pi _G$, respectively.

The length of a sequence $\vec {x}=(\bullet ,x_1,x_2,\ldots ,x_M)$ is defined as the number of nucleotides in $\vec {x}$ and is denoted by $|\vec {x}|=M$ (with the immortal link alone corresponding to $M=0$). When $M\ge 1$, we omit the immortal link for simplicity and write $\vec {x}=(x_1,x_2,\ldots ,x_M)$.

The TKF91 edge process is reversible (Thorne et al. 1991). Suppose furthermore that

$$\begin{aligned} 0< \lambda < \mu , \end{aligned}$$

an assumption we make throughout. Then, it has an stationary distribution$\Pi$, given by

$$\begin{aligned} \Pi (\vec {x})= \left( 1-\frac{\lambda }{\mu }\right) \left( \frac{\lambda }{\mu }\right) ^M\prod _{i=1}^M\pi _{x_i} \end{aligned}$$

for each $\vec {x}=(x_1,x_2,\ldots ,x_M)\in \{A,T,C,G\}^M$ where $M\ge 1$, and $\Pi (``\bullet \text {''}) = \big (1-\frac{\lambda }{\mu }\big )$. In words, under $\Pi$, the sequence length is geometrically distributed and, conditioned on the sequence length, all sites are independent with distribution $(\pi _{\sigma })_{\sigma \in \{A,T,C,G\}}$.

The TKF91 edge process is a building block in the definition of the sequence evolution model on a tree. Let $T= (V,E,\rho ,\ell )$ be a phylogeny (or, simply, tree), that is, a finite, edge-weighted, rooted tree, where V is the set of vertices, E is the set of edges oriented away from the root $\rho$, and $\ell :E \rightarrow (0,+\,\infty )$ is a positive edge-weighting function. We denote by $\partial T$ the leaf set of T. No assumption is made on the degree of the vertices. We think of T as a continuous object, where each edge e is a line segment of length $\ell _{e}$ and whose elements $\gamma \in e$ we refer to as points. We let $\Gamma _T$ be the set of points of T. We consider the following stochastic process indexed by the points of T.

Definition 2

(TKF91 sequence evolution model on a tree) The root is assigned a state $\vec {X}_{\rho }\in {\mathcal {S}}$, which is drawn from the stationary distribution $\Pi$ of the TKF91 edge process. The state is then evolved down the tree according to the following recursive process. Moving away from the root, along each edge $e = (u,v) \in E$, conditionally on the state $\vec {X}_u$, we run an independent TKF91 edge process as described in Definition 1 started at $\vec {X}_u$ for an amount of time $\ell _{(u,v)}$. We denote by $\vec {X}_\gamma$ the resulting state at $\gamma \in e$. We call the process $(\vec {X}_\gamma )_{\gamma \in \Gamma _T}$ a TKF91 process on tree T .

Our main interest is in the following statistical problem.

2.2 Root reconstruction and the big bang condition

In the root reconstruction problem, we seek to estimate the root state $\vec {X}_\rho$ based on the leaf states $\vec {X}_{\partial T}=\{\vec {X}_{v}:\,v\in \partial T\}$ of a TKF91 process on a known tree T. More formally, we look here for a consistent estimator, as defined next. Fix mutation parameters $(\nu ,\,\lambda ,\,\mu )\in (0,\infty )^3$ with $\lambda < \mu$ and $(\pi _A,\,\pi _T,\,\pi _C,\,\pi _G)\in [0,\infty )^4$ and let $\{T^k = (V^k, E^k, \rho ^k, \ell ^k)\}_{k \ge 1}$ be a sequence of trees with $|\partial T^k| \rightarrow +\,\infty$. Let ${\mathcal {X}}^k = (\vec {X}^k_\gamma )_{\gamma \in \Gamma _{T^k}}$ be a TKF91 process on $T^k$ defined on a probability space with probability measure ${{\mathbb {P}}}$.

Definition 3

(Consistent root estimator) A sequence of root estimators

$$\begin{aligned} F_k:{\mathcal {S}}^{\partial T^k} \rightarrow {\mathcal {S}}, \end{aligned}$$

is said to be consistent for the TKF91 process on $\{T^k\}_k$ if

$$\begin{aligned} \liminf _{k \rightarrow +\,\infty } {{\mathbb {P}}}\left[ F_k\left( \vec {X}^k_{\partial T^k}\right) = \vec {X}^k_{\rho ^k} \right] = 1. \end{aligned}$$

The mutation parameters and the sequence of trees are assumed to be known; that is, the estimators $F_k$ may depend on them. On the other hand, the leaf sequences $\vec {X}^k_{\partial T^k}$ are the only components of the process ${\mathcal {X}}^k$ that are actually observed.

As shown in Fan and Roch (2018), in general a sequence of consistent estimators may fail to exist. Building on the work of Gascuel and Steel (2010), necessary and sufficient conditions for consistent root reconstruction are derived in Fan and Roch (2018, Theorem 1) in the context of bounded-height nested tree sequences with a growing number of leaves, which we refer to as the taxon-rich setting. These conditions have a combinatorial component (the big bang condition) and a stochastic component (initial-state identifiability, to which we come back in Sect. 3). To state the combinatorial condition formally, we need a few more definitions:

• (Restriction) Let $T = (V,E,\rho ,\ell )$ be a tree. For a subset of leaves $L \subset \partial T$, the restriction of T to L is the tree obtained from T by keeping only those points on a path between the root $\rho$ and a leaf $u \in L$.

• (Nested trees) We say that $\{T^k\}_{k}$ is a nested sequence if for all $k > 1$, $T^{k-1}$ is a restriction of $T^{k}$. Without loss of generality, we assume that $|\partial T^k| = k$, so that $T^k$ is obtained by adding a leaf edge to $T^{k-1}$. (More general sequences can be obtained as subsequences.) In a slight abuse of notation, we denote by $\ell$ the edge-weight function for all k. For $\gamma \in \Gamma _T$, we denote by $\ell _{\gamma }$ the length of the unique path from the root $\rho$ to $\gamma$. We refer to $\ell _\gamma$ as the distance from $\gamma$ to the root.

• (Bounded height) We further say that $\{T^k\}_{k}$ has uniformly bounded height if

  $$\begin{aligned} h^* := \sup _{k}h^{k} < +\,\infty , \end{aligned}$$

  (2)

  where $h^{k}:=\max \{\ell _x:\,x\in \partial T^k\}$ is the height of $T^k$.

• (Big bang) For a tree $T = (V,E,\rho ,\ell )$, let

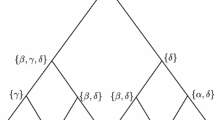
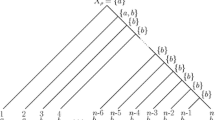
  $$\begin{aligned} T(s)=\{\gamma \in \Gamma _T:\ell _\gamma \le s\} \end{aligned}$$

  denote the tree obtained by truncating T at distance s from the root. We refer to T(s) as a truncation of T. (See the left side of Fig. 1 for an illustration.) We say that a sequence of trees $\{T^k\}_k$ satisfies the big bang condition if, for all $s\in (0,+\,\infty )$, we have $|\partial T^k(s)|\rightarrow +\,\infty$ as $k\rightarrow +\,\infty$. (See Fig. 2 for an illustration.) In words, the big bang condition ensures the existence of a large number of leaves that are “almost conditionally independent” given the root state, which is shown in Fan and Roch (2018) to be necessary for consistency.

Fig. 1

On the left side, $T^k(s)$ is shown for the tree $T^k$ on the right, where the subtree ${\tilde{T}}^{k,s}$ is highlighted

Fig. 2

A sequence of trees $\{T^k\}_k$ (from left to right) satisfying the big bang condition. The distance from $v_k$ to the root is $2^{-k}$

Finally, we are ready to state our main combinatorial assumption.

Assumption 1

(Taxon-rich setting: big bang condition) We assume that $\{T^k\}_{k}$

• 1. Is a nested sequence of trees with common root $\rho$;

• 2. Has uniformly bounded height; and

• 3. Satisfies the big bang condition.

We record the following consequence of Fan and Roch (2018, Theorem 1) (see Sect. 3):

Under Assumption 1, there exists a sequence of root estimators that is consistent for the TKF91 process on $\{T^k\}_k$.

However, this result is essentially existential and that sequence of estimators is in general not directly computable [see Section 5.2 in Fan and Roch (2018, Theorem 1) for the details of the estimator]. The main contribution here is the design of a sequence of estimators which are not only consistent but also explicit and computationally tractable. This is a first step toward designing practical estimators with consistency guarantees.

Important simplification Without loss of generality, we can assume that all leaves are at height $h^*$. This can be achieved artificially by simulating the TKF91 process from the original leaf sequences up to time $h^*$ and using the output as the new leaf sequences. We make this assumption throughout the rest of the paper, that is, from now on

$$\begin{aligned} \ell _v = h^*, \quad \forall v\in \partial T^k,\;\; \forall k. \end{aligned}$$

Alternatively, one could make use of the conditional law of the sequences at height $h^*$ given the sequences at the leaves of $T^k$; however, this would unnecessarily complicate the presentation of our estimator.

2.3 Main results

In our main result, we devise and analyze a sequence of explicit, consistent root estimators for the TKF91 model under Assumption 1. We first describe the root reconstruction algorithm.

Root reconstruction algorithm The input data are the mutation parameters $(\nu ,\lambda ,\mu )\in (0,\infty )^3$ and $(\pi _A,\pi _T,\pi _C,\pi _G)\in [0,\infty )^4$ with $\pi _A+\pi _T+\pi _C+\pi _G=1$ and, for $k\ge 1$, the tree $T^k$ together with the leaf states $\{\vec {X}_{v}:v\in \partial T^{k}\}$. Our root reconstruction algorithm has three main steps: To control correlations among leaves, we follow (Fan and Roch 2018) and extract a “well-spread” restriction of $T^k$ (step 1); then, using only the leaf states on this restriction, we estimate the root sequence length (step 2) and finally the root sequence itself (step 3). The intuition behind the construction of the estimator is discussed in Sect. 3.

We fix $t_j=j$ for all j (although we could use any $0 \le t_1< t_2< \cdots < +\,\infty$).¹ The following functions will help simplify some expressions:

$$\begin{aligned} \eta (t)&= \frac{1- \mathrm{e}^{(\lambda -\mu )t}}{1-\gamma \mathrm{e}^{(\lambda -\mu )t}},\\ \phi (t)&=\frac{(1-\gamma \eta (t))\,\big [ \mathrm{e}^{-\mu t} (1-\mathrm{e}^{-\nu t})+ \big (1-\mathrm{e}^{-\mu t} - \eta (t)\big )\big ]}{1-\eta (t)},\\ \psi (t)&= \big (1-\gamma \eta (t)\big )\,\mathrm{e}^{-(\mu +\nu )t}, \end{aligned}$$

where $\gamma =\lambda /\mu$. Note that the function $\eta (t)$ is in fact the probability that a nucleotide dies and has no descendant at time t. (See Thorne et al. 1991.) For simplicity, we write

$$\begin{aligned} \eta _j=\eta (h^*+t_j),\quad \phi _j= \phi (h^*+t_j) \quad \text {and}\quad \psi _j=\psi (h^*+t_j), \end{aligned}$$

(3)

where recall that $h^*$ was defined in (2). We use the notation [[x]] for the unique integer such that $[[x]]-1/2 \le x < [[x]]+1/2$. Finally, we let $T^k_{[z]}$ be the subtree of $T^k$ rooted at z.

Root estimator

Our estimator $F_{k,s}$ will depend on a fixed chosen $s\in (0,h^*)$ and on the index k of the tree.

• Step 1: restriction

  • Fix $s\in (0,h^*)$ and denote $\partial T^k(s) = \{z_1,\ldots ,z_m\}$, where $m=|\partial T^k(s)|$.

  • For each $z_i$, pick an arbitrary leaf $x_i \in \partial T^k_{[z_i]}$.

  • Set ${\tilde{T}}^{k,s}$ to be the restriction of $T^k$ to $\{x_1,\ldots ,x_m\}$. See Fig. 1 where $m=3$.

• Step 2: length estimator

  • Compute the root sequence-length estimator

    $$\begin{aligned} {\widehat{M}}^{\,k} =\Bigg [\Bigg [\,\frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}}\bigg ( |\vec {X}_v|\mathrm{e}^{(\mu -\lambda )h^*}-\frac{\lambda }{\mu -\lambda } (\mathrm{e}^{(\mu -\lambda )h^*}-1) \bigg )\,\Bigg ]\Bigg ]. \end{aligned}$$

    (4)

• Step 3: sequence estimator

  • Compute the conditional frequency estimator

    $$\begin{aligned} f^{k,s}_{\sigma }(t_j)= \frac{1}{m}\,\sum _{v\in \partial {\tilde{T}}^{k,s}} p^{\sigma }_{\vec {X}_{v}}(t_j) \end{aligned}$$

    (5)

    for $1\le j\le {\widehat{M}}^{\,k}$ and $\sigma \in \{A,T,C,G\}$, where

    $$\begin{aligned} p^{\sigma }_{\vec {x}}(t)= \pi _{\sigma }\,\phi (t)\,\big [1-\big (\eta (t)\big )^{|\vec {x}|}\big ]\,+\,\psi (t)\sum _{i=1}^{|\vec {x}|}1_{\{x_i=\sigma \}}\big (\eta (t)\big )^{i-1} \,+\,\pi _{\sigma }\gamma \,\eta (t),\nonumber \\ \end{aligned}$$

    (6)

    when $\vec {x}=(x_i)_{i=1}^{|\vec {x}|}$.

  • Set U to be the ${\widehat{M}}^{\,k}\times 4$ matrix with entries

    $$\begin{aligned} U_{j, \sigma }=f^{k,s}_{\sigma }(t_j)- \pi _{\sigma }\,\phi _j\,\big [1-\eta _j^{{\widehat{M}}^{\,k}}\big ]\,-\,\pi _{\sigma }\,\gamma \,\eta _j; \end{aligned}$$

    (7)

    set $\Psi$ to be the ${\widehat{M}}^{\,k}\times {\widehat{M}}^{\,k}$ diagonal matrix whose diagonal entries are $\{\psi _j\}_{j=1}^{{\widehat{M}}^{\,k}}$; and set $V:=V_{t_1,\ldots ,t_{{\widehat{M}}^{\,k}}}$ to be the ${\widehat{M}}^{\,k}\times {\widehat{M}}^{\,k}$ Vandermonde matrix

    $$\begin{aligned} V_{t_1,\ldots ,t_{{\widehat{M}}^{\,k}}}= \begin{pmatrix} 1&{}\quad \eta _1&{}\quad \eta _1^2&{}\quad \dots &{}\quad \eta _1^{{\widehat{M}}^{\,k}-1}\\ 1&{}\quad \eta _2&{}\quad \eta _2^2&{}\quad \dots &{}\quad \eta _2^{{\widehat{M}}^{\,k}-1}\\ &{}&{}\quad \vdots \\ 1&{}\quad \eta _{{\widehat{M}}^{\,k}}&{}\quad \eta _{{\widehat{M}}^{\,k}}^2&{}\quad \dots &{}\quad \eta _{{\widehat{M}}^{\,k}}^{{\widehat{M}}^{\,k}-1}\\ \end{pmatrix}, \end{aligned}$$

    where recall that $\eta _j$, $\phi _j$ and $\psi _j$ were defined in (3).

  • Define $F_{k,s}(\vec {X}_{\partial T^k})$ to be an element in $\{A,T,C,G\}^{{\widehat{M}}^{\,k}}$ such that the ith site satisfies

    $$\begin{aligned} \left[ F_{k,s}\left( \vec {X}_{\partial T^k}\right) \right] _i \in \arg \max \left\{ (V^{-1}\Psi ^{-1} U)_{i,\sigma } : \sigma \in \{A,T,C,G\}\right\} . \end{aligned}$$

    (8)

    If there is more than one choice, pick one uniformly at random.

Statement of results Finally, our main claim is Theorem 1, which asserts that the root estimator we just described provides a consistent root estimator in the sense of Definition 3. Recall the sequence space ${\mathcal {S}}$ defined in (1).

Theorem 1

Suppose $\{T^k\}_k$ satisfies Assumption 1. Let $(s_k)_k$ be any sequence such that $s_k > 0$ and $s_k \downarrow 0$ as $k \rightarrow +\,\infty$, and let $F_k:=F_{k,s_k}$ be as defined in (8). Then, $\{F_k\}_k$ is a sequence of consistent root estimators for $\{T^k\}_k$.

In the more general context of continuous-time countable-space Markov chains on bounded-height nested trees (Fan and Roch 2018), consistent root estimators were shown to exist under the big bang condition of Assumption 1 when, in addition, the edge process satisfies initial-state identifiability, i.e., the state of the process at time 0 is uniquely determined by the distribution of the state at any time $t > 0$. (In fact, these conditions are essentially necessary; see Fan and Roch 2018 for details.) Moreover, reversibility of the TKF91 process together with an observation of Fan and Roch (2018) implies that the TKF91 process does indeed satisfy initial-state identifiability.

In that sense, Theorem 1 is not new. However, the root estimators implicit in Fan and Roch (2018) have a major drawback from an algorithmic point of view. They rely on the computation of the total variation distance between the leaf distributions conditioned on different root states—and we are not aware of a tractable way to do these computations in the TKF91 model. In our main contribution, we give explicit root estimators that are statistically consistent under Assumption 1. Specifically, our main novel contribution lies in step 3 above, which is based on the derivation of explicit formulas to invert the mapping from the root sequence to the distribution of the leaf sequences. Moreover, our estimator is computationally efficient in that the number of arithmetic operations needed scales like a polynomial of the total input sequence length. See Sect. 3 for an overview.

In a second novel contribution, we also derive a quantitative error bound. Throughout this paper, we let ${{\mathbb {P}}}^{\vec {x}}$ be the probability measure when the root state is $\vec {x}$. If the root state is chosen according to a distribution $\Pi$, then we denote the probability measure by ${{\mathbb {P}}}^{\Pi }$. Finally, we denote by ${{\mathbb {P}}}_M$ the conditional probability measure for the event that the root state has length M.

Theorem 2

(Error bound) Suppose $\{T^k\}_k$ satisfies Assumption 1 and $\{F_{k,s}\}_k$ are the root estimators described in (8).

Then, for any $\epsilon \in (0,\infty )$, there exist positive constants $\{C_i\}_{i=1}^3$ such that

$$\begin{aligned} {{\mathbb {P}}}^{\Pi }\left[ F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {X}^k_{\rho }\right]&\le \epsilon + C_1\,\exp {\left( -C_2\,|\partial T^{k}(s)|\right) }\,+\,C_3\,s \end{aligned}$$

(9)

for all $s\in (0,h^*/2]$ and $k\ge 1$.

More concretely, if we seek an error probability of at most, say, $3\epsilon$ where $\epsilon >0$, then we pick

$$\begin{aligned} s< \min {\left\{ \frac{\epsilon }{C_3},\, \frac{h^*}{2}\right\} } \end{aligned}$$

and construct root estimator $F_{k,s}$ as described in (8). Theorem 2 guarantees that

$$\begin{aligned} {{\mathbb {P}}}^{\Pi }\left[ F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {X}^k_{\rho }\right] \le 3\epsilon \end{aligned}$$

whenever k is large enough such that

$$\begin{aligned} |\partial T^k(s)| \ge \frac{1}{C_2}\ln \left( \frac{C_1}{\epsilon } \right) . \end{aligned}$$

3 Key ideas in the construction of the root estimator

In our main contribution, we give explicit, computationally efficient root estimators that are consistent under Assumption 1. The estimators were defined in Sect. 2.3. In this section, we motivate these estimators by giving an alternative, constructive proof of initial-state identifiability in the TKF91 process. At a high level, Theorems 1 and 2 are then established along the following lines: The big bang condition ensures the existence of a large number of leaves whose states are “almost independent” conditioned on the root state, and concentration arguments imply that the sample version of the inversion formula derived in Lemma 2 is close to the root state. See Sect. 4 for details.

The key ideas are encapsulated in the following lemmas about the edge process—that is, there is no tree yet at this point of the exposition. Let ${\mathbb {E}}_{M}[|{\mathcal {I}}_{t}|]$ be the expected length of a sequence ${\mathcal {I}}$ after running the TKF91 edge process for time t, starting from a sequence of length M. Recall the definition of $p^{\sigma }_{\vec {x}}(t)$ in (6). We will show in Lemma 1 that $p^{\sigma }_{\vec {x}}(t)$ is equal to the probability of observing the nucleotide $\sigma \in \{A,T,C,G\}$ as the first nucleotide of a sequence at time t, under the TKF91 edge process with initial state $\vec {x}$. Formally, let ${\mathcal {I}}_t(1)$ denote the first nucleotide of the sequence ${\mathcal {I}}$ at time t and let $\{{\mathcal {I}}_t(1) = \sigma \}$ be the event that this first nucleotide is $\sigma$.

Lemma 1

(Distribution of the first nucleotide) The probability that $\sigma$ is the first nucleotide at time t is

$$\begin{aligned} {{\mathbb {P}}}^{\vec {x}}(\mathbf{{\mathcal {I}}_t(1)} = \sigma ) = p^{\sigma }_{\vec {x}}(t), \end{aligned}$$

(10)

for all $\sigma \in \{A,T,C,G\}$, sequence $\vec {x}\in {\mathcal {S}}$ and time $t\in (0,\infty )$, where $p^{\sigma }_{\vec {x}}(t)$ is defined in (6).

Proof

We use some notation of Thorne et al. (1991), where a nucleotide is also referred to as a “normal link” and a generic such nucleotide is denoted $``\star \text {''}$. We define

$$\begin{aligned} p_k:=p_k(t)&:={{\mathbb {P}}}_{\star }\,(\text {normal link }``\star \text {''} \text { survives and has }k\,\text { descendants including itself}),\\ p^{(1)}_k :=p^{(1)}_k(t)&:={{\mathbb {P}}}_{\star }\,(\text {normal link }``\star \text {''} \text { dies and has }k\text { descendants}),\\ p^{(2)}_k :=p^{(2)}_k(t)&:={{\mathbb {P}}}_{\bullet }\,(\text {immortal link }``\bullet \text {''} \,\text {has }k\text { descendants including itself}). \end{aligned}$$

These probabilities are explicitly found in Thorne et al. (1991, Eqs. (8)–(10)) by solving the differential equations governing the underlying birth and death processes:

$$\begin{aligned}&\left\{ \begin{array}{ll} p_n(t) &{}= \mathrm{e}^{-\mu t}(1-\gamma \eta (t))[\gamma \eta (t)]^{n-1}\\ p^{(1)}_n(t) &{}= (1-\mathrm{e}^{-\mu t}-\eta (t))(1-\gamma \eta (t))[\gamma \eta (t)]^{n-1}\\ p_n^{(2)}(t) &{}= (1-\gamma \eta (t))[\gamma \eta (t)]^{n-1} \end{array}\quad \text {for }n\ge 1,\right. \\&\left\{ \begin{array}{ll} p_0(t) &{}=0\\ p^{(1)}_0(t) &{}= \eta (t)\\ p_0^{(2)}(t) &{}= 0. \end{array}\right. \end{aligned}$$

Let ${\mathcal {K}}_{\bullet }$ be the event that the first nucleotide ${\mathcal {I}}_t(1)$ is the descendant of the immortal link $``\bullet \text {''}$, and let ${\mathcal {K}}_i$ be the event that the first nucleotide is the descendant of $v_i$ for $1\le i\le |\vec {v}|$. By the law of total probability,

$$\begin{aligned}&{{\mathbb {P}}}^{\vec {v}}\left( {\mathcal {I}}_t(1) = \sigma \right) = {{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma ,\,{\mathcal {K}}_{\bullet }) + \sum _{i=1}^{|\vec {v}|} {{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma ,\,{\mathcal {K}}_i). \end{aligned}$$

(11)

We now compute each term on the RHS. In the rest of the proof of Lemma 1, to simplify the notation we set $\eta :=\eta (t)$.

We have that ${{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,|\,{\mathcal {K}}_{\bullet })= \pi _{\sigma }$, because any descendant of the immortal link corresponds to an insertion and any inserted nucleotide is independent of the other variables with distribution $(\pi _A,\pi _T,\pi _C,\pi _G)$. We note that ${{\mathbb {P}}}^{\vec {v}}({\mathcal {K}}_{\bullet })=1-p^{(2)}_1= \gamma \eta$, because ${\mathcal {K}}_{\bullet }$ occurs if and only if $``\bullet \text {''}$ has at least two descendants including itself. Hence,

$$\begin{aligned} {{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma ,\,{\mathcal {K}}_{\bullet })=\pi _{\sigma }\,\gamma \eta , \end{aligned}$$

(12)

For $1\le i\le |\vec {v}|$, ${\mathcal {K}}_i$ is the event that the normal link $v_i$ either survives or dies but has at least 1 descendant, while the offspring of all previous links die. Further, let $S_i$ be the event that $v_i$ survives, which has probability $\mathrm{e}^{-\mu t}$. Then,

$$\begin{aligned} {{\mathbb {P}}}^{\vec {v}}({\mathcal {K}}_i \cap S_i)=p^{(2)}_1(p^{(1)}_0)^{i-1}\mathrm{e}^{-\mu t}=(1-\gamma \eta )\eta ^{i-1}\mathrm{e}^{-\mu t}, \end{aligned}$$

since $p^{(2)}_1$ is the probability that the immortal link has exactly 1 offspring which is itself, $(p^{(1)}_0)^{i-1}$ is the probability that all $\{v_j\}_{j=1}^{i-1}$ were deleted and left no descendant and $S_i$ is independent of the previous events. Moreover, we have ${{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,|\,{\mathcal {K}}_i \cap S_i)= f_{v_i \sigma }$, where

$$\begin{aligned} f_{ij}:=f_{ij}(t) =\pi _{j}(1-\mathrm{e}^{-\nu t})+\mathrm{e}^{-\nu t}1_{\{i=j\}} \end{aligned}$$

is the transition probability that a nucleotide is of type j after time t, given that it is of type i initially. (Recall from Definition 1 that $\nu >0$ is the substitution rate.) Letting $S_i^c$ be the complement of $S_i$, then

$$\begin{aligned} {{\mathbb {P}}}^{\vec {v}}({\mathcal {K}}_i \cap S_i^c)=(1-\gamma \eta )\eta ^{i-1}\, \left( \sum _{k\ge 1}p^{(1)}_k \right) =(1-\gamma \eta )\eta ^{i-1}\, (1-\mathrm{e}^{-\mu t}-\eta ), \end{aligned}$$

and ${{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,|\,{\mathcal {K}}_i \cap S^c_i)=\pi _{\sigma }$. Therefore,

$$\begin{aligned}&{{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,,\,{\mathcal {K}}_i) \nonumber \\&\quad ={{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,|\,{\mathcal {K}}_i \cap S_i)\,{{\mathbb {P}}}^{\vec {v}}({\mathcal {K}}_i \cap S_i)+{{\mathbb {P}}}^{\vec {v}}({\mathcal {I}}_t(1) = \sigma \,|\,{\mathcal {K}}_i \cap S^c_i)\,{{\mathbb {P}}}^{\vec {v}}({\mathcal {K}}_i \cap S_i^c) \nonumber \\&\quad = (1-\gamma \eta )\eta ^{i-1}\,\left( f_{v_i \sigma }\mathrm{e}^{-\mu t} + \pi _{\sigma } (1-\mathrm{e}^{-\mu t}-\eta ) \right) . \end{aligned}$$

(13)

Putting (12) and (13) into (11),

$$\begin{aligned} {{\mathbb {P}}}^{\vec {v}}\left( {\mathcal {I}}_t(1) = \sigma \right)&= \pi _{\sigma }\gamma \eta + \sum _{i=1}^{|\vec {v}|} \left[ (1-\gamma \eta )\eta ^{i-1}\,\left( f_{v_i \sigma }\mathrm{e}^{-\mu t} + \pi _{\sigma } (1-\mathrm{e}^{-\mu t}-\eta ) \right) \right] \\&= (1-\gamma \eta ) \mathrm{e}^{-\mu t} \left[ \sum _{i=1}^{|\vec {v}|} \eta ^{i-1}f_{v_i \sigma }\right] \\&\quad + (1-\gamma \eta )(1-\mathrm{e}^{-\mu t} -\eta )\pi _{\sigma } \frac{1-\eta ^{|\vec {v}|}}{1-\eta } + \pi _{\sigma } \gamma \eta , \end{aligned}$$

which is exactly (10) upon further rewriting

$$\begin{aligned} \sum _{i=1}^{|\vec {v}|}\eta ^{i-1}f_{v_i \sigma } =\pi _{\sigma }(1-\mathrm{e}^{-\nu t})\frac{1-\eta ^{|\vec {v}|}}{1-\eta }+\mathrm{e}^{-\nu t}\sum _{i=1}^{|\vec {v}|}1_{\{v_i=\sigma \}}\eta ^{i-1}. \end{aligned}$$

The proof of Lemma 1 is complete.$\square$

Building on Lemma 1, our second lemma regarding the edge process gives a constructive proof of initial-state identifiability. Recall that we set $t_j = j$.

Lemma 2

(Constructive proof of initial-state identifiability) For any $h^* \ge 0$, the following mappings are one-to-one and have explicit expressions for their inverses:

• (i) The mapping $\Phi _{h^*}^{(1)}:\,{\mathbb {Z}}_+\rightarrow {\mathbb {R}}_+$ defined by

  $$\begin{aligned} \Phi _{h^*}^{(1)}(M)={\mathbb {E}}_{M}[|{\mathcal {I}}_{h^*}|]. \end{aligned}$$

• (ii) The mappings $\Phi ^{(2)}_{h^*+t_1,\ldots ,h^*+t_{M}}:\{A,T,C,G\}^M\rightarrow [0,1]^{4M}$ defined by

  $$\begin{aligned} \Phi ^{(2)}_{h^*+t_1,\ldots ,h^*+t_{M}}(\vec {x})= \left( p^{\sigma }_{\vec {x}}(h^*+t_j)\right) _{\sigma \in \{A,T,C,G\},\,1\le j\le M}, \end{aligned}$$

  (14)

  for any $\vec {x}$ with $|\vec {x}| = M \ge 1$.

Proof

(i) The sequence length of the TKF91 edge process is a well-studied stochastic process known as a continuous-time linear birth–death–immigration process $(|{\mathcal {I}}_{t}|)_{t\ge 0}$. (We give more details on this process in Sect. A.) The expected sequence length, in particular, is known to satisfy the following differential equation:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} {\mathbb {E}}_{M}[|{\mathcal {I}}_t|] = -(\mu -\lambda ) {\mathbb {E}}_{M}[|{\mathcal {I}}_t|] + \lambda , \end{aligned}$$

with initial condition ${\mathbb {E}}_{M}[|{\mathcal {I}}_0|] = M$, whose solution is given by

$$\begin{aligned} {\mathbb {E}}_{M}[|{\mathcal {I}}_t|] = \Phi _t^{(1)}(M) := M\beta _t+\frac{\gamma (1-\beta _t)}{1 -\gamma }, \end{aligned}$$

(15)

where $\beta _t = \mathrm{e}^{-(\mu -\lambda )t}$ and $\gamma =\frac{\lambda }{\mu }$. Solving (15) for M, we see that $\Phi _t^{(1)}$ is injective with inverse

$$\begin{aligned} (\Phi _t^{(1)})^{-1}(z)=\frac{1}{\beta _{t}}\left( z-\frac{\gamma (1-\beta _{t})}{1 -\gamma }\right) . \end{aligned}$$

(16)

(ii) For $\Phi ^{(2)}$, we make the following claim regarding the probability of observing $\sigma$ as the first nucleotide of a sequence at time t under the TKF91 edge process starting at $\vec {x}$ with $|\vec {x}|\ge 1$.

Recalling the functions $\phi _j$ and $\psi _j$ defined in (3), we have, by Lemma 1,

$$\begin{aligned} p^{\sigma }_{\vec {x}}(h^*+t_j)= \pi _{\sigma }\,\phi _j\,\big [1-\eta _j^{M}\big ]\,+\,\psi _j\sum _{i=1}^{M}1_{\{x_i=\sigma \}}\,\eta _j^{i-1} \,+\,\pi _{\sigma }\gamma \,\eta _j, \end{aligned}$$

(17)

for all $\sigma \in \{A,T,C,G\}$ and $1\le j\le M$, where $M = |\vec {x}|$. We then solve (17) for $\vec {x}=(x_i)\in \{A,T,C,G\}^M$. System (17) is equivalent to the matrix equation

$$\begin{aligned} H = \Psi \,V\,Y^{\vec {x}}, \end{aligned}$$

(18)

where $\Psi$ and V are the $M\times M$ matrices defined in Sect. 2.3, and

• 1. $Y^{\vec {x}}$ is the $M\times 4$ matrix whose entries are $1_{\{x_j=\sigma \}}$, and

• 2. H is the $M\times 4$ matrix with entries

  $$\begin{aligned} H_{j, \sigma }=p^{\sigma }_{\vec {x}}(h^*+t_j)- \pi _{\sigma }\,\phi _j\,\big [1-\eta _j^{M}\big ]\,-\,\pi _{\sigma }\gamma \,\eta _j. \end{aligned}$$

It is well known that the Vandermonde matrix V is invertible [see, e.g., Gautschi (1962, Theorem 1)], so we can solve the system (18) to obtain

$$\begin{aligned} Y^{\vec {x}}= V^{-1}\,\Psi ^{-1}\,H. \end{aligned}$$

(19)

Sequence $\vec {x}\in \{A,T,C,G\}^{M}$ is uniquely determined by $Y^{\vec {x}}$. Hence, from (19), we get an explicit inverse for the mappings $\Phi ^{(2)}_{h^*+t_1,\ldots ,h^*+t_{M}}$ defined in (14).

The proof of Lemma 2 is complete. $\square$

Heuristically, steps 2 and 3 in the root estimator defined in Sect. 2.3 are the sample versions of the inverses of $\Phi _{h^*}^{(1)}$ and $\Phi ^{(2)}_{h^*+t_1,\ldots ,h^*+t_{M}}$. That is, we replace the expectation ${\mathbb {E}}_{|\vec {x}|}[|{\mathcal {I}}_{h^*}|]$ and probabilities $\left( p^{\sigma }_{\vec {x}}(h^*+t_j)\right) _{\sigma \in \{A,T,C,G\},\,1\le j\le M}$ with their corresponding empirical averages—conditioned on the observations at the leaves. The reason we consider several “future times” $h^*+t_1,\ldots ,h^*+t_{M}$ is to ensure that we have sufficiently many equations to “invert the system” and obtain the full root sequence, as described in Lemma 2 (ii) and step 3 of the root estimator.

4 Proofs

To prove Theorem 2 (and Theorem 1 from which it follows), that is, to obtain the desired upper bound (9), on

$$\begin{aligned} {{\mathbb {P}}}^{\Pi }\left[ F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {X}^k_{\rho }\right] =\sum _{\vec {x}\in {\mathcal {S}}}{{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {x}\right] \,\Pi (\vec {x}), \end{aligned}$$

(20)

we first observe that from the construction of $F_{k,s}$ in Sect. 2.3, if the estimator is wrong, then either the estimated length is wrong or the length is correct but the sequence is wrong. Let $F^{(M)}_{k,s}$ denote the estimator in (8) when ${\widehat{M}}^{\,k} = M$. We have

$$\begin{aligned} {{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {x}\right]&= {{\mathbb {P}}}^{\vec {x}}\left[ \{F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {x}\}\cap \{{\widehat{M}}^{\,k}\ne |\vec {x}|\}\right] \nonumber \\&\quad +{{\mathbb {P}}}^{\vec {x}}\left[ \{F_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {x}\}\cap \{{\widehat{M}}^{\,k}= |\vec {x}|\}\right] \nonumber \\&\le {{\mathbb {P}}}_{|\vec {x}|}\left[ {\widehat{M}}^{\,k}\ne |\vec {x}|\right] +{{\mathbb {P}}}^{\vec {x}}\left[ F^{(|\vec {x}|)}_{k,s}(\vec {X}^k_{\partial T^{k}})\ne \vec {x}\right] , \end{aligned}$$

(21)

for all $\vec {x}\in {\mathcal {S}}\setminus \{``\bullet \text {''}\}$, where recall that ${{\mathbb {P}}}^{\vec {x}}$ denotes the probability law when the root state is $\vec {x}$ and ${{\mathbb {P}}}_M$ denotes the probability law when the root state has length M. The proof is therefore reduced to bounding the first and second terms on the RHS of (21), which are formulated as Propositions 1 and 2, respectively, in the next two subsections. To simplify the notation, throughout this section we let $\vec {X} := \vec {X}^k$.

4.1 Reconstructing the sequence length

In this subsection, we bound the first term on the RHS of (21), which is the probability of incorrect estimation of the root sequence length. Proposition 1 is a quantitative statement about how this error tends to zero exponentially fast in $m:=|\partial T^{k}(s)|$, as $k\rightarrow \infty$ and $s\rightarrow 0$.

Proposition 1

(Sequence length estimation error) There exist constants $C_1,\,C_2\in (0,\infty )$ which depend only on $h^*$, $\mu$ and $\lambda$ such that

$$\begin{aligned} {{\mathbb {P}}}_M({\widehat{M}}^{\,k}\ne M)&\le 2\exp {\left( -\,C_1\,|\partial T^{k}(s)|\right) }\,+\,C_2\,(M+1)\,s \end{aligned}$$

for all $s\in (0,h^*/2]$, $k\in {\mathbb {N}}$ and $M\in {\mathbb {N}}$.

Outline of proof Fix $k\ge 1$, $s>0$, and $m:=|\partial T^{k}(s)|$. Recall that

$$\begin{aligned} \beta _t = \mathrm{e}^{-(\mu -\lambda )t} \quad \text {and} \quad \gamma =\frac{\lambda }{\mu }, \end{aligned}$$

and that the definition of the length estimator is

$$\begin{aligned} {\widehat{M}}^{\,k} =\Bigg [\Bigg [\,\frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}}\bigg ( |\vec {X}_v|\mathrm{e}^{(\mu -\lambda )s}+\frac{\lambda }{\mu -\lambda } (1-\mathrm{e}^{(\mu -\lambda )s}) \bigg )\,\Bigg ]\Bigg ], \end{aligned}$$

which (up to rounding) is a linear combination of the sequence lengths at the leaves of the restriction ${\tilde{T}}^{k,s}$. To explain this expression, we note first that the expected sequence length after running the edge process for time $h^*$ is a function of the sequence length M at the root, specifically $\Phi _{h^*}^{(1)}(M)$, where we used the notation defined in Lemma 2. We can estimate the latter from the sequence lengths at the leaves of the restriction using the empirical average

$$\begin{aligned} A^{k,s}=\frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}} |\vec {X}_v| \end{aligned}$$

whose expectation is $\Phi _{h^*}^{(1)}(M)$. Lemma 2 then allows us to recover M approximately by inversion and rounding. Specifically, by linearity of $\Phi ^{(1)}$ and Eqs. (15) and (16),

$$\begin{aligned} (\Phi _{h^*}^{(1)})^{-1}(A^{k,s})&= (\Phi _{h^*}^{(1)})^{-1} \left( \frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}} |\vec {X}_v| \right) \\&= \frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}} (\Phi _{h^*}^{(1)})^{-1} \left( |\vec {X}_v| \right) \\&= \frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}} \frac{1}{\beta _{h^*}}\left( |\vec {X}_v| - \frac{\gamma (1 - \beta _{h^*})}{1-\gamma } \right) \\&= \frac{1}{m} \sum _{v\in \partial {\tilde{T}}^{k,s}} \left( |\vec {X}_v|\mathrm{e}^{(\mu -\lambda )h^*}-\frac{\lambda }{\mu -\lambda } \left( \mathrm{e}^{(\mu -\lambda )h^*} - 1\right) \right) , \end{aligned}$$

Finally, we see that ${\widehat{M}}^{\,k} = [[(\Phi _{h^*}^{(1)})^{-1}(A^{k,s})]]$. We show below that $A^{k,s}$ is concentrated around its mean $\Phi _{h^*}^{(1)}(M)$, from which we deduce that ${\widehat{M}}^{\,k}$ is concentrated around M. One technical issue is to control the correlation between the sequence lengths at the leaves of the restriction. See below for the details.

We first state as a lemma the above observations. Throughout this section, we use a generic sequence-length process $(|{\mathcal {I}}_{t}|)_{t\ge 0}$ defined on a separate probability space from $\vec {X}^k$. Its purpose is to simplify various expressions involving the law of sequence lengths.

Lemma 3

(Concentration of $A^{k,s}$ suffices)

$$\begin{aligned} {{\mathbb {P}}}_M({\widehat{M}}^{\,k}\ne M)\le {{\mathbb {P}}}_M\Big (\big |A^{k,s}-\nu _M\big | \ge \frac{\beta _{h^*}}{2}\Big ), \end{aligned}$$

(22)

for all $M\ge 0$, where

$$\begin{aligned} \nu _M:={\mathbb {E}}_M[|{\mathcal {I}}_{h^*}|]=M\beta _{h^*}+\frac{\gamma (1-\beta _{h^*})}{1 -\gamma }. \end{aligned}$$

(23)

Proof

All variables $|\vec {X}_v|$ for $v\in \partial {\tilde{T}}^{k,s}$ have the same mean $\nu _M$, where formula (23) follows from (15). Formula (15) also tells us that the function $M\mapsto \Phi _{h^*}^{(1)}(M)$ is linear with slope $\beta _{h^*}$. So if $|A^{k,s}-\nu _M| < \beta _{h^*}/2$ then the effect of the rounding is such that

$$\begin{aligned}{}[[\, (\Phi _{h^*}^{(1)})^{-1}(A^{k,s})\,]]=[[\, (\Phi _{h^*}^{(1)})^{-1}(\nu _M)\,]]=M. \end{aligned}$$

Hence, the error probability satisfies (22). $\square$

We move on to the formal proof, which follows from a series of steps. To bound the RHS of (22), note that even though the variables $|\vec {X}_v|$, for $v\in \partial {\tilde{T}}^{k,s}$, are correlated, the construction of ${\tilde{T}}^{k,s}$ guarantees that this correlation is “small” as the paths to the root from any two leaves of the restriction overlap only “above level s.” To control the correlation, we condition on the leaf states of the truncation $\vec {X}_{\partial T(s)}=\{\vec {X}_{v}:\,v\in \partial T(s)\}$. By the Markov property,

$$\begin{aligned} {\mathbb {E}}_{M}\left[ A^{k,s}\Big |\vec {X}_{\partial T^k(s)}\,\right] = \frac{1}{m}\sum _{u\in \partial T^k(s)}{\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-\,s}|], \end{aligned}$$

(24)

with $a \wedge b=\min \{a,b\}$, where note that the sum here (unlike $A^{k,s}$ itself) is over the leaves of the truncation at s. We first bound the probability that the conditional expectation (24) is close to its expectation $\nu _M$. Then, conditioned on this event, we establish concentration of $A^{k,s}$ used on conditional independence. We detail the above argument in steps A–C as follows. Properties of the length process derived in Sect. A will be employed.

(A) Decomposition from conditioning on level s We first decompose the RHS of (22) according to whether the sequence lengths at level s are sufficiently concentrated. For $\epsilon >0$, $\delta \in (0,\infty )$ and $s\in (0,\,h^*)$, we have

$$\begin{aligned} {{\mathbb {P}}}_M\left( \big |A^{k,s}-\nu _M\big | \ge \epsilon \right) \le \,{{\mathbb {P}}}_M\left( \{\big |A^{k,s}-\nu _M\big | \ge \epsilon \}\;\cap \; {\mathcal {E}}^c_{\delta ,s}\right) + {{\mathbb {P}}}_{M}( {\mathcal {E}}_{\delta ,s}), \end{aligned}$$

(25)

where

$$\begin{aligned} {\mathcal {E}}_{\delta ,s}:= \Big \{\Big |{\mathbb {E}}_{M}\big [A^{k,s}\big |\vec {X}_{\partial T^k(s)}\,\big ] - \,\nu _M\Big |> \delta \Big \} \end{aligned}$$

(26)

is the event that the conditional expectation (24) away from its expectation $\nu _M$ by $\delta$. As we shall see, Proposition 1 will be obtained by taking $\delta =\epsilon /2=\beta _{h^*}/4$.

(B) Bounding ${{\mathbb {P}}}_{M}( {\mathcal {E}}_{\delta ,s})$ The second term on the RHS of (25) is treated in Lemma 4. Because of the correlation above level s, we use Chebyshev’s inequality to control the deviation of the conditional expectation.

Lemma 4

(Conditional expectation given level s) For all $M\in {\mathbb {Z}}_+$, $\delta \in (0,\infty )$ and $s\in (0,\,h^*)$, we have

$$\begin{aligned} {{\mathbb {P}}}_{M}( {\mathcal {E}}_{\delta ,s}) \le \delta ^{-2}\,C\,(M+1)\,s, \end{aligned}$$

where $C\in (0,\infty )$ is a constant which depends only on $h^*$, $\mu$ and $\lambda$.

Proof

By (24) and Chebyshev’s inequality,

$$\begin{aligned} {{\mathbb {P}}}_{M}({\mathcal {E}}_{\delta ,s})&= {{\mathbb {P}}}_M\left[ \left| \sum _{u\in \partial T^k(s)}{\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|] - m \nu _M\right| > m\delta \right] \nonumber \\&\le \frac{1}{m^2\,\delta ^2}\,\mathrm {Var}_M\left[ \sum _{u\in \partial T^k(s)}{\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|]\right] , \end{aligned}$$

(27)

where $\mathrm {Var}_M$ is the variance conditioned on the initial sequence having length M. We will use the following simple identity for square-integrable variables

$$\begin{aligned} \mathrm {Var}\left( \sum _{b=1}^B W_b \right) \le B \sum _{b=1}^B \mathrm {Var}(W_b) \end{aligned}$$

(28)

which follows from applying Cauchy–Schwarz to the covariance terms and then the AM–GM inequality. Then, the variance above is bounded by

$$\begin{aligned} \mathrm {Var}_M\left[ \sum _{u\in \partial T^k(s)}{\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|]\right]&\le m^2 \,\mathrm {Var}_M \left[ {\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|]\right] , \end{aligned}$$

(29)

for any $u \in \partial T^k(s)$, where we used the fact that the $|\vec {X}_u|$’s for all such u’s are identically distributed.

By (15),

$$\begin{aligned} {\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|]=|\vec {X}_u|\,\beta _{h^*-s}+\frac{\gamma (1-\beta _{h^*-s})}{1 -\gamma }. \end{aligned}$$

So, plugging this last expression into the variance formula (53), we obtain

$$\begin{aligned}&\mathrm {Var}_M \left( {\mathbb {E}}_{|\vec {X}_u|}[|{\mathcal {I}}_{h^*-s}|]\right) \nonumber \\&\quad =\mathrm {Var}_M \left( |\vec {X}_u|\,\beta _{h^*-s}+\frac{\gamma (1-\beta _{h^*-s})}{1 -\gamma }\right) \nonumber \\&\quad =\beta _{h^*-s}^2\,\mathrm {Var}_M(|\vec {X}_u|) \nonumber \\&\quad =\beta _{h^*-s}^2\,\left( M\,\frac{\beta _{s}(1-\beta _{s}) (1+3\gamma -2\beta _{s})}{1-\gamma }\,+\,\frac{\gamma (1-\beta _{s}) (1-\beta _{s}\gamma )}{(1-\gamma )^2}\right) \nonumber \\&\quad \le \beta _{h^*-s}^2\,(1-\beta _{s})\,C\,(M+1)\nonumber \\&\quad \le s\,C\,(M+1), \end{aligned}$$

(30)

where $C\in (0,\infty )$ is a constant which depends only on $h^*$, $\mu$ and $\lambda$, where we used that $\gamma < 1$ and $\beta _t$ is decreasing in t.

Putting (30) into (29), the desired inequality follows from (27).$\square$

(C) Deviation of $A^{k,s}$ conditioned on ${\mathcal {E}}_{\delta ,s}^c$ The remaining step of the analysis is to control the first term on the RHS of (25) by taking advantage of the conditional independence of the leaves of the restriction given $\vec {X}_{\partial T^k(s)}$. By the definition of $A^{k,s}$, the Markov property and conditional independence, that term is equal to

$$\begin{aligned} \sum _{\vec {u} \in {\mathcal {G}}_{\delta ,s}^c} \, {{\mathbb {P}}}\left( \left| \sum _{i=1}^m L^{(u_i)}\;-\;m\nu _M\right| \ge m\epsilon \right) \,{{\mathbb {P}}}_M\left( \left| \vec {X}_{\partial T^k(s)}\right| =\vec {u}\right) , \end{aligned}$$

(31)

where the set ${\mathcal {G}}_{\delta ,s}$ (closely related to ${\mathcal {E}}_{\delta ,s}$) is defined as

$$\begin{aligned} {\mathcal {G}}_{\delta ,s}:=\Big \{\vec {u}=(u_1,\ldots ,u_m)\in {\mathbb {Z}}_+^m:\;\Big |\sum _{i}{\mathbb {E}}_{u_i}[|{\mathcal {I}}_{h^*-s}|] - m \nu _M\Big | > m\delta \Big \}, \end{aligned}$$

and $\{L^{(u_i)}\}_{i=1}^m$ are, under probability ${{\mathbb {P}}}$, independent copies of the birth–death process $|{\mathcal {I}}_{t}|$ run for time $h^*-s$ starting from $\{u_i\}_{i=1}^m$, respectively. By the triangle inequality, we have for all $s\in (0,h^*)$,

(32)

Write $t=h^*-s$ for convenience.

Each $L^{(u_i)}$ above can in fact be thought of as a sum of independent variables $L'_i + \sum _{j=1}^u L''_{ij}$ where $L'_i$ and $L_{ij}''$ are the sizes of the progenies of the immortal link and of the jth normal link, respectively, in the edge process started with sequence length u and run for time t. The expectations of $L'_i$ and $L''_{ij}$ are $\frac{\gamma (1-\beta _t)}{1 -\gamma }$ and $\beta _t$, respectively [as can be seen from (15)]. Both $L'_i$ and $L''_{ij}$ have finite exponential moments (see Sect. A), and hence, by standard results in large deviations theory (see, e.g., Durrett 1996), we have the bounds

$$\begin{aligned} {{\mathbb {P}}}\left[ \left| \sum _{i=1}^m L'_i - \frac{\gamma (1-\beta _t)}{1 -\gamma } m \right| \ge m(\epsilon -\delta )/2\right] \le \exp \left( -\,C' m \right) , \end{aligned}$$

and

$$\begin{aligned} {{\mathbb {P}}}\left[ \left| \sum _{i=1}^m \sum _{j=1}^{u_i} L''_{ij} - \beta _t \sum _{i=1}^m u_i \right| \ge m(\epsilon -\delta )/2\right] \le \exp \left( -\,C'' \sum _{i=1}^m u_i \right) , \end{aligned}$$

where $C'$ and $C''$ are strictly positive constants depending only on $\mu$, $\lambda$ and $h^*$. Note that the condition $\vec {u} \in {\mathcal {G}}_{\delta ,s}^c$ is equivalent to

$$\begin{aligned} \left| \frac{\beta _t}{m}\sum _{i=1}^m u_i\,+\frac{\gamma (1-\beta _t)}{1 -\gamma } - \nu _M\right| \le \delta , \end{aligned}$$

(33)

where we used (15). So $\sum _{i=1}^m u_i$ is of the order of mM. Let $\delta =\epsilon /2=\beta _{{h^{*}}}/4$. Plugging the two inequalities above back into (32), we see that there is a strictly positive constant $C'''$, again depending only on $\mu$, $\lambda$ and $h^*$, such that

(34)

Proof of Proposition 1

Take $\delta =\epsilon /2=\beta _{{h^{*}}}/4$. Then, apply (34) to the first term on the RHS of (25) and Lemma 4 to the second term on the RHS of (25). The proof of Proposition 1 is complete by collecting inequalities (22) and (25). $\square$

4.2 Reconstructing the root sequence given the sequence length

In this subsection, we bound the second term on the RHS of (21), which is the probability of incorrectly reconstructing the root sequence, given its length. Suppose we know that the ancestral sequence length is $M\ge 1$, that is, the ancestral state is an element of $\{A,T,C,G\}^M$. Let $F^{(M)}_{k,s}$ denote the estimator in (8) when ${\widehat{M}}^{\,k} = M$. Formally, we prove the following.

Proposition 2

(Sequence reconstruction error) For all $M\in {\mathbb {Z}}_+$, $\vec {x}\in \{A,T,C,G\}^M$ with $|\vec {x}| = M$ and $s\in (0,\,h^*)$,

$$\begin{aligned} {{\mathbb {P}}}^{\,\vec {x}}\left[ F^{(M)}_{k,s}\left( \vec {X}_{\partial T^k}\right) \ne \vec {x} \right] \le 8M\exp {\left( \frac{-\, |\partial T^{k}(s)|}{8\,{\hat{C}}}\,\right) } \,+\,C\,M^2\,{\hat{C}}\,\,s \end{aligned}$$

where ${\hat{C}}:=\Vert V^{-1}\Psi ^{-1}\Vert _{\infty \rightarrow \infty }^2\in (0,\infty )$ depends on $\mu$, $\lambda$, $h^*$ and $\{t_j\}_{j=1}^M$, and $C\in (0,\infty )$ is a constant which depends only on $\nu$, $\mu$ and $\lambda$.

Remark 1

Note that ${\hat{C}}$ depends implicitly on M.

Outline of the proof of Proposition 2 Fix $k\ge 1$, $s\in (0,h^*)$, $M\ge 1$ and $\{t_j\}_{j=1}^M$. By the construction of $F^{(M)}_{k,s}$ in (8), our sequence estimator $F^{(M)}_{k,s}\big (\vec {X}_{\partial T^k}\big )\in \{A,T,C,G\}^M$ is correct if it is close to the argmax over the columns of the matrix $V^{-1}\Psi ^{-1} U$. By the definitions of $U,\Psi ,V$, our analysis boils down to bounding the deviations of the empirical frequencies $f^{k,s}_{\sigma }(t_j)$ from their expectations $p^{\sigma }_{\vec {x}}(h^*+t_j)$. This is established using similar arguments to that of Proposition 1. Here is an outline.

(i) From deviations of frequencies to deviations of matrices Recall that $Y^{\vec {x}}$ is the $M\times 4$ matrix whose entries are $1_{\{x_j=\sigma \}}$ and recall from (8) that

$$\begin{aligned} \left[ F_{k,s}\left( \vec {X}_{\partial T^k}\right) \right] _i \in \arg \max \left\{ (V^{-1}\Psi ^{-1} U)_{i,\sigma } : \sigma \in \{A,T,C,G\}\right\} , \end{aligned}$$

a formula which is motivated by the proof of Lemma 2. Hence, $F^{(M)}_{k,s}\big (\vec {X}_{\partial T^k}\big ) = \vec {x}$ is implied by $\Vert V^{-1}\Psi ^{-1} U- Y^{\vec {x}}\Vert _{\max }<1/2$, where $\Vert A\Vert _{\max }:=\max _{i,j}|a_{ij}|$ is the maximum among the absolute values of all entries of A. Because we assume that M is known for the purposes of this analysis, the matrices V and $\Psi$ are known, while U depends on the data (Consult Sect. 2.3 for the full definitions.) To turn the inequality above into a condition on U, we note that

$$\begin{aligned} \Vert V^{-1}\Psi ^{-1} U- Y^{\vec {x}}\Vert _{\max }&=\Vert V^{-1}\Psi ^{-1} (U-\Psi \,V \,Y^{\vec {x}} )\Vert _{\max }\nonumber \\&\le \Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }\,\Vert U-\Psi \,V \, Y^{\vec {x}}\Vert _{\max }, \end{aligned}$$

(35)

where $\Vert A\Vert _{\infty \rightarrow \infty }:=\max _{i}\sum _{j}|a_{ij}|$ is the maximum absolute row sum of a matrix $A=(a_{ij})$. The above two facts give

$$\begin{aligned} {{\mathbb {P}}}^{\,\vec {x}}\left[ F^{(M)}_{k,s}\left( \vec {X}_{\partial T^k}\right) \ne \vec {x} \right]&\le \,{{\mathbb {P}}}^{\,\vec {x}}\left[ \Vert V^{-1}\Psi ^{-1} U- Y^{\vec {x}} \Vert _{\max }\ge 1/2\right] \\&\le \, {{\mathbb {P}}}^{\,\vec {x}}\left[ \Vert U-\Psi \,V \, Y^{\vec {x}}\Vert _{\max }\ge \frac{1}{2\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }}\right] . \end{aligned}$$

By definitions of $U,\Psi ,V$, we have

$$\begin{aligned} (\Psi \,V)_{ji} = \psi _j \eta _j^{i-1}, \end{aligned}$$

so that

$$\begin{aligned} (\Psi \,V\,Y^{\vec {x}})_{j} = \psi _j \sum _{i=1} 1_{\{x_i=\sigma \}} \eta _j^{i-1}, \end{aligned}$$

and, by (17),

$$\begin{aligned} p^{\sigma }_{\vec {x}}(h^*+t_j)&= \pi _{\sigma }\,\phi _j\,\big [1-\eta _j^{M}\big ]\,+\,\psi _j\sum _{i=1}^{M}1_{\{x_i=\sigma \}}\,\eta _j^{i-1} \,+\,\pi _{\sigma }\gamma \,\eta _j\\&= \pi _{\sigma }\,\phi _j\,\big [1-\eta _j^{M}\big ] \,+(\Psi \,V\,Y^{\vec {x}})_{j} \,+\,\pi _{\sigma }\gamma \,\eta _j. \end{aligned}$$

Hence, from (7),

$$\begin{aligned} \Vert U-\Psi \,V \, Y^{\vec {x}}\Vert _{\max }=\max _{\sigma \in \{A,T,C,G\}}\max _{1\le j\le M} \big |f^{k,s}_{\sigma }(t_j)-p^{\sigma }_{\vec {x}}(h^*+t_j)\big |. \end{aligned}$$

Therefore, we can bound the error probability in terms of the deviations of the empirical frequencies $f^{k,s}_{\sigma }(t_j)$ as follows:

$$\begin{aligned}&{{\mathbb {P}}}^{\,\vec {x}}\left[ F^{(M)}_{k,s}\left( \vec {X}_{\partial T^k}\right) \ne \vec {x} \right] \nonumber \\&\quad \le \sum _{\sigma \in \{A,T,C,G\}}\sum _{j=1}^M{{\mathbb {P}}}^{\,\vec {x}}\left[ \big |f^{k,s}_{\sigma }(t_j)-p^{\sigma }_{\vec {x}}(h^*+t_j)\big | \ge \frac{1}{2\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }}\right] . \end{aligned}$$

(36)

(ii) Estimating deviation of frequencies We then bound each term on the RHS of (36) using similar arguments to that of Proposition 1. As before, we let $m:=|\partial T^{k}(s)|$ for convenience. Recall from (5) that for $t\in [0,\infty )$

$$\begin{aligned} f^{k,s}_{\sigma }(t) = \frac{1}{m}\,\sum _{v\in \partial {\tilde{T}}^{k,s}} p^{\sigma }_{\vec {X}_{v}}(t). \end{aligned}$$

All the terms $p^{\sigma }_{\vec {X}_{v}}(t)$, for $v\in \partial {\tilde{T}}^{k,s}$, have expectation $p^{\sigma }_{\vec {x}}(h^*+t)$ under ${{\mathbb {P}}}^{\vec {x}}$, by the Markov property. Therefore, for $\epsilon \in (0,\infty )$ and $t\in [0,\infty )$, we have

$$\begin{aligned} {{\mathbb {P}}}^{\vec {x}}\left( |f^{k,s}_{\sigma }(t) - p_{\vec {x}}^{\sigma }(h^*+t)|>\epsilon \right) = {{\mathbb {P}}}^{\vec {x}}\left( \left| \frac{1}{m}\,\sum _{v\in \partial {\tilde{T}}^{k,s}}y_v\right| >\epsilon \right) \end{aligned}$$

(37)

where

$$\begin{aligned} y_v:=p^{\sigma }_{\vec {X}_{v}}(t) - p^{\sigma }_{\vec {x}}(h^*+t)\quad \text {for }v\in \partial {\tilde{T}}^{k,s} \end{aligned}$$

are centered but correlated random variables under ${{\mathbb {P}}}^{\vec {x}}$. To bound (37), we use the same method that we used to bound (22), namely by considering the conditional expectation of $f^{k,s}_{\sigma }(t)$ given the states $\vec {X}_{\partial T^k(s)}=\{\vec {X}_{v}:\,v\in \partial T^k(s)\}$, which by the Markov property is equal to

$$\begin{aligned} {\mathbb {E}}^{\vec {x}}\left[ f^{k,s}_{\sigma }(t)\Big |\vec {X}_{\partial T^k(s)}\,\right] = \frac{1}{m}\sum _{u\in \partial T^k(s)}p_{\vec {X}_{u}}^{\sigma }(h^*+t-\,s). \end{aligned}$$

(38)

As before, we first bound the probability of the event that this conditional expectation is close to its expectation (which is also $p_{\vec {x}}^{\sigma }(h^*+t)$), and then conditioned on this event we establish a concentration inequality for $f^{k,s}_{\sigma }(t)$, based on conditional independence. Since all $y_v$ are bounded between 1 and $-1$, we apply Hoeffding’s inequality (Hoeffding 1963) for this purpose.

We detail the above argument in steps A–C as follows.

(A) Decomposition by conditioning on levels Similarly to (25), we have

$$\begin{aligned}&{{\mathbb {P}}}^{\vec {x}}\left( |f^{k,s}_{\sigma }(t) - p_{\vec {x}}^{\sigma }(h^*+t)|>\epsilon \right) \nonumber \\&\quad \le {{\mathbb {P}}}^{\vec {x}}\left( \left\{ |f^{k,s}_{\sigma }(t) - p_{\vec {x}}^{\sigma }(h^*+t)| > \epsilon \right\} \cap ({\mathcal {F}}^t_{\delta ,s})^c\right) + {{\mathbb {P}}}^{\vec {x}}( {\mathcal {F}}^t_{\delta ,s}), \end{aligned}$$

(39)

where

$$\begin{aligned} {\mathcal {F}}^{\,t}_{\delta ,s}:= \Big \{\Big |{\mathbb {E}}^{\vec {x}}\left[ f^{k,s}_{\sigma }(t)\Big |\vec {X}_{\partial T^k(s)}\,\right] - \,p_{\vec {x}}^{\sigma }(h^*+t)\Big |> \delta \Big \}. \end{aligned}$$

(40)

As we detail next, we then control the two terms on the RHS of (39). The proof of Proposition 2 will be completed by taking

$$\begin{aligned} \epsilon =\frac{1}{2\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }},\quad \delta :=\epsilon /2 \quad \text {and}\quad t=t_j \end{aligned}$$

(41)

in (39) and combining with (36).

(B) Bounding${{\mathbb {P}}}_{M}( {\mathcal {F}}^t_{\delta ,s})$The second term on the RHS of (39) is treated in Lemma 5.

Lemma 5

(Conditional expectation given level s) There exists a constant $C\in (0,\infty )$ which depends only on $\lambda$, $\nu$ and $\mu$ such that for all $\vec {x}\in \{A,T,C,G\}^M$, $\delta \in (0,\infty )$ and $s\in (0,\,h^*)$, we have

$$\begin{aligned} \sup _{t\in (0,\infty )}{{\mathbb {P}}}^{\vec {x}}( {\mathcal {F}}^{\,t}_{\delta ,s}) \,\le \, \delta ^{-2}CMs, \end{aligned}$$

where event ${\mathcal {F}}^{\,t}_{\delta ,s}$ is defined in (40).

Proof

Similarly to the proof of Lemma 4, we use Chebyshev’s inequality to control the deviation of $m^{-1}\sum _{u\in \partial T^k(s)}p_{\vec {X}_{u}}^{\sigma }(h^*+t-\,s)$.

Using (28),

$$\begin{aligned} \mathrm {Var}_{\vec {x}}\left[ \sum _{u\in \partial T^k(s)}p_{\vec {X}_{u}}^{\sigma }(h^*+t-s)\right]&\le m^2 \,\mathrm {Var}_{\vec {x}}\left[ p_{\vec {X}_{u}}^{\sigma }(h^*+t-s)\right] , \end{aligned}$$

(42)

for any $u \in \partial T^k(s)$, where we used the fact that the $\vec {X}_u$’s for all such u’s are identically distributed. Using the explicit formula (17) together with (28) again, for each $u\in \partial T^k(s)$ we have further

$$\begin{aligned}&\mathrm {Var}_{\vec {x}}\left[ p_{\vec {X}_{u}}^{\sigma }(h^*+t-s)\right] \nonumber \\&\quad =\mathrm {Var}_{\vec {x}}\left[ -\pi _{\sigma }\,\phi (h^*+t-s)\,A^{|\vec {X}_{u}|} +\,\psi (h^*+t-s)\sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1} \right] \nonumber \\&\quad \le 2\,\pi ^2_{\sigma }\,\phi ^2(h^*+t-s)\,\mathrm {Var}_{\vec {x}}\Big [A^{|\vec {X}_{u}|}\Big ] \nonumber \\&\qquad +\,2\,\psi ^2(h^*+t-s)\,\mathrm {Var}_{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right] , \end{aligned}$$

(43)

where $A:= \eta (h^*+t-s)$. (Note that A here is distinct from that in Sect. A.)

The term $\mathrm {Var}_{\vec {x}}[A^{|\vec {X}_{u}|}]$ can be bounded as follows. Let $E_u$ be the event that the sequence never left state $\vec {x}$ along the unique path from the root to u. Then,

$$\begin{aligned} {{\mathbb {P}}}^{\vec {x}}(E_u)=\mathrm{e}^{-q_M s},\quad \text {where}\;\; q_M:=M\nu +(M+1)\lambda +M\mu , \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}^{\vec {x}}\Big [A^{|\vec {X}_{u}|}\Big ]= A^M\,{{\mathbb {P}}}^{\vec {x}}(E_u)+ {\mathbb {E}}^{\vec {x}}\Big [A^{|\vec {X}_{u}|};E_u^c\Big ]. \end{aligned}$$

Since $A \in [0,1]$, we have ${\mathbb {E}}^{\vec {x}}\Big [A^{|\vec {X}_{u}|};E_u^c\Big ]\le {{\mathbb {P}}}^{\vec {x}}(E_u^c)=1-\mathrm{e}^{-q_M s}$ and therefore

$$\begin{aligned} 0\le {\mathbb {E}}^{\vec {x}}\Big [A^{|\vec {X}_{u}|}\Big ]-A^M\,\mathrm{e}^{-q_M s}\le 1-\mathrm{e}^{-q_M s}. \end{aligned}$$

Similarly,

$$\begin{aligned} 0\le {\mathbb {E}}^{\vec {x}}\Big [A^{2|\vec {X}_{u}|}\Big ]- A^{2M}\mathrm{e}^{-q_M s}\le 1-\mathrm{e}^{-q_M s}. \end{aligned}$$

The last two displays give

$$\begin{aligned} \mathrm {Var}_{\vec {x}}\Big [A^{|\vec {X}_{u}|}\Big ]&={\mathbb {E}}^{\vec {x}}\Big [A^{2|\vec {X}_{u}|}\Big ]-\left( {\mathbb {E}}^{\vec {x}}\Big [A^{|\vec {X}_{u}|}\Big ]\right) ^2 \nonumber \\&\le \left( A^{2M}\mathrm{e}^{-q_M s}+1-\mathrm{e}^{-q_M s}\right) \;-\; (A^M\,\mathrm{e}^{-q_M s})^2 \nonumber \\&= A^{2M}\mathrm{e}^{-q_M\,s}(1-\mathrm{e}^{-q_M s}) +1-\mathrm{e}^{-q_M s} \nonumber \\&\le 2(1-\mathrm{e}^{-q_M s}). \end{aligned}$$

(44)

For the second variance term in (43), a similar argument gives

$$\begin{aligned}&{\mathbb {E}}^{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right] \\&\quad = \left( \sum _{i=1}^{M}1_{\{x_i=\sigma \}}\,A^{i-1}\right) \,{{\mathbb {P}}}^{\vec {x}}(E_u) + {\mathbb {E}}^{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1};\,E^c_u\cap \{|\vec {X}_{u}|\ge 1\}\right] \end{aligned}$$

and

$$\begin{aligned} 0\le {\mathbb {E}}^{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1};\,E^c_u\cap \{|\vec {X}_{u}|\ge 1\}\right] \le \sum _{i=1}^{\infty }A^{i-1}{{\mathbb {P}}}^{\vec {x}}\left( E^c_u\right) =\frac{1-\mathrm{e}^{-q_M s}}{1-A} \end{aligned}$$

because $A \in (0,1)$ when $h^*+t-s>0$. The last two displays immediately give

$$\begin{aligned} 0\le {\mathbb {E}}^{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right] - \left( \sum _{i=1}^{M}1_{\{x_i=\sigma \}}\,A^{i-1}\right) \mathrm{e}^{-q_M s} \le \frac{1-\mathrm{e}^{-q_M s}}{1-A}. \end{aligned}$$

Similarly, we have

$$\begin{aligned} 0&\le {\mathbb {E}}^{\vec {x}}\left[ \left( \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right) ^2\,\right] - \left( \sum _{i=1}^{M}1_{\{x_i=\sigma \}}\,A^{i-1} \right) ^2\mathrm{e}^{-q_M s}\\&= {\mathbb {E}}^{\vec {x}}\left[ \left( \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right) ^2;\,E^c_u\cap \{|\vec {X}_{u}|\ge 1\}\right] \\&\le \left( \sum _{i=1}^{\infty }A^{i-1} \right) ^2\,{{\mathbb {P}}}^{\vec {x}}\left( E^c_u\right) \\&= \frac{1-\mathrm{e}^{-q_M s}}{(1-A)^2}. \end{aligned}$$

From the above two displays, we obtain as in (44) the following estimate

$$\begin{aligned} \mathrm {Var}_{\vec {x}}\left[ \sum _{i=1}^{|\vec {X}_{u}|}1_{\{X_{u,i}=\sigma \}}\,A^{i-1}\right]&\le \, \frac{2(1-\mathrm{e}^{-q_M s})}{(1-A)^2}. \end{aligned}$$

(45)

From (43)–(45), we have

$$\begin{aligned}&\mathrm {Var}_{\vec {x}}\left[ p_{\vec {X}_{u}}^{\sigma }(h^*+t-s)\right] \\&\quad \le 4\,\pi ^2_{\sigma }\,\phi ^2(h^*+t-s)\,(1-\mathrm{e}^{-q_M s})\,+\,4\,\psi ^2(h^*+t-s)\,\frac{1-\mathrm{e}^{-q_M s}}{(1-A)^2}\\&\quad = 4\,(1-\mathrm{e}^{-q_M s})\,\left[ \pi ^2_{\sigma }\,\phi ^2(h^*+t-s)+\frac{\psi ^2(h^*+t-s)}{\left( 1-\eta (h^*+t-s)\right) ^2}\right] \\&\quad \le 4\,(1-\mathrm{e}^{-q_M s})\,\left[ \Vert \phi \Vert _{\infty }^2\pi ^2_{\sigma }+ \frac{\gamma ^2}{(1-\gamma )^2}\right] \\&\quad \le C_1Ms \end{aligned}$$

for all $s\in (0,h^*)$ and $t\in (0,\infty )$, where $C_1\in (0,\infty )$ is a constant which depends only on $\lambda$, $\nu$ and $\mu$. In the second to last inequality, we used the following facts that follow directly from the definitions: (i) $\eta$ is a strictly increasing function with $\eta (0)=0$ and $\lim _{t\rightarrow \infty }\eta (t)=1/\gamma$, (ii) the supremum norm $\Vert \phi \Vert _{\infty }<\infty$ and (iii) $\psi (t)$ is a decreasing function bounded above by 1.

The result follows by (42) and Chebyshev’s inequality. $\square$

(C) Deviation of$f^{k,s}_{\sigma }(t)$ conditioned on ${\mathcal {F}}_{\delta ,s}^t$ By the Markov property and conditional independence as in (32), the first term on the RHS of (39) is equal to

$$\begin{aligned}&{{\mathbb {P}}}^{\vec {x}}\left( \left\{ |f^{k,s}_{\sigma }(t) - p_{\vec {x}}^{\sigma }(h^*+t)|> \epsilon \right\} \;\cap \; ({\mathcal {F}}^t_{\delta ,s})^c\right) \nonumber \\&\quad = \sum _{(\vec {y}_i)_{i=1}^m \in {\mathcal {H}}_{\delta ,s}^c} \, {{\mathbb {P}}}^{\vec {x}}\left( \left| \sum _{i=1}^m p^{\sigma }_{\vec {Z}^{(\vec {y}_i)}}(t) - mp_{\vec {x}}^{\sigma }(h^*+t)\right| > m\epsilon \right) {{\mathbb {P}}}^{\vec {x}}\left( \vec {X}_{\partial T^k(s)} = (\vec {y}_i)_{i=1}^m \right) \nonumber \\&\quad \le \max _{(\vec {y}_i)_{i=1}^m \in {\mathcal {H}}_{\delta ,s}^c} {{\mathbb {P}}}\left( \left| \sum _{i=1}^m p^{\sigma }_{\vec {Z}^{(\vec {y}_i)}}(t)-mp_{\vec {x}}^{\sigma }(h^*+t)\right| \ge m\epsilon \right) , \end{aligned}$$

(46)

where

$$\begin{aligned} {\mathcal {H}}_{\delta ,s}^c:=\left\{ (\vec {y}_i)_{i=1}^m \in {\mathcal {S}}^m:\;\left| \sum _{i=1}^mp_{\vec {y}_{i}}^{\sigma }(h^*+t-s) - m \,p_{\vec {x}}^{\sigma }(h^*+t)\right| \le m\delta \right\} \end{aligned}$$

(47)

and $\{\vec {Z}^{(\vec {y}_i)}\}_{i=1}^m$ are independent copies of the TKF91 process starting from $\{\vec {y}_i\}_{i=1}^m$, respectively, evaluated at time $h^*-s$. By the triangle inequality applied to the events in (46) and (47), and then Hoeffding’s inequality (Hoeffding 1963), we have

(48)

Proof of Proposition 2

As pointed out in (41), we will take

$$\begin{aligned} \epsilon =\frac{1}{2\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }},\quad \delta :=\epsilon /2 \quad \text {and}\quad t=t_j. \end{aligned}$$

From (48), we have

Taking $t\in \{t_j\}$ in (39), we see that the terms on the RHS of (36) are of the form

$$\begin{aligned}&{{\mathbb {P}}}^{\,\vec {x}}\left[ \big |f^{k,s}_{\sigma }(t_j)-p^{\sigma }_{\vec {x}}(h^*+t_j)\big | \ge \frac{1}{2\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }}\right] \nonumber \\&\quad \le 2\,\exp {\left( \,\frac{-\,m}{8\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }^2}\,\right) }+ \,{{\mathbb {P}}}^{\vec {x}}\left[ {\mathcal {F}}^{\,t_j}_{\delta ,s}\right] ,\nonumber \\&\quad \le 2\,\exp {\left( \,\frac{-\,m}{8\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }^2}\,\right) }+ \,\left( \frac{1}{4\,\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }}\right) ^{-2}CMs, \end{aligned}$$

(49)

where the last line comes from Lemma 5 and our choice of $\delta$. The proof of Proposition 2 is completed upon plugging into (36) and summing over $\sigma$ and j. $\square$

4.3 Proof of Theorem 2

Applying Propositions 1 and 2 to the first and second terms on the RHS of (21), respectively, we obtain constants $C_1,\,C_2,\,C_3\in (0,\infty )$ which depend only on $h^*$, $\mu$ and $\lambda$ such that

$$\begin{aligned} {{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}_{\partial T^{k}})\ne \vec {x}\right]&\le 2\exp {\left( -\,C_1\,|\partial T^{k}(s)|\right) }\,+\,C_2\,M\,s \nonumber \\&\quad + 8M\exp {\left( \frac{-\, |\partial T^{k}(s)|}{8\,{\hat{C}}}\,\right) } \,+\,C_3\,M^2\,{\hat{C}}\,s \end{aligned}$$

(50)

for all $s\in (0,h^*/2]$ and $k\in {\mathbb {N}}$, where $M=|\vec {x}|$ and ${\hat{C}}:=\Vert V^{-1}\,\Psi ^{-1}\Vert _{\infty \rightarrow \infty }^2\in (0,\infty )$ is a constant which depends only on $\mu$, $\lambda$, $h^*$ and $\{t_j\}_{j=1}^M$.

For any $\epsilon \in (0,\infty )$, there exists $M_{\epsilon }$ such that $\sum _{\{\vec {x}:\,|\vec {x}|>M_{\epsilon }\}}\Pi (\vec {x}) <\epsilon /2$. Hence,

$$\begin{aligned} {{\mathbb {P}}}^{\Pi }\left[ F_{k,s}(\vec {X}_{\partial T^{k}})\ne \vec {X}_{\rho }\right]&< \sum _{\{\vec {x}:\,|\vec {x}|\le M_{\epsilon }\}}{{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}_{\partial T^{k}})\ne \vec {x}\right] \,\Pi (\vec {x})\,+\frac{\epsilon }{2}\\&\le \max _{\{\vec {x}:\,|\vec {x}|\le M_{\epsilon }\}}{{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}_{\partial T^{k}})\ne \vec {x}\right] \,+\frac{\epsilon }{2}. \end{aligned}$$

From (50), there exist constants $C_4,\,C_5,\, C_6\in (0,\infty )$ which depend only on $\mu$, $\lambda$, $h^*$, $\epsilon$ and $\{t_j\}_{j=1}^{M_{\epsilon }}$ such that

$$\begin{aligned} \max _{\{\vec {x}:\,|\vec {x}|\le M_{\epsilon }\}}{{\mathbb {P}}}^{\vec {x}}\left[ F_{k,s}(\vec {X}_{\partial T^{k}})\ne \vec {x}\right] \le C_4 \exp {\left( -\, C_5\, |\partial T^{k}(s)|\,\right) } \,+\,C_6\,s \end{aligned}$$

for all $s\in (0,h^*/2]$ and $k\in {\mathbb {N}}$. Inequality (9) follows from this. The proof of Theorem 2 is complete.

4.4 Proof of Theorem 1

Theorem 1 follows from Theorem 2 upon taking sequences $\epsilon _m \downarrow 0$ and $s_m \downarrow 0$ and then a subsequence $k_m \rightarrow +\,\infty$ such that the error in (9) goes to 0. This is possible thanks to the big bang condition, which guarantees $|\partial T^k(s_m)| \rightarrow +\,\infty$ as $k \rightarrow \infty$.

5 Discussion

In this paper, we considered the ancestral sequence reconstruction (ASR) problem in the taxon-rich context for the TKF91 process. It has been known from previous work (Fan and Roch 2018, Theorem 1) that the Big Bang condition is necessary for the existence of consistent estimators. In this paper, we design the first estimator which is not only consistent but also explicit and computationally tractable. Our ancestral reconstruction algorithm involves two steps: We first estimate the length of the ancestral sequence and then estimate the nucleotides conditioned on the sequence length.

The novel observation that leads to the design of our estimator is a new constructive proof of initial-state identifiability, formulated in Lemma 2, which says that one can explicitly invert the mapping from the root sequence to the distribution of the leaf sequences. This is nontrivial for evolutionary models with indels. Our estimator is computationally efficient in the sense that the number of arithmetic operations required scales like a polynomial in the size of the input data. Indeed, the length estimator is linear in the number of input sequences and the matrix manipulations in the sequence estimator are polynomial in the length of the longest input sequence.

We believe this is a first step toward designing practical estimators with consistency guarantees, which are lacking under indel models. We leave the nontrivial task of implementation and validation for future work. On the theoretical side, it would be of interest to explore whether our techniques can be applied to more general indel models, for instance those allowing multiple simultaneous insertions and deletions.

Appendices

Some properties of the TKF91 length process

Recall the TKF91 edge process ${\mathcal {I}}=({\mathcal {I}}_t)_{t\ge 0}$ in Definition 1, which has parameters $(\nu ,\,\lambda ,\,\mu )\in (0,\infty )^3$ with $\lambda < \mu$ and $(\pi _A,\,\pi _T,\,\pi _C,\,\pi _G)\in [0,\infty )^4$ with $\pi _A +\pi _T + \pi _C + \pi _G = 1$. The sequence length of the TKF91 edge process is a continuous-time linear birth–death–immigration process $(|{\mathcal {I}}_{t}|)_{t\ge 0}$ with infinitesimal generator $Q_{i,i+1}=\lambda +i\lambda$ (for $i\in {\mathbb {Z}}_+$), $Q_{i,i-1}=i\mu$ (for $i\ge 1$) and $Q_{i,j}=0$ otherwise. This is a well-studied process for which explicit forms for the transition density $p_{ij}(t)$ and probability generating functions $G_i(z,t)=\sum _{j=0}^{\infty }p_{ij}(t)z^j$ are known. See, for instance, Anderson (1991, Section 3.2) or Karlin and Taylor (1981, Chapter 4) for more details. This process was also analyzed in Thatte (2006) in the related context of phylogeny estimation.

We collect here a few properties that will be useful in our analysis. The probability generating function is given by

$$\begin{aligned} G_i(z,t)=\left[ \frac{1-\beta -z(\gamma -\beta )}{1-\beta \gamma -\gamma z(1-\beta )}\right] ^i\,\left[ \frac{1-\gamma }{1-\beta \gamma -\gamma z(1-\beta )}\right] \end{aligned}$$

for $i\in {\mathbb {Z}}_+$ and $t>0$, where

$$\begin{aligned} \beta =\beta _t = \mathrm{e}^{-(\mu -\lambda )t}\quad \text {and}\quad \gamma =\frac{\lambda }{\mu }. \end{aligned}$$

Fix $t\ge 0$ and let $\varphi _i(\theta )={\mathbb {E}}_i[\mathrm{e}^{\theta \,|{\mathcal {I}}_{t}|}]$ be the characteristic function of $|{\mathcal {I}}_{t}|$ starting at i. Then, for $\lambda \ne \mu$ (i.e., $\gamma \ne 1$),

$$\begin{aligned} \varphi _i(\theta )&=G_i(\mathrm{e}^{\theta },t)=\left[ \frac{1-\beta -\mathrm{e}^{\theta }(\gamma -\beta )}{1-\beta \gamma -\gamma \mathrm{e}^{\theta }(1-\beta )}\right] ^i\,\left[ \frac{1-\gamma }{1-\beta \gamma -\gamma \mathrm{e}^{\theta }(1-\beta )}\right] \nonumber \\&=(1-\gamma )\frac{A^i}{B^{i+1}}, \end{aligned}$$

(51)

where

$$\begin{aligned} A=1-\beta -\mathrm{e}^{\theta }(\gamma -\beta ) \quad \text {and}\quad B=1-\beta \gamma -\gamma \mathrm{e}^{\theta }(1-\beta ). \end{aligned}$$

Differentiating with respect to $\theta$ gives

$$\begin{aligned} \varphi '_i(\theta )&=(1-\gamma )\frac{A^{i-1}\mathrm{e}^{\theta }\big \{i(\beta -\gamma )B -(i+1)\gamma (\beta -1)A\big \}}{B^{i+2}} \nonumber \\&=(1-\gamma )\frac{A^{i-1}\mathrm{e}^{\theta }\big \{\beta (1-\gamma )^2i +\gamma (1-\beta )^2 + \mathrm{e}^{\theta }(\gamma -\beta )\gamma (\beta -1)\big \}}{B^{i+2}} \nonumber \\&= \frac{A^{i-1}}{B^{i+2}}(C\mathrm{e}^{\theta }+D\mathrm{e}^{2\theta }), \end{aligned}$$

(52)

where

$$\begin{aligned} C=(1-\gamma )[\beta (1-\gamma )^2i +\gamma (1-\beta )^2] \quad \text {and}\quad D=(1-\gamma )(\gamma -\beta )\gamma (\beta -1). \end{aligned}$$

Differentiating with respect to $\theta$ once more gives

$$\begin{aligned} \varphi ''_i(\theta )&=\frac{A^{i-2}\mathrm{e}^{\theta }}{B^{i+3}}\Big \{BA(C+2D\mathrm{e}^{\theta }) \,+\,(C\mathrm{e}^{\theta }+D\mathrm{e}^{2\theta })\\&\quad \times \big [(i-1)B(\beta -\gamma )+(i+2)A\gamma (1-\beta )\big ]\Big \}. \end{aligned}$$

The expected value and the second moment are given by

$$\begin{aligned} {\mathbb {E}}_{i}[|{\mathcal {I}}_{t}|]=\varphi '_i(0)&= i\beta +\frac{\gamma (1-\beta )}{1 -\gamma }=i\beta +\frac{\lambda }{\lambda -\mu }(\beta -1) \quad \text { and}\\ {\mathbb {E}}_{i}[|{\mathcal {I}}_{t}|^2]=\varphi ''_i(0)&= i^2\beta ^2+i\,\frac{\beta (3\gamma +1)(1-\beta )}{1-\gamma } +\frac{(1-\beta )\gamma [1+(1-2\beta )\gamma ]}{(1-\gamma )^2}. \end{aligned}$$

From these, we also have the variance

$$\begin{aligned} \mathrm {Var}_i(|{\mathcal {I}}_{t}|)&={\mathbb {E}}_i[|{\mathcal {I}}_{t}|^2]-({\mathbb {E}}_i[|{\mathcal {I}}_{t}|])^2 \nonumber \\&=i^2\beta ^2+i\,\frac{\beta (3\gamma +1)(1-\beta )}{1-\gamma } +\frac{(1-\beta )\gamma [1+(1-2\beta )\gamma ]}{(1-\gamma )^2}\nonumber \\&\quad - \left( i\beta +\frac{\gamma (1-\beta )}{1 -\gamma }\right) ^2\nonumber \\&= i\,\frac{\beta (1-\beta )(1+3\gamma -2\beta )}{1-\gamma }\,+\,\frac{\gamma (1-\beta )(1-\beta \gamma )}{(1-\gamma )^2}. \end{aligned}$$

(53)

Consider the function

$$\begin{aligned} \psi _i(\theta )&=\varphi '_i(0)-\frac{\varphi '_i(\theta )}{\varphi _i(\theta )}\\&=i\beta +\frac{\gamma (1-\beta )}{1 -\gamma } \,- \frac{C\mathrm{e}^{\theta }+D\mathrm{e}^{2\theta }}{(1-\gamma )AB} \\&=\left( \beta -\frac{C_1\mathrm{e}^{\theta }}{(1-\gamma )AB}\right) i\,+\,\frac{\gamma (1-\beta )}{1 -\gamma } - \frac{C_2\mathrm{e}^{\theta }+D\mathrm{e}^{2\theta }}{(1-\gamma )AB} \\&=\left( \beta -\frac{\beta (1-\gamma )^2\mathrm{e}^{\theta }}{AB}\right) i\,+\,\frac{\gamma (1-\beta )}{1 -\gamma } \,- \frac{\gamma (1-\beta )^2\mathrm{e}^{\theta }+(\gamma -\beta )\gamma (\beta -1)\,\mathrm{e}^{2\theta }}{AB} \\&= F(\theta )i+G(\theta ) \end{aligned}$$

where we wrote $C=C_1i+C_2$, with $C_1=\beta (1-\gamma )^3$ and $C_2=(1-\gamma )\gamma (1-\beta )^2$, and the last line is a definition. Functions F and G can be simplified to

$$\begin{aligned} F(\theta )&= \frac{-\,(\mathrm{e}^{\theta } - 1) \beta (1-\beta )[(1-\beta \gamma )-\mathrm{e}^{\theta }\gamma (\gamma -\beta )]}{AB} \end{aligned}$$

(54)

$$\begin{aligned} G(\theta )&= \frac{-\,(\mathrm{e}^{\theta }-1) \gamma (1-\beta )(1-\beta \gamma )[(1-\beta )-\mathrm{e}^{\theta }(\gamma -\beta )]}{(1-\gamma )AB}. \end{aligned}$$

(55)

Since $\varphi _i(0)=1$, we have $\psi (0)=0$. We consider the case $\mu \in (\lambda ,\infty )$, that is, $\gamma \in (0,1)$. Then, both A and B are strictly positive for all $t\in [0,\infty )$, provided that $\mathrm{e}^\theta <\mu /\lambda$. Moreover, F and G are continuous on $[0,\,\mu /\lambda )$, smooth on $(0,\,\mu /\lambda )$ and $F(0)=G(0)=0$.

Notation

For the reader’s convenience, we list some frequently used notation here (Tables 1, 2 and 3).

Table 1 TKF91 edge process ${\mathcal {I}}=({\mathcal {I}}_t)_{t\ge 0}$ in Definition 1

Table 2 TKF91 process on trees

Table 3 Probabilities, expectations and other notations