Phase transition in the sample complexity of likelihood-based phylogeny inference

Abstract

Reconstructing evolutionary trees from molecular sequence data is a fundamental problem in computational biology. Stochastic models of sequence evolution are closely related to spin systems that have been extensively studied in statistical physics and that connection has led to important insights on the theoretical properties of phylogenetic reconstruction algorithms as well as the development of new inference methods. Here, we study maximum likelihood, a classical statistical technique which is perhaps the most widely used in phylogenetic practice because of its superior empirical accuracy. At the theoretical level, except for its consistency, that is, the guarantee of eventual correct reconstruction as the size of the input data grows, much remains to be understood about the statistical properties of maximum likelihood in this context. In particular, the best bounds on the sample complexity or sequence-length requirement of maximum likelihood, that is, the amount of data required for correct reconstruction, are exponential in the number, n, of tips—far from known lower bounds based on information-theoretic arguments. Here we close the gap by proving a new upper bound on the sequence-length requirement of maximum likelihood that matches up to constants the known lower bound for some standard models of evolution. More specifically, for the r-state symmetric model of sequence evolution on a binary phylogeny with bounded edge lengths, we show that the sequence-length requirement behaves logarithmically in n when the expected amount of mutation per edge is below what is known as the Kesten-Stigum threshold. In general, the sequence-length requirement is polynomial in n. Our results imply moreover that the maximum likelihood estimator can be computed efficiently on randomly generated data provided sequences are as above. Our main technical contribution, which may be of independent interest, relates the total variation distance between the leaf state distributions of two trees with a notion of combinatorial distance between the trees. In words we show in a precise quantitative manner that the more different two evolutionary trees are, the easier it is to distinguish their output.

1 Introduction

1.1 Background

Reconstructing evolutionary trees, or phylogenies, from biomolecular data is a fundamental problem in computational biology [13, 19, 51, 57, 61]. Roughly, in the basic form of the problem, sequences from a common gene (or other DNA region) are collected from representative individuals of contemporary species of interest. From that sequence data (which is usually aligned to account for insertions and deletions), a phylogeny depicting the shared history of the species is inferred.

From a formal statistical point of view, one typically assumes that each site in the (aligned) data has evolved independently according to a common Markov model of substitution along the tree of life. The problem then boils down to reconstructing this generating model from i.i.d. samples at the leaves of the tree. Such models are closely related to spin systems that have been extensively studied in statistical physics [20, 30] and that connection has led to new insights on the amount of data required for accurately reconstructing phylogenies [56]. More specifically, under broad modeling assumptions, algorithmic upper bounds have been obtained on the sample complexity of the phylogenetic reconstruction problem, together with matching information-theoretic (i.e., applying to any method) lower bounds  [10, 32, 34, 35, 42, 47]. In particular it was established that the best achievable sample complexity undergoes a phase transition as the maximum branch length varies. That phase transition is closely related to the well-studied problem of reconstructing the root sequence of a Markov model on a tree given the leaf sequences [36], a tool which plays a key role in the above results.

The algorithmic results in [4, 10, 32, 47] concern ad hoc methods of inference. On the other hand, little is known about the precise sample complexity of reconstruction methods used by evolutionary biologists in practice (with some exceptions [29]). Here we consider maximum likelihood (ML), introduced in phylogenetics in [18], where one computes (or approximates) the tree most likely to have produced the data among a class of allowed models. Likelihood-based methods are perhaps the most widely used and most trusted methods in current phylogenetic practice [54]. In previous theoretical work, upper bounds were derived on the sample complexity of ML that were far from the lower bound [50]—in some regimes, doubly exponentially far in the number of species. Here we close the gap by proving a new upper bound on the sample complexity of maximum likelihood that matches up to constants the known information-theoretic lower bound for some standard models of evolution.

1.2 Overview of main results and techniques

In order to state our main results more precisely, we briefly describe the model of evolution considered here (See Sect. 2 for more details). The unknown phylogeny T is a weighted binary tree with n leaves labeled by species names, one leaf for each species of interest. Without loss of generality, we assume that the leaf labels are $[n] = \{1,\ldots ,n\}$. The weights on the edges (or branches), $\{w_e\}_{e \in E}$ where E is the set of edges of T, are assumed to be discretized and bounded between two constants $f < g$. The quantity $w_e$ can be interpreted as the expected number of mutations per site along edge e. We denote by $\mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$ the set of all such phylogenies, where $\frac{1}{\Upsilon }$ is the discretization.

Let $\rho$ be the root of the tree, that is, the most recent common ancestor to the species at the leaves (which formally can be chosen arbitrarily as it turns out not to affect the distribution of the data). Let $\mathcal {R}$ be a state space of size r. A typical choice is $\mathcal {R}= \{\mathrm {A}, \mathrm {G},\mathrm {C},\mathrm {T}\}$ and $r=4$, but we consider more general spaces as well. Define

$$\begin{aligned} \delta _e = \frac{1}{r}\left( 1 - e^{-w_e}\right) . \end{aligned}$$

In the r-state symmetric model, we start at $\rho$ with a sequence of length k chosen uniformly in $\mathcal {R}^k$. Moving away from the root, each vertex v in T is assigned the sequence $(s_u^i)_{i=1}^k$ of its parent u randomly “mutated” as follows: letting e be the edge from u to v, for each i, with probability $(r-1) \delta _e$ set $s_v^i$ to a uniform state in $\mathcal {R}-\{s_u^i\}$ (corresponding to a substitution), or otherwise set $s_v^i = s_u^i$. Let $(s^i_{[n]})_{i=1}^k \in (\mathcal {R}^{[n]})^k$ be the sequences at the leaves. Those are the sequences that are observed. We let $\mu _{[n]}^T(s^i_{[n]})$ be the probability of observing $s^i_{[n]}$ under T.

In the phylogenetic reconstruction problem, we are given sequences $(s^i_{[n]})_{i=1}^k$, assumed to have been generated under the r-state symmetric model on an unknown phylogeny T, and our goal is to recover T (without the root) as a leaf-labeled tree (that is, we care about the locations of the species on the tree). This problem is known to be well-defined in the sense that, under our assumptions, the phylogeny is uniquely identifiable from the distribution of the data at the leaves [7]. A useful proxy to assess the “accuracy” of a reconstruction method is its sample complexity or sequence-length requirement, roughly, the smallest sequence length k (as a function of n) such that a perfect reconstruction is guaranteed with probability approaching 1 as n goes to $+\infty$ (See Sect. 2 for a more precise definition.). A smaller sequence-length requirement is an indication of superior statistical performance. We denote by $k_0(\Psi ,n)$ the sequence-length requirement of method $\Psi$.

Here we analyze the sequence-length requirement of ML which, in our context, we define as

$$\begin{aligned} \Psi ^{\mathrm {ML}}_{n,k}\left( \left( s^i_{[n]}\right) _{i=1}^k\right) \in \mathop {{{\mathrm{arg\,min}}}}\limits _{T \in \mathbb {Y}^{(n)}_{f,g}\left[ \frac{1}{\Upsilon }\right] } \mathscr {L}_T\left[ \left( s^i_{[n]}\right) _{i=1}^k\right] , \end{aligned}$$

where $\mathscr {L}_T[(s^i_{[n]})_{i=1}^k] = - \sum _{i=1}^k \ln \mu ^T_{[n]}(s^i_{[n]})$ is the log-likelihood (breaking ties arbitrarily). In words ML selects a phylogeny that maximizes the probability of observing the data. This method is known to be consistent, that is, the reconstructed phylogeny is guaranteed to converge on the true tree as k goes to $+\infty$. The previous best known bound on the sequence-length requirement of ML in this context is $k_0(\Psi ^{\mathrm {ML}},n) \le \exp (K n)$, for a constant K, as proved in [50].

Our first main result is that, for any constant $f,g, \frac{1}{\Upsilon }$, the ML sequence-length requirement $k_0(\Psi ^{\mathrm {ML}}, n)$ grows at most polynomially in n, where the degree of the polynomial depends on g. Such a bound had been previously established for other reconstruction methods, including certain types of distance-matrix methods [15], and it was a long-standing open problem to show that a polynomial bound holds for ML as well. Interestingly, our simple proof in fact uses the result of [15]. (The argument is detailed in Sect. 2.) Further, it is known that no method in general achieves a better bound (up to a constant in the degree of the polynomial) [34].

On the other hand, our second—significantly more challenging—result establishes a phase transition on the sequence-length requirement of ML. We show that when the maximum branch length of the true phylogeny is constrained to lie below a given threshold, an improved sequence-length requirement is achieved, namely that

$$\begin{aligned} k_0(\Psi ^{\mathrm {ML}}, n) = O(\log n),\quad \text { if }g < g^* := \ln \sqrt{2}. \end{aligned}$$

(1)

The same sequence-length requirement has been obtained previously for other methods [4, 10, 32, 35, 47], but as we mentioned above our result is the first one that concerns an important method in practice and greatly improves previous bound for ML. It is known further that a sub-logarithmic sequence-length requirement is not possible in general for any method [34]. That can be seen by the following back-of-the-envelope calculation: when $k = \Theta (\log n)$, the total number of datasets is $e^{\Theta (n\log n)}$, which is asymptotically of the same order as the number of phylogenies in $\mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$ (see, e.g., [51]); and, intuitively, we need at least as many datasets as we have possible phylogenies. Note that not all methods achieve the logarithmic sequence-length requirement in (1). The popular distance-matrix method Neighbor-Joining [49], for instance, has been shown to require exponential sequence lengths in general for any g [29].

The question of whether the threshold in (1) is tight, however, is not completely resolved and we do not address this issue here. The quantity $g^*$ corresponds to what is sometimes known as the Kesten-Stigum threshold [28], which is roughly speaking the threshold at which reconstructing the root state from a “weighted majority” of the leaf states becomes no better than guessing at random as the depth of the (binary) tree diverges. See, e.g., [14, 36] for some background on this problem. See also [27] for a different characterization of the threshold. For $r=2$, no root state inference method has a better threshold than weighted majority [25] and the bound in (1) is known to be tight [35]. In general, the question is not settled [33, 42, 48]. In the case $r=4$, the most relevant in the biological context, the threshold $g^*$ translates into a $22\%$ substitution probability along each edge. In general, many factors affect the maximum branch length of a phylogeny, including how densely sampled the species are and which genes (whose mutation rates vary widely) are used.

To understand the connection between root state reconstruction and phylogenetic reconstruction, a connection which was first articulated by Steel [56], note that the depth of the phylogeny plays a key role in phylogenetic reconstruction. That is because we only have access to the sequences at the leaves of the tree. When good estimates of internal sequences are available, the phylogeny is “shallower” and reconstructing the deeper parts of the tree is significantly easier, leading to a better sequence-length requirement for some methods. That the phase transition in root state reconstruction should translate into a phase transition in the sequence-length requirement of phylogenetic reconstruction, namely from logarithmic in n in the “reconstruction phase” to polynomial in n in the “non-reconstruction phase”, is known as Steel’s Conjecture [56]. It was first established rigorously by Mossel [35] in the case of balanced binary trees with $r=2$.

In [4, 10, 32, 35, 47], in order to achieve logarithmic sequence-length requirement in the Kesten-Stigum regime, new inference methods that explicitly estimate internal sequences were devised. In ML, by contrast, the internal sequences play a more implicit role in the definition of the likelihood and our analysis of ML proceeds in a very different manner. Our main technical contribution, which may be of independent interest, is a quantitative bound on the total variation distance between the leaf state distributions of two phylogenies as a function of a notion of combinatorial distance between them. In words, the more different are the trees, the more different are the data distributions at their leaves. We prove this new bound by constructing explicit tests that distinguish between the leaf distributions. For general trees, this turns out to present serious difficulties, as sketched in Sect. 2. The bound on the total variation distance in turn gives a bound on the probability that ML returns an incorrect tree and allows us to perform a union bound over all such trees.

It is worth pointing out that the reconstruction methods of [4, 10, 32, 35, 47] have the advantage of running in polynomial time, while computing the ML phylogeny is in the worst-case NP-hard [8, 45]. So why care about ML? Of course, worst-case computational complexity results are not necessarily relevant in practice as real data tend to be more structured. Actually, good heuristics for ML have been developed that have achieved considerable practical success in large-scale phylogenetic analyses and are now seen as the standard approach [53, 54]. A side consequence of our results is that, on randomly generated data of sufficient sequence length, using the methods of [4, 10, 32, 35, 47] we are in fact guaranteed to recover what happens to be the ML phylogeny with high probability in polynomial time. Although this is not per se an algorithmic result in that we do not directly solve the ML problem, it does show that computing the ML phylogeny is easier than previously thought in an average sense and may help explain the success of practical heuristics.

Although the discretization assumption above may not be needed, removing it in the logarithmic regime appears to present significant technical challenges. Note that this assumption is also needed for the results of [4, 10, 32, 47].

1.3 Further related work

There exists a large literature on the sequence-length requirement of phylogenetic reconstruction methods, stemming mainly from the seminal work of Erdös et al. [15] which were the first to highlight the key role of the depth in inferring phylogenies. Sequence-length requirement results—both upper and lower bounds—have been derived for more general models of sequence evolution [3, 9, 16, 34, 39], including models of insertions and deletions [2, 12], for partial or forest reconstruction [6, 11, 22, 37, 59], and for reconstructing mixtures of phylogenies [40, 41]. These results have in some cases also inspired successful practical heuristics [24].

The connection between root state reconstruction and phylogenetic reconstruction has also been studied in more general models of evolution where mutation probabilities are not necessarily symmetric [42, 46, 47]. A good starting point for the extensive literature on root state reconstruction is [36, 44].

Some bounds on the total variation distance between leaf distributions that are related to our techniques were previously obtained in the special case of pairs of random trees, which are essentially at maximum combinatorial distance [52]. Similar ideas were also used to reconstruct certain mixtures of phylogenies in [40].

The sample complexity of maximum likelihood when all internal vertices are also observed was studied in [58].

1.4 Organization

The paper is organized as follows. Basic definitions are provided in Sect. 2. In Sect. 2 we also state formally our main results and give a sketch of the proof. The probabilistic aspects of the proof are sketched in Sect. 3. The combinatorial aspects are illustrated first in a special case in Sect. 4. The general case is detailed in Sect. 5. A few useful lemmas can be found in the Appendix for ease of reference.

2 Definitions, results, and proof sketch

In this section, we introduce formal definitions and state our main results.

2.1 Basic definitions

2.1.1 Phylogenies

A phylogeny is a graphical representation of the speciation history of a collection of organisms. The leaves correspond to current species (i.e., those that are still living). Each branching indicates a speciation event. Moreover we associate to each edge a positive weight. As we will see below, this weight corresponds roughly to the amount of evolutionary change on the edge. More formally, we make the following definitions. See e.g. [51] for more background. Fix a set of leaf labels (or species names) $X = [n] = \{1,\ldots ,n\}$.

Definition 2.1

(Phylogeny) A weighted binary phylogenetic X-tree (or phylogeny for short) $T = (V,E;\phi ;w)$ is a tree with vertex set V, edge set E, leaf set L with $|L| = n$, edge weights $w: E \rightarrow (0,+\infty )$, and a bijective leaf-labeling $\phi : X \rightarrow L$ (that assigns “species names” to the leaves). We assume that the degree of all internal vertices $V-L$ is exactly 3. We let $\mathcal {T}_l[T] = (V,E;\phi )$ be the leaf-labelled topology of T. We denote by $\mathbb {T}_n$ the set of all leaf-labeled trees on n leaves with internal degrees 3 and we let $\mathbb {T}= \{\mathbb {T}_n\}_{n\ge 1}$. We say that two phylogenies are isomorphic if there is a graph isomorphism between them that preserves the edge weights and the leaf-labeling.

We restrict ourselves to the following setting introduced in [10].

Definition 2.2

(Regular phylogenies) Let $0< \frac{1}{\Upsilon }\le f \le g < +\infty$. We denote by $\mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$ the set of phylogenies $T = (V,E; \phi ;w)$ with n leaves such that $f \le w_e \le g$, $\forall e\in E$, where moreover $w_e$ is a multiple of $\frac{1}{\Upsilon }$. We also let $\mathbb {Y}_{f,g}[\frac{1}{\Upsilon }] = \bigcup _{n \ge 1} \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$. (We assume for simplicity that f and g are themselves multiples of $\frac{1}{\Upsilon }$.)

To illustrate our techniques, we also occasionally appeal to the special case of homogeneous phylogenies. For an integer $h \ge 0$ and $n = 2^h$, a homogeneous phylogeny is an h-level complete binary tree $T^{(h)}_{\phi ,w} = (V^{(h)}, E^{(h)}; \phi ; w)$ where the edge weight function $w$ is identically g and $\phi$ may be any one-to-one labeling of the leaves.

2.1.2 Substitution model

We use the following standard model of DNA sequence evolution. See e.g. [51] for generalizations. Fix some integer $r > 1$.

Definition 2.3

(r-State Symmetric Model of Substitution) Let $T = (V,E;\phi ;w)$ be a phylogeny and $\mathcal {R}= [r]$. Let $\pi = (1/r,\ldots , 1/r)$ be the uniform distribution on [r] and let $\delta _e = \frac{1}{r}\left( 1 - e^{-w_e}\right) .$ Consider the following stochastic process. Choose an arbitrary root $\rho \in V$. Denote by $E_\downarrow$ the set E directed away from the root. Pick a state for the root at random according to $\pi$. Moving away from the root toward the leaves, apply the following Markov transition matrix to each edge $e = (u,v)$ independently:

$$\begin{aligned} (M(e))_{ij} = (e^{w_e Q})_{ij} = \left\{ \begin{array}{ll} 1 -(r - 1) \delta _e &{}\quad \text{ if } i=j\\ \delta _e &{}\quad \text{ o.w. } \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} Q_{ij} = \left\{ \begin{array}{ll} -\frac{r - 1}{r} &{} \quad \text{ if } i=j\\ \frac{1}{r} &{}\quad \text{ o.w. } \end{array} \right. \end{aligned}$$

(Or equivalently run a continuous-time Markov jump process with rate matrix Q started at the state of u.) Denote the state so obtained by $s_V = (s_v)_{v\in V}$. In particular, $s_{L}$ is the state vector at the leaves, which we also denote by $s_X$. The joint distribution of $s_V$ is given by

$$\begin{aligned} \mu ^T_V(s_V) = \pi (s_\rho ) \prod _{e = (u,v) \in E_\downarrow } \left[ M(e)\right] _{s_{u} s_{v}}. \end{aligned}$$

For $W \subseteq V$, we denote by $\mu ^T_W$ the marginal of $\mu ^T_V$ at W. We denote by $\mathcal {D}[T]$ the probability distribution of $s_V$. (It can be shown that the choice of the root does not affect this distribution. See e.g. [55].) We also let $\mathcal {D}_l[T]$ denote the probability distribution of $s_X := \left( s_{\phi (a)}\right) _{a\in X}.$ More generally we take k independent samples $(s^{i}_{V})_{i=1}^k$ from the model above, that is, $s^1_V, \ldots ,s^k_V$ are i.i.d. $\mathcal {D}[T]$. We think of $(s_v^i)_{i=1}^k$ as the sequence at node $v \in V$. When considering many samples $(s^i_V)_{i=1}^k$, we drop the superscript to refer to a single sample $s_V$.

The case $r=4$, known as the Jukes–Cantor (JC) model [26], is the most natural choice in the biological context where, typically, $\mathcal {R}= \{\mathrm {A}, \mathrm {G},\mathrm {C},\mathrm {T}\}$ and the model describes how DNA sequences stochastically evolve by point mutations along an evolutionary tree under the assumption that each site in the sequences evolves independently and identically. For ease of presentation, we restrict ourselves to the case $r=2$, known as the Cavender-Farris-Neyman (CFN) model [5, 17, 43], but our techniques extend to a general r in a straightforward manner. The CFN model is equivalent to a ferromagnetic Ising model with a free boundary (see e.g. [14]). For now on, we fix $r=2$. We denote by $\mathbb {E}_T, \mathbb {P}_T$ the expectation and probability under the CFN model on a phylogeny T. We will also use a random cluster representation of the CFN model, which we recall in Lemma 3. It will be convenient to work on the state space $\{-1,+1\}$ rather than $\{1,2\}$. To avoid confusion, we introduce a separate notation. Let $\nu = (1,-1)$. Given samples $(s^i_X)_{i=1}^k$, we define $\varvec{\sigma }_X = (\sigma _X^i)_{i=1}^k$ with $\sigma _a^i = \nu _{s_a^i}$ for all a, i.

2.1.3 Phylogenetic reconstruction

In the phylogenetic tree reconstruction (PTR) problem, we are given a set of sequences $(\sigma ^i_X)_{i=1}^k$ and our goal is to recover the unknown generating tree. An important theoretical criterion in designing a PTR algorithm is the amount of data required for an accurate reconstruction. At a minimum, a reconstruction algorithm should be consistent, that is, the output should be guaranteed to converge on the true tree as the sequence length k goes to $+\infty$. Beyond consistency, the sequence-length requirement (SLR) of a PTR algorithm is the sequence length required for a guaranteed high-probability reconstruction. Formally:

Definition 2.4

(Phylogenetic Reconstruction Problem) A phylogenetic reconstruction algorithm is a collection of maps $\Psi = \{\Psi _{n,k}\}_{n,k \ge 1}$ from sequences $(\sigma ^i_{X})_{i=1}^k \in (\{-1,+1\}^{X})^k$ to leaf-labeled trees in $\mathbb {T}_n$, where $X = [n]$. Fix $\delta > 0$ (small) and let k(n) be an increasing function of n. We say that $\Psi$ solves the phylogenetic reconstruction problem on $\mathbb {Y}_{f,g}[\frac{1}{\Upsilon }]$ with sequence length $k = k(n)$ if for all $n \ge 1$, and all $T \in \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$,

$$\begin{aligned} \mathbb {P}\left[ \Psi _{n,k(n)}\left( \left( \sigma ^i_{X}\right) _{i=1}^{k(n)}\right) = \mathcal {T}_l[T]\right] \ge 1 - \delta , \end{aligned}$$

where $(\sigma ^i_{X})_{i=1}^{k(n)}$ are i.i.d. samples from $\mathcal {D}_l[T]$. We let $k_0(\Psi ,n)$ be the smallest function k(n) such that the above condition holds (for fixed $f, g, \frac{1}{\Upsilon }, \delta$).

We call the function $k_0(\Psi ,n)$ the sequence-length requirement (SLR) of $\Psi$. For simplicity we emphasize the dependence on n. Intuitively the larger the tree, the more data is required to reconstruct it. One can also consider the dependence of $k_0$ on other structural parameters. In the mathematical phylogenetic literature, the SLR has emerged as a key measure to compare the statistical performance of different reconstruction methods. A lower $k_0$ suggests a better statistical performance. Note that, ideally, one would like to compute the probability that a method succeeds given a certain amount of data, but that probability is a complex function of all parameters. Instead the SLR, which can be bounded analytically, is a proxy that measures how effective a method is at extracting phylogenetic signal from molecular data.

2.1.4 Maximum likelihood estimation

The maximum likelihood (ML) estimator for phylogenetic reconstruction is given (in our setting) by

$$\begin{aligned} \Psi ^{\mathrm {ML}}_{n,k}\left( \left( \sigma ^i_X\right) _{i=1}^k\right) \in \mathop {{{\mathrm{arg\,min}}}}\limits _{T \in \mathbb {Y}^{(n)}_{f,g}\left[ \frac{1}{\Upsilon }\right] } \mathscr {L}_T\left[ \left( \sigma ^i_X\right) _{i=1}^k\right] , \end{aligned}$$

(2)

where $\mathscr {L}_T[(\sigma ^i_X)_{i=1}^k] = - \sum _{i=1}^k \ln \mu ^T_{X}(\sigma ^i_{X})$ (breaking ties arbitrarily). In words the ML selects a phylogeny which maximizes the probability of observing the data. Computation of the likelihood on a given phylogeny can be performed efficiently, but solving the maximization problem above over tree space is computationally intractable [8, 45]. Fast heuristics have been developed and are widely used [21, 54]. Despite the practical importance of ML, much remains to be understood about its statistical properties. Consistency, that is, the convergence of the ML estimate $\hat{T}^{\mathrm {ML}}_k$ on the true tree as the number of sites $k \rightarrow \infty$, has been established [7]. But obtaining tight bounds on the SLR of ML has remained an outstanding open problem in mathematical phylogenetics. The best previous known bound, due to [50] was that under the CFN model there exists $K > 0$ such that $k_0(\Psi ^{\mathrm {ML}},n) \le \exp (K n)$.

2.2 Main results

Our main result is the following.

Theorem 1

(Sequence-length requirement of maximum likelihood) Let $0< \frac{1}{\Upsilon }< f < g^* := \ln \sqrt{2}$. Then the sequence-length requirement of maximum likelihood for the phylogenetic tree reconstruction problem on $\mathbb {Y}_{f,g}[\frac{1}{\Upsilon }]$ is

$$\begin{aligned} k_0(\Psi ^{\mathrm {ML}}, n) = {\left\{ \begin{array}{ll} O(\log n), &{} \text {if }\,g < g^*,\\ \mathrm {poly}(n), &{} \text {if }\,g \ge g^*. \end{array}\right. } \end{aligned}$$

Combined with the results of [10], this bound implies that the ML estimator can be computed in polynomial time with high probability as long as $k \ge k_0(\Psi ^{\mathrm {ML}},n)$. Note that our definition of the ML estimator implicitly assumes that we know (or have bounds on) the parameters $f,g,\frac{1}{\Upsilon }$ as the search is restricted over the space $\mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$. In practice it is not unnatural to restrict the space of possible models in this way. We note finally that our proof in the regime $g \ge g^*$ holds under a much weaker discretization assumption (see below).

2.3 Proof overview

2.3.1 Known results: identifiability, consistency and the Steel-Székely bound

Before sketching the proof of Theorem 1, we first mention previously known facts about the statistical properties of ML in phylogenetics. Fix $f,g,\frac{1}{\Upsilon }, n$ and let $\mathbb {Y}= \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$. Let $T^0 \in \mathbb {Y}$ be the generating phylogeny and denote by $\varvec{\sigma }_X = (\sigma _X^i)_{i=1}^k$ a set of k samples from the corresponding CFN model. Under our assumptions, the model is known to be identifiable [7], that is,

$$\begin{aligned} T^0 \ne T^\# \in \mathbb {Y}\implies \mathcal {D}_l[T^0] \ne \mathcal {D}_l[T^\#]. \end{aligned}$$

Moreover the ML estimator is known to converge on $T^0$ almost surely as $k \rightarrow \infty$ [7]. That fact follows from the law of large numbers by which

$$\begin{aligned} \frac{1}{k}\mathscr {L}_{T^\#}(\varvec{\sigma }_X) \rightarrow -\mathbb {E}_{T^0}\left[ \ln \mu ^{T^\#}_X(\sigma _X)\right] , \end{aligned}$$

as $k \rightarrow \infty$, identifiability, the positivity of the Kullback-Leibler (KL) divergence, that is,

$$\begin{aligned} T^0 \ne T^\# \implies \mathrm {KL}(T^0\,\Vert \,T^\#) := -\mathbb {E}_{T^0}\left[ \ln \mu ^{T^\#}_X(\sigma _X)\right] + \mathbb {E}_{T^0}\left[ \ln \mu ^{T^0}_X(\sigma _X)\right] > 0, \end{aligned}$$

and a compactness argument [60].

Steel and Székely [50] also derived along the same lines a quantitative upper bound on the SLR. They used Pinsker’s inequality to lower bound the KL divergence with the total variation distance. And they appealed to concentration inequalities to bound the probability that any leaf vector state frequency is away from its expectation, thereby quantifying the speed of convergence of the log-likelihood. The argument ends up depending inversely on the lowest non-zero state probability, which is exponentially small in n, leading to an exponential SLR. The Steel-Székely bound does not make use of the structure of the phylogenetic problem and, in fact, is derived in a more general setting.

2.3.2 A polynomial bound

In order to make use of the structure of the problem, we propose a different approach. The basic idea is to design for each incorrect tree $T^\#$ a statistical test that excludes it from being selected by ML with high probability. We first illustrate this idea by sketching a polynomial bound on the SLR of ML. This proves the polynomial regime of Theorem 1.

In [15], a reconstruction algorithm was provided that, for any g, returns the correct phylogeny with probability $1 - \exp (-n^{C_1})$ as long as $k \ge n^{C_2}$ for a large enough $C_2 > 0$. We refer to this algorithm as the ESSW algorithm. Letting $T^0$ be the true phylogeny generating the data and $T^\# \ne T^0$ be in $\mathbb {Y}$, denote by $D_{T^\#}$ the event that the ESSW algorithm reconstructs (incorrectly) $T^\#$ and by $M_{T^\#}$ the event that ML prefers $T^\#$ over $T^0$ (including a tie), that is, the set of $\varvec{\sigma }_X = (\sigma ^{i}_X)_{i=1}^k$ such that $\mathscr {L}_{T^\#}(\varvec{\sigma }_X) \le \mathscr {L}_{T^0}(\varvec{\sigma }_X)$ or equivalently

$$\begin{aligned} \frac{\mu ^{T^\#}_X(\varvec{\sigma }_X)}{\mu ^{T^0}_X(\varvec{\sigma }_X)} \ge 1. \end{aligned}$$

(3)

Then, a classical result in hypothesis testing (see e.g. [31, Chapter 13]) is that the sum of Type-I and Type-II errors is minimized by the likelihood ratio test, which in our context amounts to

$$\begin{aligned} \mathbb {P}_{T^0}[M_{T^\#}] + \mathbb {P}_{T^\#}[M_{T^\#}^c] \le \mathbb {P}_{T^0}[A] + \mathbb {P}_{T^\#}[A^c], \end{aligned}$$

(4)

for any test (i.e., event) $A \subseteq [r]^{nk}$. Taking in particular $A = D_{T^\#}$, we get from [15] that

$$\begin{aligned} \mathbb {P}_{T^0}[M_{T^\#}] \le \mathbb {P}_{T^0}[D_{T^\#}] + \mathbb {P}_{T^\#}[D_{T^\#}^c] \le 2 e^{-n^{C_1}}, \end{aligned}$$

(5)

whenever $k \ge n^{C_2}$. Recall (e.g. [51]) that the number of binary trees on n labeled leaves is $(2n - 5)!! = e^{O(n \log n)}.$ For each such tree, our discretization assumption implies that there are at most $((g-f)\frac{1}{\Upsilon }+ 1)^n$ choices of branch lengths. Hence, provided we choose $C_1$ and $C_2$ large enough and taking a union bound over the $e^{O(n \log n)}$ possible trees $T^\# \ne T^0$ in $\mathbb {Y}$, we obtain: under our assumptions, there exists $K > 0$ such that $k_0(\Psi ^{\mathrm {ML}},n) \le n^K$. In fact, note that this argument still works when the discretization $\frac{1}{\Upsilon }$ is of order $n^{-C_3}$ for any $C_3 > 0$.

This new bound on $k_0(\Psi ^{\mathrm {ML}},n)$ improves significantly over the Steel-Székely bound. It has interesting computational implications as well. Although ML for phylogenetic reconstruction is NP-hard [8, 45], our polynomial SLR bound in combination with the computationally efficient ESSW algorithm indicates that the ML estimator can be computed efficiently with high probability when data is generated from a CFN model with polynomial sequence lengths.

2.3.3 A refined union bound

Dealing with logarithmic-length sequences is significantly more challenging. As the argument below suggests, certain close-by trees cannot be distinguished using logarithmic-length sequences with exponentially small failure probability. In particular the naive union bound above cannot work in this regime. Instead we use a more refined union bound.

We make two observations. We introduce $\Delta _{\mathrm {BL}}(T^\#,T^0)$, the blow-up distance between the topologies of $T^\#$ and $T^0$, that is, roughly the smallest number of edges that need to be rearranged to produce $T^\#$ from $T^0$ (See Definition 5.1 for a formal definition). The number of trees at blow-up distance D from $T^0$ is at most $O(n^{2D})$ so that it suffices to prove

$$\begin{aligned} \mathbb {P}_{T^0}[M_{T^\#}] \le C_1 e^{-C_2 k \Delta _{\mathrm {BL}}(T^\#,T^0)}, \end{aligned}$$

(6)

in order to apply a union bound over blow-up distances, when k is logarithmic in n. To prove (6), we need to use an appropriate test $A \subseteq [r]^{nk}$ in (4) and (5)—as we did before—but now the error probability of the test must depend on the blow-up distance between $T^\#$ and $T^0$. That is, we need a test $A \subseteq [r]^{nk}$ such that

$$\begin{aligned} \mathbb {P}_{T^0}[A^c] + \mathbb {P}_{T^\#}[A] \le C_1 e^{-C_2 k \Delta _{\mathrm {BL}}(T^\#,T^0)}. \end{aligned}$$

(7)

This is intuitively reasonable as we expect similar trees to be harder to distinguish.

We note in passing that (4) follows from the fact that the likelihood ratio test achieves the total variation distance between the models generated by $T^\#$ and $T^0$ under k samples, which we denote by $\Delta _{\mathrm {TV}}^k(T^\#,T^0)$. Thus, our main technical contribution can be interpreted as relating combinatorial and variational distances between trees. This claim, which may be of independent interest, is proved along with Theorem 3.

Lemma 1

(Relating combinatorial and variational distances) For $T^\#, T^0 \in \mathbb {Y}_{f,g}[\frac{1}{\Upsilon }]$ with $g < g^*$,

$$\begin{aligned} \Delta _{\mathrm {TV}}^k(T^\#,T^0) \ge 1 - C_1 e^{-C_2 k \Delta _{\mathrm {BL}}(T^\#,T^0)}. \end{aligned}$$

2.3.4 Phase transition: homogeneous case

We sketch our construction of the test A above in the special case of homogeneous trees. Fix $g, n = 2^h$ and let $\mathbb {HY}= \mathbb {HY}^{(h)}_{g}$. Let $T^0 \in \mathbb {HY}$ be the generating phylogeny and denote by $\varvec{\sigma }_X = (\sigma ^i_X)_{i=1}^k$ a set of k samples from the corresponding CFN model. In the homogeneous case, it will be more convenient to work with we call the swap distance $\Delta _{\mathrm {SW}}(T^\#,T^0)$, which is defined, roughly, as the smallest number of same-level swaps of subtrees of $T^\#$ in order to obtain $T^0$ (See Sect. 4 for a formal definition.).

Recall that a cherry is a pair of leaves with a common immediate ancestor. A result of [40] shows that if $T^\#$ is obtained from $T^0$ by applying a uniformly random permutation of the leaf labels of $T^0$ then, with high probability, there is a positive fraction (independent of n) of the cherries in $T^0$ such that the corresponding leaves in $T^\#$ are far (at least a large constant graph distance away) from each other. Let $\mathcal {C}$ be such a collection of cherries. As a result, it was shown that the total pairwise correlation over $\mathcal {C}$ as measured for instance by

$$\begin{aligned} \mathcal {Z}^i = \frac{1}{n}\sum _{(a,b) \in \mathcal {C}} \sigma _a^i \sigma _b^i, \end{aligned}$$

is concentrated on two well-separated values under $T^0$ and $T^\#$, and the event

$$\begin{aligned} A = \left\{ \frac{1}{k} \sum _{i = 1}^k \mathcal {Z}^i > z\right\} , \end{aligned}$$

for a well-chosen value of z, satisfies an exponential bound as in (7).

Returning to our context this argument suggests that, if the incorrect tree $T^\#$ is far from the generating tree $T^0$ in swap distance, a powerful enough test can be constructed from the cherries of $T^0$. One of our main contributions is to show how to generalize this idea to trees at an arbitrary combinatorial distance. This is non-trivial because $T^\#$ and $T^0$ may only differ by deep swap moves, in which case cherries cannot be used in distinguishing tests. Instead, we show how to find deep pairs of test nodes that are close under $T^0$, but somewhat far under $T^\#$ (see Proposition 2). To build a corresponding test, we reconstruct the ancestral states at the test nodes and estimate the correlation between the reconstructed values as above (see Proposition 1). Note that the reconstruction phase transition plays a critical role in this argument.

The main challenge is to find such deep test pairs and relate their number to the swap distance. For this purpose, we design a procedure that identifies dense subtrees that are shared by $T^\#$ and $T^0$, working recursively from the leaves up (see Claim 4.4) and we prove that this procedure leads to a number of tests that grows linearly in the swap distance (see Claim 4.3). A further issue is to guarantee enough independence between the tests, which we accomplish via a sparsification step (see Claim 4.5). The full argument for homogeneous trees is in Sect. 4.

2.3.5 General case

In the homogeneous case, we produce a sufficient number of deep test pairs by identifying subtrees that are matching in $T^\#$ and $T^0$. As we mentioned above, that can be done recursively starting from the leaves. In the case of general trees, the lack of symmetry makes this task considerably more challenging. One significant new issue that arises is that the matching subtrees found through the same type of procedure may in fact “overlap” in $T^\#$, that is, have a non-trivial intersection.

Hence, to construct a linear number of tests in blow-up distance, we proceed in two phases. We first attempt to identify matching subtrees similarly to the homogeneous case. We show that if the overlap produced is small, then a linear number of tests (see Claim 5.4) can be constructed in a manner similar to the homogeneous case (see Proposition 4), although several new difficulties arise. See Sect. 5.5 for details.

On the other hand, if the overlap in $T^\#$ is too large, then the first phase will fail. In that case, we show that a sufficient number of deep test pairs can be found around the “boundary of the overlap” in $T^\#$ (see Proposition 5). That construction is detailed in Sect. 5.6.

3 Distinguishing between leaf distributions

In this section, we detail our main tool for distinguishing between the leaf distributions of different phylogenies. Fix $f,g < g^*,\frac{1}{\Upsilon }, n$ and let $\mathbb {Y}= \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$. Let $T^0 \in \mathbb {Y}$ be the generating phylogeny and denote by $\varvec{\sigma }_X = (\sigma ^i_X)_{i=1}^k$ a set of k i.i.d. samples from the corresponding CFN model.

As outlined in Sect. 2.3, our strategy is to construct for each erroneous tree $T^\#\ne T^0$ a statistical test that distinguishes between the two leaf distributions. The classification error of the test will ultimately depend on the combinatorial distance between $T^\#$ and $T^0$. We show in Sects 4 (for homogeneous trees) and 5 (for general trees) how to construct such tests. Here we define formally the type of test we seek to use and derive bounds on their classification error.

3.1 Definitions

We first need several definitions. Let $T = (V,E;\phi ;w)$ be a phylogeny in $\mathbb {Y}$ and denote its leaf set by L. Recall from Definition 2.1 that $X = [n]$ is the set of leaf labels. We will work with a special type of subtrees defined as follows.

Definition 3.1

(Restricted subtree) A (connected) subtree Y of T is restricted if there exists $V_R \subseteq V$ such that Y is obtained by keeping only those edges of T lying on the path between two vertices in $V_R$. We typically restrict T to a subset of the leaves (in which case we denote $V_R$ by $L_R$ instead). When $|V_R| = 4$, Y is called a quartet. The topology of a binary quartet on $V_R = \{u,v,x,y\}$ is characterized by the pairs in $V_R$ lying on each side of the internal edge, e.g., we write uv|xy if $\{u,v\}$ and $\{x,y\}$ are on opposite sides. Let Y and Z be restricted subtrees of T. We let $Y\cap Z$ (respectively $Y \cup Z$) be the intersection (respectively the union) of the edge sets of Y and Z.

We will need to compare restricted subtrees in $T^\#$ and $T^0$. For this purpose, we will use the following metric-based definition. We first recall the notion of a tree metric.

Definition 3.2

(Tree metric) A phylogeny $T = (V,E;\phi ;w)$ is naturally equipped with a tree metric $\mathrm {d}_T : X\times X \rightarrow (0,+\infty )$ defined as follows

$$\begin{aligned} \forall a,b \in X,\ \mathrm {d}_T(a,b) = \sum _{e\in \mathrm {P}_T(\phi (a),\phi (b))} w_e, \end{aligned}$$

where $\mathrm {P}_T(u,v)$ is the set of edges on the path between u and v in T. We will refer to $\mathrm {d}_T(a,b)$ as the evolutionary distance between a and b. In a slight abuse of notation, we also sometimes use $\mathrm {d}_T(u,v)$ to denote the evolutionary distance between any two vertices u, v of T as defined above. We will also let $\mathrm {d}^{\mathrm {g}}_T(a,b)$ denote the graph distance between a and b in T, that is, the number of edges on the path between a and b in T.

Tree metrics satisfy the following four-point condition: $\forall a_1,a_2,a_3,a_4 \in X$,

$$\begin{aligned} \mathrm {d}_T(a_1,a_2) + \mathrm {d}_T(a_3,a_4) \le \max \{ \mathrm {d}_T(a_1,a_3) + \mathrm {d}_T(a_2,a_4), \mathrm {d}_T(a_1,a_4) + \mathrm {d}_T(a_3,a_2) \}. \end{aligned}$$

(8)

In the non-degenerate case, one of the three sums above is strictly smaller than the other two, which are equal. From the four-point condition, it can be shown that to each tree metric corresponds a unique phylogeny (with positive edge weights). See e.g. [51].

Definition 3.3

(Matching subtrees) Let $T = (V,E;\phi ;w)$ and $T'= (V',E';\phi ';w')$ be trees in $\mathbb {Y}$ with n leaves L and $L'$ respectively (and the same leaf label set $X = [n]$). Let Y and $Y'$ be subtrees of T and $T'$ restricted respectively to leaf sets $L_R \subseteq L$ and $L_R' \subseteq L'$ spanning the same leaf labels, that is, $\phi (L_R) = \phi (L_R')$. We say that Y and $Y'$ are metric-matching or simply matching if: the tree metrics corresponding to Y and $Y'$ are identical. Note that, even if Y and $Y'$ are metric-matching, their vertex and edge sets may differ. E.g., an edge in Y may correspond to a (non-trivial) path in $Y'$, and vice versa. However, thinking of Y and $Y'$ as continuous objects, for each vertex $v \in Y$, we can create a corresponding extra vertex $v'$ in $Y'$.

As we mentioned above, we will assign a distinguished vertex to each subtree included in the tests. We think of these as roots. The following definitions apply to such rooted subtrees.

Definition 3.4

(Dense subtree) Let $\ell$ and $\wp \le 2^{\ell }$ be nonnegative integers. Let Y be a restricted subtree of T rooted at y. The $\ell$-completion $\lfloor Y\rfloor _\ell$ of Y is obtained by adding complete binary subtrees with 0-length edges below the leaves of Y so that all leaves in $\lfloor Y\rfloor _\ell$ are at the same graph distance from y and the height of $\lfloor Y\rfloor _\ell$ is the smallest multiple of $\ell$ greater than the height of Y. We say that Y is $(\ell ,\wp )$-dense in T if: the number of vertices on the $(i\ell )$-th level of $\lfloor Y\rfloor _\ell$ is at least $(2^{\ell } - \wp )^i$ for all $i \ge 0$ such that $i\ell$ is smaller than the height of $\lfloor Y\rfloor _\ell$.

Definition 3.5

(Co-hanging subtrees) Two rooted restricted subtrees Y and Z of a tree T with empty (edge) intersection are co-hanging if the path between their roots does not intersect the edges in their union. The linkage $Y \oplus Z$ of co-hanging rooted restricted subtrees Y and Z is the (unrooted) restricted subtree obtained by adding to Y and Z the path joining their roots.

We need one last definition.

Definition 3.6

(Topped subtree) Let T be rooted. Let $\gamma \in \mathbb {N}$ and Y be a restricted subtree of T rooted at y. The $\gamma$-topping $\lceil Y \rceil ^\gamma$ of Y is obtained from Y by adding the $\gamma$ edges immediately above y on the path to the root of T (or the entire path if it is has fewer than $\gamma$ edges), which we refer to as the hat of $\lceil Y \rceil ^\gamma$.

3.2 Batteries

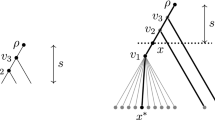
In the proof below, we will compare the true phylogeny $T^0 = (V^0,E^0;\phi ^0;w^0)$ to an incorrect phylogeny, which will be denoted by $T^\# = (V^\#,E^\#;\phi ^\#;w^\#)$. Assume that $T^0$ and $T^\#$ are rooted at $\rho ^0$ and $\rho ^\#$ respectively. The comparison will be based on the following combinatorial definition and the associated statistical test below. A test pair in $T^0$ is a pair of vertices (leaf or internal; possibly extra) $(y^0, z^0)$ in $T^0$, which we will refer to as test roots, as well as a pair of restricted subtrees $(Y^0, Z^0)$ of $T^0$ rooted at $y^0$, $z^0$ respectively, which we will refer to as test subtrees. Similarly we define a test pair in $T^\#$. We call a test panel two corresponding test pairs in $T^0$ and $T^\#$. See Fig. 1 for an illustration.

Fig. 1

A test panel: proximal in $T^0$ and non-proximal in $T^\#$

At a high level, the idea behind our distinguishing statistic is to consider pairs of subtrees, the test pairs, that are shared between $T^\#$ and $T^0$ in the sense of Definition 3.3 (Condition 2(a) below) and that further have the property that the distance between their roots differ in $T^\#$ and $T^0$ (Condition 2(d) below). The test itself (defined formally in Eqs. (12), (13) and (14) below) involves reconstructing the ancestral states at the roots of the pairs and comparing their correlation on $T^\#$ and $T^0$. To ensure a strong enough signal, we require that the subtrees are dense enough in the sense Definition 3.4 (Condition 1(a) below) to guarantee accurate reconstruction of ancestral states and that the roots are close (within a parameter $\Gamma$) in either $T^0$ or $T^\#$ (Condition 2(c) below). Although each test panel contains at least one pair whose roots are close, the other pair may not be—potentially producing unwanted dependencies between the test panels in cases where the roots are particularly far from each other (at distance at least $\gamma _t$). Such dependencies are dealt with in Proposition 1 below. Another requirement of the test is that the paths connecting the roots of each pair do not intersect the corresponding subtrees, in the sense of Definition 3.5 (Condition 2(b) below). That last property ensures that the errors of the ancestral state estimates are conditionally independent given the root states.

Definition 3.7

(Battery of Tests) Fix nonnegative integers $\ell \ge 2$, $0 \le \wp \le 2^\ell - 1$, $\Gamma \ge 1$ and $\gamma _t \ge 1$. We say that a collection of test panels

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I \text { in }T^0\quad \text {and }\quad \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I \text { in }T^\# \end{aligned}$$

form an $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery if:

• 1. Cluster requirements

  • (a) (Dense subtrees) All test subtrees are $(\ell ,\wp )$-dense.

• 2. Pair requirements

  • (a) (Matching subtrees) The subtrees $Y^0_i$ and $Y^\#_i$ are matching for all $i = 1, \ldots , I$, and similarly for $Z^0_i$ and $Z^\#_i$.

  • (b) (Co-hanging) For $i=1,\ldots ,I$, we require that $Y^0_i$ and $Z^0_i$ be co-hanging. Similarly for the pairs in $T^\#$.

  • (c) (Proximity) For $i=1,\ldots ,I$, if the graph distance between $y^0_i$ and $z^0_i$ is less than $\Gamma$, we say that the corresponding pair is proximal. (If $y^0_i$ or $z^0_i$ is an extra vertex we use the graph distance in $T^0$ to the closest neighbor.) Else, if the graph distance between $y^0_i$ and $z^0_i$ is less than $\gamma _t$, we say that the corresponding pair is semi-proximal. In both proximal and semi-proximal cases, we let

    $$\begin{aligned} \mathcal {F}^0_i = Y^0_i \oplus Z^0_i. \end{aligned}$$

    (9)

    Else, if the graph distance between $y^0_i$ and $z^0_i$ is greater than $\gamma _t$, in which case we say that the corresponding pair is non-proximal, we define (with a slight abuse of notation)

    $$\begin{aligned} \mathcal {F}^0_i = \left\lceil Y^0_i \right\rceil ^{\gamma _t} \cup \left\lceil Z^0_i \right\rceil ^{\gamma _t}, \end{aligned}$$

    (10)

    to be the forest with corresponding edge set. We refer to the path between $y^0_i$ and $z^0_i$ in $T^0$ as the connecting path of the test pair. (In the non-proximal case, the hats of $Y^0_i$ and $Z^0_i$ may not lie entirely on the connecting path.) We similarly define $\mathcal {F}_i^\#$s from the pairs in $T^\#$.

  • (d) (Evolutionary distance) For each $i = 1, \ldots , I$, we have

    $$\begin{aligned} \left| \mathrm {d}_{T^0}\left( y^0_i,z^0_i\right) - \mathrm {d}_{T^\#}\left( y^\#_i,z^\#_i\right) \right| \ge \frac{1}{\Upsilon }, \end{aligned}$$

    and at least one of the corresponding pairs is proximal. Further, we let

    $$\begin{aligned} \alpha _i = {\left\{ \begin{array}{ll} +1, &{} if~\mathrm {d}_{T^0}\left( y^0_i,z^0_i\right) < \mathrm {d}_{T^\#} \left( y^\#_i,z^\#_i\right) \\ -1, &{} o.w. \end{array}\right. } \end{aligned}$$

    (11)

• 3. Global requirements

  • (a) (Global intersection) The $\mathcal {F}^0_i$s have empty pairwise intersection. Similarly for the $\mathcal {F}^\#_i$s.

3.2.1 Tests

For a restricted subtree Y rooted at y, we denote by X[Y] the leaf labels of Y and we let

$$\begin{aligned} \hat{\sigma }_y^j = {\left\{ \begin{array}{ll} +1, &{} \text {if }\mathbb {P}_Y\left[ \sigma _y = +1\,\Big |\,\sigma _{X[Y]}^j\right] > \mathbb {P}_Y\left[ \sigma _y = -1\,\Big |\,\sigma _{X[Y]}^j\right] ,\\ -1, &{} \text {o.w.} \end{array}\right. } \end{aligned}$$

(12)

be the MLE of the state at y on site j, given $\sigma _{X[Y]}^j$. Let

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I \text { in }T^0\text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I \text { in }T^\# \end{aligned}$$

form a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery with corresponding $\alpha _i$s (as defined in (11)). The distinguishing statistics of the battery are defined as

$$\begin{aligned} \widehat{\mathcal {D}}^0 = \sum _{i=1}^I \sum _{j=1}^k \alpha _i\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}, \quad \text {and} \quad \widehat{\mathcal {D}}^\# = \sum _{i=1}^I \sum _{j=1}^k \alpha _i\hat{\sigma }^j_{y^\#_i}\hat{\sigma }^j_{z^\#_i}. \end{aligned}$$

(13)

We observe that, because the subtrees in $T^0$ and $T^\#$ are matching (that is, they are identical as sub-phylogenies as remarked after Definition 3.2), $\widehat{\mathcal {D}}^0$ and $\widehat{\mathcal {D}}^\#$ are in fact identical as a function of the leaf states, which we denote by $\widehat{\mathcal {D}}$. However their distributions, in particular their means $\mathcal {D}^0 = \mathbb {E}_{T^0}[\widehat{\mathcal {D}}]$ and $\mathcal {D}^\# = \mathbb {E}_{T^\#}[\widehat{\mathcal {D}}]$ respectively, differ as we quantify below. The distinguishing event is then defined as

$$\begin{aligned} A = \left\{ \widehat{\mathcal {D}}- \frac{\mathcal {D}^0 + \mathcal {D}^\#}{2} > 0 \right\} . \end{aligned}$$

(14)

3.2.2 Properties of batteries

We show that the distinguishing event A is likely to occur under $T^0$, but unlikely to occur under $T^\#$. The proof is in the next section.

Proposition 1

(Batteries are distinguishing) For any positive integers $\wp$ and $\Gamma$, there exist constants $\ell = \ell (g,\wp ) \ge 2$ large enough, $\gamma _t = \gamma _t(g, \wp , \ell , \Gamma , \Upsilon )$ large enough, and $C = C(g, \wp , \ell , \Gamma , \Upsilon , \gamma _t) > 0$ small enough such that the following holds. If

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I \text { in }T^0\text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I \text { in }T^\#, \end{aligned}$$

form a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery with corresponding $\alpha _i$s, $\widehat{\mathcal {D}}$, $\mathcal {D}^0$, $\mathcal {D}^\#$, and A, then

$$\begin{aligned} \max \left\{ \mathbb {P}_{T^0}[A^c], \mathbb {P}_{T^\#}[A] \right\} \le \exp \left( - C k I \right) , \end{aligned}$$

for all I and k.

3.3 Proof of Proposition 1

We give a proof of Proposition 1. The proof has several steps:

• 1. We bound the accuracy of the ancestral state estimator (12) using Lemma 2 from Appendix A.1.

Claim 3.1

(Accuracy of ancestral reconstruction) There is $\ell \ge 2$ large enough and a constant $0< \beta _{g,\wp } < +\infty$ depending on g and $\wp$ such that for any subtree Y in the battery, it holds that

$$\begin{aligned} \mathbb {P}_Y[\hat{\sigma }_y = \sigma _y] \ge \frac{1 + e^{-\beta _{g,\wp }}}{2}, \end{aligned}$$

(15)

where y is the root of Y.

Crucially $\beta _{g,\wp }$ does not depend on n, that is, the accuracy of the reconstruction does not deteriorate as one considers larger, deeper trees.

• 2. We show that the distinguishing statistics (13) have well-separated expectations. That follows from the fact that, by the assumption 2(d) in Definition 3.7, the evolutionary distances between the roots of the corresponding subtrees differ on $T^\#$ and $T^0$. The accuracy of the ancestral state estimation in Claim 3.1 also guarantees that the signal is strong enough at the leaves.

Claim 3.2

(Separation of expectations) There exists $\mathcal {D}_\delta > 0$ depending on g, $\wp$, $\Gamma$ and $\Upsilon$ such that

$$\begin{aligned} \mathcal {D}^0 - \mathcal {D}^\# \ge \mathcal {D}_\delta k I. \end{aligned}$$

(16)

• 3. Finally, in the more delicate step of the argument, we establish that the distinguishing statistics (13) are concentrated around their respective means.

Claim 3.3

(Concentration) There is $\gamma _t >0$ large enough and $C > 0$ small enough such that

$$\begin{aligned} \max \left\{ \mathbb {P}_{T^0}[A^c], \mathbb {P}_{T^\#}[A] \right\} \le \exp \left( - C k I \right) , \end{aligned}$$

for all I and k, where A is defined in (14).

Proving concentration is complicated by the fact that the terms in the sums (13) are not independent. That is the result of the non-proximal pairs having connecting paths that may intersect with other test subtrees. When the number of non-proximal pairs is not small, we show that the corresponding terms are “almost independent” of the other terms by bounding the probability that their hat is closed. A related argument is used in [40].

Proof of Proposition 1

Proposition 1 follows immediately from Claim 3.3.

It remains to prove the claims.

Proof of Claim 3.1 (Accuracy of ancestral reconstruction)

Let Y be any subtree in the battery and let y be its root. To obtain a bound on the probability of erroneous ancestral reconstruction through Lemma 2 (Appendix A.1), it suffices to bound the denominator in (61) for the $\ell$-completion $\lfloor Y \rfloor _\ell$. Choose a unit flow $\Psi$ such that the flow through each vertex on level $i\ell$ of $\lfloor Y \rfloor _\ell$ splits evenly among its descendant vertices on level $(i+1)\ell$. Let $\mathcal {E}(\lfloor Y \rfloor _\ell )$ denote the edges of $\lfloor Y \rfloor _\ell$ and let $R_y(e) = \left( 1 - \theta _e^2\right) \Theta _{y,x}^{-2}$ where $\Theta _{\rho ,y} = e^{-\mathrm {d}_T(y,x)}$ and $\theta _e = e^{-w_e}$ (as defined in (60) of Appendix A.1). Note that $0 \le \left( 1 - \theta _e^2\right) \le 1$. Hence we have

$$\begin{aligned} \sum _{e = (x',x) \in \mathcal {E}(\lfloor Y \rfloor _\ell )} R_y(e) \Psi (e)^2\le & {} \sum _{e = (x',x) \in \mathcal {E}(\lfloor Y \rfloor _\ell )} \Theta _{y,x}^{-2} \Psi (e)^2\\\le & {} \sum _{i=0}^{+\infty } \sum _{j=1}^\ell 2^{i\ell + j} \left( e^{- (\ell i + j) g}\right) ^{-2} \\&\times \left( \frac{1}{(2^\ell - \wp )^i \max \{1,2^{\ell -j} -\wp \}}\right) ^2\\\le & {} \sum _{i=0}^{+\infty } 2^{i\ell } e^{2 \ell i g} \left( \frac{1}{(2^\ell - \wp )^i}\right) ^2\\&\times \left[ \sum _{j=1}^\ell 2^{j} e^{2 j g} \left( \frac{1}{\max \{1,2^{\ell -j} -\wp \}}\right) ^2\right] , \end{aligned}$$

where, in the second inequality, the quantity $\max \{1,2^{\ell -j} -\wp \}$ is a lower bound on the number of descendants on level $(i+1)\ell$ of a vertex at graph distance j below level $i\ell$. The term in square bracket on the last line is bounded by a positive constant $0< K_{\ell ,\wp ,g} < +\infty$ depending only on $\ell ,\wp ,g$. Recall that $g < g^* = \ln \sqrt{2}$ and let $g' = \frac{g^* + g}{2}$. Choose $\ell$ large enough (depending only on g and $\wp$) such that

$$\begin{aligned} \frac{2^{\ell }}{(2^\ell - \wp )^{2}} \le \frac{1}{e^{2 \ell g'}}, \end{aligned}$$

which is possible because $g' < g^*$ and $e^{2 g^*} = 2$. Then

$$\begin{aligned} \sum _{e = (x',x) \in \mathcal {E}(\lfloor Y \rfloor _\ell )} R_y(e) \Psi (e)^2\le & {} K_{\ell ,\wp ,g} \sum _{i=0}^{+\infty } e^{2\ell i(g - g')}\\= & {} \frac{K_{\ell ,\wp ,g}}{1 - e^{-2\ell (g' - g)}}\\= & {} \frac{K_{\ell ,\wp ,g}}{1 - e^{-\ell (g^* - g)}} < +\infty . \end{aligned}$$

Hence by Lemma 2 (Appendix A.1) the probability of correct ancestral reconstruction is bounded away from 1 / 2 from below. Let $\beta _{g,\wp }$, depending on g and $\wp$ (and implicitly on $\ell$), such that

$$\begin{aligned} \mathbb {P}_Y[\hat{\sigma }_y = \sigma _y] =: \frac{1 + e^{-\beta _Y}}{2} \ge \frac{1 + e^{-\beta _{g,\wp }}}{2}, \end{aligned}$$

(17)

where the first equality is a definition.

Proof of Claim 3.2 (Separation of expectations)

Let ((y, z); (Y, Z)) be a test pair in the battery with corresponding tree T (equal to either $T^0$ or $T^\#$). Then, by the co-hanging requirement of the battery, the Markov property, and (15), we have

$$\begin{aligned} -\ln \mathbb {E}_T[\hat{\sigma }_{y}\hat{\sigma }_{z}]= & {} -\ln \left[ \mathbb {E}_T[\mathbb {E}_T[\hat{\sigma }_{y}\hat{\sigma }_{z} \,|\,\sigma _y,\sigma _z]] \right] \nonumber \\= & {} -\ln \left[ \mathbb {E}_T[\mathbb {E}_T[\hat{\sigma }_{y}\,|\,\sigma _y]\mathbb {E}_T[\hat{\sigma }_{z} \,|\,\sigma _z]] \right] \nonumber \\= & {} -\ln \left[ \mathbb {E}_T[e^{-\beta _Y}\sigma _y e^{-\beta _Z}\sigma _{z}] \right] \nonumber \\= & {} \beta _Y + \beta _Z + \mathrm {d}_T(y,z), \end{aligned}$$

(18)

where $\beta _Y, \beta _Z \le \beta _{g,\wp }$, as defined in (17). The last equality follows from

$$\begin{aligned} \mathbb {E}_T[\sigma _{y}\sigma _{z}]= & {} \mathbb {E}_T[\mathbb {E}_T[\sigma _{y}\sigma _{z}\,|\,\sigma _y]]\\= & {} \mathbb {E}_T[\sigma _{y}\mathbb {E}_T[\sigma _{z}\,|\,\sigma _y]]\\= & {} \mathbb {E}_T[\sigma _{y} e^{-\mathrm {d}_T(y,z)} \sigma _y]\\= & {} e^{-\mathrm {d}_T(y,z)}\mathbb {E}_T[\sigma _{y}^2]\\= & {} e^{-\mathrm {d}_T(y,z)}, \end{aligned}$$

where the third equality follows from the fact that $\mathbb {P}_T[\sigma _z = \sigma _y\,|\,\sigma _y] = \frac{1 + e^{-\mathrm {d}_T(y,z)}}{2}$, which can be deduced from Definition 2.3. In the proximal case, we have further that

$$\begin{aligned} -\ln \mathbb {E}_T[\hat{\sigma }_{y}\hat{\sigma }_{z}]= & {} \beta _Y + \beta _Z + \mathrm {d}_T(y,z)\nonumber \\\le & {} 2 \beta _{g,\wp } + g \Gamma \nonumber \\=: & {} \chi _{g,\wp ,\Gamma }. \end{aligned}$$

(19)

Recall that the expected difference of $\widehat{\mathcal {D}}$ under $T^0$ and $T^\#$ is given by

$$\begin{aligned} \mathcal {D}^0 - \mathcal {D}^\#= & {} \sum _{i=1}^I \sum _{j=1}^k \alpha _i \left( \mathbb {E}_{T^0}\left[ \hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}\right] -\mathbb {E}_{T^\#}\left[ \hat{\sigma }^j_{y^\#_i}\hat{\sigma }^j_{z^\#_i}\right] . \right) \end{aligned}$$

Each term in the sum, whether it corresponds to a proximal-proximal, semi-proximal-proximal, or non-proximal-proximal case, is at least

$$\begin{aligned} \mathcal {D}_\delta := e^{-\chi _{g,\wp ,\Gamma }}(1 - e^{-\frac{1}{\Upsilon }}), \end{aligned}$$

by (11), (18), (19), and the fact that

$$\begin{aligned} |\mathrm {d}_{T^0}\left( y^0_i,z^0_i\right) - \mathrm {d}_{T^\#}\left( y^\#_i,z^\#_i\right) | \ge \frac{1}{\Upsilon }, \end{aligned}$$

(20)

by the evolutionary distance requirement of the battery. Hence,

$$\begin{aligned} \mathcal {D}^0 - \mathcal {D}^\# \ge \mathcal {D}_\delta k I. \end{aligned}$$

Proof of Claim 3.3 (Concentration)

Consider $\widehat{\mathcal {D}}$ on $T^0$. (The argument is the same on $T^\#$.) Let $\mathcal {I}^0_{np}$ be the set of non-proximal pairs in $T^0$ and let $\mathcal {I}^0_p$ be the set of pairs that are either semi-proximal or proximal. We also let

$$\begin{aligned} \mathcal {J}^0_{np} = \left\{ (i,j) : i \in \mathcal {I}^0_{np}, j \in \{1,\ldots ,k\}\right\} , \end{aligned}$$

and

$$\begin{aligned} \mathcal {J}^0_p = \left\{ (i,j) : i \in \mathcal {I}^0_p, j \in \{1,\ldots ,k\}\right\} . \end{aligned}$$

Fix $0< \varepsilon < 1$ small (to be determined below).

We first illustrate our argument in the easier case where the number of non-proximal pairs is small:

$$\begin{aligned} |\mathcal {I}^0_{np}| < \varepsilon I. \end{aligned}$$

We define the following sum

$$\begin{aligned} \widetilde{\mathcal {D}}= \sum _{(i,j) \in \mathcal {J}^0_p} \alpha _i\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i} - \left| \mathcal {J}^0_{np}\right| , \end{aligned}$$

that is, we set the terms in $\mathcal {J}^0_{np}$ to their worst-case value, $-1$, which implies $\widehat{\mathcal {D}}\ge \widetilde{\mathcal {D}}$. We claim that the remaining terms in the sum are independent. To prove this, we first make an observation. For all $(i,j) \in \mathcal {J}^0_p$, the term $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$ is independent of the state $\sigma ^j_{x^0_i}$ at the root $x^0_i$ of $\mathcal {F}^0_i$, where the latter is defined in (9). This follows by the symmetry of the substitution process between the $+1$ and $-1$ states. To prove the independence claim above, we then proceed by generating the substitution process as follows, for each $j =1,\ldots ,k$ independently. Define $\mathcal {X}$ to be the set of those roots $x^0_i$ such that $(i,j) \in \mathcal {J}^0_p$.

• 1. Let $\mathcal {H}$ be the set of those i such that: (i) $(i,j) \in \mathcal {J}^0_p$ and (ii) the root $x^0_i$ does not have an ancestor in $T^0$ among $\mathcal {X}$. Pick the states $\sigma ^j_{x^0_i}$, $i \in \mathcal {H}$, and the corresponding quantities $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$, which depend only on the states within $\mathcal {F}^0_i$. By the Markov property and the condition on $\mathcal {H}$, the quantities $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$, for $i \in \mathcal {H}$, are mutually independent.

• 2. Then let $\mathcal {H}'$ be the set of those $i \notin \mathcal {H}$ such that: (i) $(i,j) \in \mathcal {J}^0_p$ and (ii) the root $x^0_i$ does not have an ancestor in $\mathcal {X}-\{x^0_i\,:\, i\in \mathcal {H}\}$. Conditioned on the previously assigned states, pick the states $\sigma ^j_{x^0_i}$, $i \in \mathcal {H}'$, and the corresponding quantities $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$, which depend only on the states within $\mathcal {F}^0_i$. By the global requirement of the battery, the $\mathcal {F}^0_i$s in $\mathcal {H}'$ have empty edge intersection with the $\mathcal {F}^0_i$s in $\mathcal {H}$. Together with the observation above, it follows that the quantities $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$, for $i \in \mathcal {H}'$, are independent of each other as well as of the quantities $\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i}$, for $i \in \mathcal {H}$.

• 3. Add $\mathcal {H}'$ to $\mathcal {H}$, and proceed similarly to the previous step until all terms in $\mathcal {J}^0_p$ have been generated.

The event

$$\begin{aligned} A^c = \left\{ \widehat{\mathcal {D}}- \frac{\mathcal {D}^0 + \mathcal {D}^\#}{2} \le 0 \right\} , \end{aligned}$$

implies the event

$$\begin{aligned} \widetilde{\mathcal {D}}\le \frac{\mathcal {D}^0 + \mathcal {D}^\#}{2}, \end{aligned}$$

or, after rearranging,

$$\begin{aligned} \widetilde{\mathcal {D}}- \mathbb {E}_{T^0}[\widetilde{\mathcal {D}}] \le - \frac{\mathcal {D}^0 - \mathcal {D}^\#}{2} + \left\{ \mathcal {D}^0 - \mathbb {E}_{T^0}[\widetilde{\mathcal {D}}]\right\} , \end{aligned}$$

(21)

which in turn implies

$$\begin{aligned} \widetilde{\mathcal {D}}- \mathbb {E}_{T^0}[\widetilde{\mathcal {D}}] \le - \frac{\mathcal {D}_\delta }{2} k I + 2\varepsilon k I, \end{aligned}$$

where we used the fact that the $\mathcal {J}^0_p$-terms cancel out in the expression in curly brackets in (21). Choose $\varepsilon$ small enough so that the RHS is less than $- \frac{\mathcal {D}_\delta }{3} k I$. Then, by Lemma 4 (Appendix A.3),

$$\begin{aligned} \mathbb {P}_{T^0}[A^c]\le & {} 2 \exp \left( -\frac{\left( \frac{\mathcal {D}_\delta }{3} k I\right) ^2}{2(2)^2 (kI)}\right) \nonumber \\= & {} \exp \left( - \Omega (k I)\right) . \end{aligned}$$

(22)

Consider now the case where

$$\begin{aligned} |\mathcal {I}^0_{np}| \ge \varepsilon I. \end{aligned}$$

We show how to deal with the extra complication that non-proximal pairs have connecting paths that may intersect with other test subtrees, thereby creating unwanted dependencies.

Let ((y, z); (Y, Z)) be a non-proximal test pair in $T^0$ and consider the $\gamma _t$-toppings $\lceil Y \rceil ^{\gamma _t}$ and $\lceil Z \rceil ^{\gamma _t}$. Note that at least one of $\lceil Y \rceil ^{\gamma _t}$ and $\lceil Z \rceil ^{\gamma _t}$ has a hat of length $\gamma _t/2$ as otherwise Y and Z would be connected through the root at distance at most $\gamma _t$, contradicting the non-proximal assumption. We refer to the corresponding hat as the hat of the pair. If both toppings have long enough hats, choose the lowest one of the two so that the hat is necessarily part of the connecting path. The probability that all edges in this hat are open under the random cluster representation of the model described in Lemma 3 (Appendix A.2), which we refer to as an open hat, is at most $e^{-f \gamma _t/2}$. If at least one such edge is closed, in which case we say the hat is closed, $\hat{\sigma }_{y}$ and $\hat{\sigma }_{z}$ are independent. Hence, we have in the non-proximal case

$$\begin{aligned} -\ln \mathbb {E}_T[\hat{\sigma }_{y}\hat{\sigma }_{z}] \ge -\ln \left\{ (e^{-f\gamma _t/2})(1) + (1)(0)\right\} \ge f \gamma _t/2, \end{aligned}$$

(23)

where the first term in curly brackets accounts for the fact that, under an open hat, the correlation between the reconstructed states is at most 1, while the second term accounts for the fact that, under a closed hat, the reconstructed states are independent and therefore have 0 correlation.

Let $[\mathcal {J}^0_{np}]_c$ be the random set corresponding to those pairs in $\mathcal {J}^0_{np}$ with a closed hat and let $[\mathcal {J}^0_{np}]_o$ be the random set corresponding to those pairs in $\mathcal {J}^0_{np}$ with an open hat. We consider the following sum

$$\begin{aligned} \widetilde{\mathcal {D}}= \sum _{(i,j) \in \mathcal {J}^0_p\cup \left[ \mathcal {J}^0_{np}\right] _c} \alpha _i\hat{\sigma }^j_{y^0_i}\hat{\sigma }^j_{z^0_i} - \left| \left[ \mathcal {J}^0_{np}\right] _o\right| , \end{aligned}$$

that is, we set the terms with open hats to their worst-case value $-1$ which implies $\widehat{\mathcal {D}}\ge \widetilde{\mathcal {D}}$. We claim that the remaining terms in the sum are conditionally independent given $[\mathcal {J}^0_{np}]_c$.

Indeed, considering only the proximal and semi-proximal test subtrees and their connecting paths as well as the non-proximal test subtrees whose hat is closed, we claim that the roots of the former and the hats of the latter form a separating set in the sense that any path between two of these subtrees must go through one of the roots or an entire hat. Indeed, a path between any two of these test subtrees must enter one of them from above. Moreover if one of the two subtrees is non-proximal but the path does not visit its entire hat, then the other test subtree must also be entered from above (as the path must deviate downwards from the hat) and its entire hat be visited if non-proximal (otherwise the two hats would intersect). Arguing as in the small number of non-proximal pairs, this implies mutual independence.

By the argument above (23),

$$\begin{aligned} \mathbb {E}_{T^0}[|[\mathcal {J}^0_{np}]_c|] \ge (1 - e^{-f \gamma _t/2}) |\mathcal {J}^0_{np}|. \end{aligned}$$

(24)

Hence, by Lemma 4 (Appendix A.3), letting $0< \varepsilon ' < 1 - e^{-f\gamma _t/2}$ (determined below)

$$\begin{aligned} \mathbb {P}_{T^0}\left[ |[\mathcal {J}^0_{np}]_c| < \mathbb {E}_{T^0}[|[\mathcal {J}^0_{np}]_c|] - \varepsilon '|\mathcal {J}^0_{np}|\right]\le & {} 2 \exp \left( - \frac{(\varepsilon ' |\mathcal {J}^0_{np}|)^2}{2 (1)^2 |\mathcal {J}^0_{np}|} \right) \nonumber \\= & {} \exp \left( - \Omega ((\varepsilon ')^2|\mathcal {J}^0_{np}|)\right) \nonumber \\= & {} \exp \left( - \Omega ((\varepsilon ')^2 \varepsilon k I)\right) . \end{aligned}$$

(25)

On the event

$$\begin{aligned} \mathcal {C}= \{|[\mathcal {J}^0_{np}]_c| \ge \mathbb {E}_{T^0}[|[\mathcal {J}^0_{np}]_c|] - \varepsilon ' |\mathcal {J}^0_{np}|\}, \end{aligned}$$

we have, using (24),

$$\begin{aligned} \left| [\mathcal {J}^0_{np}]_o\right|= & {} \left| \mathcal {J}^0_{np}\right| - \left| [\mathcal {J}^0_{np}]_c\right| \nonumber \\\le & {} \left| \mathcal {J}^0_{np}\right| - \mathbb {E}_{T^0}[|[\mathcal {J}^0_{np}]_c|] + \varepsilon ' |\mathcal {J}^0_{np}|\nonumber \\\le & {} (e^{-f \gamma _t/2} + \varepsilon ') |\mathcal {J}^0_{np}|\nonumber \\\le & {} (e^{-f \gamma _t/2} + \varepsilon ') kI\nonumber \\\le & {} - \frac{\mathcal {D}_\delta }{6} k I, \end{aligned}$$

(26)

for $\varepsilon '$ small enough and $\gamma _t$ large enough. The rest of the argument follows similarly to the small $|\mathcal {I}^0_{np}|$ case by bounding

$$\begin{aligned} \mathbb {P}_{T^0}[A^c]= & {} \mathbb {P}_{T^0}[A^c\,|\,\mathcal {C}^c] \mathbb {P}_{T^0}[\mathcal {C}^c] + \mathbb {P}_{T^0}[A^c\,|\,\mathcal {C}] \mathbb {P}_{T^0}[\mathcal {C}] \le \mathbb {P}_{T^0}[\mathcal {C}^c] \\&+ \mathbb {E}_{T^0}[\mathbb {P}_{T^0}[A^c | | [\mathcal {J}^0_{np}]_c, \mathcal {C}] | \mathcal {C}], \end{aligned}$$

using (25) for the first term, and (26) along with Claim 3.2 for the second one. $\square$

4 Homogeneous trees

We first detail our techniques for constructing batteries of tests on a special case: homogeneous trees. Formally, we define homogeneous phylogenies as follows.

Definition 4.1

(Homogeneous phylogenies) For an integer $h \ge 0$ and $n = 2^h$, we denote by $\mathbb {HY}^{(h)}_{g}$ the subset of $\mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$ comprised of all h-level complete binary trees $T^{(h)}_{\phi ,w} = (V^{(h)}, E^{(h)}; \phi ; w)$ where the edge weight function $w$ is identically g and $\phi$ may be any one-to-one labeling of the leaves. We denote by $\rho ^{(h)}$ the natural root of $T^{(h)}_{\phi ,w}$. For $0\le h'\le h$, we let $L^{(h)}_{h'}$ be the vertices on level $h - h'$ (from the root). In particular, $L^{(h)}_{0} = L^{(h)}$ denotes the leaves of the tree and $L^{(h)}_{h} = \{\rho ^{(h)}\}$ denotes the root.

Fix $g, n = 2^h$ and let $\mathbb {HY}= \mathbb {HY}^{(h)}_{g}$ be the set of homogeneous phylogenies with h levels and branch lengths g. Let $T^0 \in \mathbb {HY}$ be the generating phylogeny and denote by $\varvec{\sigma }_X = (\sigma ^i_X)_{i=1}^k$ a set of k i.i.d. samples from the corresponding CFN model. We first need an appropriate notion of distance between homogeneous trees. Note that tree operations routinely used in phylogenetics, such as subtree-prune-regraft or nearest-neighbor interchange (see e.g. [51]), may not result in homogeneous trees. It will be more convenient to work with the following definition. We say that two homogeneous trees T and $T'$ are equivalent, denoted by $T\sim T'$, if $\forall a,b \in [n], \mathrm {d}_T(a,b) = \mathrm {d}_{T'}(a,b)$, that is, if they agree as tree metrics. (Recall that tree metrics are defined in Definition 3.2.)

Definition 4.2

(Swap distance) We call a swap the operation of choosing two (non-sibling) vertices u and v on the same level of a homogeneous tree and exchanging the subtrees rooted at u and v. The swap distance $\Delta _{\mathrm {SW}}(T,T')$ between T and $T'$ in $\mathbb {HY}$ is the smallest number of swaps needed to transform T into $T'$ (up to $\sim$).

Because a swap operation is invertible, we have $\Delta _{\mathrm {SW}}(T',T) = \Delta _{\mathrm {SW}}(T,T')$. By simply re-ordering the leaves, it holds that $\Delta _{\mathrm {SW}}(T,T') \le n-1$. We need a bound on the size of the neighborhood around a tree. Since for each swap operation, we choose one of $2n-2$ vertices, then choose one of at most $n-2$ non-sibling vertices on the same level, we have:

Claim 4.1

(Neighborhod size: swap distance) Let T be a phylogeny in $\mathbb {HY}$. The number of phylogenies at swap distance $\Delta$ of T is at most $(2n^{2})^\Delta$.

In the following subsections, we prove the existence of a sufficiently large battery of distinguishing tests.

Proposition 2

(Existence of batteries) Let $\wp = 1$, $\ell = \ell (g,\wp ) \ge 2$ as in Proposition 1, $\Gamma = 2 \ell ,$ and $\gamma _t \ge \Gamma$ and C as in Proposition 1. For all $T^\# \ne T^0 \in \mathbb {HY}$, there exists a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0) \quad \text {and }\quad \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in }T^\#), \end{aligned}$$

with

$$\begin{aligned} I \ge \frac{\Delta _{\mathrm {SW}}(T^0,T^\#)}{ C_\mathcal {S}(1 + 2^{2\gamma _t + 2}) }, \end{aligned}$$

where $C_\mathcal {S}> 0$ is a constant (defined in Claim 4.3 below).

The formal proof of this proposition can be found in Sect. 4.3.

From Propositions 1 and 2 as well as Claim 4.1, we obtain our main theorem in this special case.

Theorem 2

(Sequence-length requirement of ML: homogeneous trees) For all $\delta > 0$, there exists $\kappa > 0$ depending on $\delta$ and g such that the following holds. For all $h \ge 2$, $n = 2^h$ and generating phylogeny $T^0 \in \mathbb {HY}^{(h)}_g$, if $\varvec{\sigma }_X = (\sigma ^i_X)_{i=1}^k$ is a set of $k = \kappa \log n$ i.i.d. samples from the corresponding CFN model, then the probability that MLE fails to return $T^0$ is at most $\delta$.

Proof of Theorem 2

For $T^\# \ne T^0$ in $\mathbb {HY}^{(h)}_g$, let $M_{T^\#}$ be the event that the MLE prefers $T^\#$ over $T^0$ (including a tie), that is, the set of $\varvec{\sigma }_X = (\sigma ^{i}_X)_{i=1}^k$ such that $\mathscr {L}_{T^\#}(\varvec{\sigma }_X) \le \mathscr {L}_{T^0}(\varvec{\sigma }_X)$. Combining Propositions 1 and 2, for all $T^\# \ne T^0 \in \mathbb {HY}^{(h)}_g$, there exists an event $A_{T^\#}$ such that

$$\begin{aligned} \max \{\mathbb {P}_{T^\#}[A_{T^\#}^c], \mathbb {P}_{T^0}[A_{T^\#}]\} \le e^{-C_1 k \Delta _{\mathrm {SW}}(T^0,T^\#)}, \end{aligned}$$

(27)

where $C_1$ depends only on g. Then, by a union bound, (4), (27), and Claim 4.1,

$$\begin{aligned} \mathbb {P}_{T^0}[\exists T^\# \ne T^0,\ M_{T^\#}]\le & {} \sum _{T^\# \ne T^0}\mathbb {P}_{T^0}[M_{T^\#}]\nonumber \\\le & {} \sum _{T^\# \ne T^0} [\mathbb {P}_{T^0}[A_{T^\#}] + \mathbb {P}_{T^\#}[A_{T^\#}^c]]\\\le & {} \sum _{\Delta = 1}^{n-2} (2 n^{2})^\Delta [2 e^{-C_1 k \Delta }]\\\le & {} \sum _{\Delta = 1}^{+\infty } e^{-(C_1 \kappa \log n - 2 \log n - \log 2)\Delta }\\\le & {} \frac{e^{-(C_1 \kappa \log n - 2 \log n - \log 2)}}{1 - e^{-(C_1 \kappa \log n - 2 \log n - \log 2)}}\\\le & {} \frac{1}{e^{(C_1 \kappa - 2)\log n - \log 2} - 1}\\\le & {} \delta , \end{aligned}$$

for $\kappa$ large enough, depending only on g and $\delta$, for all $n \ge 2$.

4.1 Finding matching subtrees

We now describe a procedure to construct a battery of distinguishing tests on homogeneous trees. To be clear, the procedure is not carried out on data. It takes as input the true (unknown) generating phylogeny $T^0$ and an alternative tree $T^\# \ne T^0$. It merely serves to prove the existence of a distinguishing statistic that, in turn, implies a bound on the failure probability of maximum likelihood as detailed in the proof of Theorem 2. In essence, the procedure attempts to build maximal matching subtrees between $T^0$ and $T^\#$ and pair them up appropriately to construct distinguishing tests.

Definition 4.3

($\ell$-vertices) For a fixed positive integer $\ell$, we call $\ell$-vertices those vertices in $T^0$ whose graph distance from the root is a multiple of $\ell$. The sets of all $\ell$-vertices at the same distance from the root are called $\ell$-levels. For an $\ell$-vertex x, its descendant $\ell$-vertices on the next $\ell$-level (that is, farther from the root) are called the $\ell$-children of x, which we also refer to as a family of $\ell$-siblings.

Let $\wp = 1$ and $\ell = \ell (g,\wp ) \ge 2$ be as in Proposition 1. Assume for simplicity that the total number of levels h in $T^0$ is a multiple of $\ell$. Extending the analysis to general h is straigthforward.

4.1.1 Procedure

Our goal is to color each $\ell$-vertex x of $T^0$ with the following intended meaning:

• Green $\mathtt{G}$: indicating a matching subtree rooted at x that can be used to reconstruct ancestral states reliably on both $T^0$ and $T^\#$ using the same function of the leaf states.

• Red $\mathtt{R}$: indicating the presence among the $\ell$-children of x of a pair of matching subtrees that can be used in a distinguishing test as their pairwise distance differs in $T^0$ and $T^\#$.

• Yellow $\mathtt{Y}$: none of the above.

We call $\mathtt{G}$-vertices (respectively $\mathtt{G}$-children) those $\ell$-vertices (respectively $\ell$-children) that are colored $\mathtt{G}$, and similarly for the other colors. Before describing the coloring procedure in details, we need a definition.

Definition 4.4

($\mathtt{G}$-cluster) Let x be a $\mathtt{G}$-vertex. Assume that each $\ell$-vertex below x in $T^0$ has been colored $\mathtt{G}$, $\mathtt{R}$, or $\mathtt{Y}$ and that the leaves have been colored $\mathtt{G}$. The $\mathtt{G}$-cluster rooted at x is the restricted subtree of $T^0$ containing all vertices and edges (not necessarily $\ell$-vertices) lying on a path between x and a leaf below x that traverses only $\ell$-vertices colored $\mathtt{G}$.

We now describe the coloring procedure.

• 1. Initialization

  • (a) All leaves of $T^0$ are colored $\mathtt{G}$.

• 2. For each $\ell$-vertex x in the $\ell$-level furthest from the root that has yet to be colored, do:

  • (a) Vertex x is colored $\mathtt{G}$ if:

    • at most one of its $\ell$-children is non-$\mathtt{G}$ and;

    • the resulting $\mathtt{G}$-cluster rooted at x and the corresponding restricted subtree in $T^\#$, that is, the subtree of $T^\#$ restricted to the same leaf set, are matching.

  • (b) Else, vertex x is colored $\mathtt{R}$ if:

    • at most one of its $\ell$-children is non-$\mathtt{G}$;

    • but, if x were colored $\mathtt{G}$, the resulting $\mathtt{G}$-cluster rooted at x and the corresponding restricted subtree in $T^\#$ would not be matching.

  • (c) Else, vertex x is colored $\mathtt{Y}$.

In particular observe that, if x is colored $\mathtt{Y}$, at least two of its $\ell$-children are non-$\mathtt{G}$.

As explained above, we are interested in $\mathtt{R}$-vertices because tests can be constructed from them. We prove that the number of $\mathtt{R}$-vertices scales linearly in the swap distance. More precisely, we show that

$$\begin{aligned} \#\mathtt{R}\ge 2^{-\ell - 2}\, \Delta _{\mathrm {SW}}\left( T^0,T^\#\right) . \end{aligned}$$

4.1.2 Relating combinatorial distance and the number of matching subtrees

We relate the swap distance between $T^0$ and $T^\#$ to the number of $\mathtt{R}$-vertices in the procedure above. Let $\#\mathtt{G}$ be the number of $\mathtt{G}$-vertices in $T^0$ in the construction, and similarly for the other colors. For an $\ell$-vertex x in $T^0$, we let $T^0_x$ be the subtree of $T^0$ rooted at x and we let $\mathcal {V}_\ell (T^0_x)$ be the set of $\ell$-vertices in $T^0_x$. Recall from Definition 3.2 that we denote by $\mathrm {d}^{\mathrm {g}}_{T^0}$ the graph distance on $T^0$. We first bound the number of $\mathtt{Y}$-vertices.

Claim 4.2

(Bounding the number of yellow vertices) We have

$$\begin{aligned} \#\mathtt{Y}\le \#\mathtt{R}. \end{aligned}$$

Proof

From our construction, each $\mathtt{Y}$-vertex in $T^0$ has at least two non-$\mathtt{G}$-children. Hence, intuitively, one can think of the $\mathtt{Y}$-vertices as forming the internal vertices of a forest of multifurcating trees whose leaves are $\mathtt{R}$-vertices.

The inequality follows.

Formally, if x is a $\mathtt{Y}$-vertex, from the observation above we have

$$\begin{aligned} \sum _{y \in \mathcal {V}_\ell (T^0_x)} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{\ell }} \mathbf {1}\{y \text { is a } \mathtt{R}\text {- vertex} \} \ge 1, \end{aligned}$$

(28)

by induction on the $\ell$-levels starting with the level farthest away from the root. Similarly if y is an $\mathtt{R}$-vertex,

we have

$$\begin{aligned} \sum _{x : y \in \mathcal {V}_\ell (T^0_x)} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{\ell }} \mathbf {1}\{x\text { is a } \mathtt{Y}\text {- vertex}\} < 1, \end{aligned}$$

(29)

where the inequality follows from the fact that the sum is over a path from x to the root of $T^0$. Summing (28) over $\mathtt{Y}$-vertices x and (29) over $\mathtt{R}$-vertices y gives the same quantity on the LHS, so that the RHS gives the inequality. $\square$

We can now relate the swap distance to the output of the procedure.

Claim 4.3

(Relating swaps and $\#\mathtt{R}$) We have

$$\begin{aligned} \Delta _{\mathrm {SW}}\left( T^0,T^\#\right) \le C_\mathcal {S}\#\mathtt{R}, \end{aligned}$$

where $C_\mathcal {S}= 2^{\ell + 2}$.

Proof

Pick a lowest non-$\mathtt{G}$-vertex u in $T^0$. Being lowest, all $\ell$-children of u must be colored $\mathtt{G}$. In fact, all $\ell$-vertices on the level below u must be colored $\mathtt{G}$. Make u a $\mathtt{G}$-vertex by transforming the subtree below u in $T^\#$ to match the corresponding subtree in $T^0$. This takes at most $2^{\ell +1}$ swaps.

Repeat until $T^0$ and $T^\#$ match. The inequality then follows from Claim 4.2. $\square$

4.2 Constructing a battery of tests

We now construct a battery of tests from the $\mathtt{R}$-vertices. The basic idea is that each $\mathtt{R}$-vertex has two $\mathtt{G}$-children which satisfy many of the requirements of a battery and therefore can potentially be used as a test pair. In particular, they are the roots of dense subtrees that are matching with their corresponding restricted subtrees in $T^\#$, but their evolutionary distance differs in $T^0$ and $T^\#$. Note that we also have a number of $\mathtt{R}$-vertices that scales linearly in the swap distance by Claim 4.3. However one issue to address is the global requirement of the battery. In words, we need to ensure that the test pairs do not intersect. We achieve this by sparsifying the battery. A similar argument was employed in [40].

In this section, $T^0$ and $T^\#$ are fixed. To simplify notation, we let $\Delta = \Delta _{\mathrm {SW}}\left( T^0,T^\#\right)$. Fix $\wp = 1$. Choose $\ell = \ell (g,\wp ) \ge 2$ as in Proposition 1. Then take $\Gamma = 2\ell ,$ and set $\gamma _t \ge \Gamma$ and C as in Proposition 1. In the rest of this subsection, we build a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0) \text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in } T^\#) \end{aligned}$$

with corresponding $\alpha _i$s. We number the $\mathtt{R}$-vertices $i=1,\ldots ,I'$ and we build one test panel for each $\mathtt{R}$-vertex. Here $I' \ge I$ as we will later need to reject some of the test panels to avoid unwanted correlations.

4.2.1 Co-hanging pairs in $T^\#$

We first construct test panels that satisfy the pair and cluster requirements of the battery. Let $x^0_i$ be an $\mathtt{R}$-vertex in $T^0$ and let $x^\#_i$ be the corresponding vertex in $T^\#$. Because $x^0_i$ is colored $\mathtt{R}$, by construction it has at least $2^\ell - 1$ $\mathtt{G}$-children, but its $\mathtt{G}$-children are “connected in different ways” in $T^\#$. In particular, at least one pair of $\mathtt{G}$-children $(y^0_i,z^0_i)$ must be at a different evolutionary distance in $T^0$ than the corresponding pair $(y^\#_i,z^\#_i)$ in $T^\#$ (see the remark after Definition 3.2). We use these pairs as our test panel.

Claim 4.4

(Test panels) For each $\mathtt{R}$-vertex $x^0_i$ we can find a test pair of $\mathtt{G}$-children $(y^0_i,z^0_i)$ of $x^0_i$, with corresponding test pair $(y^\#_i,z^\#_i)$ in $T^\#$, such that the test panel satisfy the cluster and pair requirements of a battery.

Proof

By construction, the test subtrees, that is, the $\mathtt{G}$-clusters rooted at the test vertices, are $(\ell ,1)$-dense. The test subtrees are also matching, co-hanging and their roots are at different evolutionary distances in $T^0$ and $T^\#$. Finally, the test pair in $T^0$ is proximal as

$$\begin{aligned} \mathrm {d}^{\mathrm {g}}_{T^0}(y^0_i, z^0_i) \le 2\ell \le \Gamma . \end{aligned}$$

$\square$

4.2.2 Sparsification in $T^\#$

It remains to satisfy the global requirements of the battery. By construction the test subtrees are non-intersecting in both $T^0$ and $T^\#$ (see the proof of Claim 4.5). However we must also ensure that proximal/semi-proximal connecting paths and non-proximal hats do not intersect with each other or with test subtrees from other test panels. By construction, this is automatically satisfied in $T^0$ where all test pairs are proximal. To satisfy this requirement in $T^\#$, we make the collection of test pairs sparser by rejecting a fraction of them.

Claim 4.5

(Sparsification in $T^\#$) Assume $\ell \ge 2$. Let $\mathcal {H}' = \{(y^0_i,z^0_i); (y^\#_i,z^\#_i)\}_{i=1}^{I'}$ be the test panels constructed in Claim 4.4. We can find a subset $\mathcal {H}\subseteq \mathcal {H}'$ of size

$$\begin{aligned} |\mathcal {H}| = I \ge \frac{1}{1 + 2^{2\gamma _t + 2}} I' \ge \frac{\Delta }{C_\mathcal {S}(1 + 2^{2\gamma _t + 2})} \end{aligned}$$

such that the test panels in $\mathcal {H}$ satisfy all global requirements of a battery.

Proof

Let $\{(Y^0_i,Z^0_i); (Y^\#_i,Z^\#_i)\}_{i=1}^{I'}$ be the test subtrees corresponding to $\mathcal {H}'$. Let $W^0_1$ and $W^0_2$ be two test subtrees in $T^0$ (not necessarily from the same test pair) and let $W^\#_1$ and $W^\#_2$ be their matching subtrees in $T^\#$. We argue that these subtrees are non-intersecting in both $T^0$ and $T^\#$. We start with $T^0$. By construction (see Claim 4.4), $W^0_1$ is a maximal $\mathtt{G}$-cluster: its root $w^0_1$ is a $\mathtt{G}$-vertex whose parent $\ell$-vertex is colored $\mathtt{R}$; all $\mathtt{G}$-children of $w^0_1$ are in $W^0_1$, as well as all of their $\mathtt{G}$-children and so forth. The same goes for $W^0_2$, whose root we denote by $w^0_2$. If neither $w^0_1$ nor $w^0_2$ is a descendant of the other, then $W^0_1$ and $W^0_2$ are necessarily non-intersecting. Assume instead, w.l.o.g., that $w^0_2$ is a descendant of $w^0_1$. Because the parent $\ell$-vertex of $w^0_2$ is colored $\mathtt{R}$, then by construction $w^0_2$ and all of its decendants (including the subtree $W^0_2$) cannot be in $W^0_1$. Note in particular that $W^0_1$ and $W^0_2$ share no leaf. We move on to $T^\#$. Because $T^\#$ is in $\mathbb {HY}$, the subtrees $W^\#_1$ and $W^\#_2$ are isomorphic as graphs to $W^0_1$ and $W^0_2$. In particular, their structure is the same as the one described above. Let $w^\#_1$ and $w^\#_2$ be the vertices corresponding to $w^0_1$ and $w^0_2$ in $T^\#$. Again, if neither $w^\#_1$ nor $w^\#_2$ is a descendant of the other one, then $W^\#_1$ and $W^\#_2$ are non-intersecting. Assume instead, w.l.o.g., that $w^\#_2$ is a descendant of $w^\#_1$. If $W^\#_1$ and $W^\#_2$ share a vertex, say z, then the parent $\ell$-vertex of z, say $\tilde{z}$, is also shared because of the structure of $W^\#_1$ and $W^\#_2$. But then $W^\#_1$ and $W^\#_2$ contain at least $2^\ell -1$ $\mathtt{G}$-children of $\tilde{z}$—so they must have at least one such $\mathtt{G}$-child in common (recall that $\ell \ge 2$). The same holds for the $\mathtt{G}$-children of these common $\mathtt{G}$-children, and so on. As a result, $W^\#_1$ and $W^\#_2$ must share at least one leaf, which contradicts the fact that $W^0_1$ and $W^0_2$ (which have the same leaf sets as $W^\#_1$ and $W^\#_2$) share no leaf.

As discussed above, it remains to appropriately sparsify the set $\mathcal {H}'$ of test pairs. We proceed as follows. Start with test panel $((y^0_1,z^0_1); (y^\#_1,z^\#_1))$. Remove from $\mathcal {H}'$ all test panels $i \ne 1$ such that

$$\begin{aligned} \min \left\{ \mathrm {d}^{\mathrm {g}}_{T^\#}(v,w)\ :\ v \in \left\{ y^\#_1,z^\#_1\right\} , w \in \mathcal {V}(Y^\#_i)\cup \mathcal {V}(Z^\#_i)\right\} \le 2\gamma _t. \end{aligned}$$

(30)

Because there are at most $2\cdot 2^{2\gamma _t + 1}$ vertices in $T^\#$ satisfying the above condition and that the test subtrees are non-overlapping in $T^\#$, we remove at most $2^{2\gamma _t + 2}$ test panels from $\mathcal {H}'$.

Let i be the smallest index remaining in $\mathcal {H}'$. Proceed as above and then repeat until all indices in $\mathcal {H}'$ have been selected or rejected.

At the end of the procedure, there are at least

$$\begin{aligned} \frac{1}{1 + 2^{2\gamma _t + 2}} I' \end{aligned}$$

test panels remaining, the set of which we denote by $\mathcal {H}$. Recalling that $\gamma _t \ge \Gamma$, note that, in $\mathcal {H}$, the connecting paths of proximal/semi-proximal pairs and the hats of non-proximal pairs cannot intersect with each other or with any of the test subtree rooted at test vertices in $\mathcal {H}$ by (53). $\square$

4.3 Proof of Proposition 2

It remains to prove Proposition 2. Recall that $\wp = 1$, $\ell = \ell (g,\wp )$ is chosen as in Proposition 1, $\Gamma = 2 \ell$, and $\gamma _t \ge \Gamma$ and C are also chosen as in Proposition 1.

By Claim 4.3, the number of $\mathtt{R}$-vertices is at least $\frac{1}{C_\mathcal {S}}\, \Delta _{\mathrm {SW}}\left( T^0,T^\#\right)$. By Claim 4.4, for each $\mathtt{R}$-vertex, we can construct a test panel satisfying the pair and cluster requirements of the battery. By Claim 4.5, we can further choose a fraction $\frac{1}{1 + 2^{2\gamma _t + 2}}$ of these test panels that also satisfy the global requirement of the battery. To sum up, we have built a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0) \text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in } T^\#) \end{aligned}$$

with

$$\begin{aligned} I \ge \frac{\Delta }{C_\mathcal {S}(1 + 2^{2\gamma _t + 2})}. \end{aligned}$$

That concludes the proof of Proposition 2.

5 General trees

We now prove our main result in the case of general trees. Once again, we use the tests introduced in Sect. 3. We also use a procedure similar to that in the homogeneous case to construct dense subtrees shared by $T^\#$ and $T^0$. However, as described in the next subsections, a number of new issues arise, mainly the possibility of overlapping subtrees and non-co-hanging pairs. Fix $f,g < g^*,\frac{1}{\Upsilon }$ and let $\mathbb {Y}= \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$.

5.1 Blow-up distance

We first need an appropriate notion of distance between general trees. Although standard definitions exist [51], the following definition (related to tree bisection and reconnection [1]) will be particularly convenient for our purposes.

Definition 5.1

(Blow-up distance) A B-blowup operation on a phylogeny consists in two steps:

• Remove a subset of B edges. The non-leaf, isolated vertices resulting from this first step are also removed.

• Add B new weigthed edges to form a new phylogeny with the same leaf set.

The blowup distance $\Delta _{\mathrm {BL}}(T,T')$ between phylogenies T and $T'$ is defined as the smallest B such that there is a B-blowup operation transforming T into $T'$ up to isomorphism.

Because the blowup operation is invertible, we have $\Delta _{\mathrm {BL}}(T,T') = \Delta _{\mathrm {BL}}(T',T)$. Observe that the blow-up distance is a metric. We will need a bound on the size of the neighborhood around a tree.

Claim 5.1

(Neighborhood size: blowup distance) Let T be a phylogeny in $\mathbb {Y}$. The number of phylogenies that can be obtained from T by a $\Delta$-blowup operation is at most $(12 g\Upsilon n^{2})^\Delta$.

Proof

There are $2n-3$ edges in T so there are at most $(2n-3)^\Delta$ choices for the first step of the blowup operation.

For the second step, we add edges one by one. The weight of each edge can take at most $g\Upsilon$ values. Each new edge must further be incident with a vertex existing at the end of the first step or adjacent to a newly added edge. Observe that the edge removal in the first step produces at most $2\Delta$ vertices which can be used in the second step to attach a new edge. Moreover, each edge addition produces at most one new vertex to which subsequent edges can be attached. Since we add a total of $\Delta$ edges, there are at any stage at most $3\Delta$ choices for an attachment. That is, there are at most $(3\Delta g\Upsilon )^\Delta$ choices for the second step of the operation.

Since clearly the blowup distance is $\le 2n-3$, there are overall at most

$$\begin{aligned} (2n-3)^\Delta (3\Delta g\Upsilon )^\Delta \le (3 g\Upsilon (2n-3)^2)^\Delta \le (12 g\Upsilon n^{2})^\Delta , \end{aligned}$$

phylogenies that can be produced with a $\Delta$-blowup operation. $\square$

5.2 Main steps of the proof

In the following subsections, we prove the existence of a sufficientlty large battery of distinguishing tests.

Proposition 3

(Existence of batteries) Let $\wp = 5$, $\ell = \ell (g,\wp )$ as in Proposition 1,

$$\begin{aligned} \Gamma = \max \left\{ (6 + 2\Upsilon g) \ell , 6 g \Upsilon \log _2 \left( \frac{8}{1 - 1/\sqrt{2}}\right) + 2\ell g \Upsilon + 4\right\} , \end{aligned}$$

and $\gamma _t \ge \Gamma$, a multiple of $\ell$, and C as in Proposition 1. For all $T^\# \ne T^0 \in \mathbb {Y}$, there exists a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0)\quad \text { and } \quad \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in }T^\#), \end{aligned}$$

with

$$\begin{aligned} I \ge \frac{\Delta _{\mathrm {BL}}(T^0,T^\#)}{ 20 C_\mathcal {O}(1 + 2^{6\gamma _t + C_w + 3}g\Upsilon ) }, \end{aligned}$$

where

$$\begin{aligned} C_w = 3 g \Upsilon \log _2 \left( \frac{8}{1 - 1/\sqrt{2}}\right) + \ell g \Upsilon + 2, \end{aligned}$$

and $C_\mathcal {O}$ is a constant (defined in Claim 5.4 below).

Proof

This follows from Propositions 4 and 5 below. $\square$

The choice of $\Gamma$ above will be justified in Claim 5.6 and in (57).

From Propositions 1 and 3 we obtain of our main bound in the general case.

Theorem 3

(Sequence-length requirement of ML: general trees) For all $\delta > 0$, there exists $\kappa > 0$ depending on $\delta$, g and $\Upsilon$ such that the following holds. For all $n \ge 2$ and generating phylogeny $T^0 \in \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$, if $\varvec{\sigma }_X = (\sigma ^i_X)_{i=1}^k$ is a set of $k = \kappa \log n$ i.i.d. samples from the corresponding CFN model, then the probability that MLE fails to return $T^0$ is at most $\delta$.

Proof

For $T^\# \ne T^0$, let $M_{T^\#}$ be the event that the MLE prefers $T^\#$ over $T^0$ (including a tie), that is, the set of $\varvec{\sigma }_X = (\sigma ^{i}_X)_{i=1}^k$ such that $\mathscr {L}_{T^\#}(\varvec{\sigma }_X) \le \mathscr {L}_{T^0}(\varvec{\sigma }_X)$. By Propositions 1 and 3, for all $T^\# \ne T^0 \in \mathbb {Y}^{(n)}_{f,g}[\frac{1}{\Upsilon }]$, there exists an event $A_{T^\#}$ such that

$$\begin{aligned} \max \{\mathbb {P}_{T^\#}[A_{T^\#}^c], \mathbb {P}_{T^0}[A_{T^\#}]\} \le e^{-C_1 k \Delta _{\mathrm {BL}}(T^0,T^\#)}, \end{aligned}$$

(31)

where $C_1$ depends only on g and $\Upsilon$. Then, by a union bound, (4), (31) and Claim 5.1, arguing as in the proof of Theorem 2

$$\begin{aligned} \mathbb {P}_{T^0}[\exists T^\# \ne T^0,\ M_{T^\#}] \le \delta , \end{aligned}$$

for $\kappa$ large enough, depending only on g, $\Upsilon$ and $\delta$, for all $n \ge 2$. (This also proves Lemma 1 in Sect. 2.) $\square$

Finally:

Proof of Theorem 1

Combining Theorem 3 and the polynomial bound from Sect.2.3 immediately gives Theorem 1.

5.3 Finding matching subtrees

We now describe our procedure to construct a battery of distinguishing tests for general trees. As in the homogeneous case, the procedure attempts to build dense, maximal subtrees shared by $T^0$ and $T^\#$. These subtrees are paired up appropriately to construct distinguishing tests. For general trees, however, care must be taken to deal with possible “overlaps” in $T^0$ and $T^\#$ (see Definition 5.4). Such overlaps produce unwanted dependencies between the test pairs.

As a result, we proceed in two stages:

• 1. First, similarly to the homogeneous case, pairs of matching subtrees are constructed.

• 2. Second, if the overlap between the tests is too large, new distinguishing tests are constructed along the “boundary of the overlap”.

The first stage is described below. Analysis of the size of the overlap is presented in Sect. 5.4. The more delicate second stage is described in Sects. 5.5 and 5.6.

We root $T^0$ arbitrarily.

Definition 5.2

($\ell$-vertices) For a fixed positive integer $\ell$, we call $\ell$-vertices those vertices in $T^0$ whose graph distance from the root is a multiple of $\ell$. The sets of all $\ell$-vertices at the same distance from the root are called $\ell$-levels. For an $\ell$-vertex x, its descendant $\ell$-vertices on the next $\ell$-level (that is, farther from the root) are called the $\ell$-children of x. We also refer to the $\ell$-children of x as a family of $\ell$-siblings. By convention, the leaves of $T^0$ are also considered $\ell$-vertices irrespective of their distance from the root. They belong to the $\ell$-level immediately below them.

Our goal is to color each $\ell$-vertex x with the following interpretation:

• Green $\mathtt{G}$: indicating a matching subtree rooted at x that can be used to reconstruct ancestral states on $T^0$ and $T^\#$ using the same function of the leaf states.

• Red $\mathtt{R}$: indicating the presence among the $\ell$-children of x of a pair of matching subtrees that can be used as a distinguishing test because the distance between their roots differs in $T^0$ and $T^\#$.

• Yellow $\mathtt{Y}$: none of the above.

As before, we call $\mathtt{G}$-vertices (respectively $\mathtt{G}$-children) those $\ell$-vertices (respectively $\ell$-children) that are colored $\mathtt{G}$, and similarly for the other colors. Before describing the coloring procedure in details, we need a definition.

Definition 5.3

($\mathtt{G}$-cluster) Let x be a $\mathtt{G}$-vertex. Assume that each $\ell$-vertex below x in $T^0$ has been colored $\mathtt{G}$, $\mathtt{R}$, or $\mathtt{Y}$ and that the leaves have been colored $\mathtt{G}$. The $\mathtt{G}$-cluster rooted at x is the restricted subtree of $T^0$ containing all vertices and edges (not necessarily $\ell$-vertices) satisfying the following property: they lie on a path between x and a leaf below x that traverses only $\ell$-vertices colored $\mathtt{G}$.

We now describe the coloring procedure. Below, when counting the $\ell$-children of an $\ell$-vertex x with a specified property, each leaf among the $\ell$-children of x counts as $2^{\ell -d}$ vertices if d is the graph distance between x and that leaf.

• 1. Initialization

  • (a) Root $T^0$ at an arbitrary vertex. (Note that $T^\#$ remains unrooted for this part of the proof where we are concerned with metric-matching as defined in Definition 3.3.)

  • (b) All leaves of $T^0$ are colored $\mathtt{G}$.

• 2. For each $\ell$-vertex x in the $\ell$-level furthest from the root that is not yet colored, do the following:

  • (a) Vertex x is colored $\mathtt{G}$ if:

    • at most one of its $\ell$-children is non-$\mathtt{G}$ and;

    • the resulting $\mathtt{G}$-cluster rooted at x and the subtree of $T^\#$ restricted to the same leaf set are matching.

  • (b) Else, vertex x is colored $\mathtt{R}$ if:

    • at most one of its $\ell$-children is non-$\mathtt{G}$;

    • and the following condition holds: if x were colored $\mathtt{G}$, the resulting $\mathtt{G}$-cluster rooted at x and the corresponding matching subtree in $T^\#$ would not be matching.

  • (c) Else, vertex x is colored $\mathtt{Y}$.

In particular observe that, if x is colored $\mathtt{Y}$, at least two of its $\ell$-children are non-$\mathtt{G}$.

5.4 Relating combinatorial distance, the number of matching subtrees and the overlap size

Let $\#\mathtt{G}$ be the number of $\mathtt{G}$-vertices in $T^0$ in the construction, and similarly for the other colors. For an $\ell$-vertex x in $T^0$, we let $T^0_x$ be the subtree of $T^0$ rooted at x and we let $\mathcal {V}_\ell (T^0_x)$ be the set of $\ell$-vertices in $T^0_x$. Recall from Definition 3.2 that we denote by $\mathrm {d}^{\mathrm {g}}_{T^0}$ the graph distance on $T^0$.

Unlike the homogeneous case (see the proof of Claim 4.5), observe that it is possible for $\mathtt{G}$-clusters to “overlap” in $T^\#$, that is, pairwise intersect. We define the overlap formally as follows. See Figs. 2 and 3 for an illustration.

Fig. 2

Test subtrees overlap in $T^\#$. Matching subtrees are labeled with the same number

Fig. 3

A more detailed view of an overlap. The black solid and dashed subtrees are matching in $T^0$ and $T^\#$. The edges that are simultaenously solid and dashed in $T^\#$ are in the overlap. Note that an edge in $T^0$ may correspond to a path in $T^\#$. For instance $e_0$ is matched to the path formed by $e_{0,1}$ and $e_{0,2}$. On the other hand, an edge in the overlap in $T^\#$ corresponds to several edges in $T^0$. For instance, $e_{0,1}$ corresponds to both $e_0$ and $e_1$. The subtrees in $T^0$ are rooted at $\rho _s$ and $\rho _d$ respectively. This rooting is consistent with the global rooting of $T^\#$ at vertex $\rho ^\#$

Definition 5.4

(Overlap) An edge $e^\#$ in $T^\#$ is in the overlap if it belongs to the matching restricted subtrees in $T^\#$ (the collection of which we denote by $\{\mathcal {M}_i\}_i$) of at least two distinct maximal $\mathtt{G}$-clusters in $T^0$ (the collection of which we denote by $\{\mathcal {G}_i\}_i$, where $\mathcal {G}_i$ and $\mathcal {M}_i$ are matching). The edge $e^\#$ is on a path of some $\mathcal {M}_i$ corresponding to an edge $e^0$ in the matching $\mathcal {G}_i$. We also say that $e^0$ is in the overlap. Let $\mathcal {O}^\#$ (respectively $\mathcal {O}^0$) denote the overlap, as a set of edges, in $T^\#$ (respectively $T^0$). We say that a vertex in $T^0$ is in the overlap if it is adjacent to an edge in $\mathcal {O}^0$, and similarly for $T^\#$.

The following bound allows us to work with the overlap in either $T^0$ or $T^\#$, whichever is more convenient depending on the context. Notice that it is not immediately clear that $\mathcal {O}^0$ and $\mathcal {O}^\#$ are roughly the same size because, by definition, each edge in $\mathcal {O}^\#$ corresponds to several edges in $\mathcal {O}^0$.

Claim 5.2

(Overlaps in $T^0$ and $T^\#$) We have

$$\begin{aligned} \left| \mathcal {O}^0\right| = \Theta \left( \left| \mathcal {O}^\#\right| \right) , \end{aligned}$$

where the constants depend on $f, g, \frac{1}{\Upsilon }, \ell$.

Proof

One direction is straightforward. Let $e^\#$ be an edge in $\mathcal {O}^\#$. There is an edge $e^0$ (in fact at least two) in a $\mathtt{G}$-cluster in $T^0$ whose corresponding path in $T^\#$ includes $e^\#$. See Fig. 3 for an illustration. Note that $e^0$ has weight at most g and therefore can be identified in this way with at most $g\Upsilon$ edges in $\mathcal {O}^\#$. That is, for every edge in $\mathcal {O}^0$ there are at most $g\Upsilon$ edges in $\mathcal {O}^\#$, or

$$\begin{aligned} \left| \mathcal {O}^0\right| \ge \frac{1}{g\Upsilon } \left| \mathcal {O}^\#\right| . \end{aligned}$$

The other direction is trickier because each edge in $\mathcal {O}^\#$ corresponds, by definition, to several edges in $\mathcal {O}^0$. However we claim that, in fact, only a small number of maximal $\mathtt{G}$-clusters can “overlap on a given edge” in $\mathcal {O}^\#$. To prove this we note that, being on a tree, most edges in the overlap are close to the “boundary of the overlap,” that is, they are close to vertices outside the overlap. But vertices outside the overlap necessarily belong to a single $\mathtt{G}$-cluster—which leads to a bound on the number of clusters overlapping on a given edge in $\mathcal {O}^\#$.

We first formalize what we mean by “being close to the boundary of the overlap.” Root $T^\#$ at an arbitrary vertex $\rho ^\#$. Let $\mathcal {G}$ be a maximal $\mathtt{G}$-cluster in $T^0$ and re-root $\mathcal {G}$ consistently with the rooting in $T^\#$, that is, at the vertex corresponding to the root of the matching subtree in $T^\#$. See Fig. 3 for an illustration. (Observe that there is no global rooting in $T^0$ that is consistent with the global rooting in $T^\#$. Instead, for this proof, each maximal $\mathtt{G}$-cluster in $T^0$ is rooted separately as explained above.) Let $\mathcal {V}^\mathcal {G}$ and $\mathcal {W}^{\mathcal {G}}$ be the vertices in $\mathcal {G}$ and the vertices in the overlap in $\mathcal {G}$ respectively. Let $\mathcal {W}^\mathcal {G}_x$ (respectively $\mathcal {V}^\mathcal {G}_x$) be the vertices in $\mathcal {W}^\mathcal {G}$ (respectively $\mathcal {V}^\mathcal {G}$) below vertex x (including x).

Definition 5.5

(Overlap-shallow vertices) We say that x is overlap-shallow (with parameter $\beta$) if

$$\begin{aligned} \sum _{y \in \mathcal {W}^\mathcal {G}_x} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{2}} < \frac{\beta }{1 - 1/\sqrt{2}}. \end{aligned}$$

(32)

We let $\mathcal {S}^\mathcal {G}$ be the set of overlap-shallow vertices in $\mathcal {G}$.

To see why this condition characterizes shallowness in the overlap, let $C > 0$ be a constant and say that y is a witness for x if 1) $y \in (\mathcal {V}^\mathcal {G}{\setminus } \mathcal {W}^{\mathcal {G}}) \cup (\mathcal {V}^\mathcal {G}\cap L)$, that is, y is in $\mathcal {G}$ outside the overlap or is a leaf in $\mathcal {G}$, and if 2) y is at graph distance at most C below x. Because a $\mathtt{G}$-cluster is $(\ell ,1)$-dense (that is, nearly bifurcating), the sum

$$\begin{aligned} \sum _{y \in \mathcal {V}^\mathcal {G}_x} \sqrt{\frac{1}{2^{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}}}, \end{aligned}$$

increases unboundedly as y moves away from x—until the leaves are reached. Thus there is a C depending only on $\ell$ and $\beta$ such that, if x is overlap-shallow, a witness is guaranteed to exist. In other words, x is close to a vertex outside of the overlap or to a leaf. If $y^\#$ is the vertex in $T^\#$ corresponding to witness y, we say that $y^\#$ is a $\#$-witness for x.

We proceed in two steps. For the rest of this claim, we let $\beta = 2$. (We will need the same definition with a different value of $\beta$ in Sect. 5.6.) Our starting point is the bound

$$\begin{aligned} \left| \mathcal {O}^0\right| \le \sum _{\mathcal {G}} \left| \mathcal {W}^{\mathcal {G}}\right| , \end{aligned}$$

(33)

where the sum runs through all maximal $\mathtt{G}$-clusters $\mathcal {G}$ in $T^0$. Indeed, the overlap forms a sub-forest of $T^0$ and, therefore, it has more vertices than edges.

• 1. A large fraction of vertices in the overlap are shallow. We first relate $|\mathcal {W}^{\mathcal {G}}|$ and $|\mathcal {S}^\mathcal {G}|$. Summing the criterion in (32) over all vertices in a maximal $\mathtt{G}$-cluster $\mathcal {G}$, we get

  $$\begin{aligned} \sum _{x \in \mathcal {W}^\mathcal {G}} \left[ \sum _{y \in \mathcal {W}^\mathcal {G}_x} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{2}} \right] = \sum _{y \in \mathcal {W}^\mathcal {G}} \left[ \sum _{x : y \in \mathcal {W}^\mathcal {G}_x} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{2}} \right] , \end{aligned}$$

  (34)

  by interchanging the sum. Note that the expression in square brackets on the r.h.s. is a sum over the overlap on the path from y towards the root of $\mathcal {G}$. Because the sum is geometric, we obtain the bound

  $$\begin{aligned} \sum _{y \in \mathcal {W}^\mathcal {G}} \left[ \sum _{x : y \in \mathcal {W}^\mathcal {G}_x} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{2}} \right] \le \sum _{y \in \mathcal {W}^\mathcal {G}} \left[ \frac{1}{1 - 1/\sqrt{2}} \right] = \frac{\left| \mathcal {W}^\mathcal {G}\right| }{1 - 1/\sqrt{2}}, \end{aligned}$$

  (35)

  where we used that $\sum _{z \ge 0} (1/\sqrt{2})^{z} = (1 - 1/\sqrt{2})^{-1}$. It follows, by contradiction, that

  $$\begin{aligned} |\mathcal {S}^\mathcal {G}| > \frac{1}{2} |\mathcal {W}^\mathcal {G}|. \end{aligned}$$

  (36)

  Indeed, if that were not the case, that is, if $|\mathcal {W}^\mathcal {G}{\setminus } \mathcal {S}^\mathcal {G}| > \frac{1}{2} |\mathcal {W}^\mathcal {G}|$, then the sum on the l.h.s. of (34) would be $> \frac{1}{2} |\mathcal {W}^\mathcal {G}| \frac{2}{1 - 1/\sqrt{2}}$ by (32), contradicting (35). Combining (33) and (36), we get the bound

  $$\begin{aligned} \left| \mathcal {O}^0\right| < 2 \sum _{\mathcal {G}} \left| \mathcal {S}^{\mathcal {G}}\right| . \end{aligned}$$

  (37)

• 2. Overlap-shallow vertices in $T^0$ can be mapped to vertices in the overlap in $T^\#$ with little duplication. It remains to relate $|\mathcal {S}^\mathcal {G}|$ and $|\mathcal {O}^\#|$. This step is delicate because the definition of the overlap (Definition 5.4) differs somewhat in $T^0$ and $T^\#$. Note, in particular, that a vertex $x^0$ in the overlap in $T^0$ is matched to a vertex $x^\#$ in $T^\#$ which may not itself be in the overlap. Instead, all we can say is that $x^0$ is incident with an edge in $T^0$ whose corresponding path in $T^\#$ contains a vertex $\tilde{x}^\#$ in the overlap. To each vertex $x^0$ in $\cup _\mathcal {G}\mathcal {S}^\mathcal {G}$, associate a vertex $\tilde{x}^\#$ in the overlap in $T^\#$ as we just described, with the following extra condition: two vertices $x^0 \ne z^0$ in the same $\mathtt{G}$-cluster $\mathcal {G}$ must be associated with distinct vertices $\tilde{x}^0 \ne \tilde{z}^0$ in the overlap in $T^\#$. This is always possible because, if $\tilde{x}^0, \tilde{z}^0$ are incident with the same edge, we can associate to them distinct vertices from the overlap on the corresponding path in $T^\#$ (say, the closest in graph distance to the matching vertex). Let $\mathcal {S}^\#$ be the set of all these $\tilde{x}^\#$s and observe that

  $$\begin{aligned} |\mathcal {S}^\#| \le 2 |\mathcal {O}^\#|. \end{aligned}$$

  (38)

  Note however that we cannot directly bound the size of $\cup _\mathcal {G}\mathcal {S}^\mathcal {G}$ with the size of $\mathcal {S}^\#$ because some vertices in $\mathcal {S}^\#$ may be associated with vertices in different $\mathtt{G}$-clusters in $T^0$. Let $\tilde{x}^\# \in \mathcal {S}^\#$ and let $x^0_1, \ldots , x^0_h$ be the vertices in $\cup _{\mathcal {G}}\mathcal {S}^\mathcal {G}$ to which it is associated. What we need is to bound h. This will follow from a number of observations. See Fig. 4

  • (a) By the construction above, each $x^0_i$ belongs to a distinct maximal $\mathtt{G}$-cluster $\mathcal {G}_i$.

  • (b) Let $y_i^0$ and $y^\#_i$ be a witness and $\#$-witness for $x^0_i$ respectively. The existence of such witnesses was established immediately after Definition 5.5.

  • (c) Each $y^\#_i$ belongs to a single $\mathtt{G}$-cluster, that is, $\mathcal {G}_i$. Indeed, by definition, either $y^\#_i$ is outside the overlap in $\mathcal {G}_i$, or it is a leaf in $\mathcal {G}_i$. (Because of the way the $\mathtt{G}$-clusters are constructed in $T^0$, each leaf belongs to one maximal $\mathtt{G}$-cluster.)

  • (d) Combining (a) and (c), $y_1^\#, \ldots , y^\#_h$ must be distinct vertices in $T^\#$.

  • (e) Because $x_i^0$ and $y_i^0$ are at graph distance C and each edge in $T^\#$ corresponds to at most $g\Upsilon$ edges in $T^0$, the graph distance between $\tilde{x}^\#$ and $y_i^\#$ is at most $(C+1)g\Upsilon$. Here the $+1$ accounts for the fact that, as explained above, $x_i^0$ and $\tilde{x}^\#$ may not be matching.

  • (f) There are at most $3(2^{(C+1)g \Upsilon +1}-1) + 1$ vertices in $T^\#$ at graph distance $(C+1) g \Upsilon$ from $\tilde{x}^\#$. That follows from the fact that an h-level (counting the root) complete binary tree has $2^{h+1} - 1$ vertices.

  • (g) Combining (d), (e) and (f), we have established that $h \le 3(2^{(C+1) g \Upsilon +1}-1)$.

  Thus, using (38),

  $$\begin{aligned} \sum _{\mathcal {G}}|\mathcal {S}^\mathcal {G}| \le |\mathcal {S}^\#| \cdot 3(2^{(C+1) g \Upsilon +1}-1) \le 2 |\mathcal {O}^\#| \cdot 3 (2^{(C+1) g \Upsilon +1}-1). \end{aligned}$$

  (39)

It remains to combine (37) and (39) to obtain

$$\begin{aligned} |\mathcal {O}^0| \le 12 (2^{(C+1) g \Upsilon +1}-1) |\mathcal {O}^\#|. \end{aligned}$$

That concludes the proof.$\square$

Fig. 4

Witnesses outside the overlap. Here $x_i^0$ and $x_j^0$ are associated to $\tilde{x}^\#$. Their respective $\#$-witnesses are $y_i^\#$ and $y_j^\#$. The dotted lines surround the overlap

We now relate the blow-up distance between $T^0$ and $T^\#$ to the number of $\mathtt{R}$-vertices, from which tests can potentially be constructed, and the size of the overlap. We first bound the number of yellow vertices.

Claim 5.3

(Bounding the number of yellow vertices) We have

$$\begin{aligned} \#\mathtt{Y}\le \#\mathtt{R}. \end{aligned}$$

Proof

From our construction, each $\mathtt{Y}$-vertex in $T^0$ has at least two non-$\mathtt{G}$-children. Hence, intuitively, one can think of the $\mathtt{Y}$-vertices as forming the internal vertices of a forest of multifurcating trees whose leaves are $\mathtt{R}$-vertices.

The inequality follows.

Formally, if x is a $\mathtt{Y}$-vertex, from the observation above we have

$$\begin{aligned} \sum _{y \in \mathcal {V}_\ell (T^0_x)} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{\ell }} \mathbf {1}\{y \text { is a } \mathtt{R}\text {- vertex} \} \ge 1, \end{aligned}$$

(40)

by induction on the $\ell$-levels starting with the level farthest away from the root. Similarly if y is an $\mathtt{R}$-vertex,

we have

$$\begin{aligned} \sum _{x : y \in \mathcal {V}_\ell (T^0_x)} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{\ell }} \mathbf {1}\{x \text { is a } \mathtt{Y}\text {- vertex}\} < 1, \end{aligned}$$

(41)

where the inequality follows from the fact that the sum is over a path from x to the root of $T^0$. Summing (40) over $\mathtt{Y}$-vertices x and (41) over $\mathtt{R}$-vertices y gives the same quantity on the LHS, so that the RHS gives the inequality. $\square$

Claim 5.4

(Relating blowup, $\#\mathtt{R}$, and overlap) There is a constant $0< C_\mathcal {O}< +\infty$, depending on $\ell$, g and $\Upsilon$, such that

$$\begin{aligned} \Delta _{\mathrm {BL}}\left( T^0,T^\#\right) \le C_\mathcal {O}\left( \#\mathtt{R}+ \left| \mathcal {O}^\#\right| \right) . \end{aligned}$$

Proof

Our goal is to display a blowup from $T^0$ to $T^\#$ whose number of edges is bounded by a constant times the number of $\mathtt{R}$-vertices plus the size of the overlap in $T^\#$. We proceed in two steps:

• Edge removals. First we remove all edges in $T^0$ that are not in a maximal $\mathtt{G}$-cluster. To count how many such edges there are, we observe that there are at most $2^{\ell +1} - 2$ edges between a non-$\mathtt{G}$-vertex and its $\ell$-children. The edge above each non-$\mathtt{G}$-vertex is also removed if its parent $\ell$-vertex is colored $\mathtt{G}$. Hence, we need to remove at most $(2^{\ell +1} - 1) (\#\mathtt{R}+ \#\mathtt{Y})$ edges. We also remove all edges in the overlap, which adds at most an extra $|\mathcal {O}^0|$ edges to the total of those removed.

  Next we remove every edge adjacent to a degree-2 vertex produced by the removals above. Each edge removed above produces at most 4 such edges, bringing the total number of edges removed so far to at most

  $$\begin{aligned} 5[(2^{\ell +1} - 1)(\#\mathtt{R}+ \#\mathtt{Y}) + |\mathcal {O}^0|] \le 5\cdot 2^{\ell +1}(\#\mathtt{R}+ |\mathcal {O}^0|), \end{aligned}$$

  (42)

  where we used Claim 5.3.

  We call what is left the backbone. Because the backbone is a subset of the $\mathtt{G}$-clusters, every vertex of the backbone corresponds to a (non-extra) vertex in $T^\#$. (Recall that extra vertices were defined in Definition 3.3.) Every edge in the backbone, on the other hand, corresponds to a path in $T^\#$ with at most $g\Upsilon$ edges. Because $T^0$ and $T^\#$ have the same overall number of edges, the number of edges in $T^\#$ that do not lie on the backbone is at most $5\cdot 2^{\ell +1}(\#\mathtt{R}+ |\mathcal {O}^0|)$ by (42). Each such edge may be incident (in $T^\#$) to at most 2 edges in the backbone that are a path of length at least 2 in $T^\#$. We also remove all such edges from the backbone, finally bringing the total of edges removed to at most $15\cdot 2^{\ell +1}(\#\mathtt{R}+ |\mathcal {O}^0|)$.

• Edge additions. All edges and vertices left after the edge removals above correspond to (non-path) edges and (non-extra) vertices of $T^\#$. Because $T^0$ and $T^\#$ have the same overall number of edges, the number of edge additions needed to obtain $T^\#$ at this point is at most $15\cdot 2^{\ell +1}(\#\mathtt{R}+ |\mathcal {O}^0|)$.

From Claim 5.2, the constant $C_\mathcal {O}$ in the statement can be taken to be a function of $\ell$, g and $\Upsilon$.$\square$

Our next goal is to construct batteries with a number of tests scaling linearly in the blowup distance between $T^0$ and $T^\#$. Using Claim 5.4, we first divide the analysis into two cases depending on the values of $\#\mathtt{R}$ and $|\mathcal {O}^\#|$.

• Large overlap. If

  $$\begin{aligned} |\mathcal {O}^\#| \ge \frac{1}{10} \frac{\Delta _{\mathrm {BL}}(T^0,T^\#)}{C_\mathcal {O}}, \end{aligned}$$

  (43)

  we say that we are in the large overlap case. We will show in Sect. 5.6 that a linear (in the blowup distance) number of tests can be built “around the periphery of the overlap.” The choice of the factor 1 / 10 will be justified in Claim 5.5.

• Many $\mathtt{R}$-vertices. If, instead,

  $$\begin{aligned} |\mathcal {O}^\#| < \frac{1}{10} \frac{\Delta _{\mathrm {BL}}(T^0,T^\#)}{C_\mathcal {O}}, \end{aligned}$$

  (44)

  we say that we are in the many-$\mathtt{R}$ case. To justify the name we note that by Claim 5.4, if (44) holds, then

  $$\begin{aligned} \#\mathtt{R}\ge \frac{9}{10}\frac{\Delta _{\mathrm {BL}}(T^0,T^\#)}{C_\mathcal {O}}. \end{aligned}$$

  (45)

  In that case, we proceed similarly to the homogeneous case and construct a distinguishing test for a linear fraction of $\mathtt{R}$-vertices. See Sect. 5.5.

5.5 Constructing a battery of tests: many-$\mathtt{R}$ case

We now construct a battery of tests in the many-$\mathtt{R}$ case. This case is similar to the homogeneous case although many new difficulties arise. The basic idea remains the same: each $\mathtt{R}$-vertex has two $\mathtt{G}$-children which satisfy many of the requirements of a battery and therefore can potentially be used as a test pair. In particular, they are the roots of dense subtrees that are matching with their corresponding restricted subtrees in $T^\#$ and their evolutionary distance differs in $T^0$ and $T^\#$. Note that, in the many-$\mathtt{R}$ case, we also have a number of $\mathtt{R}$-vertices that scales linearly in the blowup distance. Compared to the homogeneous case, however, there are new issues to address to construct a battery of tests, mainly the possibility of overlapping $\mathtt{G}$-clusters and of non-co-hanging pairs in $T^\#$.

In this section, $T^0$ and $T^\#$ are fixed. To simplify notation, we let $\Delta = \Delta _{\mathrm {BL}}\left( T^0,T^\#\right)$. Fix $\wp = 1$. Choose $\ell = \ell (g,\wp )$ as in Proposition 1. Then take

$$\begin{aligned} \Gamma = (6 + 2\Upsilon g) \ell , \end{aligned}$$

(46)

and set $\gamma _t \ge \Gamma$, a multiple of $\ell$, and C as in Proposition 1.

Choosing non-overlapping $\mathtt{G}$-clusters. To satisfy the requirements of the battery, the test subtrees must be non-intersecting in $T^\#$. (By construction, the test subtrees are non-intersecting in $T^0$.) We proceed by showing that sufficiently many non-overlapping $\mathtt{G}$-clusters can be found. For this purpose, we use a re-coloring procedure. Re-color $\mathtt{B}$ (for black) those $\mathtt{R}$-vertices that have at least one $\mathtt{G}$-child who is the root of a $\mathtt{G}$-cluster that intersects with another $\mathtt{G}$-cluster in $T^\#$. (This recoloring procedure is performed only once.) Intuitively, if too many $\mathtt{R}$-vertices are lost in this recoloring step, then the overlap must be large. That cannot be the case by (44). Indeed, we prove the following.

Claim 5.5

(Re-coloring) In the many-$\mathtt{R}$ case, after re-coloring, we have

$$\begin{aligned} \#\mathtt{R}\ge \frac{\Delta }{2C_\mathcal {O}}, \end{aligned}$$

where $C_\mathcal {O}$, which depends on $\ell$, g and $\Upsilon$, was defined in Claim 5.4.

Proof

Assume maximal $\mathtt{G}$-cluster $\mathcal {G}_i$ intersects with a distinct maximal $\mathtt{G}$-cluster in $T^\#$ and let $\mathcal {M}_i$ be the matching subtree corresponding to $\mathcal {G}_i$ in $T^\#$. Consider a shortest path in graph distance between a leaf in $\mathcal {M}_i$ and the overlap in $T^\#$. Let $v_i$ be the vertex in $T^\#$ where this path enters the overlap. Because 1) $T^\#$ is bifurcating, 2) at least one edge adjacent to $v_i$ must be in $\mathcal {O}^\#$, and 3) at least one edge adjacent to $v_i$ must be in $\mathcal {M}_i$ outside the overlap,

it follows that $v_i$ can arise as the entrance vertex to the overlap for at most two maximal $\mathtt{G}$-clusters. Hence, each maximal $\mathtt{G}$-clusters intersecting with another maximal $\mathtt{G}$-cluster is associated an entrance vertex in the overlap that can be used at most twice. So the number of such clusters is bounded by

$$\begin{aligned} 2 \cdot 2\left| \mathcal {O}^\#\right| \le 4\frac{1}{10} \frac{\Delta }{C_\mathcal {O}}, \end{aligned}$$

where we used (44) and where we took into account that the number of vertices in the overlap is at most twice the number of edges in the overlap. Moreover, observe that each such cluster contributes to the recoloring of at most one $\mathtt{R}$-vertex. That implies that the number of recolored $\ell$-vertices is at most $4\frac{1}{10} \frac{\Delta }{C_\mathcal {O}}$. After recoloring we therefore have

$$\begin{aligned} \#\mathtt{R}\ge \frac{9}{10}\frac{\Delta }{C_\mathcal {O}} - 4\frac{1}{10} \frac{\Delta }{C_\mathcal {O}} = \frac{\Delta }{2 C_\mathcal {O}}, \end{aligned}$$

where we used (45). $\square$

In the rest of this subsection, we build a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0)\text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in }T^\#) \end{aligned}$$

with corresponding $\alpha _i$s as defined in Definition 3.7. We number the $\mathtt{R}$-vertices $i=1,\ldots ,I'$ after recoloring and we build one test panel for each $\mathtt{R}$-vertex. Here it will turn out that $I' \ge I$ as we will later need to reject some of the test panels to avoid unwanted correlations. We root $T^\#$ at an arbitrary vertex $\rho ^\#$. (The rootings of $T^0$ and $T^\#$ need not be consistent at this point.)

5.5.1 Constructing co-hanging test panels

Let $x^0_i$ be an $\mathtt{R}$-vertex (after recoloring) in $T^0$. Because $x^0_i$ is colored $\mathtt{R}$, by definition it has at least $2^\ell - 1$ $\mathtt{G}$-children, but its $\mathtt{G}$-children are connected in a different way in $T^\#$. We distinguish between two cases:

• 1. An appropriate co-hanging pair can be found: All pairs of $\mathtt{G}$-children of $x^0_i$ are the roots of co-hanging, non-overlapping matching subtrees in $T^\#$. In that case at least one pair of $\mathtt{G}$-children $(y^0_i,z^0_i)$ must be at a different evolutionary distance in $T^0$ than the corresponding pair $(y^\#_i,z^\#_i)$ in $T^\#$. We use these pairs as our test panel, modulo the following re-rooting. If a test subtree is not rooted consistently in $T^0$ and $T^\#$, we move the corresponding test vertices to one of their corresponding $\mathtt{G}$-children where the rooting is consistent. This can always be done as there is at most one $\mathtt{G}$-child of a $\mathtt{G}$-vertex between itself and the root of $T^\#$. All other choices lead to a consistent rooting. See Fig. 5 for an illustration.

• 2. There exists a non-co-hanging pair: Otherwise at least one pair $(\tilde{y}^0_i,\tilde{z}^0_i)$ of $\mathtt{G}$-children of $x^0_i$, with corresponding pair $(\tilde{y}^\#_i,\tilde{z}^\#_i)$, has a connecting path in $T^\#$ that intersects with the corresponding matching test subtrees, $\tilde{Y}^\#_i$ or $\tilde{Z}^\#_i$ (or both). Indeed, although by construction the test subtrees are matching in $T^0$ and $T^\#$, the path connecting them may be “positioned differently”. See Fig. 6 for an illustration of such a case. The main goal of the next claim is to show how to construct an appropriate co-hanging test panel in this case.

Fig. 5

Construction of the test in the co-hanging sub-case of the many-$\mathtt{R}$ case. The root of the cluster in $T^\#$ is denoted by $\rho _i^\#$. Moving the test pair to the $\mathtt{G}$-children $y_i^0$ and $y_i^\#$ has the effect of making the new test subtrees rooted consistently

Fig. 6

Construction of the test in the non-co-hanging sub-case of the many-$\mathtt{R}$ case when $\tilde{y}^\#_i,\tilde{z}^\#_i$ are “far”. The root of the cluster in $T^\#$ is denoted by $\rho _i^\#$

Fig. 7

Construction of the test in the non-co-hanging sub-case of the many-$\mathtt{R}$ case when $\tilde{y}^\#_i,\tilde{z}^\#_i$ are “close”. The root of the cluster in $T^\#$ is denoted by $\rho _i^\#$

Claim 5.6

(Co-hanging pairs) In the many-$\mathtt{R}$ case, after recoloring, for each remaining $\mathtt{R}$-vertex $x^0_i$ we can find a test pair of $\mathtt{G}$-vertices $(y^0_i,z^0_i)$ in the subtree rooted at $x^0_i$ in $T^0$, with corresponding test pair $(y^\#_i,z^\#_i)$ in $T^\#$, such that the test panel satisfy the cluster and pair requirements of a battery.

Proof

We consider again the two cases above.

An appropriate co-hanging pair can be found We proceed as we described above the statement of the claim. By construction the test subtrees, that is, the $\mathtt{G}$-clusters rooted at the test vertices, are $(\ell ,1)$-dense. The test subtrees are also matching, co-hanging and their roots are at different evolutionary distances in $T^0$ and $T^\#$ by (48). Finally, the test pair in $T^0$ is proximal as

$$\begin{aligned} \mathrm {d}^{\mathrm {g}}_{T^0}\left( y^0_i, z^0_i\right) \le 4\ell \le \Gamma , \end{aligned}$$

where we note that re-rooting procedure may increase the distance by at most $2\ell$.

There exists a non-co-hanging pair For the second case, we use the notation of Item 2 above the statement of the claim. Because $T^\#$ has no cycle, the path between $\tilde{y}^\#_i$ and $\tilde{z}^\#_i$ must be of the following form: there is a vertex $v^\#$ in $\tilde{Y}^\#_i$ (possibly equal to $\tilde{y}^\#_i$) and a vertex $w^\#$ in $\tilde{Z}^\#_i$ (possibly equal to $\tilde{z}^\#_i$) such that the path between $\tilde{y}^\#_i$ and $\tilde{z}^\#_i$ 1) intersects with $\tilde{Y}^\#_i$ between $\tilde{y}^\#_i$ and $v^\#$, 2) does not intersect with either $\tilde{Y}^\#_i$ or $\tilde{Z}^\#_i$ between $v^\#$ and $w^\#$, and 3) intersects with $\tilde{Z}^\#_i$ between $w^\#$ and $\tilde{z}^\#_i$. See Figs. 6 and 7 for an illustration. We let $v^0$ and $w^0$ be the extra vertices corresponding respectively to $v^\#$ and $w^\#$ in $T^0$. (Recall that extra vertices were defined in Definition 3.3.) We consider two subcases:

• 1. $\tilde{y}^\#_i,\tilde{z}^\#_i$ are “far” in $T^\#$. Suppose first that

  $$\begin{aligned} \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i,\tilde{z}^\#_i\right) > 2g\ell . \end{aligned}$$

  (47)

  That case is illustrated in Fig. 6. We construct a co-hanging test panel by choosing appropriate $\mathtt{G}$-children as follows. Recall that we must ensure in particular that our chosen pairs are co-hanging and at different evolutionary distances in $T^0$ and $T^\#$. If $v^\# = \tilde{y}^\#_i$, we simply set $y^\#_i = \tilde{y}^\#_i$. If $v^\# \ne \tilde{y}^\#_i$, let $y^0_i$ be a $\mathtt{G}$-child of $\tilde{y}^0_i$ which satisfies the following:

  • Observe that one of the two children of $\tilde{y}^0_i$ is the root of a subtree containing $v^0$. We choose $y^0_i$ in the other subtree. This is to guarantee that the path joining $y^0_i$ and $z^0_i$ (below) does not intersect the resulting subtrees. See Fig. 6.

  • We also choose $y^0_i$ so that the test subtree rooted at $y^0_i$ and the test subtree rooted at the corresponding vertex $y^\#_i$ in $T^\#$ are rooted consistently. This can always be done as there is at most one $\mathtt{G}$-child of $\mathtt{G}$-vertex between itself and the root of $T^\#$. All other choices, of which there are overall at least $2^\ell /2 - 1$ satisfying the first property above, lead to a consistent rooting. We pick $y_i^0$ arbitrarily among them.

  We define $z^0_i$ and $z^\#_i$ similarly. As a result of this construction, the subtrees rooted at $y^\#_i$ and $z^\#_i$ are co-hanging in $T^\#$ by construction.

  Moreover, the evolutionary distance between $y_i^0$ and $z_i^0$ satisfies

  $$\begin{aligned} \mathrm {d}_{T^0}\left( y^0_i, z^0_i\right)= & {} \mathrm {d}_{T^0}\left( y^0_i, \tilde{y}^0_i\right) + \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{z}^0_i\right) + \mathrm {d}_{T^0}\left( \tilde{z}^0_i, z^0_i\right) \nonumber \\\le & {} \mathrm {d}_{T^0}\left( y^0_i, \tilde{y}^0_i\right) + 2g\ell + \mathrm {d}_{T^0}\left( \tilde{z}^0_i, z^0_i\right) \nonumber \\< & {} \mathrm {d}_{T^\#}\left( y^\#_i, \tilde{y}^\#_i\right) + \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i,\tilde{z}^\#_i\right) + \mathrm {d}_{T^\#}\left( \tilde{z}^\#_i, z^\#_i\right) \nonumber \\= & {} \mathrm {d}_{T^\#}\left( y^\#_i,z^\#_i\right) , \end{aligned}$$

  (48)

  where, on the second line, we used that $\tilde{y}^0_i$, $\tilde{z}^0_i$ were chosen to be $\mathtt{G}$-children of $x_i^0$ in $T^0$ and, on third line, we used (47) and the fact that $\mathrm {d}_{T^0}(y^0_i, \tilde{y}^0_i) = \mathrm {d}_{T^\#}(y^\#_i, \tilde{y}^\#_i)$ and $\mathrm {d}_{T^0}(\tilde{z}^0_i, z^0_i) = \mathrm {d}_{T^\#}(\tilde{z}^\#_i, z^\#_i)$ by the matching condition. That is, $\mathrm {d}_{T^0}(y^0_i, z^0_i) \ne \mathrm {d}_{T^\#}(y^\#_i,z^\#_i)$ as required. Hence the pairs $(y^0_i, z^0_i)$ and $(y^\#_i, z^\#_i)$ satisfy the cluster and pair requirements of the battery. Indeed by construction the test subtrees are $(\ell ,1)$-dense. The test subtrees are also matching, co-hanging and their roots are at different evolutionary distances in $T^0$ and $T^\#$ by (48). Finally, the test pair in $T^0$ is proximal as

  $$\begin{aligned} \mathrm {d}^{\mathrm {g}}_{T^0}\left( y^0_i, z^0_i\right) \le 4\ell \le \Gamma , \end{aligned}$$

  because $y^0_i, z^0_i$ are $\mathtt{G}$-grandchildren of $x^0_i$.

• 2. $\tilde{y}^\#_i,\tilde{z}^\#_i$ are “close” in $T^\#$. Assume instead that

  $$\begin{aligned} \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i,\tilde{z}^\#_i\right) \le 2g\ell . \end{aligned}$$

  (49)

  That case is illustrated in Fig. 7. We consider two sub-cases:

  • (a) If

    $$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{z}^0_i\right) \ne \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i,\tilde{z}^\#_i\right) , \end{aligned}$$

    (50)

    we proceed as in the “far” case above. The argument then follows in the same way with (50) playing the role of (47) in (48).

  • (b) If instead

    $$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{z}^0_i\right) = \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i,\tilde{z}^\#_i\right) , \end{aligned}$$

    (51)

    we choose the test pairs below $v^0$ and $w^0$ respectively, as shown in Fig. 7. Formally, let $y^0_i$ be the closest $\mathtt{G}$-vertex below $v^0$ resulting in a consistent rooting. Let $z^0_i$ be defined similarly. Such vertices exist within graph distance at most $2\ell$ of $v^0$ and $w^0$. (Note that the latter are not in general $\mathtt{G}$-vertices themselves which, in addition to the $(\ell ,1)$-density assumption, explains the $2 \ell$.) Let $y^\#_i$ and $z^\#_i$ be the corresponding vertices in $T^\#$.

    Then, the path connecting $y_i^\#$ and $z_i^\#$ in $T^\#$ goes through $v^\#$ and $w^\#$, and we have

    $$\begin{aligned} \mathrm {d}_{T^\#}\left( y^\#_i,z^\#_i\right)= & {} \mathrm {d}_{T^\#}\left( y^\#_i,v^\#\right) + \mathrm {d}_{T^\#}\left( v^\#,w^\#\right) + \mathrm {d}_{T^\#}\left( w^\#,z^\#_i\right) \nonumber \\< & {} \mathrm {d}_{T^0}\left( y^0_i,\tilde{y}^0_i\right) + \mathrm {d}_{T^0}\left( \tilde{y}^0_i,\tilde{z}^0_i\right) + \mathrm {d}_{T^0}\left( \tilde{z}^0_i,z^0_i\right) \nonumber \\= & {} \mathrm {d}_{T^0}\left( y^0_i,z^0_i\right) , \end{aligned}$$

    (52)

    where the inequality holds term by term. For the first term, we note that the path from $y_i^0$ to $\tilde{y}_i^0$ in $T^0$ goes through $v^0$, and similarly for the third term. For the second term, we use (51) and the fact that the path connecting v and w is a sub-path of the path connecting $\tilde{y}_i^0$ and $\tilde{z}_i^0$. Hence, we have established that $\mathrm {d}_{T^0}(y^0_i, z^0_i) \ne \mathrm {d}_{T^\#}(y^\#_i,z^\#_i)$. Moreover note that the subtrees rooted at $y^\#_i$ and $z^\#_i$ are co-hanging in $T^\#$. The resulting test subtrees are also matching and $(\ell ,1)$-dense by construction. It remains to check the proximality condition. From the choice of $y^\#_i$, $z^\#_i$,

    $$\begin{aligned} \mathrm {d}^{\mathrm {g}}_{T^0}\left( y^0_i,z^0_i\right)= & {} \mathrm {d}^{\mathrm {g}}_{T^0}\left( y^0_i,v^0\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( v^0,\tilde{y}^0_i\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( \tilde{y}^0_i,\tilde{z}^0_i\right) \\&+ \mathrm {d}^{\mathrm {g}}_{T^0}\left( \tilde{z}^0_i,w^0\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( w^0,z^0_i\right) \\= & {} \mathrm {d}^{\mathrm {g}}_{T^0}\left( \tilde{y}^0_i,\tilde{z}^0_i\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( y^0_i,v^0\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( w^0,z^0_i\right) \\&+ \left[ \mathrm {d}^{\mathrm {g}}_{T^0}\left( v^0,\tilde{y}^0_i\right) + \mathrm {d}^{\mathrm {g}}_{T^0}\left( \tilde{z}^0_i,w^0\right) \right] \\\le & {} 2\ell + 2\ell + 2\ell + 2\Upsilon g\ell \\= & {} \left( 6 + 2\Upsilon g\right) \ell \\\le & {} \Gamma , \end{aligned}$$

    where the equality on the second line is a rearrangement of terms and the inequality on the third line holds term by term: the first term follows from the fact that $\tilde{y}_i^0$ and $\tilde{z}_i^0$ are both $\mathtt{G}$-children of $\tilde{x}_i^0$; the second and third terms follow from the choice of $y_i^0$ and $z^0_i$ as described above; and the term in square brackets is an application of (49) and (51) converted into graph distance through a multiplication by $\Upsilon$, together with the observation that the paths from $v^0$ to $\tilde{y}_i^0$ and from $\tilde{z}_i^0$ to $w^0$ match the paths from $v^\#$ to $\tilde{y}_i^\#$ and from $\tilde{z}_i^\#$ to $w^\#$, which are themselves sub-paths of the path from $\tilde{y}_i^\#$ to $\tilde{z}_i^\#$. Recall that $\Gamma$ is defined in (46). Hence the pairs $(y^0_i, z^0_i)$ and $(y^\#_i, z^\#_i)$ satisfy the cluster and pair requirements of the battery.

That concludes the proof.$\square$

5.5.2 Sparsification in $T^\#$

It remains to satisfy the global requirements of the battery. By the construction in Claim 5.6 the test subtrees are non-intersecting in both $T^0$ and $T^\#$. However we must also ensure that proximal/semi-proximal connecting paths and non-proximal hats do not intersect with each other or with test subtrees from other test panels. By construction, this is automatically satisfied in $T^0$ where all test pairs are proximal. To satisfy this requirement in $T^\#$, we make the collection of test pairs “sparser” by rejecting an appropriate fraction of them.

Claim 5.7

(Sparsification in $T^\#$) Let $\mathcal {H}' = \{(y^0_i,z^0_i); (y^\#_i,z^\#_i)\}_{i=1}^{I'}$ be the test panels constructed in Claim 5.6. We can find a subset $\mathcal {H}\subseteq \mathcal {H}'$ of size

$$\begin{aligned} |\mathcal {H}| = I \ge \frac{1}{1 + 2^{2\gamma _t + 2}} I' \ge \frac{\Delta }{2 C_\mathcal {O}(1 + 2^{2\gamma _t + 2})} \end{aligned}$$

such that the test panels in $\mathcal {H}$ satisfy all global requirements of a battery.

Proof

We sparsify the set $\mathcal {H}'$ of test pairs as follows. Let $\{(Y^0_i,Z^0_i); (Y^\#_i,Z^\#_i)\}_{i=1}^{I'}$ be the test subtrees corresponding to $\mathcal {H}'$. Start with test panel $((y^0_1,z^0_1); (y^\#_1,z^\#_1))$. Remove from $\mathcal {H}'$ all test panels $i \ne 1$ such that

$$\begin{aligned} \min \left\{ \mathrm {d}^{\mathrm {g}}_{T^\#}(v,w)\ :\ v \in \{y^\#_1,z^\#_1\}, w \in \mathcal {V}(Y^\#_i)\cup \mathcal {V}(Z^\#_i)\right\} \le 2\gamma _t. \end{aligned}$$

(53)

Because there are at most $2\cdot 2^{2\gamma _t + 1}$ vertices w in $T^\#$ satisfying the above condition and that the test subtrees are non-overlapping in $T^\#$ (so that any such vertex belongs to at most one test subtree), we remove at most $2^{2\gamma _t + 2}$ test panels from $\mathcal {H}'$.

Let i be the smallest index remaining in $\mathcal {H}'$. Proceed as above and then repeat until all indices in $\mathcal {H}'$ have been selected or rejected.

At the end of the procedure, there are at least

$$\begin{aligned} \frac{1}{1 + 2^{2\gamma _t + 2}} I' \end{aligned}$$

test panels remaining, the set of which we denote by $\mathcal {H}$. Recall that $\gamma _t \ge \Gamma$. Hence by (53), in $\mathcal {H}$, the connecting paths of proximal/semi-proximal pairs and the hats of non-proximal pairs cannot intersect with each other or with any of the test subtree rooted at test vertices in $\mathcal {H}$.$\square$

5.5.3 Summary of many-$\mathtt{R}$ case

We have proved the following in the many-$\mathtt{R}$ case. Recall that $\wp = 1$, $\ell = \ell (g,\wp )$ is chosen as in Proposition 1, $\Gamma = (6 + 4\Upsilon g) \ell$, and $\gamma _t \ge \Gamma$, a multiple of $\ell$, and C are chosen as in Proposition 1.

Proposition 4

(Battery in the many-$\mathtt{R}$ case) In the many-$\mathtt{R}$ case, we can build a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in } T^0)\quad \text {and }\quad \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in }T^\#) \end{aligned}$$

with

$$\begin{aligned} I \ge \frac{\Delta }{2 C_\mathcal {O}(1 + 2^{2\gamma _t + 2})}. \end{aligned}$$

Proof

The result follows from Claims 5.5, 5.6, and 5.7.$\square$

5.6 Constructing a battery of tests: large overlap case

We now construct a battery of tests in the large overlap case. By assumption we have,

$$\begin{aligned} |\mathcal {O}^\#| \ge \frac{1}{10} \frac{\Delta _{\mathrm {BL}}(T^0,T^\#)}{C_\mathcal {O}}. \end{aligned}$$

Moreover, by the proof of Claim 5.2, a significant fraction of the vertices in the overlap are in fact shallow, that is, they are close to the boundary of the overlap. To build a battery in this case, we show that a test pair can be found near each shallow vertex. As in the many-$\mathtt{R}$ case, we need to deal with a number of issues, including the overlap of $\mathtt{G}$-clusters, the possibility of non-co-hanging pairs, and the proximity of the matching subtrees.

In this section, $T^0$ and $T^\#$ are fixed. To simplify notation, we let $\Delta = \Delta _{\mathrm {BL}}\left( T^0,T^\#\right)$. Recall that $T^0$ is rooted. We also root $T^\#$ arbitrarily. Fix $\wp = 5$. Choose $\ell = \ell (g,\wp )$ as in Proposition 1. Then take

$$\begin{aligned} \Gamma = 6 g \Upsilon \log _2 \left( \frac{8}{1 - 1/\sqrt{2}}\right) + 2\ell g \Upsilon + 4, \end{aligned}$$

and set $\gamma _t \ge \Gamma$, a multiple of $\ell$, and C as in Proposition 1.

Fig. 8

Construction of the test in the large overlap case. The region inside the dotted lineis part of the overlap in $T^\#$

5.6.1 Test pairs near the boundary of the overlap

Let $v^\#$ in $T^\#$ be in the overlap. Intuitively, vertex $v^\#$ can be used to construct a test pair for the following two reasons:

• It corresponds to (at least) two vertices $v^0_i$, $v^0_j$ in $T^0$ from distinct clusters. The evolutionary distance between these vertices differs in $T^0$, where it is $> 0$, and in $T^\#$, where it is 0.

• The vertex $v^\#$ is in the matching $\mathtt{G}$-clusters of those including $v^0_i$ and $v^0_j$. Hence its sequence can be reconstructed using the same estimator on $T^0$ and $T^\#$.

However, to avoid unwanted correlations between the ancestral reconstructions on $T^\#$, one must be careful to construct appropriate co-hanging test subtrees that further satisfy all requirements of a battery. We proceed instead by identifying pairs of edges in $T^0$ that overlap close to its boundary.

• 1. Bounding the number of overlap-shallow edges in $T^0$. Recall the definition of an overlap-shallow vertex from Definition 5.5 (in Claim 5.2). We further say that an edge $e = (x,w)$ in $\mathcal {O}^0$ is overlap-shallow with parameter $\beta$ if both x and w are overlap-shallow with parameter $\beta$. We call deep those vertices and edges that are not overlap-shallow. Proceeding as in (35), we see that at most a fraction $1 - 1/\beta$ of vertices in the overlap are deep. Each such vertex prevents at most 3 edges in $\mathcal {O}^0$ from being overlap-shallow. From the fact there are at most twice as many vertices in the overlap as there are edges, we get that the number of overlap-shallow edges in $T^0$ is at least

  $$\begin{aligned} \left[ 1 - 6 \left( 1- \frac{1}{\beta }\right) \right] |\mathcal {O}^0|. \end{aligned}$$

  (54)

  We will later choose $\beta > 1$ close enough to 1 that the above fraction is positive.

• 2. Bounding the number of intersecting pairs of shallow edges. For reasons that will be explained below, our test construction is based on finding pairs of shallow edges that intersect. Formally, we say that $e_1, e_2 \in \mathcal {O}^0$ intersect if the corresponding paths in $T^\#$ share an edge. We say that an edge $e_1 \in \mathcal {O}^0$ is useful if it is overlap-shallow and if it intersects with at least one other overlap-shallow edge $e_2 \ne e_1$. Note that here $e_1$ and $e_2$ must belong to distinct maximal $\mathtt{G}$-clusters (otherwise the corresponding cluster would not be matching in $T^\#$). Let $e_0 \in \mathcal {O}^0$ be deep. Recall that $e_0$ corresponds to a path of length at most $g\Upsilon$ in $T^\#$. Let $e_1, e_2$ are overlap-shallow edges intersecting with $e_0$ but not with each other. Then the paths corresponding to each of $e_1$ and $e_2$ in $T^\#$ must intersect with different edges on the path corresponding to $e_0$. Put differently, any deep edge $e_0$ can prevent at most $g\Upsilon$ shallow edges from intersecting with any other shallow edge. Combining this with (54), we get that the number of useful edges in $T^0$ is at least

  $$\begin{aligned} \left[ 1 - 6 g \Upsilon \left( 1- \frac{1}{\beta }\right) \right] |\mathcal {O}^0|. \end{aligned}$$

  (55)

• 3. Existence of four close witnesses. Let $e_i = (w_i^+,w_i^-)$ be a useful edge in $\mathcal {G}_i$. Let $e_j = (w_j^+,w_j^-)$ in $\mathcal {G}_j$ be an overlap-shallow edge intersecting with $e_i$ and let $e^\#$ be an edge in $T^\#$ lying on the paths corresponding to both $e_i$ and $e_j$. Assume that, for $\iota = i,j$, $w_\iota ^+$ is the parent of $w_\iota ^-$. By definition of a useful edge, both $w_i^+$ and $w_j^+$ are overlap-shallow. In the proof of Claim 5.2, we argued that (32) implies the existence of a close witness, that is, a leaf or vertex not in the overlap at a constant graph distance. By restricting the sum in (32) to those vertices that are on only one side below $w_\iota ^+$ (that is, below one of its immediate children), we can find in fact two distinct witnesses $\tilde{y}^0_\iota$ and $\tilde{z}^0_\iota$ at constant graph distance $C' = C'(g, \Upsilon )$ from $w_\iota ^+$, one on each side. The four witnesses $\tilde{y}^0_i$, $\tilde{z}^0_i$, $\tilde{y}^0_j$, $\tilde{z}^0_j$ jointly satisfy the following properties:

  • They are not in the overlap.

  • For $\iota = i,j$, $\tilde{y}^0_\iota$ and $\tilde{z}^0_\iota$ are in $\mathcal {G}_\iota$.

  • For $x = y,z$, the vertices in $T^\#$ corresponding to $\tilde{x}^0_i$ and $\tilde{x}^0_j$ are on the same side of $e^\#$, that is, the path between them does not cross $e^\#$.

  Let $\tilde{y}^\#_i$, $\tilde{y}^\#_j$, $\tilde{z}^\#_i$, and $\tilde{z}^\#_j$ be the corresponding vertices in $T^\#$.

• 4. Key observation: quartet topologies differ on $T^0$ and $T^\#$. We construct a test pair nearby $e_i$ as follows. The key observation is the following: by construction, the topology of $T^0$ restricted to the witnesses $\{\tilde{y}^0_i, \tilde{y}^0_j, \tilde{z}^0_i, \tilde{z}^0_j\}$ is $\tilde{y}^0_i \tilde{z}^0_i | \tilde{y}^0_j \tilde{z}^0_j$ while the topology of $T^\#$ restricted to the corresponding vertices $\{\tilde{y}^\#_i, \tilde{y}^\#_j, \tilde{z}^\#_i, \tilde{z}^\#_j\}$ is $\tilde{y}^\#_i \tilde{y}^\#_j | \tilde{z}^\#_i \tilde{z}^\#_j$. Indeed, on $T^0$, the pairs $\{\tilde{y}^0_i, \tilde{z}^0_i\}$, $\{\tilde{y}^0_j, \tilde{z}^0_j\}$ belong to distinct co-hanging clusters and their most recent common ancestors are therefore separated by the path joining the roots of those clusters. On $T^\#$, on the other hand, by construction $e^\#$ separates $\{\tilde{y}^\#_i, \tilde{y}^\#_j\}$ from $\{\tilde{z}^\#_i, \tilde{z}^\#_j\}$. See Fig. 8 for an illustration and refer to Definition 3.1 for quartet topology notation.

• 5. Existence of witnesses at different evolutionary distances on $T^0$ and $T^\#$. The reason the above observation is significant is that it allows us to find a pair among the witnesses whose evolutionary distance differs on $T^0$ and $T^\#$, as we show next. Note that

  $$\begin{aligned} \mathrm {d}_{T^0}(\tilde{y}^0_\iota , \tilde{z}^0_\iota ) = \mathrm {d}_{T^\#}(\tilde{y}^\#_\iota , \tilde{z}^\#_\iota ) \end{aligned}$$

  (56)

  for $\iota = i, j$ by definition of the matching subtree of $\mathcal {G}_\iota$. Moreover, by the four-point condition (8) in the non-degenerate case,

  $$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{y}^0_j\right) + \mathrm {d}_{T^0}\left( \tilde{z}^0_i, \tilde{z}^0_j\right) > \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{z}^0_i\right) + \mathrm {d}_{T^0}\left( \tilde{y}^0_j, \tilde{z}^0_j\right) , \end{aligned}$$

  and

  $$\begin{aligned} \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i, \tilde{z}^\#_i\right) + \mathrm {d}_{T^\#}\left( \tilde{y}^\#_j, \tilde{z}^\#_j\right) > \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i, \tilde{y}^\#_j\right) + \mathrm {d}_{T^\#}\left( \tilde{z}^\#_i, \tilde{z}^\#_j\right) , \end{aligned}$$

  which, with (56), implies

  $$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{y}^0_j\right) + \mathrm {d}_{T^0}\left( \tilde{z}^0_i, \tilde{z}^0_j\right) > \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i, \tilde{y}^\#_j\right) + \mathrm {d}_{T^\#}\left( \tilde{z}^\#_i, \tilde{z}^\#_j\right) . \end{aligned}$$

  Hence one of the following must hold

  $$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{y}^0_j\right)> \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i, \tilde{y}^\#_j\right) \quad \text {or} \quad \mathrm {d}_{T^0}\left( \tilde{z}^0_i, \tilde{z}^0_j\right) > \mathrm {d}_{T^\#}\left( \tilde{z}^\#_i, \tilde{z}^\#_j\right) . \end{aligned}$$

  Without loss of generality, assume that $\mathrm {d}_{T^0}(\tilde{y}^0_i, \tilde{y}^0_j) > \mathrm {d}_{T^\#}(\tilde{y}^\#_i, \tilde{y}^\#_j).$

• 6. Distance to witnesses. We will also need to bound $\mathrm {d}_{T^\#}(\tilde{y}^\#_i, \tilde{y}^\#_j)$. It suffices to bound $C'$ above.

Claim 5.8

(Distance to witnesses) We have

$$\begin{aligned} C' \le 3 \log _2 \left( \frac{4\beta }{1 - 1/\sqrt{2}}\right) , \end{aligned}$$

for $\ell$ large enoug.

Proof

We use the notation of Claim 5.2. Assume all vertices in $\mathcal {V}^{\mathcal {G}_i}_{w_i^-}$ within graph distance $C' - 1$ are in $\mathcal {W}^{\mathcal {G}_i}_{w_i^-}$. Because $\mathcal {G}_i$ is $(\ell ,1)$-dense, we have that within graph distance $C'$ of $w_i^+$ there is at least

$$\begin{aligned} \frac{1}{2} (2^\ell - 1)^{\frac{C'}{\ell }} \end{aligned}$$

vertices in $\mathcal {W}^{\mathcal {G}_i}_{w_i^+}$ below $w_i^-$, where we counted only the furthest vertices within this ball. Hence the sum in (32) restricted to vertices below $w_i^-$ satisfies

$$\begin{aligned} \sum _{y \in \mathcal {W}^{\mathcal {G}_i}_{w_i^-}} 2^{-\frac{\mathrm {d}^{\mathrm {g}}_{T^0}(x,y)}{2}} \ge \frac{1}{2} (2^\ell - 1)^{\frac{C'}{\ell }} 2^{-\frac{C'}{2}} \ge \frac{1}{2} 2^{\frac{C'}{3}} > \frac{\beta }{1 - 1/\sqrt{2}}, \end{aligned}$$

for $\ell$ large enough, if

$$\begin{aligned} C' > 3 \log _2 \left( \frac{4\beta }{1 - 1/\sqrt{2}}\right) . \end{aligned}$$

$\square$

We repeat the procedure above for each useful edge and get a collection of pre-test panels. To satisfy the requirements of the battery we then proceed, similarly to the many-$\mathtt{R}$ case, by re-rooting and sparsification. We describe these steps next.

5.6.2 Co-hanging pairs

Note that the roots of $T^0$ and $T^\#$ may not be consistent, in the sense that the $\mathtt{G}$-clusters and their matching subtrees may not be rooted at corresponding vertices. However we can make it so that the test subtrees are rooted consistently and ensure that the test subtrees are co-hanging.

For every pre-test panel constructed above, using the same notation, we proceed as follows. If $\tilde{y}^0_i$ is on the path between the root of $\mathcal {G}_i$ in $T^0$ and the (possibly extra) vertex corresponding to the root of the matching subtree in $T^\#$, we move $\tilde{y}^\#_i$ over to one of its immediate children such that the corresponding vertex $\tilde{y}^0_i$ is not on this path—unless $\tilde{y}^0_j$ is a descendant of that vertex. In that case, we instead move $\tilde{y}^\#_i$ over to the child of its other immediate child such that the corresponding vertex $\tilde{y}^0_i$ is not on the path above. The reason we need these two cases is that we seek to preserve the inequality

$$\begin{aligned} \mathrm {d}_{T^0}\left( \tilde{y}^0_i, \tilde{y}^0_j\right) > \mathrm {d}_{T^\#}\left( \tilde{y}^\#_i, \tilde{y}^\#_j\right) . \end{aligned}$$

In both cases, the two sides of the inequality increase by the same amount, at most 2g. We do the same on $\mathcal {G}_j$.

At this point, 1) the $\mathtt{G}$-cluster of $T^0$ rooted at $\tilde{y}^0_i$ and the matching subtree rooted at $\tilde{y}^\#_i$ are rooted consistently (and similarly for $\tilde{y}^0_j$ and $\tilde{y}^\#_i$) and 2) the $\mathtt{G}$-clusters rooted at $\tilde{y}^0_i$ and $\tilde{y}^0_j$ are co-hanging (and similarly for the matching subtrees in $T^\#$).

Let $y^0_i$ be a closest $\mathtt{G}$-vertex below $\tilde{y}^0_i$ on $\mathcal {G}_i$ and similarly for $y^0_j$. Let $y^\#_i$ and $y^\#_j$ be the corresponding vertices in $T^\#$. Then the test subtrees (that is the $\mathtt{G}$-clusters) $\bar{Y}^0_i$, $\bar{Y}^0_j$ $\bar{Y}^\#_i$ and $\bar{Y}^\#_j$ rooted respectively at $y^0_i$, $y^0_j$ $y^\#_i$ and $y^\#_j$ are such that $(\bar{Y}^0_i, \bar{Y}^0_j)$ and $(\bar{Y}^\#_i, \bar{Y}^\#_j)$ are co-hanging. In particular, they are non-intersecting by construction. Indeed, $(\bar{Y}^0_i, \bar{Y}^0_j)$ belong to different $\mathtt{G}$-clusters in $T^0$ and $(\bar{Y}^\#_i, \bar{Y}^\#_j)$ are on different sides below $v^\#$ in $T^\#$.

Moreover, by Claim 5.8, we have

$$\begin{aligned} \mathrm {d}^{\mathrm {g}}_{T^\#}(y^\#_i, y^\#_j) \le 6 g\Upsilon \log _2 \left( \frac{4\beta }{1 - 1/\sqrt{2}}\right) + 2\ell g \Upsilon + 4 \le \Gamma , \end{aligned}$$

(57)

where the first term corresponds to the distance to the closest witnesses, the second term corresponds to the distance to the closest $\mathtt{G}$-vertex, and the third term corresponds to the re-rooting operation above. We also used that each edge in $T^0$ corresponds to at most $g\Upsilon$ edges in the matching cluster. Hence the test pair $(y^\#_i, y^\#_j)$ is proximal. We also have

$$\begin{aligned} \mathrm {d}_{T^0}(y^0_i, y^0_j) > \mathrm {d}_{T^\#}(y^\#_i, y^\#_j), \end{aligned}$$

because $\mathrm {d}_{T^0}(\tilde{y}^0_i, \tilde{y}^0_j) > \mathrm {d}_{T^\#}(\tilde{y}^\#_i, \tilde{y}^\#_j),$ $\mathrm {d}_{T^0}(\tilde{y}^0_\iota , y^0_\iota ) = \mathrm {d}_{T^\#}(\tilde{y}^\#_\iota , y^\#_\iota ),$ for $\iota =i,j$, and $y^*_\iota$ is below $\tilde{y}^*_\iota$ for $*=0,\#$ and $\iota = i,j$.

5.6.3 Sparsification

It remains to satisfy the global requirements of the battery. Unlike the many-$\mathtt{R}$ case, we need to make the collection of test pairs sparser in both $T^\#$ and $T^0$. Indeed, although there is no overlap between the $\mathtt{G}$-clusters in $T^0$, in constructing the tests we may have used the same maximal $\mathtt{G}$-cluster repeatedly. Hence there is in fact no guarantee that the test subtrees are not overlapping in $T^0$. In $T^\#$, test subtrees may also be overlapping, whether or not they belong to the same $\mathtt{G}$-cluster. Moreover, although the test subtrees are co-hanging and proximal in $T^\#$, we must ensure that the connecting paths do not intersect with other test subtrees or their connecting paths.

Let $\{(y^0_i,y^0_j); (y^\#_i,y^\#_j)\}_{(i,j)\in \mathcal {H}'}$ be the test panels constructed above. By (43), (55), and Claim 5.2, we have

$$\begin{aligned} |\mathcal {H}'|\ge & {} \left[ 1 - 6 g \Upsilon \left( 1- \frac{1}{\beta }\right) \right] |\mathcal {O}^0|\\\ge & {} \left[ 1 - 6 g \Upsilon \left( 1- \frac{1}{\beta }\right) \right] \cdot \frac{1}{g\Upsilon } |\mathcal {O}^\#|\\\ge & {} \left[ 1 - 6 g \Upsilon \left( 1- \frac{1}{\beta }\right) \right] \cdot \frac{1}{g\Upsilon } \cdot \frac{1}{10} \frac{\Delta }{C_\mathcal {O}}. \end{aligned}$$

We choose

$$\begin{aligned} \beta = \frac{12g \Upsilon }{12 g \Upsilon - 1}, \end{aligned}$$

so that the expression in square brackets above is 1 / 2 and we have

$$\begin{aligned} \left| \mathcal {H}'\right| \ge \frac{\Delta }{20 g \Upsilon C_\mathcal {O}}. \end{aligned}$$

We note that because $g\Upsilon \ge 1$, we have $\beta \le 2$. Let $\{(\bar{Y}^0_i,\bar{Y}^0_j); (\bar{Y}^\#_i,\bar{Y}^\#_j)\}_{(i,j)\in \mathcal {H}'}$ be the test subtrees corresponding to $\mathcal {H}'$.

Claim 5.9

(Sparsification) Let

$$\begin{aligned} C_w = 3 g \Upsilon \log _2 \left( \frac{8}{1 - 1/\sqrt{2}}\right) + \ell g\Upsilon + 2. \end{aligned}$$

There is a subset $\mathcal {H}\subseteq \mathcal {H}'$ of size

$$\begin{aligned} |\mathcal {H}| \ge \frac{1}{1 + 2^{6\gamma _t + C_w + 3}g\Upsilon } |\mathcal {H}'| \ge \frac{\Delta }{20 g \Upsilon C_\mathcal {O}(1 + 2^{6\gamma _t + C_w + 3}g\Upsilon )} \end{aligned}$$

and $(\ell ,5)$-dense modified test subtrees $\{(Y^0_i,Y^0_j); (Y^\#_i,Y^\#_j)\}_{(i,j)\in \mathcal {H}}$ such that the test panels in $\mathcal {H}$ satisfy the requirements of a battery.

Proof

We proceed in two phases. First we choose a subset of test panels such that the test vertices in different panels are far away from each other. Then we cleave subtrees of the $\mathtt{G}$-clusters rooted at the test vertices to ensure that proximal/semi-proximal connecting paths and non-proximal hats do not intersect with test subtrees.

Start with an arbitrary test panel $((y^0_i,y^0_j); (y^\#_i,y^\#_j))$ in $\mathcal {H}'$. Remove from $\mathcal {H}'$ all test panels $(i',j')$ such that

$$\begin{aligned} \min \left\{ \mathrm {d}^{\mathrm {g}}_{T^\#}(v,w)\ :\ v \in \left\{ y^\#_i,y^\#_j\right\} , w \in \left\{ y^\#_{i'}, y^\#_{j'}\right\} \right\} \le 6 \gamma _t, \end{aligned}$$

(58)

or

$$\begin{aligned} \min \left\{ \mathrm {d}^{\mathrm {g}}_{T^0}(v,w)\ :\ v \in \left\{ y^0_i,y^0_j\right\} , w \in \left\{ y^0_{i'}, y^0_{j'}\right\} \right\} \le 6 \gamma _t. \end{aligned}$$

(59)

There are at most $2\cdot 2^{6\gamma _t+1}$ vertices within graph distance $2\gamma _t$ of a test pair. Note, however, that some vertices may be used as a test vertex multiple times. Nevertheless we claim that each vertex can be used at most a constant number of times. Indeed, consider a vertex $y^0_{i'}$ in $T^0$ with corresponding vertex $y^\#_{i'}$ in $T^\#$. Recall that each test panel is obtained from an overlap-shallow edge within graph distance $C_w$ in $T^0$ and that each such overlap-shallow edge produces at most $g\Upsilon$ test panels. Hence $y^0_{i'}$ can arise in this way at most $2^{C_w+1}g\Upsilon$ times. Therefore we remove at most $2^{6\gamma _t + C_w + 3}g\Upsilon$ test panels.

Pick a remaining test pair in $\mathcal {H}'$. Proceed as above and then repeat until all pairs in $\mathcal {H}'$ have been picked or removed. At the end of the procedure, there are at least

$$\begin{aligned} \frac{1}{1 + 2^{6\gamma _t + C_w + 3}g\Upsilon } |\mathcal {H}'| \end{aligned}$$

test panels remaining, the set of which we denote by $\mathcal {H}$. Recalling that $\gamma _t \ge \Gamma$, in $\mathcal {H}$, the connecting paths of proximal/semi-proximal pairs and the hats of non-proximal pairs cannot intersect with each other by (58) and (59) as it would imply the existence of test vertices in different panels at graph distance less than $2\gamma _t \le 6\gamma _t$.

For each $(i,j) \in \mathcal {H}$, it remains to define the corresponding test subtrees $((Y^0_i,Y^0_j); (Y^\#_i,Y^\#_j))$. Let $((\bar{Y}^0_i,\bar{Y}^0_j); (\bar{Y}^\#_i,\bar{Y}^\#_j))$ be as above and note that, since we may have re-used the same $\mathtt{G}$-clusters multiple times, these subtrees may not satisfy the global requirements of a battery as they may intersect with each other or with connecting paths and hats. We modify $\bar{Y}^0_i$ as follows, and proceed similarly for $\bar{Y}^0_j$. For each $(i',j') \in \mathcal {H}$ not equal to (i, j) and each subtree $Z \in \{\bar{Y}^0_{i'}$, $\bar{Y}^0_{j'}\}$, if Z has its root below the root of $\bar{Y}^0_i$, remove from $\bar{Y}^0_i$ all those nodes in Z as well as all descendants of the vertices on the upward path of length $2\gamma _t$ starting at the root of Z. Note that the latter path cannot reach $y^0_i$ because both $y^0_{i'}$ and $y^0_{j'}$ are at graph distance at least $6\gamma _t$ from $y^0_i$ from the construction of $\mathcal {H}$.

We let $Y^0_i$ be the remaining subtree in $T^0$ and $Y^\#_i$, its matching subtree in $T^\#$. We claim that the resulting restricted subtrees $(Y^0_i,Y^0_j)$ are $(\ell ,3)$-dense. Note first that the subtrees in $(\bar{Y}^0_i,\bar{Y}^0_j)_{(i,j)\in \mathcal {H}}$ are $(\ell ,1)$-dense as they were obtained from the procedure in Sect. 5.3. Moreover, because 1) the roots of the removed subtrees are at graph distance at most $2\gamma _t$ from a $\ell$-vertex in $(y^0_i,y^0_j)_{(i,j)\in \mathcal {H}}$, 2) test vertices in different pairs are at graph distance at least $6\gamma _t$ from each other, and 3) $\gamma _t$ is a multiple of $\ell$, if we remove a subtree rooted at a $\mathtt{G}$-child of a $\mathtt{G}$-vertex in $(\bar{Y}^0_i,\bar{Y}^0_j)$ we cannot remove more than one other subtree rooted at another $\mathtt{G}$-child of the same $\mathtt{G}$-vertex as that would imply the existence of two test vertices in different pairs at graph distance less than

$$\begin{aligned} 2(2\gamma _t) + 2g\ell < 6\gamma _t, \end{aligned}$$

in $T^0$, a contradiction.

We then proceed similarly in $T^\#$. The resulting restricted subtrees

$$\begin{aligned} \left\{ \left( Y^0_i,Y^0_j\right) ; \left( Y^\#_i,Y^\#_j\right) \right\} _{(i,j)\in \mathcal {H}}, \end{aligned}$$

are then $(\ell ,5)$-dense (in fact, $(\ell ,4)$-dense as there are no non-proximal pairs in $T^\#$).

$\square$

5.6.4 Summary of the large overlap case

We have proved the following in the large overlap case. Recall that $\wp = 5$, $\ell = \ell (g,\wp )$ is chosen as in Proposition 1,

$$\begin{aligned} \Gamma = 6 g \Upsilon \log _2 \left( \frac{8}{1 - 1/\sqrt{2}}\right) + 2\ell g \Upsilon + 4, \end{aligned}$$

and $\gamma _t \ge \Gamma$, a multiple of $\ell$, and C are chosen as in Proposition 1.

Proposition 5

(Battery in the large overlap case) In the large overlap case, we can build a $(\ell ,\wp ,\Gamma ,\gamma _t,I)$-battery

$$\begin{aligned} \left\{ \left( \left( y^0_i,z^0_i\right) ;\left( Y^0_i,Z^0_i\right) \right) \right\} _{i=1}^I (\text {in }T^0) \text { and } \left\{ \left( \left( y^\#_i,z^\#_i\right) ;\left( Y^\#_i,Z^\#_i\right) \right) \right\} _{i=1}^I (\text {in } T^\#) \end{aligned}$$

with

$$\begin{aligned} I \ge \frac{\Delta }{ 20 g\Upsilon C_\mathcal {O}(1 + 2^{6\gamma _t + C_w + 3}g\Upsilon ) }. \end{aligned}$$

Proof

The result follows from Claim 5.9.$\square$

Preliminary lemmas

In this section, we collect a few useful lemmas.

1.1 Ancestral reconstruction

An important part of our construction involves reconstructing ancestral states. We will use the following lemma from [14] which we typically apply to a rooted subtree. Let $T = (V,E;\phi ;w) \in \mathbb {Y}$ rooted at $\rho$. Let $e = (x,y) \in E$ and assume that x is closest to $\rho$ (in topological distance). We define $\mathrm {P}(\rho ,e) = \mathrm {P}(\rho ,y)$, $|e|_\rho = |\mathrm {P}(\rho ,e)|$, and

$$\begin{aligned} R_\rho (e) = \left( 1 - \theta _e^2\right) \Theta _{\rho ,y}^{-2}, \end{aligned}$$

(60)

where $\Theta _{\rho ,y} = e^{-\mathrm {d}_T(\rho ,y)}$ and $\theta _e = e^{-w_e}$.

Lemma 2

(Ancestral reconstruction [14]) For any unit flow $\Psi$ from $\rho$ to [n],

$$\begin{aligned} \mathbb {E}_T\left| \mathbb {P}_T[\sigma _\rho = +1|\sigma _X] - \mathbb {P}_T[\sigma _\rho = -1|\sigma _X] \right| \ge \frac{1}{1+ \sum _{e \in E} R_\rho (e) \Psi (e)^2}, \end{aligned}$$

(61)

where the LHS is the difference between the probability of correct and incorrect reconstruction using MLE. (See [14, Equation (14), Lemma 5.1 and Theorem 1.2’].)

1.2 Random cluster representation

We use a convenient percolation-based representation of the CFN model known as the random cluster model (see e.g. [23]). Let $T = (V,E;\phi ;w) \in \mathbb {Y}$ with corresponding $(\delta _e)_{e\in E}$.

Lemma 3

(Random cluster representation) Run a percolation process on T where edge e is open with probability $1 - 2 \delta _e$. Then associate to each open connected component a state according to the uniform distribution on $\{+1,-1\}$. The state vector on the vertices so obtained $(\sigma _v)_{v\in V}$ has the same distribution as the corresponding CFN model.

1.3 Concentration inequalities

Recall the following standard concentration inequality (see e.g. [38]):

Lemma 4

(Azuma-Hoeffding Inequality) Suppose $\mathbf{Z}=(Z_1,\ldots ,Z_m)$ are independent random variables taking values in a set S, and $h:S^m \rightarrow \mathbb {R}$ is any t-Lipschitz function: $|h(\mathbf{z}) - h(\mathbf{z'})|\le t$ whenever $\mathbf{z}, \mathbf{z'} \in S^m$ differ at just one coordinate. Then, $\forall \zeta > 0$,

$$\begin{aligned} \mathbb {P}\left[ |h(\mathbf{Z}) - \mathbb {E}[h(\mathbf{Z})]| \ge \zeta \right] \le 2\exp \left( -\frac{\zeta ^2 }{2 t^2 m}\right) . \end{aligned}$$