Introduction

Over the last decade, surface plasmon polaritons (SPPs) have been the subject of research for their various unique features to design nanoscale electronic and photonic devices [1,2,3,4,5,6,7,8]. It is an emerging field of science and technology. Aside from sensing purposes [9,10,11], SPPs can also be used to control switches [12] and to build signal amplifiers and modulators [13,14,15,16,17]. In contrast to other conventional focusing techniques like dielectric lenses, a fundamental characteristic of SPPs is able to confining electromagnetic fields to smaller scales, which distinguishes it from them [1, 18]. It is possible to greatly reduce the size of devices and systems by replacing free-space propagating electromagnetic (EM) waves with SPPs. When photons and electrons interact, the SPPs exhibit a larger wave vector than free space waves [19]. Metal-based structure plays an important role in determining the frequency range and propagation loss of SPPs modes [20]. Krokhin et al. studied the SPPs behavior in an anisotropic photonic crystal deposited on a thin metallic film to increase the efficiency of plasmonic devices [21]. Gric and Rafailov studied the SPPs propagation at metal free metamaterial with anisotropy of semiconductor to control the propagation length of SPPs [7]. Umair et al. presented the numerical analysis of plasmon modes in metallic filled parallel plate waveguide (PPWG) to investigate the effect of tensorial permittivity on the characteristics of EM surface wave [22]. Bousbih et al. studied the plasmon mode at chiroplasma-metal interface in the THz frequency regime [23]. Guangcan Mi and Vien Van studied the numerical investigation of SPPs at chiral-metal planar structure [24]. The propagation range of metallic based plasmonic structures is generally limited by Joule losses [21]. Additionally, the metal-based structures have a higher propagation loss, a lower tunability, and a lower confinement [25]. Currently, the plasmonic community is seeking 2D optical materials with low propagation losses. The introduction of graphene material is intended to address these bottleneck problems.

An atom-thick layer of carbon atoms known as graphene has recently attracted attention in the fields of plasmonic community [26, 27]. It has been demonstrated that graphene supports the surface plasmons in the mid-infrared (MIR) and terahertz (THz) ranges of the EM spectrum [28,29,30,31,32]. In comparison with noble metals, graphene has unique and remarkable optical properties including low losses, long propagation lengths, extreme confinement of light, and tunable conductivity [26, 28, 32]. Furthermore, the conductivity of graphene-based structures can be tuned much more easily than those of metallic and photonic crystal structures. Graphene’s tunable conductivity allows the resonance characteristics to be altered without having to re-fabricate the device [33,34,35,36]. In graphene-based plasmonic devices, electrical gating is crucial for modulating the carrier concentration in the graphene layers, which alters graphene’s electronic properties. As a result of this ability to control carrier concentration, graphene is an extremely versatile material for wide variety of technological applications, including transistors, sensors, and photonics [37]. Different authors used different geometries and different optical materials for the propagation of SPPs [24, 31, 38,39,40,41,42,43].

A substantial amount of literature has been devoted to electromagnetic propagation in chiral materials [44,45,46,47]. In the case of such an isotropic chiral material, the degree of chirality can be controlled only a limited extent once it has been created. Thus, it is imperative to develop methods for controlling chirality. The incorporation of certain forms of anisotropy enables the realization of such method. The composite chiroferrite material is made of isotropic chiral and a nonreciprocal ferrite material in which chiral material is encapsulated in a magnetically biased ferrite [48]. The permeability tensor can be modified by adjusting the tensor values, thereby controlling the chirality of SPPs waves at CF-G-CF interface.

Mathematical Formulation

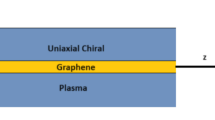
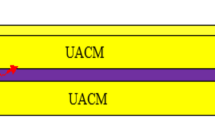
Consider the propagation of SPPs in z direction as depicted in Fig. 1.

Fig.1
figure 1

Geometry for graphene loaded chiroferrite waveguide

Full size image

Here are the constitutive relationships for chiroferrite medium.

$$D=\varepsilon {\varvec{E}}+i\xi {\varvec{B}}$$
(1)
$$H=i\xi E+\overline\mu{}^{-1}B$$
(2)
$$\overline{\mu }=\left|\begin{array}{ccc}{\mu }_{1}& -ik& 0\\ ik& {\mu }_{1}& 0\\ 0& 0& {\mu }_{3}\end{array}\right|$$
(3)

In the chiroferrite medium:

$${E}_{z}={A}_{1}{e}^{{-q}_{1}x}+{A}_{2}{e}^{{-q}_{2}x}$$
(4)
$${H}_{z}=i({A}_{1}{\alpha }_{1}{e}^{{-q}_{1}x}+{A}_{2}{{\alpha }_{2}e}^{{-q}_{2}x})$$
(5)

The rest of field components can be obtained from [49]. Based on the source-free Maxwell equations, coupled wave equations are presented below.

$${\nabla }_{t}^{2}{E}_{z}+{P}_{1}{E}_{z}+iP2{H}_{z}=0$$
(6)
$${\nabla }_{t}^{2}{H}_{z}+{iP}_{3}{E}_{z}+P4{H}_{z}=0$$
(7)

The coefficients for Eqs. 6 and 7 are

$${P}_{1}=\frac{\omega (d({\varepsilon }_{0}+{\mu }_{z}{\xi }^{2})-{\mu }_{z}\xi b)}{{D}_{2}}$$
(8)
$${P}_{2}=\frac{\omega {\mu }_{z}(b-d\xi )}{{D}_{2}}$$
(9)
$${P}_{3}=\frac{\omega (b({\varepsilon }_{0}+{\mu }_{z}{\xi }^{2})+f0{\mu }_{z}\xi )}{{D}_{2}}$$
(10)
$${P}_{4}=\frac{\omega {\mu }_{z}(b\xi +f0)}{{D}_{2}}$$
(11)

where

$$a=\left[{\beta }^{3}+3\omega k\xi {\beta }^{2}+2{\omega }^{2}{\xi }^{2}\beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+{\omega }^{2}{\mu }_{1}{\varepsilon }_{0}\beta \right]/{D}_{1}$$
(12)
$$b=[\omega \beta \left({\mu }_{1}\xi \beta +\omega {\varepsilon }_{0}k\right)+{\omega }^{3}{\varepsilon }_{0}\xi ({{\mu }_{1}}^{2}-{k}^{2})]/{D}_{1}$$
(13)
$$c=[2{\omega }^{2}\xi \beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+\omega k{\beta }^{2}]/{D}_{1}$$
(14)
$$d=[-\omega {\mu }_{1}{\beta }^{2}-{\omega }^{3}{\varepsilon }_{0}({{\mu }_{1}}^{2}-{k}^{2})]/{D}_{1}$$
(15)
$$e=-\omega [\xi \beta \left(2\omega {\varepsilon }_{0}{\mu }_{1}+\xi k\beta \right)+2\omega {\xi }^{3}\beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+{\omega }^{2}{{\varepsilon }_{0}}^{2}k] /{D}_{1}$$
(16)
$$f0=\left[\omega {\beta }^{2}\left({\varepsilon }_{0}+{\mu }_{1}{\xi }^{2}\right)-2{\omega }^{2}{\varepsilon }_{0}\xi c\beta k-{\omega }^{3}{\xi c}^{2}{\varepsilon }_{0}\left({{\mu }_{1}}^{2}-{k}^{2}\right)-{\omega }^{3}{{\varepsilon }_{0}}^{2}{\mu }_{1}\right]/{D}_{1}$$
(17)
$${D}_{1}={\beta }^{4}+4{\omega }^{2}{\xi }^{2}{\beta }^{2}({k}^{2}-{{\mu }_{1}}^{2})-2{\omega }^{2}{\beta }^{2}{\mu }_{1}{\varepsilon }_{0}+{\omega }^{4}{{\varepsilon }_{0}}^{2}({{\mu }_{1}}^{2}-{k}^{2})-4\omega \xi {\beta }^{3}k$$
(18)
$${D}_{2}={b}^{2}+df$$
(19)
$${q}_{1}=\sqrt{\frac{{P}_{1}+{P}_{4}+\sqrt{{({P}_{1}-{P}_{4})}^{2}-4{P}_{2}{P}_{3}}}{2}}$$
(20)
$${q}_{2}=\sqrt{\frac{{P}_{1}+{P}_{4}-\sqrt{{({P}_{1}-{P}_{4})}^{2}-4{P}_{2}{P}_{3}}}{2}}$$
(21)
$${\alpha }_{1}=\frac{{P}_{1}-{({q}_{1})}^{2}}{{P}_{2}}$$
(22)
$${\alpha }_{2}=\frac{{P}_{1}-{({q}_{2})}^{2}}{{P}_{2}}$$
(23)
$$\widehat{x}\times \left[{H}_{1}-{H}_{2}\right]=\sigma E$$
(24)
$$\widehat{x}\times \left[{E}_{1}-{E}_{2}\right]=0$$
(25)

The conductivity of graphene is described as follows:

$$\sigma =\frac{j{e}^{2}\left(\omega -j{\tau }^{-1}\right)}{\pi {h}^{2}}\times \left[\frac{1}{{\left(\omega -j{\tau }^{-1}\right)}^{2}}{\int }_{0}^{\infty }\times \xi \left(\frac{\sigma {f}_{d}\left(\xi ,{\mu }_{c},T\right)}{\sigma \xi }-\frac{\sigma {f}_{d}\left(-\xi ,{\mu }_{c},T\right)}{\sigma \xi }\right)d\xi -{\int }_{0}^{\infty }\times \frac{{f}_{d}\left(-\xi ,{\mu }_{c},T\right)-{f}_{d}\left(\xi ,{\mu }_{c},T\right)}{{\left(\omega -j{\tau }^{-1}\right)}^{2}-4{\left({~}^{\xi }\!\left/ \!{~}_{\hslash }\right.\right)}^{2}}d\xi \right]$$
(26)

Using Eqs. 26 and 27, the following characteristic is obtained:

$$i\sigma {q}_{1}\left(b-d{\alpha }_{1}\right)+{q}_{2}\left(-ib\sigma +{\alpha }_{2}\left(id\sigma +2\left({b}^{2}+df0\right){q}_{1}\right)-2\left({b}^{2}+df0\right){q}_{1}{\alpha }_{1}\right)=0$$
(27)

Numerical Results

In this section, numerical results have been carried out to obtain the deeper understanding the features of SPPs at the CF-G-CF planar interface. Combining both optical materials, i.e., (graphene and chiroferrite), enables us to gain a deeper understanding of the engineerable properties of SPPs. Monolayer graphene is sandwiched between chiroferrite layers as depicted in Fig. 1. To understand the plasmonic features of plasmon mode at a CF-G-CF interface, dispersion relation is plotted between EMI and wave frequency in THz regime under the different graphene as well as chiroferrite parameters. In this context, Maxwell’s equations for planar structure are used to derive the dispersion relation. In our calculation, we have set numerical parameters as \({\mu }_{c}\)=0.5 eV, \(T=300 K\), \({\xi }_{c}=0.2\), \(\tau =12ps\), and \({\mu }_{2}=0.52{\mu }_{0}\). The EMI spectra for different magnitude of graphene’s chemical potential and graphene layers are displayed in Fig. 2a and b, respectively. According to Fig. 2a, to achieve the plasmonic properties, chemical potential extends from \({\mu }_{c}=0.3 eV\) to \({\mu }_{c}=0.6 eV\) indicated by black, green, red, and blue peaks. The rise in chemical potential shifts the characteristics peaks towards higher frequency spectrum. In addition, as chemical potential increases, the frequency band starts to narrow. The squeezing of the frequency band gap with an increasing amount of chemical potential provides an additional degree of freedom for modulating EM surface waves. Moreover, lower chemical potential leads to higher EMI as reported [6, 43, 50, 51]. Because when the concentration of graphene carriers is low enough, both the valence band and the conduction band overlap at the Dirac point in the Brillouin zone. Upon reaching this point, the relationship between energy and momentum becomes linear, resulting in distinct electronic properties for plasmonic community. Linear dispersion is a key component of nanoscale devices that facilitates strong coupling between light and matter, as well as efficient energy transfer. The carrier concentration of graphene can be modified by electrostatic gating or chemical doping [31, 42, 52], thereby allowing dynamic control of plasmon response enabled the advanced technological applications for plasmonic sector. Figure 2b illustrates the EMI under different graphene layers. According to a recent study, only 2.3% of the incident light is absorbed by single layer of graphene [37, 53]. It can be noted that EMI reduces with the number of layers of graphene. Based on the numerical analysis, it is clearly manifest that single-layer graphene (N = 1) exhibits lower energy losses than multilayered graphene as reported in [53,54,55,56]. Furthermore, numerical analysis shows that multilayer graphene causes to shifts the characteristic peak toward the high frequency region. The influence of chirality on EMI is graphically depicted in Fig. 3a under different chirality range \({\xi }_{c}=0.2\), \({\xi }_{c}=0.3\), \({\xi }_{c}=0.4\), and \({\xi }_{c}=0.5\). Figure 3a illustrates how EMI decreases with the increment of chirality parameter. As chirality increases, wave frequency decreases, and dispersion curves reflect lower EMI [23]. Thus, the frequency and EMI of the CF-G-CF structure can be controlled by adjusting the chirality values. It is of peculiar of interest to note that the slope of dispersion curve is smaller for higher chirality values. To illustrate the effect of gyrotropy on the behavior of SPPs, Fig. 4b illustrates the influence of gyrotropy on EMI as a function of wave frequency. It is obvious that as gyrotropy increases, frequency band broadened, and dispersion curves reflect higher EMI. Recently, Razzaz et al. presented the numerical analysis of EM surface wave in graphene filled waveguide bounded by magnetic material [56]. In our proposed structure, the introduction of chirality in the ferrite medium provides an additional degree of freedom. It is important to note that when a wave interacts with a gyrotropic medium, its velocity is altered, affecting its speed of propagation. Changing the direction of the polarization plane reduces propagation losses and allows the wave to interact more effectively with the material. These extraordinary features of ferrite mediums with increased gyrotropy are widely used in optics community to fabricate nano plasmonic devices. The choice of an appropriate gyrotropy of medium is crucial for the design of nanophotonic devices based on chiroferrite-graphene in a specific frequency band. Figure 4a depicts the effects of chemical potential on phase velocity. As chemical potential increases, the dispersion curves shift from low to high frequency region. Thus, it is concluded that the phase velocity and frequency band of the proposed structure can be adjusted through the tuning of graphene’s chemical potential. The effect of number of graphene layers on phase velocity of EM surface waves with respect to EM frequency is graphically demonstrated in Fig. 4b. It is observed that multilayer graphene support high frequency as compared with monolayer graphene. To analyze, the variation in phase velocity for different values of chirality and gyrotropy is shown in Fig. 5a and b, respectively. Figure 5a illustrates how phase velocity varies with chirality. Obviously, as magnitude of chirality increases, EM waves frequency increases and bandgap starts squeezing. Furthermore, it is of peculiar of interest to note that highest slope of variation is observed for lowest chirality value, i.e., \({\xi }_{c}=0.2\). In Fig. 5b, we demonstrate the impact of varying gyrotropy of chiroferrite medium on the phase velocity. In this regard, frequency range is taken from 1 to 6 THz. As gyrotropy increase, the EM wave frequency decreases, but bandgap becomes broadened. Figure 6a and b describes the impact of chemical potential and EM wave frequency on EMI versus graphene conductivity, respectively, by using dispersion relation 27. It is possible to tune the chemical potential of a compound by doping it or applying external fields to it as reported in [39, 41, 42]. According to Fig. 6a, as chemical potential rises, graphene conductivity decreases. It is important to note that graphene’s carrier density increases in proportion to its chemical potential. Increasing carrier density may result in more scattering events. As a result of these scattering events, charge carriers have a lower mobility, which results in a lower conductivity.

Fig. 2
figure 2

The influence of chemical potential and number of graphene layers on EMI versus EM wave frequency

Full size image
Fig. 3
figure 3

The influence of chirality and gyrotropy on EMI versus EM wave frequency

Full size image
Fig. 4
figure 4

The impact of chemical potential and number of graphene layers on phase velocity versus EM wave frequency

Full size image
Fig. 5
figure 5

The impact of chirality and gyrotropy on phase velocity versus EM wave frequency

Full size image
Fig. 6
figure 6

The influence of chemical potential and EM wave frequency on EMI versus graphene conductivity

Full size image

Impact of different EM wave frequencies on EMI versus graphene conductivity is presented in Fig. 6b. It is clearly manifest that as EM wave frequency increases, graphene conductivity decreases. Increasing EM wave frequency hinders the dynamic response of charge carriers, increases scattering, and causes energy to be absorbed by interband transitions and other processes, reducing graphene’s conductivity. The effect of chirality and gyrotropy on EMI versus graphene conductivity by using dispersion relation 27. The influence of chirality on EMI versus graphene conductivity is plotted in Fig. 7a. Clearly, the conductivity of graphene decreases with increasing chirality. Furthermore, slope of dispersion curve is smaller for higher chirality value. It is important to note that graphene’s electronic properties are highly dependent on its surroundings medium. The effect of gyrotropy on EMI versus graphene conductivity is shown in Fig. 7b. As gyrotropy of chiroferrite medium increases, the dispersion curves shifted towards higher conductivity. Since, gyrotropic nature of the chiroferrite medium generates magneto-optical effects, such as the Faraday effect, which causes light’s polarization plane to rotate. As a result of these effects, the charge carriers in graphene are aligned, resulting in reduced resistive losses and increased graphene conductivity.

Fig. 7
figure 7

The influence of chirality and gyrotropy on EMI versus graphene conductivity

Full size image

Concluding Remarks

This study focuses on the features of electromagnetic surface waves generation at the CF-G-CF planar interface. It is demonstrated that the propagation characteristics associated with surface waves are strongly influenced by the chiroferrite and graphene parameters. These characteristics of the CF-G-CF structure are EMI, phase velocity, and characteristics curve. Additionally, frequency fluctuations offer flexibility in modifying and altering the propagation of surface waves for the proposed structure. The calculated numerical results of this research work may be useful in plasmonic community to design the innovative optical sensors, plasmonic platforms, detectors, and surface waveguides in the THz frequency region and provide active control due to additional degree of freedom in graphene and anisotropy of chiral medium.