Introduction

Data transmission systems increasingly rely on photonic devices due to rapid technological advancements in optical techniques. In the future, reducing the element size will be expected to allow for 10 Tbits/s/1 of data transmission by reducing the size of nanophotonic devices to nanometer; in this way, data storage will be up to 1Tbit per inch. Because Abbe’s diffraction limit reaches approximately one-half of the optical wavelength, it is extremely difficult to reduce the element sizes to nanometers in conventional photonic devices. A promising method of controlling propagation and dispersion of light on the nanometer scale is through excitation of surface plasmon polaritons (SPPs) that can defeat the diffraction limit [1]. SPPs are a special kind of electromagnetic waves existing between metal and dielectric interface [2,3,4,5,6,7]. So far, numerous plasmonic components based on metal have been studied [8,9,10,11]. However, metal-based plasmonic structures have been hindered by higher intrinsic losses, low mode of confinement, and poor tenability [12]. In the last few years, graphene has gained much attention due to its excellent optical and electronic properties, providing compact, strong mode confinement, low propagation loss, and tunable components. Due to their superior tuning and compactness, graphene is considered a superb candidate for use in next-generation nano-plasmonic chips and optical devices. Additionally, these features can be tailored by tailoring graphene conductivity [13]. Numerous graphene-based devices have been proposed, including bends, splitters, optical waveguides, metasurface absorbers, logic gates, lenses, filters, switches, and directional couplers [14]. Guangcan Mi and Vien Van analyzed the analyze the numerical calculation of EM wave at chiral-metal interface for on-chip chiral sensing and enantiomer detection application [15]. M Z Yaqoob presented theoretical analysis of planar structure at chiral-graphene interface for chiral sensing applications [16]. Further control on plasmon chiroferrite-graphene planar structure is analyzed which is not presented yet.

It was discovered in the nineteenth century that some biological or crystalline materials exhibited optical activity, and by the middle of the century, it was hypothesized that this phenomenon was attributed to the chirality of their molecules. Several studies have been conducted on electromagnetic propagation in chiral materials. Chiral medium can rotate the plane of polarization of an electromagnetic wave to the right or left depending on its handedness. Creating an isotropic chiral material allows very limited control over its chirality. The development of methods to achieve chirality control is therefore of utmost importance. This can be accomplished by introducing specific types of anisotropy. A chiral medium and a nonreciprocal ferrite medium can be combined to form a composite chiroferrite medium by immersing chiral objects in a magnetically biased ferrite whose permeability is gyrotropic. By modifying the biased static magnetic field, one can control gyrotropy of the permeability and thus control the chirality within the waveguide. The longitudinal components and eigenmode solution of this electromagnetic problem are complex in chiroferrite media due to the intrinsic coupling between electric and magnetic fields [17]. Chiroferrite materials can be used to control the radiation properties of printed circuit antennas. Additionally, chiroferrite material has numerous applications in optical communication and integrated optics. In this manuscript, hybrid plasmon modes are studied at chiroferrite-graphene planar interface. Frequency-dependent normalized propagation constant for various values of chemical potential, relaxation time, number of graphene layers, temperature, chirality, and gyrotropy are analyzed. The presented research may be useful for chiral sensing, microwave devices, antennas, and magnetic resonance imaging in the terahertz (THz) frequency band.

Methodology

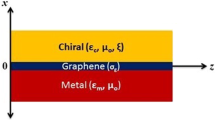
The analytical formulation of chiroferrite-graphene has been presented in this section. SPP wave is propagating in z axis as shown in Fig. 1.

Fig. 1
figure 1

Geometry for chiroferrite-graphene interface

Full size image

Constitutive relations for chiroferrite material [18] as follow:

$$D=\varepsilon E+i\xi B$$
(1)
$$H=i\xi {{E}}+{\overline{\mu }}^{-1}{{B}}$$
(2)

\(\varepsilon\) and \(\xi\) represent the permittivity and chirality respectively of chiroferrite medium. \({\overline{\mu }}^{-1}\) represents permeability tensor as reported in [18].

$$\overline{\mu }=\left|\begin{array}{ccc}{\mu }_{1}& -ik& 0\\ ik& {\mu }_{1}& 0\\ 0& 0& {\mu }_{3}\end{array}\right|$$
(3)

The EM field components for chiroferrite medium are:

$${E}_{z}={A}_{1}{e}^{{-q}_{1}x}+{A}_{2}{e}^{{-q}_{2}x}$$
(4)
$${H}_{z}=i({A}_{1}{\alpha }_{1}{e}^{{-q}_{1}x}+{A}_{2}{{\alpha }_{2}e}^{{-q}_{2}x})$$
(5)

Remaining EM fields components for chiroferrite medium can be derived from [19].

$${E}_{x}=-i{{e}^{{-i-x(q}_{1}+{q}_{2})}(A}_{1}{q}_{1}{e}^{{q}_{2}x}(a+c{\alpha }_{1})+{A}_{2}{q}_{2}{e}^{{q}_{1}x}(a+c{\alpha }_{2}))$$
(6)
$${E}_{y}={{e}^{{-i-x(q}_{1}+{q}_{2})}(A}_{1}{q}_{1}{e}^{{q}_{2}x}(b-d{\alpha }_{1})+{A}_{2}{q}_{2}{e}^{{q}_{1}x}(b-d{\alpha }_{2}))$$
(7)
$${H}_{x}={{e}^{{-i-x(q}_{1}+{q}_{2})}(-A}_{1}{q}_{1}{e}^{{q}_{2}x}\left(e-a{\alpha }_{1}\right)-{A}_{2}{q}_{2}{e}^{{q}_{1}x}(e-a{\alpha }_{2}))$$
(8)
$${H}_{y}={{ie}^{{-i-x(q}_{1}+{q}_{2})}(A}_{1}{q}_{1}{e}^{{q}_{2}x}\left(f+b{\alpha }_{1}\right)+{A}_{2}{q}_{2}{e}^{{q}_{1}x}(f+b{\alpha }_{2}))$$
(9)

Following are coupled wave equations obtained from the source-free Maxwell equations.

$${\nabla }_{t}^{2}{E}_{z}+{P}_{1}{E}_{z}+i{P}_{2}{H}_{z}=0$$
(10)
$${\nabla }_{t}^{2}{H}_{z}+{iP}_{3}{E}_{z}+{P}_{4}{H}_{z}=0$$
(11)

The EM wave coefficients of 6 and 7 are given below.

$${P}_{1}=\frac{\omega (d({\varepsilon }_{0}+{\mu }_{z}{\xi }^{2})-{\mu }_{z}\xi b)}{{D}_{2}}$$
(12)
$${P}_{2}=\frac{\omega {\mu }_{z}(b-d\xi )}{{D}_{2}}$$
(13)
$${P}_{3}=\frac{\omega (b({\varepsilon }_{0}+{\mu }_{z}{\xi }^{2})+f{\mu }_{z}\xi )}{{D}_{2}}$$
(14)
$${P}_{4}=\frac{\omega {\mu }_{z}(b\xi +f)}{{D}_{2}}$$
(15)

where,

$$a=\left[{\beta }^{3}+3\omega k\xi {\beta }^{2}+2{\omega }^{2}{\xi }^{2}\beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+{\omega }^{2}{\mu }_{1}{\varepsilon }_{0}\beta \right]/{D}_{1}$$
(16)
$$b=[\omega \beta \left({\mu }_{1}\xi \beta +\omega {\varepsilon }_{0}k\right)+{\omega }^{3}{\varepsilon }_{0}\xi ({{\mu }_{1}}^{2}-{k}^{2})]/{D}_{1}$$
(17)
$$c=[2{\omega }^{2}\xi \beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+\omega k{\beta }^{2}]/{D}_{1}$$
(18)
$$d=[-\omega {\mu }_{1}{\beta }^{2}-{\omega }^{3}{\varepsilon }_{0}({{\mu }_{1}}^{2}-{k}^{2})]/{D}_{1}$$
(19)
$$e=-\omega [\xi \beta \left(2\omega {\varepsilon }_{0}{\mu }_{1}+\xi k\beta \right)+2\omega {\xi }^{3}\beta \left({{\mu }_{1}}^{2}-{k}^{2}\right)+{\omega }^{2}{{\varepsilon }_{0}}^{2}k] /{D}_{1}$$
(20)
$$\begin{aligned}f&=\Bigg[\omega {\beta }^{2}\left({\varepsilon }_{0}+{\mu }_{1}{\xi }^{2}\right)-2{\omega }^{2}{\varepsilon }_{0}\xi c\beta k\\&-{\omega }^{3}{\xi c}^{2}{\varepsilon }_{0}\left({{\mu }_{1}}^{2}-{k}^{2}\right)-{\omega }^{3}{{\varepsilon }_{0}}^{2}{\mu }_{1}\Bigg]/{D}_{1}\end{aligned}$$
(21)
$$\begin{aligned}{D}_{1}&={\beta }^{4}+4{\omega }^{2}{\xi }^{2}{\beta }^{2}({k}^{2}-{{\mu }_{1}}^{2})\\&-2{\omega }^{2}{\beta }^{2}{\mu }_{1}{\varepsilon }_{0}+{\omega }^{4}{{\varepsilon }_{0}}^{2}({{\mu }_{1}}^{2}-{k}^{2})-4\omega \xi {\beta }^{3}k\end{aligned}$$
(22)
$${D}_{2}={b}^{2}+df$$
(23)
$${q}_{1}=\sqrt{\frac{{P}_{1}+{P}_{4}+\sqrt{{({P}_{1}-{P}_{4})}^{2}-4{P}_{2}{P}_{3}}}{2}}$$
(24)
$${q}_{2}=\sqrt{\frac{{P}_{1}+{P}_{4}-\sqrt{{({P}_{1}-{P}_{4})}^{2}-4{P}_{2}{P}_{3}}}{2}}$$
(25)
$${\alpha }_{1}=\frac{{P}_{1}-{({q}_{1})}^{2}}{{P}_{2}}$$
(26)
$${\alpha }_{2}=\frac{{P}_{1}-{({q}_{2})}^{2}}{{P}_{2}}$$
(27)

Electromagnetic field components for free space are given below:

$${E}_{z}={A}_{3} {e}^{\alpha mx}$$
(28)
$${H}_{z}={A}_{4} {e}^{\alpha mx}$$
(29)

Here, \(\alpha m=\sqrt{{\beta }^{2}-{\omega }^{2}{\varepsilon }_{0}{\mu }_{0}}\). The remaining EM field components can be derived from [16]. Following boundary conditions to be enforced at chiroferrite-graphene interface.

$$\widehat{x}\times \left[{H}_{1}-{H}_{2}\right]=\sigma E$$
(30)
$$\widehat{x}\times \left[{E}_{1}-{E}_{2}\right]=0$$
(31)

\(\sigma\) is the conductivity of monolayer graphene as follows:

$$\begin{aligned}\sigma \left(\mu ,\tau ,T\right)&=\frac{i{e}^{2}\left(\omega -j{\tau }^{-1}\right)}{\pi {h}^{2}}\\&\times \Bigg[\frac{1}{{\left(\omega -i{\tau }^{-1}\right)}^{2}}{\int }_{0}^{\infty }\\&\times {\xi }_{en}\left(\frac{\sigma {f}_{d}\left({\xi }_{en},\mu ,T\right)}{\sigma \xi }-\frac{\sigma {f}_{d}\left(-{\xi }_{en},\mu ,T\right)}{\sigma \xi }\right)d{\xi }_{en}\\&-{\int }_{0}^{\infty }\times \frac{{f}_{d}\left(-{\xi }_{en},\mu ,T\right)-{f}_{d}\left({\xi }_{en},\mu ,T\right)}{{\left(\omega -i{\tau }^{-1}\right)}^{2}-4{\left(\nicefrac{\xi }{\hslash}\right)}^{2}}d{\xi }_{en}\Bigg]\end{aligned}$$
(32)

where \(\mu\) is chemical potential, \(\tau\) is relaxation rate, \(\mathrm{T}\) is temperature, \(e\), charge on electron, \({f}_{d}\) is Fermi–Dirac, \(\omega\) is operating frequency, \({\xi }_{en}\), energy, and \(\hslash\) represent the reduced Plank’s constant [20]. By applying boundary conditions, the following dispersion relation is obtain.

$$\begin{aligned}\alpha m&(\omega {q}_{1}(f+b{\alpha }_{1}){\alpha }_{2}{\mu }_{0}-\omega {q}_{2}{\alpha }_{1}(f+b{\alpha }_{2}){\mu }_{0}\\&-({b}^{2}+df){q}_{1}{q}_{2}(-{\alpha }_{1}+{\alpha }_{2})(\alpha m-i\sigma \omega {\mu }_{0}))\\-&(i\alpha m\sigma +{\varepsilon }_{0}\omega )(\omega ({\alpha }_{1}-{\alpha }_{2}){\mu }_{0}+{q}_{1}(b-d{\alpha }_{1})\\&(\alpha m-i\sigma \omega {\mu }_{0})-{q}_{2}(b-d{\alpha }_{2})(\alpha m-i\sigma \omega {\mu }_{0}))=0\end{aligned}$$
(33)

Results and Discussion

This section presents the analytical results to explore the characteristics of hybrid plasmon modes at chiroferrite-graphene planar structure. In all graphs, the chemical potential of monolayer graphene is set to be \(\mu =0.1 eV\), relaxation time \(\tau =20\times {10}^{-13} s\), temperature \(T=300 K\), chirality \(\xi =0.002\), and gyrotropy of ferrite medium \(k=0.6 {\mu }_{0}\). Characteristic curve analysis is utilized to study the behavior of electromagnetic surface waves on graphene planar interface loaded with semi-infinite chiroferrite medium. Normalized propagation constant \(Re(\frac{\beta }{{k}_{0}})\) is a powerful parameter for designing the plasmonic devices, which shows the factor of confinement in the plasmonic structure. \(\beta\) represents propagation constant and \({k}_{0}=\) \(\sqrt{{\omega }^{2}{\varepsilon }_{0}{\mu }_{0}}\). Two propagating modes (upper and lower) appeared.

due to the existence of chiroferrite medium. Frequency dependent normalized propagation constant under the different graphene features, chirality, and gyrotropy of the ferrite medium are studied. Since graphene supports THz frequencies [13, 17,18,19,20,21,22], numerical results are taken in THz frequency range. To study the factor of confinement, which is a very crucial parameter for the practical point of view to fabricate nanophotonic devices, it is analyzed in Fig. 2a for three various values of chemical potential. The upper mode shows greater variation in characteristic curves as compared to lower mode. Characteristic curves for both modes start squeezing for higher magnitude of chemical potential. For the case of the upper mode, normalized propagation starts decreasing by increasing of chemical potential as reported [16, 21,22,23] and characteristic curves start shifting toward low frequency region as reported in [16]. The slope of variation of characteristic curve is greater for smaller value of chemical potential as reported in [22]. It can be noted that the frequency band for both modes can be tuned by varying chemical potential. Furthermore, lower mode shows a smaller variation in band gap as compared to the upper mode. As the chemical potential rises, the propagation constant decreases. This can be understood by considering the behavior of the energy bands in graphene. At low carrier concentrations, the valence and conduction bands in graphene meet at a single point in the Brillouin zone, known as the Dirac point. At this point, the energy–momentum relation for electrons becomes linear, leading to unique electronic properties. However, as chemical potential increases, electron density also increases, the energy bands shift, and the Dirac point moves away from the zero-energy level. At this point, the energy–momentum relation for electrons becomes linear, leading to unique electronic properties. However, as chemical potential increases, electron density also increases, the energy bands shift, and the Dirac point moves away from the zero-energy level. In other words, at higher electron densities (higher chemical potentials), the plasmons experience more damping, causing them to lose their energy faster and leading to a shorter propagation for the electromagnetic wave.

Fig. 2
figure 2

Influence of chemical potential and relaxation time on normalized propagation constant

Full size image

At this point, the energy–momentum relation for electrons becomes linear, leading to unique electronic properties. However, as chemical potential increases, electron density also increases, the energy bands shift, and the Dirac point moves away from the zero-energy level. In other words, at higher electron densities (higher chemical potentials), the plasmons experience more damping, causing them to lose their energy faster and leading to a shorter propagation for the electromagnetic wave. Therefore, there is a trade-off for choosing a suitable chemical potential to achieve the desired values of normalized propagation constant. The variation in Frequency dependent normalized propagation constant under the different values of relaxation time is depicted in Fig. 2b. As relaxation time increases, the characteristic curves for both modes start moving toward a low-frequency region. The bandgap between the upper and lower modes starts squeezing as the relaxation time increases; this confirms that electromagnetic surface.

waves are strongly dependent on the quality and traits of monolayer graphene layer. In the respect that normalized propagation increases with decreasing relaxation time, the variation of upper mode is almost the same, like in the chemical potential case, but the difference lies in their lower modes. Furthermore, the slope of variation of characteristic curve is greater for smaller value of relaxation time. It can be noted that, as relaxation time increases, normalized propagation starts decreasing as reported in [24, 25], and characteristic curves starts shifting towards low-frequency region. Furthermore, the lower mode becomes more dominant as compared to the higher mode. By optimizing relaxation time, it is possible to enhance the performance and reliability of nanophotonic devices. As the relaxation time increases, the scattering of electrons by phonons becomes more frequent and prominent. These scattering events cause the electrons to lose energy and momentum, resulting in a decrease in the propagation constant. Furthermore, the scattering process leads to a decrease in the overall conductivity of graphene and affects the propagation of electromagnetic waves in the material. Figure 3a analyzes the influence of the number of graphene layers on the normalized propagation constant since a monolayer of graphene absorbs only 2.3% of incident light as reported in [24, 26]. For the case of the upper mode, as number of graphene layers increases, normalized propagation constant starts decreasing as reported in [24, 25, 27]. The slope variation is greater for monolayer graphene as compared to multilayers. For the case of the upper mode, by increasing number of graphene layers the EM wave frequency decreases and characteristic curves exhibit smaller variation. After some higher frequencies, an unphysical region starts that has no practical importance in the plasmonics community. Additionally, the monolayer graphene exhibits higher variation characteristic curves. For the case of the lower mode, the variation in characteristic curves is shown at some higher frequencies. To demonstrate the influence of temperature on the normalized propagation constant, it is depicted in Fig. 3b. For the case of the upper mode, higher propagation constant could be achieved for lower temperature values. For the case of the lower mode, characteristic curves show very small variation in characteristic curves. The decrease in the normalized propagation constant with increasing temperature of graphene conductivity can be attributed to the increased scattering of electrons due to thermal energy and the enhanced electron–phonon interactions. These factors disrupt electron motion and reduce the overall conductivity of graphene. It is concluded that as temperature rises, normalized propagation constant starts decreasing for the upper mode and vice versa for the lower mode, as shown in Fig. 3a. But the difference lies in their frequency band gap. Frequency dependent normalized propagation constant of under the different values of chirality parameter is analyzed in Fig. 4a. It is worth mentioning that as the chirality parameter increases, the normalized propagation constant starts increasing as reported in [18]. Lower mode characteristic curves begin to level off at lower frequencies while the upper mode at higher frequencies has practical importance. In optics, chiral materials can be used to manipulate the propagation of light in unique ways. By controlling the chirality of a material, researchers can effectively control the speed at which light propagates through it, leading to applications such as chiral optics and chiral metamaterials. Frequency dependent normalized propagation constant for the various values of gyrotropy (permeability tensor parameter) in certain THz frequency band is illustrated in Fig. 4b. The upper mode shows higher variation in characteristic curves as compared to lower mode. By increasing gyrotropy, the frequency band starts squeezing, and characteristic curves are shifted from low-frequency to high-frequency region. It is noted that from the above discussion, gyrotropy and chirality show the same trend for normalized propagation constant, but the difference lies in their frequency band gap. Furthermore, for the case of gyrotropy, lower mode characteristic curves level off at 0.51 THz. As the wave interacts with the gyrotropic medium, its velocity changes, affecting the rate at which it propagates through the material. The rotation of the polarization plane reduces losses and allows for a more efficient interaction between the wave and the material. Additionally, the alteration of the refractive index contributes to a higher propagation speed. These combined effects make ferrite mediums with increased gyrotropy particularly useful in applications such as microwave devices, antennas, and magnetic resonance imaging. This is an important matter for designing chiroferrite-graphene-based nanophotonic devices in the specific frequency band by choosing the appropriate gyrotropy of medium.

Fig. 3
figure 3

Influence of number of graphene layers and temperature on normalized propagation constant

Full size image
Fig. 4
figure 4

Influence of chirality and gyrotropy on normalized propagation constant

Full size image

Conclusion

Theoretical investigations were carried out to explore hybrid plasmon modes at the chiroferrite-graphene interface. Maxwell’s equations in differential form were used to find the model field equations, and impedance boundary conditions were applied to obtain dispersion relation. Frequency dependence normalized propagation constant under the different values of graphene chemical potential, relaxation, number of graphene layers, temperature, chirality, and gyrotropy of the chiroferrite medium were analyzed. It is concluded that normalized propagation constant can be tailored by tailoring the abovementioned parameters to fabricate nanophotonic devices in THz frequency range.