1 Introduction

A large number of existing reservoirs may be categorized as naturally fractured [5, 15, 16, 21, 22, 24,25,26, 32,33,34, 44, 45]. By this, we usually refer to materials with distributed discontinuities that they exhibit two very distinct porous networks. Roughly speaking, the first porous network is formed of penny-shaped cracks or fissures mainly due to tectonic activities, while the second is formed of rounded pores [20]. As for their characteristics, the fracture networks are characterized by low storage and high permeability, whereas the porous blocks are characterized by high storage and low permeability [55]. As a result, the behaviors of fractured reservoirs are considerably different from those of conventional reservoirs [25], which could be reflected in the soil consolidation, groundwater flow, solute transport, and gas/oil production [3]. Until now, the modeling of fractured reservoirs is still one of the most challenging activities in geomechanics and geosciences.

Over the last 50 years, numerous models with different degrees of sophistication have been proposed for porous materials, which can be divided into three categories. In the earliest category, a fractured system was grossly treated as an equivalent single-porosity continuum [40], and the existence of fractures or cracks is reflected in the material coefficients such as stiffness, which may be orders of magnitude different from those of a homogeneous medium [3]. However, this approach has a number of drawbacks such as the identification of the representative blocks and the determination of equivalent permeability values [3, 32]. On the contrary, the second category is known as the explicit (direct) modeling approach such as the discrete fracture network [6, 23, 27, 47], which allows one to account for each length scale directly within a model. However, the very large number of micro-fractures in the unconventional reservoir [37] could make the direct simulation of discrete fracture networks computationally prohibitive [1, 2].

The third category is the double-porosity model [4, 50], which assumed that two pore regions overlap in a computational domain. The main idea is that for every physical point in space, there may be two scales of porosity, one representing the average porosity in the fracture network and the other in the porous blocks [20]. This idealization may be thought of as an extreme case of the crack density model of Wong [53] when the micro-fracture density becomes very high. The mathematical basis for this model is known as mixture theory in which any material in a composite medium that is significantly different from those of other intervening materials deserves a separate description. This leads to two mass conservation equations, one for each of the foregoing porosity regions. These equations are coupled by a leakage (source/sink) term [30, 36, 37, 42]. Nowadays, the double-porosity concept has been widely used in civil engineering, energy resource engineering, and many other related fields of engineering [3, 32].

Previous formulations of poroelasticity in double-porosity media have assumed isotropy in both deformation and fluid flow [3, 7, 18, 19, 25, 29, 31, 35, 36, 46, 52, 59]. However, many geologic materials have exhibited anisotropy in either or both deformation and fluid flow responses [14, 28, 41, 43, 49, 54, 57, 60]. In this work, we consider a special case of anisotropy known as transverse isotropy, or cross-anisotropy, which is characterized by a plane on which the response is isotropic and an axis perpendicular to this plane on which the response is anisotropic. For a single-porosity medium, the effect of transverse isotropy has already been incorporated into the poroelasticity equations [17, 49, 58]. For a double-porosity medium, however, its effect has not been clearly elucidated in light of the limitations imposed by current laboratory testing procedures.

The aim of this paper is to address the above-mentioned knowledge gap in the poroelasticity of anisotropic double-porosity media. A novel feature of the mathematical formulation is the use of the principle of superposition in combination with mixture theory to arrive at the governing mass balance equations. The mathematical formulation is innovative because it leads to a result that is identical to what has been developed previously using continuum principles of thermodynamics [58], but following a different route. It is the first time, to the authors’ knowledge, that these new formulas and interpretations are presented within the context of poromechanics.

However, we emphasize at the outset that the principle of superposition is applied in this paper at a fixed hydromechanical state where only mechanical deformation is involved, and not from one hydromechanical state to another where dissipative processes would render the principle inapplicable. Furthermore, we restrict the developments to linear elasticity. Nevertheless, even with the assumption of poroelasticity, the parameters or coefficients of a model are usually arbitrarily assumed in the literature, and their fundamental origins were not clearly established. In this respect, the results of this paper are useful in shedding light onto the physical meaning of the governing conservation equations and the relevant poroelastic coefficients.

The paper is organized as follows. Based on mixture theory, mass conservation equations are first formulated in Sect. 2 for single-porosity media, where the evolution laws for the volume fractions are derived. To this end, we make use of the principle of superposition for anisotropic single-porosity media to obtain the poroelastic coefficients and compare them with those derived in [17, 58]. In Sect. 3, we extend the formulation to anisotropic double-porosity media and derive the corresponding poroelastic coefficients analytically. The elastic moduli for transversely isotropic materials are discussed in Sect. 4, where the relevant poroelastic coefficients for two types of rock are also calculated and compared with those derived by prominent authors [8, 29]. Finally, conclusions are given in Sect. 5.

2 Single-porosity media

In the following discussion and throughout this paper, we assume that the solid deformation is infinitesimal in the sense that the domain of the problem does not change appreciably. We denote by V a representative elementary volume (REV) consisting of a mixture of solid and fluid. Let \(\phi ^s\) and \(\phi ^f\) represent the volume fractions of solid and fluid, respectively, defined as

$$\begin{aligned} \phi ^s = \frac{V_s}{V}\,, \qquad \phi ^f = \frac{V_f}{V}\,, \end{aligned}$$
(1)

where \(V_s\) and \(V_f\) are volumes of solid and fluid in V, respectively. The closure condition on the volume fractions is

$$\begin{aligned} \phi ^s + \phi ^f = 1\,. \end{aligned}$$
(2)

The partial mass densities of the solid and fluid are given by

$$\begin{aligned} \rho ^s = \phi ^s \rho _s \,, \qquad \rho ^f = \phi ^f \rho _f\,, \end{aligned}$$
(3)

where \(\rho _s\) and \(\rho _f\) are the intrinsic mass densities of solid and fluid, respectively. The total mass density of the mixture is given by the sum

$$\begin{aligned} \rho = \rho ^s + \rho ^f\,. \end{aligned}$$
(4)

We denote the material time derivatives following the motions of solid and fluid by \(\mathrm {d}(\cdot )/ \mathrm {d}t\) and \(\mathrm {d}^f (\cdot )/ \mathrm {d}t\), respectively. The mass balance equations for solid and fluid, assuming no mass exchanges between them, take the form

$$\begin{aligned}&\frac{\mathrm {d}{\rho ^s}}{\mathrm {d} {t}} + \rho ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\mathrm {d}^{f} {\rho ^f}}{\mathrm {d} {t}} + \rho ^f \nabla \cdot \mathbf {v}_f = 0\,, \end{aligned}$$
(6)

where \(\mathbf {v}\) and \(\mathbf {v}_f\) are the intrinsic velocities of solid and fluid particles, respectively. Written in terms of \(\rho _s\) and \(\rho _f\), the conservation equations take the form

$$\begin{aligned}&\frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} + \frac{\phi ^s}{\rho _s} \frac{\mathrm {d}{\rho _s}}{\mathrm {d} {t}} + \phi ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\mathrm {d}^{f} {\phi ^f}}{\mathrm {d} {t}} + \frac{\phi ^f}{\rho _f} \frac{\mathrm {d}^{f} {\rho _f}}{\mathrm {d} {t}} + \phi ^f \nabla \cdot \mathbf {v}_f = 0\,. \end{aligned}$$
(8)

Assuming barotropic flow, the constitutive equation relating density and pressure in the solid is given by

$$\begin{aligned} \frac{1}{\rho _s}\frac{\mathrm {d} {\rho _s}}{\mathrm {d} {t}} = \frac{1}{K_s} \frac{\mathrm {d} {p_s}}{\mathrm {d} {t}}\,, \end{aligned}$$
(9)

where \(p_s\) and \(K_s\) are the intrinsic pressure and bulk modulus in the solid. Substituting in Eq. (7) yields

$$\begin{aligned} \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} + \frac{\phi ^s}{K_s} \frac{\mathrm {d} {p_s}}{\mathrm {d} {t}} + \phi ^s \nabla \cdot \mathbf {v} = 0\,. \end{aligned}$$
(10)

For the fluid, we take a similar intrinsic constitutive relation of the form

$$\begin{aligned} \frac{1}{\rho _f} \frac{\mathrm {d}^{f} {\rho _f}}{\mathrm {d} {t}} = \frac{1}{K_f} \frac{\mathrm {d}^{f} {p}}{\mathrm {d} {t}}\,, \end{aligned}$$
(11)

where \(p = p_f\) is the intrinsic pressure in the fluid. Substituting into Eq. (8) gives

$$\begin{aligned} \frac{\mathrm {d}^{f} {\phi ^f}}{\mathrm {d} {t}} + \frac{\phi ^f}{K_f} \frac{\mathrm {d}^{f} {p}}{\mathrm {d} {t}} + \phi ^f \nabla \cdot \mathbf {v}_f = 0\,. \end{aligned}$$
(12)

We recall that the material time derivative following the fluid motion is related to the material time derivative following the solid motion through the equation

$$\begin{aligned} \frac{\mathrm {d}^{f} {(\cdot )}}{\mathrm {d} {t}} = \frac{\mathrm {d} {(\cdot )}}{\mathrm {d} {t}} + \nabla (\cdot )\cdot \tilde{\mathbf {v}}_f\,, \end{aligned}$$
(13)

where \(\tilde{\mathbf {v}}_f = \mathbf {v}_f - \mathbf {v}\) is the relative velocity of fluid with respect to solid. Thus, for the fluid we obtain

$$\begin{aligned} \frac{\mathrm {d} {\phi ^f}}{\mathrm {d} {t}} + \frac{\phi ^f}{K_f} \frac{\mathrm {d} {p}}{\mathrm {d} {t}} + \frac{1}{K_f}\left( {\nabla p}\right) \cdot \mathbf {q} + \nabla \cdot \mathbf {q} + \phi ^f \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(14)

where

$$\begin{aligned} \mathbf {q} = \phi ^f \tilde{\mathbf {v}}_f \end{aligned}$$
(15)

is the superficial Darcy velocity.

The total Cauchy stress tensor \({\varvec{\sigma }}\) may be written as the sum of partial stress tensors in the form

$$\begin{aligned} {\varvec{\sigma }} = \phi ^s {\varvec{\sigma }}_s - \phi ^f p {\mathbf{1}}\,, \end{aligned}$$
(16)

where \({\varvec{\sigma }}_s\) is the intrinsic stress in the solid (force in solid per unit area of solid), and \({\mathbf{1}}\) is the second-order identity tensor. We note that the intrinsic solid stress has the form

$$\begin{aligned} {\varvec{\sigma }}_s = - p_s {\mathbf{1}} + {\varvec{s}}_s\,, \end{aligned}$$
(17)

where \(p_s\) is the intrinsic solid pressure and \({\varvec{s}}_s\) is the deviatoric component of \({\varvec{\sigma }}_s\). However, it is also common knowledge that part of the total stress tensor \({\varvec{\sigma }}\) may be ascribed to an effective stress \({\varvec{\sigma }}'\) that depends on solely on the deformation of the solid frame. For linear elasticity, the relation takes the form

$$\begin{aligned} {\varvec{\sigma }}' = {\mathbb {C}}^e : {\varvec{\epsilon }}\,, \end{aligned}$$
(18)

where \({\varvec{\epsilon }}\) is the small strain tensor describing the deformation of the solid frame, and \({\mathbb {C}}^e\) is a rank-four tensor (with major and minor symmetries) characterizing the elastic isotropy or anisotropy of the porous material, see Sect. 4.

Fig. 1
figure 1

Superposition in poroelasticity: Phase diagram for a single-porosity volume with solid represented by the shaded area and pores represented by the white area. Volume is subjected to a tensorial stress indicated above each diagram; number inside the white area is the generated pore fluid pressure

Full size image

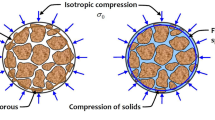
To determine the component of fluid pressure p that complements the effective stress \({\varvec{\sigma }}'\), we make use of the principle of superposition shown in Fig. 1. In loading configuration (a) of this figure, the porous volume is subjected to a total stress of \(\left( {{\varvec{\sigma }} + p{\mathbf{1}}}\right)\) with no internal fluid pressure within the pores, thus resembling a dry condition. In this case, the load is borne completely by the solid frame. In loading configuration (b), on the other hand, a total stress of \(-p{\mathbf{1}}\) is applied to the same volume that generates an internal fluid pressure p within it. This second load is borne completely by the solid constituent. Superposition of these two loading configurations yields the original problem.

Since the internal fluid pressure is zero for loading configuration (a), the strain in the solid matrix can be calculated as

$$\begin{aligned} {\varvec{\epsilon }}^{(a)} = \left( {{\mathbb {C}}^e}\right) ^{-1}:\left( {{\varvec{\sigma }} + p{\mathbf{1}}}\right) \,, \end{aligned}$$
(19)

where \(\left( {{\mathbb {C}}^e}\right) ^{-1}\) is the elastic compliance tensor under dry (or drained) condition. For loading configuration (b), on the other hand, the solid matrix is subjected to isotropic deformation equal to the isotropic strain in the solid constituent, i.e.,

$$\begin{aligned} {\varvec{\epsilon }}^{(b)} = - \frac{p}{3K_s}{\mathbf{1}}\,. \end{aligned}$$
(20)

The sum of these two strains represents the total strain in the solid frame, i.e.,

$$\begin{aligned} {\varvec{\epsilon }} = {\varvec{\epsilon }}^{(a)} + {\varvec{\epsilon }}^{(b)} = \left( {{\mathbb {C}}^e}\right) ^{-1}:\left( {{\varvec{\sigma }} + p{\mathbf{1}}}\right) - \frac{p}{3K_s}{\mathbf{1}}\,. \end{aligned}$$
(21)

Pre-multiplying both sides by \({\mathbb {C}}^e\) yields the effective Cauchy stress,

$$\begin{aligned} {\varvec{\sigma }}' = {\mathbb {C}}^e : {\varvec{\epsilon }} = {\varvec{\sigma }} + p{\varvec{b}} \qquad \Rightarrow \qquad {\varvec{\sigma }} = {\varvec{\sigma }}' - p {\varvec{b}}\,, \end{aligned}$$
(22)

where

$$\begin{aligned} {\varvec{b}} = {\mathbf{1}} - \frac{{\mathbb {C}}^e : {\mathbf{1}}}{3K_s} \end{aligned}$$
(23)

is the same Biot tensor derived by Zhao and Borja [58]. However, it must be noted that Zhao and Borja employed continuum thermodynamics to arrive at the above result, whereas the present formulation makes use of the superposition principle. That the same result is obtained via two different methods is noteworthy since one result verifies the other, see also the expression derived by Cheng [17]. We note that for isotropic elasticity the Biot tensor reduces to

$$\begin{aligned} {\varvec{b}} = \left( {1 - \frac{K}{K_s}}\right) {\mathbf{1}} = \alpha {\mathbf{1}}\,, \end{aligned}$$
(24)

where K is the elastic bulk modulus of the solid frame and \(\alpha = 1 - {K}/{K_s}\) is the familiar Biot coefficient, see Borja [10]. For rocks, typical values of \(\alpha\) range from 0.6 to 0.9 [39].

We next use the same superposition principle to evaluate the remaining dependent variable in the balance of mass for the solid phase, namely, either the mass density \(\rho _s\) in Eq. (7) or the pressure \(p_s\) in Eq. (10). Let us first define \(\theta _s\) as the intrinsic volumetric strain in the solid constituent, which can be decomposed into \(\theta _s^{(a)}\) and \(\theta _s^{(b)}\) following the superposition procedure. For loading configuration (a) shown in Fig. 1, the intrinsic Cauchy stress in the solid constituent is \(\left( {{\varvec{\sigma }} + p{\mathbf{1}}}\right) /\phi ^s\), while the intrinsic mean normal stress is \(\left( {\sigma + p}\right) /\phi ^s\), where \(\sigma = \mathrm{tr}({\varvec{\sigma }})/3\). Thus, the intrinsic volumetric strain in the solid (assuming a constant \(K_s\)) is

$$\begin{aligned} \theta _s^{(a)} = \frac{1}{K_s} \frac{\sigma + p}{\phi ^s} = \frac{1}{K_s} \frac{-\phi ^s p_s - \phi ^f p + p}{\phi ^s} = \frac{p - p_s}{K_s}\,. \end{aligned}$$
(25)

For loading configuration (b), the solid constituent is subjected to the fluid pressure p, so

$$\begin{aligned} \theta _s^{(b)} = -\frac{p}{K_s}\,. \end{aligned}$$
(26)

Adding the two and taking the material time derivative following the solid motion yields

$$\begin{aligned}\frac{\mathrm {d}{\theta _s}}{\mathrm {d} {t}} &= \frac{\mathrm {d}{\theta _s^{(a)}}}{\mathrm {d} {t}} + \frac{\mathrm {d}{\theta _s^{(b)}}}{\mathrm {d} {t}}\nonumber \\& = \frac{1}{\phi ^s K_s} \left[ {\frac{\mathrm {d}{\sigma }}{\mathrm {d} {t}} + \phi ^f \frac{\mathrm {d} {p}}{\mathrm {d} {t}} - \left( {p - p_s}\right) \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}}}\right] \,. \end{aligned}$$
(27)

From solid mechanics, we know the intrinsic volumetric strain rate in solid \(\mathrm {d}\theta _s / \mathrm {d}t\) is related to the change in \(\rho _s\) through the following equation, assuming the solid mass is conserved

$$\begin{aligned} \frac{\mathrm {d} {\theta _s}}{\mathrm {d} {t}} = - \frac{1}{\rho _s} \frac{\mathrm {d} {\rho _s}}{\mathrm {d} {t}}\,. \end{aligned}$$
(28)

After substituting Eqs. (27) and (28) into Eq. (7) and collecting terms, we obtain

$$\begin{aligned} \left( {1 + \frac{p - p_s}{K_s}}\right) \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} - \frac{1}{K_s} \left( {\frac{\mathrm {d} {\sigma }}{\mathrm {d} {t}} + \phi ^f \frac{\mathrm {d} {p}}{\mathrm {d} {t}}}\right) + \phi ^s \nabla \cdot \mathbf {v} = 0\,. \end{aligned}$$
(29)

We note that

$$\begin{aligned} \frac{p - p_s}{K_s} = \theta _s^{(a)} \ll 1\,, \end{aligned}$$
(30)

see [58]. Thus, the balance of mass for solid takes the simpler form

$$\begin{aligned} \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} - \frac{1}{K_s} \left( {\frac{\mathrm {d} {\sigma }}{\mathrm {d} {t}} + \phi ^f \frac{\mathrm {d} {p}}{\mathrm {d} {t}}}\right) + \phi ^s \nabla \cdot \mathbf {v} = 0\,. \end{aligned}$$
(31)

The final step is to determine an expression for \(\mathrm {d}\sigma /\mathrm {d}t\).

From the effective stress relation Eq. (22), we obtain

$$\begin{aligned} \frac{{\mathbf{1}}:{\mathbb {C}}^e : {\varvec{\epsilon }}}{3} = \sigma + \left( {1 - \frac{{\mathbf{1}}:{\mathbb {C}}^e:{\mathbf{1}}}{9 K_s}}\right) p \end{aligned}$$
(32)

by taking the trace of both sides. Next, by taking the material time derivatives of both sides and solving, we obtain

$$\begin{aligned} \frac{\mathrm {d} {\sigma }}{\mathrm {d} {t}} = \frac{{\mathbf{1}}:{\mathbb {C}}^e}{3}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} - \left( {1 - \frac{{\mathbf{1}}:{\mathbb {C}}^e:{\mathbf{1}}}{9 K_s}}\right) \frac{\mathrm {d} {p}}{\mathrm {d} {t}}\,. \end{aligned}$$
(33)

Substituting back into Eq. (31) and collecting terms yields

$$\begin{aligned} \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} + \frac{\beta }{K_s} \frac{\mathrm {d} {p}}{\mathrm {d} {t}} - \frac{{\mathbf{1}}:{\mathbb {C}}^e}{3 K_s}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \phi ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(34)

where

$$\begin{aligned} \beta = 1 - \phi ^f - \frac{{\mathbf{1}}:{\mathbb {C}}^e:{\mathbf{1}}}{9 K_s}\,. \end{aligned}$$
(35)

For the fluid phase, we add Eqs. (14) and (34) to obtain

$$\begin{aligned} {\varvec{b}}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \frac{1}{{\mathcal {M}}} \frac{\mathrm {d} {p}}{\mathrm {d} {t}} + \frac{1}{K_f}\left( {\nabla p}\right) \cdot \mathbf {q} + \nabla \cdot \mathbf {q} = 0\,, \end{aligned}$$
(36)

where \({\mathcal {M}}\) is the Biot modulus, defined as

$$\begin{aligned} \frac{1}{{\mathcal {M}}} = \frac{\beta }{K_s} + \frac{\phi ^f}{K_f}\,. \end{aligned}$$
(37)

Equation (36) can be used in combination with balance of linear momentum to solve coupled systems with the \(\mathbf {u}/p\) formulation [51, 58].

3 Double-porosity media

We denote by V a representative elementary volume (REV) consisting of a mixture of solid with double porosity. Let \(\phi ^s\), \(\phi ^m\), and \(\phi ^M\) represent the volume fractions of solid, nanopores, and micro-fractures, respectively, defined as

$$\begin{aligned} \phi ^s = \frac{V_s}{V}\,, \quad \phi ^m = \frac{V_m}{V}\,, \quad \phi ^M = \frac{V_M}{V}\,, \end{aligned}$$
(38)

where \(V_s\), \(V_m\), and \(V_M\) are the volumes of solid, nanopores, and micro-fractures contained in V. The closure condition on the volume fractions is

$$\begin{aligned} \phi ^s + \phi ^m + \phi ^M = 1\,. \end{aligned}$$
(39)

The pore fractions represent the proportion of pore volume occupied by the nanopores and micro-fractures and are given by

$$\begin{aligned} \psi ^m = \frac{\phi ^m}{1 - \phi ^s}\,, \qquad \psi ^M = \frac{\phi ^M}{1 - \phi ^s}\,. \end{aligned}$$
(40)

The denominator in these two expressions, \(1 - \phi ^s\), is the porosity \(\phi\) of the mixture. The closure condition on the pore fractions is

$$\begin{aligned} \psi ^m + \psi ^M = 1\,. \end{aligned}$$
(41)

In what follows, we assume that the nanopores and micro-fractures are filled with the same type of fluid, which could be either liquid or gas. The partial mass densities of the solid, fluid in the nanopores, and fluid in the micro-fractures are given by

$$\begin{aligned} \rho ^s = \phi ^s \rho _s \,, \qquad \rho ^m = \phi ^m \rho _m\,, \qquad \rho ^M = \phi ^M \rho _M\,, \end{aligned}$$
(42)

where \(\rho _s\), \(\rho _m\), and \(\rho _M\) are the intrinsic mass densities of the solid, fluid in the nanopores, and fluid in the micro-fractures, respectively. The total mass density of the mixture is given by the sum

$$\begin{aligned} \rho = \rho ^s + \rho ^m + \rho ^M\,. \end{aligned}$$
(43)

Denoting the material time derivatives following the motions of solid and fluids by \(\mathrm {d}\left( {\cdot }\right) /\mathrm {d}t\), \(\mathrm {d}^m\left( {\cdot }\right) /\mathrm {d}t\), and \(\mathrm {d}^M\left( {\cdot }\right) /\mathrm {d}t\), the mass balance equations take the form

$$\begin{aligned}&\frac{\mathrm {d} {\rho ^s}}{\mathrm {d} {t}} + \rho ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(44)
$$\begin{aligned}&\frac{\mathrm {d}^{m} {\rho ^m}}{\mathrm {d} {t}} + \rho ^m \nabla \cdot \mathbf {v}_m = c^m\,, \end{aligned}$$
(45)
$$\begin{aligned}&\frac{\mathrm {d}^{M} {\rho ^M}}{\mathrm {d} {t}} + \rho ^M \nabla \cdot \mathbf {v}_M = c^M\,, \end{aligned}$$
(46)

where \(\mathbf {v}\), \(\mathbf {v}_m\), and \(\mathbf {v}_M\) are the velocities of solid, fluid in the nanopores, and fluid in the micro-fractures, respectively. We assume in the foregoing equations that the solid mass is conserved, and that the nanopores and micro-fractures exchange mass at the rates if \(c^m\) and \(c^M\) per unit total volume. For a closed system,

$$\begin{aligned} c^m + c^M = 0\,. \end{aligned}$$
(47)

Assuming barotropic flow on the solid and fluids once again, we can write the solid mass balance equation in terms of \(\theta _s\) defined in Sect. 2 as

$$\begin{aligned} \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} - \phi ^s \frac{\mathrm {d} {\theta _s}}{\mathrm {d} {t}} + \phi ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(48)

and the fluid mass balance equations in terms of the intrinsic fluid pressures \(p_m\) and \(p_M\) as

$$\begin{aligned}&\frac{\mathrm {d} {\phi ^m}}{\mathrm {d} {t}} + \frac{\phi ^m}{K_m} \frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} + \frac{1}{K_m}\left( {\nabla p_m}\right) \cdot \mathbf {q}_m + \nabla \cdot \mathbf {q}_m\nonumber \\&\quad + \phi ^m \nabla \cdot \mathbf {v} = \frac{c^m}{\rho _m}\,, \end{aligned}$$
(49)
$$\begin{aligned}&\frac{\mathrm {d} {\phi ^M}}{\mathrm {d} {t}} + \frac{\phi ^M}{K_M} \frac{\mathrm {d} {p_M}}{\mathrm {d} {t}} + \frac{1}{K_M}\left( {\nabla p_M}\right) \cdot \mathbf {q}_M + \nabla \cdot \mathbf {q}_M\nonumber \\&\quad + \phi ^M \nabla \cdot \mathbf {v} = \frac{c^M}{\rho _M}\,, \end{aligned}$$
(50)

where

$$\begin{aligned} \mathbf {q}_m = \phi ^m \left( {\mathbf {v}_m - \mathbf {v}}\right) \,, \qquad \mathbf {q}_M = \phi ^M \left( {\mathbf {v}_M - \mathbf {v}}\right) \end{aligned}$$
(51)

are the superficial Darcy velocities; and \(K_m\) and \(K_M\) are the intrinsic fluid bulk moduli.

Fig. 2
figure 2

Statistically distributed pores allow a double-porosity structure to be replaced with a single-porosity structure with mean pore fluid pressure \({\bar{p}}\)

Full size image

To derive the effective stress equation, a key aspect is to recognize the statistically distributed nature of the pores, which allows the double-porosity structure to be represented by a single-porosity structure with a weighted pore fluid pressure. Consider, for example, the superposition shown in Fig. 2. Here, the double-porosity structure is replaced with a statistically equivalent single-porosity structure with a weighted pore fluid pressure of \({\bar{p}}\) given by [11]

$$\begin{aligned} {\bar{p}} = \psi ^M p_M + \psi ^m p_m\,. \end{aligned}$$
(52)

Thus, we can use the results from Sect. 2 directly by replacing p with \({\bar{p}}\) rather than repeating the whole process of Sect. 2. Specifically, from Eq. (22), we have

$$\begin{aligned} {\varvec{\sigma }} = {\varvec{\sigma }}' - {\bar{p}} {\varvec{b}} = {\varvec{\sigma }}' - \psi ^M p_M {\varvec{b}} - \psi ^m p_m {\varvec{b}}\,, \end{aligned}$$
(53)

where \({\varvec{b}}\) is the same Biot tensor given in Eq. (23). From Eq. (34), we have

$$\begin{aligned} \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} + \frac{\beta }{K_s} \frac{\mathrm {d} {{\bar{p}}}}{\mathrm {d} {t}} - \frac{{\mathbf{1}}:{\mathbb {C}}^e}{3 K_s}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \phi ^s \nabla \cdot \mathbf {v} = 0\,, \end{aligned}$$
(54)

where \(\beta\) is already defined in Eq. (35) with \(\phi ^f\) replaced by total porosity \(\phi=\phi^M + \phi^m\). Note here the time derivative of \({\bar{p}}\) generates an additional term which is the time derivative of pore fraction \(\mathrm {d}\psi ^M/\mathrm {d}t\), and this term is unique to double-porosity formulation.

Remark

An alternative approach that does not explicitly employ volume averaging of the pore pressures, such as that shown in Eq. (52), is presented in "Appendix". This latter formulation reinforces the understanding that the principle of superposition does not depend on the sequence of loading, and that there is more than one way by which one can get to the same result.

In order to evaluate \(\mathrm {d}\phi ^m/\mathrm {d}t\) and \(\mathrm {d}\phi ^M/\mathrm {d}t\) of Eqs. (49) and (50), we must develop a constitutive law for \(\mathrm {d}\psi ^M/\mathrm {d}t\). We refer to the phase diagram shown in Fig. 3, where the REV is partitioned into two superimposed regions representing the nanopore and micro-fracture skeletons. These two regions must be distinguished from the nanopore and micro-fracture volumes, which are mainly pore spaces occupied by fluids. The nanopore and micro-fracture skeletons are themselves superimposed solids and pore spaces. Let \(V_{np}\) and \(V_{mf}\) represent respective portions of the total volume V occupied by the nanopore and micro-fracture skeletons. The corresponding volume fractions are

$$\begin{aligned} \varphi ^m = \frac{V_{np}}{V}\,, \quad \varphi ^M = \frac{V_{mf}}{V}\,, \quad \varphi ^m + \varphi ^M = 1\,. \end{aligned}$$
(55)

Since both volume fractions are statistically distributed throughout the entire volume, we would require the porosities are the same for the nanopore and micro-fracture skeletons, i.e.,

$$\begin{aligned} \frac{\phi ^m}{\varphi ^m} = \frac{\phi ^M}{\varphi ^M}\,, \end{aligned}$$
(56)

which implies that \(\varphi ^m \equiv \psi ^m\) and \(\varphi ^M \equiv \psi ^M\).

Fig. 3
figure 3

Representation of double-porosity structure in terms of superimposed nanopore and micro-fracture skeletons or matrices

Full size image

We next consider following trivial decomposition

$$\begin{aligned} {\varvec{\sigma }} = \psi ^m {\varvec{\sigma }} + \psi ^M {\varvec{\sigma }}\,, \end{aligned}$$
(57)

and assume the following decomposition for \({\varvec{\sigma }}'\)

$$\begin{aligned} {\varvec{\sigma }}' = \psi ^m {\varvec{\sigma }}_m' + \psi ^M {\varvec{\sigma }}_M'\,, \end{aligned}$$
(58)

where \({\varvec{\sigma }}_m'\) and \({\varvec{\sigma }}_M'\) are effective stresses in the nanopore and micro-fracture skeletons of Fig. 3. Rewriting the effective stress relation Eq. (53) in the expanded form using above two equations gives

$$\begin{aligned} \psi ^m \left( {{\varvec{\sigma }} + p_m {\varvec{b}}}\right) + \psi ^M \left( {{\varvec{\sigma }} + p_M {\varvec{b}}}\right) = \psi ^m {\varvec{\sigma }}_m' + \psi ^M {\varvec{\sigma }}_M'\,. \end{aligned}$$
(59)

This equation holds for any \(\psi ^M\) (and \(\psi ^m\)), so we must have

$$\begin{aligned} {\varvec{\sigma }} + p_m {\varvec{b}} = {\varvec{\sigma }}_m'\,, \quad {\varvec{\sigma }} + p_M {\varvec{b}} = {\varvec{\sigma }}_M'\,, \end{aligned}$$
(60)

which means that

$$\begin{aligned} {\varvec{\sigma }}_m' - p_m {\varvec{b}} = {\varvec{\sigma }}_M' - p_M {\varvec{b}}\,. \end{aligned}$$
(61)

Taking the trace and applying the material time derivative with respect to solid motion gives

$$\begin{aligned} \frac{\mathrm {d} {\sigma _m'}}{\mathrm {d} {t}} - \frac{\mathrm {d} {\sigma _M'}}{\mathrm {d} {t}} = \left( {\frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} - \frac{\mathrm {d} {p_M}}{\mathrm {d} {t}}}\right) b\,, \end{aligned}$$
(62)

where \(\sigma _m' = \mathrm{tr}({\varvec{\sigma }}_m')/3\), \(\sigma _M' = \mathrm{tr}({\varvec{\sigma }}_M')/3\), and \(b = \mathrm{tr}({\varvec{b}})/3\).

In terms of the volumetric strain in the nanopore and micro-fracture skeletons, \(\theta _m\) and \(\theta _M\), respectively, we assume linear elasticity and rewrite the foregoing equations as

$$\begin{aligned} K_m^e \frac{\mathrm {d} {\theta _m}}{\mathrm {d} {t}} - K_M^e \frac{\mathrm {d} {\theta _M}}{\mathrm {d} {t}} = \left( {\frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} - \frac{\mathrm {d} {p_M}}{\mathrm {d} {t}}}\right) b\,, \end{aligned}$$
(63)

where \(K_m^e\) and \(K_M^e\) are the elastic bulk moduli of the nanopore and micro-fracture skeletons, respectively (not to be confused with the fluid bulk moduli \(K_m\) and \(K_M\)). Finally, from Fig. 3, we recognize that if the height of the REV remains unchanged, we can represent \(\mathrm {d}\theta _m/\mathrm {d}t\) and \(\mathrm {d}\theta _M/\mathrm {d}t\) as

$$\begin{aligned} \frac{\mathrm {d} {\theta _m}}{\mathrm {d} {t}} = - \frac{1}{1 - \psi ^M} \frac{\mathrm {d} {\psi ^M}}{\mathrm {d} {t}}\,, \quad \frac{\mathrm {d} {\theta _M}}{\mathrm {d} {t}} = \frac{1}{\psi ^M} \frac{\mathrm {d} {\psi ^M}}{\mathrm {d} {t}}\,. \end{aligned}$$
(64)

Substituting Eqs. (64) into (63) yields the poroelastic equation

$$\begin{aligned} \frac{\mathrm {d} {\psi ^M}}{\mathrm {d} {t}} = \frac{1}{{\mathcal {C}}} \left( {\frac{\mathrm {d} {p_M}}{\mathrm {d} {t}} - \frac{\mathrm {d} {p_m}}{\mathrm {d} {t}}}\right) \,, \end{aligned}$$
(65)

where

$$\begin{aligned} {\mathcal {C}} = \frac{1}{b} \left( {\frac{K_m^e}{1 - \psi ^M} + \frac{K_M^e}{\psi ^M}}\right) \end{aligned}$$
(66)

is a modulus describing the change in internal structure of the material. We remark that a constitutive law relating the variation of pore fraction \(\psi ^M\) with pore pressure difference \(p_M - p_m\) is consistent with the internal energy equation for double-porosity media developed by Borja and Choo [13]. We also note that only one combined coefficient \({\mathcal {C}}\) is needed to describe the material response, although its physical meaning is based on the two elasticity constants \(K_m^e\) and \(K_M^e\).

Now, we can rewrite Eqs. (49) and (50) in terms of the primary unknown variables \(p_m\), \(p_M\), and \({\varvec{\epsilon }}\). Recall that

$$\begin{aligned} \frac{\mathrm {d} {\phi ^m}}{\mathrm {d} {t}} = -\psi ^m \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} - \phi \frac{\mathrm {d} {\psi ^M}}{\mathrm {d} {t}} \end{aligned}$$
(67)

and

$$\begin{aligned} \frac{\mathrm {d} {\phi ^M}}{\mathrm {d} {t}} = -\psi ^M \frac{\mathrm {d} {\phi ^s}}{\mathrm {d} {t}} + \phi \frac{\mathrm {d} {\psi ^M}}{\mathrm {d} {t}}\,. \end{aligned}$$
(68)

Thus, we can combine Eqs. (54) and (65) to obtain equivalent forms of Eqs. (49) and (50) as

$$\begin{aligned}&\psi ^m{\varvec{b}}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \frac{1}{K_m}\left( {\nabla p_m}\right) \cdot \mathbf {q}_m + \nabla \cdot \mathbf {q}_m\nonumber \\&\quad + S_{mM} \frac{\mathrm {d} {p_M}}{\mathrm {d} {t}}+S_{mm} \frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} = \frac{c^m}{\rho _m} \end{aligned}$$
(69)

and

$$\begin{aligned}&\psi ^M{\varvec{b}}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \frac{1}{K_M}\left( {\nabla p_M}\right) \cdot \mathbf {q}_M + \nabla \cdot \mathbf {q}_M\nonumber \\&\quad + S_{MM} \frac{\mathrm {d} {p_M}}{\mathrm {d} {t}}+ S_{Mm} \frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} = \frac{c^M}{\rho _M}\,. \end{aligned}$$
(70)

where

$$\begin{aligned} \left. \begin{array}{l} S_{mm} = \dfrac{\beta \psi ^m\psi ^m}{K_s} + \dfrac{\phi ^m}{K_m}-\dfrac{\omega ^m-\phi }{{{\mathcal {C}}}}\\ S_{MM} = \dfrac{\beta \psi ^M\psi ^M}{K_s} + \dfrac{\phi ^M}{K_M}+\dfrac{\omega ^M+\phi }{{{\mathcal {C}}}}\\ S_{mM}= \dfrac{\beta \psi ^m \psi ^M}{K_s}+\dfrac{\omega ^m-\phi }{{{\mathcal {C}}}}\\ S_{Mm}= \dfrac{\beta \psi ^m \psi ^M}{K_s}-\dfrac{\omega ^M+\phi }{{\mathcal {C}}} \end{array}\;\right\} \end{aligned}$$
(71)

are storage coefficients. Equations (69) and (70) can then be used in combination with balance of linear momentum to solve coupled systems based on a \(\mathbf {u}/p_M/p_m\) formulation [18, 19, 56].

In calculating the coefficients of Eqs. (69) and (70), we can further assume that

$$\begin{aligned} \omega ^m&=\frac{\beta \left( {p_M - p_m}\right) \psi ^m}{K_s}\ll 1\,,\nonumber \\ \omega ^M&= \frac{\beta \left( {p_M - p_m}\right) \psi ^M}{K_s}\ll 1\,, \end{aligned}$$
(72)

since \(\left| {p_M - p_m}\right| /K_s\) is on the order of intrinsic strain [9]. In this case, the storage coefficients reduce to the forms

$$\begin{aligned} \left. \begin{array}{l} S_{mm} = \dfrac{\beta \psi ^m\psi ^m}{K_s} + \dfrac{\phi ^m}{K_m}+\dfrac{\phi }{{{\mathcal {C}}}}\\ S_{MM} = \dfrac{\beta \psi ^M\psi ^M}{K_s} + \dfrac{\phi ^M}{K_M}+\dfrac{\phi }{{{\mathcal {C}}}}\\ S_{mM}= S_{Mm}= \dfrac{\beta \psi ^m \psi ^M}{K_s}-\dfrac{\phi }{{\mathcal {C}}} \end{array}\;\right\} \,, \end{aligned}$$
(73)

i.e., the matrix of storage coefficients becomes symmetric. Thus, all the coefficients of \(\mathrm {d}{\varvec{\epsilon }}/\mathrm {d}t\), \(\mathrm {d}p_M/\mathrm {d}t\), and \(\mathrm {d}p_m/\mathrm {d}t\) are “constants” in the sense that they do not depend on the primary unknown variables. Furthermore, it is also reasonable to assume that the pressures \(p_M\) and \(p_m\) do not affect the density terms in \(\mathbf {q}_M\) and \(\mathbf {q}_m\), i.e., \(\mathbf {q}_M = \mathbf {q}_M\left( {\nabla p_M, \rho _{\mathrm{ref}}\mathbf {g}}\right)\) and \(\mathbf {q}_m = \mathbf {q}_m\left( {\nabla p_m, \rho _{\mathrm{ref}}\mathbf {g}}\right)\), where \(\rho _{\mathrm{ref}}\) is the reference (constant) fluid density and \(\mathbf {g}\) is the gravity acceleration vector.

Finally, we can combine Eqs. (69) and (70) to obtain the total flow equation. The result reads

$$\begin{aligned}&{\varvec{b}}:\frac{\mathrm {d} {{\varvec{\epsilon }}}}{\mathrm {d} {t}} + \frac{1}{{\mathcal {M}}_m} \frac{\mathrm {d} {p_m}}{\mathrm {d} {t}} + \frac{1}{{\mathcal {M}}_M}\frac{\mathrm {d} {p_M}}{\mathrm {d} {t}}+\frac{1}{K_m}\left( {\nabla p_m}\right) \cdot \mathbf {q}_m \nonumber \\&\quad + \frac{1}{K_M}\left( {\nabla p_M}\right) \cdot \mathbf {q}_M + \nabla \cdot \mathbf {q}_t = \frac{c^m}{\rho _m} + \frac{c^M}{\rho _M}\,, \end{aligned}$$
(74)

where \({\mathcal {M}}_m\) and \({\mathcal {M}}_M\) are the Biot moduli defined as

$$\begin{aligned} \frac{1}{{\mathcal {M}}_m} &= \left( {\frac{\beta }{K_s} + \frac{\phi }{K_m}}\right) \psi ^m-\frac{\beta (p_M-p_m)}{K_s{{{\mathcal {C}}}}}\,,\nonumber \\ \frac{1}{{\mathcal {M}}_M} &= \left( {\frac{\beta }{K_s} + \frac{\phi }{K_M}}\right) \psi ^M+\frac{\beta (p_M-p_m)}{K_s{{{\mathcal {C}}}}}\,, \end{aligned}$$
(75)

\(\phi\) is the porosity, and \(\mathbf {q}_t = \mathbf {q}_m + \mathbf {q}_M\) is the resultant total flux vector. Eq. (74) is analogous to the pressure equation of multiphase flow through porous media [48].

4 Poroelastic coefficients

4.1 Elastic coefficients

Before illustrating how Eqs. (69) and (70) may be used, we first consider a transversely isotropic elastic solid characterized by an elastic moduli tensor \({\mathbb {C}}^e\) of the form

$$\begin{aligned}{\mathbb {C}}^e =& \lambda ^e {\mathbf{1}}\otimes {\mathbf{1}} + 2\mu _T {\mathbb {I}} + a^e \left( {{\mathbf{1}}\otimes {\varvec{M}} + {\varvec{M}}\otimes {\mathbf{1}}}\right) \nonumber \\ & + b^e {\varvec{M}}\otimes {\varvec{M}} + 2\left( {\mu _L - \mu _T}\right) \left( {{\varvec{M}}\odot {\mathbf{1}} + {\mathbf{1}}\odot {\varvec{M}}}\right) \,, \end{aligned}$$
(76)

where \(\left( {{\varvec{A}}\odot {\varvec{B}}}\right) _{ijkl} = \left( {A_{ik}B_{jl} + A_{il} B_{jk}}\right) /2\), \({\mathbb {I}}\) is the symmetric fourth-order identity tensor, \({\varvec{M}} = \mathbf {n} \otimes \mathbf {n}\) is the microstructure tensor, \(\mathbf {n}\) is the unit normal vector to the bedding plane, and \(\lambda ^e\), \(\mu _L\), \(\mu _T\), \(a^e\), and \(b^e\) are the five material elastic constants. The subscript \(\left( {\cdot }\right) _{T}\) (bed-parallel BP) pertains to the plane of isotropy, and subscript \(\left( {\cdot }\right) _{L}\) (bed-normal BN) pertains to the direction perpendicular to the plane of isotropy.

In practice, we do not determine \(\lambda ^e\), \(\mu _L\), \(\mu _T\), \(a^e\), and \(b^e\) directly from laboratory experiments. Instead, we obtain these constants indirectly from the following procedure. First, we perform the following matrix inversion

$$\begin{aligned} \left[ \begin{array}{cc} \ {\mathbf {C}}^e_{11}\ &\ {\mathbf {0}}\\ {\mathbf {0}} &\ {\mathbf {C}}^e_{22}\ \end{array}\right] = \begin{bmatrix} \ {\mathbf {S}}^e_{11}\ &{\mathbf {0}} \\ {\mathbf {0}} &\ {\mathbf {S}}^e_{22}\ \end{bmatrix}^{-1}\,, \end{aligned}$$
(77)

where \(\mathbf {0}\) represents a \(3\times 3\) null matrix. The remaining submatrices are

$$\begin{aligned} {\mathbf {C}}^e_{11} = \begin{bmatrix} \ \lambda ^e + 2\mu _T\ &\ \lambda ^e\ &\ \ \lambda ^e + a^e\ \\ \lambda ^e & \lambda ^e + 2\mu _T & \lambda ^e + a^e\\ \lambda ^e + a^e & \lambda ^e + a^e & \lambda ^e + 2{\widetilde{\mu }}\\ \end{bmatrix}\,, \end{aligned}$$
(78)

where \({\widetilde{\mu }} = 2\mu _L-\mu _T + a^e + b^e/2\), and

$$\begin{aligned} {\mathbf {C}}^e_{22} = \begin{bmatrix} \ \mu _T\ & 0 & 0 \\ 0 &\ \mu _L\ & 0 \\ 0 & 0 &\ \mu _L\ \end{bmatrix}\,. \end{aligned}$$
(79)

The compliance submatrices are

$$\begin{aligned} {\mathbf {S}}^e_{11} = \begin{bmatrix} 1/E_h &\ -\nu _{hh}/E_h \ &\ -{\nu _{vh}}/{E_v}\ \\ \ -{\nu _{hh}}/{E_h} & {1}/{E_h} & -{\nu _{vh}}/{E_v} \\ -{\nu _{hv}}/{E_h} & -{\nu _{hv}}/{E_h} & {1}/{E_v} \\ \end{bmatrix} \end{aligned}$$
(80)

and

$$\begin{aligned} {\mathbf {S}}^e_{22} = \begin{bmatrix} \ {2\left( {1+\nu _{hh}}\right) }/{E_h}\ & 0 & 0 \\ 0 &\ {1}/{G_{vh}}\ & 0 \\ 0 & 0 &\ {1}/{G_{vh}}\ \end{bmatrix}\,. \end{aligned}$$
(81)

In the above four submatrices, \(E_v\) and \(E_h\) are Young’s moduli in v and h directions, \(\nu _{hh}\), \(\nu _{vh}\), and \(\nu _{hv}\) are Poisson’s ratios, and \(G_{vh}\) is the shear modulus. These constants are directly measurable in laboratory experiments [38]. Poisson’s ratios \(\nu _{hv}\) and \(\nu _{vh}\) are not independent because we have

$$\begin{aligned} \frac{\nu _{vh}}{E_v} = \frac{\nu _{hv}}{E_h}\,, \end{aligned}$$
(82)

which guarantees symmetry of the compliance matrix. Note the matrix on the LHS of Eq. (77) is exactly the Voigt form of \({\mathbb {C}}^e\) in Eq. (76) when \(\mathbf {n} = \mathbf {e}_z = [0, 0, 1]^T\).

4.2 Comparison of poroelastic coefficients

To further illustrate the use of formulas (69) and (70), we compare the calculated values of the poroelastic coefficients with those obtained by Berryman and Pride [8] and Khalili and Selvadurai [29]. To this end, we elucidate the differences in the mathematical formulations adopted in their models. Berryman and Pride considered an isotropic double-porosity material with six basic variables, namely, the mean total stress \(\sigma\), volumetric strain \(\epsilon\), fluid pressures \(p_M\) and \(p_m\), and fluid content variations \(\zeta _M\) and \(\zeta _m\). In terms of these variables, they formulated a set of linear constitutive equations of the form

$$\begin{aligned} \left\{ \begin{array}{c} \epsilon \\ -\zeta _m \\ -\zeta _M \end{array}\right\} = \left[ \begin{array}{ccc} \ a_{11}\ & a_{12}\ &\ a_{13}\ \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{array}\right] \left\{ \begin{array}{c} \sigma \\ -p_m \\ -p_M \end{array}\right\} \,, \end{aligned}$$
(83)

where \(a_{11}\) through \(a_{33}\) are all constant coefficients. The flow continuity equations are given as [37]

$$\begin{aligned} {\frac{\partial \zeta _m}{\partial t}} + \nabla \cdot \mathbf {q}_m = \gamma \left( {p_M - p_m}\right) \,, \end{aligned}$$
(84)
$$\begin{aligned} {\frac{\partial \zeta _M}{\partial t}} + \nabla \cdot \mathbf {q}_M = \gamma \left( {p_m - p_M}\right) \,, \end{aligned}$$
(85)

where \(\gamma\) is the leakage parameter. This approach is a phenomenological or micromechanical approach for obtaining the poroelastic coefficients, which is different from what we have presented in Sect. 3.

In order to rewrite Eqs. (84) and (85) in terms of the primary unknown variables adopted in our formulation, we need to move the term \(\sigma\) in Eq. (83) to the LHS and the term \(\epsilon\) to the RHS. The result reads

$$\begin{aligned}&\sigma = \frac{\epsilon }{a_{11}} + \frac{a_{12}}{a_{11}} p_m + \frac{a_{13}}{a_{11}} p_M\,, \end{aligned}$$
(86)
$$\begin{aligned}&\zeta _m = - \frac{a_{12}}{a_{11}} \epsilon + s_{mm} p_m + s_{mM} p_M \,, \end{aligned}$$
(87)

and

$$\begin{aligned} \zeta _M = - \frac{a_{13}}{a_{11}} \epsilon + s_{Mm}p_m + s_{MM} p_M \,. \end{aligned}$$
(88)

where the storage coefficients are given by

$$\begin{aligned} \left. \begin{array}{l} s_{mm} = a_{22} - \dfrac{a_{12}^2}{a_{11}}\\ s_{MM} = a_{33} - \dfrac{a_{13}^2}{a_{11}}\\ s_{mM} = s_{Mm} = a_{23} - \dfrac{a_{12} a_{13}}{a_{11}} \end{array}\;\right\} \,. \end{aligned}$$
(89)

From the above three equations, we identify the scalar Biot coefficients of the Berryman–Pride isotropic double-porosity model as \(-a_{12}/a_{11}\) (for nanopores or matrix) and \(-a_{13}/a_{11}\) (for micro-fractures). As for the formulation proposed by Khalili and Selvadurai [29], we tune the values of \(K_p\) (bulk modulus of the porous blocks), \(K_b\), and \(K_s\) in their formulation so as to obtain the same Biot coefficients \(-a_{12}/a_{11}\) and \(-a_{13}/a_{11}\) of the Berryman–Pride model. The result reads

$$\begin{aligned} K_b = \frac{1}{a_{11}}\,, \quad K_p = \frac{K_b}{1 + \left( {a_{13}/a_{11}}\right) }\,, \quad K_s = \frac{1}{a_{11} + a_{12} + a_{13}}\,. \end{aligned}$$
(90)

while the fluid content variations are given by

$$\begin{aligned} \mathring{\zeta }_m = \alpha _1 \epsilon + \mathring{s}_{mM} p_M + \mathring{s}_{mm} p_m \end{aligned}$$
(91)

and

$$\begin{aligned} \mathring{\zeta }_M = \alpha _2 \epsilon + \mathring{s}_{Mm} p_m + \mathring{s}_{MM}p_M\,, \end{aligned}$$
(92)

where the storage coefficients are

$$\begin{aligned} \left. \begin{array}{l} \mathring{s}_{mm} = \dfrac{\alpha _2 - \phi ^M}{K_p} + \dfrac{\alpha _1 - \phi ^m - \alpha _2 + \phi ^M}{K_s} + \dfrac{\phi ^m}{K_m}\\ \mathring{s}_{MM} =\dfrac{\alpha _2 - \phi ^M}{K_p} + \dfrac{\phi ^M}{K_M}\\ \mathring{s}_{mM}=\mathring{s}_{Mm}=\dfrac{\alpha _2 - \phi ^M}{K_s} - \dfrac{\alpha _2 - \phi ^M}{K_p} \end{array}\;\right\} \,, \end{aligned}$$
(93)

and where \(\alpha _1 = K_b/K_p - K_b/K_s = -a_{12}/a_{11}\) and \(\alpha _2 = 1 - K_b/K_p = -a_{13}/a_{11}\). Note that we have modified the notation for \(\zeta _m\) and \(\zeta _M\) to indicate that the Khalili–Selvadurai constitutive formulation is not the same as the Berryman–Pride formulation. By substituting these constitutive laws into Eqs. (84) and (85), it is now possible to compare the poroelastic coefficients with those used in Eqs. (69) and (70).

Table 1 presents a set of input parameters used in these constitutive relations. We consider two types of material, Chelmsford granite and Weber sandstone, since they are well-characterized by laboratory data. Tables 2, 3 and 4 display the results of calculations using the above three double-porosity frameworks. By comparing these three frameworks, we find that the Biot coefficients of our method are quite different from the other two methods, which is because we use pore fractions (\(\psi ^M\) and \(\psi ^m\)) as weights to obtain \({\bar{p}}\) in Fig. 2, while different weighting schemes were adopted in [8, 29]. Nevertheless, the total Biot coefficient matches well among the three methods. The main dependence on the last three rows of Table 2 (i.e., the storage coefficients, ignoring the \(\varphi ^m\) and \(\varphi ^M\) terms) is in the value of \({\mathcal {C}}\), and by tuning the value of \({\mathcal {C}}\), we find that the agreement of the storage coefficients with those of the other two methods is quite good for both the granite and sandstone examples. In particular, we find the off-diagonal storage coefficients \(S_{Mm}\), \(s_{Mm}\), and \(\mathring{s}_{Mm}\) have a negative value for both rocks, which might also be true for other parameter settings. Furthermore, it must be emphasized that our approach is the only one that can handle an anisotropic macroscopic system. In terms of the time derivative, our approach adopts the material time derivative for solid and fluid, while the other two approaches simply use partial time derivative as an approximation, compare Eqs. (69) and (70) with Eqs. (84) and (85), for example. This facilitates an easier extension of our theory to the finite deformation regime since the material time derivative already carries the convected term.

Table 1 Material parameters
Full size table
Table 2 Double-porosity and state variables for the proposed formulation
Full size table
Table 3 Berryman and Pride [8] double-porosity coefficients
Full size table
Table 4 Khalili and Selvadurai [29] double-porosity coefficients
Full size table

5 Closure

We have utilized the principle of superposition to derive poroelastic coefficients for single- and double-porosity media. The resulting conservation laws are exact for single-porosity media and are consistent with those derived in [17, 58]. For double-porosity media, we derived an evolution law for total porosity \(\phi\) by introducing the weighted pore fluid pressure \({\bar{p}} = \psi ^M p_M + \psi ^m p_m\) in the equivalent single-porosity structure, which is consistent with the results of Borja and Koliji [11]. We then adopted the effective stress partition concept to derive an evolution law for the pore fraction \(\psi ^M\) or \(\psi ^m\). Identical results were obtained by using different loading paths, thus affirming the invariance of the principle of superposition with respect to sequence of loading.

The resulting formulas for double-porosity media require fewer material parameters than those proposed by other authors while delivering a comparable performance. Thus, the proposed approach is useful whenever the unknown parameters cannot be readily determined in the laboratory. Provided that the processes involved are reversible, extension of this work to multi-field coupling, such as thermo-hydro-chemo-mechanical (THCM) coupling, is possible. However, the principle of superposition cannot be applied to irreversible or path-dependent processes, such as processes involving elastoplastic deformations. In this case, the formulation must be complemented by thermodynamical principles to accommodate the effect of plastic dissipation [12]. Nevertheless, the theory presented in this paper is still very useful for a wide variety of applications given the prominent role of poroelasticity in the scientific literature.