1 Introduction

Piles are always designed in a group to transfer dynamic loads to competent soil layers, which covers the issue of how each pile interacts with its surrounding soil (pile-to-soil interaction) [1, 3, 4, 11, 19, 20], and of interaction between piles in the same group (pile-to-pile interaction) [7, 10, 15, 18, 21]. The effects of pile-to-soil and pile-to-pile interaction phenomena on load transfer mechanisms are coupled sophisticatedly, rendering a number of numerical methods such as the finite element method (FEM) [13, 16] and the boundary element method (BEM) [2, 9, 14]. The complex geometry of pile groups with large group members and dense mesh discretization of the domain and its boundaries, especially for dynamic problems involving wave propagation, lead to large systems of equations and therefore to computationally expensive effort. This is not surprising that some approximate wave propagation methods [5, 6, 8, 12, 15, 17] are still in use to reveal load transfer mechanisms of pile-to-soil and pile-to-pile interaction.

Principle of superposition pioneered by Poulos [15] offers a method to calculate settlement of pile groups with arbitrary number of piles, by considering the interaction between two floating piles subjected to static vertical loads. The interaction factor is defined as a ratio of the additional displacement of a pile due to the presence of a source pile, over the displacement of the same pile under its own load. Later, Dobry and Gazetas [5] extended the static interaction factor of two piles to dynamic problems to serve as a basis for further studies on vertical, lateral and rocking vibrations of pile groups. These solutions were proposed based on a simple three step to calculate the dynamic interaction factor, while assuming that cylindrical waves are emanated from the source pile and spread radially to strike an adjacent pile, and that a receiver pile follows exactly the soil attenuation function. These assumptions suggest that secondary waves generated by the receiver pile vibration are ignored when the radially spreading incident waves strike the adjacent pile, and that the interaction between the receiver pile and its surrounding soil is neglected. Mylonakis and Gazetas [10] refined the pile-to-pile interaction model of Dobry and Gazetas [5] to account for the diffraction effect of the arriving wave by simulating the pile as a Winkler beam supported by springs and dashpots, while they did not consider the generated secondary waves.

In all the above-mentioned studies, only incident waves are considered when evaluating the pile-soil-pile interaction of pile groups subjected to vertical dynamic loads. In reality, secondary waves which are generated by the vibration of the receiver pile also exist in the soil layer after the incident waves striking the receiver pile, which tends to interfere with the incident waves form the source pile. Intuitively, the contribution of the secondary wave to the responses of the pile group will depend on the pile spacing S and the number of piles in the same group. To the authors’ knowledge, this mechanism is ignored in all existing analytical solutions used to evaluate dynamic responses of a pile group. In the following, we address a four-step process for the dynamic analysis of pile-soil-pile systems that considers both the incident waves and the secondary waves, and use the new analytical model to define a “coupling factor” that accounts for the coupling effect of the source and receiver pile vibrations. Accordingly, we employ this coupling factor to obtain a new expression for the pile-to-pile interaction factor, which is used for dynamic responses of a pile group subjected to vertical loads. Finally, we discuss the effect of the refinement introduced in this paper on the popular interaction factor of two identical piles and the impedance of pile groups via comparison with existing solutions of Mylonakis and Gazetas [10].

2 A new proposed model for mutual interaction of piles in a group

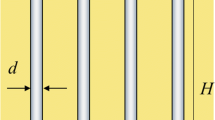
The problem addressed in this paper is illustrated in Fig. 1: a group of m vertical circular piles with length H, diameter d (d = 2r0), cross-sectional area Ap, modulus of elasticity Ep and mass density ρp are embedded in soil layers and subjected to a vertical harmonic load PGeiωt. ω is the excited frequency; \(i = \sqrt { - 1}\). The soil layer is modelled as linear viscoelastic material, with damping ratio βs, complex Lame constants λ = λ*(1 + 2iβs) and G = G*(1 + 2iβs) and mass density ρs. The pile members spaced with S are connected through a rigid weightless pile cap which is not in contact with the soil, rendering this model competent for high-rise pile groups. A right-handed cylindrical (r − θ − z) coordinate system, shown in Fig. 1b, is used to cast the governing equations of the problem. The origin of the system lies at the centre of the pile head, and the z-axis coincides with the pile axis which points downwards, with clockwise polar angles θ taken as positive. In addition, we introduce the following assumption that the pile members are simulated as Winkler beams; no slippage takes place at the pile-soil interface and that the pile group is rested on the rigid bedrock.

Fig. 1
figure 1

Schematic of a pile group subjected to a vertical dynamic load: a side view of the pile group and b coordinate system used to cast the governing equations

Full size image

As discussed above, secondary waves also exist in the soil after the incident waves striking receiver piles, which tends to amplify or de-amplify the free soil displacement at location of the source pile. In order to depict this mechanism mathematically, the development of pile-to-pile coupled interaction is decomposed into the following four steps with reference to Fig. 2, which follows from the model proposed by Dobry and Gazetas [5] and Mylonakis and Gazetas [10]:

Fig. 2
figure 2

Schematic illustration of the proposed model to account for pile-to-pile mutual interaction

Full size image

  • Step 1: The response (vertical displacement W11(z)) of a solitary source pile subjected to a time-harmonic vertical load is determined using an analytical method.

  • Step 2: Cylindrical waves are generated along the source pile and spread radially with the vertical soil displacement U21(S, z) given by:

    $$U_{21} \left( {S,z} \right) = \psi \left( S \right)W_{11} \left( z \right)$$
    (1)

    in which ψ(S) is the soil attenuation function:

    $$\psi \left( S \right) = \frac{{U_{21} \left( {S,z} \right)}}{{U_{21} \left( {\frac{d}{2},z} \right)}} = \frac{{H_{0}^{\left( 2 \right)} \left( {\frac{S}{d}\frac{{a_{0} }}{{\sqrt {1 + 2i\beta_{s} } }}} \right)}}{{H_{0}^{\left( 2 \right)} \left( {\frac{1}{2}\frac{{a_{0} }}{{\sqrt {1 + 2i\beta_{s} } }}} \right)}}$$
    (2)

    where a0 = ωd/Vs, Vs is shear wave velocity of the soil layer, and H20 () is the Hankel function of zero order and the second kind.

  • Step 3: The unloaded receiver pile is modelled as a Winkler beam to account for diffraction effect of the arriving wave. Notice that the mechanics of step 3 is in a sense the reverse to that in step 1: in step 1 the source pile induces displacements on soil, whereas in step 3, the incident wave field induces displacements on the receiver pile.

  • Step 4: The soil reaction at location of the source pile arising from the receiver pile interferes with the incident free displacement, rendering responses of the source pile different. To account in a simple realistic way for this interaction, the source pile is modelled as a Winkler beam, and the soil displacement U12(S, z) induced by the receiver pile is applied at the distributed soil springs and dashpots.

For a harmonically vibrating source pile, the dynamic equilibrium of the infinitesimal pile segment gives the following governing equation:

$$E_{p} A_{p} \frac{{d^{2} W_{11} \left( z \right)}}{{dz^{2} }} - \left( {k_{z} + i\omega c_{z} - m\omega^{2} } \right)W_{11} \left( z \right) = 0$$
(3)

where W11(z) denotes the axial displacement of the vibrating source pile, kz and cz are frequency-dependent springs and dashpots, respectively, m = ρpAp. The general solution of Eq. (3) is:

$$W_{11} \left( z \right) = A_{11} e^{\lambda z} + B_{11} e^{ - \lambda z}$$
(4)

where \(\lambda^{2} = \frac{{k_{z} + i\omega c_{z} - m\omega^{2} }}{{E_{p} A_{p} }}\), A11 and B11 are constants relating with boundary conditions of the source vibrating pile. For special end-bearing piles, we introduce the boundary conditions at the top and bottom of the pile as:

$$\left. {\frac{{dW_{11} \left( z \right)}}{dz}} \right|_{z = 0} = - \frac{{P_{1} }}{{E_{p} A_{p} }}$$
(5)
$$\left. {W_{11} \left( z \right)} \right|_{z = H} = 0$$
(6)

where P1 denotes the harmonic vertical load atop the source pile.

Substituting Eqs. (5) and (6) into Eq. (4) yields:

$$A_{11} = - \frac{{P_{1} }}{{E_{p} A_{p} \lambda \left( {1 + e^{2H\lambda } } \right)}}$$
(7)
$$B_{11} = \frac{{e^{2H\lambda } P_{1} }}{{E_{p} A_{p} \lambda \left( {1 + e^{2H\lambda } } \right)}}$$
(8)

Similarly, the dynamic equation of a receiver pile can be governed as:

$$E_{p} A_{p} \frac{{d^{2} W_{21} \left( z \right)}}{{dz^{2} }} + m\omega^{2} W_{21} \left( z \right) - \left( {k_{z} + i\omega c_{z} } \right)\left[ {W_{21} \left( z \right) - U_{21} \left( {S,z} \right)} \right] = 0$$
(9)

where \(U_{21} \left( {S,z} \right) = \psi \left( S \right)W_{11} \left( z \right) = \psi \left( S \right)\left( {A_{11} e^{\lambda z} + B_{11} e^{ - \lambda z} } \right)\) W21(z) is the displacement of the receiver pile induced by vibration of the source pile.

The solution of Eq. (9) is:

$$W_{21} \left( z \right) = \frac{{k_{z} + i\omega c_{z} }}{{2\lambda E_{p} A_{p} }}\psi \left( S \right)z\left( { - A_{11} e^{\lambda z} + B_{11} e^{ - \lambda z} } \right) + A_{21} e^{\lambda z} + B_{21} e^{ - \lambda z}$$
(10)

in which A21 and B21 are integration constants. A21 and B21 are calculated considering zero force atop the receiver pile and fixed bottom of the receiver pile i.e.

$$\left. {\frac{{dW_{21} \left( z \right)}}{dz}} \right|_{z = 0} = 0$$
(11)
$$\left. {W_{21} \left( z \right)} \right|_{z = H} = 0$$
(12)

Accordingly,

$$A_{21} = \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi \left( S \right)\left( {A_{11} - B_{11} - B_{11} \lambda H + A_{11} \lambda He^{2\lambda H} } \right)}}{{2E_{p} A_{p} \lambda^{2} \left( {1 + e^{2H\lambda } } \right)}}$$
(13)
$$B_{21} = \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi \left( S \right)\left( { - A_{11} e^{2\lambda H} + B_{11} e^{2\lambda H} - B_{11} \lambda H + A_{11} \lambda He^{2\lambda H} } \right)}}{{2E_{p} A_{p} \lambda^{2} \left( {1 + e^{2H\lambda } } \right)}}$$
(14)

Considering the secondary waves striking the source pile, the governing equation for this step can be expressed as:

$$E_{p} A_{p} \frac{{d^{2} W_{12} \left( z \right)}}{{dz^{2} }} + m\omega^{2} W_{12} \left( z \right) - \left( {k_{z} + i\omega c_{z} } \right)\left[ {W_{12} \left( z \right) - U_{12} \left( {S,z} \right)} \right] = 0$$
(15)

In which \(U_{12} \left( {S,z} \right) = \psi \left( S \right)W_{21} \left( z \right) = \psi \left( S \right)\left[ {\frac{{k_{z} + i\omega c_{z} }}{{2\lambda E_{p} A_{p} }}\psi \left( S \right)z\left( { - A_{11} e^{\lambda z} + B_{11} e^{ - \lambda z} } \right) + A_{21} e^{\lambda z} + B_{21} e^{ - \lambda z} } \right];\) W12(z) is a displacement induced by the secondary wave, which points upwards.

The solution of Eq. (15) is:

$$\begin{aligned} W_{12} \left( z \right) & = z\left[ {\frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{2} E_{p}^{2} A_{p}^{2} }}A_{11} z - \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi }}{{2E_{p} A_{p} \lambda }}A_{21} - \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{3} E_{p}^{2} A_{p}^{2} }}A_{11} } \right]e^{\lambda z} \\ & \quad + z\left[ {\frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{2} E_{p}^{2} A_{p}^{2} }}B_{11} z + \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi }}{{2E_{p} A_{p} \lambda }}B_{21} + \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{3} E_{p}^{2} A_{p}^{2} }}B_{11} } \right]e^{ - \lambda z} \\ & \quad + A_{12} e^{\lambda z} + B_{12} e^{ - \lambda z} \\ \end{aligned}$$
(16)

in which A12 and B12 are integration constants. A12 and B12 are calculated considering zero force atop the pile head and fixed bottom of the pile i.e.

$$\left. {\frac{{dW_{12} \left( z \right)}}{dz}} \right|_{z = 0} = 0$$
(17)
$$\left. {W_{12} \left( z \right)} \right|_{z = H} = 0$$
(18)

Therefore,

$$A_{12} = - \frac{{M_{1} + e^{H\lambda } M_{2} \lambda }}{{\lambda + \lambda e^{2H\lambda } }}$$
(19)
$$B_{21} = \frac{{e^{H\lambda } \left( {e^{H\lambda } M_{1} - M_{2} \lambda } \right)}}{{\lambda + \lambda e^{2H\lambda } }}$$
(20)

where \(M_{1} = - \frac{{A_{11} \psi^{2} \left( {k_{z} + i\omega c_{z} } \right)^{2} }}{{8A_{p}^{2} E_{p}^{2} \lambda^{3} }} - \frac{{A_{21} \psi \left( {k_{z} + i\omega c_{z} } \right)}}{{2A_{p} E_{p} \lambda }} + \frac{{B_{11} \psi^{2} \left( {k_{z} + i\omega c_{z} } \right)^{2} }}{{8A_{p}^{2} E_{p}^{2} \lambda^{3} }} + \frac{{B_{21} \psi \left( {k_{z} + i\omega c_{z} } \right)}}{{2A_{p} E_{p} \lambda }},\) \(M_{2} = H\left[ \begin{aligned} \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{2} E_{p}^{2} A_{p}^{2} }}A_{11} H -\hfill \\ \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi }}{{2E_{p} A_{p} \lambda }}A_{21} - \hfill \\ \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{3} E_{p}^{2} A_{p}^{2} }}A_{11} \hfill \\ \end{aligned} \right]e^{\lambda H} + H\left[ \begin{aligned} \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{2} E_{p}^{2} A_{p}^{2} }}B_{11} H + \hfill \\ \frac{{\left( {k_{z} + i\omega c_{z} } \right)\psi }}{{2E_{p} A_{p} \lambda }}B_{21} + \hfill \\ \frac{{\left( {k_{z} + i\omega c_{z} } \right)^{2} \psi^{2} }}{{8\lambda^{3} E_{p}^{2} A_{p}^{2} }}B_{11} \hfill \\ \end{aligned} \right]e^{ - \lambda H}.\)

Since Mylonakis and Gazetas [10] only considered the incident wave emanating from the source pile, the ratio of α1 = W21(0)/W11(0) was defined as the popular interaction factor of two piles. However, to account for the secondary waves due to vibrations of the receiver pile, we need to introduce a coupling factor \(\kappa\), which is equal to the source pile head displacement due to vibration of the receiver pile, over the pile head displacement of the source pile:

$$\kappa = \frac{{W_{12} \left( 0 \right)}}{{W_{11} \left( 0 \right)}}$$
(21)

Considering the coupled interaction between the source and receiver pile, the value of W11(0) − W12(0) is the finally desired displacement of the source pile. Therefore, the interaction factor which accounts for secondary waves propagating from the receiver pile can be expressed as:

$$\alpha = \frac{{W_{21} \left( 0 \right)}}{{W_{11} \left( 0 \right) - W_{12} \left( 0 \right)}} = \frac{{W_{21} \left( 0 \right)}}{{\left( {1 - \kappa } \right)W_{11} \left( 0 \right)}}$$
(22)

3 Mutual interaction of pile group

Every single pile in a pile group acts both as a source and receiver pile, simultaneously. On basis of principle of superposition, displacement of every solitary pile comprises two components: (1) The source pile displacement induced by load applied on its own head i.e. \(\left( {1 - \sum\nolimits_{j = 1,j \ne i}^{m} {\kappa_{ij} } } \right)W_{i}\); (2) The receiver pile displacement induced by neighbouring piles i.e. \(\sum\nolimits_{j = 1,j \ne i}^{m} {\alpha_{1,ij} } W_{j}\), where κij is a factor accounting for the coupling effect of pile j on pile i; α1,ij denotes the traditional interaction factor between pile j and pile i as defined by Mylonakis and Gazetas [10]; Wi and Wj are the displacement of pile i and j, respectively, due to the atop vertical loads Pi and Pj. Therefore, the resultant displacement Di of each pile i in the pile group can be cast as:

$$D_{i} = \left( {1 - \sum\limits_{j = 1,j \ne i}^{m} {\kappa_{ij} } } \right)W_{i} + \sum\limits_{j = 1,j \ne i}^{m} {\alpha_{1,ij} } W_{j}$$
(23)

For m identical piles, pile displacement can be expressed mathematically in matrix as:

$$\left[ D \right] = \left[ {\rm A} \right]\left[ P \right]$$
(24)

where

$$\begin{aligned} \left[ D \right] &= \left[ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ . \\ . \\ . \\ {D_{m} } \\ \end{array} } \right] ,\quad \left[ {\rm A} \right] = \frac{1}{K}\left[ {\begin{array}{*{20}c} {1 - \sum\limits_{j = 1,j \ne 1}^{m} {\kappa_{1j} } } & {\alpha_{1,12} } & {\alpha_{1,13} } & . & . & . & {\alpha_{1,1m} } \\ {\alpha_{1,21} } & {1 - \sum\limits_{j = 1,j \ne 2}^{m} {\kappa_{2j} } } & {\alpha_{1,23} } & . & . & . & {\alpha_{1,2m} } \\ . & . & . & . & {} & {} & . \\ . & . & . & {} & . & {} & . \\ . & . & . & {} & {} & . & . \\ {\alpha_{1,m1} } & {\alpha_{1,m2} } & . & . & . & . & {1 - \sum\limits_{j = 1,j \ne m}^{m} {\kappa_{mj} } } \\ \end{array} } \right] ,\\ \left[ P \right] &= \left[ {\begin{array}{*{20}c} {P_{1} } \\ {P_{2} } \\ . \\ . \\ . \\ {P_{m} } \\ \end{array} } \right]. \end{aligned}$$

Vertical loads atop the pile can be expressed as:

$$\left[ P \right] = \left[ {\rm A} \right]^{ - 1} \left[ D \right]$$
(25)

Pile members are connected through a rigid pile cap, which yields:

$$P_{G} e^{i\omega t} = \sum\limits_{i = 1}^{m} {P_{i} }$$
(26)

and

$$D_{1} = D_{2} = \cdots = D_{m} = D_{G}$$
(27)

The pile group impedance can be defined as:

$$K_{G} = \frac{{P_{G} e^{i\omega t} }}{{D_{G} }}$$
(28)

which can be recast in the summation of a real component and an imaginary component:

$$K_{G} = {{E_{p} }}{d}\left( {k_{G} + ic_{G} } \right)$$
(29)

4 Results and discussion

The aim of this section is twofold: first, we present examples to illustrate secondary waves generated by the vibration of the receiver pile on dynamic responses of the source pile through the coupling factor. Next, we use the introduced coupling factor to combine with the two-pile interaction factor to shed some light on how the refinement of the receiver pile affects dynamic responses of a pile group via selected arithmetic examples. Unless otherwise stated, the parameters considered in the analysis are presented as follows: elasticity modulus of pile Ep= 25GPa, mass density of pile ρp= 2500 kg/m3, mass density of soil ρs= 2000 kg/m3, shear modulus of soil Gs= 10 MPa, damping ratio of soil βs= 0.02 and Poisson’s ratio of soil νs= 0.4. In addition, the results are presented in terms of the normalized frequency a0 = ωd/Vs, where \(V_{s} = \sqrt {{{G_{s} } \mathord{\left/ {\vphantom {{G_{s} } {\rho_{s} }}} \right. \kern-0pt} {\rho_{s} }}}\).

4.1 Effect of receiver pile vibration on the source pile and the interaction factor

First, variations of the real and imaginary components of the coupling factor κ with the dimensionless frequency a0 for different pile spacing and different pile slenderness ratio are, respectively, illustrated in Figs. 3 and 4. Notice in Fig. 3 that resonance amplitude of the coupling factor (both the real component and the imaginary component) tends to decrease with the increasing pile spacing. The variation of the coupling factor with pile spacing is not trivial, suggesting that the effect of secondary waves on responses of the source pile is important, especially for closely spaced pile groups. Also notice in Fig. 4 that the coupling factor is, as expected, dependent on the pile slenderness: large slenderness ratio results in significant coupling effect. This is owing to the fact that the interaction between the receiver pile and its surrounding soil becomes obvious with the increasing pile length, leading to increased secondary waves. This coupling effect between the source pile and the receiver pile cannot be captured by the conventional model, as it does not consider the secondary waves caused by the existence of the receiver pile.

Fig. 3
figure 3

Effects of pile spacing on the coupling factor a real component and b imaginary component. The results for H/d = 20

Full size image
Fig. 4
figure 4

Effects of slenderness ratio of the pile on the coupling factor a real component and b imaginary component. The results for S/d = 2

Full size image

Next, we will investigate the effect of secondary waves generated by the vibration of the receiver pile on its calculated interaction factor, by comparing results of the presented solution against those obtained by Mylonakis and Gazetas [10]. Interaction factors calculated through the two solutions, which are both expressed via α uniformly here, are illustrated in Figs. 5 and 6 for different pile spacing and slenderness ratio, respectively. Comparatively noticeable discrepancies are observed for the case of S/d = 2 in Fig. 5 and H/d = 50 in Fig. 6, while as expected, the two solutions converge as the pile spacing increases and the pile slenderness ratio decreases (see S/d = 5 in Fig. 5 and H/d = 20 in Fig. 6). Therefore, (1) secondary waves emanating from the receiver pile become important for pile groups with close pile spacing or with large slenderness ratio, and (2) the presented solution agrees well with the established solutions proposed by Mylonakis and Gazetas [10] when the pile spacing is sufficiently large enough or the pile slenderness ratio is comparatively small. It is noteworthiness that the secondary waves of the receiver pile on the interaction factor may not significant e.g. cases of S/d = 5 and H/d = 20, as only two piles are used to obtain the interaction factor. However, this coupling effect tends to be noticeable when calculating impedance of the pile group with increased group members, and we will demonstrate this in the following part through a selected arithmetic example.

Fig. 5
figure 5

Comparison of the interaction factor computed using the proposed model and the solution of Mylonakis and Gazetas [10] for the case of S/d = 2 and S/d = 5: a real component b imaginary component. The results for H/d = 50

Full size image
Fig. 6
figure 6

Comparison of the interaction factor computed using the proposed model and the solution of Mylonakis and Gazetas [10] for the case of H/d = 20 and H/d = 50: a real component b imaginary component. The results for S/d = 2

Full size image

4.2 Effect of receiver pile vibration on pile group impedance

Effects of the receiver pile vibration on the impedance of a symmetrical nine-pile group are illustrated in Figs. 7 and 8, via making comparisons between the proposed solutions and the results obtained from Mylonakis and Gazetas [10]. Arithmetic results are presented for different pile spacing in Fig. 7 and different pile slenderness ratio in Fig. 8. Notice that the solution at hand agrees well with the pile group impedance resulting from that neglecting effects of the receiver pile, for the case of large-spaced pile group e.g. S/d = 10 in Fig. 7. However, notable discrepancies are observed with the decreased pile spacing e.g. S/d = 2, which confirm the important role of the receiver pile vibration. In addition, comparatively significant discrepancies, as expected, are observed for the case of H/d = 20 and H/d = 30 in Fig. 8, and this difference becomes more prominent for the case of H/d = 30. Notice in Fig. 6 that effect of the receiver pile vibration on the interaction factor is negligible small for the case of H/d = 20. However, discrepancies between the proposed solution and that from Mylonakis and Gazetas [10] in evaluating the impedance of a nine-pile group are still not trivial for the case of H/d = 20 in Fig. 8. Therefore, effects of the receiver pile vibration in a pile group with large group members become important for pile slenderness of practical interests.

Fig. 7
figure 7

Comparison of impedance of a symmetrical nine-pile group computed using the proposed solution with that obtained by Mylonakis and Gazetas [10] for the case of a S/d = 2, b S/d = 2. The results for H/d = 30

Full size image
Fig. 8
figure 8

Comparison of impedance of a symmetrical nine-pile group computed using the proposed solution with that obtained by Mylonakis and Gazetas [10] for the case of a H/d = 20, b H/d = 30. The results for S/d = 2

Full size image

5 Concluding remarks

We presented a simple physical model for describing the dynamic response of end-bearing pile groups subjected to harmonic vertical loads. The model is based on a pile-to-pile coupling interaction which allows considering the radially spreading waves emanated from the source pile and considering the secondary waves generated by the receiver pile vibration. The model allows calculating the coupling effect of the source and receiver pile through an introduced coupling factor, and permits the impedance of pile groups with arbitrary number of cylindrical piles to be obtained analytically. Apart from illustrating coupling factor between the source and receiver pile, which allows us to gain insight into the physical mechanics of the problem, we also presented arithmetic results to verify validation of the method and to quantify effects of the receiver pile vibration on dynamic responses of the pile group. Unquestionably, limitations of the model stem from certain assumptions introduced in the solution, such as the rigid weightless cap which is not in contact with soil and the perfect bonding at pile-soil interaction. Nevertheless, the main advantage of this model is that it is relatively easy to program, and is suitable for dealing with large closely spaced pile groups or pile groups with large members.