Progressive degradation of rock properties and time-dependent behavior of deep tunnels

Abstract

Time-dependent response of deep tunnels is studied considering the progressive degradation of the mechanical properties of the rock mass. The constitutive model is based on a rock-aging law for the uniaxial strength of the rock and for the Young’s modulus. A semi-analytical solution is developed for the stresses and displacements around a deep circular tunnel taking into account the face advance. The evolution of the plastic and damage zones over time is determined. Numerical examples are presented for the case of Saint-Martin-La-Porte access adit in France of the Lyon–Turin Base Tunnel. The computed results which are compared with the field data in terms of the convergence of tunnel wall and of the displacements inside the rock mass monitored by multi-point extensometers show the efficiency of the approach to simulate the time-dependent deformation of a tunnel excavated in squeezing ground. Simple relationships are proposed to evaluate the parameters of the constitutive model directly from those of the empirical convergence law presented in previous work.

1 Introduction

Time-dependent behavior of rocks has a significant impact on the stability of underground excavations. In many case studies, the tunnel closure and the stresses in tunnel supports increase for months or years after the excavation. This results in great difficulties for completing tunneling projects, with increased delays and construction costs. As one of the typical phenomena associated with time-dependent deformation of rocks, “squeezing” grounds have intrigued experts for years and tunneling in such grounds is always seen as a challenging task for engineers. There are many interesting cases of tunnels over the world where the squeezing phenomenon has been observed as, for example, in the Alps, the Lötschberg and Gotthard base tunnels [19], the Frejus tunnel [27, 32], and more recently the Saint-Martin-la-Porte access adit of the Lyon–Turin Base Tunnel [5, 9].

A number of methods are available for the analysis of the tunnel response, from the earliest closed-form solutions to the most recent numerical simulations [4]. We will focus here on analytical solutions. Although often requiring simplifications regarding the rock behavior and the geometry of the problem, closed-form solutions are of great interest for a quick evaluation of stresses and displacements around underground excavations and are very useful in the early design process. Many works have been devoted to the analysis of time-dependent deformations for both lined and unlined tunnels using linear viscoelastic models [15, 17, 21, 23–25, 38], empirical creep laws [1, 28, 32, 33], viscoplastic models [8, 12, 13, 16, 22, 29] and considering also hydro-mechanical couplings in porous media [14, 39]. As mentioned by Barla [3], the analysis of tunnels in squeezing ground requires considering the evolution of the yielding zone which develops around the tunnel, with the tunnel face advance and with time.

In this paper, we present a new analytical solution for stresses and displacements around a circular tunnel excavated in a rock mass which exhibits time-dependent behavior. This time-dependent behavior is modeled here by considering the progressive degradation of the rock strength as in materials aging constitutive models. The time-dependent solution takes into account the face advance, and the evolution of the plastic zone around the tunnel with time is explicitly obtained. We first present the constitutive model and derive a semi-analytical solution for stresses and displacements in the case of a deep circular tunnel. We then apply the obtained solution to the case study of the Saint-Martin-la-Porte access adit (France) of the Lyon–Turin Base Tunnel. The computed displacements of the tunnel wall and inside the rock mass are compared to the field data. We show that the values of the parameters of the proposed model can be directly deduced from the convergence data recorded in situ.

2 A model for rock mass progressive degradation

The long-term strength concept proposed by Ladanyi [20] is often applied in tunnel practice. In this approach, it is assumed that the surrounding rock mass undergoes a continuous deterioration, involving a decrease in its modulus of deformation and a gradual loss of strength [21]. However, only two limiting states, i.e., the short-term response and the long-term response, are generally considered in the analysis. Using this approach, Vu et al. [36] have analyzed the short-term and long-term convergences in the Saint-Martin-la-Porte access adit and found that the long-term convergences are obtained from the short-term ones by only reducing the cohesion of the rock mass. The main drawback of such analyses is that it does not provide any information on the intermediate states. In order to fill the gap between the short-term and long-term rock mass response, we propose here a degradation model considering the effect of rock-aging on the parameters of a Mohr–Coulomb elastic perfectly plastic material. The advantage of the approach is that the evolution in time of stresses and strains as well as the one of the extent of the plastic zone around the excavation can be modeled.

Time-dependent deformation around tunnels is commonly observed and is attributed to various phenomena such as viscous creep of the rock mass, consolidation effects in the presence of fluids, progressive failure of the rock. Squeezing behavior which induces large deformation around the excavation and severe loading conditions of the support systems is generally associated with poor rock mass deformability and strength properties and is encountered in altered rock complexes. In the following, we will focus on the effect of progressive degradation of the elastic and strength properties of the material. This time-dependent evolution of the mechanical parameters of the rock may be attributed to subcritical propagation of existing and induced cracks [2]. This subcritical crack growth is responsible for brittle creep of rocks and for delayed failure. We generally distinguish between the short-term and long-term strength properties. When the state of stress is beyond the long-term strength and below the short-term strength, the rock deforms and eventually fails after a time delay that depends upon the applied stress. Subcritical crack propagation is a physical mechanism that can describe such a phenomenon as studied experimentally in the recent paper of Brantut et al. [10]. This phenomenon is affected by many factors (applied state of stress, presence of pore fluid, chemical composition of the pore fluid, temperature, etc.). In this paper, we shall emphasize the role of the deviatoric stress on time-dependent behavior of a rock mass in the absence of pore fluid and temperature change. There is currently no model that can include all the complexity of the physical processes that govern time-dependent behavior of rocks. Micromechanical models can take into account the physical mechanisms involved in the initiation and growth of microcracks but present difficulties for implementation in numerical codes for practical engineering applications. Therefore, a phenomenological approach based on damage and plasticity continuum theory provides a convenient macroscopic constitutive framework. The basic idea of the model developed here is the following: When the state of stress exceeds a given threshold, time-dependent degradation of the elastic properties (i.e., time-dependent damage) and of the strength properties occurs. This degradation process can be related to the progressive development of cracks in the material as discussed above, but the advantage of the phenomenological approach is that cracks’ development is smeared at the scale of the representative elementary volume (REV) of the model in order to be described in the framework of (homogenized) continuum theories.

The Mohr–Coulomb failure criterion is classically written as follows

$$\sigma_{1} - K_{\text{p}} \sigma_{3} - \sigma_{\text{c}} = 0$$

(1)

where σ ₁ and σ ₃ are the major and minor principal stresses, respectively, K _p is the passive coefficient, which depends on the friction angle $\varphi$ through the relation ${K_{\text{p}} = ({1 + \sin \varphi }) /({1 - \sin \varphi }})$, and σ _c is the unconfined compressive strength ($\sigma_{\text{c}} = 2c\sqrt {K_{\text{p}} }$, where c is the cohesion). The plastic deformation is controlled by the dilatancy parameter $K_{\psi } =({1 + \sin \psi }) / ({1 - \sin \psi })$, where ψ is the dilation angle.

The proposed model follows the idea of Tran et al. [34] who have considered a rock-aging law to study the behavior of a rockfill dam by describing the time-evolving resistance of the rock blocks. Following the same lines of thoughts, we define here a rock-aging law for the evolution of the unconfined compressive strength with time

$$\sigma_{\text{c}} = \sigma_{\text{c}}^{0} \left( {1 - \beta_{1} \int\limits_{{t_{0} }}^{t} {\kappa {\text{d}}t} } \right)$$

(2)

where

$$\kappa = \left\{ {\begin{array}{*{20}l} {\exp \left( {\beta_{2} \frac{{\left( {\sigma_{1} - K_{\text{p}} \sigma_{3} - \sigma_{\text{c}}^{0} } \right)}}{{\left( {\sigma_{1} - K_{\text{p}} \sigma_{3} - \sigma_{\text{c}}^{\infty } } \right)}}} \right)} \hfill & {{\text{if}}\;\sigma_{1} - K_{\text{p}} \sigma_{3} \ge \sigma_{\text{c}}^{\infty } } \hfill \\ 0 \hfill & {\text{else}} \hfill \\ \end{array} } \right.\;{\text{and}}\;\sigma_{\text{c}}^{\infty } = \beta_{3} \sigma_{\text{c}}^{0} \quad{\text{with}} \quad 0 \le \beta_{3} \le 1$$

where $\sigma_{\text{c}}^{0}$ and $\sigma_{\text{c}}^{\infty }$ are, respectively, the short-term and long-term unconfined compressive strength. When the stress state reaches a damage initiation criterion (which is identified here to the long-term yield criterion), the unconfined compressive strength starts to decrease over time. The rate of degradation decreases as the unconfined compressive strength gets closer to its long-term value $\sigma_{\text{c}}^{\infty }$. It should be noted that in this model the passive coefficient K _p (or the friction angle φ) remains constant. Two positive parameters β ₁ and β ₂ are introduced to characterize the velocity of the rock degradation. The time to failure can be derived as follows

$$T = t - t_{0} = \frac{{1 - \beta_{3} }}{{\beta_{1} \exp \left( {\beta_{2} \frac{{\sigma_{1} - K_{\text{p}} \sigma_{3} - \sigma_{\text{c}}^{0}}}{{\sigma_{1} - K_{\text{p}} \sigma_{3} - \sigma_{\text{c}}^{\infty }}}} \right)}}$$

(3)

The physical processes that control the degradation of the rock strength may also affect the rock stiffness. Thus, degradation of the rock mass is not limited to the rock strength but also affects the rock elastic properties. Therefore, we introduce a scalar variable, D, which represents a damage index of the rock mass which is defined as:

$$D = \frac{{\sigma_{\text{c}}^{0} - \sigma_{\text{c}} }}{{\sigma_{\text{c}}^{0} - \sigma_{\text{c}}^{\infty } }},\quad (0 \le D \le 1)$$

(4)

A damage law is postulated for the Young’s modulus with the following expression

$$E = (1 - D)E_{0} + DE_{\infty }$$

(5)

where E ₀ and E _∞ are the short-term and long-term Young’s modulus, respectively. An additional parameter is introduced as β ₄ = E _∞/E ₀ with 0 ≤ β ₄ ≤ 1. Assuming constant Poisson’s ratio ν, the elastic shear modulus of the rock G follows the same evolution as the Young’s modulus. The decrease in the Young’s modulus in time (Eq. 5) controls the creep of the rock when the stress state is below the plastic yield criterion.

3 Problem description

We consider a deep tunnel with a circular cross section of radius R ₀ excavated in an isotropic elasto-plastic medium. It is assumed that the rock mass exhibits a time-dependent behavior described with the above rock mass progressive degradation law. The initial state of stress is hydrostatic and the tunnel is deep enough so that gravity effect is neglected. Under these assumptions the problem can be considered as axisymmetric and displacement, strains and stresses are only functions of the distance r to the center of the cross section. In plane-strain conditions, the equilibrium equation in the absence of body forces can be written in cylindrical coordinates as follows

$$\frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = 0$$

(6)

The Mohr–Coulomb yield criterion is written as

$$f(\sigma_{\theta } ,\sigma_{r} ) = \sigma_{\theta } - \sigma_{r} K_{\text{p}} - \sigma_{\text{c}} = 0$$

(7)

In the practice of tunnel support design, the 3D problem is commonly approached by considering a section behind the face as a 2D plane-strain problem. The effect of face advance is taken into account by applying a varying fictitious internal pressure p _f on the tunnel wall [26]

$$p_{\rm f} = (1 - \lambda )\sigma_{0}$$

(8)

where σ ₀ is the in situ stress and λ is the deconfinement rate which depends on the distance from the face. The λ parameter varies between 0 and 1 (λ = 1 for the sections far from the tunnel face) and is commonly evaluated from the following empirical expression

$$\lambda = \lambda_{0} + (1 - \lambda_{0} )\left[ {1 - \left( {\frac{{R_{0} \alpha }}{{R_{0} \alpha + x}}} \right)^{2} } \right]$$

(9)

where λ ₀ and α are two empirical parameters that depend on the rock mass behavior and x is the distance to the face. In order to keep the model simple and following Panet [26], fixed values are assumed for these two parameters $(\lambda_{0} = 0.25,\;\alpha = 0.75)$. Of course, other mathematical expressions can be considered for describing the deconfinement process.

The boundary conditions are

$$\begin{aligned} & \lim_{r \to \infty } \sigma_{r} (r,t) = \sigma_{0} \\ & \sigma_{r} (R_{0} ,t) = p(t) = (1 - \lambda (t)) \sigma_{0} \\ \end{aligned}$$

(10)

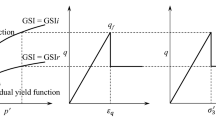
Figure 1 depicts the stress path at the tunnel wall. Before the excavation, the initial stress state around the tunnel is homogeneous and isotropic (point A). When the deconfinement rate is small enough, the stress state is below the long-term failure criterion and the rock surrounding the tunnel behaves elastically. In this zone, the stress path is linear. As the face advances, the deconfinement rate increases and a (elastic) damage zone is created at the tunnel wall when the internal pressure is less than a critical value $p_{\rm D}^{ * }$ (point B)

$$p_{\text{D}}^{*} = \frac{{2\sigma_{0} - \sigma_{\text{c}}^{\infty } }}{{K_{\text{p}} + 1}}$$

(11)

Fig. 1

Stress path (A–B elastic zone, B–C damage zone and C–D plastic zone)

In this damage zone, the unconfined compressive strength σ _c and the Young’s modulus E start to decrease with time from their initial values ($\sigma_{\text{c}}^{0}$ and E ₀, respectively). A plastic zone develops around the tunnel when the current yield criterion is reached at the tunnel wall (point C). We denote by $p_{\text{P}}^{ * }$ the critical value for the internal pressure corresponding to the initiation of the plastic zone. A damage zone with radius R _D and a plastic zone with radius R _P are formed around the tunnel as can be seen in Fig. 2. Time-dependent strains only occur in the damage and in the plastic zones. Obviously, the time-dependent effect is more pronounced in the plastic zone as both the stiffness and the strength decrease with time.

Fig. 2

Scheme of the different zones formed around the tunnel

The following conditions are always fulfilled

$$\begin{aligned} \sigma_{r} (R_{\text{D}} ,t) & = p_{\text{D}}^{ * } \;{\text{on}}\;{\text{the}}\;{\text{elastic{-}damage}}\;{\text{interface}} \\ \sigma_{r} (R_{\text{P}} ,t) & = p_{\text{P}}^{ * } \; {\text{on}}\;{\text{the}}\;{\text{damage{-}plastic}}\;{\text{interface}} \\ \end{aligned}$$

(12)

In the long term, when the tunnel is fully excavated (λ = 1), the stress path tends to point D. The final value of the plastic and damage radius are calculated from the elasto-plastic solution [30]

$$\left. {R_{\text{D}} } \right|_{t \to \infty } = \left. {R_{\text{P}} } \right|_{t \to \infty } = R_{\infty } = R_{0} \left[ {\frac{2}{{K_{\text{p}} + 1}}\left( {(K_{\text{p}} - 1)\frac{{\sigma_{0} }}{{\sigma_{\text{c}}^{\infty } }} + 1} \right)} \right]^{{\frac{1}{{K_{\text{p}} - 1}}}}$$

(13)

The equilibrium equation (Eq. 6) and the boundary conditions (Eq. 10) permit the evaluation of the stress state around the tunnel. However, the extents of the plastic zone and of the damage zone are unknown and evolve with time. In the following, we present an incremental scheme for the computation in time of the radius of the plastic zone and the radius of the damage zone, together with the computation of the stress and displacement fields.

4 Semi-analytical solution process

Let’s define t ₀ as the time when the fictitious internal pressure attains the critical value $p_{\text{D}}^{ * }$. For t < t ₀, the rock is elastic and the solution is time-independent. The stresses and displacement can be calculated from the Lamé’s solution and only depend upon the distance to the tunnel face

$$\sigma_{r} = \sigma_{0} - (\sigma_{0} - p_{\text{f}} )\left( {\frac{{R_{0} }}{r}} \right)^{2}$$

$$\sigma_{\theta } = \sigma_{0} + \left( {\sigma_{0} - p_{\text{f}} } \right)\left( {\frac{{R_{0} }}{r}} \right)^{2}$$

$$\frac{{u_{r} }}{{R_{0} }} = \frac{{\left( {\sigma_{0} - p_{\text{f}} } \right)}}{{2G_{0} }}\frac{{R_{0} }}{r}$$

(14)

For t > t ₀, an excavation damage zone (EDZ) is created around the tunnel. The material properties of rock mass inside this zone are no longer homogeneous, and the rock mass behavior is nonlinear and time-dependent. Stresses and displacements distributions around the tunnel can be obtained by adopting a stepwise solution [11, 31]. As shown in Fig. 3, the medium surrounding the tunnel between R ₀ and R _N is discretized into N concentric circular rings. R _N is chosen in such a way that the final value of the plastic and the damage radii do not exceed R _N . For R > R _N , the displacement and stresses field are given by the elastic solution. The ith ring is limited by the inner radius R _i−1 and outer radius R _i . For the initial mesh, a constant step d is adopted

$$R_{i} = R_{0} + id\;{\text{with}}\;i = 1,N\;{\text{and}}\;d = (R_{N} - R_{o} )/N$$

(15)

Fig. 3

Discretization of the rock mass surrounding the tunnel

It is assumed that inside each ring, the material properties are homogeneous. Time discretization is performed with t _n  = t _n−1 + Δt _n . During the nth step of calculation, the pressure acting on the tunnel wall (r = R ₀) decreases from $p_{\text{f}}^{n - 1}$ to $p_{\text{f}}^{n}$. The parameters related to the degradation of the rock mass (the unconfined compressive strength and the Young’s modulus) in the damage zone decrease with time but are assumed to be homogeneous in each ring. In the following, we denote by $\cdot^{i,n}$ the corresponding quantities (stresses and displacements) inside the ith annulus at the nth time step. The continuity conditions in terms of displacements and radial stresses at the annulus’ boundaries are written as

$$u_{r}^{i,n} = u_{r}^{i + 1,n} \;{\text{and}}\;\sigma_{r}^{i,n} = \sigma_{r}^{i + 1,n} \quad {\text{for}}\;r = R_{i} (i = 1,N - 1)$$

(16)

If the thickness of the rings is small enough, we can assume that at time t _n , the radius of the plastic zone R _P and the radius of the damage zone R _D practically coincide with the outer boundaries of given rings (kth and qth ring, respectively). As the damage and the plastic zones evolve with time, k and q must be updated during the computation. In the following, the numerical solution procedure is sketched. Details of the derivations are given in “Appendixes 1 and 2.”

During each step of calculation, the mechanical parameters inside each annulus in the damage zone and in the plastic zone are first updated. For a ring located in the plastic zone (R _i  ≤ R _P), the unconfined compressive strength $\sigma_{c}^{i,n}$ is calculated as

$$\sigma_{c}^{i,n} = \sigma_{c}^{i,n - 1} - \Delta t_{n} \sigma_{c}^{0} \beta_{1} \exp \left( {\beta_{2} \frac{{\left( {\sigma_{c}^{i,n - 1} - \sigma_{c}^{0} } \right)}}{{\left( {\sigma_{c}^{i,n - 1} - \sigma_{c}^{\infty } } \right)}}} \right)\quad {\text{for}}\;i = 1,k$$

(17)

For a ring located in the damage zone (R _P ≤ R _i  ≤ R _D),

$$\sigma_{\text{c}}^{i,n} = \sigma_{\text{c}}^{i,n - 1} - \Delta t_{n} \sigma_{\text{c}}^{0} \beta_{1} \exp \left( {\beta_{2} \frac{{\left( {\left. {\left( {\sigma_{\theta }^{i,n - 1} - K_{\text{p}} \sigma_{r}^{i,n - 1} } \right)} \right|_{{r = R_{i} }} - \sigma_{\text{c}}^{0} } \right)}}{{\left( {\left. {\left( {\sigma_{\theta }^{i,n - 1} - K_{\text{p}} \sigma_{r}^{i,n - 1} } \right)} \right|_{{r = R_{i} }} - \sigma_{\text{c}}^{\infty } } \right)}}} \right)\quad {\text{for}}\;i = k + 1,q$$

(18)

The damage index and Young’s modulus are calculated from Eqs. 4 and 5. During this step, the ith annulus undergoes a decrease in stress $\Delta p_{i - 1}^{n} \left( { = \sigma_{0} - p_{i - 1}^{n} } \right)$ and $\Delta p_{i}^{n} \left( { = \sigma_{0} - p_{i}^{n} } \right)$ at the inner and outer boundaries, respectively. In the following, the equations of the displacements and stresses in the damage zone and the plastic zone are presented.

4.1 Solution in the damage zone

The radial displacement and the stresses inside the ith annulus in the damage zone (i = k + 1,q) are given by:

$$\Delta u_{r}^{i,n} = - \frac{1}{{2G_{i}^{n} \left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}}\left( {\frac{{\Delta p_{i}^{n} R_{i}^{2} - \Delta p_{i - 1}^{n} R_{i - 1}^{2} }}{1 - 2v}r + \frac{{\left( {\Delta p_{i}^{n} - \Delta p_{i - 1}^{n} } \right)R_{i - 1}^{2} R_{i}^{2} }}{r}} \right)$$

(19)

and

$$\Delta \sigma_{r}^{i,n} = \sigma_{0} - \sigma_{r}^{i,n} = \frac{{\Delta p_{i}^{n} R_{i}^{2} - \Delta p_{i - 1}^{n} R_{i - 1}^{2} }}{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}} - \frac{{\left( {\Delta p_{i}^{n} - \Delta p_{i - 1}^{n} } \right)R_{i - 1}^{2} R_{i}^{2} }}{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)r{}^{2}}}$$

$$\Delta \sigma_{\theta }^{i,n} = \sigma_{0} - \sigma_{\theta }^{i,n} = \frac{{\Delta p_{i}^{n} R_{i}^{2} - \Delta p_{i - 1}^{n} R_{i - 1}^{2} }}{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}} + \frac{{\left( {\Delta p_{i}^{n} - \Delta p_{i - 1}^{n} } \right)R_{i - 1}^{2} R_{i}^{2} }}{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)r^{2} }}\quad {\text{with}}\;R_{i - 1} \le r \le R_{i}$$

(20)

Writing the continuity of the radial displacement

$$\left. {\Delta u_{r}^{i,n} } \right|_{{r = R_{i} }} = \left. {\Delta u_{r}^{i + 1,n} } \right|_{{r = R_{i} }} \quad {\text{for}}\;i = k+1,q$$

(21)

we obtain

$$\Delta p_{i}^{n} = h^{i,n} \Delta p_{q}^{n}\quad {\text{for}}\;i = k,q$$

(22)

with

$$h^{i,n} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{for}}\;i = q} \hfill \\ {\frac{{(1 + (1 - 2v)\xi_{q,n} )}}{2(1 - v)}\left( {\frac{{R_{q} }}{{R_{q - 1} }}} \right)^{2} + \frac{{(1 - \xi_{q,n} )}}{2(1 - v)}(1 - 2v)} \hfill & {{\text{for}}\;i = q - 1} \hfill \\ {h_{1}^{i,n} h^{i + 1,n} + h_{2}^{i,n} h^{i + 2,n} } \hfill & {{\text{for}}\;i = k,q - 2} \hfill \\ \end{array} } \right.$$

(23)

where

$$h_{1}^{i - 1,n} = \left( {1 + \xi_{i,n} \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}}{{\left( {R_{i + 1}^{2} - R_{i}^{2} } \right)}}} \right)\frac{{R_{i}^{2} }}{{R_{i - 1}^{2} }} - \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)\left( {1 - \xi_{i,n} } \right)}}{{2R_{i - 1}^{2} \left( {1 - v} \right)}}$$

$$h_{2}^{i - 1,n} = - \xi_{i,n} \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)R_{i + 1}^{2} }}{{\left( {R_{i + 1}^{2} - R_{i}^{2} } \right)R_{i - 1}^{2} }}$$

(24)

and

$$\xi_{i,n} = \frac{{E_{i}^{n} }}{{E_{i + 1}^{n} }} = \frac{{G_{i}^{n} }}{{G_{i + 1}^{n} }}$$

(25)

Equation 22 shows the relationship between the radial stress at the outer boundary of the ith annulus in the damage zone $(\Delta p_{i}^{n} )$ and the radial stress at the elastic–damage interface $(\Delta p_{q}^{n} )$. This equation obviously allows to derive the radial stress at the elastic–damage interface $(\Delta p_{q}^{n} )$ from the radial stress at the damage–plastic interface $(\Delta p_{k}^{n} )$ which is calculated by using the solution in the plastic zone (Sect. 4.2). Once the radial stresses at the outer boundary of each annulus are obtained, the displacement and the stress fields are calculated using Eqs. 19 and 20. The radial stress $\sigma_{r}^{i,n}$ in the elastic zone is compared with the critical value $p_{\text{D}}^{ * }$ (Eq. 12), and the radius of the damage zone is updated.

4.2 Solution in the plastic zone

For a ring in the plastic zone (i = 1,k), the solution of the equilibrium Eq. (6) is obtained as

$$\sigma_{r}^{i,n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {\left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + p_{i - 1}^{n} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}}$$

$$\sigma_{\theta }^{i,n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {K_{\text{p}} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + K_{\text{p}} p_{i - 1}^{n} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} \quad {\text{with}}\;R_{i - 1} \le r \le R_{i} ,\;i = 1,k$$

(26)

where $p_{i}^{n}$ is the radial stress at the outer boundary of the ith annulus (r = R _i ) at the nth time step (note that $p_{0}^{n} = p_{\text{f}}^{n}$ at the tunnel wall (Eq. 8)) and is calculated from the following relation

$$p_{i}^{n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {\left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + p_{i - 1}^{n} \left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} \quad {\text{with}}\;i = 1,k$$

(27)

The general solution for the radial displacement is

$$\frac{{\Delta u_{r}^{i,n} }}{r} = \frac{1}{{2G_{i}^{n} }}\left[ {\frac{{B_{1}^{i,n} }}{{K_{\text{p}} + K_{\psi } }}\left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} + C^{i,n} \left( {\frac{{R_{i} }}{r}} \right)^{{K_{\psi } + 1}} + \frac{{B_{2}^{i,n} }}{{K_{\psi } + 1}}} \right]$$

(28)

where

$$B_{1}^{i,n} = \left( {\frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}} + p_{i - 1,n} } \right)\left( {A_{1} + K_{\text{p}} A_{2} } \right),\quad B_{2}^{i,n} = - \left( {A_{1} + A_{2} } \right)\left( {\sigma_{0} + \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}} \right)$$

(29)

$$A_{1} = 1 - v(K_{\psi } + 1),\quad A_{2} = (1 - v)K_{\psi } - v$$

(30)

and C ^i,n is an integration constant which is calculated by applying the condition of displacement continuity at the interface between two adjacent rings

$$\begin{aligned} C_{i,n} & = \frac{1}{{K_{p} + K_{\psi } }}\left[ {B_{1}^{i + 1,n} \xi_{i,n} - B_{1}^{i,n} \left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{p} - 1}} } \right] + C_{i + 1,n} \xi_{i,n} \left( {\frac{{R_{i + 1} }}{{R_{i} }}} \right)^{{K_{\psi } + 1}} \\ & \quad + \frac{{B_{2}^{i + 1,n} \xi_{i,n} - B_{2}^{i,n} }}{{K_{\psi } + 1}}\quad {\text{with}}\;i = 1,k - 1 \\ \end{aligned}$$

(31)

By applying the displacement continuity condition at the plastic–damage interface (r = R _P), we get

$$C_{k,n} = \left. {\xi_{k,n} \Delta u_{r}^{k + 1,n} } \right|_{{r = R_{k} }} - \left[ {\frac{{B_{1}^{k,n} }}{{K_{\text{p}} + K_{\psi } }}\left( {\frac{{R_{k} }}{{R_{k - 1} }}} \right)^{{K_{\text{p}} - 1}} + \frac{{B_{2}^{k,n} }}{{K_{\psi } + 1}}} \right]$$

(32)

The numerical algorithm is sketched in Fig. 4 and can be summarized as follows: After updating the parameters related to the rock mass degradation, the stresses in the plastic zone are calculated and the plastic radius is updated. By applying the normal stress continuity condition at the plastic–damage interface, the radial stress at the boundary of each annulus in the damage zone is then calculated. Therefore, the stresses and displacement field in the damage and elastic zone are derived and the damage radius is updated. Finally, the radial displacement in the plastic zone is computed by using the displacement continuity condition. It is important to note that large displacement computation must be applied for tunnels which exhibit large values of the convergence. Therefore, following an updated Lagrangian approach, the radius of each ring is updated after each computation step. The computation step is small enough so that a small strain formulation can be adopted for each increment. The implementation of this numerical algorithm into computing codes (e.g., MATLAB, Maple, Mathematica) is straightforward, and results can be obtained in a quick and accurate manner. The convergence of the numerical procedure and the appropriate choice of the space and time steps are discussed in “Appendix 3.”

Fig. 4

Flowchart for the sequence of calculations

5 Application to Saint-Martin-la-Porte access adit

As part of the Lyon–Turin project, the excavation of the Saint-Martin-La-Porte access adit between 2003 and 2010 encountered severe operational difficulties in the coal schists section associated with an extreme squeezing condition. Careful instrumentation of displacement measurements of the tunnel walls along different directions clearly showed a high time-dependent deformation behavior of rock mass. In this paper, the analysis of the convergence measurements is performed for the sections between chainage 1250 and 1550 m where the largest displacements have been recorded.

5.1 Geological conditions and difficulties encountered during excavation

Apart from recent superficial formations, the rock masses encountered in the Saint-Martin-La-Porte access adit belong to the internal structural zones of the Alps, characterized by an extreme geological complexity from both lithological and structural points of view. The section of the access gallery is characterized by the overlapping of the “Houillère Briançonnaise” zone on the “Sub-briançonnaise” zone, originating a contact marked by Triassic formations (gypsum and anhydrite), called “Front du Houiller” (Fig. 5a). In particular, the tunnel has been excavated in the “Productive Carboniferous Formation” (Encombres Unit) which is composed of schists and/or carboniferous schists (45–55 %), sandstone (40–50 %), and a significant proportion of cataclastic rocks (up to 15 %) [5]. A characteristic feature of the ground observed at the face during excavation is the anisotropic, highly heterogeneous, disrupted and fractured conditions of the rock mass, which exhibits a very severe squeezing behavior.

Fig. 5

a Simplified geological longitudinal view of the gallery. b Geological plan view at the base tunnel level

Tunneling works in the Jurassic carbonated rocks and in the Triassic dolomites did not face any particular problem, including in the Houiller Front. Indeed, excavation using traditional methods reached a rate of 10 m/day. Then, when the Houiller sandstones and schists were encountered, very severe squeezing behavior appeared. Several traditional support systems were used, but it soon became apparent that a stiff support could not cope with this phenomenon. Subsequent to the metric convergences encountered in the coal schists section, the geometrical layout (in plan and elevation) of the gallery was modified as shown in Fig. 5b. Initially, a “soft” support (named P7-3), consisting of steel ribs with sliding joints, 8-m-long rock dowels, and a 20-cm shotcrete primary lining was installed from chainage 1267 m. The tunnel sections with such a support system installed up to chainage 1384 m underwent very large deformations, with convergences up to 2 m and the need of extensive re-shaping of the tunnel. A novel excavation and support method (named DSM) was finally adopted with highly deformable elements inserted in the shotcrete lining which allowed for controlled deformation and stress in the rock mass and in the supports [5, 9].

5.2 Monitoring data

The excavation of the Saint-Martin-La-Porte access adit has been associated with a program of intensive geological and geotechnical monitoring. Convergence measurements were carried out by optical ranging on regularly spaced sections equipped each with five monitoring points along the perimeter of the section. Figure 6 shows typical relative convergence curves at chainage 1311 m in an area of large convergence. This provides a clear example of the time-dependent behavior of the rock mass with convergence of the tunnel walls that continues to increase even during a stop of the face advance.

Fig. 6

Example of convergence measurements at chainage 1311 m

Starting with a quasi-circular initial cross section, the convergence data and the in situ observations clearly show an ovalization of the cross section. In order to describe the anisotropy observed in the gallery, a method for geometrical processing of the measurement data was proposed [37]. The evolution of the cross section is described by fitting the cross section with an ellipse and its principal axes give directly the principal directions of deformation mode. The convergences along each semi-axis have been back-analyzed using the semiempirical law [37] or the semi-analytical model [36] and numerical simulations [35]. In the present version of the model, the proposed semi-analytical solution does not consider the anisotropy of the rock mass. Therefore, we analyze the evolution of the mean value of the convergence over the two principal directions by defining the equivalent radius of tunnel section as

$$R_{\text{eq}} = \sqrt {ab}$$

(33)

where a and b are, respectively, the major semi-axis and the minor semi-axis of the elliptical cross section of tunnel which were determined in [37]. The mean value of the convergence is deduced as $C = 2(R_{0} - R_{\text{eq}} )$, where R ₀ is the initial value of equivalent radius of tunnel section. The mean convergence of deformed sections is then interpreted by applying the convergence law proposed by Sulem et al. [32, 33], where the convergence is expressed as a function of the distance x to the face and of the time t

$$C(x,t) = C_{\infty x} \left[ {1 - \left( {\frac{X}{x + X}} \right)^{2} } \right]\left[ {1 + m\left( {1 - \left( {\frac{T}{t + T}} \right)^{n} } \right)} \right]$$

(34)

This convergence law depends on five parameters C _∞x , X, T, m and n, where X characterizes the distance of influence of the excavation, T is a characteristic time related to time-dependent properties of the ground, C _∞x is the “instantaneous” convergence as obtained in the case of an infinite rate of face advance (no time-dependent effect), C _∞x (1 + m) is the total (long term) closure, and n is a constant (often taken equal to 0.3). The calibration of the four parameters of the convergence law has been performed for sections between chainage 1250 and 1550 m where the largest displacements have been recorded. All the fitting procedures are performed using a least squares algorithm. From the curve fitting results, it is observed that the parameters X, T, and m do not change for all sections in six different “quasi-homogeneous” zones which were previously identified (see [35, 37]). Therefore, an average constant value for these three parameters can be assumed in each zone and only the parameter C _∞x changes to account for the heterogeneity of the field conditions from one section to another. For all the studied sections, we obtain an excellent fit of the measured convergence data. Table 1 summarizes the results of this calibration for each section of the studied zone.

Table 1 Curve fitting of the convergence law

A number of sections in the tunnel have also been equipped with multi-position borehole extensometers to measure the displacement distribution in the rock mass. The extensometers were installed in boreholes of 9–24 m length oriented in different directions around the tunnel. Each extensometer includes from 3 to 6 measurement points. Figure 7 shows the most significant extensometer measurements at chainage 1331 m where a total of six multi-position borehole extensometers, each 18 m long, were installed, one at the invert and crown, and two on each sidewall, left and right. It is interesting to note that the radial displacement is not symmetric (the maximal displacement is on the right side of the section), and the length of the extensometers is not sufficient to take into account the total radial displacement, which means that the extent of the plastic zone exceeded the length of the extensometers.

Fig. 7

Radial displacements from multi-point borehole extensometers installed at chainage 1331 m after a 45 and b 135 days from installation

5.3 Back-analysis of the convergence data using the proposed semi-analytical model

This section describes the back-analysis of the convergence data of the Saint-Martin-la-Porte access adit using the proposed model. The main scope is to highlight the potential of our semi-analytical solution for the analysis of time-dependent deformation behavior of tunnels in squeezing conditions.

In the studied sections, the overburden is approximately 300 m and the initial state of stress σ ₀ in the ground is assumed to be hydrostatic and equal to 8.5 MPa [6, 36]. Two geometric configurations corresponding to a radius of the opening section of R ₀ = 5.5 m and R ₀ = 6 m, respectively, have been considered to describe the two profiles P7-3 and DSM between chainage 1250 and 1550 m [6]. The recorded convergence data correspond to the stage for which the soft support system was installed, i.e., before re-profiling and installation of the yield support system equipped with compressible blocks. As mentioned above, this soft support could not cope with the large convergence of the tunnel walls and failed. Therefore, in the numerical analysis we neglect the effect of the shotcrete lining.

The face advance history during the time window considered (Fig. 8) alternates between the standstills and the excavation phases, with an advance rate of 0.67–1.0 m/day. For consistency with previous numerical works on the simulation of the Saint-Martin-la-Porte access adit [7, 35, 37], we consider the following numerical values for the elasto-plastic parameters of the rock mass: Young’s modulus E ₀ = 650 MPa; Poisson’s ratio ν = 0.30; friction angle φ = 26°; zero dilatancy is assumed (ψ = 0°). The remaining parameters are the initial cohesion c ₀ and the four parameters β ₁, β ₂, β ₃ and β ₄ which describe the time-dependent behavior of the rock matrix. In order to reduce the number of parameters to be fitted, we assume here that β ₃ = β ₄. Of course, one can assume different values for these parameters, but as we shall see in the following, acceptable numerical results are obtained under this assumption. The remaining parameters are fitted on the convergence data.

Fig. 8

Face advance in the part of the gallery considered in the analysis

As discussed in “Appendix 3,” the numerical simulation is performed using a discretization of the medium surrounding the tunnel into 500 rings with a thickness d from 0.025 to 0.030 m. The time step Δt is constant and taken equal to 0.5 day. This choice gives sufficiently accurate results. Note that the large displacement approach is used by updating the rings radii as mentioned above. A comparison between the small and large displacement approach is presented in “Appendix 4” and illustrated in Fig. 13. When the convergence of the tunnel walls is over 2 m, the small displacement approach overestimates the convergence of about 20 %.

The calibration of the four parameters c ₀, β ₁, β ₂ and β ₃ is done as follows: For each zone as identified in Table 1, these four parameters are evaluated by the back-analysis of convergence data of the first section of each zone; then, following the idea that for the fitting of the convergence law (Eq. 34) only C _∞x changes from one section to another in a given zone, whereas X, m and T are kept constant, the data of the other sections of the zone are simulated by keeping β ₁, β ₂, β ₃ unchanged and by only adjusting the initial cohesion c ₀ in order to account for the heterogeneity of the local field conditions.

A comparison between computed and measured radial displacements at the tunnel wall for all the studied sections is shown in Fig. 9. The agreement of the numerical results with the observed values over a period of approximately 160 days is very good. After 20 days the relative error between the computed and the recorded displacements is less than 10 %. As, in the calibration procedure, we have emphasized the good simulation of the long-term convergence, the relative error is only of few % in the long term. Better results could be obtained for the simulation of the very short-term data (after few days) by adjusting the empirical law describing the deconfinement process (Eq. 9). However, the proposed solution can well capture the measured data during the stop of the face and also the increase in convergence rate when the tunnel advances. It means that the solution correctly takes into account the effect of the face advance and of the time-dependent behavior of rock mass.

Fig. 9

Comparison between measured convergences and computed convergences using the convergence law and the proposed solution for different sections between chainage 1250 and 1550 m

A good agreement between computed and monitored radial displacements around the tunnel up to a depth of 18 m, at chainage 1331 m, is also shown in Fig. 10. The two diagrams illustrate the measured and computed displacements 45 days (Fig. 10a) and 135 days (Fig. 10b) after the installation of the multi-point extensometers. Note that the measured values are relative displacements to the reference point at the depth of 18 m which is considered as a fixed point. Therefore, in order to compare the computed values with measured displacements, the computed displacement of the reference point must be subtracted.

Fig. 10

Computed and monitored radial displacements at depth at chainage 1331 m after a 45 days and b 135 days from installation of the multi-point extensometers

A total of 19 monitoring section have been considered, and the constitutive parameters obtained are reported in Table 2. This permits to distinguish the same six zones as defined from the analysis of convergence data using the empirical law presented above. These six zones are characterized with different values of the two parameters β ₂ and β ₃ which describe the time-dependent behavior of rock mass. Parameter β ₁ is the same everywhere. The heterogeneity of the rock mass from one section to another is described with different values of the initial cohesion c ₀. At this point, we can see that there is a correspondence between the parameters of constitutive model and the ones of the semiempirical convergence law: Parameters c ₀ (in the model) and C _∞x (in the convergence law) characterize the “instantaneous” response, β ₂ (in the model) and T (in the convergence law) are related to time-dependent properties of the ground, and finally β ₃ (in the model) and m (in the convergence law) describe the ratio between the “instantaneous” response and the final one. Therefore, it is interesting to compare the constitutive parameters with the parameters of the semiempirical convergence law. As can be seen in Fig. 11, a linear fit can describe the relationship between the cohesion c ₀ and the parameter C _∞x for each homogeneous zone. A linear fit can also approximate the relationship between the parameters β ₃ and m. The relation between the two parameters β ₂ and T is clearly nonlinear. Thus, we have here a simple way to infer the constitutive parameters of the rock mass directly from the convergence data.

Table 2 Constitutive parameters of the proposed model between chainage 1250 and 1550 m

Fig. 11

Relation between the constitutive parameters and the ones of the empirical convergence law

6 Conclusion

In this paper, a semi-analytical solution for stresses and displacements around a circular tunnel excavated in a rock mass with time-dependent mechanical properties is proposed. The approach is based on a rock-aging model. It is capable of modeling both the time-dependent deformation and the time-dependent extent of the yielding zone as often observed for tunnels excavated in squeezing ground. The constitutive model considers a degradation of the elastic and strength properties with time when the stress state reaches a damage initiation criterion. A semi-analytical solution process based on the discretization of rock mass around the tunnel in circular rings and on a progressive unloading of the inner boundary of the tunnel is proposed by deriving closed-form solutions inside each ring. Large displacement analysis is also implemented to account for squeezing ground conditions. The proposed solution is used to back-analyze convergence data from the Saint-Martin-La-Porte access adit. The numerical examples show that the time-dependent deformation behavior of the rock mass observed in the Saint-Martin-La-Porte access adit can be very well captured using the proposed solution. Simple relationships are obtained between the model parameters and those of the empirical convergence law of Sulem et al. [32, 33]. Therefore, the observational method proposed in [37] and [18] can be extended. The parameters of the empirical convergence law can be determined from continuous monitoring of the convergence data, and the corresponding values of the parameters of the proposed constitutive model can be subsequently evaluated. This procedure would permit an assessment of the material properties of the ground and their variability along the tunnel and an adjustment of the excavation and lining design.

Appendices

Appendix 1: Derivation of the governing equations in the (elastic) damage zone

Let’s consider the loading step for which the ith annulus inside the damage zone undergoes a decrease in stress $\Delta p_{i - 1}^{n} \;\left( { = \sigma_{0} - p_{i - 1}^{n} } \right)$ and $\Delta p_{i}^{n} \;\left( { = \sigma_{0} - p_{i}^{n} } \right)$ at the inner and outer boundaries, respectively. The constitutive relationships are written for each annulus

$$\begin{aligned} \Delta \sigma_{r}^{i,n} & = M_{i}^{n} \Delta \varepsilon_{r}^{i,n} + (M_{i}^{n} - 2G_{i}^{n} )\Delta \varepsilon_{\theta }^{i,n} \\ \Delta \sigma_{\theta }^{i,n} & = (M_{i}^{n} - 2G_{i}^{n} )\Delta \varepsilon_{r}^{i,n} + M_{i}^{n} \Delta \varepsilon_{\theta }^{i,n} \\ \end{aligned}$$

(35)

with $M_{i}^{n} = \frac{{E_{i}^{n} (1 - v)}}{(1 + v)(1 - 2v)}$; $G_{i}^{n} = \frac{{E_{i}^{n} }}{2(1 + v)}.$

For axisymmetric conditions $\Delta \varepsilon_{\theta }^{i,n} = \frac{{\Delta u_{r}^{i,n} }}{r}$ and under the assumption of small displacement,

$$\Delta \varepsilon_{r}^{i,n} = \frac{{{\text{d}}\Delta u_{r}^{i,n} }}{{{\text{d}}r}}; \Delta \varepsilon_{\theta}^{i,n}=\frac{\Delta u_{r}^{i,n}}{r}$$

(36)

This assumption is justified by the fact that the elastic damage zone is beyond the plastic zone and therefore undergoes small displacements.

Replacing Eq. 36 with Eq. 35 and the equilibrium equation (Eq. 16), one gets

$$\frac{{{\text{d}}^{2} \Delta u_{r}^{i,n} }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{{\text{d}}\Delta u_{r}^{i,n} }}{{{\text{d}}r}} - \frac{{\Delta u_{r}^{i,n} }}{r} = 0$$

(37)

The general solution is

$$\Delta u_{r}^{i,n} = Ar + \frac{B}{r}$$

(38)

The boundary conditions $\left( {\Delta \sigma_{r}^{i,n} = \Delta p_{i - 1}^{n} \;{\text{at}}\;r = R_{i - 1} \;{\text{and}}\;\Delta \sigma_{r}^{i,n} = \Delta p_{i}^{n} \;{\text{at}}\;r = R_{i} } \right)$ are applied to obtain the integration constants A and B

$$\begin{aligned} A = - \frac{{\Delta p_{i}^{n} R_{i}^{2} - \Delta p_{i - 1}^{n} R_{i - 1}^{2} }}{{2G_{i}^{n} (1 - 2v)\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}} \hfill \\ B = - \frac{{\left( {\Delta p_{i}^{n} - \Delta p_{i - 1}^{n} } \right)R_{i - 1}^{2} R_{i}^{2} }}{{2G_{i}^{n} \left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}} \hfill \\ \end{aligned}$$

(39)

Hence, the radial displacement and the stress state inside this annulus in the damage zone can be calculated as Eqs. 19 and 20.

The continuity of the radial displacement,

$$\left. {\Delta u_{r}^{i,n} } \right|_{{r = R_{i} }} = \left. {\Delta u_{r}^{i + 1,n} } \right|_{{r = R_{i} }} \quad {\text{for}}\;i = k,q - 1$$

(40)

yields

$$\Delta p_{i - 1}^{n} = h_{1}^{i,n} \Delta p_{i}^{n} + h_{2}^{i,n} \Delta p_{i + 1}^{n} \quad {\text{for}}\;i = k,q - 1$$

(41)

with

$$h_{1}^{i - 1,n} = \left( {1 + \xi_{i,n} \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)}}{{\left( {R_{i + 1}^{2} - R_{i}^{2} } \right)}}} \right)\frac{{R_{i}^{2} }}{{R_{i - 1}^{2} }} - \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)\left( {1 - \xi_{i,n} } \right)}}{{2R_{i - 1}^{2} \left( {1 - v} \right)}}$$

$$h_{2}^{i - 1,n} = - \xi_{i,n} \frac{{\left( {R_{i}^{2} - R_{i - 1}^{2} } \right)R_{i + 1}^{2} }}{{\left( {R_{i + 1}^{2} - R_{i}^{2} } \right)R_{i - 1}^{2} }}$$

(42)

and

$$\xi_{i,n} = \frac{{E_{i}^{n} }}{{E_{i + 1}^{n} }} = \frac{{G_{i}^{n} }}{{G_{i + 1}^{n} }}$$

(43)

In the elastic zone (r ≥ R _D), the radial displacement is obtained from the Lamé’s solution

$$\frac{{\Delta u_{r}^{q + 1,n} }}{{R_{\text{D}}^{n} }} = \frac{{\Delta p_{q}^{n} }}{{2G_{0} }}\frac{{R_{\text{D}}^{n} }}{r}\quad {\text{with}}\;i = q,N$$

(44)

the continuity of the displacement on the elastic–damage interface

$$\left. {\Delta u_{r}^{q,n} } \right|_{{r = R_{q} }} = \left. {\Delta u_{r}^{q + 1,n} } \right|_{{r = R_{q} }}$$

(45)

yields

$$\Delta p_{q - 1}^{n} = h_{q - 1,n} p_{q}^{n}$$

(46)

with

$$h^{q - 1,n} = \frac{{(1 + (1 - 2v)\xi_{q,n} )}}{2(1 - v)}\left( {\frac{{R_{q} }}{{R_{q - 1} }}} \right)^{2} + \frac{{(1 - \xi_{q,n} )}}{2(1 - v)}(1 - 2v)$$

(47)

We obtain the following relation from Eqs. 21 and 27

$$\Delta p_{i}^{n} = h^{i,n} \Delta p_{q}^{n} \quad {\text{for}}\;i = k,q - 2$$

(48)

with

$$h^{i,n} = h_{1}^{i,n} h^{i + 1,n} + h_{2}^{i,n} h^{i + 2,n}$$

(49)

Appendix 2: Derivation of governing equations in the plastic zone

For a ring in the plastic zone (i = 1,k), the plastic criterion $\left( {\sigma_{\theta }^{i,n} - \sigma_{r}^{i,n} K_{\text{p}} - \sigma_{\text{c}}^{i,n} = 0} \right)$ is satisfied. Replacing with the equilibrium equation (Eq. 6), we obtain

$$\frac{{{\text{d}}\sigma_{r}^{i,n} }}{{{\text{d}}r}} + \frac{{(1 - K_{\text{p}} )\sigma_{r}^{i,n} - \sigma_{\text{c}}^{i,n} }}{r} = 0$$

(50)

Integration of the above equation gives the classical expression of the radial and hoop stresses for a Mohr–Coulomb elasto-plastic medium

$$\sigma_{r}^{i,n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {\left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + p_{i - 1}^{n} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} \quad {\text{with}}\;R_{i - 1} \le r \le R_{i} ,\;i = 1,k$$

$$\sigma_{\theta }^{i,n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {K_{\text{p}} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + K_{\text{p}} p_{i - 1}^{n} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}}$$

(51)

where $p_{i}^{n}$ is the radial stress at the inner boundary of the ith annulus (r = R _i ) at the nth time step [note that at the tunnel wall (Eq. 8)] and is calculated from the following relation

$$p_{i}^{n} = \frac{{\sigma_{\text{c}}^{i,n} }}{{K_{\text{p}} - 1}}\left[ {\left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + p_{i - 1}^{n} \left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{\text{p}} - 1}} \quad {\text{with}}\;i = 1,k$$

(52)

The new position of the plastic–damage interface must be determined. We first assume that this interface is still on the outer boundary of the kth annulus. The decrease in the radial stress $\Delta p_{k}^{n} ( = \sigma_{0} - p_{k}^{n} )$ at the plastic boundary is calculated from Eq. 52. The stress state and displacement are obtained by replacing $\Delta p_{0}^{n}$ and R ₀ by $\Delta p_{k}^{n}$ and R _k, respectively, in the elastic–damage solution presented above, and we have

$$\Delta p_{k + 1}^{n} = \frac{{h^{k + 1,n} }}{{h^{k,n} }}\Delta p_{k}^{n}$$

(53)

Then the stress state on the outer boundary of the (k + 1)th annulus is calculated from Eq. 51, and the plastic criterion must be checked $\left( {\left. {f = (\sigma_{\theta }^{k + 1,n} - K_{\text{p}} \sigma_{r}^{k + 1,n} )} \right|_{{r = R_{k + 1} }} - \sigma_{\text{c}}^{k + 1,n} } \right)$. If f < 0, the plastic boundary is still on the outer boundary of the kth annulus, and the stress state surrounding the tunnel is determined. Otherwise, it is assumed that this interface is now on the outer boundary of the annulus where the radial stress is

$$p_{k + 1}^{n} = \frac{{\sigma_{\text{c}}^{k + 1,n} }}{{K_{\text{p}} - 1}}\left[ {\left( {\frac{{R_{k + 1} }}{{R_{k} }}} \right)^{{K_{\text{p}} - 1}} - 1} \right] + p_{k}^{n} \left( {\frac{{R_{k + 1} }}{{R_{k} }}} \right)^{{K_{\text{p}} - 1}}$$

(54)

The elastic–damage solution process is again applied to calculate the stress state from the (k + 1)th annulus to the qth one with a stress decrease $\Delta p_{k + 1}^{n} \left( { = \sigma_{0} - p_{k + 1}^{n} } \right)$ at $r = R_{k + 1}$. The yield criterion on the outer boundary of the (k + 2)th annulus must be checked. If $\left( {\left. {f = (\sigma_{\theta }^{k + 2,n} - K_{\text{p}} \sigma_{r}^{k + 2,n} )} \right|_{{r = R_{k + 1} }} - \sigma_{\text{c}}^{k + 2,n} < 0} \right)$, the plastic boundary is on the outer boundary of the (k + 1)th annulus and the plastic radius is updated. Otherwise this process is repeated successively for rings k + 3, k + 4 … until the extent the plastic zone is reached. Once the new position of the plastic–damage interface is determined, the stress field in the plastic–damage and in the elastic–damage one is determined. In the damage zone, the displacement is again calculated with Eq. 19.

In the plastic zone, strains are classically written as the sum of the elastic part and the plastic part

$$\dot{\varepsilon }_{r} = \dot{\varepsilon }_{r}^{e} + \dot{\varepsilon }_{r}^{p} ;\quad \dot{\varepsilon }_{\theta } = \dot{\varepsilon }_{\theta }^{e} + \dot{\varepsilon }_{\theta }^{p}$$

(55)

where the elastic strains are determined by using Hooke’s law and the plastic strains derived from a plastic potential

$$g(\sigma_{\theta } ,\sigma_{r} ) = \sigma_{\theta } - \sigma_{r} K_{\psi }$$

(56)

according to

$$\dot{\varepsilon }_{r}^{p} = \dot{\varLambda }\frac{\partial g}{{\partial \sigma_{r} }} = - \dot{\varLambda }K_{\psi }$$

$$\dot{\varepsilon }_{\theta }^{p} = \dot{\varLambda }\frac{\partial g}{{\partial \sigma_{\theta } }} = \dot{\varLambda }$$

(57)

where $\dot{\varLambda }$ is a plastic multiplier. Thus, we can write

$$\dot{\varepsilon }_{r}^{p} + K_{\psi } \dot{\varepsilon }_{\theta }^{p} = 0$$

(58)

In an axisymmetric configuration,

$$\dot{\varepsilon }_{r}^{i,n} = \frac{{{\text{d}}\Delta \dot{u}_{r}^{i,n} }}{{{\text{d}}r}};\quad \dot{\varepsilon }_{\theta }^{i,n} = \frac{{\Delta \dot{u}_{r}^{i,n} }}{r}$$

(59)

From Eqs. 55, 58, and 59, and considering that $K_{\psi }$ remains unchanged during the loading process (no hardening effect), the above rate equations can be integrated in time to obtain the equation that governs the radial displacement

$$\frac{{\partial \Delta u_{r}^{i,n} }}{\partial r} + K_{\psi } \frac{{\Delta u_{r}^{i,n} }}{r} = \Delta \varepsilon_{r}^{e,i,n} + K_{\psi } \Delta \varepsilon_{\theta }^{e,i,n} \quad {\text{with}}\;R_{i - 1} \le r \le R_{i} ,\;i = 1,k$$

(60)

In the left-hand side of the equation, the accumulated elastic strains are assumed to be small enough so that the small strain constitutive relationships (Eq. 35) hold.

Finally, it is obtained that the radial displacement is the solution of following differential equation

$$\frac{{\partial \Delta u_{r}^{i,n} }}{\partial r} + K_{\psi } \frac{{\Delta u_{r}^{i,n} }}{r} = \frac{1}{{2G_{i}^{n} }}\left[ {A_{1} \Delta \sigma_{r}^{i,n} + A_{2} \Delta \sigma_{\theta }^{i,n} } \right]\quad {\text{with}}\;R_{i - 1} \le r \le R_{i} ,\;i = 1,k$$

(61)

with

$$A_{1} = 1 - v(K_{\psi } + 1),\quad A_{2} = (1 - v)K_{\psi } - v$$

(62)

Thus,

$$\frac{{\partial \Delta u_{r}^{i,n} }}{\partial r} + K_{\psi } \frac{{\Delta u_{r}^{i,n} }}{r} = \frac{1}{{2G_{i}^{n} }}\left[ {B_{1}^{i,n} \left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{p} - 1}} + B_{2}^{i,n} } \right]$$

(63)

with

$$B_{1}^{i,n} = \left( {\frac{{\sigma_{c}^{i,n} }}{{K_{p} - 1}} + p_{i - 1,n} } \right)\left( {A_{1} + K_{p} A_{2} } \right),\quad B_{2}^{i,n} = - \left( {A_{1} + A_{2} } \right)\left( {\sigma_{0} + \frac{{\sigma_{c}^{i,n} }}{{K_{p} - 1}}} \right)$$

(64)

The general solution for the radial displacement is

$$\frac{{\Delta u_{r}^{i,n} }}{r} = \frac{1}{{2G_{i}^{n} }}\left[ {\frac{{B_{1}^{i,n} }}{{K_{p} + K_{\psi } }}\left( {\frac{r}{{R_{i - 1} }}} \right)^{{K_{p} - 1}} + C^{i,n} \left( {\frac{{R_{i} }}{r}} \right)^{{K_{\psi } + 1}} + \frac{{B_{2}^{i,n} }}{{K_{\psi } + 1}}} \right]$$

(65)

where C ^i,n is an integration constant and is found by applying the condition of displacement continuity at the interface between two adjacent rings

$$\begin{aligned} C_{i,n} & = \frac{1}{{K_{\text{p}} + K_{\psi } }}\left[ {B_{1}^{i + 1,n} \xi_{i,n} - B_{1}^{i,n} \left( {\frac{{R_{i} }}{{R_{i - 1} }}} \right)^{{K_{p} - 1}} } \right] + C_{i + 1,n} \xi_{i,n} \left( {\frac{{R_{i + 1} }}{{R_{i} }}} \right)^{{K_{\psi } + 1}} \\ & \quad + \frac{{B_{2}^{i + 1,n} \xi_{i,n} - B_{2}^{i,n} }}{{K_{\psi } + 1}}\quad {\text{with}}\;i = 1,k - 1 \\ \end{aligned}$$

(66)

By applying the displacement continuity condition at the plastic–damage interface (r = R _P), we get

$$C_{k,n} = \left. {\xi_{k,n} \Delta u_{r}^{k + 1,n} } \right|_{{r = R_{k} }} - \left[ {\frac{{B_{1}^{k,n} }}{{K_{\text{p}} + K_{\psi } }}\left( {\frac{{R_{k} }}{{R_{k - 1} }}} \right)^{{K_{\text{p}} - 1}} + \frac{{B_{2}^{k,n} }}{{K_{\psi } + 1}}} \right]$$

(67)

Appendix 3: Convergence of solution

We study here the effect of the discretization around the tunnel and of the time step on the convergence curve. For that, we assume a constant excavation rate of 1 m/day and we take the following numerical values for the parameters describing the behavior of the rock matrix: E ₀ = 650 MPa; ν = 0.3; c ₀ = 1 MPa, φ = 26°, ψ = 0°, β ₁ = 0.01 day⁻¹, β ₂ = 0.85, β ₃ = 0.50. Different computations have been performed with a number of ring between 20 and 1000 and a time step between 0.5 and 10 days (Fig. 12).

Fig. 12

Effect of the time step (a) and the number of annulus (b) on the computed diametrical convergence (E ₀ = 650 MPa; ν = 0.3; c ₀ = 1 MPa, φ = 26°, ψ = 0°, β ₁ = 0.01, β ₂ = 0.85, β ₃ = 0.50, excavation rate of 1 m/day)

It is obtained that for a time step smaller than Δt = 1 day, the obtained diametrical closure of the tunnel after 100 days differs from less than 0.25 % as compared to the one computed with a time step Δt = 0.5 day (Fig. 12a).

On the other hand, Fig. 12b shows the results for different number of rings. We observe that the numerical solution converges with increasing number of rings and that a discretization with 500 rings ensures a very accuracy of the numerical results. Therefore, we choose a time step Δt = 0.5 day and a number of ring of 500 in all the computations.

Appendix 4: Comparison between the small and large displacement approach

Figure 13 presents a comparison of the computed convergence curve with and without updating the spatial discretization. This example corresponds to a section for which a convergence of more than 2 m was recorded. The computations show a difference of about 20 % between the two computations after 100 days (2484 mm without updating the mesh and 2040 mm with updating it). Therefore, the large displacement approach is needed for the sections of the Saint-Martin-la-Porte access adit exhibiting metric convergences as encountered in the coal schists zone.

Fig. 13

Comparison of convergence computed using small and large displacement approach (E ₀ = 650 MPa; ν = 0.3; c ₀ = 1 MPa, φ = 26°, ψ = 0°, β ₁ = 0.01, β ₂ = 0.85, β ₃ = 0.50, excavation rate of 1 m/day)