Analytical Solution for Deep Circular Tunnels in Rock with Consideration of Disturbed zone, 3D Strength and Large Strain

Abstract

This paper presents a new analytical solution for deep circular tunnels in rock with consideration of disturbed zone, 3D strength and large strain. The rock is assumed to be elastic–brittle–plastic and governed by a 3D Hoek–Brown yield criterion. To take the large displacement around a tunnel into account, the large-strain theory is adopted to determine the displacement of rock in the plastic zone. Based on the equilibrium equation, constitutive law and large-strain theory, the governing equations for the stresses and radial displacement around the tunnel were derived and solved by using MATLAB. The proposed solution was validated by using it to analyze a tunnel and comparing the results with those from numerical analysis using a finite difference code. Finally, extensive parametric studies were performed on tunnels in both poor-quality and good-quality rock masses with respect to stresses and radial displacement. The results indicate that the disturbed zone and the flow rule both have significant effects on the stress and displacement distributions around the tunnel.

1 Introduction

To understand the response of rock around an excavated tunnel and provide appropriate design for tunnel support, it is necessary to analyze the stress and displacement distributions around the tunnel. Cavity contraction theory has been widely used to analyze tunnels by considering the tunnel as a cylindrical cavity (Mair and Taylor 1993; Wang 1996; Carranza-Torres and Fairhurst 1999; Yu 2000). Early studies on cavity contraction were mostly based on the linear Mohr–Coulomb criterion (Florence and Schwer 1978; Kennedy and Lindberg 1978). Then, the solutions for stresses and displacements around a tunnel were developed based on the original Hoek–Brown criterion with some simplifying assumptions (Brown et al. 1983; Wang 1996). Carranza-Torres and Fairhurst (1999) seem to be the first to present an analytical solution to the cavity contraction problem in the original Hoek–Brown criterion-based rock mass without additional assumptions, but only the elastic–perfectly plastic behavior of rock mass was considered. Later, Carranza-Torres (2004) updated their 1999 solution based on the generalized Hoek–Brown criterion. Thereafter, Sharan (2003, 2005, 2008) also presented solutions to the cavity contraction problem in an elastic–brittle–plastic rock mass based on both the original and generalized Hoek–Brown criteria. Park and Kim (2006) provided a solution to tunnel in an elastic–brittle–plastic rock mass, but the Mohr–Coulomb criterion rather than the Hoek–Brown criterion was adopted as the potential function in their solution. Alonso et al. (2003) adopted a piecewise function to describe the strain-softening behavior of rock mass and presented a corresponding solution to the cavity contraction problem. Since both the Mohr–Coulomb and Hoek–Brown criteria are 2D strength criterion with respect to the major and minor principal stresses, the intermediate principal stress was ignored in the abovementioned solutions. Wang et al. (2012) proposed a more general solution to the cavity contraction problem in a Mohr–Coulomb criterion-based rock mass by considering the out-of-plane stress, but the plastic strain in the out-of-plane direction was simply assumed to be zero. More recently, to consider the large strain around a tunnel, solutions based on the Mohr–Coulomb criterion were presented to analyze excavated tunnels (Park 2014; Zhang et al. 2019).

Although many solutions have been developed for the rock mass around a tunnel based on the Hoek–Brown criterion, none of those solutions can truly consider the 3D strength and the 3D plastic behavior after failure. Furthermore, the small-strain theory was adopted in most Hoek–Brown criterion-based solutions for the calculation of displacement, which may overpredict the deformation of a tunnel with low support and large convergence (Yu and Houlsby 1995). To overcome those limitations, in this paper, a 3D version of the Hoek–Brown criterion, the newly modified generalized Zhang-Zhu (GZZ) criterion (Chen et al. 2020), is selected to characterize the 3D strength of rock mass, and the large-strain theory is applied to the plastic region near the tunnel. Since rock mass experiences strain softening during excavation, it is assumed as an elastic–brittle–plastic material. Besides, considering the significant influence of tunnel excavation on the rock mass, a disturbed zone with a disturbance factor D is considered. Based on those assumptions, an analytical solution to the cavity contraction problem in rock mass is developed by considering the disturbed zone, 3D strength, and large strain of rock mass. The derived solution is validated by comparing the results with those from numerical simulations using the finite-difference code FLAC3D. Finally, extensive parametric studies have been performed on tunnels in both poor-quality and good-quality rock masses, regarding the stress and displacement distributions.

2 Rock Mass Model

The rock mass in this study is assumed to be an elastic–brittle–plastic material, and the brittle behavior of the rock mass is controlled by the decrease in the Geological Strength Index (GSI). In this context, the rock mass will be governed first by an initial value GSI_i and then a residual value GSI_r (Fig. 1). The initial yield surface is related to GSI_i and the residual yield surface is related to GSI_r as shown in Fig. 1. The rock mass around a tunnel is strongly affected by the excavation activity, and thus a disturbed zone is included in the inner part of the plastic zone. A disturbance factor D ($0<D\le 1$) is assigned to the disturbed zone, and D = 0 is set for the rest of the plastic zone.

Fig. 1

Simplified yield surface, stress–strain relation and brittle behavior of elastic–brittle–plastic material

2.1 Elastic Behavior of Rock Mass

The elastic behavior of the rock mass is assumed to obey Hooke’s law:

$${\text{d}}{\varvec\sigma} ={\textbf{D}}d{{\varvec\varepsilon}}^{e}={\textbf{D}}\left({\text{d}}{\varvec\varepsilon}-{\text{d}}{{\varvec\varepsilon}}^{p}\right)$$

(1a)

$${\varvec\sigma} =\left[{\sigma }_{x},{\sigma }_{y},{\sigma }_{z},{\tau }_{xy},{\tau }_{xz},{\tau }_{yz}\right]$$

(1b)

$$\begin{array}{c}{\textbf{D}}=\left[\begin{array}{cc}\begin{array}{ccc}{a}_{1}& {a}_{2}& {a}_{2}\\ {a}_{2}& {a}_{1}& {a}_{2}\\ {a}_{2}& {a}_{2}& {a}_{1}\end{array}& \begin{array}{ccc}& & \\ & & \\ & & \end{array}\\ \begin{array}{ccc}& & \\ & & \\ & & \end{array}& \begin{array}{ccc}G& & \\ & G& \\ & & G\end{array}\end{array}\right]\end{array}$$

(1c)

$${a}_{1}=K+\frac{4}{3}G$$

(1d)

$${a}_{2}=K-\frac{2}{3}G$$

(1e)

$$K=\frac{E}{3\left(1-2\nu \right)}$$

(1f)

$$G=\frac{E}{2\left(1+\nu \right)}$$

(1g)

where $\mathbf{D}$ is the elastic constitutive matrix; $E$ and $\nu$ are Young’s modulus and Poisson’s ratio, respectively; and the superscripts e and p mean elastic and plastic, respectively.

2.2 Yield and Potential Functions

Considering the effect of intermediate effective principal stress on rock behavior, Zhang and Zhu (2007) and Zhang (2008) extended the Hoek–Brown criterion into a 3D version and, to be simple, the criterion is called the GZZ criterion in this paper following Priest (2012). To address the smoothness and nonconvexity problems of the GZZ criterion in a simple way, the GZZ criterion was modified by Chen et al. (2020) and denoted as the newly modified GZZ criterion. The newly modified GZZ criterion not only inherits the advantages of the Hoek–Brown criterion but also extends the Hoek–Brown criterion to a more general case and thus is adopted in this paper as the yield function, $f$, as expressed below:

$$f=\frac{1}{{\sigma }_{c}^{\left(1/a-1\right)}}{\left(\sqrt{{I}_{1}^{*2}-3{I}_{2}^{*}}\right)}^{1/a}+\frac{{m}_{b}}{2}\sqrt{{I}_{1}^{*2}-3{I}_{2}^{*}}-\frac{{m}_{b}}{2}\sqrt{\frac{\left({I}_{1}^{*}{I}_{2}^{*}-{I}_{3}^{*}\right)\left({I}_{1}^{*2}-3{I}_{2}^{*}\right)}{{I}_{1}^{*}{I}_{2}^{*}-9{I}_{3}^{*}}}=0$$

(2)

where the three transformed stress invariants ${I}_{1}^{*}$, ${I}_{2}^{*}$, and ${I}_{3}^{*}$ are defined by

$${I}_{1}^{*}={\sigma }_{1}^{*}+{\sigma }_{2}^{*}+{\sigma }_{3}^{*}$$

(3a)

$${I}_{2}^{*}={\sigma }_{1}^{*}{\sigma }_{2}^{*}+{\sigma }_{2}^{*}{\sigma }_{3}^{*}+{\sigma }_{3}^{*}{\sigma }_{1}^{*}$$

(3b)

$${I}_{3}^{*}={\sigma }_{1}^{*}{\sigma }_{2}^{*}{\sigma }_{3}^{*}$$

(3c)

$${\sigma }_{1}^{*}={\sigma }_{1}^{\prime}+\frac{{\sigma }_{c}}{{m}_{b}}s; \,\,{\sigma }_{2}^{*}={\sigma }_{2}^{\prime}+\frac{{\sigma }_{c}}{{m}_{b}}s;\,\,{\sigma }_{3}^{*}={\sigma }_{3}^{\prime}+\frac{{\sigma }_{c}}{{m}_{b}}s$$

(3d)

in which ${\sigma }_{1}^{\prime}$, ${\sigma }_{2}^{\prime}$ and ${\sigma }_{3}^{\prime}$ represent the effective major, intermediate, and minor principal stresses, respectively; ${m}_{b}$, $s$ and $a$ are three constants for rock mass; and ${\sigma }_{c}$ is the unconfined compressive strength of intact rock. The ${m}_{b}$, $s$ and $a$ can be related to GSI by (Hoek et al. 2002)

$${m}_{b}={m}_{i}\cdot \exp\left(\frac{{\text{GSI}}-100}{28-14D}\right)$$

(4a)

$$s=\exp\left(\frac{{\text{GSI}}-100}{9-3D}\right)$$

(4b)

$$a=\frac{1}{2}+\frac{1}{6}\left[\exp\left(-\frac{{\text{GSI}}}{15}\right)-\exp\left(-\frac{20}{3}\right)\right]$$

(4c)

in which $D$ is the disturbance factor representing the level of blast damage and stress relaxation to the rock mass.

To simplify the derivation, all the effective principal stresses are normalized by ${\sigma }_{c}$ as follows

$${\stackrel{\sim }{\sigma }}_{i}=\frac{{\sigma }_{i}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}};\quad i=\mathrm{1,2},3$$

(5)

Similarly, the newly modified GZZ criterion can be expressed in a dimensionless form as

$$f={\left(\sqrt{{\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}}\right)}^{1/a}+\frac{{m}_{b}}{2}\sqrt{{\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}}-\frac{{m}_{b}}{2}\sqrt{\frac{\left({\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-{\stackrel{\sim }{I}}_{3}^{*}\right)\left({\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}\right)}{{\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-{9\stackrel{\sim }{I}}_{3}^{*}}}$$

(6)

The potential function, $g$, controls the post-failure behavior of the rock mass. When $g=f$, the flow rule is associated; otherwise, the flow rule is unassociated. A detailed description of the potential function for the unassociated case is provided in “Appendix”.

2.3 Plastic Behavior of Rock Mass

The plastic strain increment is determined by (Lubliner 1990)

$${\dot{\varepsilon }}_{ij}^{p}=\lambda \frac{\partial g}{\partial {\sigma }_{ij}^{\prime}}$$

(7)

where $\lambda$ is the plastic multiplier and $\dot{\left(\right)}$ denotes the rate of a plastic strain; e.g., ${\dot{\varepsilon }}_{r}^{p}$ denotes the plastic strain rate in the radial direction. $\lambda$ can be determined based on the so-called consistency condition (Lubliner 1990), as detailed in Sect. 3.3.

2.4 Brittle Behavior of Rock

As shown in Fig. 1, the stress state of rock mass will degrade to its residual value once it reaches the initial yield function. For a criterion involving only two principal stresses such as the Mohr–Coulomb and Hoek–Brown criteria, the residual stress can be easily determined, because only the major effective principle stress degrades when the initial yield function is reached. However, for a 3D strength criterion, the deviatoric shear stress, q, which is a function of the three effective principal stresses, degrades. Therefore, to properly describe the brittle behavior related to the 3D strength criterion, two assumptions are made:

• 1. the minor effective principal stress does not change when the brittle behavior takes place, which is the same as that used for the brittle behavior of 2D strength criterion-based material (Sharan 2003, 2005; Park and Kim 2006);

• 2. both the major and intermediate effective principal stresses decrease when the brittle behavior takes place, and the relationship between the two stress components is determined by deformation condition, i.e., plane strain condition for the cylindrical cavity contraction problem (Wang et al. 2012; Zou et al. 2016; Singh et al 2019).

3 Proposed Solution to Cavity Contraction Problem

3.1 Cavity Contraction Problem

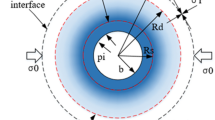
Figure 2 schematically shows a cylindrical cavity contraction problem in an infinite rock mass. The cavity (tunnel) with an initial radius of ${r}_{a0}$ in a rock mass is under initial effective stress equal to ${\sigma }_{0}^{\prime}$. When the effective cavity pressure ${\sigma }_{a}^{\prime}$ at the cavity wall decreases, the rock mass around the cavity will experience elastic deformation until the initial yielding occurs. If the cavity keeps on contracting, a plastic region will form around the cavity. The ${r}_{\mathrm{p}}$ in the figure refers to the radius of the elastic–plastic boundary (EPB), which is originally located at the radial location of ${r}_{\mathrm{p}0}$. Within the plastic zone, a so-called disturbed zone due to tunnel excavation and at a radius of $d\times {r}_{\mathrm{p}}$ ($0\le d\le 1$) is considered. During the contraction process, an arbitrary rock particle moves inward from its initial radial position ${r}_{x0}$ to the current radial position ${r}_{x}$ and the following equilibrium equation should be satisfied (Yu and Rowe 1999)

Fig. 2

Schematic diagram of cavity contraction problem

$$\frac{{\text{d}}{\sigma }_{\mathrm{r}}^{\prime}}{{\text{d}}r}+\frac{{\sigma }_{\mathrm{r}}^{\prime}-{\sigma }_{\uptheta }^{\prime}}{r}=0$$

(8)

where ${\sigma }_{\mathrm{r}}^{\prime}$ and ${\sigma }_{\uptheta }^{\prime}$ denote the effective radial and circumferential stresses, respectively.

To maintain consistency with the scaled criterion, the initial in situ stress and internal pressure are scaled as

$${\stackrel{\sim }{\sigma }}_{0}=\frac{{\sigma }_{0}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}$$

(9a)

$${\stackrel{\sim }{\sigma }}_{a}=\frac{{\sigma }_{a}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}$$

(9b)

Similarly, the Young’s modulus $E$, shear modulus $G$ and the radial distance are normalized as follows:

$$\stackrel{\sim }{E}=\frac{E}{{\sigma }_{c}}$$

(10a)

$$\stackrel{\sim }{G}=\frac{G}{{\sigma }_{c}}=\frac{E}{2{\sigma }_{c}\left(1+\nu \right)}$$

(10b)

$$\xi =\stackrel{\sim }{r}=\frac{r}{{r}_{p}}$$

(10c)

where $\xi$ is the dimensionless radial distance. In this way, the equilibrium Eq. (8) can be rewritten as

$$\frac{{\text{d}}{\stackrel{\sim }{\sigma }}_{r}}{{\text{d}}\xi }+\frac{{\stackrel{\sim }{\sigma }}_{r}-{\stackrel{\sim }{\sigma }}_{\theta }}{\xi }=0$$

(11)

3.2 Elastic Region Solution

Considering the boundary conditions of the far-field stresses, the radial, circumferential and out-of-plane stresses, and the radial displacement, at location r, can be derived as (Yu 2000):

$${\sigma }_{r}^{\prime}={\sigma }_{0}^{\prime}+\left({\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}\right){\left(\frac{{r}_{p}}{r}\right)}^{2}$$

(12a)

$${\sigma }_{\theta }^{\prime}={\sigma }_{0}^{\prime}-\left({\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}\right){\left(\frac{{r}_{p}}{r}\right)}^{2}$$

(12b)

$${\sigma }_{x}^{\prime}={\sigma }_{0}^{\prime}$$

(12c)

$${u}_{r}=\frac{{\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}}{2G}{r}_{p}\left(\frac{{r}_{p}}{r}\right)$$

(12d)

where ${\sigma }_{rp}^{\prime}$ is the radial stress at the EPB and ${\sigma }_{x}^{\prime}$ is the effective out-of-plane stress. So, the out-of-plane stress ${\sigma }_{x}^{\prime}$ remains constant during the elastic stage. If ${\sigma }_{a}^{\prime}$ is larger than ${\sigma }_{rp}^{\prime}$, no plastic region will occur; in this case, by substituting ${\sigma }_{rp}^{\prime}={\sigma }_{a}^{\prime}$ and ${r}_{p}={r}_{a}$ into Eq. (12), the solution for the whole region is determined. Equation (12) can also be expressed in a dimensionless form as

$${\stackrel{\sim }{\sigma }}_{r}={\stackrel{\sim }{\sigma }}_{0}+\left({\stackrel{\sim }{\sigma }}_{rp}-{\stackrel{\sim }{\sigma }}_{0}\right){\left(\frac{1}{\xi }\right)}^{2}$$

(13a)

$${\stackrel{\sim }{\sigma }}_{\theta }={\stackrel{\sim }{\sigma }}_{0}-\left({\stackrel{\sim }{\sigma }}_{rp}-{\stackrel{\sim }{\sigma }}_{0}\right){\left(\frac{1}{\xi }\right)}^{2}$$

(13b)

$${\stackrel{\sim }{\sigma }}_{x}={\stackrel{\sim }{\sigma }}_{0}$$

(13c)

$${\stackrel{\sim }{u}}_{r}=\frac{{\stackrel{\sim }{\sigma }}_{rp}-{\stackrel{\sim }{\sigma }}_{0}}{2\stackrel{\sim }{G}}\frac{1}{\xi }$$

(13d)

3.3 Plastic Region Solution

For the Hoek–Brown criterion-based solutions, the out-of-plane stress and strain are ignored due to the absence of the intermediate effective principal stress in the Hoek–Brown criterion. This problem can be addressed by adopting the newly modified GZZ criterion to describe the rock mass behavior. Since the deformation in the periphery of the cavity (tunnel) can be large, the large-strain theory is utilized to define the increment of the three strain components following Chadwick (1959):

$${\dot{\varepsilon }}_{r}=-\left[\dot{\mathrm{ln}\left(\frac{{\text{d}}r}{{\text{d}}{r}_{0}}\right)}\right]=-\left[\dot{\mathrm{ln}\left(\frac{{\text{d}}r}{{\text{d}}r-{\text{d}}{u}_{r}}\right)}\right]=-\frac{1}{1-\frac{{\text{d}}{u}_{r}}{{\text{d}}r}}\frac{{\text{d}}{\dot{u}}_{r}}{{\text{d}}r}=-\frac{1}{1-\frac{{\text{d}}{\stackrel{\sim }{u}}_{r}}{{\text{d}}\xi }}\frac{{\text{d}}{\dot{\stackrel{\sim }{u}}}_{r}}{{\text{d}}\xi }$$

(14a)

$${\dot{\varepsilon }}_{\theta }=-\dot{\left[\mathrm{ln}\left(\frac{r}{{r}_{0}}\right)\right]}=\dot{\left[\mathrm{ln}\left(1-\frac{{u}_{r}}{r}\right)\right]}=-\frac{1}{1-\frac{{u}_{r}}{r}}\frac{{\dot{u}}_{r}}{r}=-\frac{1}{1-\frac{{\stackrel{\sim }{u}}_{r}}{\xi }}\frac{{\dot{\stackrel{\sim }{u}}}_{r}}{\xi }$$

(14b)

$${\dot{\varepsilon }}_{x}=0$$

(14c)

It is noted that the $\frac{{\text{d}}{\sigma }_{\mathrm{r}}^{\prime}}{dr}$ in Eq. (8) denotes the derivation of ${\sigma }_{\mathrm{r}}^{\prime}$ with respect to the radial distance at a specific location, while $\dot{\left(\right)}$ in Eq. (14) describes the rate of strain and is evaluated by a time variable. Since the cavity contraction problem is self-similar (Carranza-Torres and Fairhurst 1999), Eqs. (8) and (14) can be converted to differential equations in terms of the same similar variable by some mathematical manipulations. Then, a series of differential equations with respect to the same variable can be established as the governing equations.

To evaluate the rate of strain, the normalized radius of the elastic–plastic boundary, ${R}_{0}$, a kinematic parameter defined by Detournay (1986), is adopted as the time variable

$${R}_{0}=\frac{{r}_{p}}{{r}_{a}}$$

(15)

Therefore, the rate of a mechanical quantity, such as stress, strain, and displacement, can be expressed as

$$\dot{\left(\right)}=\frac{\partial \left(\right)}{\partial {R}_{0}}$$

(16)

Note that the kinematic parameter, ${R}_{0}$, can also be expressed by the dimensionless distance $\xi$ as

$${R}_{0}=\frac{{r}_{p}}{{r}_{a}}=\frac{{r}_{p}}{r}\frac{r}{{r}_{a}}=\frac{r}{{r}_{a}}\frac{1}{\xi }$$

(17)

By using Eq. (17), both the partial derivation with respect to ${R}_{0}$ and $r$ can now be converted to the derivation with respect to $\xi$ via the chain rule as

$$\dot{\left(\right)}=\frac{\partial \left(\right)}{\partial {R}_{0}}=-\frac{\xi }{{R}_{0}}\frac{\partial \left(\right)}{\partial \xi }$$

(18a)

$$\frac{\partial \left(\right)}{\partial r}=\frac{1}{{{r}_{a}R}_{0}}\frac{\partial \left(\right)}{\partial \xi }$$

(18b)

Therefore, the dimensionless distance, $\xi$, can be taken as the similar variable to establish the governing equations for the cavity contraction problem. Specifically, the rates of radial displacement and stress components are

$${\dot{u}}_{r}=\frac{\partial {u}_{r}}{\partial {R}_{0}}=\frac{\partial \left({\stackrel{\sim }{u}}_{r}\frac{r}{\xi }\right)}{\partial {R}_{0}}=-\frac{\xi }{{R}_{0}}\frac{\partial \left({\stackrel{\sim }{u}}_{r}\frac{r}{\xi }\right)}{\partial \xi }=-{r}_{a}\xi \frac{\partial {\stackrel{\sim }{u}}_{r}}{\partial \xi }+{r}_{a}{\stackrel{\sim }{u}}_{r}$$

(19a)

$${\dot{\stackrel{\sim }{\sigma }}}_{i}=-\frac{\xi }{{R}_{0}}\frac{\partial {\stackrel{\sim }{\sigma }}_{i}}{\partial \xi };\quad i=r,\theta ,x$$

(19b)

Substituting Eq. (19a) back into Eq. (14), the rates of strain components can be rewritten as

$${\dot{\varepsilon }}_{r}={\dot{\varepsilon }}_{r}^{e}+{\dot{\varepsilon }}_{r}^{p}=-\frac{1}{1-\frac{{\text{d}}{\stackrel{\sim }{u}}_{r}}{{\text{d}}\xi }}\frac{{\text{d}}{\dot{\stackrel{\sim }{u}}}_{r}}{{\text{d}}\xi }=\frac{1}{1-\frac{{\text{d}}{\stackrel{\sim }{u}}_{r}}{{\text{d}}\xi }}\frac{\xi }{{R}_{0}}\frac{{\partial }^{2}{\stackrel{\sim }{u}}_{r}}{\partial {\xi }^{2}}$$

(20a)

$${\dot{\varepsilon }}_{\theta }={\dot{\varepsilon }}_{\theta }^{e}+{\dot{\varepsilon }}_{\theta }^{p}=\frac{1}{1-\frac{{\stackrel{\sim }{u}}_{r}}{\xi }}\left(-\frac{1}{{R}_{0}\xi }{\stackrel{\sim }{u}}_{r}+\frac{1}{{R}_{0}}\frac{\partial {\stackrel{\sim }{u}}_{r}}{\partial \xi }\right)$$

(20b)

$${\dot{\varepsilon }}_{x}={\dot{\varepsilon }}_{x}^{e}+{\dot{\varepsilon }}_{x}^{p}=0$$

(20c)

It should be noted that the plastic strain rates in different directions should obey the flow rule given in Eq. (7). And the so-called consistency condition should be satisfied for the stress state on the yield surface as (Lubliner 1990)

$$\dot{f}=\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{r}}{\dot{\stackrel{\sim }{\sigma }}}_{r}+\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\dot{\stackrel{\sim }{\sigma }}}_{\theta }+\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{x}}{\dot{\stackrel{\sim }{\sigma }}}_{x}=0$$

(21)

Considering Eq. (1), flow rule, Eq. (7), and the consistency condition, Eq. (21), one has

$${-\dot{\varepsilon }}_{r}+{A}_{3}{\dot{\varepsilon }}_{\theta }={A}_{4}{\dot{\stackrel{\sim }{\sigma }}}_{r}+{A}_{5}{\dot{\stackrel{\sim }{\sigma }}}_{\theta }$$

(22a)

$${\dot{\stackrel{\sim }{\sigma }}}_{x}=-\frac{2\stackrel{\sim }{G}\left(1+\nu \right)}{{A}_{2}\nu +1}{A}_{2}{\dot{\varepsilon }}_{\theta }+\frac{\nu -\nu {A}_{2}}{{A}_{2}\nu +1}{\dot{\stackrel{\sim }{\sigma }}}_{r}+\frac{\nu +{A}_{2}}{{A}_{2}\nu +1}{\dot{\stackrel{\sim }{\sigma }}}_{\theta }$$

(22b)

$${\dot{\stackrel{\sim }{\sigma }}}_{\theta }=-\frac{{A}_{6}}{{A}_{8}}{\dot{\varepsilon }}_{\theta }+\frac{{A}_{7}}{{A}_{8}}{\dot{\stackrel{\sim }{\sigma }}}_{r}$$

(22c)

$$\lambda =\frac{{\dot{\varepsilon }}_{\theta }-\left[{\dot{\stackrel{\sim }{\sigma }}}_{\theta }-\nu \left({\dot{\stackrel{\sim }{\sigma }}}_{r}+{\dot{\stackrel{\sim }{\sigma }}}_{x}\right)\right]/\stackrel{\sim }{E}}{\partial g/\partial {\stackrel{\sim }{\sigma }}_{\theta }}$$

(22d)

where

$${A}_{1}=\frac{\partial g/\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial g/\partial {\stackrel{\sim }{\sigma }}_{\theta }}$$

(23a)

$${A}_{2}=\frac{\partial g/\partial {\stackrel{\sim }{\sigma }}_{x}}{\partial g/\partial {\stackrel{\sim }{\sigma }}_{\theta }}$$

(23b)

$${A}_{3}={A}_{1}+\nu \frac{1-{A}_{1}}{{A}_{2}\nu +1}$$

(23c)

$${A}_{4}=\frac{1}{2\stackrel{\sim }{G}\left(1+\nu \right)}\left\{-\left(1+\nu {A}_{1}\right)+\frac{\nu -\nu {A}_{2}}{{A}_{2}\nu +1}\left(\nu -\nu {A}_{1}\right)\right\}$$

(23d)

$${A}_{5}=\frac{1}{2\stackrel{\sim }{G}\left(1+\nu \right)}\left\{\left(\nu +{A}_{1}\right)+\frac{\left({A}_{2}+\nu \right)}{{A}_{2}\nu +1}\left(\nu -\nu {A}_{1}\right)\right\}$$

(23e)

$${A}_{6}=-\frac{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{z}}}{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}}\frac{2\stackrel{\sim }{G}\left(1+\nu \right)}{{A}_{2}\nu +1}{A}_{2}$$

(23f)

$${A}_{7}=-\frac{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{r}}}{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}}-\frac{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{z}}}{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}}\frac{\nu -\nu {A}_{2}}{{A}_{2}\nu +1}$$

(23g)

$${A}_{8}=1+\frac{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{z}}}{\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}}\frac{\nu +{A}_{2}}{{A}_{2}\nu +1}$$

(23h)

Substituting Eq. (20) into Eq. (22a) yields

$$\frac{1}{1-\frac{d{\stackrel{\sim }{u}}_{r}}{d\xi }}\frac{{\partial }^{2}{\stackrel{\sim }{u}}_{r}}{\partial {\xi }^{2}}=\frac{{A}_{3}}{\xi }\frac{1}{1-\frac{{\stackrel{\sim }{u}}_{r}}{\xi }}\frac{\partial {\stackrel{\sim }{u}}_{r}}{\partial \xi }-{{A}_{3}\frac{1}{1-\frac{{\stackrel{\sim }{u}}_{r}}{\xi }}\frac{{\stackrel{\sim }{u}}_{r}}{{\xi }^{2}}+{A}_{4}}\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial \xi }+{A}_{5}\frac{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\partial \xi }$$

(24)

To reduce the order of the governing equation for displacement, Eq. (24) can be rewritten as:

$$\frac{\partial {y}_{1}}{\partial \xi }={A}_{3}{\frac{1-{y}_{1}}{\xi -{y}_{2}}{y}_{1}}-{{A}_{3}\frac{1-{y}_{1}}{\xi -{y}_{2}}\frac{{y}_{2}}{\xi }+{A}_{4}}(1-{y}_{1})\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial \xi }+{A}_{5}(1-{y}_{1})\frac{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\partial \xi }$$

(25a)

$$\frac{\partial {y}_{2}}{\partial \xi }={y}_{1}$$

(25b)

$${y}_{1}=\frac{\partial {\stackrel{\sim }{u}}_{r}}{\partial \xi };\,\,{y}_{2}={\stackrel{\sim }{u}}_{r}$$

(25c)

And the governing equations for the three stress components can be determined by recasting the equilibrium Eqs. (11) and (22) as:

$$\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial \xi }=-\frac{{{\stackrel{\sim }{\sigma }}_{r}-\stackrel{\sim }{\sigma }}_{\theta }}{\xi }$$

(26a)

$$\frac{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\partial \xi }=\frac{{A}_{6}}{{A}_{8}}\frac{1}{\xi -{y}_{2}}\left({y}_{1}-\frac{{y}_{2}}{\xi }\right)+\frac{{A}_{7}}{{A}_{8}}\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial \xi }$$

(26b)

$$\frac{\partial {\stackrel{\sim }{\sigma }}_{x}}{\partial \xi }=\frac{2\stackrel{\sim }{G}\left(1+\nu \right)}{{A}_{2}\nu +1}\frac{{A}_{2}}{\xi -{y}_{2}}\left({y}_{1}-\frac{{y}_{2}}{\xi }\right)+\frac{\nu -\nu {A}_{2}}{{A}_{2}\nu +1}\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial \xi }+\frac{\nu +{A}_{2}}{{A}_{2}\nu +1}\frac{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\partial \xi }$$

(26c)

Now, the governing equations with respect to the similar variable $\xi$ for the cylindrical cavity contraction problem in the plastic zone are established as Eqs. (25) and (26). It should be noted that the governing equations are established with the general form of the yield function $f$ and the potential function $g$ and thus can be seen as the generalized formation for different 3D criteria-based cylindrical contraction solutions. Details about the derivation of the yield and potential functions are given in Appendix. The governing equations have been solved as an initial problem by using MATLAB. Since the rock mass in the plastic zone first experiences elastic deformation before yielding and then elastic–plastic deformation during contraction of the cavity (tunnel), the stress and displacement at the EPB are taken as the initial conditions for the governing equations in the plastic zone. As for the plastic zone, the parameters of the rock mass within and outside the disturbed zone are different due to the excavation effect, and stress degradation also takes place at the disturbed zone boundary (DZB). An iterative algorithm is proposed to calculate the residual stresses at the DZB, as detailed later.

3.4 Elastic–Plastic Boundary Conditions

As discussed earlier, the stress and displacement conditions at the EPB should be taken as the initial values for the governing equations in the plastic zone. Also, both the elastic and plastic solutions should be applicable at the EPB. For a poor-quality rock mass, an elastic–perfectly plastic model can be used and, in this case, all the stress components should be continuous at the EPB. Therefore,

$${y}_{1}\left(1\right)=\frac{\partial {\stackrel{\sim }{u}}_{rp}}{\partial \xi }=-\frac{{\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}}{2G}$$

(27a)

$${y}_{2}\left(1\right)={\stackrel{\sim }{u}}_{rp}=\frac{{\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}}{2G}$$

(27b)

$${\stackrel{\sim }{\sigma }}_{rp}=\frac{{\sigma }_{rp}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}$$

(27c)

$${\stackrel{\sim }{\sigma }}_{\theta p}=\frac{{\sigma }_{\theta p}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}=\frac{2{\sigma }_{0}^{\prime}-{\sigma }_{rp}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}$$

(27d)

$${\stackrel{\sim }{\sigma }}_{xp}=\frac{{\sigma }_{0}^{\prime}+\frac{s{\sigma }_{c}}{{m}_{b}}}{{\sigma }_{c}}$$

(27e)

where ${\sigma }_{rp}^{\prime}$ can be obtained using a Newton’s method-based algorithm as shown in Fig. 3a.

Fig. 3

a Newton’s method-based algorithm for determination of radial stress and b bisection method-based algorithm for determination of residual circumferential stress at elastic–plastic boundary

However, a good-quality rock mass may experience a significant strength degradation after yielding as shown in Fig. 1. As stated in Sect. 2.4, only the radial stress (the minor effective principal stress) and displacement would be continuous at the EPB. Both the circumferential stress and the out-of-plane stress reduce to their residual values according to the plane strain condition (Wang et al. 2012; Zou et al. 2016; Singh et al 2019)

$$\Delta {\varepsilon }_{z}=\frac{1}{E}\left[{\sigma }_{xpr}^{\prime}-\nu \left({\sigma }_{rp}^{\prime}+{\sigma }_{\theta pr}^{\prime}\right)-\left(1-2\nu \right){\sigma }_{0}^{\prime}\right]=0$$

(28)

or

$${\sigma }_{xpr}^{\prime}= \nu \left({\sigma }_{rp}^{\prime}+{\sigma }_{\theta pr}^{\prime}\right)+\left(1-2\nu \right){\sigma }_{0}^{\prime}$$

(29)

Therefore, the residual yield function can be seen as a function with only one variable, ${\sigma }_{\theta pr}^{\prime}$. A bisection method-based algorithm is proposed to determine ${\sigma }_{\theta pr}^{\prime}$ as shown in Fig. 3b. Finally, the obtained ${\sigma }_{\theta pr}^{\prime}$ and ${\sigma }_{xpr}^{\prime}$ can be used to replace the ${\sigma }_{\theta p}^{\prime}$ and ${\sigma }_{xp}^{\prime}$ in Eq. (27) to determine the EPB of the elastic–brittle–plastic response.

3.5 Disturbed Zone Boundary Conditions

Within the disturbed zone, the disturbance factor D is in the range of (0, 1], and outside the disturbed zone, D = 0. Hence, stress degradation also takes place at the disturbed zone boundary (DZB). In this case, by replacing ${\sigma }_{rp}^{\prime}$, ${\sigma }_{\theta p}^{\prime}$ and ${\sigma }_{xp}^{\prime}$ in Eq. (28) with the initial stresses ${\sigma }_{rB}^{\prime}$, ${\sigma }_{\theta B}^{\prime}$ and ${\sigma }_{xB}^{\prime}$ at the DZB, the residual stresses ${\sigma }_{rBr}^{\prime}$, ${\sigma }_{\theta Br}^{\prime}$ and ${\sigma }_{xBr}^{\prime}$ at the DZB can be determined following the same procedure as shown in Fig. 3b. However, the initial stresses and the normalized displacement ${\xi }_{B}$ at the DZB cannot be explicitly expressed due to the complex stress–displacement relation within the plastic zone. Therefore, an iterative algorithm as shown in Fig. 4 is proposed for the case when the plastic zone contains a disturbed zone with d < 1.

Fig. 4

Flow chart for solving plastic region with consideration of disturbed zone

3.6 Rock Mass Parameters in Elastic, Plastic and Disturbed Zones

The rock mass parameters in the various zones (elastic, plastic and disturbed) are different due to the excavation disturbance and the brittle behavior considered in the study. To be clear, Table 1 summarizes the parameters in each zone for both poor-quality and good-quality rock masses. With the GSI and D in Table 1, other rock mass parameters can be determined by using Eq. (4). For poor-quality rock masses, GSI is a constant for the whole region, while GSI_i and GSI_r are defined separately for the good-quality rock masses. Hence, the poor-quality rock mass can be regarded as an elastic–perfectly plastic material, while good-quality rock masses exhibit brittle properties.

Table 1 Rock mass properties for different zones

4 Validation of Proposed Solution

To validate the proposed solution for both elastic–perfectly plastic (EPP) and elastic–brittle–plastic (EBP) rock masses, a cylindrical cavity (tunnel) contraction problem studied by Carranza-Torres and Fairhurst (1999) is analyzed. The tunnel has a diameter of 10 m and is buried 400 m deep in a rock mass. Table 2 summarizes the rock mass properties for the EPP and EBP models, respectively, for both the proposed solution and numerical simulations. The numerical simulation was conducted using finite-difference code FLAC3D with a user-defined constitutive model based on the newly modified GZZ criterion (Chen et al. 2020). Figure 5 shows the quarter model used for the numerical simulation. The model consists of 3600 elements with increasing size away from the tunnel. The symmetric boundaries are restricted in the normal direction, while the displacement of the far-field boundary is set as zero. In the numerical simulation, the initial stress state is first applied throughout the domain, and then the tunnel is excavated.

Table 2 Rock mass properties for verification

Fig. 5

FLAC3D model of a tunnel problem

Figure 6 presents the comparison between the numerical results, the analytical solution based on the Hoek–Brown criterion from Carranza-Torres and Fairhurst (1999) and the proposed solution for the cylindrical cavity contraction problem with the EPP model, all considering the small-strain condition to keep consistency with Carranza-Torres and Fairhurst (1999). As can be seen, the proposed solution is in good agreement with the numerical results, which verifies the correctness of the proposed solution. A careful inspection of the proposed solution and that based on the Hoek–Brown criterion reveals the slight difference in the magnitude of radial displacements and the range of the plastic zone between those two solutions. Specifically, the proposed solution gives slightly smaller radial displacement but slightly higher circumferential stress than the Hoek–Brown criterion-based solution. This is because of the ignorance of the out-of-plane stress and the adoption of the infinitesimal strain theory in the Hoek–Brown criterion-based solution.

Fig. 6

Comparison proposed analytical solution, Hoek–Brown criterion-based solution, and numerical results from FLAC3D with elastic–perfectly plastic model: a distribution of normalized stress components and b distribution of normalized radial displacement around a tunnel in a rock mass with GSI = 50, D = 0, and at small-strain condition

Figure 7 compares the numerical results and the proposed solution for the cavity contraction problem with the EBP model at the large-strain condition. Again, the proposed solution is in good agreement with the numerical results regarding both stresses and radial displacements.

Fig. 7

Comparison of the proposed analytical solution and numerical results from FLAC3D with elastic–brittle–plastic model: a distribution of normalized stress components and b distribution of normalized radial displacement around a tunnel in a rock mass with GSI = 50, D = 0, and at large-strain condition

5 Applications

To demonstrate the applications of the proposed solution, it is applied to analyze two tunnels, one in a poor-quality rock mass and the other in a good-quality rock mass. The two application examples also systematically study the effect of main factors on the tunneling-induced ground response.

5.1 Tunnel in Poor-Quality Rock Mass

Following Carranza-Torres and Fairhurst (1999), a 10-m-radius tunnel in a poor-quality rock mass at 400 m below the ground surface, with in situ stress of 10 MPa, is analyzed. The related rock mass parameters are summarized in Table 3. For the poor-quality rock mass, the GSI value is assumed to be constant during the excavation process. The size of the disturbed zone where the disturbance factor D is assigned is affected by the specific tunneling method and often roughly estimated (Hoek et al. 2002). For instance, Hedayat and Weems (2019) assumed a disturbed zone to be half of the plastic region. In this study, to be general, the size of the disturbed zone is described by the disturbed zone radius to plastic zone radius ratio (d) as shown in Fig. 2. The effects of rock properties, disturbance factor D (representing the effect of construction), large strain, flow rule and ratio d are systematically studied. For the case with an unassociated flow rule, a dilation angle of 0° is used.

Table 3 Tunnel geometry and rock mass parameters (case 1)

5.1.1 Effect of GSI

Figure 8 compares the predicted stress and radial displacement distributions around the tunnel in poor-quality rock mass with different GSI values, D = 0, d = 1, using both associated and unassociated flow rules, and considering both small-strain and large-strain conditions. As GSI increases, the radial stress is larger in both the plastic and elastic zones but the circumferential stress is larger in the plastic zone and slightly larger close to the EPB and smaller in the elastic zone. As for the out-of-plane stress, it is larger in the plastic zone and remains the same in the elastic zone when GSI is larger. As expected, at a higher GSI, both the plastic zone size and the radial displacement are smaller. The flow rules show no influence on the distribution of stresses, while the radial displacement within the plastic zone is much smaller when the unassociated flow rule is applied. The adoption of small strain or large stain does not affect the stress distribution results, but the small-strain solution predicts slightly larger radial displacement. The difference between the small-strain and large-strain solutions regarding the radial displacement increases with smaller GSI or larger total displacement.

Fig. 8

Distribution of a stresses and b radial displacement around tunnel in poor-quality rock mass with different GSI values, D = 0 and d = 1

Figure 9 plots the normalized wall radial displacement and EPB location versus the normalized cavity pressure for a tunnel in poor-quality rock mass with different GSI values, D = 0, d = 1, using both associated and unassociated flow rules, and considering large-strain condition. This figure can be used to estimate both the extent of the plastic zone and the convergence of a tunnel at different equivalent support pressures denoted by the normalized cavity pressure and thus can serve as a design chart for tunnel engineers. Due to the smaller deformation modulus and lower strength, the tunnel convergence in a rock mass with smaller GSI increases much more remarkably with the decrease in the cavity pressure. To control the tunnel convergence, stronger support is needed for a tunnel in a poor-quality rock mass with smaller GSI. The size of the plastic zone increases when the GSI is smaller or the cavity pressure is lower. The wall radial displacement under the associated flow rule is much larger than that under the unassociated flow rule, but the flow rule does not affect the size of the plastic zone.

Fig. 9

a Wall radial displacement and b elastic–plastic boundary radius versus cavity pressure in poor-quality rock mass with different GSI values, D = 0, d = 1, and at large-strain condition

5.1.2 Effect of Disturbance Factor

To explore the effect of disturbance factor D on the tunneling-induced ground response, the tunnels in a rock mass with GSI = 50, different D values, and d = 1 are analyzed using both associated and unassociated rules and considering both small-strain and large-strain conditions. Figure 10 shows the distribution of the three normalized stress components, ${\sigma}'_{r}/{\sigma}'_{0}$, ${\sigma}'_{\theta}/{\sigma}'_{0}$ and ${\sigma}'_{x}/{\sigma}'_{0}$, and the normalized radial displacement ${u}_{r}/{r}_{a0}$ versus the normalized radial distance from the tunnel wall $r/{r}_{a}$. As clearly seen from Fig. 10a, when D increases, the plastic zone becomes larger. At a higher D, the radial stress decreases in both the plastic and elastic zones, while the circumferential stress decreases in the plastic zone and increases within the elastic zone. As for the out-of-plane stress, it decreases in the plastic zone and keeps constant within the elastic zone when D increases. It needs to be noted that the stresses at the specific EPB locations do not change with D. As for the radial displacement, as shown in Fig. 10b, it increases significantly, especially in the plastic zone, when D increases (i.e., poorer excavation method). The radial wall displacement (at $r/{r}_{a}$ = 0) more than doubles when D goes from 0 to 0.8. As expected, the stress distributions of the associated and unassociated cases are the same, while the radial displacement is much larger when the associated flow rule is applied. Hence, using a proper flow rule should be given particular attention in the analysis and design of a tunnel. Again, the adoption of small strain or large strain does not affect the stress distribution results, but the small-strain solution gives slightly larger radial displacement as expected. The difference between the small-strain and large-strain solutions regarding the radial displacement increases with larger D or larger total displacement.

Fig. 10

Distribution of a stresses and b radial displacement around tunnel in poor-quality rock mass with GSI = 50, different disturbance factor D values and d = 1

Figure 11 depicts the normalized wall radial displacement and EPB location versus the normalized cavity pressure for a tunnel in poor-quality rock mass with GSI = 50, different D values d = 1, using both associated and unassociated rules, and considering large-strain condition. When the cavity pressure (i.e., the tunnel support) is high enough, ${\sigma}'_{a}/{\sigma}'_{0} >0.279$ in this case, no plastic zone is formed and the disturbance factor has no effect on the wall radial displacement because the disturbance factor is only assigned in the plastic zone. However, if the cavity pressure is not high enough and the plastic zone forms, a larger disturbance factor D (or poorer excavation method) increases the wall radial displacement and the effect of D becomes more significant at a smaller cavity pressure. This again confirms the importance of sufficient cavity pressure (or tunnel support). On the other hand, as expected, the flow rule does not affect the linear elastic segment of the wall radial displacement curve but adopting the associated flow rule results in much larger wall radial displacement within the plastic zone as shown in Fig. 11a. When the cavity pressure is small, ${\sigma}'_{a}/{\sigma}'_{0} <0.279$ in this case, the plastic zone is formed and the size of the plastic zone increases with lower cavity pressure or larger disturbance factor D (or poorer excavation method), as shown in Fig. 11b. Again, the flow rule has no effect on the size of the plastic zone.

Fig. 11

a Wall radial displacement and b elastic–plastic boundary radius versus cavity pressure in poor-quality rock mass with GSI = 50, different disturbance factor D, d = 1, and at large-strain condition

5.1.3 Effect of Disturbed Zone Size

Figure 12 shows the distribution of stresses and radial displacement around a tunnel in a poor-quality rock mass with GSI = 50, D = 0.8, different disturbed zone sizes represented by the disturbed zone radius/plastic zone radius ratio (d), using both associated and unassociated rules, and considering large-strain condition. As d increases, the plastic zone expands, and the stresses remain the same in the disturbed zone and decrease within the undisturbed plastic zone. In the elastic zone, the radial stress decreases, the circumferential stress increases and the out-of-plane stress remains the same with increasing d. As expected, the radial displacement increases with a higher ratio d for both associated and unassociated cases.

Fig. 12

Distribution of a stresses and b radial displacement around tunnel in poor-quality rock mass with GSI = 50, D = 0.8, different disturbed zone radius/plastic zone radius ratio d values, and at large-strain condition

5.2 Tunnel in Good-Quality Rock Mass

Following Alejano et al. (2009), a 14-m-diameter tunnel excavated at a depth of 1000 m in a good-quality rock mass is analyzed in this section. Besides using the initial GSI = 64.9 considered by Alejano et al. (2009), two other initial GSI values of 55 and 75 are also used to study the effect of the initial GSI. Considering the residual strength of the same rock mass with different initial GSI values to be identical, GSI_r = 27.8 is assigned to all the three cases considered. The dilation angle for the unassociated case is assumed to be 0°. Three disturbed zone sizes represented by the disturbed zone radius/plastic zone radius ratio d are considered in the analysis. The properties of the rock mass and tunnel are summarized in Table 4. In the following, only the results at large-strain condition are presented because the difference between small and large-strain solutions is almost negligible for good-quality rock masses.

Table 4 Tunnel geometry and rock mass parameters (case 2)

5.2.1 Effect of Initial GSI

Figure 13 shows the distribution of normalized stresses and normalized radial displacement around the tunnel with different initial GSI values, D = 0, d = 1, using both associated and unassociated flow rules, and considering large-strain condition. The effect of the initial GSI on the stresses and radial displacement is similar to that in the poor-quality rock mass case shown in Fig. 8, but the size of plastic zone and the radial displacement are both smaller and the circumferential stress at the EPB is higher due to the higher strength of the rock mass. As for the flow rule, just like the case in the poor-quality rock mass, it only affects the radial displacement within the plastic zone, with the associated flow rule giving much larger radial displacement than the unassociated flow rule.

Fig. 13

Distribution of a stresses and b radial displacement around tunnel in good-quality rock mass with different GSI_i values and D = 0, d = 1, and at large-strain condition

Figure 14 shows the normalized wall radial displacement and EPB location versus the normalized cavity pressure in good-quality rock mass with different initial GSI values, D = 0, d = 1, using both associated and unassociated flow rules, and considering the large-strain condition. The trend is very similar to that in the poor-quality rock mass case shown in Fig. 9, except the cavity pressure at which the plastic zone starts to form, the size of the plastic zone and the wall radial displacement (tunnel convergence) are all much smaller due to the good quality of rock mass.

Fig. 14

a Wall radial displacement and b elastic–plastic boundary radius versus cavity pressure in good-quality rock mass with different GSI_i values, D = 0, d = 1, and at large-strain condition

5.2.2 Effect of Disturbance Factor

Figure 15 illustrates the normalized stress distributions and normalized radial displacement around the tunnel with different D values, d = 1, using both associated and unassociated rules, and considering large-strain condition. All the cases are analyzed with the initial GSI = 75. The effect of the disturbance factor D and flow rule on the stresses and radial displacement is similar to that in the poor-quality rock mass case shown in Fig. 10. However, due to the good quality of the rock mass, the size of the plastic zone and the radial displacement are both much smaller.

Fig. 15

Distribution of a stresses and b radial displacement around tunnel in good-quality rock mass with GSI_i = 75, different disturbance factor D, d = 1 and at large-strain condition

Figure 16 shows the normalized wall radial displacement and EPB location versus the normalized cavity pressure for a tunnel in good-quality rock mass with the initial GSI = 75, different disturbance factor D values, d = 1, using both associated and unassociated rules, and considering large-strain condition. The trend is very similar to that in the poor-quality rock mass case shown in Fig. 11. The major difference is that, due to the good quality of rock mass, at the cavity pressure at which the plastic zone starts to form, the size of the plastic zone and the wall radial displacement (tunnel convergence) are all much smaller.

Fig. 16

a Wall radial displacement and b elastic–plastic boundary radius versus cavity pressure in good-quality rock mass with GSI_i = 75, different disturbance factor D, d = 1 and at large-strain condition

5.2.3 Effect of Disturbed Zone Size

Figure 17 shows the distribution of normalized stresses and radial displacement around the tunnel with GSI_i= 75, D = 0.8, different d values, using both associated and unassociated flow rules, and considering the large-strain condition. The effect of the disturbed zone size represented by d is very similar to that in Fig. 12 for poor-quality rock mass. However, due to the higher strength of good-quality rock mass, the size of the plastic zone and the radial displacement value are both much smaller and the effect of the disturbed zone is smaller compared with that for the poor-quality rock mass.

Fig. 17

Distribution of a stresses and b radial displacement around tunnel in good-quality rock mass with GSI_i = 75, D = 0.8, different disturbed zone radius/plastic zone radius ratios d and at large-strain condition

6 Conclusion

A new analytical solution for deep circular tunnels in rock is developed by using the newly modified GZZ criterion and considering the effects of disturbed zone, 3D strength and large strain of the rock mass around the tunnel. The proposed solution is validated by comparing it with the numerical results obtained from simulations using finite-difference code FLAC3D. Finally, extensive parametric studies are performed by using the proposed solution to analyze tunnels in both poor-quality and good-quality rock masses. The following conclusions can be drawn based on the study:

• 1. Ignoring the intermediate principal stress could overpredict the plastic zone and the radial displacement of the ground.

• 2. While the flow rule does not affect the stress distribution and the size of the plastic zone, the radial displacement predicted using the associated flow rule could be much larger than that using the unassociated flow rule with a dilation angle of ${0}^{^\circ }$. Hence, it is important to use a proper flow rule in the analysis and design of a tunnel.

• 3. The GSI, disturbance factor D (related to construction method) and disturbed zone radius/plastic zone radius ratio d all have significant effects on the stress distribution, the size of the plastic zone and the radial displacement. It is therefore important to determine the right GSI, D and d for the analysis and design of a tunnel.

• 4. The cavity pressure (tunnel support) has a significant effect on the size of the plastic zone and the radial displacement when the cavity pressure is smaller than the one at which the plastic zone starts to form. The cavity pressure at which the plastic zone starts to form is closely related to the rock mass quality; the one for a good-quality rock mass could be much smaller than that for a poor-quality rock mass.

Appendix

1.1 Derivatives of Yield Function and Potential Function

For the consistency condition, Eq. (21), the derivatives in the three directions can be given as

$$\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{i}}=\frac{\partial f}{\partial {\stackrel{\sim }{I}}_{1}^{*}}+\frac{\partial f}{\partial {\stackrel{\sim }{I}}_{2}^{*}}\left({\stackrel{\sim }{I}}_{1}^{*}-{\stackrel{\sim }{\sigma }}_{i}\right)+\frac{\partial f}{\partial {\stackrel{\sim }{I}}_{3}^{*}}\frac{{\stackrel{\sim }{I}}_{3}^{*}}{{\stackrel{\sim }{\sigma }}_{i}};\quad i=r,\theta ,x$$

(30)

where

$$\frac{{\partial f}}{{\partial \tilde{I}_{1}^{*} }} = \frac{{m_{b} \tilde{I}_{1}^{*} }}{{2\sqrt {\tilde{I}_{1}^{{*2}} - 3v_{2}^{*} } }} - \frac{{m_{b} \left( {\tilde{I}_{1}^{{*3}} \tilde{I}_{2}^{{*2}} - 14\tilde{I}_{1}^{{*2}} \tilde{I}_{2}^{*} \tilde{I}_{3}^{*} + 9\tilde{I}_{1}^{*} \tilde{I}_{3}^{{*2}} + 12\tilde{I}_{2}^{{*2}} \tilde{I}_{3}^{*} } \right)}}{{4\left( {\tilde{I}_{1}^{*} \tilde{I}_{2}^{*} - 9\tilde{I}_{3}^{*} } \right)^{2} \tilde{\sigma }_{m}^{*} }} + \frac{{\tilde{I}_{1}^{*} }}{{a\left( {\tilde{I}_{1}^{{*2}} - 3\tilde{I}_{2}^{*} } \right)^{{1 - \frac{1}{{ {2a}}}}} }}$$

(31)

$$\frac{\partial f}{\partial {\stackrel{\sim }{I}}_{2}^{*}}=-\frac{3{m}_{b}}{4\sqrt{{\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}}}+\frac{{m}_{b}\left(8{\stackrel{\sim }{I}}_{1}^{*3}{\stackrel{\sim }{I}}_{3}^{*}+3{\stackrel{\sim }{I}}_{1}^{*2}{\stackrel{\sim }{I}}_{2}^{*2}-54{\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}{\stackrel{\sim }{I}}_{3}^{*}+27{\stackrel{\sim }{I}}_{3}^{*2}\right)}{8{\left({\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-9{\stackrel{\sim }{I}}_{3}^{*}\right)}^{2}{\stackrel{\sim }{\sigma }}_{m}^{*}} +\frac{3}{2a{\left({\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}\right)}^{1-\frac{1}{2a}}}$$

(32)

$$\frac{\partial f}{\partial {\stackrel{\sim }{I}}_{3}^{*}}=\frac{2{m}_{b}{\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}\left(-{\stackrel{\sim }{I}}_{1}^{*2}+3{\stackrel{\sim }{I}}_{2}^{*}\right)}{2{\left({\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-9{\stackrel{\sim }{I}}_{3}^{*}\right)}^{2}{\stackrel{\sim }{\sigma }}_{m}^{*}}$$

(33)

$${\stackrel{\sim }{\sigma }}_{m}^{*}=\sqrt{\frac{\left({\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-{\stackrel{\sim }{I}}_{3}^{*}\right)\left({\stackrel{\sim }{I}}_{1}^{*2}-3{\stackrel{\sim }{I}}_{2}^{*}\right)}{{\stackrel{\sim }{I}}_{1}^{*}{\stackrel{\sim }{I}}_{2}^{*}-{9\stackrel{\sim }{I}}_{3}^{*}}}$$

(34)

According to the flow rule, the plastic strain rate in the three directions can be given as

$${\dot{\varepsilon }}_{r}^{p}=\lambda \frac{\partial g}{\partial {\sigma }_{r}}=\lambda \frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{r}}\frac{\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial {\sigma }_{r}}=\lambda \frac{1}{{\sigma }_{c}}\frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{r}}$$

(35)

$${\dot{\varepsilon }}_{\theta }^{p}=\lambda \frac{\partial g}{\partial {\sigma }_{\theta }}=\lambda \frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}\frac{\partial {\stackrel{\sim }{\sigma }}_{\theta }}{\partial {\sigma }_{\theta }}=\lambda \frac{1}{{\sigma }_{c}}\frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{\theta }}$$

(36)

$${\dot{\varepsilon }}_{x}^{p}=\lambda \frac{\partial g}{\partial {\sigma }_{x}}=\lambda \frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{x}}\frac{\partial {\stackrel{\sim }{\sigma }}_{x}}{\partial {\sigma }_{x}}=\lambda \frac{1}{{\sigma }_{c}}\frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{x}}$$

(37)

For associated flow rule

$$\frac{\partial g}{\partial {\stackrel{\sim }{\sigma }}_{i}}=\frac{\partial f}{\partial {\stackrel{\sim }{\sigma }}_{i}};\quad i=r,\theta ,x$$

(38)

while for unassociated flow rule with a dilation angle, one has

$$\frac{\partial g/\partial {\stackrel{\sim }{\sigma }}_{r}}{\partial g/\partial {\stackrel{\sim }{\sigma }}_{\theta }}=-\frac{1-\mathrm{sin}\varPsi }{1+\mathrm{sin}\varPsi }$$

(39)

where $\varPsi$ is the dilation angle.

1.2 Equations for Iterative Algorithms

For the cylindrical cavity contraction problem, the yield function in terms of ${\sigma }_{rp}$ can be simplified as

$$f\left({\sigma }_{rp}^{\prime}\right)=\frac{1}{{\sigma }_{c}^{\left(1/a-1\right)}}{\left[\sqrt{3}\left({\sigma }_{0}^{\prime}-{\sigma }_{rp}^{\prime}\right)\right]}^{1/a}+\frac{\sqrt{3}{m}_{b}}{2}\left({\sigma }_{0}^{\prime}-{\sigma }_{rp}^{\prime}\right)-\frac{{m}_{b}}{2}\sqrt{4{\sigma }_{0}^{2}-{\left({\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}\right)}^{2}}$$

(40)

The corresponding derivation of yield function $f$ with respect to ${\sigma }_{rp}^{\prime}$ is

$${f}^{\prime}\left({\sigma }_{rp}^{\prime}\right)=-\frac{{3}^{\frac{1}{\left(2a\right)}}}{a{\sigma }_{c}^{\left(1/a-1\right)}}{\left({\sigma }_{0}^{\prime}-{\sigma }_{rp}^{\prime}\right)}^{1/a-1}-\frac{\sqrt{3}{m}_{b}}{2}+\frac{{m}_{b}}{2}\frac{{\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}}{\sqrt{4{\sigma }_{0}^{\prime2}-{\left({\sigma }_{rp}^{\prime}-{\sigma }_{0}^{\prime}\right)}^{2}}}$$

(41)