Introduction

Background

Climate change has posed a significant threat to the ecological environment and public health since the advent of global industrialization. Controlling greenhouse gas emissions is a critical component in addressing climate change issues under the framework of the Kyoto Protocol. Following the Protocol, the carbon trading market emerged and it was considered a new strategy to lower greenhouse gas, particularly carbon dioxide emissions. The core of the carbon trading market is the carbon pricing mechanisms. The volatility of carbon prices could release policy signals and restrict the actions of those industries that generate plenty of carbon dioxide (Lu et al. 2020). In response, many countries and regions have regarded carbon pricing mechanisms as a shift to a sustainable development pathway (Wara 2007; Zhang and Zhang 2019; Boyce 2018). Carbon pricing mechanisms differ across countries and regions. The European Union Emissions Trading System (EU ETS) is one of the world’s largest carbon pricing mechanisms (Convery 2009). It covers specific carbon-emitting industries in the 28 European Union member states as well as in Norway, Iceland, and Liechtenstein, which are part of the European Economic Area. The California Cap-and-Trade Program is the first carbon emissions trading system in the USA. It was implemented in 2013 and covers multiple carbon-emitting industries (Cushing et al. 2018). Starting from 2013, China has successively launched carbon emission quota trading pilots in seven cities, including Beijing, Shanghai, Hubei, Shenzhen, Tianjin, Chongqing, and Guangdong. On July 16, 2021, China’s carbon emission trading market was officially launched for the further carbon-constrained goal. The market has a total of 2162 key emitting units in the power generation industry, covering approximately 4.5 billion tons of carbon dioxide emissions. In 2022, the total trading volume of Chinese Emission Allowances (CEA) reached 50.88 million tons in the market. Until now, it has become the world’s largest carbon market. Implementing a low-carbon development strategy and advancing the construction of a carbon market are important measures for China to address climate change (Zhang et al. 2019; Liu et al. 2020). Research on carbon price prediction is favorable in achieving the transformation to a low-carbon economy, managing enterprise risk, and stabilizing the development of the carbon market. Besides, this research is also crucial in supporting decisions regarding carbon trading. Therefore, exploring methods to predict China’s carbon prices is particularly significant (Ji et al. 2018; Xu et al. 2020; Hao and Tian 2020; Huang and He 2020).

Previous literature

Carbon price prediction models typically relied on traditional statistical models during their initial development. For example, various types of generalized autoregressive conditional heteroskedasticity (GARCH) models have been utilized to forecast carbon prices (Paolella and Taschini 2008; Benz and Trück 2009; Byun and Cho 2013). Based on moving average (ARIMA) and least squares support vector machine (LSSVM), a combined model was carried out for carbon price prediction (Zhu and Wei 2013). Chevallier and Sévi (2011) applied a simplified HAR-RV model for carbon price prediction. Previous studies of carbon price forecasting have observed that these traditional methods could be implemented effectively and reliably. However, the carbon price data has been shown for its nonlinear and unstable characteristics, which suggests the traditional statistical models are powerless to handle the current carbon price prediction of the market (Zhu et al. 2019).

To better deal with the nonlinearity and unstability issues of sequence data, machine learning and deep learning methods have been utilized for data prediction. Fan et al. (2015) forecasted the carbon price trend by multi-layers perceptron (MLP) neural network. Sun and Zhang (2018) used extreme learning machine (ELM) and back-propagation (BP) network to estimate the EU carbon price. Ji et al. (2019) analyzed and predicted the carbon price by ARIMA-CNN-LSTM models. Compared to traditional statistical methods, many recent studies carried out in the machine learning and deep learning methods could more accurately handle nonlinear problems.

In order to enhance prediction performance, a combination of data decomposition and machine learning or deep learning models, known as hybrid models, has been increasingly utilized for forecasting problems. Decomposing the raw data sequence can effectively improve the data’s stability and reduce the impact of noise on the prediction results. Zhu (2012) used an artificial neural network (ANN) model combined with the empirical mode decomposition (EMD) method for carbon price prediction. Its prediction accuracy exceeded that of single ANN. Huang et al. (2021) enhanced the performance of carbon price prediction by incorporating the variational mode decomposition (VMD) into the GARCH and long short-term memory (LSTM) network. Zhou et al. (2019) performed a complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) with the XGBoost model to make the crude oil price prediction. As data decomposition can effectively reduce prediction difficulty, hybrid models conducted by previous research demonstrate better prediction performance.

To reduce data complexity and improve prediction accuracy, Li et al. (2021) proposed a secondary decomposition (re-decomposition) method. Sun and Huang (2020) proposed the EMD-VMD method with BP neural network for prediction. Zhou et al. (2022a) attempted to use CEEMDAN-VMD as a decomposition method and integrated it with LSTM to forecast carbon pricing, resulting in improved accuracy. Evidence from several studies identified the benefits of re-decomposition algorithm for carbon price prediction.

The re-decomposition method has shown its superiority in carbon price prediction for markets with relatively stable prices, such as Tianjin and Hubei ETS. The performance of these models fell short of expectations when it came to the more intricate carbon prices of the Beijing ETS, which experienced more substantial fluctuations. To better predict high-complexity data, we represent a multiple decomposition prediction model entitled multi-decomposition-XGBoost. Multiple decompositions refer to combining the results of the first and second decompositions based on sample entropy and then performing another round of decomposition. The following describes the innovation and contribution of this research:

  1. (1)

    Proposing the multi-decomposition algorithm to further mitigate the effects of data nonlinearity and irregularity on forecasting performance. And the multi-decomposition is a combination of VMD and CEEMDAN.

  2. (2)

    The sample entropy was used as the selection criterion for decomposing the data, and the decomposed results were recombined before further decomposition.

  3. (3)

    Proposing a hybrid model called multi-decomposition-XGBoost by combining multi-decomposition algorithm and XGBoost model. The model is validated and assessed utilizing data from Beijing and Hubei carbon market. RMSE, MAE, MAPE, Diebold-Mariano (D-M) test (Harvey et al. 1997), and time are the five indicators used to assess the model’s performance.

The remaining sections of this work are organized as follows: “Methods” describes the methodologies and theoretical foundation of the models conducted in this research. “Empirical examination” presents the data selection and the composition of the hybrid model. Besides, it carries out verification, analysis, and comparison of different models. The experimental findings are outlined in “Conclusion and discussion” along with potential areas for future research.

Methods

Complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN)

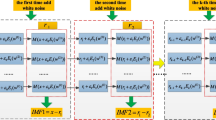
Torres et al. (2011) introduced CEEMDAN, which stands for full ensemble empirical mode decomposition with adaptive noise, as an advanced signal processing technique. It allows the dissection of a complex signal into multiple intrinsic mode functions (IMFs). The decomposition process is achieved through a combination of the empirical mode decomposition (EMD) (Wu and Huang 2009) and the ensemble EMD (EEMD) (Huang et al. 1998). The fundamental approach employed by CEEMDAN involves introducing small amounts of white noise to the original signal and subsequently performing EMD on each noisy signal. The IMFs derived from each noisy signal are then combined to form the complete ensemble IMFs, which serve as a representation of the original signal.

The significant benefit of CEEMDAN is its capability to resolve the mode mixing issue, which is prevalent in conventional EMD. This issue arises when IMFs derived through EMD contain more than one intrinsic mode, causing imprecise outcomes. By the addition of minimal units of noise to the original signal, CEEMDAN guarantees that each IMF has only one intrinsic mode, resulting in enhanced results in signal analysis and processing applications. The concrete steps of CEEMDAN are outlined below:

The initial data is noted as F(t). \({\overline{\mathrm{IMF}}}_{\mathrm{j}}\) refers to the jth IMF derived through CEEMDAN. Gaussian white noise with \(\mathcal{N}\left(0,1\right)\) is noted as ωi(t). rj(t) represents jth residue. Let \({\overline{\mathrm{EM}D}}_j\left(\cdot \right)\) be the jth IMF obtained from EMD decomposition. All above variables are long vector sequence. White noise standard deviation is noted as εj.

  1. (1)

    The first decomposition is performed using Fi(t)(i = 1, 2, 3, …, n). The definition of Fi(t) is given in formula (1-1), in which i denotes the ith noise, t denotes time point and n denotes ensemble size.

    $${F}^i(t)=\mathrm{F}(t)+{\upvarepsilon}_0{\upomega}^i(t),\mathrm{i}=1,2,3,\ldots, \mathrm{n}.$$
    (1-1)
  2. (2)

    \(\mathrm{IM}{F}_j^i(t)\left(i=1,2,3,\ldots, n\right)\) represents jth IMF that Fi(t) decomposed by EMD. Then, the first IMF obtained by CEEMDAN \({\overline{\mathrm{IMF}}}_1(t)\) can be calculated by formula (1-2).

    $${\overline{\mathrm{IMF}}}_1(t)=\frac{1}{n}{\sum}_{i=1}^n\mathrm{IM}{\mathrm{F}}_1^i(t)=\frac{1}{n}{\overline{\mathrm{EMD}}}_1\left({F}^i(t)\right).$$
    (1-2)
  3. (3)

    The first residue r1(t) can be found in formula (1-3).

    $${r}_1(t)=F(t)-\overline{\mathrm{IM}{\mathrm{F}}_1}(t).$$
    (1-3)
  4. (4)

    The first IMF that ωi(t) decomposed by EMD, \({\overline{\mathrm{EMD}}}_1\left({\omega}^i(t)\right)\), with ε1 are combined to form the adaptive noise. Then adding it to the first residue r1(t) can get a new sequence. Thereafter, decomposing this sequence by EMD again and then calculating the second IMF decomposed by CEEMDAN \({\overline{\mathrm{IMF}}}_2(t)\) via formula (1-4).

    $${\overline{\text{IMF}}}_2(t)=\frac1n\sum\limits_{i=1}^n{\overline{\text{EMD}}}_1\left(r_1(t)+\varepsilon_1{\overline{\text{EMD}}}_1\left(\omega^i(t)\right)\right).$$
    (1-4)
  5. (5)

    The jth IMF decomposed by CEEMDAN \({\overline{\mathrm{IMF}}}_j(t)\left(j=2,3,\ldots, J\right)\) can be calculated by formula (1–5). J means the total amount of IMFs obtained by CEEMDAN.

    $${\overline{\mathrm{IMF}}}_j(t)=\frac{1}{n}\sum\limits_{\mathrm{i}=1}^{\mathrm{n}}{\overline{\mathrm{EMD}}}_1\left({r}_{j-1}(t)+{\upvarepsilon}_{j-1}{\overline{\mathrm{EMD}}}_{j-1}\left({\upomega}^i(t)\right)\right).$$
    (1-5)
  6. (6)

    Next, jth residue rj(t)(j = 2, 3, …, J) be calculated by formula (1-6).

    $${r}_j(t)={\mathrm{r}}_{\mathrm{j}-1}(t)-{\overline{\mathrm{IMF}}}_j(t).$$
    (1-6)
  7. (7)

    Repeat step 5 and step 6 for next k until the residue unable to be decomposed anymore and does not possess a minimum of two extrema. The last residue is noted as R(t). Ultimately, the final decomposition result for initial data F(t) is expressed in formula (1-7).

    $$\text{F}(t)=\sum\limits_{j=1}^J{\overline{\text{IMF}}}_j(t)+R(t).$$
    (1-7)

Variational mode decomposition (VMD)

Dragomiretskiy and Zosso (2014) presented the variational mode decomposition (VMD) algorithm as a novel approach for signal analysis. The term of VMD involves breaking down a signal into its intrinsic modes using a variational method. The approach is based on the perspective that a signal can be decomposed into basic functions or modes and that these modes can be improved by minimizing a cost function. This cost function represents the discrepancy between the original signal and its approximation. VMD blends the concepts of EMD and sparse representation. It offers a more robust and dependable mode decomposition approach in comparison to conventional EMD or CEEMDAN. The concrete steps of VMD are outlined below:

The initial data is noted as F(t). The finite bandwidth is defined as uk(k = 1, 2, …, K). K represents the total amount of IMFs obtained by VMD. And instantaneous frequency is noted as ωk. The variational model with the corresponding constraints can be calculated by formula (2-1). And the width of frequency spectrum for each IMF is shown in formula (2-2).

$$\underset{\left\{{u}_k\right\},\left\{{\omega}_k\right\}}{\min}\left\{{\sum}_k{\left\Vert {\partial}_t\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast {u}_k(t)\right]{e}^{-j{\omega}_kt}\right\Vert}_2^2\right\},$$
(2-1)
$$s.t.\sum\limits_{k=1}^Ku_k(t)=F(t).$$
(2-2)

The constraint concern can be simplified into a more solvable unconstrained problem by incorporating a penalty term α and a Lagrange multiplier λ. Afterwards, the augmented Lagrange expression is derived in formula (2-3).

$$\mathrm{L}\left(\left\{{u}_k\right\},\left\{{\upomega}_k\right\},\uplambda \right)=\upalpha \sum\limits_k{\left\Vert {\partial}_t\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast {u}_k(t)\right]{e}^{-j{\omega}_kt}\right\Vert}_2^2+{\left\Vert F(t)-\sum\limits_k{u}_k(t)\right\Vert}_2^2+\left\langle \uplambda (t),F(t)-\sum\limits_k{u}_k(t)\right\rangle .$$
(2-3)

Then, utilizing the alternative direction multiplier approach to calculate the saddle point:

$${\hat{u}}_k^{n+1}\left(\upomega \right)=\frac{\hat{F}\left(\omega \right)-\sum_{i\ne k}{\hat{u}}_i\left(\omega \right)+\hat{\lambda}\left(\omega \right)/2}{1+2\upalpha {\left(\upomega -{\upomega}_k\right)}^2},$$
(2-4)
$${\hat{\uplambda}}^{n+1}\left(\upomega \right)={\hat{\uplambda}}^n\left(\upomega \right)+\uptau \left(\hat{F}\left(\upomega \right)-\sum\limits_k{\hat{u}}_k^{n+1}\left(\upomega \right)\right),$$
(2-5)

where \({\hat{u}}_k^{n+1}\left(\upomega \right)\), \(\hat{F}\left(\upomega \right)\), and \(\hat{\uplambda}\left(\upomega \right)\) respectively indicate Fourier transform of \({u}_k^{n+1}(t)\), F(t), and λ(t). And τ represents the tolerance of noise. Similarly, the method for updating the center frequency is shown in formula (2-6).

$${\hat{\upomega}}_k^{n+1}=\frac{\int_0^{\infty}\upomega {\left|{\hat{u}}_k^{n+1}\left(\upomega \right)\right|}^2d\upomega}{\int_0^{\infty }{\left|{\hat{u}}_k^{n+1}\left(\upomega \right)\right|}^2d\upomega}.$$
(2-6)

Sample entropy

Richman and Moorman (2000) presented sample entropy as a mathematical measure of the complexity and unpredictability of a time series. It is computed by comparing the similarity between patterns in a time series. Typically, it is used to analyze physiological signals and financial time series. The concrete steps of sample entropy are outlined below:

The tolerance is noted as r and m indicates the length of the compared time series. The number of data points in time series is referred to as N. Let A(m, r, N) be the number of matches, which is calculated in formula (3-1). Besides, the number of self-matches is defined as B(m, r, N), which is shown in formula (3-2).

$$A\left(m,r,N\right)=\sum\limits_{i=1}^{N-m}\left[\max\left|x_{i+j}-x_i\right|\leq r\right],j=1,2,\ldots,m.$$
(3-1)
$$B\left(m,r,N\right)=\sum\limits_{i=1}^{N-m+1}\left[\max\left|x_{i+j}-x_i\right|\leq r\right],j=1,2,\ldots,m-1.$$
(3-2)

Ultimately, the expressions for Sample Entropy, SampEn(m, r, N), is listed in formula (3-3).

$$\mathrm{SampEn}\left(m,r,N\right)=-\ln \frac{A\left(m,r,N\right)}{B\left(m,r,N\right)}.$$
(3-3)

XGBoost algorithm

XGBoost, proposed by Chen and Guestrin (2016), is a gradient boosting algorithm for machine learning. It is an enhanced version of the gradient boosting decision tree (GBDT) algorithm. XGBoost is a model that is formed by combining multiple decision trees. The core of the training process involves continuously adding trees, where each new tree is constructed based on the residuals of the previous tree. It trains data by fitting weak decision trees and obtains the combined prediction result by weighted majority voting. Compared to traditional GBDT algorithms, XGBoost achieves enhanced data fitting by performing a second-order Taylor expansion on the loss function. Additionally, it incorporates L1 regularization (lasso) and L2 regularization (ridge) into the model to avoid overfitting issues. The principle of XGBoost is outlined below:

Let ℂ = {(xi, yi)} be the initial data with m examples and n features, where |C| = n, xi ∈ ℝn and yi ∈ ℝ. \(\mathcal{F}\) indicates the space of the classification and regression tree. XGBoost predicts by adding K functions:

$$\left\{\begin{array}{l}{\hat{y}}_i=\phi \left({x}_i\right)=\sum\limits_{k=1}^K{f}_k\left({x}_i\right),{f}_k\in \mathcal{F},\\ {}\mathcal{F}=\left\{{f}_k\left({x}_i\right)={\omega}_{q(x)}\right\},q:\mathbb{R}\to T,\omega \in {\mathbb{R}}^T.\end{array}\right.$$
(4-1)

In formula (4-1), q is defined as structure of each tree, T means the total leaves inside the tree. ω indicates the weights of leaves. fk(xi) represents the result of kth tree.

In XGBoost, for regression tasks, each tree is added to the model sequentially, thus enhancing the performance of the model. The newly generated tree must match the previous prediction’s residuals, and the jth tree’s iteration process is shown as follows:

$${\hat{y}}_i^j={\hat{y}}_i^{j-1}+{f}_j\left({x}_i\right),{\hat{y}}_i^0=0.$$
(4-2)

XGBoost avoids overfitting by incorporating regularization terms into the objective function. The formula (4-3) displays the regularization term, in which γ and ω are the control coefficients.

$$\Omega \left({f}_j\right)=\upgamma T+\frac{1}{2}\uplambda {\left\Vert \omega \right\Vert}^2.$$
(4-3)

Then, we can calculate the objective function as below:

$${\mathcal{L}}_{obj}^{(j)}=\sum\limits_{i=1}^ml\left({\hat{y}}_i^{(j)},{y}_i\right)+\Omega \left({f}_j\right)=\sum\limits_{i=1}^ml\left({\hat{y}}_i^{\left(j-1\right)}+{f}_j\left({x}_i\right),{y}_i\right)+\Omega \left({f}_j\right).$$
(4-4)

In order to enhance the model, fj(xi) can approximately be expanded using a second-order Taylor expansion. The improved objective function formula (4-5) as follows:

$${\mathcal{L}}_{\mathrm{obj}}^{(j)}\approx \sum\limits_{i=1}^m\left[l\left({\hat{y}}_i^{\left(j-1\right)},{y}_i\right)+{\textsf{g}}_i{f}_j\left({x}_i\right)+\frac{1}{2}{h}_i{f}_j^2\left({x}_i\right)\right]+\Omega \left({f}_j\right),$$
(4-5)

where first-order gradient statistics \({\mathrm{g}}_i={\partial}_{{\hat{y}}_i^{\left(j-1\right)}}l\left({\hat{y}}_i^{\left(j-1\right)},{y}_i\right)\) and second-order gradient statistics \({h}_i={\partial}_{{\hat{y}}_i^{\left(j-1\right)}}^2l\left({\hat{y}}_i^{\left(j-1\right)},{y}_i\right)\). As first (j − 1) trees’ residuals have a small impact on the objective function, equation (4-5) can be simplified as follows:

$${\overline{\mathcal{L}}}_{\mathrm{obj}}^{(j)}=\sum\limits_{i=1}^m\left[{\textsf{g}}_i{f}_j\left({x}_i\right)+\frac{1}{2}{h}_i{f}_j^2\left({x}_i\right)\right]+\Omega \left({f}_j\right).$$
(4-6)

Then, substituting equation (4-3) into equation (4-6) results in formula (4-7).

$${\overline{\mathcal{L}}}_{obj}^{(j)}=\sum\limits_{i=1}^m\left[{\mathrm{g}}_i{f}_j\left({x}_i\right)+\frac{1}{2}{h}_i{f}_j^2\left({x}_i\right)\right]+\upgamma T+\frac{1}{2}\uplambda \sum\limits_{\mathrm{k}=1}^{\mathrm{T}}{\upomega}_{\mathrm{k}}^2.$$
(4-7)

Afterwards, the optimum weight \({\upomega}_k^{\ast }\) can be calculated as below:

$${\upomega}_k^{\ast }=-\frac{\sum_{i\in {I}_k}{\mathrm{g}}_i}{\sum_{i\in {I}_k}{h}_i+\uplambda},$$
(4-8)

where Ik is donated to the set of leaf k. Lastly, the optimum objective function is shown as follows:

$${\overline{\mathcal{L}}}_{\mathrm{obj}}=-\frac{1}{2}\sum\limits_{k=1}^T\frac{{\left({\sum}_{i\in {I}_k}{\mathrm{g}}_i\right)}^2}{\sum_{i\in {I}_k}{h}_i+\uplambda}+\upgamma T.$$
(4-9)

Empirical examination

Data collection

Since China’s carbon trading pilot projects were carried out in October 2011, Beijing ETS and Hubei ETS have large business volume. As of December 20,2022, the business volume for Beijing ETS and Hubei ETS are up to 10.49 billion Yuan and 20.03 billion Yuan, thereby their carbon prices are representative. This paper selects Beijing and Hubei carbon price data set as sample (collected from http://www.tanjiaoyi.com/). The summary of data set is shown in Table 1. Compared to the relatively stable price curve in Hubei ETS, the price curve in Beijing fluctuates more significantly. In this case, it is worthwhile to establish an accurate price prediction model that can be utilized for expansion and implementation in other carbon markets. In other words, we employed multi-decomposition for denoising and XGBoost for effectively predicting carbon prices for Beijing and Hubei ETS. All the decomposition results are normalized by min-max scaling before being predicted by the XGBoost model.

Table 1 The summary of data set
Full size table

Empirical analyses

In order to verifying the validity of the multi-decomposition with XGBoost model, this section constructs 4 comparative experiments.

Individual models

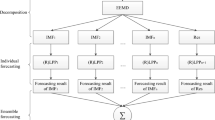
Figure 1 compares the prediction results for each individual model without using decomposition method. Individual models cover single XGBoost, LightGBM, random forests (RF), deep neural networks (DNN), ARIMA and THETA. Besides, XGBoost, LightGBM, RF, and DNN using K-folder cross-validation method to increase prediction precision. Table 2 presents the predictive performance comparison results for single models, RMSE, MAE, MAPE, and D-M test results are listed.

Fig. 1
figure 1

Beijing carbon price prediction outcomes from individual models

Full size image
Table 2 Prediction comparison of individual models
Full size table

According to the comparison results, the single XGBoost outperforms other individual models. RMSE, MAE, and MAPE for single XGBoost are 3.085, 2.615, and 2.815%. The outcomes reveal that these three evaluation criteria scored in XGBoost are optimal in this comparison respectively. The D-M test results of single DNN, AIRMA, and THETA are negative, which proves that these three models may be better than XGBoost. Compared with XGBoost, RMSE for DNN decreases by 5.099%, MAE decreases by 4.860%, and MAPE decreases by 4.629%. RMSE for ARIMA decreases by 12.089%, MAE decreases by 11.127%, and MAPE decreases by 10.643%. The RMSE value of the THETA model decreases by 4.333%, the MAE value decreases by 6.244%, and the MAPE value decreases by 7.964%. Therefore, the XGBoost shows superior predictive performance compared to other models.

Decomposition methods with XGBoost model

To improve the predictive performance, CEEMDAN and VMD methods are used to decompose the carbon price sequence. Different decomposition methods caused different predictive performances. Table 3 present the details of prediction comparison between CEEMDAN-XGBoost, VMD-XGBoost, and single XGBoost model.

Table 3 Prediction comparison of single XGBoost and decomposition methods
Full size table

Figure 2 CEEMDAN part displays that CEEMDAN divides original data into 6 IMF components and a residual component. From IMF 1 to IMF 6, the frequency and complexity of the CEEMDAN outcomes decrease. As the order of magnitude of this residual is only 1e-14, it can be ignored while making prediction and will not decrease the predictive performance. Likewise, VMD also divide original data into 6 IMF components. Raw data and VMD decomposition components IMF 1 to IMF 6 are shown in Fig. 2 VMD part. The results of the VMD decomposition increase in frequency and complexity from IMF 1 to IMF 6. The sample entropy for each IMF shown in Fig. 2. The complexity of the sequence increases with sample entropy value, making sequence prediction harder. The ultimate result is achieved by summing up the predictions for each IMF obtained from the decomposition.

Fig. 2
figure 2

CEEMDAN and VMD decomposition and sample entropy results

Full size image

After analyzing the RMSE, MAE, MAPE, and D-M test results in Table 3, CEEMDAN-XGBoost model performed better than single XGBoost and VMD-XGBoost model. The RMSE, MAE, and MAPE for VMD-XGBoost are 2.478, 2.089, and 2.260%. Compared with XGBoost, RMSE decreased 19.691%, MAE decreased 20.133% and MAPE value decreased 19.716%. Meanwhile, the RMSE, MAE, and MAPE for CEEMDAN-XGBoost are 2.697, 2.036, and 2.258%. Compared with XGBoost, RMSE decreased 12.590%, MAE decreased 22.141%, and MAPE decreased 19.787%. All these evaluation criteria performed much better than the single XGBoost model. The D-M test results of CEEMDAN-XGBoost and VMD-XGBoost are negative. The value of MAE, MAPE, and D-M test for CEEMDAN-XGBoost model get highest score in these three models. Considering the findings, CEEMDAN-XGBoost model has better predictive performance.

Figure 3 shows the price prediction results and the original price for each IMFs. According to this figure, IMF1 is almost unpredictable, with a considerable discrepancy between the forecasted and actual data and high sample entropy value of 1.12. The predictive performance of IMF2 and IMF3 is relatively good. Simultaneously, IMF4, IMF5, and IMF6 have a robust predictive performance and accurately reflect changes in the price trend. The discrepancy between the expected and actual data is minimal.

Fig. 3
figure 3

Price prediction results for each decomposition IMF

Full size image

Re-decomposition-XGBoost model

The objective of the re-decomposition is to reduce the complexity of the IMFs obtained from the initial decomposition even more. In the “Re-decomposition-XGBoost model,” the predictive performance of IMF1 was poor. To improve its predictive performance, IMF1 needs further decomposition. As CEEMDAN is derived from EMD decomposition, using a similar approach for further decomposition of IMF1 will not yield good results. Therefore, using VMD as a method for further decomposition is a good choice. In this scenario, the decomposition number is compared between 4 and 6 with all other settings set to default.

Figure 4 shows the re-decomposition results for IMF1 by using CEEMDAN. IMF1-1 to IMF1-6 refer to each component obtained by re-decomposing IMF1. The first IMF1-1 after re-decomposition of IMF1 is essentially the same as the original data. Its sample entropy value is nearly identical to the initial value, and the complexity of the data has not been reduced. Meanwhile, the values of the other IMFs are small and have little impact on the predictive performance. Therefore, using the same decomposition method during re-decomposition does not effectively improve the predictive performance. However, the re-decomposition results of VMD are entirely different. The data curves obtained through VMD re-decomposition are smooth and have low complexity. As demonstrated in Fig. 4, the sample entropy value of each VMD decomposed IMFs are significantly lower than that of IMF1. As a result, employing VMD to decompose IMF1 can make data prediction easier while also enhancing model performance. Predict each of the IMF1-1 to IMF1-4 or IMF1-6 obtained from the re-decomposition, and the remaining IMF2 to IMF6, using the XGBoost model. The ultimate prediction result is calculated by adding up the outcomes of each IMF's predictions.

Fig. 4
figure 4

Re-decomposition results for IMF1 by CEEMDAN and sample entropy comparison

Full size image

Table 4 shows forecasting results for different re-decomposition methods. Recall VMD4 presents the decomposition number for VMD is 4. A similar definition is for VMD6 which appears in the following part. RMSE, MAE, MAPE, D-M test, and time value for CEEMDAN-VMD6-XGBoost model are 2.694, 2.015, 2.211%, −3.672, and 418.292 according to Table 4. Compared with CEEMDAN-XGBoost, the value of RMSE just decreased 0.107%, MAE decreased 1.048%, and MAPE value decreased 2.075%. Therefore, using VMD with 6 decomposition IMFs has little effect on performance improvement. RMSE, MAE, MAPE, and time values for the CEEMDAN-VMD4-XGBoost model demonstrate superior performance compared to other models, with values of 2.534, 1.985, 2.195%, and 346.328, respectively. Compared with CEEMDAN-XGBoost, RMSE decreased 6.077%, MAE decreased 2.521%, and MAPE decreased 2.790%. The D-M test value is up to −6.461. The prediction accuracy is improved when IMF1 is replaced with 4 IMFs obtained through VMD decomposition. The D-M test value indicates that the forecasting results of CEEMDAN-VMD4-XGBoost and CEEMDAN-VMD6-XGBoost are closer to the actual values compared to CEEMDAN-XGBoost model. Figure 5 shows the price prediction results and the original price for each decomposition and re-decomposition IMF.

Table 4 Prediction comparison of decomposition and re-decomposition methods
Full size table
Fig. 5
figure 5

Prediction results for each decomposition and re-decomposition IMF

Full size image

Multi-decomposition-XGBoost model without integration

Multi-decomposition means further decomposition for re-decomposed IMFs, which is attempted to increase the prediction’s accuracy. As shown in Fig. 5, the forecasting result of IMF1-4 still has a large gap with the original data. Since IMF1-4 is obtained by VMD, CEEMDAN is selected as the method for further decomposition. Therefore, we use CEEMDAN-VMD-CEEMDAN as the specific method for multi-decomposition. IMF1-4 is decomposed into 6 IMFs, namely IMF1-4-1 to IMF1-4-6, and 1 residual. This residual can be ignored as its magnitude is only 1e-15. We use XGBoost model to predict IMF1-4-1 to IMF1-4-6 obtain from CEEMDAN multi-decomposition, IMF1-1 to IMF1-3 from VMD re-decomposition, and IMF2 to IMF6 from the first CEEMDAN decomposition separately. The ultimate multi-decomposition prediction result is obtained by summing up all the prediction outcomes.

But still, this method’s gain in prediction performance is insignificant. RMSE, MAE, MAPE, and D-M test values for this model (No integration) are 2.471, 1.849, 2.150%, and −0.527, respectively, according to Table 5. The D-M value is near to 0, indicating that the improvement in effect is not readily apparent. Compared with model CEEMDAN-VMD4-XGBoost, the value of RMSE just decreased 2.478%, MAE decreased 6.843%, and MAPE value decreased 2.045%. However, the model’s running time increased by approximately 100 s.

Table 5 Prediction results for multi-decomposition methods
Full size table

Multi-decomposition-XGBoost model with integration

Given that a third consecutive decomposition does not significantly enhance the prediction performance and requires additional resources, this section focuses on integrating IMFs before multi-decomposing. This section selects IMFs with higher sample entropy for integration to form the corresponding Co-IMF, as IMFs with higher sample entropy has a greater prediction difficulty. CEEMDAN decomposition of integrated Co-IMF results in different decomposition components, namely Co-IMF1 to Co-IMFn. Table 5 shows the prediction performance obtained from different combinations of Co-IMFs. Co-IMFs (1) presents the integration of IMF1-4 and IMF3. Co-IMFs (2) presents the integration of IMF1-4, IMF3 and IMF4. Co-IMFs (3) presents the integration of IMF1-4, IMF2, IMF3 and IMF4. The flowchart for this model is shown in Fig. 6. Co-IMFs (4) presents the integration of IMF1-3, IMF1-4, IMF2, IMF3, and IMF4. Co-IMF1 to Co-IMF4 and the remaining IMFs from the previous two decompositions are predicted using the XGBoost model. By summing up all of the prediction outcomes, this model’s ultimate prediction result is obtained.

Fig. 6
figure 6

Multi-decomposition-XGBoost flowchart for Co-IMFs (3)

Full size image

Figure 7 presents the improvement comparation results for multi-decomposition. The scores for the Co-IMFs (1) model’s RMSE, MAE, MAPE, and D-M test are 2.314, 1.793, 1.980%, and −3.876. Compared with the re-decomposition model CEEMDAN-VMD4-XGBoost, the RMSE, MAE, and MAPE reduced 8.671%, 9.692%, and 9.830% respectively. For Co-IMFs (2), the RMSE, MAE, MAPE, and D-M values are 2.164, 1.778, 1.950%, and −4.464. RMSE falls by 14.584%, MAE decreases by 10.452%, and MAPE decreases by 11.169% compared to the CEEMDAN-VMD4-XGBoost. For Co-IMFs (3) model, the four indicators are 2.146, 1.450, 1.608%, and −8.989, respectively. The improvement comparation results for RMSE, MAE, and MAPE are up to 15.289%, 26.938%, and 26.755%. For Co-IMFs (4) model, the value of RMSE, MAE, MAPE, and D-M test are 2.426, 1.974, 2.176%, and 0.916. The improvement comparison results for RMSE, MAE, and MAPE are up to 15.289%, 26.938%, and 26.755%. Compared with model CEEMDAN-VMD4, the value of RMSE merely decreased 4.233%, MAE merely decreased 0.585%, and MAPE merely decreased 0.897%.

Fig. 7
figure 7

Improvement comparation results for multi-decomposition

Full size image

Based on the comparison results, the multi-decomposition showed improved accuracy in prediction compared to the re-decomposition. Furthermore, the improvement in accuracy obtained by using multi-decomposition with integration based on sample entropy was much greater than that obtained by directly using multi-decomposition without integration.

By employing multi-decomposition with appropriate integration, the selected IMFs can be transformed into new IMFs. These new IMFs exhibit lower sample entropy values compared to the original IMFs, making them easier to predict. Table 6 displays the sample entropy values of the IMFs before integration (IMF2, IMF3, IMF4, and IMF1-4) and after multi-decomposition (Co-IMF1 to Co-IMF4) in the Co-IMFs (3) model. The sample entropy values for IMF2, IMF3, IMF4, and IMF1-4 are 0.388, 0.582, 0.454, and 0.471, respectively. After multi-decomposition with integration, the sample entropy values for the new set of four IMFs decrease to 0.316, 0.449, 0.288, and 0.006. Clearly, for the Co-IMFs (3) model, the application of multi-decomposition with integration allows the original four IMFs to be transformed into four IMFs with lower complexity, thereby reducing the difficulty of prediction.

Table 6 Sample entropy values of the IMFs before integration and after multi-decomposition in the Co-IMFs (3) model
Full size table

However, not all multi-decomposition with integration can produce good results. The combination of Co-IMFs results in different prediction performance. For example, Co-IMFs (3) improved the RMSE, MAE, and MAPE by 15.289%, 26.938%, and 26.755% respectively, compared to the CEEMDAN-VMD4-XGBoost model. Each IMF included in this model is depicted in Fig. 8(a). However, Co-IMFs (4) only improved these three indicators by 4.233%, 0.585%, and 0.897%, respectively. Co-IMFs (3) model costs 349.209 s, which is an increase of less than 1% compared to the re-decomposition model. This is because the Co-IMFs (3) model has the same total number of IMFs as the re-decomposition model. Therefore, the Co-IMFs (3) model provides the most precise forecast of all models, and it does not require additional resources to achieve this level of precision. Figure 8(b) presents the prediction results for each decomposition XGBoost model. As a result, using this method requires selecting an appropriate combination of Co-IMFs to achieve better prediction performance.

Fig. 8
figure 8

Prediction results for Co-IMFs (3) model and other decomposition models

Full size image

Validation of Hubei carbon market

This research utilizes data from the Hubei carbon market to further validate the predictive performance of multi-decomposition-XGBoost model in other carbon markets. The summary of Hubei carbon price data set is shown in Table 1.

Table 7 reveals that the multi-decomposition-XGBoost model demonstrates superior prediction performance compared to other models. Compared to the CEEMDAN-VMD6-XGBoost (re-decomposition) model, the multi-decomposition-XGBoost model exhibits a decrease in RMSE from 0.916 to 0.748, a reduction in MAE from 0.784 to 0.505, and a significant decline in MAPE from 2.727 to 1.745%. The model achieved better predictive performance compared to the re-decomposition model, while also reducing the time required by approximately 73 s. The multi-decomposition-XGBoost model recombines the six IMF components obtained from the decomposition and further applies CEEMDAN decomposition to obtain four new IMFs. With a decreasing total number of IMFs, the model requires less time for processing. Therefore, it remains applicable in other carbon markets as well.

Table 7 Prediction performance for Hubei carbon market
Full size table

Conclusion and discussion

This research offers the multi-decomposition-XGBoost model for predicting carbon price. This model employs a novel decomposition strategy called multi-decomposition, which involves recombining the results of the first and second decomposition based on sample entropy and then performing a further round of decomposition. Afterwards, the XGBoost model was employed for carbon price prediction. We could arrive at the following findings by contrasting the new hybrid model with others:

  1. (1)

    The Co-IMFs (3) multi-decomposition-XGBoost model presented in Table 5 performs the best among all the models in Beijing carbon market. Its results for RMSE, MAE, MAPE, and time are 2.146, 1.450, 1.608%, and 349.209, respectively. For the multi-decomposition-XGBoost model in Hubei carbon price prediction, the RMSE is 0.748, the MAE is 0.505, the MAPE is 1.745%, and the time value is 462.521.

  2. (2)

    The utilization of multi-decomposition with appropriate integration after re-decomposition does not significantly increase the computational time of the model. In the case of Beijing carbon price prediction, the optimal multi-decomposition model only experiences an increase in computational time of less than 1%. While in Hubei carbon price prediction, the optimal multi-decomposition model even reduces the computational time by approximately 73 s.

  3. (3)

    The multi-decomposition approach with integration based on sample entropy greatly enhances the precision of carbon price prediction. After combining multi-decomposition algorithm, XGBoost model in Beijing carbon market achieved a decrease in RMSE, MAE, and MAPE by 30.437%, 44.543%, and 42.895%. And in Hubei carbon market, the RMSE, MAE, and MAPE decreased by 28.504%, 39.356%, and 39.394%.

  4. (4)

    The integration based on sample entropy can improve the prediction performance, but it requires finding a proper integration approach. Otherwise, the improvement effect of this method is insignificant.

The multi-decomposition-XGBoost model used in this paper performs well in predicting the fluctuation of carbon price in Beijing and Hubei. However, the findings are subject to several limitations. With regard to the decomposition part, we used the classical methods of VMD and CEEMDAN. In future research, it may be worthwhile to explore updated decomposition methods, such as empirical Fourier decomposition, proposed by Zhou et al. (2022b). Regarding the recombination of decomposition results, we used sample entropy as the criterion. Considerably, more work will need to be explored on an alternative criterion for recombining the decomposition, such as permutation entropy. Ruiz-Aguilar et al. (2021) employed a model based on permutation entropy for wind speed prediction. In addition, more research is required to account for hybrid models composed of multiple deep learning or machine learning models that have gained attention recently (Li et al. 2020; Hassan et al. 2020; Liu et al. 2021; Asteris et al. 2021; Lin et al. 2021; Ahmad et al. 2022). Such hybrid models may also have good performance for price prediction.