Carbon-efficient closed-loop supply chain network: an integrated modeling approach under uncertainty

Abstract

Inspired by a circular economy paradigm, an evolving momentum of policies and legislations aims to close the loop of product lifecycles through improved level of recycling, remanufacturing, and reuse, with the objective of adding value to the economy while not endangering the environment. However, the trade-off between the environmental and economic sustainability of designing business processes is inevitable. To address this trade-off in the supply chain context, competing objectives regarding both cost minimization and reduction in carbon emission should be simultaneously considered and integrated into a comprehensive model. This complexity is however elevated when uncertainty of demand is taken into consideration. In this study, the design of a closed-loop supply chain is investigated where competing objectives of cost and sustainability of supply chain operations are evaluated under demand uncertainty. Augmented Weighted Tchebycheff (AWT) and ε-constraint methods are employed to address the multi-objectivity of the problem while a robust optimization approach is applied to deal with the demand uncertainty. The results confirm that the proposed approach provides efficient solutions for designing a green closed-loop supply chain network.

1. Introduction

Reverse logistics and closed-loop supply chain have attracted significant attention in the context of reliable and sustainable sourcing as effective managing the complexities of all integrated processes has positive environmental, social, and economic impacts (Gholipoor et al. 2019). In addition, governmental legislations in various countries have enormously put pressure on businesses to proactively devise plans for controlling and managing the waste. This is a response to the fact that the amount of waste is rapidly increasing across the world. For example, wastes regarding electrical and electronic equipment (WEEE) has reached 65 million tons by 2017 globally, which increased by approximately 33% compared to 49 million tons in 2012 (Zhang et al. 2018). By increasing concerns about the possible impacts of supply chain networks on the environment, the green closed-loop supply chain networks have become more and more popular among organization in particular global and international supply chains (Nayeri et al. 2020). In other words, conventional supply chain networks focused on maximizing the profit of network and minimizing the cost of the network at different levels namely strategic, tactical, and operational; however, more recently, environmental consideration and social challenges are incorporated in novel supply chain networks (Darbari et al. 2019). Therefore, more researchers have focused on the subject of sustainable supply chain management by taking into account environmental and social considerations (Barbosa-Povoa da Silva and Carvalho). Indeed, the traditional supply chain networks have been shifted towards the optimal trade-off between costs and environmental consideration (by developing multi-objective models) owing to the increasing focus on environmental considerations, sustainable development, and social challenges (Yu and Solvang 2020). What is more, integration of social, economic, and environmental issues has incorporated into multi-objective sustainable supply chain models for defining the long-term planning of companies and organizations (Carter and Rogers 2008). Multi-objective models have significant role in sustainable supply chain management on account of providing a compromise among several conflict goals (Tautenhain et al. 2021).

As it is not just a matter of waste management and all aspects of reworking, reusing, and recycling should be accommodated, this stream of research has been viewed from different angles such as reverse logistics (RL), closed-loop supply chain (CLSC), sustainable supply chain (SSC), and green supply chain (GSC) (Govindan et al. 2015). Compared to RL, CLSC potentially provides a more holistic view as it considers both traditional supply chain (forward logistics) and reverse logistics concurrently. However, there is a commonality in various studies concerning RL/CLSC as improving the supply chain surplus through minimization of total cost has gained special attention (Rad and Nahavandi b). On the other hand, from the sustainability perspective and to design a green supply chain, it is crucial to integrate environmental concerns into managing supply chain processes including manufacturing processes, product design, sourcing and selection of raw materials, and delivery mechanism as well as end-of-life management of the product after its useful life. With respect to just logistics and transportation aspects, it has been widely advised by government bodies such as Logistics Bureau that businesses should develop plans to reduce CO₂ emissions by modifying transport and facility usage in the supply chain (carbon footprint analysis).

It is obvious that minimizing total supply chain cost and improving the sustainability aspect of a supply chain are competing objectives which should be simultaneously considered in an attempt to identify the optimal strategies for designing an effective supply chain. Therefore, in the current study, we develop an integrated multi-objective model to minimize both CO₂ emissions and supply chain cost including cost of opening facilities, facility activities, transportation, and shortages to optimize the design of a closed-loop supply chain network. To ensure that multi-objective problem is precisely modeled, two solution approaches have been employed: augmented weighted Tchebycheff approach and ɛ-constraint method.

Another key contribution of this study is to address the concern that ignoring uncertainty could invalidate an attempt to design an optimized supply chain (Fadaki et al. 2019, 2020). In a closed-loop supply chain, demand uncertainty is one of the main drivers of supply chain design (Kim et al. 2018). Uncertainty can be incorporated into the model in various methods. There are some possible solution approaches for dealing with uncertainty, namely robust optimization (RO) (Ben-Tal and Nemirovski 1998), stochastic dynamic programming (SDP) (King 2002), fuzzy programming (FP) (Lotfi 1965), stochastic programming (SP), and some combined solution approaches such as fuzzy-robust optimization (FRO) (Pishvaee et al. 2012) and robust stochastic programming (RSP) (Chen et al. 2020). Moreover, using deterministic equivalent models is another way of coping uncertainty that contains three common methods estimated method (EM), chance constraint optimization (CCO), and expected violation penalty method (EVPM) (Keith and Ahner 2019; Yue et al. 20182018). In our study, we opt for the robust solution whereby feasibility and optimality are not enormously influenced by the change of certain input coefficient. It should be noted that shortage concept came up in this paper which can trigger the model be not only more compatible with real-world situation, but also may reduce the total network costs. Direct shifting of commodities from factories to customers without entering to warehouses is another contribution of this work that can have decisive effects on reduction of warehousing and transportations costs.

The rest of the paper is organized as follows. An extensive literature review is presented in the “Literature review” section. In the “Problem definition” section, problem statement, proposed MILP model, and the robust optimization framework are delineated. Computational results and sensitivity analysis are presented to validate and verify the proposed model in the “Results” section. Finally, the “Discussion and concluding remarks” section includes the discussions around the findings, concluding remarks, and topics for future research.

2. Literature review

The reviewed literature is generally based on the three significant clusters. Green concept of network, closed-loop network, and network uncertainty. However, the predominant focus of this work is on the Green multi-objective closed-loop supply chain network (GMOCLSN). An integrate forward-reverse logistic network had been presented by Fleischmann et al. (2001) for the first time (Rad and Nahavandi b). Moreover, a CLSCN was designed by Özceylan et al. (2017) considering multi-period feature. In 2017, Govindan et al. (2017) widely reviewed closed-loop and reverse supply chain networks. Paksoy et al. (2019) introduced a novel model for optimizing the closed-loop supply chain network. A single-objective model was proposed to minimize total costs of the network, containing fixed costs, purchase and operational costs of facilities, transportation costs, and greenhouse gas emission costs. An integrated two-layer network model was incorporated to a green closed-loop supply chain of perishable products under disruption by Yavari and Zaker (2019). In the same way, Banasik et al. (2017) established a multi-objective model to develop closed-loop supply chain for agricultural industry incorporating the environmental considerations. In addition, Reche et al. (2019) studied precisely green closed-loop supply chain network, sustainability, and product development process. Iqbal et al. (2019) investigated thoroughly green concept of supply chain. They proposed a model for the centralized supply chain system to investigate economic aspects of chain. Supply chain leagility was introduced by Fadaki et al. (2019, 2020) and they investigated the impact of uncertainty as the vital design driver of supply chain.

The substantial objective of supply chain networks is to ascertain total costs of system including purchase, production, and distribution quantities and minimizing them, while lately, environmental and social responsibility and employee’s safety and health have been entered into such models. These concerns have been incorporated to the supply chain models as second or third objective function, which give rise creation of multi-objective models. Zohal and Soleimani (2016) mapped gold supply chain into a multi-objective model. The model includes economic and environmental considerations. Meta-heuristic ant colony approach has been developed to solve the problem. In addition, Nurjanni et al. (2017) investigated a GCLSCN by presenting a multi-objective model to minimize the total cost and environmental factors of network. Recently, Mardan et al. (2019) formulated a multi-objective model to design a green closed-loop supply chain network. They developed an accelerated benders decomposition approach to solve the large-scale problem. Besides, the proposed model was implemented on wire-and-cable industry to illustrate validity of model. Beforehand, Vafaeenezhad et al. (2019) designed a sustainable multi-echelon, multi-product, multi-period closed-loop supply chain for paper industry by presenting a multi-objective model. The improved ɛ-constraint method was utilized to solve the multi-objective model. Jindal and Sangwan (2017) analyzed economic factors and carbon footprints of network by providing the multi-objective model with uncertainty nature. They addressed the multi-objective model by an interactive ɛ-constraint method.

In real-world environment, the organization may face various levels of uncertainty and perturbations. Creating a robust supply chain is a substantial matter and has been scrutinized by several authors. In the context of developing uncertain models, Govindan et al. (2017) designed a CLSCN via presenting a multi-objective model, which consists of cost minimization, performance maximization, and carbon dioxide (CO₂) emissions due to the transportation. Sun (2017) investigated some factors to decrease reverse logistic CO₂ emissions to improve sustainable developments. In addition, Shouket et al. (2019) delved into amount of carbon footprint produced by air and railway transportation on environment by using time series of data between 1975 and 2016. They concluded that the government should focus on green transportation to dwindle the detrimental impacts of carbon emissions. The development of a sustainable manufacturing system to minimize environmental effects as a decisive and radical way is run through by Ahmad et al. (2019). Furthermore, a closed-loop supply chain was proposed by Safaei et al. (2017) to examine cardboard recycling network under uncertainty of demand. However, Soleimani et al. (2017) carried out a research on developing a green closed-loop supply chain considering uncertainty of demand. In order to deal with uncertainty, fuzzy programming method was utilized. What is more, Yavari and Geraeli (2019) implemented robust optimization to solve the green closed-loop supply chain under uncertainty of demand, return rate of products, and the quality of returning products. Above all, Zhen et al. (2019) formulated a multi-objective model to address total costs and CO₂ emissions. As well, a probabilistic scenario-based approach was conducted on the model to cope with uncertain concept of problem. Furthermore, Mohseni and Pishvaee (2019) introduced a closed-loop supply chain for sustainable biodiesel production from wastewater sludge. Data-driven robust optimization approach was identified to deal with uncertainty. Additionally, Kim et al. (2018) inquired the closed-loop supply chain under uncertainty of demand and solved it via robust optimization approach. More recently, Fathollahi-Fard et al. (2020a) designed a water supply network by developing a new multi-objective stochastic model and estimated the sustainability aspect of their suggested system by using life cycle assessment method. Furthermore, Fathollahi-Fard et al. (2020b) developed a water supply and water waste system for real case study in Azarbaijan province in Iran to ensure the validity of suggested system. They utilized an adoptive lagrangian relaxation-based algorithm for this purpose. Finally, a closed-loop supply chain network is designed by Demirel et al. (2014) considering two main policies such as secondary market pricing, and incremental incentive policy. In order to cope with uncertainty, fuzzy approach is employed and a multi-objective genetic algorithm is used to solve the model for large-scale problems.

The most related papers in the literature are summarized in Table 1.

Table 1 Summary of studies in the field of closed-loop supply chain with uncertain parameters

As highlighted in Table 1, extensive review of literature confirms a gap in optimizing the green closed-loop supply chain under demand uncertainty considering shortage, direct dispatch of products from factories to the customers without entering warehouses, and their impacts on the network. That is to say, shortage in the supply chain networks is an indispensable part of such networks that can help decision makers (organizations managers or the government authorities) to make the best decisions based on the situations. For instance, in some situations, meeting the demand of some customers imposes a huge cost to the factories or sometimes, meeting the demand of customers puts the organizations or factories in highly risk situations, consequently, making decision on how much of their demand should be met to increase the profit and reduce cost considering environmental aspects, is super crucial. What is more, warehouse operations impose a lot of cost to the supply chain networks which dispatching products in some circumstances if it is possible can dwindle such expenditures. In this study, various aspects of designing an effective green closed-loop supply chain are investigated such as decisions on opening new facilities, optimizing the flow of products, and selecting the most effective transportation options to transfer products among facilities. In this regard, the amount of CO₂ emission due to transportation and operations of units is investigated as the second objective of the developed multi-objective model. Furthermore, as direct dispatch reduces the total handling costs of warehouses, this matter has also been encapsulated in the model. This study also addresses the over and under-production issues resulting from ignoring the stochastic nature of the demand and the likelihood of producing defective products.

3. Problem definition

The problem of this study is to develop a green closed-loop supply chain network in the presence of uncertain demand in order to optimize the total cost of system along with the CO₂ emissions emanating from the chain activities and transporting the products between nodes. Hence, the problem includes designing a sustainable closed-loop supply chain network, identifying facilities that should operate along the chain, determining flow of product between nodes, choosing the most suitable transportation mode to ship the products, and finally incorporating the demand uncertainty in the robust counterpart and comparing the robust and deterministic models. So, a mathematical model is developed to optimize a green closed-loop supply chain network model, considering both financial and environmental aspects. From the financial perspective, total cost of the network is evaluated while environmental aspect is assessed based on total CO₂ emission. Since two objectives are competing in this model, multi-objective optimization techniques are employed in order to convert the multi-objective model to a single objective.

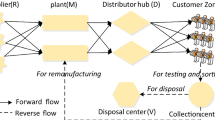
The model includes some facilities such as factories, warehouses, customers, and disassemble centers. In the forward path, products are manufactured in factories and then shipped to warehouses and finally to customers. In our model, products are also allowed to be directly shipped from factories to customers. In the backward path, the faulty products are shipped to the disassemble center and then continue their journey to the factories for remanufacturing operations. One of the main advantages of our model is its ease of generalization given that it can be applied to various real business scenarios in which a closed-loop network is used to manage the flow of products in both forward and backward paths. The uncertainty associated with demand values is one of the major challenges in designing closed-loop supply chains. We consider a number of demand scenarios given that probability distribution of demand is known.

Figure 1 is a schematic representation of the closed-loop network which comprises of factories, warehouses, customers, and disassemble centers along with the direction of product flows among the nodes. The operations of factories involve two main operations: manufacturing products and remanufacturing returned items. The produced products in factories are transported to warehouses or are delivered to the customers directly. Then, the end-of-use products (EoU) and end-of-life products (EoL) are collected from customers to deliver to disassemble centers in order to be recycled and reused in production process in factories.

Figure 1

Schematic representation of material flow in the closed-loop supply chain

Assumptions of this study are as follows: (i) a single product is manufactured; (ii) flow of the products are managed by several transportation modes (m) (road, rail, etc.); (iii) demand of all customers is uncertain (D_k); (iv) customers’ demand can be fulfilled either by warehouses or directly from the factories in order to decrease the cost of warehousing since direct shipping of products from factories to customers is allowed; (v) a specified percentage of total demand is disposed (mp₁); (vi) disposed products which are delivered to disassemble centers are successfully disassembled (mp₂); (vii) transportation modes have unlimited capacity.

3.1. Model formulation

The proposed model is formulated as a mixed integer linear programing. The model has two objectives aiming to minimizing the total cost of the network and the total CO₂ emissions concurrently. In the following section, we define the sets, parameters, and decision variables of the model. Next, the mathematical model is presented.

Sets

i:

factories I = {1, 2, ..., |I|}

j:

warehouses J = {1, 2, …..., |J|}

k:

customers K = {1, 2, ......, |K|}

h:

disassemble centers H = {1, 2, ......., |H|}

m:

transportation mode in order to dispatch product between facilities M = {1, 2, ..., |M|}

Parameters

D_k:

demand of customer k (kg)

L_k:

shortage cost of customer k ($)

A_ijm:

transportation cost in order to dispatch product from echelon i to j with transportation mode m ($)

R_ijm:

transportation rate in order to dispatch product from echelon i to j with transportation mode m ($)

G_i,j:

distance between echelon i and j (km)

F_i:

fixed cost in order to opening factory ($)

mp₁:

minimum amount of goods which collected from customers in percent (kg)

mp₂:

minimum amount of goods to be sent from a disassemble center in percent (kg)

W_i:

variable cost per unit of activity in factory ($)

B_i:

maximum capacity of factory for producing (kg)

C_i:

CO₂ emission due to the activity in factory for unit of product (kg)

T_ijm:

CO₂ emission due to the transportation for dispatch product from echelon i to j (kg)

Variables

Z_i:

equals 1 if factory i is opened, and zero, otherwise.

X_ijm:

total product transferred from echelon i to j with transportation mode m (kg)

E_k:

defect level for each customer (kg)

Based on the defined sets, parameters, and decision variable the mathematical model of this study can be developed as:

$$ \mathit{\operatorname{Min}}\ {F}_1= TC=\sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_i\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}+\sum \limits_{j\epsilon J}{w}_j\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}+\sum \limits_{k\epsilon K}{w}_k\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}+\sum \limits_{h\epsilon H}{w}_h\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}+\sum \limits_{i\epsilon I}{wr}_i\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon J}\sum \limits_{m\epsilon M}{A}_{i jm}{X}_{i jm}+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}{X}_{j km}+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}{X}_{k hm}+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}{X}_{h im}\kern0.5em +\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}{X}_{i km}+\sum \limits_{k\epsilon K}{E}_k{L}_k $$

(1)

$$ \mathit{\operatorname{Min}}{F}_2= TE=\sum \limits_{i\epsilon I}{C}_i\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}+\sum \limits_{j\epsilon J}{C}_j\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}+\sum \limits_{h\epsilon H}{C}_h\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}+\sum \limits_{i\epsilon I}{C}_r\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i j m}\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}{G}_{j k}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{k h m}\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}{G}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i p}\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}{G}_{i k}{R}_{i k m} $$

(2)

Subject to:

$$ \sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{ijm}+\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{ikm}\le {B}_i{X}_i\kern1em \forall i\epsilon I $$

(3)

$$ \sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{i jm}\le {B}_j{X}_j\kern1em \forall j\epsilon J $$

(4)

$$ \sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{jkm}\le \sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{i jm}\kern2em \forall j\epsilon J $$

(5)

$$ \sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{j km}+\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{i km}\ge {D}_k-{E}_k\kern1.75em \forall k\epsilon K $$

(6)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{khm}\ge {D}_k\kern5em \forall k\epsilon K $$

(7)

$$ \sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}\le {B}_h{Z}_h\kern1em \forall h\epsilon H $$

(8)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{khm}\ge \kern0.5em {m p}_1\ {D}_k\kern6em \forall k\epsilon K $$

(9)

$$ \sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{him}\ge {m p}_2\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}\kern2.75em \forall h\epsilon H $$

(10)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}\le {Br}_{i\kern0.75em }{Z}_i\kern1em \forall i\epsilon I $$

(11)

$$ \kern0.5em {X}_{ijm}\kern0.5em \in Int\kern2.5em \forall i\epsilon I, j\epsilon J, m\epsilon M $$

(12)

$$ {X}_{jkm}\kern0.5em \in Int\kern2.5em \forall j\epsilon J, k\epsilon K, m\epsilon M $$

(13)

$$ {X}_{khm}\kern0.5em \in Int\kern2.5em \forall k\epsilon K, h\epsilon H, m\epsilon M $$

(14)

$$ {X}_{him}\kern0.75em \in Int\kern2.25em \forall h\epsilon H, i\epsilon I, m\epsilon M $$

(15)

$$ {X}_{ikm}\kern0.75em \in Int\kern2.25em \forall i\epsilon I, k\epsilon K, m\epsilon M $$

(16)

$$ {Z}_i\in \left[0,1\right]\kern0.5em \forall i\epsilon I $$

(17)

$$ {Z}_j\in \left[0,1\right]\kern0.5em \forall j\epsilon J $$

(18)

$$ {Z}_h\in \left[0,1\right]\kern0.5em \forall h\epsilon H $$

(19)

The first objective function of this study (F₁) is developed to minimize the total cost of chain including cost of opening facilities, facility activities, transportation, and shortages (Eq. 1). To be more specific, F₁ includes the following terms: one to three: total fixed cost; four to eight: total variable cost; nine to thirteen: transportation cost; fourteen: cost of defect. The second objective function (F₂) is formulated to minimize the total CO₂ emission emanating from activities of the system and shipping of items between the nodes (Eq. 2). In the F₂, terms one to four compute the total emitted CO₂ as a result of the production, handling, disassembling, and remanufacturing activities respectively. The last five terms of F₂ are developed to estimate the total CO₂ emission due to the transportation.

Constraint 3 ensures that the total capacity of each factory is greater than the total output of the same plant. Furthermore, capacity of each warehouse should be greater than the total incoming products that the warehouse receives from factories (constraint 4). Constraint 5 supports that total flow of products to a warehouse would be greater than total flow of the products from it. Constraint 6 ensures that demands of all customers are fulfilled. The quantity of goods shipped from a customer to disassemble centers is guaranteed to be less than the same customer’s demand (constraint 7). Moreover, the capacity of each disassemble center should be greater than total quantity of goods that it receives from customers (constraint 8). At least mp₁ percentage of the total products already sent to a customer is transferred to disassembly centers (constraint 9). Similarly, at least mp₂ percentage of total products that already received by a disassembly center is delivered to factories (constraint 10). Constraint 11 ensures that remanufacturing capacity of a factory is greater than the total quantity of goods that it receives from disassemble centers. Constraints 12 to 16 are the non-negativity constraint for the decision variables regarding the shipped quantity among nodes. Finally, constraints 17 to 19 define binary variables which take one if a facility would be open and take zero otherwise.

3.2 Robust counterpart

There are several ways to cope with uncertainty. The robust optimization approach is well known among the most appropriate methods to formulate widely used method to incorporate uncertainty in an optimization problem (Sahinidis 2004). In this study, demand is uncertain and it is assumed that demand scenarios are known. We have employed the robust optimization approach to deal with demand uncertainty in the closed-loop network.

We transform the problem into another problem in which the various scenarios with certain probability of occurrence are defined. Suppose we have k scenarios. The set S^′ = {S₁, , S₂, …, S_K} is the set of scenarios and probability of occurrence of each scenario is P_S, where:

$$ \sum \limits_{S^{\prime }=1}^S{P}_S=1 $$

The value of uncertain coefficient A, B, C for scenario sϵS^′ is: (C_s و A_s و B_s)

$$ {\displaystyle \begin{array}{c}\mathit{\operatorname{Min}}\ Z= cX\\ {} st: AX=B\\ {}x\ge 0\end{array}} $$

Suppose that the objective function value in scenario s is: Q_s = C_sX

$$ \min Z=\sum \limits_{s\epsilon {S}^{\prime }}{P}_S{Q}_s+r\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left({Q}_s-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S{Q}_s+2{\theta}_s\right)+u\sum \limits_{s\epsilon {S}^{\prime }}{P}_S{\lambda}_s $$

$$ s.t: $$

$$ {\displaystyle \begin{array}{c}{A}_sX+{\lambda}_s={B}_s\\ {}{Q}_s-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S{Q}_s+{\theta}_s\ge 0\kern4.25em {\forall}_s\epsilon {s}^{\prime}\\ {}x,{\lambda}_s,{\theta}_s\ge 0\end{array}} $$

where u is the penalty for violation of constraint and r is the risk of taking distance from mean.

Mulvey et al. (1995) presented a robust optimization approach when the problem data are described by a set of scenarios for their value, instead of using point estimates. They introduced two types of robustness: “solution robustness” and “model robustness.” From the solution robustness perspective, a robust solution is the one that it stays close to the optimal for all scenarios of the input data. On the other hand, a solution is model robust if it remains “almost” feasible for all data scenarios. They defined the robust optimization (RO) that explicitly incorporates the conflicting objectives of solution and model robustness. The robust counterpart of our model is formulated as follows:

$$ \operatorname{Min}{F}_1=\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}^s+\sum \limits_{j\epsilon J}{w}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}^s+\sum \limits_{k\epsilon K}{w}_{k s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{h\epsilon H}{w}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{i\epsilon I}{wr}_{i s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon J}\sum \limits_{m\epsilon M}{A}_{i jm}^s{X}_{i jm}^s+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}^s{X}_{j km}^s+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}^s{X}_{k hm}^s+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}^s{X}_{h im}^s\kern0.75em +\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}^s{X}_{i km}^s+\sum \limits_{k\epsilon K}{E}_k^s\ast {L}_k^s\right)+r\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left[\sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}^s+\sum \limits_{j\epsilon J}{w}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}^s+\sum \limits_{k\epsilon K}{w}_{k s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{h\epsilon H}{w}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{i\epsilon I}{wr}_{i s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon J}\sum \limits_{m\epsilon M}{A}_{i jm}^s{X}_{i jm}^s+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}^s{X}_{j km}^s+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}^s{X}_{k hm}^s+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}^s{X}_{h im}^s\kern0.75em +\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}^s{X}_{i km}^s+\sum \limits_{\mathrm{k}\epsilon K}{E}_k^s\ast {L}_k^s-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}^s+\sum \limits_{j\epsilon J}{w}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}^s+\sum \limits_{k\epsilon K}{w}_{k s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{h\epsilon H}{w}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{i\epsilon I}{wr}_{i s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon \mathrm{J}}\sum \limits_{m\epsilon M}{A}_{i jm}^s{X}_{i jm}^s+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}^s{X}_{j km}^s+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}^s{X}_{k hm}^s+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}^s{X}_{h im}^s\kern0.75em +\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}^s{X}_{i km}^s+\sum \limits_{k\epsilon K}{E}_k^s\ast {L}_k^s\right)+2{\theta}_s\right]+u\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\times {\lambda}_s $$

(20)

$$ \mathit{\operatorname{Min}}{F}_2= TE=\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\sum \limits_{i\epsilon I}{C}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}^s+\sum \limits_{j\epsilon J}{C}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}^s+\sum \limits_{h\epsilon H}{C}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}^s+\sum \limits_{i\epsilon I}{C}_{rs}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}^s+\sum \limits_{m\epsilon M}{T}_{i j m}^s\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}^s{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}^s\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}^s{G}_{j k}{R}_{j k m}+\sum \limits_{m\epsilon M}{T}_{k h m}^s\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}^s{G}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i m}^s\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}^s{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}^s\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}^s{G}_{i k}{R}_{i k m}\right)+r\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left[\left(\sum \limits_{i\epsilon I}{C}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}^s+\sum \limits_{j\epsilon J}{C}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}^s+\sum \limits_{h\epsilon H}{C}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}^s+\sum \limits_{i\epsilon I}{C}_{rs}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}^s+\sum \limits_{m\epsilon M}{T}_{i j m}^s\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}^s{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}^s\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}^s{G}_{j k}{R}_{j k m}+\sum \limits_{m\epsilon M}{T}_{k h m}^s\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}^s{G}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i m}^s\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}^s{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}^s\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}^s{G}_{i k}{R}_{i k m}\right)-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\ \sum \limits_{i\epsilon I}{C}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}^s+\sum \limits_{j\epsilon J}{C}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}^s+\sum \limits_{h\epsilon H}{C}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}^s+\sum \limits_{i\epsilon I}{C}_{rs}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}^s+\sum \limits_{m\epsilon M}{T}_{i j m}^s\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}^s{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}^s\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}^s{G}_{j k}{R}_{j k m}+\sum \limits_{m\epsilon M}{T}_{k h m}^s\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}^s{\mathrm{G}}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i m}^s\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}^s{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}^s\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}^s{G}_{i k}{R}_{i k m}\right)+2{\theta}_s\right]+u\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\times {\lambda}_s $$

(21)

Subject to:

$$ \sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{ijm}+\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{ikm}\le {B}_i{X}_i\kern1em \forall i\epsilon I $$

(22)

$$ \sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{i jm}\le {B}_j{X}_j\kern1em \forall j\epsilon J $$

(23)

$$ \sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{j km}+\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{i km}+{\lambda}_s={d}_k^s-{E}_k^s\kern1.75em \forall k\epsilon K; s\epsilon S $$

(24)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{khm}-{\lambda}_s={D}_k\kern5em \forall k\epsilon K; s\epsilon S $$

(25)

$$ \sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}\le {B}_h{Z}_h\kern1em \forall h\epsilon H $$

(26)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{khm}+{\lambda}_s={m p}_1\ {D}_k\kern6em \forall k\epsilon K; s\epsilon S $$

(27)

$$ \sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{X}_{him}\ge {m p}_2\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}\kern2.75em \forall h\epsilon H $$

(28)

$$ \sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}\le {Br}_{i\kern0.75em }{Z}_i\kern1em \forall i\epsilon I $$

(29)

$$ \kern6em \sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}^s+\sum \limits_{j\epsilon J}{w}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}^s+\sum \limits_{k\epsilon K}{w}_{k s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{h\epsilon H}{w}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{i\epsilon I}{wr}_{i s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon J}\sum \limits_{m\epsilon M}{A}_{i jm}^s{X}_{i jm}^s+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}^s{X}_{j km}^s+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}^s{X}_{k hm}^s+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}^s{X}_{h im}^s\kern0.75em +\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}^s{X}_{i km}^s+\sum \limits_{k\epsilon K}{E}_k^s\ast {L}_k^s-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\sum \limits_{i\epsilon I}{F}_i{Z}_i+\sum \limits_{j\epsilon J}{F}_i{Z}_j+\sum \limits_{h\epsilon H}{F}_h{Z}_h+\sum \limits_{i\epsilon I}{w}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i jm}^s+\sum \limits_{j\epsilon J}{w}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j km}^s+\sum \limits_{k\epsilon K}{w}_{k s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{h\epsilon H}{w}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k hm}^s+\sum \limits_{i\epsilon I}{wr}_{i s}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{i\epsilon J}\sum \limits_{m\epsilon M}{A}_{i jm}^s{X}_{i jm}^s+\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{j km}^s{X}_{j km}^s+\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{A}_{k hm}^s{X}_{k hm}^s+\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}\sum \limits_{m\epsilon M}{A}_{h im}^s{X}_{h im}^s+\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{A}_{i km}^s{X}_{i km}^s+\sum \limits_{k\epsilon K}{E}_k^s\ast {L}_k^s\right)+{\theta}_s\ge 0 $$

(30)

$$ \left(\sum \limits_{i\epsilon I}{C}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}^s+\sum \limits_{j\epsilon J}{C}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}^s+\sum \limits_{h\epsilon H}{C}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}^s+\sum \limits_{i\epsilon I}{C}_{rs}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}^s+\sum \limits_{m\epsilon M}{T}_{i j m}^s\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}^s{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}^s\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}^s{G}_{j k}{R}_{j k m}+\sum \limits_{m\epsilon M}{T}_{k h m}^s\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}^s{G}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i m}^s\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}^s{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}^s\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}^s{G}_{i k}{R}_{i k m}\right)-\sum \limits_{s\epsilon {S}^{\prime }}{P}_S\left(\ \sum \limits_{i\epsilon I}{C}_{i s}\sum \limits_{j\epsilon J}\sum \limits_{m\epsilon M}{X}_{i j m}^s+\sum \limits_{j\epsilon J}{C}_{j s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{j k m}^s+\sum \limits_{h\epsilon H}{C}_{h s}\sum \limits_{k\epsilon K}\sum \limits_{m\epsilon M}{X}_{k h m}^s+\sum \limits_{i\epsilon I}{C}_{rs}\sum \limits_{h\epsilon H}\sum \limits_{m\epsilon M}{X}_{h i m}^s+\sum \limits_{m\epsilon M}{T}_{i j m}^s\sum \limits_{i\epsilon I}\sum \limits_{j\epsilon J}{X}_{i j m}^s{G}_{i j}{R}_{i j m}+\sum \limits_{m\epsilon M}{T}_{j k m}^s\sum \limits_{j\epsilon J}\sum \limits_{k\epsilon K}{X}_{j k m}^s{G}_{j k}{R}_{j k m}+\sum \limits_{m\epsilon M}{T}_{k h m}^s\sum \limits_{k\epsilon K}\sum \limits_{h\epsilon H}{X}_{k h m}^s{G}_{k h}{R}_{k h m}+\sum \limits_{m\epsilon M}{T}_{h i m}^s\sum \limits_{h\epsilon H}\sum \limits_{i\epsilon I}{X}_{h i m}^s{G}_{h i}{R}_{h i m}+\sum \limits_{m\epsilon M}{T}_{i k m}^s\sum \limits_{i\epsilon I}\sum \limits_{k\epsilon K}{X}_{i k m}^s{G}_{i k}{R}_{i k m}\right)+{\theta}_s\ge 0 $$

(31)

$$ {X}_{ijm}^s\ge 0\kern2em \forall i\epsilon I; j\epsilon J; m\epsilon M; s\epsilon S $$

(32)

$$ {X}_{jkm}^s\ge 0\kern0.5em \forall j\epsilon J; k\epsilon K; m\epsilon M; s\epsilon S $$

(33)

$$ {X}_{khm}^s\ge 0\kern0.5em \forall k\epsilon K; h\epsilon H; m\epsilon M; s\epsilon S $$

(34)

$$ {X}_{him}^s\ge 0\kern0.5em \forall h\epsilon H;\kern0.5em i\epsilon I; m\epsilon M; s\epsilon S $$

(35)

$$ {X}_{ikm}^s\ge 0\kern0.5em \forall i\epsilon I; k\epsilon K;\kern0.5em m\epsilon M; s\epsilon S $$

(36)

$$ \kern0.5em {\lambda}_s,{\theta}_s\ge 0\kern0.5em \forall s\epsilon S $$

(37)

$$ {Z}_i\in \left[0,1\right]\kern0.5em \forall i\epsilon I $$

(38)

$$ {Z}_j\in \left[0,1\right]\kern0.5em \forall j\epsilon J $$

(39)

$$ {Z}_h\in \left[0,1\right]\kern0.5em \forall h\epsilon H $$

(40)

The first objective function (Eq. 20) comprises of three components. The first term is the average of total cost of network, the second term is variance of total cost of network that represents robustness of the model regarding optimality, and the third term represents the robustness from the feasibility perspective. Similar terms are used in developing the robust counterpart of the second objective function (Eq. 21) in which the total CO₂ emission is formulated. With respect to constraints 22 to 23 and 26, no change in the mathematical expression is made compared to the deterministic model. To ensure that the penalty is applied in case of unmet demand, constraint 24 ensures that if the amount of X_ijm+ X_jkn is greater than ${d}_k^s-{E}_k^s$, then there is no unmet demand and λ_s = 0; otherwise, if X_ijm + X_jknis lower than ${d}_k^s-{E}_k^s$, then unmet demand is non-zero and penalty would be ${d}_k^s-$ ${E}_k^s-{X}_{ijm}-$ X_jkn = λ_s. Constraint 25 also ensures that if total products that a disassemble center receives from a customer exceeds the customer’s demand, then λ_s takes value. If the amount of product that each customer ships to a disassemble center is lower than mp1 * D_k then the penalty parameter takes value (constraint 28). Constraints 28 and 29 have no change compared to the deterministic model. We have included constraints 30 and 31 to convert the nonlinear objective function to a linear model. Finally, constraints 32 to 40 are the same as the respective constraints in deterministic model under scenario s.

3.3 Multi-objective formulation

As stated earlier, in this study, we are dealing with a multi-objective model. The general format of a multi-objective model can be expressed as:

$$ {\displaystyle \begin{array}{c}\operatorname{Min}\ \mathrm{F}\left(\mathrm{x}\right)=\left(\mathrm{f}1\left(\mathrm{x}\right),\mathrm{f}2\left(\mathrm{x}\right),\mathrm{f}31\left(\mathrm{x}\right),\dots, \mathrm{f}\mathrm{m}\left(\mathrm{x}\right)\right)\\ {}\mathrm{s}.\mathrm{t}.\\ {}\mathrm{C}\left(\mathrm{x}\right)\le 0\end{array}} $$

Our mathematical model contains two conflicting objectives in which both total cost of the network and the corresponding CO₂ emission are minimized. However, reduction in any objective leads to increasing the other objective. To deal with the competing objectives, augmented weighted Tchebycheff approach and ɛ-constraint method are employed to convert the multi-objective model to an equivalent single-objective model. In other words, the optimal solution will be obtained by solving the converted single-objective model. With respect to the first method (augmented weighted Tchebycheff), the approach is to minimize the deviation of each objective from its optimal value (Steuer and Choo 1983). This method ensures that each found solution is non-dominated point (Steuer and Choo 1983). The mathematical formulation is expressed as follows:

• First method: augmented weighted Tchebycheff:

  $$ {\displaystyle \begin{array}{c}\operatorname{Min}\ {\mathrm{F}}_3=\kern0.5em \upgamma +\uprho\ {\sum}_{k=1}^2\left({f}_{k\kern0.75em }-{Z}_K^{\ast \ast}\right)\\ {}\begin{array}{cc}\mathrm{St}:& \mathrm{W}1\ \left({f}_{1\kern0.75em }-{Z}_1^{\ast \ast}\right)\le \upgamma \end{array}\\ {}\begin{array}{c}{W}_2\left({f}_{2\kern0.75em }-{Z}_2^{\ast \ast}\right)\le \upgamma \\ {}\mathrm{Co}\ 3\ \mathrm{to}\ \mathrm{Co}\ 19\end{array}\end{array}} $$

where ρ>0 is a small quantity. W₁≥0 , W₂≥0 are the weights of objectives given that W₁+W₂=1. The terms f₁ and f₂ are the objectives, Z^**= (${Z}_1^{\ast \ast }$ ,${Z}_2^{\ast \ast}\Big)$ ^T= (min f₁ , min f₂)^T is a reference point. γ is an integer variable.

• Second method: ε-constraint:

The ε-constraint method is one of the well-known approaches to deal with multi-objective problems. In this approach, just one of the objectives is kept and the rest of the objectives are restricted within user-specific values (Haimes et al., 1971). The first objective is considered as the main objective of this method.

$$ {\displaystyle \begin{array}{c}\operatorname{Min}\ {\mathrm{f}}_1\left(\mathrm{x}\right)\\ {}\mathrm{x}\in X\ \\ {}\begin{array}{c}{\mathrm{f}}_2\left(\mathrm{x}\right)\le \upvarepsilon \\ {}{\mathrm{f}}_{\mathrm{n}}\left(\mathrm{x}\right)\le \upvarepsilon \end{array}\end{array}} $$

4. Results

A numerical example is conducted to analyze the developed model and assess the performance of various solution approaches. Four echelons are considered in the designed closed-loop network including factories, warehouses, disassemble centers, and customers. The smooth flow of network depends on efficiency of each node in undertaking the corresponding activities. At the starting point of the network, products are made in a factory and shipped to the warehouse and then to customers. Subsequently, end-of-life and end-of-use products are collected from customers and shipped to disassemble centers. After processing in the disassemble centers, items are returned to factories for remanufacturing. Two modes of transportation are considered: road and rail.

The developed multi-objective optimization model that addresses the competing objectives of total cost of the network and total corresponding emission resulting from the network activities is solved using augmented weighted Tchebycheff and ɛ-constraint methods. A list of parameters which have been incorporated to solve the model is listed in Table 2. With respect to the uncertain demand, three scenarios are considered: high, moderate, and low demand. Probability of occurrence of each scenario is 0.3, 0.5, and 0.2, respectively. To understand the impact of uncertainty in demand on the optimality of solution, the model is solved in two settings: deterministic and robust. Mathematical model is solved using CPLEX solver on a computer quad core with 4G ram.

Table 2 A list of parameters which have been incorporated to solve the model

4.1 Tchebycheff method

Reference point for augmented weighted Tchebycheff method is calculated considering that minimum of total cost ($) and minimum of total released CO₂ (kg) are reference points. Two objectives compete with each other as decreasing TC leads to higher value of TE. Consequently, the trade-off among these objectives should be properly addressed. A range of weights are considered by changing the weights using 0.05 steps. Using the augmented weighted Tchebycheff method, Pareto optimal frontier is shaped by computing the optimal value of objective functions considering various weights. It is noteworthy to mention that this method does not create any weakly Pareto optimal point. A summary of computational results is given in Table 3.

It should be noted that the first point of deterministic model of this table (F₁=234487.990, F₂=5793435.627) is not considered owing to the scale of the figure. Basically, to precisely show the Pareto front in Figure 2, it is plotted without the first point. Table 3 shows that by increasing the number of facilities in a closed-loop supply chain, total cost increases. There exist different transportation options with different transportation costs. For example, in some cases, transportation cost and amount of CO₂ emissions via rail option are lower than the road or other options.

Table 3 Solution of multi-objective optimization model using the augmented weighted Tchebycheff method

Figure 2

Pareto front for total cost (F1) and total emission (F2) using the Tchebycheff method for the deterministic model

To illustrate the competition among the total cost (F₁) and the total emission (F₂), the Pareto front is developed for both deterministic model (Figure 2) and robust counterpart (Figure 3).

Figure 3

Pareto front for total cost (F₁) and total emission (F₂) using the Tchebycheff method for the robust model

Both Figures 2 and 3 clearly show how improving one objective has an adverse effect on the other. Furthermore, an insight can be gleaned from the comparison between Figures 2 and 3 as the obtained optimal solution in the robust model is significantly less than the deterministic model. This stipulates that incorporating a range of scenarios in the model (robust counterpart) results in an improved optimal solution. In addition, using the deterministic setting for modeling the closed-loop supply chain might have a negative impact on the design of network.

4.1.1 Trade-off between robustness of model and solution

The parameter u in the robust counterpart facilitates a trade-off between model robustness and solution robustness. Note that in the robust optimization, infeasible constraints resulting from various demand scenarios are penalized in the objective function. For example, while the objective function attempts to minimize the λ_s value in control constraint (${d}_c^s-{B}_c$), the penalty value of zero (u=0) leads to highest amount of unsatisfied demand. As a result, optimality of the estimated solution is greatly impacted, considering higher values for the penalty (u) improves the feasibility of the solution as the objective function (F₃) is decreased. Therefore, it is crucial to investigate how the penalty cost impacts the objective function. In this regard, the result of solving the robust optimization model for various value of u is presented in Figure 4.

Figure 4

Impact of penalty cost (u) on the integrated objective function (F₃)

Figure 4 shows the changes in the optimal value of objective function (F₃) when u changes in the range of zero to one and the model is solved using the augmented weighted Tchebycheff method. This result provides a guideline for decision makers to select a suitable u in order to achieve the desired balance between feasibility and optimality of the solution.

4.2 ɛ-Constraint method

The multi-objective model including two objectives of minimizing total cost and total emission is solved using the second solution approach (ɛ-constraint). Table 4 shows the result of analysis for both deterministic and robust settings where demand could be uncertain in the latter. In addition, the model is solved for a range of various values of epsilon.

Table 4 Solution of multi-objective optimization model using the augmented weighted ɛ-constraint method

Table 4 shows optimal values of total cost of operating the network and total cost of emission resulting from the network’s operations for various epsilon values. To illustrate the trade-off among these competing objectives for various values of epsilon, the optimal values of F₁ and F₂ are depicted in the same graph. This trade-off for the deterministic and robust models is presented in Figures 5 and 6 respectively.

Figure 5

Trade-off between competing objectives of total cost (F₁) and total emission (F₂) using ɛ-constraint method for the deterministic model

Figure 6

Trade-off between competing objectives of total cost (F₁) and total emission (F₂) using ɛ-constraint method for the robust model

In both Figures 5 and 6, the trade-off between the total cost and total emission is shown as increasing one of these objectives results in decreasing the other one. This trend can be observed when either of solution approaches (deterministic or robust) is adopted.

4.3 The impact of number of scenarios

A set of numerical experiments is constructed based on a different number of scenarios (various demand values) to assess the performance of robust counterpart. Table 5 provides a summary of obtained results.

Table 5 Sensitivity analysis of demand under different scenarios

It can be observed that by increasing the number of scenarios, total cost of entire chain dramatically increases from 4.310266E+8 ($) to 1.78883E+10 ($). It then falls rapidly, declining to around 4.55732E+10 ($) when the number of scenarios reaches to 40. Similar pattern is detectable for the total carbon dioxide emissions. First, it significantly increases, then fluctuates around 2.15391E+11 and 3.29491E+11. Regarding CPU time, the consumed time under different scenarios is estimated. It can be observed that the CPU time exponentially increases with an early rise of 534 (s) for 40 scenarios and then 32520 (s) for 100 scenarios.

5. Case study

In this section, the proposed model and solution approach are implemented on real-word case to show the efficiency and effectiveness of the suggested model and method. That is to say, the proposed deterministic and robust counterparts are implemented on Iran Transfo company that is located in Zanjan province, Iran. Iran Transfo Company is the largest manufacturer and exporter of transformers under the license of Siemens Germany in the Middle East. This company is a member of the Iranian Electricity Industry Syndicate. The current supply chain of the company is open-loop without considering environmental consideration and we tried to apply green closed-loop supply chain network on the company to redesign the network and verify the effectiveness of the suggested model. Iran Transfo company groups is a huge company in the transformers production sector. The current supply chain involves two main production factories Zanjan and Parand (Tehran), two warehouses in Zanjan (Zanjan’a Industrial Estate, Prand Industrial Estate, Tehran), three main customers Iraq, Syria, and China. It should be noted that two disassemble centers are considered for designing closed-loop network at (Qazvin province, Karaj province) that the end-of-life (EoL) products and end-of-use (EoU) products are entered to these centers in order to be used in production process again. Three main scenarios are considered for the demand of customers (high, moderate, low). There are two transportation options rail and road to transfer products between sites. All transportation options (rail and road) are not available between all points of the network. According to the real data, the total cost for establishing factories and warehouses are 239,852.1 Rials and 115,583.4 Rials respectively. (It should be noted that these cost are based on the Iran’s currency value in 1961 and are estimated based on today’s currency). Maximum production capacity in factories and holding capacity in warehouses are 15,000 unit different kinds of transformers annually and can increase to 20,000 unit transformers. Moreover, it is assumed that at least 0.01% of products are flowed to disassemble and disposal centers. Demand of potential customers for Iraq, Syria, and China are 10,000–12,000–15,000 respectively. Finally, transportation cost and CO₂ emissions due to transportation and operational activities are assumed based on the historical data in the literature (Mohammadi et al., 2021; Mirzapour Al-E-Hashem et al. 2011). Table 6 provides information about distance between points of the network.

Table 6 Distance between points

Table 7 compares the results of two networks.

Table 7 Summary of comparison open and closed-loop supply chain network

According to Table 7, it is easily apparent that 92 units of products are produced at factory two, and then flowed to the second warehouse by rail transportation option under first scenario. Moreover, 84 units of products are produced at first factory and then sent to the second warehouse by rail transportation option under second scenario, and 76 units are flowed to first warehouse under third scenario. After that, the products are flowed from warehouses to the customers under different scenarios by different transportation options, rail and road, while in the closed-loop network, the products are transferred to the customers directly without entering warehouses as much as possible to reduce network costs. Furthermore, in the second network (closed-loop), the model tries to use rail transportation option rather than road that is more efficient in the context of cost and environmental considerations.

Generally speaking, redesign of company’s network imposes reasonable cost to the network (open-loop cost = 33,010.324, closed-loop cost = 33,462.165), and in the context of environmental issue, the suggested network shows outstanding performance (open-loop environmental consideration: 20,689.070, closed-loop environmental consideration: 7877.688). It should be noted that, although shortage is considered in the model, the whole demand of customers is met completely and the penalty of violation of constraints is zero in the model that ensures the performance of robust models.

6. Discussion and concluding remarks

In this study, to design a green closed-loop supply chain, a multi-objective mixed integer linear mathematical model has been developed. The proposed model aims to address the trade-off between minimizing the total cost of a closed-loop supply chain and its environmental impact that is measured by the CO₂ emission. To deal with multi-objectivity of the model, two solution approaches (augmented weighted Tchebycheff and ε-constraint) have been adopted. Furthermore, since demand uncertainty is an inevitable driver of supply chain design, robust optimization method has been employed to accommodate the realization of various demand scenarios and then compare the result of analysis with the pure deterministic model.

Comparing two solution approaches to deal with the competing objectives shows that when the deterministic model is employed, both relatively deliver the same performance. In the first method (augmented weighted Tchebycheff), the minimum value for total cost is $234,487.990 and for CO₂ emission is 2,683,455.390 (kg); whereas in second method, they are $234,487.990 and 2,683,350.127 (kg) respectively. Comparatively, in the non-deterministic model, the obtained solutions are slightly different for two methods: $4.177134E+7 and 8532387.171 (kg) resulting from employing the augmented weighted Tchebycheff method, and $4.153395E+7 and 8526602.571 (kg) when ε-constraint method is used. Although some white noises can be observed among solutions, in general they are quite similar. The degree of similarity regarding the optimal values of two objectives indicates that the gleaned insights from the developed model can be interpreted with higher confidence. Furthermore, similarity of the obtained solution from both methods provides a higher flexibility to the supply chain executives to select any of the developed methods to design a closed-loop supply chain when the trade-off between supply chain cost and the corresponding implications of supply chain operations on the environment should be simultaneously considered. Briefly, the proposed model and solution approaches help decision makers which are supply chain executives or organizational authorities to make the best decision in line with strategic and operational level of their supply chains which involves organizations, individuals, activities, and resources to control the flow of goods from one point to another and to maximize the customer value and sustain a competitive advantage. That is to say, it helps the organizations managers, supply chain owners, and authorities to reach great efficiency rate, better cooperation, increase their output, help them to manage their costs more efficiency, gain strong revenue, and provide timely and robust services. Moreover, in the context of environmental consideration, it may meet the supply chain owner’s responsibility desires.

In addition to considering the customers’ demand as a stochastic variable in the proposed model, future studies may consider to evaluate the model in the presence of uncertainty for other parameters such as unit transportation cost and unit CO₂ emission. This will improve the model from the practical perspective. Moreover, extending the current study by investigating the impact of centralization of decision making in a green closed-loop supply chain might provide a great value. Since the stochastic model will be impossible to solve in large scales, developing metaheuristics/heuristics methods is another avenue for future studies. Finally, limited access to real word data is one of the important limitations of this study that forced us to use historical data to evaluate the proposed mathematical model and solution approach. Moreover, it is important to have a sufficient sample size in order to conclude a valid research result when conducting a study; on the other hand, it requires powerful systems to code and run samples to ensure the precision of the results.