Introduction

Ultrasonic methods are commonly used to determine the high-frequency mechanical properties of materials [1, 2]. Most ultrasonic methods are based on measurements of amplitude and time-of-flight of ultrasonic waves through a sample of known thickness and density. From these two measurements are deduced the wave velocity and attenuation of ultrasonic waves in the considered medium, which makes it possible to calculate the mechanical moduli (shear and P-wave moduli using respectively transverse and longitudinal waves).

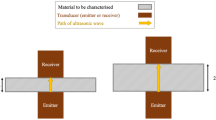
This principle can be implemented using various techniques illustrated in Fig. 1. In the transmission mode, two transducers (one emitter and one receiver) are placed face to face on both sides of the sample [3,4,5,6,7,8]. This method is quite easy to implement but has some disadvantages. It requires access to both sides of the material to be tested, which may not be possible for in-situ measurements. Moreover the precise determination of attenuation often requires several sample thicknesses (in order to avoid the influence of transmission coefficients at interfaces between transducers and material) and appropriate consideration of the ultrasonic beam geometry. The latter problem can be addressed by using transmission mode in water bath [9,10,11,12,13]: it is sufficient in this case to make measurements with and without a sample in order to determine accurately the attenuation coefficient. Another advantage of this method is that the transmission of longitudinal and transverse waves can be studied using the same couple of pressure transducers by simply rotating the sample. However, this method is obviously reserved for laboratory tests. A third method is more suitable for some in-situ tests in which only one side of the material to be tested is accessible. This method, called pulse-echo mode [14,15,16,17,18], measures the transit time and wave amplitude after reflection on the opposite side and only requires a single transducer. However, this method has some limitations. If the sample is too thin, the echo may overlap with the sensor’s emission signal. Conversely, if the sample is too thick, the amplitude of the reflected signal may be too small to be accurately measured.

Fig. 1
figure 1

Illustration of the main ultrasonic measurement modes

Full size image

Whichever of the three methods outlined above is used, the thickness of the sample must be precisely known, which is not always possible in the context of in-situ measurements. Above all, the main limitation of those three methods is that once the signal has passed through the material its amplitude has to be measurable. Ultrasonic measurement of the mechanical properties of high damping materials may therefore be impossible [1, 19].

However, a fourth method, presented in [20, 21], has been developed to overcome some of these drawbacks: the Surface Reflection Method (SRM). This method is founded on the influence of an interface change on the reflected acoustic wave. In other words, it is based on the measurement of the ratio of the amplitude of the reflected wave at the interface between two materials to the amplitude of the reflected wave at the air interface. These amplitudes depend on the mechanical properties of each medium. If one of the media (named in the following reference material) is known, this measurement makes it possible to determine the mechanical characteristics of the second. In this method, the incidence of the emitted pulse may be normal or oblique [22,23,24,25]. The measurement accuracy is increased for oblique incidence, at the expense of simplicity of implementation. Only the normal incidence method is considered in this study. A scheme illustrating how the method works is presented in Fig. 2.

Fig. 2
figure 2

Illustration of the Surface Reflection Method (SRM)

Full size image

Given the limitations of the traditional methods described previously, the conditions for the applicability of the SRM is discussed below. First, this paper focuses on the theoretical formulation of the amplitude of reflected waves at the interface between two viscoelastic media according to the latter’s mechanical characteristics. Subsequently, the analytical solution to the inverse problem (the mechanical characteristics of the tested medium based on those of the reference medium and the waves’ amplitude) is given. From this analytical solution, an analysis of the measurand error is performed and a method for choosing the reference material is proposed.

Theory

Ultrasonic Wave Propagation in Viscoelastic Medium

The propagation of a mechanical wave in a continuous and homogeneous medium is governed by Euler’s equation:

$$\nabla\sigma\ast=\rho\mathrm a\ast$$
(1)

Where \({\upsigma }^{*}\) is the complex Cauchy stress, \(\uprho\) is the density of the material, \({\mathrm{a}}^{*}\) is the complex acceleration and \(\nabla\) is the Laplacien operator.

The mechanical behaviour of the material is assumed to be linear viscoelastic in the small strain domain with a complex descriptor denoted below by \({\mathrm{D}}^{*}\) with real and imaginary parts respectively denoted as \({\mathrm{D}}^{^{\prime}}\) and \({{\mathrm{D}}^{"}}\). In case of transverse waves (respectively longitudinal waves) \({{\mathrm{D}}^{*}}\) represents the complex shear modulus \({\mathrm{G}}^{*}\) (respectively the complex P-wave modulus \({\mathrm{M}}^{*}={\mathrm{K}}^{*}+4{\mathrm{G}}^{*}/3\), with \({\mathrm{K}}^{*}\) the complex bulk modulus). In the case of a plane wave propagating in the x-direction, the complex stress is expressed according to Eq. 1.

$${\upsigma }^{*}={\mathrm{D}}^{*}\frac{\partial {\mathrm{u}}^{*}}{\partial \mathrm{x}}$$
(2)

where \({\mathrm{u}}^{*}\) represents the complex displacement.

From Eqs. 1 and 2 the well-known relationship of propagation of mechanical waves in a continuous medium is obtained [26].

$${\mathrm{D}}^{*}\frac{{\partial }^{2}{\mathrm{u}}^{*}}{\partial {\mathrm{x}}^{2}}=\uprho \frac{{\partial }^{2}{\mathrm{u}}^{*}}{\partial {\mathrm{t}}^{2}}$$
(3)

In a semi-infinite medium, the stationary solution of Eq. 3 in case of a harmonic wave of pulsation \(\upomega\) is expressed:

$${\mathrm{u}}^{*}\left(\mathrm{t},\mathrm{x}\right)={\mathrm{u}}_{0}\mathrm{exp}\left(-\alpha \mathrm{x}\right)\mathrm{exp}\left(\mathrm{j}\left(\omega \left(\mathrm{t}-\frac{\mathrm{x}}{\mathrm{c}}\right)\right)\right)$$
(4)

where \({\mathrm{u}}_{0}\) is the amplitude of displacement at x = 0, \(\alpha\) is the attenuation coefficient, \(\upomega\) is the wave pulsation and \(\mathrm{c}\) is the wave phase velocity.

By substituting the solution expressed in Eq. 4 in Eq. 2, the relationship between the real and imaginary part of \({\mathrm{D}}^{*}\) on the one hand and attenuation and wave velocity on the other hand has been revealed (Eqs. 4 and 5). This system of equations establishes the method for determining mechanical properties by ultrasonic transmission (Fig. 1).

$$\left\{\begin{array}{c}\alpha=\frac{\omega \sqrt{\rho }\sqrt{\left|{\mathrm{D}}^{*}\right|-{\mathrm{D}}^{^{\prime}}}}{\sqrt{2}\left|{\mathrm{D}}^{*}\right|}\\ \mathrm{c}=\frac{\sqrt{2}\left|{\mathrm{D}}^{*}\right|\sqrt{\left|{\mathrm{D}}^{*}\right|-{\mathrm{D}}^{^{\prime}}}}{{\mathrm{D}}^{^{\prime}{^{\prime}}}\sqrt{\rho }}\end{array}\right.$$
(5)
$$\left\{\begin{array}{c}{\mathrm{D}}^{^{\prime}}=\rho {\mathrm{c}}^{2}\frac{1-{\left(\alpha \mathrm{c}/\omega \right)}^{2}}{{\left(1+{\left(\alpha \mathrm{c}/\omega \right)}^{2}\right)}^{2}}\\ {\mathrm{D}}^{^{\prime}{^{\prime}}}=\rho {\mathrm{c}}^{2}\frac{2\alpha \mathrm{c}/\omega }{{\left(1+{\left(\alpha \mathrm{c}/\omega \right)}^{2}\right)}^{2}}\end{array}\right.$$
(6)

Reflection At the Interface of Two Viscoelastic Media

Many authors have studied the mechanisms of reflection and transmission of plane waves at the interface between two elastic or viscoelastic media [27,28,29]. Unlike these authors whose aim was to investigate the propagation of waves at the interface of two known materials, this study focuses on the inverse problem and its analytical solution.

Acoustic Impedance

In the present paper, only the case of a normal incidence is considered. When an ultrasonic wave reaches the interface between two media, it is partially reflected and transmitted. The amplitudes of transmitted (denoted \({{\mathrm{u}}_{\mathrm{t}}}^{*}\)) and reflected (denoted \({{\mathrm{u}}_{\mathrm{r}}}^{*})\) waves depend upon the acoustic impedances of the two media in contact and are proportional to the amplitude of the incident wave (denoted \({{\mathrm{u}}_{\mathrm{i}}}^{*}\)) as illustrated in Fig. 3. In what follows, subscript 1 is related to the medium of incident wave and subscript 2 to the secondary medium.

Fig. 3
figure 3

Scheme illustrating the wave propagation through a two-layer medium

Full size image

The acoustic impedance \({\mathrm{Z}}^{*}\) for a viscoelastic medium is defined by Eq. 6 [26].

$$\sigma^{*}=-\text{j} \omega \text{Z}^{*} \text{u}^{*} \ \text{with}\;\text{Z}^{*}=\text{Z}_\mathfrak{R}+\text{jZ}_\mathfrak{I}$$
(7)

From Eqs. 1 and 6 expressions of real and imaginary parts of \({\mathrm{Z}}^{*}\) in relation to \({\mathrm{D}}^{*}\) and ρ are obtained (Eq. 7).

$${\mathrm{D}}^{*}=\frac{{{\mathrm{Z}}^{*}}^{2}}{\uprho }\iff \left\{\begin{array}{c}{\mathrm{Z}}_{\mathfrak{R}}=\sqrt{\frac{\uprho }{2}}\frac{{\mathrm{D}}^{"}}{\sqrt{\left|{\mathrm{D}}^{*}\right|-{\mathrm{D}}^{^{\prime}}}}\\ {\mathrm{Z}}_{\mathfrak{I}}=\sqrt{\frac{\uprho }{2}}\sqrt{\left|{\mathrm{D}}^{*}\right|-{\mathrm{D}}^{{\mathrm{D}}^{^{\prime}}}}\end{array}\right.$$
(8)

Conservation Equation At the Interface

Displacement and stress continuity at the interface lead to the following set of equations:

$$\left\{\begin{array}{c}{{\mathrm{u}}_{\mathrm{i}}}^{*}={{\mathrm{u}}_{\mathrm{t}}}^{*}+{{\mathrm{u}}_{\mathrm{r}}}^{*}\\ {{\upsigma }_{\mathrm{i}}}^{*}={{\upsigma }_{\mathrm{t}}}^{*}+{{\upsigma }_{\mathrm{r}}}^{*}\end{array}\right.$$
(9)

By substituting the expression of stress in function of the complex impedance (Eq. 6), Eq. 9 leads to:

$$\left\{\begin{array}{c}{{\mathrm{u}}_{\mathrm{i}}}^{*}={{\mathrm{u}}_{\mathrm{t}}}^{*}+{{\mathrm{u}}_{\mathrm{r}}}^{*}\\ {{\mathrm{Z}}_{1}}^{*}{{\mathrm{u}}_{\mathrm{i}}}^{*}={{\mathrm{Z}}_{2}}^{*}{{\mathrm{u}}_{\mathrm{t}}}^{*}-{{\mathrm{Z}}_{1}}^{*}{{\mathrm{u}}_{\mathrm{r}}}^{*}\end{array}\right.$$
(10)

Which solution is:

$$\left\{\begin{array}{c}{{\mathrm{u}}_{\mathrm{r}}}^{*}=\frac{{{\mathrm{Z}}_{2}}^{*}-{{\mathrm{Z}}_{1}}^{*}}{{{\mathrm{Z}}_{2}}^{*}+{{\mathrm{Z}}_{1}}^{*}}{{\mathrm{u}}_{\mathrm{i}}}^{*}\\ {{\mathrm{u}}_{\mathrm{t}}}^{*}=\frac{2{{\mathrm{Z}}_{1}}^{*}}{{{\mathrm{Z}}_{2}}^{*}+{{\mathrm{Z}}_{1}}^{*}}{{\mathrm{u}}_{\mathrm{i}}}^{*}\end{array}\right.$$
(11)

In what follows, equations are expressed in terms of ratios \({\mathrm{U}}_{\mathrm{r}}^{*}\) and \({\mathrm{U}}_{\mathrm{t}}^{*}\) with

$$\left\{\begin{array}{c}{\mathrm{U}}_{\mathrm{r}}^{*}={{\mathrm{u}}_{\mathrm{r}}}^{*}/{{\mathrm{u}}_{\mathrm{i}}}^{*}\\ {\mathrm{U}}_{\mathrm{t}}^{*}={{\mathrm{u}}_{\mathrm{t}}}^{*}/{{\mathrm{u}}_{\mathrm{i}}}^{*}\end{array}\right.$$
(12)

The real and imaginary parts of the amplitude of transmitted and reflected waves are given by Eq. 12.

$$\left\{\begin{array}{c}\begin{array}{c}{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}=\frac{{\left|{{\mathrm{Z}}_{2}}^{*}\right|}^{2}-{\left|{{\mathrm{Z}}_{1}}^{*}\right|}^{2}}{{\left|{{\mathrm{Z}}_{1}}^{*}+{{\mathrm{Z}}_{2}}^{*}\right|}^{2}}\\ {\mathrm{U}}_{\mathrm{r}\mathfrak{I}}=\frac{2\left({\mathrm{Z}}_{\mathfrak{R}1}{\mathrm{Z}}_{\mathfrak{I}2}-{\mathrm{Z}}_{\mathfrak{R}2}{\mathrm{Z}}_{\mathfrak{I}1}\right)}{{\left|{{\mathrm{Z}}_{1}}^{*}+{{\mathrm{Z}}_{2}}^{*}\right|}^{2}}\end{array}\\ \begin{array}{c}{\mathrm{U}}_{\mathrm{t}\mathfrak{R}}=1-{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}\\ {\mathrm{U}}_{\mathrm{t}\mathfrak{I}}=-{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}\end{array}\end{array}\right.$$
(13)

Since SRM is based on echo measurements, only the reflected wave is of interest. By inverting the system it is possible to obtain the complex impedance components of medium 2 knowing those of medium 1 and by measuring the reflected wave’s amplitude (Eq. 13).

$$\left\{\begin{array}{c}{\mathrm{Z}}_{\mathfrak{R}2}=-\frac{{\mathrm{Z}}_{\mathfrak{R}1}\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right)+2{\mathrm{Z}}_{\mathfrak{I}1}{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}{{\left({\mathrm{U}}_{\mathrm{r}\mathfrak{R}}-1\right)}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}}\\ {\mathrm{Z}}_{\mathfrak{I}2}=-\frac{{\mathrm{Z}}_{\mathfrak{I}1}\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right)+2{\mathrm{Z}}_{\mathfrak{R}1}{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}{{\left({\mathrm{U}}_{\mathrm{r}\mathfrak{R}}-1\right)}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}}\end{array}\right.$$
(14)

The aim of the method exposed in the present paper is to determine the modulus of medium 2. By substituting in Eq. 14 the impedance components using their expressions in function of the components of modulus, the final relationship is obtained in Eq. 14. To the author’s knowledge, such analytical relationship between two viscoelastic media does not exist in the literature.

$$\left\{\begin{array}{c}{{\mathrm{D}}^{^{\prime}}}_{2}=\frac{{\rho }_{1}}{{\rho }_{2}}\frac{\left[\left({\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right)}^{2}-4{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}\right){{\mathrm{D}}^{^{\prime}}}_{1}+4\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right){\mathrm{U}}_{\mathrm{r}\mathfrak{I}}{{\mathrm{D}}^{^{\prime}{^{\prime}}}}_{1}\right]}{{\left({\left({\mathrm{U}}_{\mathrm{r}\mathfrak{R}}-1\right)}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}\right)}^{2}}\\ {{\mathrm{D}}^{^{\prime}{^{\prime}}}}_{2}=\frac{{\rho }_{1}}{{\rho }_{2}}\frac{\left[\left({\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right)}^{2}-4{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}\right){{\mathrm{D}}^{^{\prime}{^{\prime}}}}_{1}-4\left({{\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}-1\right){\mathrm{U}}_{\mathrm{r}\mathfrak{I}}{{\mathrm{D}}^{^{\prime}}}_{1}\right]}{{\left({\left({\mathrm{U}}_{\mathrm{r}\mathfrak{R}}-1\right)}^{2}+{{\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}^{2}\right)}^{2}}\end{array}\right.$$
(15)

Uncertainty of Measurand and Choice of Reference Material

Equation 15 being strongly non-linear, the measurand error is also non-linear and can become detrimental for some material combinations. The choice of material 1 is therefore crucial to ensure that the mechanical properties of material 2 are measured with an acceptable error margin. The way to achieve a given measurement error on \({\mathrm{U}}_{\mathrm{r}}^{*}\) is not discussed in this paper. In this section, based on the literal expression of measurand error, guidelines to assist the selection of the reference material are provided.

In order to determine the error on the components of the module (\({D}^{^{\prime}}\) and \({{D}^{"}}\)), it is first necessary to estimate the error on the components of acoustic impedance (Eq. 16 obtained from Eq. 7).

$$\left\{\begin{array}{c}\text{D}_{2}^{^{^\prime}}=\left({\text{Z}_{\mathfrak{R}2}}^{2}-{\text{Z}_{\mathfrak{I}2}}^{2}\right)/{\rho_{2}}\\{\text{D}_{2}}^{^{\prime\prime}}=2{\text{Z}}_{\mathfrak{R}2}{\text{Z}}_{\mathfrak{I}2}/{\rho_{2}}\end{array}\right.$$
(16)

For the sake of simplicity, the error on the real and imaginary part of the reflected amplitude are set equal and noted \(\Delta \mathrm{U}\). Arguments of \({{\mathrm{Z}}_{1}}^{*}\) and \({{\mathrm{Z}}_{2}}^{*}\) are respectively denoted \({\uptheta }_{1}\) and \({\uptheta }_{2}\). The acoustic impedance argument is equal, as usual, to half the angle of the loss factor \({\delta }_{2}\left(\mathrm{tan}\left({\delta }_{2}\right)={\mathrm{D}}_{2}/{\mathrm{D}}_{2}\right)\).

By differentiating Eq. 15, we obtain

$$\begin{cases}\frac{\frac{\Delta {{\mathrm{D}}_{2}}^{{^{\prime}}}}{{{\mathrm{D}}_{2}}^{{^{\prime}}}}}{\Delta \mathrm{U}}=\frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{R}2}}{{\mathrm{Z}}_{\mathfrak{R}2}}}{\Delta \mathrm{U}}*\left(\frac{2}{1-{\mathrm{tan}}^{2}\left({\uptheta }_{2}\right)}\right)+\frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{I}2}}{{\mathrm{Z}}_{\mathfrak{I}2}}}{\Delta \mathrm{U}}*\left(\frac{2{\mathrm{tan}}^{2}\left({\uptheta }_{2}\right)}{1-{\mathrm{tan}}^{2}\left({\uptheta }_{2}\right)}\right)\\ \frac{\frac{\Delta {{\mathrm{D}}_{2}}^{"}}{{{\mathrm{D}}_{2}}^{"}}}{\Delta \mathrm{U}}=\frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{R}2}}{{\mathrm{Z}}_{\mathfrak{R}2}}}{\Delta \mathrm{U}}+\frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{I}2}}{{\mathrm{Z}}_{\mathfrak{I}2}}}{\Delta \mathrm{U}}\end{cases}$$
(17)

where

$$\left\{\begin{array}{c}\frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{R}2}}{{\mathrm{Z}}_{\mathfrak{R}2}}}{\Delta \mathrm{U}}=\left(\left|\frac{\partial {\mathrm{Z}}_{\mathfrak{R}2}}{\partial {\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}\right|+\left|\frac{\partial {\mathrm{Z}}_{\mathfrak{R}2}}{\partial {\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}\right|\right)*\frac{1}{{\mathrm{Z}}_{\mathfrak{R}2}}\\ \frac{\frac{\Delta {\mathrm{Z}}_{\mathfrak{I}2}}{{\mathrm{Z}}_{\mathfrak{I}2}}}{\Delta \mathrm{U}}=\left(\left|\frac{\partial {\mathrm{Z}}_{\mathfrak{I}2}}{\partial {\mathrm{U}}_{\mathrm{r}\mathfrak{R}}}\right|+\left|\frac{\partial {\mathrm{Z}}_{\mathfrak{I}2}}{\partial {\mathrm{U}}_{\mathrm{r}\mathfrak{I}}}\right|\right)*\frac{1}{{\mathrm{Z}}_{\mathfrak{I}2}}\end{array}\right.$$
(18)

Figure 4 represents the acoustical impedance moduli ratio which corresponds to the minimal error on the determination of D2′ and D2″ for given values of impedance arguments of reference material (θ1) and material to be characterised (θ2): (a) and (b) are respectively related to real and imaginary part of \({{\mathrm{D}}_{2}}^{*}\). Impedance arguments vary in the whole physical domain from 0° (purely elastic solid behaviour) to 45°.

Fig. 4
figure 4

Impedance moduli ratio corresponding to minimal error on D2′ (left) and D2″ (right) in function of impedance arguments of reference material (θ1) and material to be characterised (θ2): (a) Determination of D2′ (b) Determination of D2”

Full size image

It appears that, whatever the impedance arguments of materials 1 and 2 are, the optimum value of the moduli ratio is always in the range 0.6 to 1.6. To this optimum ratio corresponds a minimum error that is plotted in Fig. 5. This minimal error depends mainly on the impedance argument of medium 2. The following analysis is based on the assumption of a measurement error of 1% on the reflected amplitude. In what concerns the real part of modulus D2′, a minimal error in an acceptable range (i.e. < 10%) is only obtained for an impedance argument of medium 2 lower than 25°. For the imaginary part of modulus D2″, the impedance argument of medium 2 has to be higher than 14°. Hence, with an assumption on the measurement error of 1%, both components of the modulus can only be determined accurately for an impedance argument in the range 14° to 25°, which corresponds to \(0.5<\mathrm{tan}\left({\delta }_{2}\right)<1.2\).

Fig. 5
figure 5

Minimal relative error in function of impedance arguments of reference material (θ1) and material to be characterised (θ2): (a) Determination of D2′ (b) Determination of D2”

Full size image

Two limit cases will now be investigated: loss modulus of medium 1 is null (θ1 = 0°) as illustrated in Fig. 6 and storage modulus of medium 1 null (\({\uptheta }_{1}=45^\circ\)) as presented in Fig. 7.

Fig. 6
figure 6

Error in determining the real (a) and imaginary (b) parts of the complex modulus of the material to be tested in function of moduli ratio when the reference material is purely elastic (\({\uptheta }_{1}=0^\circ\)). A profile with an isovalue of \({\uptheta }_{2}=22.5^\circ\) is represented on the right side of each plot

Full size image
Fig. 7
figure 7

Error in determining the real (a) and imaginary (b) parts of the complex modulus of the material to be tested in function of moduli ratio when the reference material is purely viscous (\({\uptheta }_{1}=45^\circ\)). A profile with an isovalue of \({\uptheta }_{2}=22.5^\circ\) is represented on the right side of each plot

Full size image

Figures 6 and 7 represent the error in determining the real (a) and imaginary (b) part of the complex modulus of material 2 in function of \({\uptheta }_{2}\) and \({\mathrm{log}}_{10}\left(\left|{\mathrm{Z}}_{2}/{\mathrm{Z}}_{1}\right|\right)\). As in the previous case, let us consider a case in which the uncertainty of amplitude measurement can be estimated at 1% and the error is expected to be less than 10%.

The frontier of the domain of acceptable error (< 10%) is symbolised by the thick black line. The fields of applicability of the method are similar for the two extreme values of θ1 considered. Whatever θ1 and the modulus component, the minimum error is in the vicinity of a moduli ratio of 1, a result in accordance with previous findings (see Fig. 4).

Nevertheless, a reasonable accuracy is maintained over an extended moduli ratio range (0.1 to 10) if material 2 is purely linear elastic (only the real part of the complex modulus has to be determined in this case) or purely viscous (in which case only the imaginary part of the complex modulus has to be determined). However, in the case of a viscoelastic medium with an angle in a median zone, the choice of medium 1 is much more restricted to achieve the desired accuracy. For instance, let us consider a viscoelastic solid whose loss factor (\(\text{tan}\left({\updelta }_{2}\right)={{\text{D}}_{2}}^{"}/{{\text{D}}_{2}{^{\prime}}}\)) is of 1. The corresponding impedance argument would be \({\uptheta }_{2}={\delta }_{2}/2=22.5^\circ\). In this case, a sufficiently accurate estimation of both D’ and D” would only be obtained for an impedance module ratio between 0.5 and 2.

The error study highlights that only the storage moduli ratio between the two contacting media had an impact on the accuracy of the measurand. From this point of view, \({{\text{D}}^{"}}_{1}\) can take on any value. By contrast, a too large viscous component (which causes a very strong attenuation in the reference medium) would be detrimental in terms of the accuracy of the measurement of the reflected waves’ amplitudes. In all cases, a high degree of accuracy in the measurement of reflected waves’ amplitudes is required: in the most favourable case, the error on the modules is four times greater than that on amplitudes. More generally speaking, this method can be applied either for longitudinal or transverse waves. In the first case, media 1 and 2 can be either fluids or solids. In the second case, media 1 must be solid and media 2 can be either solid or fluid. In the last case, the applicability of the method implies high ultrasonic frequency and high viscosity so that the acoustical impedance of the fluid is equivalent to the one of a solid.

Discussion

In the previous section, it is highlighted how to achieve the best measurand accuracy by applying the SRM. In the following, the accuracy obtained with this method is compared with that of traditional methods in order to determine the respective fields of application of the different methods.

Traditional methods (transmission mode, transmission mode in water bath, pulse-echo mode) are based, on the one hand, on the measurement of a transit time and a sample thickness in order to deduce the wave velocity and, on the other hand, on amplitude ratio measurements to deduce the attenuation. Depending on the method, the amplitude ratio most commonly used is as follows:

  • Transmission mode: ratio of wave amplitudes travelling through samples of different thicknesses

  • Transmission mode in water bath: ratio of transmitted waves’ amplitudes with and without sample

  • Pulse-echo mode: ratio of successive echo amplitudes

The wave velocity c is calculated using Eq. 18, where d represents the distance travelled by the wave and t the corresponding transit time. The attenuation coefficient α is obtained from Eq. 19, where U is the amplitude ratio determined according to the considered mode.

$$\mathrm{c}=\mathrm{d}/\mathrm{t}$$
(19)
$$\left\{\begin{array}{c}{\alpha}=\text{ln}\left(\text{U}\right)/\text{d for transmission and pulse}-\text{echo modes}\\{\alpha }=\text{ln}\left(\text{U}\right)/\text{d}+{\alpha }_{\text{w}}\text{ for transmission mode in water bath}\end{array}\right.$$
(20)

Based on Eqs. 5 and 19, the error on \({\mathrm{D}}^{^{\prime}}\) and \({\mathrm{D}}^{^{\prime}{^{\prime}}}\) is expressed in terms of the argument of the acoustic impedance of the tested material \(\mathrm{tan}\left(\uptheta \right)\) and u (Eq. 20) and is plotted in Fig. 8. Only the error associated with the determination of U is taken into account. The error on c has been considered negligible: an error of less than 1% is easily achieved, which is small compared to other sources of error.

Fig. 8
figure 8

Error in determining the real (a) and imaginary (b) parts of the complex modulus of the material to be tested against amplitude ratio. A profile with an isovalue of \(\uptheta =22.5^\circ\) is represented on the right side of each plot

Full size image
$$\left\{\begin{array}{c}\frac{\frac{\Delta {\mathrm{D}}^{^{\prime}}}{{\mathrm{D}}^{^{\prime}}}}{\Delta \mathrm{U}}=-2{\mathrm{tan}}^{2}\left(\uptheta \right)\frac{3-{\mathrm{tan}}^{2}\left(\uptheta \right)}{1-{\mathrm{tan}}^{4}\left(\uptheta \right)}\frac{1}{\mathrm{U ln }\left(\mathrm{U}\right)}\\ \frac{\frac{\Delta {\mathrm{D}}^{"}}{{\mathrm{D}}^{"}}}{\Delta \mathrm{U}}=\left|\frac{1-3{\mathrm{tan}}^{2}\left(\uptheta \right)}{1+{\mathrm{tan}}^{2}\left(\uptheta \right)}\frac{1}{\mathrm{U ln }\left(\mathrm{U}\right)}\right|\end{array}\right.$$
(21)

At a given angle, the minimum error is obtained for a value of \(\mathrm{U}=1/\mathrm{e}=0.368\). Another noteworthy value is the angle \(\uptheta =30^\circ\) for which the theoretical error on \({\mathrm{D}}^{"}\) is zero. More generally, an acceptable error (i.e. < 10%) is only obtained for sufficiently high values of U. Considering the case of a solid with \(\mathrm{tan}\left(\updelta \right)=1\) (corresponding to an angle \(\uptheta =22.5^\circ\)), an error of less than 10% can only be obtained for a value of U greater than about 0.015.

The conventional modes can be very accurate if the thickness of the samples can be adjusted to obtain a value of U sufficiently close to the optimal value of 0.368. Under specific conditions, the required sample thickness would be so small that it prevent the practical implementation of the method. For detailed demonstration, please refer to Part 2.

One way to get around this difficulty is to study the velocities and attenuations of torsion waves propagating in rigid tubes filled with the material to be studied [30]. However, to be applicable, this method requires that the material can be melted without altering its mechanical properties, which is rarely the case for polymers. In addition, the displacements have to be high enough to be measured by optical sensors, which limits the frequency range of the method.

Conclusion

The aim of this paper is to highlight the potential scope of the Surface Reflection Method (SRM). First, analytical formulas were established to relate the mechanical characteristics of a sample to be tested to those of a reference sample as well as to the amplitude of the waves reflected at the interface. The error study demonstrated that, in order to obtain a given accuracy on the measurands, the moduli ratio of the acoustic impedances of the two materials in contact had to be close (typically between 0.6 and 1.6). These conditions for the validity of the method apply to both viscoelastic and considered elastic materials. Although the error on the measurand expected with conventional methods is generally lower than that of the SRM, the conditions required to obtain a given accuracy cannot be met in some cases such as the study of the mechanical properties of polymers in rubbery state or highly viscous fluids (honey, crude oil, colloid suspensions …). The SRM makes the measurement of all mechanical moduli achievable over a wide frequency range. Other possible fields of application are quality control, the measurement of ageing or the study of the durability of materials.