On the Testing of the Dynamic Mechanical Properties of Soft Gelatins

Abstract

This research focuses on the measurement of the static and dynamic mechanical properties of ballistic gelatin. We present a simple, novel experimental setup for measuring the dynamic material properties of ballistic gelatin that includes the classic metallic incident and transmission bars as opposed to the polymeric Kolsky bars used by additional research groups. This method is mathematically validated, while providing sought out for stress–strain curves for three different ballistic gelatin concentrations. The results are then compared to two additional research groups, while being consistent with one and contradictory to the other. Finally, an empirical constitutive law is presented that is consistent with the results obtained through the experimental setup.

Introduction

Dynamic material properties must be assessed due to the fact that materials behave (and eventually fail) very differently when subjected to high rates of loading. This is especially applicable to the fields of ballistics, explosions and other impact scenarios that are of increasingly growing interest. There are several diverse, acceptable methods for determining these properties [1, 2], while the most popular is the Split Hopkinson Pressure Bar (SHPB) [3–5]. This method is highly effective for testing materials at high strain rates while enabling the researcher to implement a relatively uniform strain rate throughout most of the experiment. However, when it comes to testing materials such as rubbers, biological tissues, foams and other soft materials, several problems arise [6]. First of all, the SHPB technique requires the specimen to be in dynamic equilibrium throughout the duration of the experiment. When testing metals, this requirement is relatively easy to fulfill due to the fact that stress waves travel at speeds of the order of 5000 m/s, whereas for materials such as biological tissues, this speed is more along the lines of 1 to 100 m/s [7]. Low sound velocity is detrimental to achieving dynamic equilibrium without taking additional measures. Another problem that often arises is the impedance mismatch effect. When using SHPB techniques, it is highly recommended to ensure that the acoustic impedance of the SHPB bars, Z, defined as:

$$ Z=\rho \cdot C $$

(1)

is of a similar order to that of the material specimen under observation (ρ and C are the mass density and sound wave velocity, respectively). If the two impedances are dissimilar, the signal to noise ratio will be too high to obtain reliable results, as the sought after signal will be indiscernible from the inherent noise in the standard system. In order to overcome these problems, several different research groups have introduced a variety of methods that include introducing aluminum bars for lowering the impedance mismatch [8], titanium bars [9] magnesium bars [10], hollow bars as a geometrical amplification of the signal [11], direct force sensing for measuring dynamic equilibrium [6], and pulse shaping to insure dynamic equilibrium [6, 12]. High strain rate testing on soft biologial tissues has been observed through the use of ballistic gelatin (BG), which is a gel made from a collagen mixed with water, and is correlated to swine muscle tissue and in turn to human tissue. BG is a very extreme case, as it is much softer than other materials, such as rubbers and foams, as its consistancy includes up to 90 % water, and is therefore almost a fluid making high strain rate testing even more difficult. In addition, this material is affected greatly by the room temperature at which the experiments were conducted [13, 14], and at 40 °C will revert back to a fluid form. Therefore, several proposed modifications for soft materials such as hollow bars, are insufficient in overcoming the great impedance mismatch, and other solutions are required. Two methods for the testing and measurement of ballistic gelatin behavior at high strain rates have been published [15, 16], and both have implemeted the use of the Polymeric Split Hopkinson Pressure Bar (PSHPB) technique in which the incident and transmission bars are polymeric as opposed to the metallic bars traditionally used. This modification greatly reduces the impedance mismatch, although it does come at a certain price. The analysis required on the researchers part is much more difficult and cumbersome due to the fact that polymeric bars introduce viscoelastic effects into the system, and the stress waves travelling in the incident and transmission bars are distorted due to dispersion and attenuation phenomena that correspond to viscoelasticity [17, 18]. These effects are overcome by one research group [15] through the use of 4 strain gauges (instead of the standard 2 that are found in ‘traditional’ SHPB tests), that enable the use of an iterative deconvolution algorithm in order to determine the impulse response function of the polymeric bars, and thus measure the stresses and strains in the BG specimen. In addition, a quartz crystal gauge was used in order to verify dynamic equilibrium. The second research group [16] used acrylic bars, and a linear viscoelastic assumption, that was followed by a transformation of the stress wave equation into the frequency domain in order to obtain the solution for the actual stresses measured during the experiment. Additionally, a laser displacement system was used to measure the displacements in the gel specimen, and although accurate, may have distorted the test results due to the increased temperature of the gel specimen while the laser was used. Due to the complex nature of these two methods, we propose a novel, simple experimental setup that provides accurate results, while eliminating unnecessary elements that distort the true values that we seek to obtain. This experimental setup is presented, validated mathematically, and tested, while providing sought out for stress–strain curves for three different ballistic gelatin concentrations.

Materials and Methods

Ballistic Gelatin Preparation

The preparation of BG involves mixing gelatin powder with water at different temperatures, and then cooling the mixture in molds for several hours until ready for use. There are two types of commonly used BG mixtures, known as, 10 % and 20 % BG, while the percentage refers to the amount of powder used in each configuration. The BG powder used in this research was 250 Bloom, Type A. Bloom refers to the strength of the gel and is measured between 0 and 300 in increments of 25 through a probing test that was developed by O. T. Bloom in 1925 [19]. Type A refers to the processing in acid solution through which the gelatin was obtained (Type B would refer to a lime solution). In order to obtain adequately shaped gel specimens, a mold was designed specifically for this purpose. The most commonly used BG is 10 % solution, meaning a tenth of the mixture is the powder. It should be noted that many different types of gels are created by different groups, and they are all classified in this category. The differences between the methods are in the temperature of the added liquid, the storage temperature at which the mixture is kept, additional ingredients to dissolve the foam etc. Obviously, all of these gels will have different mechanical properties and each will efficiently simulate different types of tissue or internal organs. In other words, the ability to derive conclusions regarding living tissue only comes into effect if certain measures are taken. Essentially, certain conditions will simulate one type of tissue, while other circumstances will effectively simulate a liver if calibrated according to a certain standard. Jussila [20] developed a standard method for preparing BG that requires shooting round shot from an air gun (bb pellets), into a block of gelatin in order to validate the conclusions regarding living tissue after the desired tests have been performed. Due to the fact that in this research we are not interested at all in the similarity between tissue and BG, the terms X% BG refer to the concentration of the powder in that particular mix. The different concentrations used in this research are summarized in Table 1, and can be seen in Fig. 1.

Table 1 Ballistic gelatin concentrations used

Fig. 1

Ballistic gelatin specimens 10 %, 20 %, 30 % (from right to left)

We note that while 10 % and 20 % are known (usual) concentrations, 30 % ballistic gelatin does not actually exist. There are no standard methods for preparing it, and it does not actually simulate human or swine tissue. However, this research is dedicated to exploring different types of gel-like materials, and we were interested in creating a solution using 30 % powder and comparing its mechanical properties to those of the other gels. Therefore, we will henceforth refer to the following solution as 30 % BG while we are fully aware that this term is used for convenience only and does not refer to actual BG.

Quasi-Static Testing

All of the static testing was performed on the Instron machine model #4483 for strain rates in the range of $\overset{\cdot }{\varepsilon }={10}^{-4}-{10}^{-2}{ \sec}^{-1}$ _. 50 kg and 1.5 kg load cells were used and all of the conducted experiments were carried out under displacement control. Petroleum jelly was used as a lubricant to prevent barreling. The gel specimen was sandwiched between two steel cylinders while the upper compressed the gel and the lower was in a fixed state. The purpose of these tests was twofold: Firstly, we wished to obtain an understanding and familiarity with the material before proceeding to the high strain rates. Secondly, if only high strain rate experiments are performed, there is nothing to compare these results to. Therefore, static experiments are performed and material properties are determined in order to observe the uniqueness of these materials in the differences between the static and dynamic material properties.

Dynamic Testing for Soft Materials

While testing a soft material in the SHPB technique, several difficulties arise. The first of which is that the impedance of the specimen is much smaller compared to that of the incident and transmission bars. Due to that fact, only a very small portion of the incident wave that propagates through the specimen is transmitted to the transmission bar while most of the wave is either reflected or distorted by the material being tested. As a result, the transmitted wave has a very small magnitude and is hardly measurable. The standard conventional SHPB method is therefore not suitable for testing soft materials. Additionally, SHPB is based upon the assumption that the specimen is in an equilibrated stress state. This equilibrium is achieved after several propagations in the specimen, which takes a certain amount of time depending upon the specimen material. For very soft materials such as BG, this characteristic time may be relatively long, due to the fact that stress waves propagate much more slowly in gels than in metals, which may cause non-uniform deformation in the specimen rendering the results useless. Validation of the results requires assurances of an equilibrated specimen state for obtaining results and suggesting conclusions.

SHPB Experimental Method

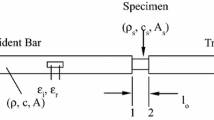
In order to overcome the previously mentioned obstacles the following method is proposed. The SHPB setup may be seen in Fig. 2.

Fig. 2

Schematic of proposed SHPB setup for the testing of the dynamic material properties of ballistic gelatin

The setup consists of aluminum incident and transmission bars which allow for elastic stress wave analysis while being on the lower end of the mechanical impedance scale for metals. A strain gauge setup consisting of 2 diametrically placed strain gauges connected in a series form on one arm of a quarter Wheatstone bridge with a gauge factor of 2.1 was implemented on the incident bar. This classical setup was complemented by two Flexiforce (Tekscan Inc.) commercial pressure sensitive force sensors on both specimen-bar interfaces. These sensors compensate for the unavoidable, poor impedance matching between the aluminum bars and ballistic gelatin specimen, due to their high sensitivity. The strain gauge and both sensors were connected to an oscilloscope in order to record time histories for the output voltages of all three channels. The force sensors were calibrated separately before each batch of tests, and additional verification was made at the commencement of the tests. This calibration consisted of placing the force sensor between the incident and transmission bars (without a specimen), and propelling the striker, while a strain gauge setup was placed on each bar. This setup provides an approximation of the single bar Hopkinson test due to the very small thickness of the force sensor and was verified through the stress wave that was nearly identical on both of the bars. Then the voltage measured by the force sensor, and the force derived from the strain gauge measurement through classic SHPB analysis provides the calibration between the voltage of the force sensor and the force in the bars as seen in Fig. 3.

Fig. 3

Typical force sensor response during calibration test repeated thrice

The aluminum striker was selected to be of 18.5mm length in order to create a large deformation in the specimen while preventing an overlap of the gauge signals. Petroleum jelly was placed on the end of the incident bar to serve as a pulse shaper for the stress wave, allowing for dynamic equilibrium in the gel specimen. All specimens were tested immediately after being removed from their refrigerated state in order to reduce temperature effects.

Proposed Method Validation

The known parameters in a standard SHPB experiment are ε _I , ε _R , ε _T . These variables define the incident, reflected and transmitted strains respectively.

The proposed methodology relies on a single strain gauge reading; therefore the following proof provides the steps in obtaining strains in the incident and transmission bars.

As seen in Fig. 4, the incident and reflected signals are measured through the incident strain gauge, and the transmitted signal is measured through the signal on the transmission bar. However, due to the very low impedance of ballistic gelatin, once the signal reaches the specimen, the strain gauge output voltage for transmitted and reflected signals will be of the same order as the noise, rendering the results virtually useless. Therefore, the only known parameter that we may infer is ε _I which will remain unchanged by the gel specimen, and is clearly discernible. The use of the incident signal alone is necessary, though not damaging to the results, due to the fact that this signal is obtained before the stress wave has traveled in the specimen and is therefore not yet distorted, unlike the reflected and transmitted signals, which have gone through some distortion and are no longer reliable.

Fig. 4

SHPB schematic for forces, strains, velocities and displacements in one-dimensional stress wave analysis

In order to determine the material properties, first, transmitted and reflected signals must be obtained. This is done through utilizing the signals retrieved from the Flexiforce force sensors Fig. 5 that are directly measuring the forces (after calibration) F ₁, F ₂ that are present on either side of the specimen. These forces relate to the signals in the following manner:

Fig. 5

SHPB Gel-bar interfaces with force sensors

$$ \begin{array}{l}{F}_1={E}_b\cdot {A}_b\cdot \left({\varepsilon}_I+{\varepsilon}_R\right)\hfill \\ {}{F}_2={E}_b\cdot {A}_b\cdot {\varepsilon}_T\hfill \end{array} $$

(2)

where E _b , A _b are the Hopkinson bar Young’s modulus and cross section area, respectively. The transmitted strain may be calculated directly:

$$ {\varepsilon}_T=\frac{F_2}{E_b\cdot {A}_b} $$

(3)

and the combination of the incident and reflected strains are also provided:

$$ {\varepsilon}_I+{\varepsilon}_R=\frac{F_1}{E_b\cdot {A}_b} $$

(4)

Therefore, the force sensors are capable of measuring the transmitted signal (rendering the strain gauge on the transmitted bar useless) and a combination of the incident and reflected signals. The separation of these two signals is done through the use the incident signal that is already known from the strain gauge on the incident bar. Re-arranging equation (4):

$$ {\varepsilon}_R=\frac{F_1}{E_b\cdot {A}_b}-{\varepsilon}_I $$

(5)

The transmitted strain ε _T is known from the second force sensor (equation (3)) and the incident strain is known from the first force sensor and the incident strain gauge (equation (5)).

Now that all three signals are known, the procedure for obtaining the stress–strain curve is presented as follows.

The dynamic equilibrium requirement (once fulfilled) provides:

$$ {F}_1={F}_2 $$

(6)

Direct measurement of the forces, allow for the nominal stress in the gel specimen to be immediately calculated:

$$ {\sigma}_g=\frac{F_1+{F}_2}{2{A}_{0g}} $$

(7)

The stress may also be expressed in terms of the transmitted signal as:

$$ {\sigma}_g=\frac{A_b\cdot {E}_b}{A_{0g}}{\varepsilon}_T $$

(8)

Where A _0g is the initial cross section area of the gel specimens. The velocities on either side of the specimen are defined as:

$$ \begin{array}{l}{v}_1={C}_b\cdot \left({\varepsilon}_I-{\varepsilon}_R\right)\hfill \\ {}{v}_2={C}_b\cdot {\varepsilon}_T\hfill \end{array} $$

(9)

With C _b as the bar wave velocity, defined as:

$$ {C}_b=\sqrt{\frac{E_b}{\rho_b}} $$

(10)

Here ρ _b is the bar density. The nominal strain rate is therefore defined as:

$$ {\overset{\cdot }{\varepsilon}}_g=\frac{v_1-{v}_2}{l_{0s}} $$

(11)

And with the addition of equations (9), (6), (2) yields the following expression:

$$ {\overset{\cdot }{\varepsilon}}_g=-\frac{2{C}_b}{l_{0g}}\cdot {\varepsilon}_R $$

(12)

Integration over time of equation (12), yields the nominal strain in the specimen:

$$ {\varepsilon}_g(t)={\displaystyle \underset{0}{\overset{t}{\int }}{\overset{\cdot }{\varepsilon}}_g\left(\tau \right) d\tau}=-\frac{2{C}_b}{l_{0g}}{\displaystyle \underset{0}{\overset{t}{\int }}{\varepsilon}_R\left(\tau \right) d\tau} $$

(13)

The previous expressions for stress and strain were are all nominal (engineering) values. The true (logarithmic) values of these expressions are:

$$ {\sigma}_t={\sigma}_g\left(1-{\varepsilon}_g\right)=\frac{A_b\cdot {E}_b}{A_{0g}}{\varepsilon}_T\cdot \left(1+\frac{2{C}_b}{l_{0g}}{\displaystyle \underset{0}{\overset{t}{\int }}{\varepsilon}_R\left(\tau \right) d\tau}\right) $$

(14)

$$ {\varepsilon}_t=- \ln \left(1-{\varepsilon}_g\right)=- \ln \left(1+\frac{2{C}_b}{l_{0g}}{\displaystyle \underset{0}{\overset{t}{\int }}{\varepsilon}_R\left(\tau \right) d\tau}\right) $$

(15)

It should be noted that this transference is done using an incompressibility assumption. The fact that ballistic gelatin has a Poisson’s ratio of at least 0.45 justifies the assumption of near incompressibility [21].

These relations have shown that the use of two force sensors, along with the incident signal ε _I , measured by the strain gauge, are alone, sufficient to determine the material properties (without the reflected and transmitted signals). This determination is contingent upon fulfillment of dynamic equilibrium in the specimen (6).

Results

Quasi-Static Testing Results

Gelatin concentrations of 10, 20 and 30 % were tested quasi-statically by compressing the specimen up to 50 % strain, and subsequently decompressing allowing the specimen to return to its original state. Three separate strain rates $\overset{\cdot }{\varepsilon }={10}^{-2},{10}^{-3},{10}^{-4}{ \sec}^{-1}$ were tested. After testing, the results were analyzed to provide stress–strain curves using engineering and true values separately. The elastic modulus was then measured by measuring the initial unloading slope, due to the fact that the unloaded material has a purely elastic response at this particular point before viscoelasticity takes a significant effect [22]. The measurement can be observed in Fig. 6 below.

Fig. 6

Typical stress–strain curve for 20 % BG at strain rate of 10^− 3 sec ^− 1. Red line indicates measurement of elastic modulus

Due to the large deformations in these tests, the true stress–strain curves are more significant, as both the specimen diameter and length experience drastic changes throughout the experiment.

Figure 7 shows a representation of all of the quasi-static test results. Each blue point on the graph represents the series of tests for the same concentration and strain rate, which include 5 separate tests for each concentration (10 %, 20 %, 30 %) at each strain rate ($\overset{\cdot }{\varepsilon }={10}^{-2},{10}^{-3},{10}^{-4}{ \sec}^{-1}$). For all three concentrations, the strain rates ascend as they climb the y-axis. It is interesting to note that there is a very high strain rate dependence, even at lower strain rates, that is correlated directly to the concentration and strain rate. Note that the results for 10 % at the lowest strain rate (10^− 4 sec ^− 1) should be observed with caution as this concentration being of the highest liquid concentration is the most temperature dependent, and was observed to not have returned to its original state after the experiment. Additionally, all of the tests for 10 and 20 % BG were very repeatable showing a standard deviation of no more than 6.5KPa (which is shown through the barely discernible error bars) as opposed to the 30 % concentration which was shown to have much higher standard deviation. This is due to the fact that the higher concentration of BG powder introduced into the creation process, didn’t absorb the liquid in an even manner, and solidified much quicker. This makes it difficult to remove the air bubbles created in the mixing process and resulted in a material that was less repeatable.

Fig. 7

Quasi-static results for BG concentrations at all three strain rates including error bars

Dynamic Testing Results

The dynamic test setup underwent a fine-tuning process prior to achieving measurable results. Several striker and specimen lengths were tested until suitable values were determined. A nominal specimen length of 1.5mm, specimen diameter of 8mm and striker length of 18.5mm, provided ample strain in the specimen while still ensuring dynamic equilibrium (Fig. 8) throughout the experiment. Such a state of equilibrium was ascertained for each tested specimen.

Fig. 8

Dynamic equilibrium shown in 20 % BG sample. Peak deviation between signals prior to unloading <5 %

This assured a repeatable experimental system that provided accurate results for the gel specimens. 10 %, 20 % and 30 % ballistic gelatin specimens were tested at strain rates ranging from 1,800 to 5,200 s⁻¹ and the results are presented in Figs. 9, 10 and 11.

Fig. 9

True stress–strain curves for 10 % BG

Fig. 10

True stress–strain curves for 20 % BG

Fig. 11

True stress–strain curves for 30 % BG

The noise observed in Figs. 8, 9, 10 and 11 is a result of the force sensors that are measuring very low forces (as low as several Newtons) in the gelatin specimen. The figures are presented in their true form, without Fourier analysis to provide the reader with a sense of the actual results obtained through these sensors.

After obtaining the stress–strain curves for the materials, the dependence of the material strength upon strain rate and concentration may be replotted as shown in Fig. 12.

Fig. 12

Semi-logarithmic representation of true stress for all three BG concentrations at a fixed strain of ε = 0.3 as a function of strain rate

This representation shows an increase in stress for both strain rate and gel concentration.

Discussion

Radial Inertia Effects

It has been observed that the impact response of soft materials may be highly affected by inertia induced stresses that are dominant during the initial stages of loading [23], and may therefore distort the specimen response if not carefully taken into account. This occurs due to the fact that the axially impacted specimen wishes to expand radially which in turn may cause an increased stress in the loaded axial direction that is not being taken into account. This phenomenon is reduced through the increase of specimen diameter—length ratio, which will reduce the radial expansion post impact, therefore, a 4:1 diameter-length ratio was implemented in all of the specimens. These effects have been summarized and observed [24, 25], with the latter presenting an analytical representation of the inertia induced stress, that includes two terms. The second term is relative to the derivative of the strain rate and is only valid for lower strains, but the interesting term is the first term that increases with increasing strain and strain rate. This term is presented as:

$$ {\sigma}_i=\frac{3\cdot \rho \cdot {a_0}^2}{16{\left(1-\varepsilon \right)}^3}{\left(\overset{\cdot }{\varepsilon}\right)}^2 $$

(16)

[25], where σ _i is the inertia induced stress, ρ is the gel density, a ₀ is the initial specimen cross section, ε is the strain in the gel specimen and $\overset{\cdot }{\varepsilon }$ is the strain rate. In order to assess this effect, a constant strain rate of $\overset{\cdot }{\varepsilon }=5100{ \sec}^{-1}$ was assumed (the highest strain rate measured with the proposed experimental setup), the specimen diameter of 8mm was used to calculate the cross section, a density of 1000gr/cm ³ was assumed and the strain was set up to ε = 0.7 (the highest achieved). This provided the results seen in Fig. 13.

Fig. 13

Inertia induced stress in gel specimen subjected to maximal strains and strain rates

This shows that although the inertia induced stress greatly increases with the strain in the specimen, under the harshest conditions this only reaches a maximal value of less than 5KPa . This is two orders of magnitude less than the stresses measured in the ballistic gelatin specimen, and is therefore deemed negligible in this case.

Method Comparison

Additional research groups have performed impact experiments on ultra-soft and gel-like materials, in order to observe their unique response to high strain rate testing. The research groups [15, 16] have both tested ballistic gelatin at high strain rates, and while our ballistic gelatin has not been calibrated to assume tissue response, the material should still have a similar dynamic response.

As may be observed in Table 2, comparison may only be made for all three methods in 10 % BG, while 20 % BG may be compared only with [16].

Table 2 Method comparison of high strain rate testing of ballistic gelatin

It should be noted that the additional methods presented here are reconstructed by the authors through the figures presented in the aforementioned articles, in order to provide the reader with an understanding of the comparison between these methods. All comparisons are made with similar strain rates so as to improve the level of similarity between the results presented.

As can be observed in Figs. 14 and 15, there is a similarity between the nature of the results obtained through the proposed method and Salisbury [16]. This is best seen Fig. 15, while for 10 % BG, the proposed method achieved a strain of 0.45, as opposed to 1.5. However, the results published by [15], are not in good agreement at all, as they present an almost metallic response of the material, and not at all rubber like as would be expected from a gel.

Fig. 14

BG high strain rate response as measured by 3 separate research groups for 10 % concentration

Fig. 15

BG high strain rate response as measured by 2 research groups for 20 % concentration

Of the advantages of the Flexiforce force sensors upon Quartz crystal gauges [15], are that the crystal gauges must be protected by an additional aluminum disc that does not allow for the measurement of the signal directly upon the specimen as is possible through the Flexiforce sensor. This additional disc must also be corrected for in the analysis, and introduces additional element into the SHPB setup that keep it from being simple. Additionally, as can be seen from Table 2, the amount of strain gauges required in the proposed setup is significantly less than both methods resulting in a much simpler setup, and no correction factors are needed which greatly simplify the post experiment analysis.

Strain Rate Dependence

All of the stress strain responses seen in the three figures above have several stages. The first is a loading stage that consists of 2 major slopes—a moderate one at first, that transforms into a much more significant slope best observed in Fig. 11. This loading stage reaches a certain plateau, and commences with an “unloading” stage. For all three of the figures, strain rate dependence is observed through the increase of the stress for a given strain as the strain rate increases. This is consistent with the previously seen observation that gels and other soft materials are highly strain rate dependent. The different slopes observed in the loading process may be attributed to the nature of the high strain rate response of these materials. Each dynamic stress–strain curve presented, has an initial range of strains (usually up to ε ≈ 0.25) that has little effect on the material, as the deformation grows, the gel begins to stiffen and the material undergoes a loading phase up till the maximal stress that it senses. Following the loading phase, we may observe a gradual decline in the stress as the strain increases. It is important to note that this is obviously not an unloading phase as seen in the static testing, firstly, because an unloading phase occurs when the stress decreases with the strain, and secondly, because the SHPB compression setup is not equipped to unload the material. This is seen very explicitly through the calculation of the strain. The strain is an integral of the strain rate, which is directly proportionate to the reflected signal from equation (13). The reflected signal is a tensile stress wave, that does not change directions, therefore, the strain which is an integral of this signal, can only be positive. In order to unload the material, the strain must decrease, which is impossible in this setup, as no component is forcing the specimen to remain in constant contact with the incident and transmission bars after the initial compression. These regions are seen clearly in the graphs for 10 % and 20 % ballistic gelatin. However, in Fig. 11 depicting the stress–strain behavior for 30 % ballistic gelatin, the decrease in specimen stress is different and looks somewhat like unloading, which is obviously impossible as explained previously. Therefore, we surmise that the “unloading” region in the 10–20 % specimens, is a representation of the “yielding” of the material, and the commencement of its plastic deformation, which is consistent with the fact that all of the 30 % BG specimens did not deform plastically, and no permanent deformation was observed, while the 10 % and 20 % specimens exhibited cracking after the SHPB test.

Empirical Constitutive Law

The aforementioned testing of different concentrations of ballistic gelatin, leads to an attempt at providing an empirical constitutive law for assessing the rate and composition dependent mechanical properties of the investigated gels. Due to the logarithmic nature of the stress strain relationship as can be seen in Fig. 12, a power law relationship in the shape of:

$$ \sigma \left(\varepsilon = const\right)=a\cdot {\overset{\cdot }{\varepsilon}}^b $$

(17)

was sought out. This relationship provided converging results that are presented in Table 3.

Table 3 Summary of the constants found in constitutive law for BG

It is very interesting to note that the integer preceding the strain rate in the first column of Table 3 is very similar for all three concentrations. This yields the following regarding the constant a:

$$ a=9.55\cdot {10}^{-3}\pm 3.1\cdot {10}^{-4} $$

(18)

As for the variable b, we propose a linear relationship attributed to the gel concentration. This provides:

$$ b=8.5\cdot {10}^{-3}\cdot C+0.3413 $$

(19)

Where C is the gel concentration. In summary, the proposed constitutive law may be presented thus far as:

$$ \sigma \left(\varepsilon = const\right)=9.55\cdot {10}^{-3}{\overset{\cdot }{\varepsilon}}^{9.55\cdot {10}^{-3}\cdot C+0.3413} $$

(20)

Finally, a dependence upon the strain must be introduced. This was done in the form:

$$ \sigma =\left(m\cdot {\varepsilon}^n\right)\cdot \left(9.55\cdot {10}^{-3}{\overset{\cdot }{\varepsilon}}^{9.55\cdot {10}^{-3}\cdot C+0.3413}\right) $$

(21)

Where m, n are material constants. Using a curve-fitting tool, the constants are obtained and presented Table 4.

Table 4 Summary of material constants relating to strain for constitutive law

The constants for 10 %, 20 % BG are grouped together due to their similarity, while the constants for 30 % are presented separately as they are very different. We speculate that this may be due to the fact that the 10 %, 20 % specimens failed during testing, while the 30 % did not. It should finally be noted that this empirical representation of the mechanical behavior of the BG at high strain rates is rather standard, of the kind used for metals, namely:

$$ \sigma =K\cdot {\varepsilon}^m\cdot {\overset{\cdot }{\varepsilon}}^n $$

(22)

where K, m, n are material constants.

Conclusions

This research presents a novel method for obtaining the high strain rate response of ballistic gelatin for three different formulations. 10 % and 20 % are known concentrations, and these dynamic responses are compared to experiments conducted by additional research groups and are found to be in good agreement with one of them. The 30 % ballistic gelatin presented a somewhat similar response, although it did not experience any plastic deformation, and therefore submitted a different response at the stress decreasing stage. The strain rate dependence is observed for all three concentrations, in addition to an increase in the stiffening of the material due to a rise in gel concentration. The proposed method implements aluminum bars which exhibit an elastic response resulting in a great simplification of the post experiment analysis, and providing the researcher with an inexpensive, simple method for determining material properties of any ultra-soft material. Finally, an empirical model for a constitutive law is presented and found to be dependent upon the strain, strain rate and ballistic gelatin concentration.