1 Introduction

It is well known that the mechanical response of polymers is strongly affected by strain-rate [1–6]. Increasing the strain-rate leads to higher elastic modulus because the polymer chains have reduced relaxation time [7]. This also results in increased yield stress. While we [8–16] and others (see for example [17–20]) have published extensively on the mechanical behavior of numerous semi-crystalline polymers, these studies have largely focused on characterizing the material in a single form. From study to study, the pedigree (record of the material including variables such as chemical composition, processing, thermal and loading histories, density, crystallinity, molecular weight, etc.) of the material being characterizing ranges from extremely well known to completely unknown. Some of this research has probed the effect of changing polymer morphology, such as changing the percent crystallinity [8] or orientation of the polymer chains [21], while others have made comparisons based on changing composition, such as polytetrafluoroethylene versus polychlorotrifluoroethylene [15].

The current work investigates three polymers with the same chemical composition in the monomer repeat unit (C2H4) n , but vastly different long-range conformations. We present the characterization and comparison of the large strain compressive behavior of three different industrial forms of polyethylene (PE): high-density polyethylene (HDPE), ultra high molecular weight polyethylene (UHMWPE), and cross-linked polyethylene (PEX). Polyethylene is a commodity thermoplastic extensively used in consumer products with over 60 million tons produced worldwide every year. It is classified into at least nine different categories based primarily on its density, molecular weight, and branching, of which we focus on three. Polyethylene with a density of ≥941 kg m3 is denoted as HDPE. It has a low degree of branching and thus stronger intermolecular forces and tensile strength. Also known as plastic #2, HDPE is often used in recyclable commercial products such as bottles, tubs, and containers. Polyethylene with a molecular weight ≥106 repeat units (∼3.1–5.7 × 106) is denoted as UHMWPE. The high molecular weight results in less efficient packing of the chains into the crystal structure resulting in lower densities than HDPE (∼930–935 kg m3) but increasing the toughness. Because of its outstanding toughness, wear and excellent chemical resistance, UHWMPE is used in a wide diversity of applications. One notable application is artificial joints, and as a result, the bio-journals contain a significant amount of work on UHMWPE (for example see [18, 22–27]). A medium- to high-density polyethylene containing cross-link bonds is denoted as PEX. Of the three forms discussed, PEX has received by far the least attention in the literature. The high-temperature properties of the polymer are improved, its creep behavior is reduced, and its chemical resistance is enhanced.

The literature contains a rich breadth of work on polyethylene in its many forms and a complete review of these contributions is beyond the scope of the current work. Here we highlight some examples of these contributions that have focused on the mechanical behavior. Lee et al. [17] studied the effect of extruding and drawing processes on the quasi-static behavior of HDPE. G’Sell and Jonas [28] proposed a constitutive model for the flow behavior of HDPE in tension and later provided a more global discussion of microstructure evolution in semi-crystalline polymers [29]. Extensive data on complex path loading of polyethylene was presented by Kitagawa et al. [30], but provided no further information on the type of PE studied. Tuttle et al. [31] studied the biaxial behavior of HDPE. A discussion on the large strain plastic deformation of HDPE has been given by Lee et al. [32] in terms of texture evolution. Boontongkong et al. [33] studied the orientation in UHMWPE compressed in a channel die and compared the results with a similar study on HDPE by Galeski et al. [34], but in neither case was the compressive mechanical response measured. Kurtz et al. [18] measured the quasi-static yielding, plastic flow, and fracture behavior of UHMWPE for use in total joint replacements, which was extended to a comparison of wear and work to failure in HDPE and UHMWPE [22]. The non-linear Poisson’s effect in UHMWPE was studied by Smith et al. [35]. Zhang et al. [36] made a direct comparison of the wear behavior of HDPE and UHMWPE, with similar data present by Yong et al. [37] nearly a decade earlier. Mourad et al. [20] measured the deformation and fracture behavior of UHMWPE as a function of high strain-rate and triaxial state of stress using a “flying-wedge” type of loading device. Khonakdar et al. [38] used DMA to compare HDPE with low density PE (LDPE). Sobieraj et al. [27] measured the effect of large deformation compression on the crystallinity of conventional and cross-linked UHMWPE by DSC. Lim et al. [39] recently studied HDPE/UHMWPE blends from pure HDPE to pure UHMWPE in 10% increments. They measured the blends in tension, but only presented engineering properties (E, σult, ɛult, etc.) rather than constructing stress-strain curves. The dynamic viscoelastic behavior of HPDE has been measured by nano-indentation by Odegard et al. [40]. While these and other studies of polyethylene are quite extensive, most of the work has focused on a single form of PE making comparisons over a wide range of temperatures and strain-rates impractical. The focus of the current work is the presentation of a direct comparison of HDPE, UHMWPE, and PEX.

In the current work samples are tested in compression as a function of temperature (−75 to +100°C) and strain-rate (10−4 to 2,600 s−1). The results of conventional mechanical load frame and split Hopkinson pressure bar (SHPB) testing are presented along with thermomechanical analysis (TMA) and differential scanning calorimetry (DSC). The dependence of the yield stress is shown to be linear for temperature and logarithmic for strain-rate. These results are discussed in terms of an empirical mapping function proposed by Siviour et al. [41] for superposition between temperature and strain-rate.

2 Experimental Procedure

2.1 Materials and Preparation

Industrial grade polyethylene extruded sheets of HDPE, UHMWPE, and PEX were obtained from Cope Plastics (Godfrey, IL). The sheets were ∼25 mm thick. The densities are 969.8 ± 1.4, 926.8 ± 1.4, and 932.46 ± 1.5 kg/m3 for HDPE, UHMWPE, and PEX, respectively as measured by He pycnometry. All compression samples were machined from the plates in the through thickness direction.

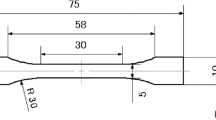
Polyethylene is a highly ductile polymer, thus large strain deformations were investigated and reported. For this reason, all strains referenced in this paper are true-strains (logarithmic strains). A constant true strain-rate was maintained for all experiments, and true-stress was calculated assuming a constant sample volume. The low- and intermediate-strain-rate compression sample geometry was 6.350 mm diameter by 6.350 mm long right-regular cylinders, while the high-strain-rate compression sample geometry was 6.350 mm diameter by 4.064 mm long right-regular cylinders.

2.2 Low and Intermediate Strain-rate Compression Testing

Quasi-static or low-strain-rate compression tests were conducted at room temperature and strain-rates from 10−4 to 1 s−1 in one decade increments and at 0.1 s−1 temperatures from −75 to 100°C. These compression tests were conducted with an MTS model 880 servo-hydraulic testing machine. For intermediate-strain-rate compression room temperature tests at 10 and 100 s−1 an MTS model 810 servo-hydraulic machine was utilized. These machines ran MTS TestStar software allowing for full control over the test profile. The tests were run in strain control and the specimen strain was measured using a displacement extensometer located near the loading platens. In all samples tested at −20°C, or higher, paraffin wax was used to lubricate the specimen ends to prevent specimen barreling [5, 42–44]. The specimens were compressed between highly polished tungsten carbide platens to further reduce frictional effects. Temperature control was carried out using either electrically heated or liquid nitrogen cooled platens and surrounding insulation was used to create a small environmental chamber. The samples were allowed to equilibrate at temperature for between 15 and 30 min prior to testing.

2.3 High-strain-rate Compression Testing

High-strain-rate data was obtained at ∼2,600 s−1 using a modified split-Hopkinson pressure bar (SHPB) [45–50]. The SHPB used for this study was equipped with 9.4 mm diameter Ti-6Al-4V bars that improve the signal-to-noise level needed to test extremely low strength materials as compared to the maraging steel bars traditionally used for SHPB studies on metals. The lower elastic modulus titanium bars help facilitate specimen stress equilibrium at lower strains and higher resolution of the low flow stress levels. The inherent oscillations in the dynamic stress-strain curves and the lack of stress equilibrium during initial load-up makes the determination of the yield strength inaccurate at best, and the determination of the elastic modulus impossible at high strain-rates. As before, paraffin wax was used to lubricate the specimen ends and the sample temperature was allowed to equilibrate prior to testing.

2.4 Validity of SHPB Testing of Polymers

The testing of these soft materials presents difficulties that are not observed during the testing of most other materials (metals and ceramics). Because of the dispersive nature of wave propagation in ductile polymers and the potential influence of specimen size on attaining a uniform stress state, the high-strain-rate constitutive response of the polymeric samples in this study were carefully probed to obtain well-posed and accurate data [45, 47–50]. Specifically, the specimen geometry and experimental techniques were modified from the standard SHPB application to obtain uniaxial stress data.

To assure valid high-rate measurements on polymers, it is necessary to examine the different analyses [45, 48] used to calculate specimen stress from the Hopkinson bar strain. In the 1-wave analysis, the specimen stress is directly proportional to the bar strain measured from the transmitted bar. The 1-wave stress analysis indicates the conditions at the sample-transmitted bar interface and is often referred to as the specimen “back stress.” This analysis results in stress-strain curves with little oscillation, especially near the yield point. Alternatively, in a 2-wave analysis, the sum of the synchronized incident and reflected bar waveforms (which are opposite in sign) is proportional to the specimen “front stress” and indicates the conditions at the incident/reflected bar-sample interface. The equations for converting these signals into stress and strain are described elsewhere [49]. Finally, a third stress-calculation variation that considers the complete set of three measured bar waveforms, the 3-wave analysis, is simply the average of the 2-wave “front” and the 1-wave “back” stress. A valid, uniaxial split Hopkinson pressure bar test requires that the stress state throughout the specimen achieves equilibrium during the test, and this condition can be checked readily by comparing the 1-wave and 2-wave (or 3-wave) stress-strain response. When the stress state is uniform throughout the specimen, then the 2-wave stress oscillates about the 1-wave stress, as seen in Fig. 1 for all three polymers. Tests that do not reach stress state equilibrium have a 2-wave profile that does not oscillate about the 1-wave profile. Once a sample achieves stress state equilibrium, it will remain in that state for most normal materials. The duration required for the sample to reach equilibrium is referred to as the ring-up period and indicated by a reduction and stabilization of the 2-wave stress oscillations about the 1-wave stress typically dominates the first 1–5% of the strain. The l/d of 0.64 employed in the current work, and several recent studies on semi-crystalline polymers [8, 11, 13, 15], for the SHPB tests yields satisfactory uniaxial stress state equilibrium for this class of polymers over the range of temperatures considered. It has previously been shown that for more compliant polymers an l/d of 0.25 to 0.5 may be necessary to achieve acceptable results [49]. Additionally, a relatively constant strain-rate is also desirable during a SHPB test. Gradually increasing or decreasing strain-rates indicate that either too much or too little energy, respectively, is available for deformation. Cases where either stress-state stability cannot be achieved during the measurement duration or a constant strain rate cannot be achieved—as can be the case for materials that exhibit significant strain hardening or softening—can be mitigated by employing pulse-shaping techniques [51, 52]. In the current study we observed the samples to reach equilibrium prior to the strain levels of interest and the strain rate evolution to be acceptable, therefore we found pulse shaping to be unnecessary.

Fig. 1
figure 1

SHPB stress-strain response at 20°C for (a) HDPE, (b) UHMWPE, and (c) PEX with 1- and 2-wave stress curves illustrating stress state stability and strain-rate

Full size image

2.5 Thermomechanical Analysis and Differential Scanning Calorimetry

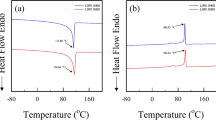
Samples of the three polymers were characterized by differential scanning calorimetry (DSC) and thermomechanical analysis (TMA). Thermomechanical analysis, using a Perkin Elmer TMA-7 was run on an ∼1 mm thick sample in the through thickness direction. DSC scans were conducted using a cryogenic Perkin Elmer DSC-7 on ∼15 mg sample of each polymer. Both tests were performed from −150 to ∼150°C at a rate of 2–10°C/min under a nitrogen purge gas. Both methods were employed to determine the glass transition temperature (T g) and melt temperature (T m).

It is worth noting that the glass transition temperature of PE has been a subject of significant debate and discussion. Davis and Eby [53] provides an excellent illustration of this disagreement in a histogram of the reported values of T g from 50 peer reviewed sources based on thermal expansion, calorimetry, NMR, mechanical testing, electron spin resonance, and small-angle X-ray. The T g of PE had been reported to be in every decade of temperature from −140 to 70°C by at least one source. At the time of Davis’s publication in 1973 most sources reported the T g to be in the range of −18 ± 18°C, with a second collection of reports suggesting ∼−123°C. The literature continues to present a discrepancy in the value of T g, see Table 1. A rough estimate can also be surmised from the simple rule-of-thumb of \( T_{g} = 2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3 \) T m, where T m is the melting temperature in Kelvin. From T m = 133°C the value of T g should be on the order of −2°C. Independent of the correct T g, these values fall well within the range of temperatures investigated.

Table 1 Literature values for T g
Full size table

3 Results and Discussion

3.1 Compressive Response

Figures 2, 3 and 4 show the compressive true-stress versus true-strain response of HDPE, UHMWPE, and PEX, respectively. In each case part (a) shows the compressive response as a function of temperature and part (b) provides the response as a function of strain-rate. For ease of comparison the same scale is used for all of the plots. All three forms of PE exhibit classic increases in initial tangent modulus and yield stress with either a decrease in temperature or increase in strain-rate. Varying of the temperature over a range from −75 to 100°C presents a much larger impact on the true-stress versus true-strain response than observed for varying the strain-rate from 10−4 to ∼2,600 s−1. While the responses of UHMWPE and PEX are very similar, they exhibit some significant differences from HDPE (see Fig. 5). The HDPE samples exhibit a higher yield stress followed by a flow behavior that is flat to first order. Conversely UHMWPE and PEX both exhibit strain-hardening after yield. However, their yield stress is significantly lower such that they do not reach the flow stress level of HDPE until between 40 and 50% true strain. Starting at 0°C HDPE exhibits a subtle post yield softening that becomes increasingly pronounced as the temperature is further decreased. Both UHMWPE and PEX exhibit a bi-linearity to their flow behavior, with the hardening rate (i.e., the slope) increasing above ∼15% true strain. This break in slope becomes more apparent as the temperature is reduced, being observable only at room temperature and below. For a given temperature and strain-rate the phenomenon is more pronounced in PEX than UHMWPE both in terms of the magnitude of the change in slope and sharpness of the transition (i.e. the change in both the first and second derivatives).

Fig. 2
figure 2

Response of HDPE as a function of (a) temperature (at 10−2 s−1) and (b) strain-rate (at 20°C)

Full size image
Fig. 3
figure 3

Response of UHMWPE as a function of (a) temperature (at 0.1 s−1) and (b) strain-rate (at 20°C)

Full size image
Fig. 4
figure 4

Response of PEX as a function of (a) temperature (at 0.1 s−1) and (b) strain-rate (at 20°C)

Full size image
Fig. 5
figure 5

Comparison of stress-strain response of HDPE, UHMWPE and PEX at a strain-rate of 0.1 s−1 and a temperature of 20°C

Full size image

Because of the ring-up period during SHPB testing—typically 1–5% strain depending on sample/bar impedance mismatch, sample sound speed, bar straightness, etc.—it is impossible to accurately measure an elastic modulus [49]. While the initial tangent modulus qualitatively evolves as expected with temperature and strain-rate, in the current work we focus on the flow response to quantify the temperature and strain-rate dependence. Since classic criteria for yield stress (i.e., the 2% offset of the tangent modulus or the intersection of the extrapolated tangent modulus and linear flow response) require the tangent modulus, we instead simply compare the stress level at specified strain levels. Figures 6, 7 and 8 show the stress level at 7.5 and 20% strain in HDPE, UHMWPE, and PEX, respectively. The lower strain value of 7.5% was chosen as a point that is high enough to ensure that the material has undergone yielding for all loading conditions investigated, but low enough to capture the maximum value prior to the subtle post yield softening seen in HDPE at low temperatures. The higher strain value of 20% is included to further elucidate the different flow behaviors. Again, for ease of comparison the same scale is used for all of the plots. Error bars indicating the standard deviation are presented for the data points corresponding 7.5% strain. For clarity they are omitted from the data points corresponding to 20% strain, although the standard deviations are similar for both strain levels.

Fig. 6
figure 6

Stress levels at 7.5 and 20% strain in HDPE as a function of (a) temperature and (b) strain-rate. The solid lines represent linear best fits for 7.5% strain, and the dashed lines represent linear best fits for 20% strain

Full size image
Fig. 7
figure 7

Stress levels at 7.5 and 20% strain in UHMWPE as a function of (a) temperature and (b) strain-rate

Full size image
Fig. 8
figure 8

Stress levels at 7.5 and 20% strain in PEX as a function of (a) temperature and (b) strain-rate

Full size image

The most noteworthy aspect of the Figs. 6, 7 and 8 is that for all three polymers the temperature dependence can be captured by a simple linear fit (\( \sigma = B + C \cdot T \)) over the full range of temperatures and the strain-rate dependence can be captured by a simple logarithmic fit (i.e., linear in log(strain-rate) space, \(\sigma = D + E\log {\left( {{\mathop \varepsilon \limits^ \cdot }} \right)}\)) over the full range of rates. In both cases the fits fall well within the error bars and fit to the average values with an accuracy of Pearson’s R = 0.99 or better. This ideal behavior is, to the author’s knowledge, unique for polymers. In previous work [8–20], on semi-crystalline polymers two deviations from these ideal behaviors have been reported. First, when plotting the yield stress as a function of temperature, a bi-linear dependence on temperature is consistently observed. This is generally due to transitioning through the glass transition temperature, T g, but can also arise from thermally induced phase transitions. Second, although a linear dependence on log(strain-rate) is generally accepted for low strain-rates, most polymers divert from this relationship exhibiting enhanced flow stress at higher strain-rates. Briscoe and Nosker [61] previously observed this lack of flow stress enhancement in HDPE.

The constants associated with the fits through the data are given in Table 2. The values B and D provide relative measures of the magnitude of the yield stress (at \(T = {\mathop \varepsilon \limits^ \cdot } = 0\)), while C and E indicate the sensitivity to temperature and strain-rate respectively. As previously indicated HDPE has a higher yield stress than the other two forms of PE (∼72% higher at 20°C and 0.1 s−1). Although it is on the level of the sample-to-sample variability, PEX appears to exhibit a marginally higher yield stress than UHMWPE (∼3% higher). We also observe that the temperature and strain-rate dependences of HDPE are significantly stronger than for UHMWPE, 72 and 67%, respectively. Conversely, the temperature dependence of PEX is only 6% greater than for UHMWPE, while the strain-rate dependence is 29% greater. This difference in strain-rate dependence is the most substantial quantitative difference between PEX and UHMWPE. Comparing the curve for stress levels at 7.5% strain with the curve for 20% strain, some observations can be made regarding the average strain hardening responses of these materials (see Fig. 9). For HDPE, the 20% strain data consistently falls above the 7.5% strain data, albeit within the error bars, indicating very little strain hardening. On the other hand, the 20% strain data falls significantly above the 7.5% strain data for UHMWPE and PEX. For both UHMWPE and PEX, the 7.5 and 20% strain data set diverge with decreasing temperature. For UHMWPE, these two data sets similarly diverge with increasing strain-rate, whereas they are nearly parallel for PEX over the range of strain-rates.

Table 2 Fit constants for temperature and strain-rate dependence at ɛ = 7.5%
Full size table
Fig. 9
figure 9

Stress levels at 7.5% strain in HDPE, UHMWPE, and PEX as a function of strain-rate

Full size image

3.2 TMA, DSC, and T g

The thermomechanical analysis and differential scanning calorimetry results for HDPE, UHMWPE, and PEX are shown in Figs. 10, 11 and 12, respectively. All three forms of PE exhibit similar melt temperatures that can be determined from the rapid volume change from TMA and the peak of the DSC melt endotherm. High-density polyethylene exhibits a T m of ∼134°C, while the T m of UHMWPE and PEX is ∼133°C. Literature values are 132–136°C [27, 29, 39]. More notably, T m in HDPE has an associated volume decrease, whereas UHMWPE and PEX exhibit the more common volume increase. This may be due to the much higher degree of crystallinity present in the HDPE compared to PEX and UHMWPE. Below T m the TMA traces of both PEX and UHMWPE exhibit smooth increases with temperature that can be described by coefficients of thermal expansion of 138.5 and 124.5 × 10−6/°C, respectively. The TMA trace of HDPE exhibits a small transition in slope at ∼3°C, indicative of a glass transition. However, neither PEX nor UHMWPE exhibited a similar transition. It is worth noting that melting in the cross-linked material only refers to disordering of the crystalline domains and does not affect the crosslink sites. In addition, the DSC traces from the three polymers exhibited no transitions in the form of endo- or exo-therms that might reflect a glass transition. As such, while HDPE appears to have a glass transition a few degrees above 0°C, no clear glass transition temperature could be identified for either PEX or UHMWPE. Integrating the area under the DSC melt endotherm from 100 to 150°C yields heat of melt of 236.9, 113.0, 109.5 J/g for HDPE, UHMWPE, and PEX, respectively. Taking the heat of melt for a perfect PE crystal to be 293 J/g from [25, 29, 33, 39, 62, 63] the percent crystallinity of the HDPE, UHMWPE, and PEX are 80.9, 38.6, and 37.4% respectively (Sobieraj et al. [27] used 288.84 J/g). All of these values are summarized in Table 3.

Fig. 10
figure 10

DSC and TMA traces for HDPE

Full size image
Fig. 11
figure 11

DSC and TMA traces for UHMWPE

Full size image
Fig. 12
figure 12

DSC and TMA traces for PEX

Full size image
Table 3 Thermal properties of the three polyethylene materials
Full size table

While there is not a clear change in slope of the yield stress versus temperature plots [Figs. 6(a), 7(a), and 8(a)] that would unequivocally define the glass transition temperature, there is an accumulation of subtle data that we can use to point at a T g. For HDPE there is the transition to post yield softening at ≥0°C [Fig. 2(a)], there is the transition in the DSC trace centered at ∼0°C (Fig. 10), and the rule-of-thumb of 2/3 T m (in K) suggests a value of −2°C. Taking these indicators we can go back to the data in Fig. 5 and see that it would be reasonable to fit the data to two straight lines, one for data at ≤−25°C and the other for ≥0°C. Unfortunately, the two linear fits actually diverge rather than crossing to indicate a precise T g. However, all of these indicators point to a T g for HDPE between the test conditions of −25 to 0°C. Similarly, for UHMWPE and PEX there is bi-linearity to their flow behavior at ≥20°C, there are the transitions in the DSC trace centered at ∼−10°C (Figs. 11 and 12) with a parallel transition in the TMA trace for PEX (Fig. 12), and the rule-of-thumb of 2/3 T m (in K) suggests a value of −1°C. Going back to the data in Figs. 7(a) and 8(a), it would be reasonable to fit the data to two straight lines, one for data at ≤0°C and the other for ≥20°C. These indicators point to a T g for UHMWPE and PEX between the test conditions of 0–20°C.

3.3 Temperature-rate Superposition

Siviour et al. [41] proposed an empirical mapping to relate temperature to strain-rate for polymer. For this mapping, the new temperature, T map, is defined as:

$$T_{{{\text{map}}}} = T_{{\exp }} + A{\left( {\log {\left( {{\mathop \varepsilon \limits^ \cdot }_{{{\text{map}}}} } \right)} - \log {\left( {{\mathop \varepsilon \limits^ \cdot }_{{\exp }} } \right)}} \right)},$$
(1)

where the subscript exp indicates the experimental values and map indicates the new values. The empirical material constant A can be determined by fitting to the experimental data. Values of A have been reported to be 17°C·log(s) for polycarbonate and polyvinylidene difluoride [41], and 8°C·log(s) for PTFE [21]. One of the challenges faced in fitting a superposition theory to temperature and strain-rate in many polymers is that the temperature response, the glass transition temperature, melting and possibly phase transitions, are not always reflected in the strain-rate data. Therefore, in many polymers, average global superposition between temperature and strain-rate is quite successful, they are often not point-wise accurate. For example PTFE exhibits two crystalline phase transitions at ∼19 and 30°C, which do not shift with increasing strain rate and have no corollary transitions with strain-rate [14]. The apparent lack of significant thermal transitions in the three forms of PE investigated lends them to being captured accurately by equation (1).

The linear (\( \sigma = B + C \cdot T \)) and logarithmic (\( \sigma = D + E\log {\left( {{\mathop \varepsilon \limits^ \cdot }} \right)} \)) fitting functions can be rewritten as:

$$ T_{{\exp }} = {{\left( {\sigma _{{\exp }} - B} \right)}} \mathord{\left/ {\vphantom {{{\left( {\sigma _{{\exp }} - B} \right)}} C}} \right. \kern-\nulldelimiterspace} C $$
(2)

and

$${\mathop \varepsilon \limits^ \cdot }{\mathop Y\limits^\prime }_{{\exp }} = 10^{{{\left( {{{\left( {\sigma _{{\exp }} - D} \right)}} \mathord{\left/ {\vphantom {{{\left( {\sigma _{{\exp }} - D} \right)}} E}} \right. \kern-\nulldelimiterspace} E} \right)}}} ,$$
(3)

where equation (2) is determined at \({\mathop \varepsilon \limits^ \cdot }_{{\exp }} = 0.1\;s^{{ - 1}} \) and equation (3) is derived for T exp = 20°C. Equations (1) and (3) can be solved to yield:

$$T_{{{\text{map}}}} = T_{{\exp }} + A{\left( {\log {\left( {{\mathop \varepsilon \limits^ \cdot }{\mathop Y\limits^\prime }_{{{\text{map}}}} } \right)} - {{\left( {\sigma - D} \right)}} \mathord{\left/ {\vphantom {{{\left( {\sigma - D} \right)}} E}} \right. \kern-\nulldelimiterspace} E} \right)}.$$
(4)

If T exp and ɛ. 0.1 s−1 in equation (4) are taken to be 20°C and 0.1 s−1, respectively, then equation (2) for the mapped temperature dependent data and equation (4) for the strain-rate data mapped into temperature dependence can be solved to find A:

$$ A = - \frac{E} {C}\frac{{\sigma - {\left( {20C + B} \right)}}} {{\sigma - {\left( {D - E} \right)}}}. $$
(5)

From this it can be seen that A will be a unique value if and only if:

$$ B + 20C = D - E. $$
(6)

This simply states that the functions for temperature and strain-rate dependence must generate a single common point at their intersection. Moreover, if this condition is fulfilled then

$$ A \equiv { - E} \mathord{\left/ {\vphantom {{ - E} {C.}}} \right. \kern-\nulldelimiterspace} {C.} $$
(7)

One non-ideal aspect of the data fitting shown above is that it does not intersect uniquely at ɛ. = 0.1 s−1 and T = 20°C, i.e. for HDPE the predicted stress level at this point from equation (2) is 37.0 MPa while equation (3) predicts 38.8 MPa. Thus equation (6) is not rigorously satisfied. Table 2 shows the deviation from this equality as δ, defined as (\( {\left( {B + 20C} \right)} - {\left( {D - E} \right)} \)). For all three polymers, the deviation at the intersection point is well within the error bars of the experimental measurements. To rigorously satisfy equation (6) one could shift the two curves to force them to intersect at the desired point, i.e., increase B by δ/2 and decrease D by δ/2. However, since shifting Band D does not effect equations (7) and (6) is satisfied to within experimental error, values of A are calculated and given in Table 2. The calculated A values are of the same magnitude as those previous reported for PC, PVDF, and PTFE. While A for HDPE and UHMWPE agree to within 3%, the value for PEX is 25% higher.

Some precautions must be considered when applying equation (1). First, if equation (6) is not absolutely satisfied, the error in the shifted data, δ’, increases faster than the error δ, as illustrated in Fig. 13. It can been seen that the experiment temperature function and the mapped temperature function (mapped from strain-rate data) are parallel curves offset by ∼3.3 MPa. If equation (6) is fulfilled, then these two curves lie on top of one another. However, it is important to keep in mind that even if δ is within experimental error, δ’ may not be. Second, A can be calculated point-wise as a function of σ (i.e., for each stress level in Fig. 13, the value of A required to shift one curve to the other can be calculated from equation (1)), as illustrated in Fig. 14 for HDPE. This method could be necessary for polymers not fit by simple functions. If the stress is not a unique value at the intersection of the temperature and strain-rate data, A(σ) will be unstable in the vicinity of the intersection stress, σX. The greater δ, the more rapidly A(σ) diverges. At σ far from σX, the function of A(σ) approaches the unique value of A. Therefore, if A is to be determined point-wise from experimental data, it is important to acquire data over a wide range of temperature and strain-rates, and to select the value of A as far possible from the intersection of the two data sets.

Fig. 13
figure 13

Fit equations for temperature and strain-rate dependence of HDPE mapped to the superposition equation

Full size image
Fig. 14
figure 14

‘A’ calculated point-wise for a HDPE with unique and non-unique sets of temperature and strain-rate curves

Full size image

3.4 T g Superposition

The current suggested construct can now be used to discuss a broader range of temperature and strain-rate phenomena in polymers. Due to the tack of a clear mechanical T g in polyethylene, this phenomenon is presented using literature data for other polymers. Numerous researchers (for example see [8, 9, 13, 15, 41, 64]) have presented data of yield stress versus temperature with a bilinear behavior indicating the glass transition temperature for a range of polymers. The T g point is shown to shift to higher temperatures with increasing strain-rate. Equation (1) can be rewritten to define the glass transition temperature under deformation as:

$$T^{{{\text{deformation}}}}_{g} = T^{{{\text{thermodynamic}}}}_{g} + A{\left( {\log {\left( {{\mathop \varepsilon \limits^ \cdot }{\mathop Y\limits^\prime }^{{{\text{deformation}}}} } \right)} - \Psi } \right)}$$
(8)

where \( T^{{{\text{thermodynamic}}}}_{g} \) is the inherent thermodynamic T g in the unloaded state as determined from DSC or similar measurement, \({\mathop \varepsilon \limits^ \cdot }{\mathop Y\limits^\prime }^{{{\text{deformation}}}} \) is the strain-rate of interest, and Ψ is a material constant. Mathematically Ψ is the log of the strain-rate associated \( T^{{{\text{thermodynamic}}}}_{g} \), which is required to be non-zero. Although the applied strain-rate is zero, it is physically intuitive that there should be a non-zero strain-rate term. On the molecular scale there is always mobility in the polymer chains that will have a non-zero energy term associated with it. On the continuum scale, polymers are always undergoing some level of creep; physically Ψ captures these rate phenomena. From literature data on Kel F-800, \( T^{{{\text{thermodyrnamic}}}}_{g} \) was reported to be 27°C and \( T^{{{\text{deformation}}}}_{g} \) was 33 and 53°C for strain-rates of 0.001 and 3,200 s−1, respectively [13]. This dependence is captured by A = 3.1, which is slightly lower than seen in this current research or in previously fit values, but is still of the same order of magnitude. Also Ψ = −5.0, which suggests an inherent mobility on the order of 10−5 s−1.

Several researchers (for example see [1, 21, 41]) have also presented data on yield stress versus strain-rate for a range of polymers showing a bilinear behavior. The location of this transition has often been estimated based on the extrapolated effect of T g. An illustration of the bi-linear temperature dependence of the yield stress and the resulting strain-rate dependence is shown in Fig. 15. As can be seen, the bi-linear dependence on temperature around T g produces the proposed bi-linearity when mapped into strain-rate space. It also illustrates that small variations in T g can lead to large changes in the strain-rate dependence. In the case described here, the break in slope in strain-rate space is increased from 10 to 316 s−1 when the T g is depressed by only 15°C. An additional effect of small changes in temperature mapping into large changes in strain-rate is that data collected over the modest temperature range of −75 to 100°C maps to strain-rates far in excess of what can be experimentally measured. In Fig. 15, this temperature range predicts strain-rates from ∼10−9 to 109 s−1. Experimentally, at strain-rates below ∼10−5 s−1, extreme care needs to be taken to avoid small temperature fluctuations over the course of long measurements. At the upper end, even the smallest miniture-SHPBs can only achieve reported strain-rates up to ∼104 s−1 [21], and the strain-rate present in strong shock waves in polymers is only ∼106 s−1. Any extrapolation beyond the strain-rates used to calibrate the model should be done with care. Despite this, the model does pose an interesting opportunity for conjecture beyond our current experimental capabilities.

Fig. 15
figure 15

Illustrative stress levels as a function of (a) temperature and (b) strain-rate from the superposition equation

Full size image

Figure 15 illustrates the source of apparent power law behavior in the rate dependence of some polymers. While the glass transition is commonly quoted as a number, the transition actually occurs over a range of temperatures. One method for determining T g is dynamic mechanical analysis, which measures the small strain tangent modulus E as a function of temperature. When E is plotted as a function of temperature, most polymers exhibit three semi-linear regimes: (I) a glassy regime at low temperatures with minimal negative slope, (II) a transition regime with a very steep negative slope, and (III) a rubbery regime at high temperatures with a modest negative slope. The value of T g is commonly defined as the midpoint of region II (which also coincides with the peak in the tan δ curve), although this region can encompass several tens of degrees Celsius. The effect of the glass transition regime on yield stress is to produce a smooth curved transition between the two slopes, rather than the idealized intersecting point. This is illustrated in Fig. 15 as a transition over a range of 25°C. At this point it should be kept in mind that few studies have had the fidelity between temperature test conditions to have more than one, or at most two, data points fall within a temperature range of 25°C. This means that this transition is not well defined experimentally, and more importantly means that it has been easily ignored. However, when mapped into strain-rate space, this small thermal transition region of 25°C is spread out between ∼0.1 and 500 s−1, indicating a possible reason for the observed power-law behavior seen in some polymers [3, 11, 15]. It is also significant that in the illustration in Fig. 15—which is representative of the polymers where this behavior has been reported—this transition occurs at strain-rates between upper range of most conventional mechanical load frames (∼0.1–1 s−1) and the lower range of the split Hopkinson pressure bar (SHPB) (∼1,000 s−1). Therefore, even in many of the studies where one simple logarithmic fit has been made to low rate data, and a second has been made to high rate data, the power-law may have provided a better fit if intermediate strain-rate data had been available.

4 Conclusions

High-density polyethylene (HDPE), ultra high molecular weight polyethylene (UHMWPE), and cross-linked polyethylene (PEX) were tested in compression as a function of temperature (−75 to +100°C) and strain-rate (10−4 to 2,500 s−1). While the responses of UHMWPE and PEX are very similar, they exhibit some significant differences from HDPE. The HDPE samples exhibit a significantly higher yield stress followed by a flow behavior that is flat to first order. Conversely, UHMWPE and PEX both exhibit significant strain-hardening after yield. However, their yield stress is sufficiently lower such that they do not reach the flow stress level of HDPE until between 40 and 50% true strain. Starting at 0°C, HDPE exhibits a subtle post yield softening that becomes increasingly pronounced as the temperature is further decreased. Both UHMWPE and PEX exhibit a bi-linearity to their flow behavior, with the hardening rate (i.e., the slope) increasing above ∼15% true strain. This break in slope becomes more apparent as the temperature is reduced and is only observed at room temperature and below. For a given temperature and strain-rate, the phenomenon is more pronounced in PEX than UHMWPE. The temperature and strain-rate dependence are captured by simple linear and logarithmic fits, respectively, over the full range of conditions investigated. The temperature and strain-rate dependences of HDPE are 72 and 67% stronger than for UHMWPE, while for PEX they are 6 and 29% greater, respectively. While clear glass transition temperatures were not observed, numerous indicators pointed to a T g between −20 to 0°C for HDPE and 0 to 20°C for UHMWPE and PEX. The yield behavior is presented in terms of an empirical mapping function that is extended to analytically solve for the mapping constant. The power-law dependence of strain-rate observed in some polymers is explained using this mapping function.