Locating pivotal connections: the K-Truss minimization and maximization problems

Abstract

In social networks, the strength of relationships between users can significantly affect the stability of the network. Two users are more likely to build the friendship if they share some common friends. Meanwhile, the breakdown or enhancement of critical connections may lead to a cascaded phenomenon and cause the social network collapsed or reinforced. In this paper, we leverage the k-truss model to measure the stability of a social network. To identify the critical edges, we propose two novel problems named k-truss minimization problem and k-truss maximization problem. Given a social network G, a positive integer k and a budget b, it aims to find b edges for deletion (resp. addition), which can lead to the maximum number of edges collapsed (resp. added) in the k-truss of G. We prove that both problems are NP-hard. To accelerate the computation, novel pruning rules and searching paradigms are developed for the corresponding problem. Comprehensive experiments are conducted over 9 real-life networks to demonstrate the effectiveness and efficiency of our proposed models and approaches.

1 Introduction

As a key problem in graph analysis, the mining of cohesive subgraphs, such as k-core, k-truss, clique, etc, can find many important real-life applications [6, 15, 16, 20, 24, 26]. The mined cohesive subgraph can serve as an important metric to evaluate the properties of a network, such as network engagement and stability. In this paper, we use the k-truss model to measure the cohesiveness of a social network. Unlike k-core, k-truss not only emphasizes the users’ engaged activities (i.e., number of friends), but also requires strong connections among users (i.e., common friends). That is, the k-truss of a graph G is the maximal subgraph where each edge is involved in at least k − 2 triangles. Note that, triangle is an important building block for the analysis of network structure [7, 19]. The number of edges in the k-truss can be utilized to measure the stability of network structure.

Motivation

The breakdown of a strong connection may affect other relationships, which can make certain relationships involved in less than k − 2 triangles and removed from the k-truss. Hence, it will lead to a cascading breakdown of relationships eventually. Likewise, the addition of new connections to the graph can also strengthen the communities in the graph and expand the size of the corresponding k-truss. To identify the critical edges, in this paper, we propose and investigate the k-truss minimization (KMIN) problem and k-truss maximization (KMAX) problem through edge manipulation. Given a graph G and a budget b, k-truss minimization (resp. maximization) problem aims to find a set B of b edges, which will lead to the largest number of edges broken (resp. engaged) in the k-truss by deleting (resp. adding) B.

Example 1

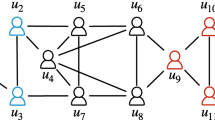
Figure 1 shows a small network with 12 users. The engagement of users in the group is affected by the number of his friends and strong connections. The withdrawal or construction of certain connections will significantly influence size of the community structure, i.e., k-truss. Suppose k = 5. The subgraph in the dotted circle is the corresponding 5-truss. If we delete the connection between u₅ and u₆, it will cause the whole community collapsed, i.e., all the connections dropped from the 5-truss. This is because they are no longer fulfilling the requirement of 5-truss. On the contrary, if we establish a new connection between u₃ and u₉, then the subgraph in the dotted rectangle, except for edges (u₃, u₄) and (u₇, u₈), will be the new 5-truss. We can see, the deletion or addition of one single edge can seriously influence the structure of the community.

Fig. 1

Motivating example

The k-truss minimization and maximization problems can find many applications in real life. For instance, given a social network, we can reinforce the community by paying more attention to the critical relationships. In addition, we can provide some incentives to users and make them build new connections in order to strength the network. This is very essential for an emerging social network platform, which requires to enlarge the number of active users inside. Also, we can detect vital connections in enemy’s network for military purpose. Moreover, in road network, facility network and biology network, we can protect the identified connections in order to enhance the corresponding network or attack them if they belong to the enemies.

Challenges and contributions

To the best of our knowledge, we are the first to investigate the k-truss minimization and maximization problems through edge manipulations. We prove both of the problems are NP-hard. Although we can compute the k-truss in polynomial time, i.e., O(m^1.5), where m is the number of edges in the graph, while the enumeration of all combination of b edges makes the problem hard to compute. To avoid verifying all the combinations, we adopt a greedy framework in the paper by selecting the best edge in each iteration. In addition, in real applications, the graph is usually large in size, which results in a large size of candidate space. Moreover, the real-life networks are usually sparse. It makes the k-truss maximization problem even harder, since the candidate space of this problem is O(n² − m) instead of O(m) for the k-truss minimization problem, where n is the number of nodes in the graph.

In the literature, there are some researches that focus on modifying important nodes or edges to influence the community, e.g., [21, 28]. However, they either aims to find important nodes (e.g., [21]) or focus on different cohesive subgraph models (e.g., [28]), which make them hard to apply for the problems investigated in this paper. Even though the greedy framework can accelerate the search and return competitive results, it is still hard to scale. In this paper, we leverage the properties of k-truss to filter the candidate space. Group structure and layer-based techniques are developed to reduce the computation cost. In addition, novel upper bound based methods are proposed to skip unpromising candidates. Our principal contributions are summarized as follows.

• To find critical connections, we conduct the first research to investigate the k-truss minimization and maximization problems. We prove both of the problems are NP-hard.

• To scale for large graphs, optimized algorithms are developed. Together with early termination and pruning techniques, we further reduce the number of candidates, which can significantly enhance performance of the algorithms.

• Extensive experiments are conducted over 9 real-world social networks to verify the performance of the proposed techniques.

2 Preliminaries

In this section, we first present some related concepts and then formally define the k-truss minimization and maximization problems, respectively. Finally, we prove the properties of the investigated problems. The notations that are frequently used throughout the paper are shown in Table 1.

Table 1 Summary of notations

2.1 Problem definition

We consider a social network G = (V, E) as an undirected graph, where V and E represent the sets of nodes and edges in G, respectively. Given a subgraph $S \subseteq G$, we use V_S (resp. E_S) to denote the set of nodes (resp. edges) in S. N(u, S) is the neighbors of u in S. D(u, S) equals |N(u, S)|, denoting the degree of u in S. m = |E| (resp. n = |V |) is the number of edges (resp. nodes) in G. Assuming the length of each edge equals 1, a triangle is a cycle of length 3 in the graph. For e ∈ E, a containing-e-triangle is a triangle that contains e, denoted by △_e. We say a node u is incident to an edge e or e is incident to u, if u is one of the endpoints of e.

Definition 1 (k-core)

Given a graph G, a subgraph S is the k-core of G, denoted by C_k, if (i) S satisfies degree constraint, i.e., deg(u, S) ≥ k for every u ∈ V_S; and (ii) S is maximal, i.e., any supergraph of S cannot be a k-core.

Definition 2 (edge support)

Given a subgraph $S \subseteq G$ and an edge e ∈ E_S, the edge support of e is the number of containing-e-triangles in S, denoted as sup(e, S).

Definition 3 (k-truss)

Given a graph G, a subgraph S is the k-truss of G, denoted by T_k, if (i) sup(e, S) ≥ k − 2 for every edge e ∈ E_S; (ii) S is maximal, i.e., any supergraph of S cannot be a k-truss; and (iii) S is non-trivial, i.e., no isolated node in S.

Definition 4 (trussness)

The trussness of an edge e ∈ E_G, denoted as τ(e), is the largest integer k that satisfies $e \in E_{T_{k}}$ and $e \notin E_{T_{k+1}}$.

Based on the definitions of k-core and k-truss, we can see that k-truss not only requires sufficient number of neighbors, but also has strict constraint over the strength of edges. It is easy to verify that a k-truss is at least a (k − 1)-core. Therefore, to compute the k-truss, we can first compute the (k − 1)-core and then find the k-truss over (k − 1)-core by iteratively removing all the edges that violate the k-truss constraint. The detailed algorithm is shown in Algorithm 1, whose time complexity is O(m^1.5) [17].

As discussed in Section 1, the deletion of certain edges in the graph G can significantly affect the structure of the community, i.e., k-truss. Given an edge set $B\subseteq E$, we use $T_{k}^{-B}$ to denote the k-truss after deleting B and $|T_{k}^{-B}|$ denotes the number of edges in $T_{k}^{-B}$. We define the followers $F(B,T_{k}^{-})$ of B as the edges that are removed from T_k due to the deletion of B. Then, we can define the k-truss minimization problem as follows.

Problem Statement 1

Given a graph G and a budget b, the k-truss minimization (KMIN) problem aims to find a set B^∗ of b edges, such that the $|T_{k}^{-B^{*}}|$ is minimized. It is also equivalent to finding an edge set B^∗ that can maximize $|{B^{*},T_{k}^{-}}|$, i.e.,

$$ B^{*} = \underset{B \subseteq E \wedge |B| = b}{\arg\max}|{B,T_{k}^{-}}| $$

Similarly, adding new edges to the graph can also enlarge the corresponding community size. Given an edge set $B \subseteq (V\times V) \setminus E$, we use $T_{k}^{+B}$ to denote the k-truss after adding B to the graph G. We use $|T_{k}^{+B}|$ to denote the number of edges in $T_{k}^{+B}$. We define the followers $F(B,T_{k}^{+})$ of B as the edges that are added to the new k-truss due to the addition of B. Then, we can define the k-truss maximization problem as follows.

Problem Statement 2

Given a graph G and a budget b, the k-truss maximization (KMAX) problem aims to find a set B^∗ of b edges, such that the $|T_{k}^{+B^{*}}|$ is maximized. It is also equivalent to finding an edge set B^∗ that can maximize $|F(B,T_{k}^{+})|$, i.e.,

$$ B^{*} = \underset{B \subseteq (V\times V) \setminus E \wedge |B| = b}{\arg\max}|F(B,T_{k}^{+})| $$

2.2 Properties of the k-truss minimization problem

Theorem 1

The k-truss minimization problem is NP-hard for k ≥ 5.

Proof

For k ≥ 5, we sketch the proof for k = 5. A similar construction can be applied for the case of k > 5. When k = 5, we reduce the k-truss minimization problem from the maximum coverage problem [10], which aims to find b sets to cover the largest number of elements, where b is a given budget. We consider an instance of maximum coverage problem with s sets T₁, T₂, .., T_s and t elements {e₁,.., e_t} = ∪_1≤i≤sT_i. We assume that the maximum number of elements inside T is R ≤ t. Then we construct a corresponding instance of the k-truss minimization problem in a graph G as follows. Figure 2(a) is a constructed example for s = 3, t = 4, R = 2.

Fig. 2

Example for the NP-hard proof of the k-truss minimization problem

We divide G into three parts, V, N and P. 1) V consists of s parts. Each part V_i corresponds to T_i in the maximum coverage problem instance. 2) N consists of t parts. Each part N_i corresponds to e_i in the maximum coverage problem instance. 3) P is a dense subgraph. The support of edges in P is no less than k − 2 + b. Specifically, suppose T_i consists of r_i ≤ R elements, V_i consists of 4R − r_i + 1 nodes and 8R − r_i edges. To construct V_i, we first construct a (4R − 2r_i)-polygon. Then, we add a node ${v^{i}_{0}}$ in the center of (4R − 2r_i)-polygon and add 4R − 2r_i edges between ${v^{i}_{0}}$ and ${v^{i}_{1}}, ..., v^{i}_{4R-2r_{i}}$. Finally, we further add r_i nodes $v^{i}_{4R-2r_{i}+1}, ..., v^{i}_{4R-r_{i}}$ and 3r_i edges $\{({v^{i}_{0}}, v^{i}_{4R-2r_{i}+1}), ({v^{i}_{1}}, v^{i}_{4R-2r_{i}+1}), ({v^{i}_{2}}, v^{i}_{4R-2r_{i}+1}), ... , ({v^{i}_{0}},$ $v^{i}_{4R-r_{i}}), (v^{i}_{2r_{i} - 1}, v^{i}_{4R-r_{i}}), (v^{i}_{2r_{i}}, v^{i}_{4R-r_{i}})\}$. With the construction, the edges in V have support no larger than 3. We use P to provide support for edges in V and make the support of edges in V to be 3. Each part in N consists of 2R + 2 nodes and the structure is a list of 4R triangles which is shown in Figure 2(a). For each element e_i in T_j, we add two triangles between N_i and V_j to make them triangle connected. The structure is shown in Figure 2(b). Note that each edge in N_i and V_j can be used at most once. We can see that edges in N have support no larger than 3. Finally, we use P to provide support for edges in N and make the support of edges in N to be 3. Then the construction is completed. The construction of V_i for R = 3 is shown in Figure 2(c).

With the construction, we can guarantee that 1) deleting any edge in V_i can make all the edges in V_i and the edges in N_j who have connections with V_i deleted from the truss. 2) Only the edges in V_i can be considered as candidates. 3) Except the followers in N, each V_i has the same number of followers. In Figure 2(a), deletion of each V_i can make 8R edges (except the edges in N) removed. Consequently, the optimal solution of k-truss minimization problem is the same as the maximum coverage problem. Since the maximum coverage problem is NP-hard, the theorem holds. □

Theorem 2

For the k-truss minimization problem, the objective function $f(x) = |F(x,T_{K}^{-})|$ is monotonic but not submodular.

Proof

Suppose $B \subseteq B^{\prime }$. For every edge e in $F(B,T_{k}^{-})$, e will be deleted from the k-truss when deleting $B^{\prime }$. Thus, $f(B) \leq f(B^{\prime })$ and f is monotonic. Given two sets A and B, if f is submodular, it must hold that f(A ∪ B) + f(A ∩ B) ≤ f(A) + f(B). We show that the inequality does not hold by constructing a counter example. In Figure 1, for k = 4, suppose A = {(u₃, u₈)} and B = {(u₈, u₉)}. We have f(A) = 2, f(B) = 2, f(A ∪ B) = 7 and f(A ∩ B) = 0. The inequation does not hold. Therefore, f is not submodular. □

2.3 Properties of the k-truss maximization problem

Theorem 3

The k-truss maximization problem is NP-hard for k ≥ 4.

Proof

We reduce the k-truss maximization problem from the maximum coverage (MC) problem [10], which is NP-hard. The MC problem is to find at most b sets to cover the largest number of elements, where b is a given budget. We consider an instance of MC with s sets T₁, T₂, ..., T_s and t elements {e₁, ... , e_t} = ∪_1≤i≤sT_i. We assume that T_i consists of x_i elements, and e_i belongs to y_i sets. Let R be the maximum number of elements in T, i.e., R = max(x_i). Then we construct a corresponding instance of the k-truss maximization problem in a graph G as follows. Figure 3(a) is a constructed example for s = 3, t = 4, R = 2 and k = 4.

Fig. 3

Example for the NP-hard proof of k-truss maximization problem

We divide G into three parts, V, N and P. 1) The part V corresponds to T_i contains s set of nodes. For each set, we construct $\lceil \frac {R}{2k-5}\rceil$ k-cliques that lack an edge (named le-clique), and all le-cliques share the same two nodes (named s-nodes) without edge between them, for example in Figure 3(c). 2) The part N contains t sets of nodes corresponding to e_i. For each set, we construct a triangle with three nodes ${n^{i}_{1}}$, ${n^{i}_{2}}$ and ${n^{i}_{3}}$. 3) The part P is a k-clique. Specifically, for each element e_j contained in T_i, we add the structure in Figure 3(b) between an edge in V_i and edge $({n^{j}_{1}},{n^{j}_{2}})$ to make them triangle connected. Note that every edge in V_i can only be used once and only 2k − 5 edges in each le-clique in V_i can be constructed. Finally, we need to use P to ensure that the support of each edge in Figure 3(b) satisfy their corresponding conditions, making sure the support of $({n^{j}_{1}}, {n^{j}_{3}})$ and $({n^{j}_{2}}, {n^{j}_{3}})$ is k − 1, and the support of $({n^{j}_{1}}, {n^{j}_{2}})$ is k − 3 + y_j. Then the construction is completed.

With the construction, we can guarantee that 1) every edge in P with stay in k-truss. 2) edges $({n^{j}_{1}}, {n^{j}_{3}})$ and $({n^{j}_{2}}, {n^{j}_{3}})$ are in k-truss. 3) edges (a, c) and (b, d) in Figure 3(b) are in k-truss. 4) there must be an edge in V_i with support equal to k − 3. 5) Add an edge between s-nodes in V_i can make V_i and the edge $({n^{j}_{1}}, {n^{j}_{2}})$ in N_j who have connections with V_i join in the k-truss. 6) Only the edge between s-nodes in V_i can be considered as candidates. 3) Except the followers in N, each V_i has the same number of followers, i.e., itself. Consequently, the optimal solution of k-truss maximization problem is the same as the maximum coverage problem. Since the maximum coverage problem is NP-hard, the theorem holds. □

Theorem 4

For the k-truss maximization problem, the objective function $f(x) = |F(x,T_{k}^{+})|$ is monotonic but not submodular.

Proof

Suppose $B \subseteq B^{\prime }$. For every edge e in $F(B,T_{k}^{+})$, e will be added to the new k-truss when adding $B^{\prime }$. Thus, $f(B) \leq f(B^{\prime })$ and f is monotonic. Given two sets A and B, if f is submodular, it must hold that f(A ∪ B) + f(A ∩ B) ≤ f(A) + f(B). We show that the inequality does not hold by constructing a counter example. In Figure 1, for k = 4, suppose A = {(u₁, u₄)} and B = {(u₃, u₉)}. We have f(A) = 0, f(B) = 0, f(A ∪ B) = 1 and f(A ∩ B) = 0. The inequation does not hold. Therefore, f is not submodular. □

3 Solution to the KMIN problem

3.1 Baseline algorithm

For the k-truss minimization problem, a naive solution is to enumerate all the possible edge sets of size b, and return the best one. However, the size of a real-world network, i.e., m, is usually very large. The number of combinations is enormous. Due to the complexity and non-submodular property of the problem, we resort to the greedy framework. Algorithm 2 shows the baseline greedy algorithm. It is easy to verify that we only need to consider the edges in the k-truss as candidates (Line 1). The algorithm iteratively finds the edge with the largest number of followers in the current k-truss (Line 3). The algorithm terminates when b edges are found. The time complexity of the baseline algorithm is O(bm^2.5).

3.2 Group based solution

The baseline method can greatly accelerate the search compared with the naive solution. However, it is hard to scale for large networks. In this section, novel pruning techniques are developed to speedup the search in baseline algorithm. Before introducing the pruning rules, we first present some definitions involved.

Definition 5 (triangle adjacency)

Given two triangles △₁, △₂ in G, they are triangle adjacent if △₁ and △₂ share a common edge, which means $\triangle _{1} \cap \triangle _{2} \neq \varnothing$.

Definition 6 (triangle connectivity)

Given two triangles △_s, △_t in G, they are triangle connected, denoted as $\triangle _{s} \leftrightarrow \triangle _{t}$, if there exists a sequence of θ triangles △₁, △₂, ... , △_θ in G, such that △_s = △₁, △_t = △_θ, and for 1 ≤ i < θ, △_i and △_i+ 1 are triangle adjacent.

For two edges e and $e^{\prime }$, we also say they are triangle adjacent, if e and $e^{\prime }$ belong to the same triangle. As shown in the baseline algorithm, we only need to consider the edges in T_k as candidates. Lemma 1 shows that we only need to explore the edges in Q.

Lemma 1

Given a k-truss T_k, let P = {e | sup(e, T_k) = k − 2}. If an edge e has at least one follower, e must be in Q, where $Q = \{e~|~e \in T_{k} \wedge \exists e^{\prime } \in P$ where e and $e^{\prime }$ are triangle adjacent}.

Proof

We prove the lemma by showing that edges in E_G ∖ Q do not have followers. We divide E_G ∖ Q into two sets. i) For edge with trussness less than k, it will be deleted during the k-truss computation. ii) For an edge e in T_k, if e is not triangle adjacent with any edge in P, it means e is triangle adjacent with edges such as $e^{\prime }$ whose $sup(e^{\prime }{T_{k}} > k-2$. If we delete e, all the edges triangle adjacent with e will still have support at least k − 2 in T_k. Thus, e has no follower. The lemma is correct. □

Based on Lemma 2, we can skip the edges that are the followers of the explored ones.

Lemma 2

Given two edges e₁, e₂ ∈ T_k, if $e_{1} \in F(e_{2},T_{k}^{-})$, then we have $F(e_{1},T_{k}^{-})$ $\subseteq F(e_{2},T_{k}^{-})$.

Proof

$e_{1} \in F(e_{2},T_{k}^{-})$, it implies that e₁ will be deleted during the deletion of e₂. Therefore, each edge in $F(e_{1},T_{k}^{-})$ will be deleted when e₂ is deleted. Consequently, we have $F(e_{1},T_{k}^{-}) \subseteq F(e_{2},T_{k}^{-})$. □

To further reduce the searching space, we introduce a pruning rule based on k-support group.

Definition 7 (k-support group)

Given a k-truss T_k, a subgraph $S \subseteq T_{k}$ is a k-support group if it satisfies: (i) ∀e ∈ S, sup(e, T_k) = k − 2. (ii) ∀e₁, e₂ ∈ S, suppose e₁ ∈△_s, e₂ ∈△_t. There exists a sequence of θ triangles △₁, ... , △_θ with △_s = △₁, △_t = △_θ. For i ∈ [1, θ), △_i ∩△_i+ 1 = e and sup(e, T_k) = k − 2. (iii) S is maximal, i.e., any supergraph of S cannot be a k-support group.

Lemma 3 shows that edges in the same k-support group are equivalent. The deletion of any edge in a k-support group can lead to the deletion of the whole k-support group.

Lemma 3

S is a k-support group of T_k. For ∀e ∈ S, if we delete e, we can have S deleted from T_k.

Proof

Since S is a k-support group of T_k, for $\forall e, e^{\prime } \in S$, suppose that $e \in \triangle _{s}, e^{\prime } \in \triangle _{t}$, there exists a sequence of θ triangles △₁, ... , △_θ with △_s = △₁, △_t = △_θ. For i ∈ [1, θ), △_i ∩△_i+ 1 = e_i and sup(e_i, T_k) = k − 2. The deletion of any edge inside the group will destroy the corresponding triangles and decrease the support of triangle adjacent edges by 1. It will lead to a cascading deletion of subsequent triangle edges in the group due to the violation of truss constraint. Therefore, the lemma holds. □

According to Lemma 3, we only need to add one edge from a k-support group to the candidate set, and the other edges in the group can be treated as the followers of the selected edge. In the following lemma, we can further prune the edges that are adjacent with multiple edges in a k-support group.

Lemma 4

Suppose that e ∈ T_k and sup(e, T_k) = w > k − 2. For a k-support group S, if e belongs to more than w − k + 2 triangles, each of which contains at least one edge in S, then e is a follower of S.

Proof

According to Lemma 3, by removing an edge from S, we have S deleted from T_k. Since e belongs to more than w − k + 2 triangles, each of which contains at least one edge in S, the support of e will decrease by more than w − k + 2 due to the deletion of S. So its support will be less than k − 2 and it will be deleted due to the support constraint. Thus, e is a follower of S. □

Group-based algorithm

We improve the baseline algorithm by integrating all the pruning rules above, and the details are shown in Algorithm 3. In each iteration, we first find k-support groups of current T_k and compute the candidate set T according to Lemma 3 (Line 4). This process, i.e., FindGroup function, corresponds to Lines 12-19. It can be done by conducting BFS search from edges in T_k. We use a hash table to maintain the group id (i.e., gID) for each edge and the gID starts from 0 (Line 13). For each unvisited edge with support of k − 2, we conduct a BFS search from it by calling function GroupExpansion (Lines 20-32). During the BFS search, we visit the edges that are triangle adjacent with the current edge, and push the edges with support of k − 2 into the queue if they are not visited (Lines 25 and 28). The edges, which are visited in the same BFS round, are marked with the current gID. For the visited edges with support larger than k − 2, we use a hash table to record its coverage with the current k-support group, and update the candidate set based on Lemma 4 (Line 31). According to Lemma 2, we can further update the candidate set after computing the followers of edges (Line 7).

3.3 Upper bound based algorithm

The group based algorithm reduces the size of candidate set by excluding the edges in the same k-support group and the followers of k-support groups, which greatly accelerates the baseline method. However, for each candidate edge, we still need lots of computation to find its followers. Given an edge, if we can obtain the upper bound of its follower size, then we can speed up the search by pruning unpromising candidates. In this section, we present a novel method to efficiently calculate the upper bound required. Before introducing the lemma, we first present some basic definitions. Recall that τ(e) denotes the trussness of e.

Definition 8 (k-triangle)

A triangle △_uvw is a k-triangle, if the trussness of each edge is no less than k.

Definition 9 (k-triangle connectivity)

Two triangles △_s and △_t are k-triangle connected, denoted as $\triangle _{s} \overset {k}\leftrightarrow \triangle _{t}$, if there exists a sequence of θ ≥ 2 triangles △₁, ... , △_θ with △_s = △₁, △_t = △_θ. For i ∈ [1, θ), △_i ∩△_i+ 1 = e and τ(e) = k.

We say two edges $e, e^{\prime }$ are k-triangle connected, denoted as $e \overset {k} \leftrightarrow e^{\prime }$, if and only if 1) e and $e^{\prime }$ belong to the same k-triangle, or 2) $e \in \triangle _{s}, e^{\prime } \in \triangle _{t}$, with $\triangle _{s} \overset {k}\leftrightarrow \triangle _{t}$.

Definition 10 (k-truss group)

Given a graph G and an integer k ≥ 3, a subgraph S is a k-truss group if it satisfies: 1) ∀e ∈ S, τ(e) = k. 2) $\forall e, e^{\prime } \in S, e \overset {k}\leftrightarrow e^{\prime }$. 3) S is maximal, i.e., there is no supergraph of S satisfying conditions 1 and 2.

Based on the definition of k-truss group, Lemma 5 gives an upper bound of $|F(e,T_{k}^{-})|$.

Lemma 5

If e is triangle adjacent with θ k-truss groups g₁, g₂, ... , g_θ, we have $|F(e,T_{k}^{-})| \leq \sum \limits _{i=1}^{\theta } |{E}_{{g}_{i}}|$.

Proof

Suppose sup(e, T_k) = w, we have w ≥ k − 2, so e is contained by w triangles and is triangle adjacent with 2w edges. We divide the edges which are triangle adjacent with e in T_k into two parts. 1) $\tau (e^{\prime }) > k$. Since the deletion of e may cause $\tau (e^{\prime })$ to decrease at most 1 , we have $\tau (e^{\prime }) \geq k$ after deleting e, which means $e^{\prime }$ has no contribution to $F(e,T_{k}^{-})$. 2) $\tau (e^{\prime }) = k$. Suppose $e^{\prime } \in g_{i}$. The deletion of e can cause trussness of each edge in g_i to decrease at most 1. Then $e^{\prime }$ can contribute to $|F(e,T_{k}^{-})|$ with at most $|{E}_{{g}_{i}}|$. Thus, $\sum \limits _{i=1}^{\theta } |{E}_{{g}_{i}}|$ is an upper bound of $|F(e,T_{k}^{-})|$. □

Based on Lemma 5, we can skip the edges whose upper bound of follower size is less than the best edge in the current iteration. However, given the trussness of each edge, it may still be prohibitive to find the k-truss group that contains an edge e, since in the worst case we need to explore all the triangles in the graph. To compute the upper bound efficiently, we construct an index to maintain the relationships between edges and their k-truss groups. To find the k-truss group for a given edge e, we extend the GroupExpansion function in Lines 20-32 of Algorithm 3. It also follows the BFS search manner. The difference is that when we explore an adjacent triangle, it must satisfy the k-triangle constraint, and we only enqueue an edge, whose trussness satisfies k-triangle connectivity constraint. After the BFS search starting from e, its involved k-truss groups can be found.

After deleting an edge e in the current iteration, the constructed k-truss groups may be changed. Therefore, we need to update the k-truss groups for the next iteration. The update algorithm consists of two parts, i.e., update the trussness and update the groups affected by the changed trussness. Given the edges with changed trussness, we first find the subgraph induced by these edges. Then we reconstruct the k-truss groups for the induced subgraph and update the original ones. Based on the k-truss groups constructed, we can compute the upper bound of followers for edges efficiently. The final algorithm, named MinEdge, integrates all the techniques proposed above for the KMIN problem.

4 Solution to the KMAX problem

Different from the k-truss minimization problem, which aims to minimize the size of k-truss through edge deletion, the k-truss maximization problem aims to add new connections to the graph in order to enlarge the k-truss. In addition, for the KMIN problem, we only need to consider the edges in T_k, i.e., O(m). However, for the KMAX problem, the candidate space is (V × V ) ∖ E, i.e., O(n² − m). In real-life networks, graphs are usually sparse, which makes the KMAX problem even harder, due to the larger searching space. Moreover, some techniques, such as group strategy, are no longer applied for the problem, since the edges are newly added to the graphs. In this section, a baseline framework is first presented. Then, novel techniques are developed to speedup the processing.

4.1 Baseline algorithm

For the k-truss maximization problem, the candidate space is (V × V ) ∖ E. A naive method is to enumerate all the combinations of edge set of size b, i.e., $O({{n^{2}-m} \choose b})$, and return optimal result. As discussed, the KMAX is much more challenging than the KMIN problem due to the larger candidate space. For example, for the small graph Wildbird used in the experiments with 149 nodes and 2,837 edges, the naive method requires 28,884.7s to find the result for k = 10 and b = 2. While, for the KMIN problem, the naive method only takes 1,941.7s to find the result. Due to the hardness of the problem, we turn to the greedy heuristic by iteratively selecting the best edge for addition and the greedy algorithm terminates when b edges are selected. Algorithm 4 presents the details of the greedy framework. The algorithm terminates when b edges are selected, which time complexity is O((n² − m)bm^1.5). However, even equipped with greedy strategy, Algorithm 4 is still hard to perform on large graphs. Therefore, we further integer Lemma 6, which will be presented later, into Algorithm 4 to serve as the baseline, named BaselineMax.

4.2 Candidate reduction

The greedy algorithm significantly reduce the time complexity by applying the greedy heuristic, but it still cannot handle large graphs due to the huge searching space. In fact, the greedy framework cannot even perform on small graphs because of the large candidate size. In this section, we propose some pruning rules to reduce the size of candidates. Before introducing the detailed lemmas, we first present some basic concepts.

Definition 11 (k-hull)

Given a graph G, the k-hull of G, denoted by H_k, is the subset of edges that belongs to T_k but not T_k+ 1, i.e., H_k = T_k ∖ T_k+ 1.

We say an edge e can have followers, if it has triangle adjacent edges that satisfy Lemma 6.

Lemma 6

Given a graph G, an edge e can have followers in current iteration, if it satisfies that (i) sup(e, G) ≥ k − 2 after e added to graph G, (ii) it can find at least one containing-e-triangle △_e such that $\forall e^{\prime } \in \triangle _{e} \setminus e$, $e^{\prime } \in T_{k-1}$ and $\exists e^{\prime \prime } \in \triangle _{e} \setminus e$, $e^{\prime \prime }$ is in (k − 1)-hull.

Proof

We prove the lemma by showing that the edge e will have no follower if any constraint is violated. For the first constraint, assume its support sup(e, G) < k − 2 after adding the edge e. Based on the definition of k-truss, it will not be involved in the k-truss or contribute to the support of other edges. Therefore, the edge will not have any follower. For the second constraint, if the edges in △_e ∖ e are both in k-truss but not in (k − 1)-hull, which means that they are already in k-truss initially, they will not be the followers of e. And if one of the edges $e^{\prime }$ in △_e ∖ e is not in (k − 1)-truss, then $e^{\prime }$ cannot be included in k-truss because the trussness of each edge will change at most by one after one edge insertion [14]. Then, the edge e also have not any follower. Therefore, at least one of edges in △_e ∖ e should be in (k − 1)-hull. Thus, the lemma is correct. □

Based on Lemma 6, the candidate space is reduced significantly. By integrating Lemma 6 with the greedy framework (i.e., Algorithm 4), we come up with the baseline approach for the KMAX problem, denoted as BaselineMax. That is, for each iteration, we only consider the edges that satisfy the lemma. To further filter the searching space, we leverage the layer structure in the T_k− 1. That is, we iteratively peeling the edges in T_k− 1 and maintain the edges in s + 1 layers. The layer construction procedure is shown in Algorithm 5. In each iteration, we only peel the edges with support smaller than k − 2 currently, until all the edges in H_k− 1 are added to the corresponding layer. The final layer, i.e., ${\mathscr{L}}_{s+1}$ consists of the edges in T_k.

Given an edge e, we use l(e) to denote its layer number in ${\mathscr{L}}$. Let G_e be the subgraph induced by edges in $\bigcup _{i\geq l(e)} {\mathscr{L}}_{i}$ and s⁺(e) = sup(e, G_e). Then, an edge can have followers if it satisfies the following lemma.

Lemma 7

Given a graph G, a candidate edge e can have followers, if it satisfies that there exists a containing-e-triangle $\triangle _{e,e_{1},e_{2}}$, such that l(e₁) ≤ l(e₂) and s⁺(e₁) = k − 3.

Proof

Since s⁺(e₁) = k − 3 and l(e₁) ≤ l(e₂), it means the added edge e can contribute support to e₁ when peeling the edges in T_k− 1. Then, e₁ will be follower of e. Thus, the lemma is correct. □

Example 2

Suppose k = 4. As shown in Figure 4(a), the graph is a 3-truss initially, i.e., T_k− 1. Based on the layer structure, we know that all the red edges consist of the first layer ${\mathscr{L}}_{1}$, whose support equals 1 currently. After peeling the edges in ${\mathscr{L}}_{1}$, the blue edges form the second layer ${\mathscr{L}}_{2}$. Then, all the other edges belong to ${\mathscr{L}}_{3}$, i.e., T_k. As observed, the edge (v₁, v₄), i.e., the dashed edge in Figure 4(b), satisfies the Lemma 7, where the newly constructed triangle {v₁, v₃, v₄} has l(v₁, v₃) ≤ l(v₃, v₄) and s⁺(v₁, v₃) = k − 3 = 1 hold. Figure 4(b) shows the 4-truss after adding the edge (v₁, v₄).

Fig. 4

Layer structure example

In the k-truss minimization problem, we can leverage Lemma 2 to skip the edge that belongs to the followers of previous computed edges. However, this rule does not hold for the k-truss maximization problem, since the candidate edge set of the KMAX problem does not exist in the graph originally. To compute the follower set for a newly added edge, we can conduct a BFS from the added edge by leveraging triangle connection. The BFS is processed layer by layer. Given a newly added edge e, let $F_{1}({e,T_{k}^{+}})$ be the follower set of e in the first layer of the BFS, i.e., the edges can form triangles with e and join the new k-truss. Then, we can skip some unpromising edge based on Lemma 8.

Lemma 8

Given two candidate edges e₁, e₂, the follower set of e₂ is computed. Then, we can skip e₁, if $F_{1}({e_{1},T_{k}^{+}}) \subseteq F({e_{2},T_{k}^{+}})$.

Proof

When adding a new edge e, it will first provide support for the edges that can form new triangles with the edge, i.e., $F_{1}(e,T_{k}^{+})$. Then, $F_{1}(e,T_{k}^{+})$ will further influence the other edges in cascade. Therefore, if $F_{1}({e_{1},T_{k}^{+}}) \subseteq F({e_{2},T_{k}^{+}})$, it means e₂ can provide the same support for $F(e,T_{k}^{+})$. That is, $F(e,T_{k}^{+})$ will be the subset of $F({e_{2},T_{k}^{+}})$. Thus, the lemma is correct. □

Based on Lemma 8, we can skip some unpromising edges by only explore $F_{1}(e,T_{k}^{+})$. By integrating the pruning strategies above, we introduce the layer-based algorithm, which details are shown in Algorithm 6. For each iteration, we construct the layer structure and prune the candidate space based on the property of layer. In addition, we leverage Lemma 8 to further reduce the computation.

4.3 Upper bound based strategy

To further skip the unpromising edges, in this section, we propose the upper bound based strategy by leveraging the concept of hull group.

Definition 12 (hull group)

Given a graph G and an integer k, g is a hull group if it satisfies the following conditions: (i) ∀e ∈ g, e is in (k − 1)-hull, (ii) $\forall e, e^{\prime } \in g, e \overset {k-1}\leftrightarrow e^{\prime }$, (iii) g is maximal, i.e., there is no supergraph of g that fulfills the first two constraints.

When adding a new edge e to the graph, new triangles will be generated. For a new triangle, if the original two edges of this triangle belong to a hull group, we consider the edge e is triangle adjacent to the group. Then, we can derive the upper bound based on Lemma 9. The lemma is similar to that in Lemma 5, which correctness can be easily verified. Thus we omit the detailed proof here.

Lemma 9

If an edge e is inserted to the graph G and e is triangle adjacent with d hull group g₁, g₂, ... , g_d, we have $|F(e,T_{k}^{+})| \leq \sum \limits _{i=1}^{d} |E_{g_{i}}|$.

Based on Lemma 9, we can skip the edges whose upper bound is smaller than the current best result. By further integrating the lemma with the layer-based method, we propose the optimized algorithm for KMAX, denoted as MaxEdge. We omit the detailed pseudocode here due to the space limitation.

5 Experiments

In this section, comprehensive experiments are conducted on 9 datasets to evaluate the efficiency and effectiveness of the proposed models and techniques.

5.1 Experiment Setup

Algorithms

To the best of our knowledge, there is not existing work on k-truss minimization and maximization problem through edge manipulation. In the experiments, we implement and evaluate the following algorithms.

• ExactMin/ExactMax. Naive algorithm for the KMIN/KMAX problem by enumerating all the combinations.

• Support. Heuristic method for the KMIN problem. In each iteration, it selects the edge that is triangle adjacent with the edge with minimum support in the k-truss.

• HullValue. Heuristic method for the KMAX problem. In each iteration, it selects the edge with the largest sum score of the two end nodes. The score of a node is the number adjacent edges in the k-hull.

• BaselineMin/BaselineMax. The baseline algorithm for the KMIN/KMAX problem introduced in Sections 3.1/4.1.

• MinEdge/MaxEdge. Optimized method for the KMIN/KMAX problem by integrating all the developed techniques.

• MinEdge-/MaxEdge-. MinEdge/MaxEdge method without upper bound based strategy in Sections 3.3/4.3 for the KMIN/KMAX problem.

Dataset and workloads

We employ 9 real-life networks (i.e., Bitcoin, Email, Facebook, Brightkite, Gowalla, DBLP, Youtube, Orkut and LiveJournal) in our experiments to evaluate the performance of the proposed methods. The datasets are public available on SNAP¹ and DBLP². Table 2 present the statistic details of the datasets. Due to the different properties of datasets, we set the default k as 15 for 6 datasets (i.e., Email, Facebook, Brightkite, Gowalla, Dblp and Youtube), and set the default k as 10, 60 and 64 for Bitcoin, LiveJournal and Orkut, respectively. For each setting, we run the algorithm 10 times and report the average value. All programs are implemented in standard C++ and compiled with gcc-4.8. All experiments are performed on a machine with an Intel i5-9600KF 3.7GHz CPU and 64 GB memory.

Table 2 Statistics of datasets

5.2 Effectiveness Evaluation for the KMIN Problem

Compare with exact solution

To evaluate the performance of the proposed greedy framework, we conduct the experiments compared with ExactMin and Support approaches by deleting b edges, where the follower size is reported. Since MinEdge only improve the efficiency of BaselineMin and MinEdge-, we only report the results of MinEdge here. Due to high-computation cost of the exact solution, we only conduct the experiment on two small datasets, i.e., Bitcoin and Artificial network for b = 3 and b = 4, respectively. The artificial network is generated by GTGraph with 500 nodes and 5,000 edges. We set k = 11 and 8 for Bitcoin and Artificial network, respectively. For the convenience, we report the inclined ratio here. That is, the ratio of ExactMin is 100%, and for the other approaches, we report the ratio compared with ExactMin. The results are shown in Table 3. As observed, compared with ExactMin, there is only slight drop for MinEdge. In addition, MinEdge is much faster than ExactMin. For b = 2 on bitcoin, ExactMin requires 10.537s to find the result, while it only takes 0.019s for MinEdge, which is 554.58X speedup. Moreover, MinEdge is much better than the support based heuristic. It verifies that the proposed method can greatly speedup the processing and provide competitive results.

Table 3 Effectiveness evaluation compared with ExactMin and Support

Effectiveness evaluation by varying k and b

To further evaluate the effectiveness, we report the experiment results by varying k and b compared with Support. Figures 5 and 6 show the result by varying k and b, respectively. As observed, MinEdge always outperforms Support significantly, which verifies the advantage of developed greedy framework. Furthermore, the follower size of the two algorithms increases as b grows, sine more edges are selected. In addition, the parameter k can greatly influence the results, since the size of T_k decreases when k increases, and the candidate space also varies a lot.

Fig. 5

Effectiveness evaluation of the KMIN problem by varying k

Fig. 6

Effectiveness evaluation of the KMIN problem by varying b

Case study for the KMIN problem

Figure 7 shows a case study on DBLP with k = 10, b = 1. We can see that the edge between Lynn A. Volk and David W. Bates is the most critical relationship. This edge has 264 followers (grey edges in the figure). Moreover, it is interesting to observe that most followers have no direct connection with them.

Fig. 7

Case study on DBLP for KMIN with k= 10 and b= 1

5.3 Efficiency evaluation for the KMIN problem

To evaluate the efficiency of proposed techniques, we report the response time of MinEdge, MinEdge- and BaselineMin by varying k and b. Figures 8 and 9 show the results by varying k and b, respectively. We can see that MinEdge and MinEdge- significantly outperform BaselineMin in all the datasets because of the pruning techniques developed. As more pruning techniques equipped, the algorithms run faster. In particular, MinEdge speedups BaselineMin by two orders of magnitude on LiveJournal for any k and b. When b grows, the response time increases for the algorithms since more edges need to be selected. When k increases, the response time decreases for the most cases, since the searching space becomes smaller.

Fig. 8

Efficiency evaluation of the KMIN problem by varying k

Fig. 9

Efficiency evaluation of the KMIN problem by varying b

5.4 Effectiveness evaluation for the KMAX problem

Compare with exact solution

To evaluate the effectiveness of proposed greedy framework, we first conduct the experiments compared with ExactMax and HullValue. Compared with the KMIN problem, the searching space of KMAX is much larger, which is cost-prohibitive even for ExactMax on very small b and network. Thus, we conduct the experiments on two small datasets, i.e., Species³ and Wildbird⁴, with 65/149 nodes and 1,139/2,837 edges, respectively. We set k equals 10 for the two datasets. Table 4 shows the experiment results, where the inclined ratio is reported. As observed, the greedy framework can achieve very competitive results, and is much better than HullValue. When b = 2, ExactMax requires 557.493s to find the result on Species, while MaxEdge only needs 0.021442s.

Table 4 Effectiveness evaluation compared with ExactMax and HullValue

Effectiveness evaluation by varying k and b

To evaluate the performance, we report the follower size by varying k and b. Figures 10 and 11 present the corresponding results. Clearly, MaxEdge outperforms HullValue significantly under all settings. In addition, for many cases, HullValue can only reports few followers. This is because, for the KMAX problem, the candidate space is huge. Even though HullValue seems to be a good heuristic, it still cannot be effective under such a large candidate space. When b grows, the follower size returned increases, since more edges are selected. Due to the different distributions of edge support and k-truss, the results vary a lot by changing k.

Fig. 10

Effectiveness evaluation of the KMAX problem by varying k

Fig. 11

Effectiveness evaluation of the KMAX problem by varying b

Case study

Figure 12 shows a case study on DBLP with k = 23, b = 1. We can see that the edge between Jeffrey M. Rothchild and Julia M. Fiskio is the most critical relationship for the KMAX problem, i.e., the dark edge in the figure. This edge has 251 followers, which are in dark gray color. As observed from the results of case studies, by changing a single connection, we can influence the community of the network a lot.

Fig. 12

Case study on DBLP, k= 23, b= 1

5.5 Efficiency Evaluation for the KMAX Problem

In Figures 13 and 14, we report the response time of proposed methods by varying k and b. Note that, we does not report the greedy framework in Algorithm 4, which is still hard to perform even on small datasets. The BaselineMax method is Algorithm 4 by integrating Lemma 6. As we can see, MaxEdge is much faster than MaxEdge- and BaselineMax under all the settings due to the optimized techniques developed. The algorithms run faster when more techniques are integrated, which verifies the effectiveness of developed strategies. The response time is proportional to the size of b, as more edges are returned. When increasing k, the response time decreases for most cases, since larger k will lead to smaller k-truss and k-hull.

Fig. 13

Efficiency evaluation of the KMAX problem by varying k

Fig. 14

Efficiency evaluation of the KMAX problem by varying b

6 Related work

Graph is widely used to model the complex relationships among entities [4, 5, 18]. Cohesive subgraph identification is of great importance to social network analysis. In the literature, different cohesive subgraph models are proposed, such as k-core [13], k-truss [8]. The k-truss model not only emphasize the engagement of users, but also requires strong connections among them. In the literature, numerous research is conducted for the k-truss decomposition problem under different settings, including in-memory algorithms [6], external-memory algorithms [17], distributed algorithms [3], etc. Huang et al. [9] investigate the truss decomposition problem in uncertain graphs. In [23], authors extend the k-truss model for signed graph. In [8], authors leverage the k-truss property to mine required communities. Recently, some research focuses on modifying the graph in order to maximize/minimize the corresponding metric, e.g., [1, 12, 25, 28]. In [22], Zhang et al.develop layer based techniques for the anchored k-core and anchored k-truss problems. Bhawalkar et al. [1] propose the anchored k-core problem, which tries to maximize the k-core by anchoring b nodes. Zhang et al. [21] investigate the k-truss and k-core minimization through node deletion. In [2, 28], authors study the problem of k-core minimization via edge modification. In [11], a game theory approach is considered for core resilience. In [12], Medya et al.try to maximize the node centrality by adding new edges to the graph. In [27], authors aim to minimize the number of butterflies in bipartite graphs. As we can see, in the previous studies, they either focus on finding important nodes or emphasize different cohesive subgraph models, which makes them difficult to support the problem studied in this paper.

7 Conclusion

In this paper, we investigate and propose the k-truss minimization and maximization problems. Given a graph G and a budget b, the problems aim to find a set of b edges in a network, such that the size of the resulting k-truss is minimized or maximized We prove both problems are NP-hard. Integrating with novel pruning strategies, greedy algorithms and optimized searching approaches are developed to speedup the processing. Finally, extensive experiments on 9 real-life network datasets demonstrate the effectiveness and efficiency of the proposed models and techniques.