Critical Nodes Identification in Large Networks: The Inclined and Detached Models

Abstract

In social networks, the departure of some users can lead to the dropout of others from the community in cascade. Therefore, the engagement of critical users can significantly influence the stability of a network. In the literature, the anchored/collapsed k-core problem is proposed, which aims to enlarge/collapse the community by anchoring/deleting certain nodes. While, in real social networks, nodes are usually associated with different preferences, such as close or conflict interest. Intuitively, a community will be more stable if more nodes share close interest and fewer of them carry conflict interest. However, most existing researches simply treat all users equally, and the inclination property is neglected. To fill the gap, in this paper, we propose two novel problems, named inclined anchored k-core (IAK) problem and minimum detached k-core (MDK) problem, to better characterize the real scenarios. We prove that both problems are NP-hard. To facilitate the computation, novel search strategies are proposed. Comprehensive experiments are conducted on 9 networks to demonstrate the effectiveness and efficiency of the proposed techniques.

1 Introduction

In recent years, modeling user engagement for user behavior has attracted great interest from researchers [2, 6, 7, 10,11,12, 28]. In social network analysis, the k-core model is widely used in the study of network stability or engagement, e.g., [2, 7, 28]. Given a graph G, k-core is the maximal subgraph, in which each node has at least k neighbors. The size of k-core plays an important role in graph analysis. To enlarge (resp. collapse) the size of k-core, the anchored (collapsed) k-core problem are proposed in the literature [2, 29]. By giving users some incentives, the anchored k-core problem aims to anchor b nodes, i.e., stay in k-core regardless of the neighbor size constraint, in order to maximize the corresponding k-core size. The selected nodes are called anchored nodes. On the contrary, the collapsed k-core problem attempt to delete certain nodes in order to minimize the corresponding k-core. In real applications, users in a network are usually associated with different properties, such as close or conflict interest, towards the community. However, the previous models treat each node equally and may fail to characterize the propensity and stability of the network.

Intuitively, a community is more stable if more nodes inside share close interest and fewer nodes hold conflict interest [3]. It will also assist more new users to join the community if the community is strongly inclined. Motivated by this, in this paper, we propose two new models, i.e., inclined anchored $k$-core(IAK) and minimum detached $k$-core(MDK), to fill the gap. For the IAK problem, we consider the nodes outsides the k-core are marked with labels, i.e., close, conflict or unlabeled. When anchoring nodes, both nodes with close and conflict interest may join the k-core community. In the IAK problem, we aim to find b anchor nodes, such that more close nodes but fewer conflict nodes will involve in the anchored k-core. For MDK problem, we consider a set $\mathcal {E}$ of nodes in the k-core are attached with conflict interest. To maintain the harmony in the community, we aim to collapse or detach the minimum number of nodes, such that all the nodes in $\mathcal {E}$ are removed from the k-core. As observed, we not only consider the size of resulting k-core, but also pore over the inclination of the returned community. Through this way, we can better portray the resilience of networks. Following are two motivating examples.

Figure 1

Motivation example

Example 1

As shown in Figure 1, there is a social network with 12 users and their corresponding connections. Suppose k = 3, the close node set F = $\{u_1, u_2,$ $u_3, u_{12}\}$ (blue nodes), the conflict node set $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$ (red nodes), and the others are marked as unlabeled. The willingness of a user to engage in the group depends on the number of his neighbors. If a user leaves the group, the willingness of his neighbors will decrease, which may lead to a cascade of others to drop out the community. Given $k=3$, only nodes $u_4, u_5, \dots , u_8$ belong to the 3-core. To enhance the inclination and stability of the group, we can anchor the critical nodes by giving them incentives. If we anchor $u_1$, there will be three close followers $\{u_1, u_2, u_3\}$ (i.e., join the anchored k-core) and no conflict followers. When $u_{12}$ is anchored, there will be four followers $\{u_9, u_{10}, u_{11}, u_{12}\}$, but three of them are from the conflict group. Thus, for b = 1, we can select $u_1$ as the optimal node to anchor. It can also be observed, simply enlarging the k-core size will not guarantee the increase of nodes with close interest.

Example 2

Reconsider the graph in Figure 1. Suppose the conflict node set $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$ and $k=2$. Then, all nodes in the graph except $u_1$ belong to the 2-core. To make the group more harmonious, i.e., not contain any conflict nodes, we need to detach some nodes from the group. Considering the cost of detaching, we need to choose as few detached nodes as possible. Thus, in the example, $\{u_9, u_{12}\}$ is the best detached node set. After deleting $\{u_9, u_{12}\}$, all the nodes in the conflict node set will be removed from the 2-core.

Challenges and Contributions In this paper, we propose and investigate the inclined anchored k-core and minimum detached $k$-coreproblems. We prove that both problems are NP-hard, which implies that it is non-trivial to solve them within polynomial time. Thus, following the routine in previous studies, in this paper, we aim to design heuristic strategies that can return competitive results efficiently. In addition, due to the different properties of the objective functions, lots of pruning rules in previous studies no longer hold for our problems. Secondly, in real-world social networks, the search space is usually quite large, which is time-consuming to conduct the exploration. To enhance the processing, different search approaches and pruning techniques are considered. The main contributions of the paper are summarized as follows.

• To the best of our knowledge, we are the first to investigate the inclined anchored k-core and minimum detached $k$-coreproblems. We formally define the problems and prove the hardness of the problems.

• For the inclined anchored k-core problem, a layer-based method is adopted to accelerate the exploration, and upper bound based techniques are integrated to further speedup the procedure.

• For the minimum detached $k$-coreproblem, two heuristic strategies, i.e., conflict remove heuristic and degree decline heuristic, are proposed by leveraging different properties of the model.

• We conduct extensive experiments over 9 datasets to evaluate the efficiency and effectiveness of proposed methods.

Roadmap The rest of this paper is organized as follows. In Sect. 2, we formally define the problems studied and show their properties. In Sect. 3, we present the solutions for the IAK problem. In Sect. 4, novel heuristic strategies are proposed for MDK problem. We report the experiment results in Sect. 5. We introduce the related work in Section 6 and conclude the paper in Sect. 7.

2 Preliminaries

In this section, we first formally define the inclined anchored $k$-coreand minimum detached $k$-coreproblems. Then, we present the analysis about the proprieties and hardness of the problems. Table 1 summarizes the notations frequently used throughout the paper.

Table 1 Summary of notations

2.1 Problem definition

We consider an unweighted and undirected graph G = (V, E), where V and E represent the sets of nodes and edges, respectively. We denote n = |V| and m = |E|. Given a subgraph $S\subseteq G$, N(u, S) is the set of adjacent nodes of u in S. deg(u, S) is the degree of u in S, i.e., $deg(u,S) =|N(u,S)|$. To measure the cohesiveness of subgraph, we employ the concept of k-core in this paper.

Definition 1

Given a graph G, a subgraph S is the k-core of G, denoted by $C_k(G)$, if 1) $deg(u,S)\ge k$ for each node $u\in S$; 2) S is maximal, i.e., any supergraph $S' \supset S$ is not a k-core.

Definition 2

Given a graph G, the coreness of a node $u \in G$, denoted by core(u), is the largest k such that u belongs to k-core, i.e.,$core(u) = \max \{k | u \in C_k(G)\}$.

The k-core of a graph G can be obtained by recursively removing the node whose degree is less than k with a time complexity of $\mathcal {O}(m)$ [1, 22]. The pseudo code is shown in Algorithm 1.

Definition 3

Given a graph G, the k-peel of G, denoted by $\mathcal {P}_k(G)$, is the set of nodes that have coreness equal to k, i.e., $\mathcal {P}_k(G)$ = $C_k(G)\backslash C_{k+1}(G)$.

The k-core model is widely used to measure the properties of the graph. In order to enlarge the k-core, we can offer some incentives to a set $\mathcal {A}$ of nodes, named the anchored nodes, to make them stay in the k-core community. That is, once a node is anchored, it is always reserved in the k-core, i.e., with infinite large degree. Through anchoring these nodes, some other nodes will join the k-core in cascade and finally the k-core is enlarged.

Definition 4

Given a graph G and an anchored node set $\mathcal {A}\subseteq V$, the anchored k-core, denoted by $C_k(G\oplus \mathcal {A})$, is the corresponding k-core of G with nodes in $\mathcal {A}$ anchored.

We use $\mathcal {F}(u,G)$ to denote the set of nodes that join the k-core when u is anchored, i.e., $\mathcal {F}(u,G) = C_k(G\oplus u) \backslash C_k(G)$, and call $\mathcal {F}(u,G)$ as the followers of u. As discussed, a community may have its own preferences, such as nodes with close or conflict interests. When selecting anchored nodes, we would like to preserve more users with close interests and less users with conflict interests. Given the set F (resp. $\mathcal {E}$) of nodes with close (resp. conflict) interests, we use $\mathcal {F}^+(\mathcal {A},G)$ (resp. $\mathcal {F}^-(\mathcal {A},G)$) to denote the close (resp. conflict) followers of $\mathcal {A}$, i.e., $\mathcal {F}(\mathcal {A},G)\cap F$ (resp. $\mathcal {F}(\mathcal {A},G)\cap \mathcal {E}$). To enlarge a community through anchoring nodes, intuitively, we want to involve more users with close interests and fewer ones with conflict interests. Then, we define the inclined score as follows.

Definition 5

[inclined score] Given a graph G, an anchored node set $\mathcal {A}$, and the close and conflict node sets F and $\mathcal {E}$, the inclined score of $\mathcal {A}$, denoted as Score($\mathcal {A}$, G), is the difference between the number of close followers and that of conflict followers, i.e., Score($\mathcal {A}$, G) = $\mathcal {F}^+(\mathcal {A},G) - \mathcal {F}^-(\mathcal {A},G)$.

We propose the concept of inclined score to better judge the effectiveness of anchored nodes by considering the inclination. When the context is clear, we omit the second parameter, i.e., G, from the notations.

Problem 1 (IAK problem) Given a graph G, the close and conflict node sets F and $\mathcal {E}$, the degree constraint k and a budget b, the inclined anchored k-core (IAK) problem aims to anchor a set of b nodes $\mathcal {A}^*$ with the largest inclined score, i.e.,

$$\begin{aligned} \mathcal {A}^* = \mathop {\arg \max }_{\mathcal {A}\subseteq G \wedge |\mathcal {A}|=b} Score(\mathcal {A}) \end{aligned}$$

Example 3

Reconsider the graph in Figure 1. Assume $k=3$ and $b=1$. The close and conflict node sets are F = $\{u_1, u_2, u_3, u_{12}\}$ and $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$, respectively. By anchoring the node $u_1$, we can obtain the anchored k-core $\{u_1, u_2, \dots , u_8\}$ with inclined score 3. The inclined score is -2, if we anchor $u_{12}$.

Contrary to the anchor k-core problem, the dropout of certain nodes could collapse the k-core community, i.e., the collapsed k-core problem. As discussed, sometimes we may enforce the leaving of certain nodes to detach the conflict users from the community. Motivated by this, we introduce the minimum detached k-core problem as follows.

Problem 2 (MDK problem) Given a graph G, the conflict node set $\mathcal {E}$ and the degree constraint k, the minimum detached k-core (MDK) problem aims to find the smallest node set of $\mathcal {D}^* \subseteq G$, such that after the deletion of $\mathcal {D}^*$, the k-core of G contains no nodes in $\mathcal {E}$. That is, $C_k(G \backslash \mathcal {D}^*)$ does not contain any nodes in $\mathcal {E}$, i.e.,

$$\begin{aligned} \mathcal {D}^* = \mathop {\arg \min }_{\mathcal {D}\subseteq G \wedge C_k(G \backslash \mathcal {D})\cap \mathcal {E}=\varnothing } |\mathcal {D}| \end{aligned}$$

Example 4

Reconsider the graph in Figure 1. Suppose $k=2$ and the conflict node set is $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$. The detached node set $\mathcal {D} = \{u_9, u_{12}\}$ is optimal result for MDK problem with size of 2, and $C_k(G \backslash \mathcal {D})$ does not contain any node in $\mathcal {E}$.

2.2 Problem properties

In this section, theoretical analysis is conducted about the hardness and properties of the studied problems. According to Theorems 1 and 2, the inclined anchored k-core problem is NP-hard, and the objective function is non-monotonic and non-submodular. Then, we prove the minimum detached k-core problem is also NP-hard in Theorem 3.

Theorem 1

The IAK problem is NP-hard for $k \ge 3$.

Proof

When there are only close nodes in the graph, the inclined anchored k-core problem can be reduced to the traditional anchored k-core problem, which is NP-hard for $k\ge 3$ [2]. Hence, the inclined anchored k-core problem studied in this paper is also NP-hard.

Theorem 2

The objective function of IAK problem is non-monotonic and non-submodular.

Proof

Non-monotonic. We prove Score(X) is non-monotonic by constructing a counter example. Reconsider the graph in Figure 1. For k = 3, $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$ and F = $\{u_1, u_2, u_3, u_{12}\}$, suppose $\mathcal {A} = \{u_3\}$. We have $Score(\mathcal {A}) = 2$. By adding $u_{12}$ to $\mathcal {A}$, the inclined score becomes 0. While, the score becomes 3, if we add $u_{1}$ to $\mathcal {A}$. Thus, the objective function is non-monotonic.

Non-submodular. Given two sets A and B, we say the function Score(X) is submodular if $Score(A) + Score(B) \ge Score(A\cup B) + Score(A\cap B)$. We also show the inequality does not hold by constructing a counter example. In Figure 1, for k = 3, $\mathcal {E}$ = $\{u_9, u_{10}, u_{11}\}$ and F = $\{u_1, u_2, u_3, u_{12}\}$, suppose A = $\{u_{10}\}$ and B = $\{u_{12}\}$. We have $Score(A) = -2$, $Score(B) = -2$, $Score(A\cap B) = 0$ and $Score(A\cup B) = -2$. Hence, the inequation does not hold. Therefore, the theorem is correct.

Figure 2

Construction example for NP-hard proof, where $m = 6$, $n = 4$ and $k = 3$

Theorem 3

The MDK problem is NP-hard for $k \ge 2$.

Proof

We prove this theorem by reducing set cover problem [15] to MDK problem. Given an element set $\mathcal {Q} = \{e_1,e_2,\cdots ,e_m\}$ with m elements and a collection $\mathcal {T} = \{T_1,T_2,\cdots ,T_n\}$ of n sets whose union equals $\mathcal {Q}$. The set cover problem aims to identify the smallest sub-collection $R \subseteq \mathcal {T}$ whose union equals $\mathcal {Q}$. Then we construct a graph G such that we can find a minimum detached node set $\mathcal {D}$ for MDK problem if and only if the set cover problem is answered. Following is the construction procedure.

First, we create some nodes. For each element $e_i$ in $\mathcal {Q}$, we generate a node $u_i$ and let conflict set $\mathcal {E} = \{u_i | 1 \le i \le m\}$. For each set $T_j \in \mathcal {T}$, we generate a node $v_j$. Let $V = \{v_j | 1 \le j \le n\}$. We add a k-core M with at least $(m+n) \times k$ nodes. Then, we build some edges between these nodes. If an element $e_i \in T_j$, we add an edge between $u_i$ and $v_j$. Let t be the max $deg(u_i, V)$ for any $u_i \in \mathcal {E}$. For each node $v_j$ in V, let it be connected to k nodes in M. For each node $u_i$ in $\mathcal {E}$, let it connected to $k - deg(u_i, V)$ nodes in M. Consequently, the construction is completed. Figure 2 is a construction example with $m = 6$, $n = 4$ and $k = 3$.

With the construction, we can ensure that i) M is always a k-core, no matter how many nodes in V and $\mathcal {E}$ are deleted; ii) $v_j$ always in k-core, no matter how many nods in $V \backslash \{v_j\}$ and $\mathcal {E}$ are deleted; iii) once $v_j$ is deleted, all its neighbors $u_i$ in $\mathcal {E}$ will not belong to k-core.

By doing this, for any $k \ge t$, the sub-set $\mathcal {D}$ of V corresponding to the smallest sub-collection $R \subseteq \mathcal {T}$ whose union equals $\mathcal {Q}$ of set cover problem is the optimal solution of MDK problem. Hence, this theorem is correct.

3 Solution for IAK problem

In this section, a baseline search framework is firstly proposed. Then, optimized solutions are developed to accelerate the computation.

3.1 Baseline algorithm

For the inclined anchored k-core problem, a native method is to enumerate all possible node sets $\mathcal {A}$ with size b and compute the corresponding inclined score. Then, we just return the result with the largest score. However, the exact algorithm is time-consuming because of the large number of combinations. Due to the NP-hardness of the inclined anchored k-core problem, we resort to the greedy heuristic as the traditional anchored k-core solution does [28]. The details are shown in Algorithm 2. It iteratively finds the node with the largest score in current k-core. It is easy to verify that we only need to consider the nodes not in the k-core as candidates.

3.2 Follower computation

Because of the non-monotonic property, the pruning techniques developed for the traditional anchored k-core problem are no longer held for our inclined case. For our problem, an essential task is to compute the followers of an anchored node.

Lemma 1

By anchoring a node, all of its followers are from $\mathcal {P}_{k-1}$.

Proof

By anchoring a node, the coreness of a node increases at most 1 [28]. Therefore, if one node u is not in $(k-1)$-core, then anchoring a node x can increase the coreness of u to $k-1$ at most, and u cannot appear in the k-core. Thus, it cannot be the follower of x.

Peel layer Based on the definition of $(k-1)$-peel, we can divide the nodes in $\mathcal {P}_{k-1}$ into different layers. Motivated by the onion layer structure [28], we recursively remove the node with degree less than k and organize the nodes in $\mathcal {P}_{k-1}$ in a peel layer structure P. Thus, the set of nodes which are deleted in the i-th batch belong to the i-layer, denoted by $P_i$. Specifically, $P_1$ = $\{u~|~deg(u, C_{k-1}(G)) < k \wedge u \in C_{k-1}(G)\}$. Due to the deletion of $P_1$, we can get $P_2$ in the same manner. Similarly, we recursively get all $P_i$. So, the peel layer structure $P = \bigcup _{i=1}^{t}{P_i}$, where t represents the recursion times. We use p(u) to denote the layer index of a node u, i.e., $p(u) = i$ when $u \in P_i$.

According to the peel layer structure P and Lemma 1, we have that the valid candidate anchored nodes with at least one follower must belong to P, which can significantly reduce the size of candidates. We propose an effective candidate pruning technique based on peel layer structure based on Observation 1. To better explain the pruning rule, we first represent the definition of ladder path.

Definition 6

Given an anchored node x, there is a ladder path from x to u, denoted by $x \leadsto u$, where (i) all nodes are from P; (ii) $p(v) < p(w)$ for every two consecutive nodes v and w along this path.

Observation 1

Given a graph G, if a candidate anchor x has at least one follower u, we have that there exists a ladder path $x \leadsto u$.

Clearly, if there is no one ladder path $x \leadsto u$ for a node x, it cannot be considered as a candidate anchor. Then, we compute the followers for each candidate anchor based on the radiate search after candidate reduction. We give the definition involved before presenting the details.

Definition 7

[distance] Give a graph G and a node u, the distance of u, denoted as dis(u), is the difference between degree constraint k and the number of neighbors of u in k-core, i.e., dis(u) = $k - deg(u, C_k(G))$. The distance of u represents that u still need dis(u) nodes to satisfy the requirement of degree not less than k.

Radiate Search We find the followers of anchors by radiate search, which is similar to breadth-first search. During the search procedure, each node has four states. When we start to anchor a node u, then other nodes will be listening l(v). Due to the degree of anchored node u is infinity, which satisfies the degree constraint, i.e. $dis(u) \le 0$, u is received r(u). A node is activated a(v) when its neighbor is received or activated. In addition, if $p(v) \ge p(u)$, then the node v cannot be activated based on the layer structure P. After anchoring a node u, the distance of each neighbor v of u subtract 1, and we check whether the distance of v is 0. If the distance is 0, then v is received, so we continue to check the neighbors of v. Otherwise, we need to check that whether the neighbors of v can participate in the k-core to decrease dis(v). Note that, if $dis(v) > a(v) + r(v) + l(v)$, then the distance of v cannot be 0, thus, v is closed c(v). The details are described in Algorithm 3.

At first, we set the status of anchored node x as received (Line 1). Then, we process all other nodes in G (Lines 2-4). For each node, we compute the degree of v in $C_k(G)$ (Line 3) and obtain the distance of v. Then, we set the status of v as listening (Line 4). After that, we set queue Q as empty in Line 5. In Lines 6-9, for each node w who is the neighbor of x or belongs to layer structure P with $p(w) > p(x)$, we push it into the queue Q (Line 7). Then, we update the distance for both w and x by subtracting 1 (Line 8). If the distance of w is no larger than 0, we set the status of it as received (Line 9). In Lines 10-21, we process all nodes in Q until it becomes empty. In Line 11, we pop a node u from Q. If the distance of u is larger than $a(u)+r(u)+l(u)$ which means the node u cannot be the follower, we set the status of u as closed, and use the Shrink of Algorithm 4 to update its neighbors’ distance and status (Lines 12-13). Otherwise, we set the status of u as activated (Line 15) and process each listening node z who is the neighbors of u (Lines 16-21). If node z is not in the k-core and $p(z)>p(u)$, we push z into Q and update the distance u and z by subtracting 1. Then, we judge the distance of z. If dis(z) is no larger than 0, we set the status of z as received. Finally, we return all received nodes in P until Q is empty.

Figure 3

Example of radiate search

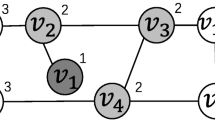
Example 5

As shown in Figure 3, given the part of a graph G and the distance d(u) for each u, when we anchor the node $u_3$, then $u_3$ is received and its neighbors are activated and other nodes are listening. The distance of $u_2$ subtract 1, i.e., $d(u_2)$ = 4 and the distance of neighbors {$u_5, u_7, u_4, u_1$} of $u_2$ subtract 1. We have that $d(u_5)$ = 0, $d(u_2)$ = 0. Thus, the node $u_2$ and $u_5$ are received. Similarly, activating $u_1$ can activate its neighbors and make their distance subtract 1. Finally, we find that all nodes are received except $u_8$.

3.3 Search algorithm

Let CC(u) be the connected component of u. The number of close nodes in CC(u) is denoted by $f^+(u)$. Then, we can use $f^+(u)$ to serve as an upper bound to filter the candidate. It is easy to verify the correctness of Lemma 2.

Lemma 2

Let $\alpha$ denote the largest marginal score currently after anchoring a candidate node. If $f^+(u) < \alpha$, we can remove u from the candidate.

By further extending the result in Lemma 2, we can maintain a tighter upper bound when conducting the radiate search. That is, when exploring the layer structure, we can decease the upper bound value $f^+(u)$ by if we meet a node in the conflict set. Then, we can terminate the computation when the updated upper bound violates Lemma 2. By integrating all optimization techniques, we present the KSM algorithm as shown in Algorithm 5. We skip a node u, if $f^+(u)$ is no large than $\alpha$. Otherwise, we conduct a radiate search that integrates the extended Lemma 2. At the end of current iteration, we have the best anchor $u^*$ with maximum score and merge it into $\mathcal {A}$. Lastly, Algorithm 5 returns the set $\mathcal {A}$ of b anchored nodes after b iterations.

4 Solution for MDK problem

In this section, we first present an exact algorithm by enumerating all the combinations. Then, we propose two heuristic algorithms based on the properties of the problem.

4.1 Exact Algorithm

Recall that the MDK problem is to find the smallest node set $\mathcal {D}$ from G so that $C_k(G \backslash \mathcal {D})$ does not contain any nodes in the conflict node set $\mathcal {E}$.

Observation 2

The deletion of node in $G\backslash C_k(G)$ will not influence the structure of k-core.

Observation 3

Given a graph G and the conflict set $\mathcal {E}$, for the MDK problem, the size of the optimal solution $\mathcal {D}$ is no larger than that of $\mathcal {E}$.

The observation is easy to verify, since 1) the node in $G\backslash C_k(G)$ will be deleted when computing the k-core, and 2) $C_k(G \backslash \mathcal {E})$ must not contain $\mathcal {E}$. Therefore, to find the optimal solution of MDK, we can first compute the k-core of G, and then enumerate all subsets $\mathcal {D}'\subseteq V(C_k(G))$ with size from 1 to $|\mathcal {E}|$. Then, we select the first encountered node set $\mathcal {D}'$ such that $C_k(G \backslash \mathcal {D}')$ does not contain any nodes in $\mathcal {E}$. In the worst case, the time complexity of the algorithm is $\mathcal {O}(2^{|V(C_k(G))|}|E(C_k(G))|)$. The above solution is too cost to be adopted in real applications, especially when $|\mathcal {E}|$ is large. In the next sections, we turn to heuristic solutions, which can return a competitive result efficiently.

4.2 Conflict removing heuristic

For any node $v \in V(C_k(G))$, if we want v to not be contained in $C_k(G)$, there are two approaches, 1) one is to delete v directly, and 2) the other is to delete $deg(v,C_k(G))-k+1$ v’s neighbors in $C_k(G)$. Considering that we aim to find the smallest node set $\mathcal {D}$, the latter method usually requires more nodes than the former method, unless $deg(v,C_k(G))=k$. Before introducing the detailed heuristic method, we first show a property of k-core in Lemma 3.

Lemma 3

Let S be a subset of k-core but not in $(k+1)$-core of G. Then, there must exist a node u in S such that $S \backslash u$ does not satisfy the degree constraint of k-core.

Proof

Let v be a node in S with the minimum degree. Then, deg(v, S) must equal k, otherwise S should also be inside $(k+1)$-core. Suppose u is a neighbor of v in S. After u is removed, the degree of v in S will be $k-1$. Thus, $S \backslash u$ cannot be a k-core, and the lemma holds.

Since $\mathcal {D} = \mathcal {E}$ is a solution for MDK problem, although not necessarily the optimal one, in this heuristic method, we try to optimize this solution by shrinking its cardinality. According to Lemma 3, for a node $v \in \mathcal {E} \cap \mathcal {P}_k$, i.e.,$deg(v,C_k(G)) = k$, if one of its neighbor u in $C_k(G)$ is deleted, v cannot stay in $C_k(G)$ due to the degree constraint. Moreover, all neighbors of u in $\mathcal {E} \cap \mathcal {P}_k$ cannot exist in $C_k(G)$ either. Therefore, $\mathcal {D}' = (\mathcal {E} \backslash (\mathcal {E} \cap \mathcal {P}_k\cap N(u,G))) \cup \{u\}$ is a superior solution compared with $\mathcal {D} = \mathcal {E}$. Based on this idea, we propose our conflict removing heuristic (CRH) algorithm, which tries to reduce the result size iteratively. The details of this algorithm is shown in Algorithm 6.

In Algorithm 6, we first compute the k-core of G (line 1). Then, we iteratively select nodes to be removed from $C_k(G)$ until $C_k(G)$ does not contain any node in $\mathcal {E}$ (lines 3-21). Let $\mathcal {E}_k$ be the nodes in $\mathcal {E}$ with degree equal k (line 4) in the k-core, and $N_k$ be the neighbors of each node in $\mathcal {E}_k$ (line 5). If there exist nodes in $\mathcal {E}_k$, we delete the node from $N_k$ that has the largest number of neighbors in $\mathcal {E}_k$. Otherwise, we delete the node from $\mathcal {E}$ that has the largest coreness (lines 7-18). Note that, the nodes in $N_k$ may also belong to $\mathcal {E}$, so they need to be handled differently (lines 9-16). After each iteration, we update k-core and $\mathcal {E}$ (lines 20-21). Finally, we returned the detached node set $\mathcal {D}$ in line 22.

4.3 Degree decline heuristic

The CRH algorithm is based on the idea that to make a node $v \in V(C_k(G))$ dropout of $C_k(G)$, we need to delete $deg(v,C_k(G))-k+1$ v’s neighbors in $C_k(G)$, i.e., local perspective. However, it is undesirable to put all these neighbors of each node in $\mathcal {E}$ into $\mathcal {D}$. Considering the effect of cascade in the k-core, i.e., global perspective, it may be enough to remove only a very small number of nodes from $C_k(G)$, such that the degree of each node in $\mathcal {E}$ is less than k in $C_k(G)$. Motivated by this, for each node u in $C_k(G)$, we use Dec(u) to measure the contribution of deleting u in the MDK problem. Specifically, Dec(u) is the number of neighbors of the nodes in $\mathcal {E}$ that are removed with the deletion of u, i.e.,

$$\begin{aligned} \text {Dec}(u) = \sum _{v \in \mathcal {E}}deg(v,C_k(G))-deg(v,C_k(G \backslash \{u\})) \end{aligned}$$

Based on the concept of Dec(u), we introduce our degree decline heuristic (DDH) algorithm. The details of the algorithm is shown in Algorithm 7. In line 1, we first compute the k-core of G. Then, we iteratively select a node $u^*$ from $C_k(G)$ with the maximum Dec(u) for deletion, until all nodes in $\mathcal {E}$ do not exist in k-core (lines 3-9). Finally, we return the set of detached nodes in line 10.

Note that, in Algorithm 7, we need to compute Dec(u) for each node in candidate set. Let $\mathcal {I}(u)$ be the set of nodes that are removed from the k-core after u is deleted, i.e.,

$$\begin{aligned} \mathcal {I}(u) = V(C_k(G)) \backslash V(C_k(G \backslash u)) \end{aligned}$$

To speed up the selection of the node with the largest Dec from $V(C_k(G))$ at each iteration, we propose the following lemma to avoid the computation of Dec for some nodes.

Lemma 4

Given two nodes u and v in G, we have Dec$(v) \le$ Dec(u), if $v \in \mathcal {I}(u)$.

Proof

Since $v \in \mathcal {I}(u)$, it implies that $\mathcal {I}(v) \subseteq \mathcal {I}(u)$. Hence, Dec$(v) \le$ Dec(u), and the lemma holds.

5 Experiments

Table 2 Statistics of datasets

In this section, comprehensive experiments are conducted over 9 datasets to evaluate the efficiency and effectiveness of proposed techniques.

5.1 Experiment setup

Algorithms In the experiments, we implement and compare the following algorithms. The first 5 algorithms is for the IAK problem.

• Rand: select b nodes that are not in the k-core randomly.

• Exact-IAK: enumerate all possible combinations with the optimal result.

• Traditional: obtain the node set with traditional anchored k-core model.

• BL: the baseline greedy algorithm, i.e., Algorithm 2.

• KSM: the optimized algorithm i.e., Algorithm 5.

Then, the following 3 algorithms is for the MDK problem.

• Exact-MDK: enumerate all possible combinations with size from 1 to $|\mathcal {E}|$ and return the optimal solution.

• CRH: The conflict removing heuristic algorithm, i.e.,Algorithm 6.

• DDH: The degree decline heuristic algorithm, i.e.,Algorithm 7.

Note that, for MDK problem, there is no random and traditional solutions. This is because, the results returned by random and traditional solutions may be far from satisfied due to the removal of all the nodes in conflict set $\mathcal {E}$.

Table 3 Inclined score ratio of Exact-IAK and KSM

Table 4 Response time of Exact-IAK and KSM

Datasets and workloads We conduct experiments on 8 real-world networks, which are public available in Networkrepository¹ and SNAP². We also employ 1 artificial graph, which is generated by GTGraph with 500 nodes and 5000 edges. Table 2 shows the statistic details of the datasets. Note that, nodes in the original graphs have no close or conflict properties, so we use a method similar to BFS to assign the labels to each node in the datasets. For each connected component in the original graph, we randomly select an initial node and regard it as a close, and each neighbor of the initial node has a 50% probability of being close, a 20% probability of being conflict, and a 30% probability of being unchanged (i.e., no label). For an unchanged node, each of its neighbor is set as unchanged. Then, we repeat the process for the encountered nodes in BFS. In our experiment, both k and b vary from 5 to 25. For each setting, we run the algorithm 20 times and take the average performance as the final result. All the programs are implemented in standard C++. All the experiments are performed on a PC with an Intel i5-9600KF 3.7GHz CPU and 64 GB main memory.

Figure 4

Effectiveness evaluation compared with Rand and Traditional for IAK problem

Figure 5

Case study for IAK problem

Figure 6

Effectiveness evaluation compared with Exact-MDK

5.2 Effectiveness evaluation for IAK problem

To evaluate the effectiveness of algorithms for IAK problem, we report the ratio of inclined score of KSM and Exact-IAK by anchoring b nodes. This is because KSM only enhances the efficiency compared to BL. Then, we compare the results obtained by the traditional anchored k-core and our inclined anchored k-core problems. In addition, case studies are also conducted.

Figure 7

Compare the size of detached node set by varying k

5.2.1 Compared with Exact-IAK

Table 3 reports the inclined score ratio of KSM and Exact-IAK by anchoring b nodes, where k = 10 and b varies from 1 to 3. We set the inclined score ratio of Exact-IAK as 100% and that of KSM is $\frac{\text {score returned by KSM}}{\text {score returned by Exact-IAK}}\times 100\%$. Note that, due to the high computational cost of Exact-IAK, we only test Exact-IAK on small datasets with small b values. As observed, KSM only slightly drops in one setting. In addition, Table 4 reports the running time of Exact-IAK and KSM. We can see KSM achieves significant speedup compared with Exact-IAK, which further verifies the effectiveness of the greedy framework.

Figure 8

Compare the size of detached node set by varying $|\mathcal {E}|$

5.2.2 Compared with rand and traditional

Compared with Rand In Figure 4(a), we report the inclined score compared with Rand on 6 larger datasets, i.e., Email, Facebook, Brightkite, Arxiv, Gowalla, YouTube with $b = 10$ and $k = 10$. The datasets are ordered by their network sizes, i.e., the number of edges. Note that, the larger the inclined score is, the more effective the algorithm will be. As we can see, KSM outperforms Rand by a big margin. This is because, there is usually few followers for anchored nodes that are selected in random.

Compared with Traditional We report the results by compared the inclined model with the traditional model. The corresponding inclined scores are shown in Figure 4(b). Traditional does not consider the properties of different nodes, and only focuses on enlarging the total k-core. As observed, Traditional may lead to a very small inclined score, even a negative score, such as Youtube. Thus, it is necessary to develop algorithms to handle the inclined case.

Figure 9

Compare the size of remaining k-core by varying k

Figure 10

Compare the size of remaining k-core by varying $|\mathcal {E}|$

5.2.3 Case study

We conduct a case study on Facebook dataset with $k = 20$ and $b = 1$. Figure 5(a) and (b) are the results obtained by KSM and Traditional, respectively, where blue/red nodes denotes the close/conflict nodes, and white nodes are the ones without labels. As shown in Figure 5(a), the best anchored node is the one with id 2300. It has 5 followers and all of them are close nodes, i.e., the inclined score is 5. As shown in Figure 5(b), the returned anchor is with id 1611. It has 9 followers, where there are 3 close and 4 conflict nodes, i.e., the inclined score is -1. Compared with the anchored node 2300, though the node 1611 has more followers, it has smaller inclined score.

5.3 Effectiveness evaluation for MDK problem

To evaluate the effectiveness of the proposed two heuristic algorithms for MDK problem, we compare them with Exact-MDK on a small dataset. Then, we conduct experiments on the large datasets to further evaluate the performance of the two strategies.

5.3.1 Compare heuristic solutions with Exact-MDK

Due to the prohibitive time cost for Exact-MDK algorithm, in this experiment, we select a small dataset, i.e.,Eco-mahindas, to evaluate the performance of the heuristic solutions and Exact-MDK by varying k and $|\mathcal {E}|$. The results are shown in Figure 6. The number on the bar is the corresponding response time. Since both heuristics take less than $10^{-3}$ seconds to complete, we only mark the time cost for Exact-MDK in the figure. As we can see, the two heuristics perform as well as the Exact-MDK in most settings. Moreover, the heuristic algorithms are much faster than Exact-MDK, which verifies the advantage of proposed heuristic strategies.

5.3.2 Compare detached node set size

In this experiment, we report the size of detached node set, i.e.,$|\mathcal {D}|$, retrieved by CRH and DDH in Figures 7 and 8 by varying k and the number of conflict nodes on the largest 6 datasets, respectively. Recall that, $\mathcal {D} = \mathcal {E}$ is an answer of MDK problem. Therefore, we use $|\mathcal {E}|$ as a benchmark to measure the effectiveness of CRH and DDH, i.e.,the gray bar in Figures 7 and 8. As we have seen, in most cases, both CRH and DDH are able to obtain smaller $\mathcal {D}$. DDH performs better than CRH, because CRH is able to select nodes from global perspective, i.e., leveraging the cascade phenomenon of k-core. While, DDH is based on local observation, i.e., only replace part of nodes in $\mathcal {D} = \mathcal {E}$. For example, in Figure 7(d) with $k=25$, $|\mathcal {E}|$ is 300, while the size of $\mathcal {D}$ retrieved by CRH and DDH are 128 and 115, respectively. The results of CRH and DDH are similar only when k or $|\mathcal {E}|$ is small. This is because, the cascading phenomenon becomes more prominent for larger k and $|\mathcal {E}|$.

5.3.3 Compare size of remaining k-core

In this experiment, we report the size of remaining k-core, i.e., i.e.,$|C_k(G \backslash \mathcal {D})|$, after the deletion of detached node set from graph G for CRH and DDH. The result are shown in Figures 9 and 10 by varying k and the number of conflict nodes on the largest 6 datasets, respectively. We use the size of original k-core as a benchmark, i.e.,$|C_k(G)|$. It can be seen from the results that the remaining k-core becomes smaller due to the removal of $\mathcal {D}$, and the variation increases gradually with the increase of k and $|\mathcal {E}|$. Although DDH takes into account the cascade effect when selecting nodes, the final remaining k-core is usually larger than that of CRH. For example, in Figure 9(e) with $k=25$, the size of remaining k-core of DDH is 2138, while CRH is only 313. From this perspective, it also reflects that DDH is more effective than CRH.

5.4 Efficiency evaluation for IAK problem

To evaluate the efficiency of our algorithms for IAK problem, we report the response time of BL and KSM by varying b and k on the largest 6 datasets. The results are shown in Figures 11 and 12, respectively. It is clear that KSM constantly outperforms BL on all datasets, and can achieve up to 2 orders of magnitude speedup. As observed, the response time of both methods increases when b increases. This is because more iterations need to be conducted. When k increases, the response time also grows. This is because when k is larger, the nodes in the layer structure have a larger degree, which leads to the need to explore more neighbors and greater time consumption.

Figure 11

Efficiency evaluation for IAK problem by varying b

Figure 12

Efficiency evaluation for IAK problem by varying k

5.5 Efficiency evaluation for MDK problem

In this experiment, we report the response time of CRH and DDH algorithms for MDK problem by varying k and the size of conflict node set on the largest 6 datasets. The results are shown in Figures 13 and 14. As can be seen from the results, CRH is basically faster than DDH by at least one order of magnitude. This is because CRH only needs to visit the nodes in $\mathcal {E}$ and their neighbors, i.e., local observation, while DDH needs to traverse all the nodes in $C_k(G)$. However, DDH is also able to finish in a competitive time, and takes only about 100 seconds for the largest graph. Since CRH only needs to traverse $\mathcal {E}$, the time required for CRH is essentially constant when k varies. Moreover, the response time CRH slightly increases when the size of $\mathcal {E}$ becomes larger. The response time of DDH, on the other hand, is sensitive to the change of k and $|\mathcal {E}|$. With the increase of k, DDH runs faster, because there are fewer nodes in k-core. However, as $|\mathcal {E}|$ increases, the response time of DDH become larger. This is because it takes more iterations to exclude all the nodes in $\mathcal {E}$ from k-core.

Figure 13

Efficiency evaluation for MDK problem by varying k

Figure 14

Efficiency evaluation for MDK problem by varying $|\mathcal {E}|$

6 Related work

As a common data structure, graphs are widely used to model the relationships among different entities, such as IoT [14], social network [27] and brain network [24]. In social network analysis, different cohesive subgraph models have been proposed to accommodate different scenarios, such as k-core [20, 21], k-truss [13, 30] and clique [5, 23]. The k-core model is firstly proposed by Seidman [20], which has been widely adopted for social network analysis with numerous applications, such as protein function prediction [26], social contagion [25] and influence study [16].

In social networks, the engagement and breakdown of certain nodes/edges can greatly influence the corresponding community. Due to the unique applications, the problems of finding critical nodes or edges have attracted significant attention in the recent, and different cohesive subgraph models and settings are studied, e.g., [2, 8, 28, 29]. These problems are usually NP-hard. Therefore, heuristic strategies are widely adopted in the previous studies. Bhawalkar et al. [2] propose the anchored k-core problem, which aims to maximize the size of k-core by anchoring b nodes. The authors also prove the problem is NP-hard. To accelerate the computation, [28] develops an efficient algorithm for the anchored k-core problem on large-scale graphs. [11] proposes the directed anchored k-core problem by considering the case in directed graphs. In [17], authors further investigate the anchored k-core problem by minimizing the total budget. Different from the anchored k-core problem, the collapsed k-core problem aims to minimize the size of k-core community by deleting certain nodes [29]. In [7, 32], authors attempt to minimize the corresponding k-core by removing the critical edges from the graph. [18, 19] consider the k-core minimization problem based on the game theory model. Besides k-core model, the collapsed problems are also investigated under different models, such as k-truss model [9, 33] and bipartite graph settings [31]. However, none of them considers the different property of nodes, i.e., close or conflict.

7 Conclusion

Anchored/collapsed k-core problem has attracted great attentions in the recent. However, the previous studies usually treat the nodes equally, which may fail to better characterize the real scenarios. Motivated by this, in this paper, we propose and study the inclined anchored $k$-coreand minimum detached $k$-coreproblems by considering the node properties, i.e., close or conflict. We formally define the problem and prove their hardness. To facilitate the computations, different search methods and heuristic strategies are developed. Finally, comprehensive experiments on real-life networks are conducted to verify the effectiveness and efficiency of the developed techniques.