On flexible cohesive subgraph mining

Abstract

When characterizing the cohesion of a subgraph, many cohesive subgraph models impose various constraints on the relationship between the minimum degree of vertices and the number of vertices in the subgraph. However, the constraints imposed by the clique, quasi-clique and k-core models are so rigid that they cannot simultaneously characterize cohesive subgraphs of various scales in a graph. This paper characterizes the flexibility of a cohesive subgraph model by the constraint it imposes on this relationship and proposes f -constraint core (f -CC), a new model that can flexibly characterize cohesive subgraphs of different scales. We formalize the FlexCS problem that finds r representative f -CCs in a graph that are most diversified. This problem is NP-hard and is even NP-hard to be approximated within |V |^1−𝜖 for any 𝜖 > 0. To solve the problem efficiently, a divide-and-conquer algorithm is proposed together with some effective techniques including f -CC generation, sub-problem filtering, early termination, and index-based connected component retrieval. Extensive experiments verify the flexibility of the f -CC model and the effectiveness of the proposed algorithm.

1 Introduction

Cohesive subgraph mining aims at finding cohesively connected vertices in a massive graph. It plays important roles in many applications such as community detection, graph compression and graph visualization [8]. So far, a considerable number of cohesive subgraph models have been proposed in the literature, e.g. clique [12], quasi-clique [13], k-core [17], k-truss [6], and nucleu [16].

When characterizing the cohesion of a subgraph, many cohesive subgraph models commonly consider two key features, namely the minimum degree of vertices and the number of vertices in the subgraph. Different models often impose different constraints on the relationship between these two features. To be more specific, let us first review some well-known cohesive subgraph models in the literature and take a deeper look at their respective constraints imposed on the relationship.

Let G = (V, E) be a graph, where V is the set of vertices, and E is the set of edges. Two vertices u and v are adjacent if (u, v) ∈ E. The subgraph of G induced by a vertex subset $Q \subseteq V$, denoted by G[Q], is (Q, E[Q]), where E[Q] is the set of edges with both endpoints in Q. Let us consider three classical cohesive subgraph models, namely clique, quasi-clique and k-core.

• A clique [12] in G is a set of vertices where every two vertices are adjacent to each other. Each vertex in a clique Q is of degree |Q|− 1 in G[Q].

• A (degree-based) γ-quasi-clique [13] in G is a subset of vertices $Q \subseteq V$ where every vertex is adjacent to at least ⌈γ ⋅ (|Q|− 1)⌉ other vertices, where γ ∈ [0,1]. Specially, a clique is a γ-quasi-clique for γ = 1.

• A k-core [17] in G is a subset of vertices $Q \subseteq V$ where every vertex is of degree at least k in G[Q].

Figure 1 illustrates the relationships between the minimum degree of vertices and the number of vertices in a cohesive subgraph restricted by these models. For the clique and quasi-clique models, the minimum degree is required to be linear to the number of vertices, which is obviously very strict. In practice, it is nearly impossible to find a cohesive subgraph with hundreds of vertices in a real graph under these two models due to the sparsity of real graphs. Thus, the clique and quasi-clique models are only suitable for modeling small cohesive subgraphs. On the contrary, the k-core model imposes a very loose constraint: the minimum vertex degree is required to be at least k, which is independent of the number of vertices. In fact, in a real graph, k-cores are generally large and sparsely connected, and therefore, this model is only suitable for modeling large cohesive subgraphs.

Fig. 1

Relationships between the minimum degree of vertices and the number of vertices in a cohesive subgraph under various cohesive subgraph models

Inspired by these observations, we characterize the flexibility of a cohesive subgraph model by the constraint it imposes on the relationship between the minimum degree of vertices and the number of vertices. In fact, the clique/quasi-clique model and the k-core model stay at two extremes of flexibility. The rigidity of these models prevents them from simultaneously characterizing cohesive subgraphs varying from small scales to large scales, so each model is only suitable for a limited scope of applications. Therefore, we focus on flexible cohesive subgraph models which can be applied to flexibly model cohesive subgraphs in a wide range of applications. To the best of our knowledge, no prior work has been done on this problem in the literature.

This paper proposes f -constraint core (f -CC), a new cohesive subgraph model. Given a graph G = (V, E) and a monotonically increasing function $f: \mathbb {N} \to \mathbb {R}$, a subset of vertices $Q \subseteq V$ is an f -CC if every vertex in G[Q] is adjacent to at least ⌈f(|Q|)⌉ other vertices. Rather than a special new model, the f -CC model is a generalization of the clique, quasi-clique and k-core models. When f(x) = x − 1, an f -CC is a clique; When f(x) = γ(x − 1) where γ ∈ [0,1], an f -CC is a γ-quasi-clique; When f(x) = k where $k \in \mathbb {N}$, an f -CC is a k-core. Section 6.2 shows that by carefully specifying f, the f -CC model attains more flexibility than other classical models mentioned above. Here, we illustrate the flexibility of the f -CC model by an example.

Example 1

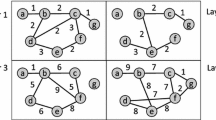
Consider the graph shown in Figure 2. First, we depict the constraints imposed by the clique, $\sqrt x$-CC and 3-core models in Figure 3. For the $\sqrt x$-CC model, as the number of vertices increases, the required minimum vertex degree increases more and more slowly, which is consistent with users’ expectations on cohesive subgraphs: When a cohesive subgraph is small (like a micro-cluster), the constraint on the minimum vertex degree should be strict; when it is large (like a community), this constraint should be relaxed.

Fig. 2

An example graph

Fig. 3

Relationships between the minimum degree of vertices and the number of vertices restricted by the clique model, the $\sqrt x$-CC model and the 3-core model, and the cohesive subgraphs characterized by these models

Moreover, we illustrate some cohesive subgraphs characterized by these models, particularly, the maximum clique, two maximal $\sqrt {x}$-CCs and the maximal 3-core. Obviously, there are two groups of cohesively connected vertices in the graph, namely S₁ = {c, d, e, f, g, h, i, j, k, l, m} and S₂ = {n, o, p, q, r, s, t, u}. The maximum clique only contains partial vertices in S₁ and excludes the vertices i, j, k, l, m that are also cohesively connected to the maximum clique. The maximal 3-core merges S₁ and S₂. This is also not reasonable because S₁ and S₂ are only linked through the cut vertex n. The $\sqrt {x}$-CC model circumvents the shortcomings of the clique and k-core models. Two maximal $\sqrt {x}$-CCs shown in Figure 3 precisely characterize S₁ and S₂, respectively.

As with cliques and quasi-cliques, mining all f -CCs on a large graph is often a tough task due to the following reasons: (1) The number of all f -CCs can be exponential to the number of vertices in the graph; (2) There always exists huge overlap between f -CCs in the graph, which will be illustrated by the following example.

Example 2

In the example graph shown in Figure 2, there are a large number of $\sqrt {x}$-CCs, e.g. {c, d, e, f, g, h, i, j, k, l, m}, {d, e, g, h, j, k, l, n}, {e, f, g, h, j, k, l, n}, and so on. As illustrated in Figure 4, they are overlapped with each other significantly.

Fig. 4

The f -CCs {c, d, e, f, g, h, i, j, k, l, m}, {d, e, g, h, j, k, l, n} and {e, f, g, h, j, k, l, n} have significant overlaps

To avoid the huge but uninformative result set of the enumeration paradigm, [9, 19, 21] provide a way to formalize the problem that extracts not only individually large but also lowly overlapped cohesive subgraphs. They characterize the quality of the result set by its diversity, i.e., the number of vertices it covers, and extract r cohesive subgraphs that are most diversified. Motivated by this, we formalize the flexible cohesive subgraph mining (FlexCS) problem with respect to our f -CC model: We extract r representative f -CCs that attain the highest diversity, i.e., these f -CCs can cover the largest number of vertices. We show that the FlexCS problem is NP-hard and is even NP-hard to be approximated within |V |^1−𝜖 for any 𝜖 > 0.

Due to the extremely high computational complexity of the FlexCS problem, we develop a heuristic algorithm that extracts a collection of qualified f -CCs in a divide-and-conquer manner and selects r representative f -CCs on the fly that approximately attain the highest diversity. To this end, the constraint on the relationship between the minimum vertex degree and the number of vertices is equivalently translated into a series of simple constraints. Based on these simple constraints, the FlexCS problem on the input graph G is decomposed into a series of sub-problems called ConsCS on the connected components of the maximal k-cores of G. An advanced filtering method is proposed to eliminate a portion of ConsCS problem instances that are unpromising to produce any informative f -CCs to improve the diversity of the result set. The remaining ConsCS problem instances are handled in different ways depending on the size of the input connected component. Problem instances on small connected components are easy to solve. For problem instances on large connected components, we develop a heuristic algorithm to generate qualified f -CCs. This algorithm takes both greediness and randomness into the f -CC generation process. In addition, we propose an early termination mechanism and an index-based connected component retrieval method to speed up the algorithm for the FlexCS problem.

The main contributions of this paper can be summarized as follows:

• We propose the f -CC model that can flexibly characterize cohesive subgraphs of various scales and formalize the FlexCS problem that extracts r representative f -CCs attaining the highest diversity.

• We prove the NP-hardness and the inapproximability of the FlexCS problem and develop a divide-and-conquer approach to solving it efficiently.

• Extensive experiments were conducted to verify that the f -CC model is flexible in simultaneously characterizing cohesive subgraphs varying from small scales to large scales, and the proposed algorithm can efficiently discover top-r f -CCs that approximately have the highest diversity.

The paper is organized as follows. Section 2 defines the f -CC model and formalizes the FlexCS problem. Section 3 presents the main procedure of our algorithm, followed by the important subroutines described in Section 4 and the optimization techniques in Section 5. The experiments are reported in Section 6. The related work is reviewed in Section 7. Finally, the paper is concluded in Section 8.

2 Model and problem definition

This section introduces the f -constraint core (f -CC) model and the flexible cohesive subgraph mining (FlexCS) problem. In this paper, we only consider simple undirected graphs. Let G = (V, E) be a graph. The degree of a vertex v ∈ V in G, denoted by d_G(v), is the number of edges adjacent to v in G. The neighborhood of a vertex v ∈ V in G, denoted by N_G(v), is the set of vertices connected to v by an edge in G. We have d_G(v) = |N_G(v)|. For a vertex subset $Q \subseteq V$, the subgraph of G induced by Q, denoted by G[Q], is (Q, E[Q]), where E[Q] is the set of edges with both endpoints in Q.

We first define the notion of f -constraint core (f -CC) that can flexibly characterize cohesive subgraphs of various scales simultaneously in a graph.

Definition 1

(f-constraint core) Given a graph G = (V, E) and a monotonically increasing function $f: \mathbb {N} \to \mathbb {R}$, a subset of vertices $Q \subseteq V$ is an f-constraint core (f-CC for short) if the degree of every vertex in the induced subgraph G[Q] is at least ⌈f(|Q|)⌉.

Since connectivity is often expected in research and practice, we require that G[Q] is connected. Note that the notion of f -CC is a generalization of the notions of clique, quasi-clique and k-core. Specifically,

• For f(x) = x − 1, an f -CC is a clique.

• For f(x) = γ(x − 1) where 0 ≤ γ ≤ 1, an f -CC is a γ-quasi-clique.

• For f(x) = k where $k \in \mathbb {N}$, an f -CC is a k-core.

Let F_f(G) be the set of all f -CCs in G. As mentioned in Section 1, |F_f(G)| could be exponential to the size of G, so we usually cannot expect to retrieve all f -CCs in G. In addition, f -CCs in G often overlap with each other, so it is not a rational choice to return all f -CCs in F_f(G) due to the huge redundancy. Therefore, we try to find a small number of informative f -CCs that are qualified to represent F_f(G) as the existing work [9, 19, 21] did. Similar to [9, 19, 21], we use the diversity (i.e., the size of the coverage of the result set defined in Definition 2) to measure the quality of the result set.

Definition 2

(coverage) Given a set of f-CCs $\mathcal {R} = \{Q_{1}, Q_{2}, \ldots \}$ in graph G, the coverage of $\mathcal {R}$, denoted by $\mathsf {cov}(\mathcal {R})$, is the set of vertices in G covered by f-CCs in $\mathcal {R}$, i.e., $\mathsf {cov}(\mathcal {R}) = \bigcup _{Q \in \mathcal {R}} Q$.

Apparently, the smaller $|\mathsf {cov}(F_{f}(G)) - \mathsf {cov}(\mathcal {R})|$ is, the better $\mathcal {R}$ approximates F_f(G). Thus, the problem in this paper called the flexible cohesive subgraph mining (FlexCS) can be formally defined as follows.

Problem Definition 1

Given a graph G = (V, E), a monotonically increasing function $f: \mathbb {N} \to \mathbb {R}$ and $r\in \mathbb {N}$, the goal of the flexible cohesive subgraph mining (FlexCS) problem is to find a subset $\mathcal {R}\subseteq F_{f}(G)$ such that $|\mathcal {R}| = r$ and $|\mathsf {cov}(\mathcal {R})|$ is maximized (i.e., $|\mathsf {cov}(F_{f}(G)) - \mathsf {cov}(\mathcal {R})|$ is minimized).

Example 3

Given the example graph shown in Figure 2, $f(x) = \sqrt x$ and r = 2, two $\sqrt x$-CCs {c, d, e, f, g, h, i, j, k, l, m} and {n, o, p, q, r, s, t, u} shown in Figure 3 are returned as $\mathcal {R}$, and $|\mathsf {cov}(\mathcal {R})| = 19$, which is maximized.

Theorem 1

The FlexCS problem is NP-hard and is even NP-hard to be approximated within |V |^1−𝜖 for all 𝜖 > 0.

Proof

Let η-APPROX-π denote the approximation version of an optimization problem π with approximation ratio η. Since an f-CC is a clique when f(x) = x − 1, the maximum clique problem (MCP) and the η-APPROX-MCP problem are special cases of FlexCS and η-APPROX-FlexCS, respectively. Therefore, MCP and η-APPROX-MCP are polynomial-time many-to-one reducible to FlexCS and η-APPROX-FlexCS, respectively. Due to the NP-hardness of MCP [10], FlexCS is also NP-hard. In addition, for all 𝜖 > 0, it is NP-hard to approximate MCP within |V |^1−𝜖 [23], so does FlexCS. The theorem thus holds. □

3 Our method

This section introduces our method to solve the FlexCS problem. Due to the huge search space of the enumeration process for enumerating all f -CCs and its exponential-scale output, we cannot extend the clique enumeration paradigm to enumerate all f -CCs in a graph G and then choose r of them that cover the largest number of vertices. Therefore, we develop a heuristic algorithm that first finds a set of qualified f -CCs $S \subseteq F_{f}(G)$ and then chooses r f -CCs attaining the highest diversity from S. In the rest of this section, we present two key components of our method, namely the qualified f -CCs generation (Section 3.1) and the diversified top-r f -CCs selection (Section 3.2).

3.1 Qualified f -CCs generation

The first component of our method is to find a set of f -CCs $S \subseteq F_{f}(G)$ that is qualified to represent F_f(G), from which the diversified top-r f -CCs are further selected. To this end, we adopt a divide-and-conquer approach to generating S. The generation process is decomposed into solving a series of sub-problem instances, and a core-based filtering method is developed to eliminate some useless sub-problem instances that are unpromising to return informative f -CCs.

3.1.1 Problem decomposition

To begin with, we introduce a generalized inverse function of a monotonically increasing function F presented in [7] as follows:

$$ F^{-1}(x) = \sup\{y|F(y)\le x\} $$

(1)

Based on this generalized inverse function, we have the following theorem:

Theorem 2

Given a graph G = (V, E) and a monotonically increasing function $f: \mathbb {N} \to \mathbb {R}$, let $g : \mathbb {N} \rightarrow \mathbb {N}$ be a function such that g(x) = ⌈f(x)⌉. For a vertex subset $Q \subseteq V$, the following conditions are equivalent:

• Q is an f-CC;

• The minimum degree of vertices in G[Q] is at least g(|Q|);

• |Q|≤ g^− 1(k), where k is the minimum degree of vertices in G[Q] and g^− 1 is the generalized inverse function of g defined by (1).

Proof

Condition 1 and Condition 2 are equivalent due to Definition 1. Condition 2 and Condition 3 are equivalent due to (1). According to the transitivity, the theorem holds. □

Based on Theorem 2, the degree constraint imposed on vertices in an f -CC can be translated into the following pair of constraints parameterized by k:

• (Minimum degree constraint): The degree of every vertex in G[Q] is at least k.

• (Maximum size constraint): |Q|≤ g^− 1(k).

For brevity, we use C^k to represent both $\mathbf {C_{1}^{\mathit {k}}}$ and $\mathbf {C_{2}^{\mathit {k}}}$. Certainly, an f -CC must satisfy C^k for some 1 ≤ k ≤|V |− 1. Hence, we define the following sub-problem called the constrained cohesive subgraph mining (ConsCS) problem:

Problem Definition 2

Given a graph G = (V, E), a monotonically increasing function $f: \mathbb {N} \to \mathbb {R}$ and k ∈ [1,|V |− 1], the goal of the constrained cohesive subgraph mining (ConsCS) problem is to find the set of f-CCs in G satisfying C^k.

Theorem 3

Given a graph G, for k ∈ [1,|V |− 1], let F_{f, k}(G) be the set of f-CCs satisfying constraint C^k in G. We have

$$ F_{f}(G) = {\bigcup}_{k = 1}^{|V| - 1} F_{f,k}(G). $$

(2)

Proof

(1) Obviously, by definition, ${\bigcup }_{k = 1}^{|V| - 1} F_{f,k}(G) \subseteq F_{f}(G)$. (2) For each f-CC Q ∈ F_f(G), let k be the minimum degree of vertices in G[Q]. Definitely, 1 ≤ k ≤|V |− 1. Based on Theorem 2, Q satisfies C^k. Therefore, Q ∈ F_{f, k}(G). Thus, we have $F_{f}(G) \subseteq {\bigcup }_{k = 1}^{|V| - 1} F_{f,k}(G)$. Therefore, the theorem holds. □

According to Theorem 3, F_f(G) can be obtained by solving each ConsCS problem instance 〈G, f, k〉 for k = 1,2,…,|V |− 1. Note that, given a ConsCS instance 〈G, f, k〉, the number of f -CCs in G satisfying C^k can be exponential to the size of G. It is nearly impossible to enumerate all such f -CCs in G. Therefore, we cannot merge all exact result sets of ConsCS instances as the qualified f -CCs set S and further select diversified top-rf -CCs from it. To tackle this, we develop a heuristic method to approximately extract representative f -CCs that attain high diversity (i.e., cover a large number of vertices) for solving the ConsCS problem, which will be described in Section 4. And then, we merge all these result sets of ConsCS instances to obtain S.

3.1.2 Elimination of ConsCS problem instances

Next, we present a filtering method to eliminate some ConsCS problem instances that are unpromising to produce informative f -CCs that have contributions to the diversity of the final result set. This method is based on the k-core model [17]: a set Q of vertices is a k-core of a graph G if every vertex in G[Q] is of degree at least k. A k-core is maximal if none of its proper supersets is a k-core. A key concept related to the k-core model is shown in Definition 3.

Definition 3

(core number) The core number of G, denoted by κ(G), is the largest integer k such that the maximal k-core of G is nonempty. The core number of a vertex v ∈ V in G, denoted by κ_G(v), is the largest integer k such that there exists a nonempty maximal k-core containing v in G. κ_G(v) can be simplified as κ(v) if G is clear in the context.

The k-core model has two elegant properties:

• Uniqueness: The maximal k-core is unique.

• Hierarchy: The maximal k-core is a subset of the maximal k^′-core if k^′≤ k.

In the following, we use ${K_{k}^{G}}$ to denote the maximal k-core of G. When G is clear in the context, ${K_{k}^{G}}$ can be simplified as K_k.

Lemma 1

Any f-CC satisfying the constraint C^k is contained in a connected component of the maximal k-core K_k of G.

Proof

The lemma holds due to the minimum degree constraint $\mathbf {C_{1}^{\mathit {k}}}$. □

Based on Lemma 1, the ConsCS problem instance 〈G, f, k〉 can be solved on G[K_k] instead of on G. Moreover, since f -CCs are connected, we can solve the instance 〈G[K_k], f, k〉 on each connected component of G[K_k] independently.

Lemma 2

Let C be a connected component of the maximal k-core K_k of G. Given the ConsCS problem instance 〈G[C], f, k〉, if |C|≤ g^− 1(k), C is an f-CC in the result and is a superset of any other f-CC in the result.

Proof

The lemma holds due to the maximum size constraint $\mathbf {C_{2}^{\mathit {k}}}$ and Lemma 1. □

Since the goal of our FlexCS problem is to extract representative f -CCs that attain high diversity and avoid uninformative ones, it is not reasonable to include two f -CCs with inclusion relationship in the result set. Accordingly, also for speeding up the proceeding diversified top-rf -CCs selection, it is necessary to keep S succinct, i.e., for two f -CCs Q₁ and Q₂ in S, if $Q_{1} \subseteq Q_{2}$, Q₁ can be removed from S without sacrificing diversity but making S smaller. According to Lemma 2, if there exists a connected component C in G[K_k] with |C|≤ g^− 1(k), C is certainly an f -CC, and any f -CC in G[C] is a subset of C. If C is already contained in S, any subset of C can be removed from S. All ConsCS problem instances $\langle G[C^{\prime }], f, k^{\prime }\rangle$ for $C^{\prime }\subseteq C$ and $k \le k^{\prime }$ can thus be eliminated. Consequently, we have the following core-based filtering method:

• 1. We compute all nonempty maximal k-cores in G for k ≥ 1 by the fast core decomposition algorithm [3].

• 2. We deal with each maximal k-core in ascending order of k. For each maximal k-core K_k with 1 ≤ k ≤ κ(G), we first compute its connected components. Then, for each connected component C, if |C|≤ g^− 1(k), we add C into S and remove all vertices in C from the k^′-cores for k^′≥ k.

Now, we only need to solve the ConsCS problem instances on each remaining connected component of each nonempty maximal k-core after applying the core-based filtering.

Example 4

Consider the example graph shown in Figure 2 and $f(x) = \sqrt x$. When k = 4, the maximum size constraint w.r.t. k is |Q|≤ g^− 1(k) = 16. Since the only one connected component of the maximal 4-core is K₄ = {c, d, e, f, g, h, i, j, k, l, m} with size 11, K₄ is an f-CC. We add K₄ into S and all ConsCS problem instances $\langle G[C^{\prime }], f, k^{\prime }\rangle$ for $C^{\prime }\subseteq K_{4}$ and $k^{\prime } \ge 4$ can be eliminated.

3.2 Diversified top-r f -CCs selection

The second component of our method is to choose from S, the set of qualified f -CCs, r most diversified ones that can cover the largest number of vertices. Because it is extremely expensive to enumerate all r-combinations of f -CCs in S and then select the most diversified one, we design a method that approximately identifies the best r-combination of f -CCs. Our algorithm maintains a set $\mathcal {R}$ of temporary diversified top-r f -CCs. Initially, $\mathcal {R} = \emptyset$. When a new f -CC Q is found, we use Procedure Update (Algorithm 1) to update $\mathcal {R}$ with Q according to the following rules:

• R₁ If $|\mathcal {R}| < r$, we add Q to $\mathcal {R}$ (lines 1–2).

• R₂ If $|\mathcal {R}| = r$, we replace an f -CC in $\mathcal {R}$ by Q if such replacement can significantly expand $\mathsf {cov}(\mathcal {R})$ (lines 3–6). Specifically, let $Q^{*} \in \mathcal {R}$ be the f -CC that covers the least number of vertices exclusively by itself among all f -CCs in $\mathcal {R}$. Replace Q^∗ by Q if $\mathcal {R}$ can cover at least $|\mathsf {cov}(\mathcal {R})|/r$ more vertices after applying the replacement.

Theorem 4

Let S = {Q₁, Q₂,…, Q_n} be a set of f-CCs and $\mathcal {R}^{*} \subseteq S$ be the set of r f-CCs in S that covers the largest number of vertices. Let $\mathcal {R}$ be the final set of r f-CCs updated with Q₁, Q₂,…, Q_n in an arbitrary order according to the rules R₁ and R₂. We have $|\mathsf {cov}(\mathcal {R})|\ge |\mathsf {cov}(\mathcal {R^{*}})|/4$.

Proof

For the proof of Theorem 4, please refer to [2]. □

By implementing the PNP-Index introduced in [21], the space and time complexity of Update is O(r|V |) and O(|V |), respectively [21].

3.3 Description of algorithm

Our algorithm for solving the FlexCS problem is presented in Algorithm 2. It first initializes the result set $\mathcal {R}$ and the set S of qualified f -CCs to be empty (line 1). For ease of presentation, let g(x) = ⌈f(x)⌉. Then, it computes all nonempty maximal k-cores $K_{1}, K_{2}, \dots , K_{\kappa (G)}$ in G by the fast core decomposition algorithm CORE [3] (line 3). Next, the algorithm carries out the core-based filtering (lines 4–12). The filtering process stops when all vertices in the maximal k-core K_k have been removed. After applying the core-based filtering, the algorithm finds qualified f -CCs on the updated maximal k-cores (lines 13–18) in descending order of k. It first recomputes the connected components in K_k (line 15). Then, it invokes Procedure ConsCS to solve the ConsCS problem instance on each connected component of K_k (line 17) and adds the discovered f -CCs to S (line 18). The details of Procedure ConsCS will be presented in Section 4. After S has been obtained, the algorithm uses each f -CC in S to update $\mathcal {R}$ (lines 19–20). Finally, $\mathcal {R}$ is outputted (line 21).

The space and time complexity of Algorithm 2 are O(r|V |) and O(|V |³), respectively. Since the analysis of the space and time complexity of Algorithm 2 requires the procedures and the results presented in Sections 4 and 5, we give the analysis in Appendix A.

4 Solving the ConsCS problem

In this section, we present our algorithm for solving the ConsCS problem. We only study the problem instances 〈G[C], f, k〉 for |C| > g^− 1(k) because the other instances for |C|≤ g^− 1(k) have been eliminated by the core-based filtering. In the following, we present how to generate an f -CC in Section 4.1 and describe the algorithm for solving the ConsCS problem in Section 4.2.

4.1 f -CC generation

We first introduce how to generate an f -CC in G[C] satisfying the constraint C^k enforced in Section 3.1. To avoid the huge search space of the enumeration paradigm and the large overlap between the enumerated f -CCs, we design a heuristic method inspired by [15] that leverages both greediness and randomness: It first generates a series of vertex subsets by progressively adding vertices starting from a seed vertex and then outputs the most diversified one.

Algorithm 3 shows the proposed algorithm FccGen to generate an f -CC starting from a seed vertex s. The selection of seeds will be discussed in Section 4.2. At first, the current selected vertex subset Q and the maximum f -CC discovered so far Q_max are initialized in line 1. To make all vertices in G[Q] have their degrees at least k as early as possible, we design the following strategy to add a new vertex to Q. Let $Q_{k} \subseteq Q$ be the set of vertices of degree less than k in G[Q] (line 2). For a vertex v ∈ C − Q, let $d_{Q_{k}}(v)$ be the number of vertices in Q_k that are adjacent to v in G[C]. The larger $d_{Q_{k}}(v)$ is, the more vertices in Q_k can have their degrees increased after adding v to Q. However, selecting v with the largest $d_{Q_{k}}(v)$ may lead the search to a sub-optimal cohesive subgraph. Hence, we select v with $d_{Q_{k}}(v) \ge (1 - \alpha ) \min \limits _{u \in C-Q} d_{Q_{k}}(u) + \alpha \max \limits _{u \in C-Q} d_{Q_{k}}(u)$ uniformly at random, where α ∈ [0,1] (lines 5–8). Parameter α controls the trade-off between greediness and randomness: when α = 1, the vertex v with the largest $d_{Q_{k}}(v)$ is selected; when α = 0, an arbitrary vertex adjacent to a vertex in Q_k is chosen randomly.

When the degree of every vertex in G[Q] becomes at least k, the generation step continues adding new vertices to Q to form an even larger f -CC. We now have Q_k = ∅, so the heuristic strategy described above is not applicable any more. Alternatively, we select a vertex v with $d_{Q}(v) \ge (1 - \alpha ) \min \limits _{u \in C-Q} d_{Q}(u) + \alpha \max \limits _{u \in C-Q} d_{Q}(u)$ uniformly at random, where α ∈ [0,1] (lines 10–13), since v is expected to be cohesively linked to Q.

As long as a new vertex v has been selected, we add it to Q (line 14) and recalculate Q_k (line 15). When Q_k is empty, Q is the current largest f -CC satisfying the constraint C^k. We hence copy Q to Q_max (lines 16–17). According to the maximum size constraint ${\mathbf {C}_{\mathbf {2}}^{\mathit {k}} }$, the generation process stops when |Q| = g^− 1(k) (line 3). Q_max must be a subset of C and satisfy the constraint C^k, so it is returned as the result (line 18).

We now analyze the space and time complexity of FccGen. Apparently, the procedure only requires O(|C|) space to keep Q, Q_max and candidate vertices in C to be added to Q. Therefore, the space complexity of FccGen is O(|C|). Then, we consider its time complexity. In each iteration, the procedure selects a vertex from C − Q to add to Q, which runs in O(|C|) time. Since the generation process consists of at most |C| iterations, it therefore takes O(|C|²) time. Overall, the time complexity of FccGen is O(|C|²).

4.2 Algorithm for the ConsCS problem

As presented in Section 4.1, the f -CC generation procedure FccGen starts from a seed vertex and generates an f -CC in the proximity of the seed. Since FccGen is fast and randomized, we can repeat it many times starting from different seeds to get more diversified f -CCs.

To approximately solve a ConsCS problem instance 〈G[C], f, k〉, a trivial method is to designate each vertex in C as a seed and generate an f -CC starting from the seed. However, this method often carries out a lot of redundant computation and produces many overlapping f -CCs. For efficiency consideration, we adopt the following seed selection strategies to reduce redundancy.

• The vertices in a generated f -CC will not be chosen as seeds any more.

• The vertices in the maximal (k + 1)-core K_k+ 1 of G will not be selected as seeds because these vertices have been considered as seeds when solving the problem instances $\langle G[C^{\prime }],f,k^{\prime } \rangle$ for $k^{\prime } \ge k + 1$ and $C^{\prime } \subseteq C$.

Based on the f -CC generation procedure FccGen presented in Algorithm 3 and the seed selection strategies described above, we develop an algorithm for approximately solving the ConsCS problem in Algorithm 4. The procedure is self-explanatory. We now analyze the space and time complexity of ConsCS. As analyzed in Section 4.1, the FccGen procedure invoked in line 4 requires O(|C|) space and O(|C|²) time, so the space complexity of ConsCS is O(|C|). Since the for loop in lines 3–6 is executed at most |C| times, and each loop runs in O(|C|²) time, the time complexity of ConsCS is O(|C|³).

Example 5

Consider the example graph shown in Figure 2 and a ConsCS problem instance $\langle G[K_{3}], f(x) = \sqrt x, k = 3 \rangle$ on the connected 3-core K₃. We consider S = {n, o, p, q, r, s, t, u} as initial seeds since $\{c, d, e, f, g, h, i, j, k, l, m\} \subseteq K_{4}$. First, we select the vertex n as seed and execute FccGen. Assume that FccGen returns Q₁ = {d, e, g, h, j, k, l, n}, we add Q₁ into T and remove n from S. Then, we select the vertex o as seed and execute FccGen. Assume that FccGen returns Q₂ = {n, o, p, q, r, s, t, u}, we add Q₂ into T and remove vertices in Q₂ from S. Now, S = ∅, the procedure terminates and returns T.

5 Optimization techniques

This section introduces some optimization techniques that help speed up the proposed FlexCS algorithm.

5.1 On-the-fly result set updating

For ease of presentation, in FlexCS (Algorithm 2), we keep the qualified f -CCs in the set S in memory (lines 9 and 18) and later update the result set $\mathcal {R}$ with the f -CCs in S at the end of the algorithm (lines 19–20). In fact, it is not necessary to keep S in memory. In our implementation, whenever a new f -CC Q is found in line 9 of FlexCS (Algorithm 2) or in line 4 of ConsCS (Algorithm 4), we immediately update $\mathcal {R}$ with Q using Procedure Update (Algorithm 1). The on-the-fly updating of $\mathcal {R}$ is correct because the order in which the f -CCs in S are used to update $\mathcal {R}$ does not affect the approximation ratio of $\mathcal {R}$ (see Theorem 4). The on-the-fly updating of $\mathcal {R}$ can significantly reduce memory overhead because |S| is usually very large for a large input graph G.

5.2 Early termination mechanism

With the on-the-fly result set updating, the result set $\mathcal {R}$ can be filled with r f -CCs at an early stage of the FlexCS algorithm (Algorithm 2). It enables us to design a mechanism to early terminate the execution of ConsCS (Algorithm 4) and FlexCS (Algorithm 2) if they are not possible to generate any useful f -CCs to improve the coverage $\mathsf {cov}(\mathcal {R})$ of $\mathcal {R}$. For ease of notation, let $\mathsf {minCov}(\mathcal {R})$ denote the least number of vertices exclusively contained in an individual f -CC in $\mathcal {R}$, that is, $\mathsf {minCov}(\mathcal {R}) = \min \limits _{Q\in \mathcal {R}}|\mathsf {cov}(\mathcal {R})-\mathsf {cov}(\mathcal {R}-\{Q\})|$. We have the following theorem:

Theorem 5

Given an instance 〈G[C], f, k〉 of the ConsCS problem, none of the f-CCs generated by Procedure ConsCS (Algorithm 4) on G[C] can update the result set $\mathcal {R}$ if the following conditions hold:

$$ \left\{ \begin{array}{lr} |\mathcal{R}| = r, \\ \mathsf{minCov}(\mathcal{R}) + \frac{1}{r}|\mathsf{cov}(\mathcal{R})| > g^{-1}(k). \end{array} \right. $$

(3)

Proof

Let Q^∗ be the f-CC in $\mathcal {R}$ that covers the least number of vertices exclusively by itself, i.e., $|\mathsf {cov}(\mathcal {R})-\mathsf {cov}(\mathcal {R}-\{Q^{*}\})| = \mathsf {minCov}(\mathcal {R})$. If the conditions presented in (3) hold, for each f-CC Q in the result set of the ConsCS problem instance 〈G[C], f, k〉, replacing Q^∗ with Q leads to a new result set $\mathcal {R}'$ such that:

$$ \begin{array}{@{}rcl@{}} |\mathsf{cov}(\mathcal{R}\prime)| &= &|\mathsf{cov}(\mathcal{R}-\{Q^{*}\}) \cup \{Q\}| \\ &\le &|\mathsf{cov}(\mathcal{R})| - \mathsf{minCov}(\mathcal{R}) + g^{-1}(k) \text{// According to} \mathbf{C}_{2}^{{k}} \\& < &\left( 1+\frac{1}{r}\right)|\mathsf{cov}(\mathcal{R})|. \end{array} $$

According to the rule R₂ presented in Section 3.2, Q cannot be used to update $\mathcal {R}$. The theorem thus holds. □

Theorem 5 naturally indicates the following early termination mechanism for ConsCS (Algorithm 4). In Algorithm 4, we check the conditions presented in (3) before executing FccGen in line 4 and terminate Algorithm 4 if the conditions hold because no more useful f -CCs can be generated to update $\mathcal {R}$.

We can further extend this early termination mechanism to FlexCS (Algorithm 2). In Algorithm 2, we check the conditions presented in (3) before executing line 15 and terminate Algorithm 2 if the conditions hold. If Algorithm 2 is early terminated for some value of k, it completely avoids executing ConsCS on the connected components of the maximal k^′-cores for k^′≤ k because no more useful f -CCs can be generated on any connected component in these maximal k^′-cores to update $\mathcal {R}$. This also explains why k is considered from $k_{\max \limits }$ downward to 1 in line 14 of Algorithm 2 (just for early termination).

5.3 Index-based connected component retrieval

Note that FlexCS (Algorithm 2) computes the connected components of each maximal k-core K_k in G twice (line 6 and line 15). In line 6, it computes the connected components of K_k to realize the core-based filtering (see Section 3.1.2) that removes small connected components of K_k (in ascending order of k). Since K_k is changed in line 11, we must re-compute the connected components of K_k in line 15 and execute ConsCS to generate qualified f -CCs on each large connected component of K_k (in descending order of k). Obviously, large amount of redundant computation has to be carried out in line 15.

To reduce such redundant computation, one available alternative is to compute all connected components of K_k in line 6 and save them in memory for future use. However, this approach requires O(κ(G)|V |) space to keep all large-sized connected components, where κ(G) is the core number of G (Definition 3). To make a trade-off between time and space, we design the connected component index (CCIndex for short) to facilitate the retrieval of the connected components of K_k. The CCIndex only requires O(|V |) space, and with the help of it, we can avoid the redundant computation caused by re-computing connected components performed in line 15 of Algorithm 2.

5.3.1 Connected component index (CCIndex)

A CCIndex is composed of two arrays A and CC:

• 1. The array A holds all vertices in G in a specific order which will be introduced below.

• 2. The array CC serves as an access path to the information stored in A.

The key to designing the CCIndex is the ordering of vertices in the array A. The central idea is that all vertices in a connected component C of the maximal k-core K_k are consecutively placed in A so that C can be efficiently retrieved by doing a sequential read on A. To retrieve C, we only need to know the offset s_C of the first vertex in C within A and the size |C| of C because C = {A[i]|s_C ≤ i < s_C + |C|}. Such ordering of vertices in A can be realized based on the hierarchical structure described in the following lemma.

Lemma 3

Each connected component of the maximal k-core K_k is a subset of a connected component of the maximal $k^{\prime }$-core $K_{k^{\prime }}$ if $k^{\prime }\le k$.

Proof

Let C be a connected component of K_k and $C^{\prime }$ be a connected component of $K_{k^{\prime }}$ that overlaps with C. Suppose $C \not \subseteq C^{\prime }$. We have that $C \cup C^{\prime }$ is a $k^{\prime }$-core and $C \cup C^{\prime }$ is connected. It contradicts with the fact that $C^{\prime }$ is a connected component of $K_{k^{\prime }}$. Thus, the lemma holds. □

Figure 5 illustrates how we order the vertices in the array A according to the hierarchical structure described in Lemma 3. By leveraging the hierarchical structure among connected components, the overlaps between connected components are stored in A only once. Therefore, the array A can be regarded as a redundancy-free compression of all connected components of all maximal k-cores of G. The details of constructing the array A will be presented in the next subsection.

Fig. 5

Illustration of the ordering of vertices in the array A in the CCIndex. The maximal 1-core K₁ of graph G has two connected components C_1,1 and C_1,2; The maximal 2-core K₂ has three connected components C_2,1, C_2,2 and C_2,3; The maximal 3-core K₃ has three connected components C_3,1, C_3,2 and C_3,3. The hierarchical structure of these connected components is illustrated by the nested circles. The dotted lines depict the mapping from a connected component to a sub-array of A

After the order of vertices in A has been determined, the information required for retrieving each connected component is kept in the array CC. As mentioned above, for each connected component C of the maximal k-core K_k, it can be identified by the offset s_C of the first vertex in C within A and the size |C| of C. The pair (s_C,|C|) is thus recorded in the element CC[k]. Since K_k may be composed of several connected components, CC[k] actually records a list of pairs (s_C,|C|) for all connected components C in K_k.

Example 6

Figure 6 shows a CCIndex for the example graph given in Figure 2. The vertices in the array A are ordered such that all vertices in a connected component of the maximal k-core K_k are consecutively placed in A. For k = 4, the maximal 4-core in the graph is K₄ = {c, d, e, f, g, h, i, j, k, l, m}. There is only one connected component in K₄, i.e., K₄ itself. The size of K₄ is 11, and the first vertex (m) in K₄ within A is placed in A[0]. Therefore, the pair (0,11) is recorded in the element CC[4]. According to the pair (0,11), this connected component can be retrieved as $A[0 {\dots } 10]$.

Fig. 6

A CCIndex for the example graph given in Figure 2

Furthermore, to efficiently support the core-based filtering (Section 3.1.2) and the early termination mechanism (Section 5.2), the pairs (s_C,|C|) in CC[k] are sorted in ascending order of |C|. The core-based filtering can be implemented by examining each pair (s_C,|C|) in CC[k] and removing it from CC[k] if |C|≤ g^− 1(k). Procedure ConsCS is then executed on each connected component C represented by each remaining pair (s_C,|C|) in CC[k].

5.3.2 Construction of CCIndex

The algorithm for constructing a CCIndex is presented in Algorithm 5. The input of the algorithm includes the graph G = (V, E), the core number κ(G) of G and the core number κ(v) of every vertex v ∈ V. The output of the algorithm is a CCIndex of G. The algorithm works as follows. First, we set up the array A and the array CC in the CCIndex (line 1). The length of A is |V |, and the length of CC is κ(G). For ease of notion, let A[s : t] denote the sub-array of A starting from A[s] and ending at A[t], where 1 ≤ s ≤ t ≤|V |. Then, we add all vertices in V to A in an arbitrary order (lines 2–5). The key step of the algorithm is reordering the vertices in A (line 6) so that they satisfy the criterion of ordering described in Section 5.3.1.

The reordering of A is realized by the recursive procedure Reorder. The procedure takes as input a sub-array A[s : t], the array CC and an integer k ∈ [0, κ(G)]. As will be shown later, this procedure has the following invariant: all vertices in A[s : t] form a connected component of the maximal k-core K_k of G for k = 1,2,…, κ(G). Therefore, we have κ(v) ≥ k for all v ∈ A[s : t]. The procedure works as follows. First, the vertices in A[s : t] form a connected component of K_k, and its size is t − s + 1. To enable fast access to this connected component, we add the pair (s, t − s + 1) to the element CC[k] of the array CC (line 8). Then, we move all vertices v ∈ A[s : t] with κ(v) > k to the front of A[s : t] (lines 9–16). Suppose there are l vertices v ∈ A[s : t] with κ(v) > k.

If l = 0, all vertices in A[s : t] have core number k. According to the invariant of the procedure, all vertices in A[s : t] form a connected component of K_k. This connected component is now consecutively placed in A[s : t], which satisfies the criterion of the ordering described in Section 5.3.1. Since all vertices in A[s : t] have core number k, none of the connected components of $K_{k^{\prime }}$ with $k^{\prime } > k$ is nested in A[s : t]. Therefore, the reordering of A[s : t] is done, and the procedure returns (line 18).

If l > 0, some of the connected components of $K_{k^{\prime }}$ with $k^{\prime } > k$ are nested in A[s : s + l − 1], so we must recursively reorder the vertices in A[s : s + l − 1]. First, we compute the connected components of the subgraph of G induced by the vertices in A[s : s + l − 1] (line 19). Let $C_{1}, C_{2}, \dots , C_{m}$ be these connected components. Then, we reorder the vertices in A[s : s + l − 1] so that the vertices in each connected component C_i are consecutively placed in A. Particularly, we move the vertices in C_i to the sub-array A[s_i : t_i], where $s_{i} = s + {\sum }_{j = 1}^{i - 1} |C_{j}|$ and t_i = s_i + |C_i|− 1 (lines 20–24). The order of vertices in A[s_i : t_i] is arbitrary. Next, for i = 1,2,…, m, we recursively reorder the vertices in A[s_i : t_i] by calling Procedure Reorder with input A[s_i : t_i], CC and k + 1 (lines 25–29).

In line 6 of the CCIndex construction algorithm (Algorithm 5), we call Procedure Reorder with input A, CC and k = 0 to start reordering all vertices in A. When the procedure returns, the construction of the CCIndex is completed. The algorithm outputs the arrays A and CC (line 7).

The correctness of Algorithm 5 is ensured by the invariant of Procedure Reorder stated in the following theorem.

Theorem 6

All vertices in A[s : t] form a connected component of the maximal k-core K_k of G for k = 1,2,…, κ(G).

Proof

We prove this theorem by induction on k. First, we consider the inductive base for k = 1. When Procedure Reorder is called at line 6 of Algorithm 5, it moves all vertices v in A with κ(v) ≥ 1 to A[1 : l] (lines 9–16) and computes the connected components $C_{1}, C_{2}, \dots , C_{m}$ of the subgraph of G induced by the vertices in A[1 : l] (line 19). Certainly, $K_{1} = C_{1} \cup C_{2} \cup {\dots } \cup C_{m}$. Therefore, C_i is a connected component of K₁ for 1 ≤ i ≤ m. Each connected component C_i is consecutively stored in A[s_i : t_i] (lines 20–24), and A[s_i : t_i] is recursively reordered by calling Procedure Reorder with input A[s_i : t_i] and k = 1 (line 28). Therefore, all vertices in A[s_i : t_i] form a connected component of K₁. The base case holds.

Assume that when Procedure Reorder is called with input A[s : t] and k, all vertices in A[s : t] form a connected component of K_k. Certainly, we have κ(v) ≥ k for all vertices v in A[s : t]. Procedure Reorder moves all vertices v in A[s : t] with κ(v) > k to A[s : s + l − 1] (lines 9–16) and computes the connected components $C_{1}, C_{2}, \dots , C_{m}$ of the subgraph of G induced by the vertices in A[s : s + l − 1] (line 19). We have κ(v) ≥ k + 1 for all v ∈ C_i. Therefore, C_i is a connected component of K_k+ 1. Procedure Reorder consecutively stores C_i in A[s_i : t_i] (lines 20–24) and reorders A[s_i : t_i] by recursively calling Procedure Reorder with input A[s_i : t_i] and k + 1 (line 28). Thus, all vertices in A[s_i : t_i] form a connected component of K_k+ 1. The induction holds. □

Given the graph G = (V, E), Algorithm 5 outputs the arrays A and CC in the CCIndex of G. The array A stores all vertices in V, so it takes O(|V |) space. The array CC stores a pair of integers (s_C,|C|) for each connected component C of each maximal k-core in G. As will be shown in the following theorem, there are totally at most |V | such connected components. Thus, CC requires O(|V |) space. Consequently, it takes O(|V |) space to store the CCIndex.

Theorem 7

Given the graph G = (V, E), let n_k be the number of connected components of the maximal k-core K_k of G. We have ${\sum }_{i = 0}^{\kappa (G)} n_{k} \le |V|$.

Proof

According to the definition of k-core, a k-core must be composed of at least k + 1 vertices. Therefore, K_κ(G) contains at least (κ(G) + 1)n_κ(G) vertices. For 0 ≤ k < κ(G), by Lemma 3, there are at least $\max \limits \{0, (n_{k} - n_{k+1})\}$ connected components in K_k that do not contain any connected component in K_k+ 1. Each of these connected components is a k-core, which contains at least k + 1 vertices. Therefore, $|K_{k} - K_{k + 1}| \ge (k + 1) \max \limits \{0, (n_{k} - n_{k+1})\}$. Hence, we have

$$ \begin{array}{@{}rcl@{}} |V| &=& |K_{\kappa(G)}| + \sum\limits_{k = 0}^{\kappa(G) - 1} |K_{k} - K_{k + 1}| \\ &\ge& (\kappa(G) + 1) n_{\kappa(G)} + \sum\limits_{k = 0}^{\kappa(G) - 1} (k + 1) \max\{0, (n_{k} - n_{k+1})\}\\ &\ge& n_{\kappa(G)} + n_{\kappa(G) - 1} + {\dots} + n_{1} + n_{0}. \end{array} $$

(4)

The last inequality (4) is derived based on the arguments shown in Appendix B. Thus, the theorem holds. □

We now analyze the space complexity of Algorithm 5. Given as input the sub-array A[s : t], Procedure Reorder needs O(l) space to compute and keep the connected components $C_{1}, C_{2}, \dots , C_{m}$ of the subgraph of G induced by the vertices in A[s : s + l − 1] (line 19). We have l ≤ t − s + 1 ≤|V |. This space can be released as soon as $C_{1}, C_{2}, \dots , C_{m}$ have been consecutively stored in A[s : s + l − 1] (lines 20–24). In addition to the O(|V |) space taken by the CCIndex, Algorithm 5 totally requires O(|V |) space.

Next, we analyze the time complexity of Algorithm 5. It takes O(|V |) time to add all vertices in V to the array A (lines 2–5). The execution time of line 6 is O(κ(G)(|V | + |E|)), which is analyzed as follows. For 0 ≤ k ≤ κ(G), let ${C^{k}_{1}}, {C^{k}_{2}}, \dots , C^{k}_{n_{k}}$ be all connected components of K_k. We have ${\sum }_{i = 1}^{n_{k}} |{C^{k}_{i}}| = |K_{k}|$. Suppose ${C^{k}_{i}}$ has been consecutively placed in $A[{s^{k}_{i}}:{t^{k}_{i}}]$. Given $A[{s^{k}_{i}}:{t^{k}_{i}}]$ and k as input, Procedure Reorder takes $O(|{C^{k}_{i}}|)$ time to move all vertices v in $A[{s^{k}_{i}}:{t^{k}_{i}}]$ with κ(v) > k to the front of $A[{s^{k}_{i}}:{t^{k}_{i}}]$ (lines 9–16). If Procedure Reorder does not return in line 18, it computes connected components of K_k+ 1 nested in C_i (line 19) and places these connected components consecutively in $A[{s^{k}_{i}}:{t^{k}_{i}}]$ (lines 20–24). For all ${C^{k}_{1}}, {C^{k}_{2}}, \dots , C^{k}_{n_{k}}$, it totally takes $O({\sum }_{i = 1}^{n_{k}} |{C^{k}_{i}}| = |K_{k}|)$ time to execute lines 9–16, $O({\sum }_{i = 1}^{n_{k+1}} |C^{k+1}_{i}| = |K_{k + 1}|)$ time to execute lines 20–24 and $O({\sum }_{i = 1}^{n_{k+1}} (|C^{k+1}_{i}| + |E[C^{k+1}_{i}]|)) = O(|K_{k + 1}| + |E[K_{k + 1}]|)$ time to execute line 19, where E[S] represents the set of edges in G with both endpoints in S. By Theorem 7, Algorithm 5 adds at most |V | integer pairs to the array CC (line 8), which totally takes O(|V |) time. Therefore, line 6 runs in $O(|V| + {\sum }_{k = 0}^{\kappa (G)} (|K_{k}| + |E[K_{k}]|)) = O(\kappa (G)(|V|+|E|))$ time. Consequently, the time complexity of Algorithm 5 is O(κ(G)(|V | + |E|)).

6 Experiments

In this section, we evaluate the proposed f -CC model and the FlexCS algorithm. First, we show the flexibility of the f -CC model compared with the clique model and the k-core model. Then, we evaluate the practical performance of the algorithm FlexCS with respect to its parameters. Next, we examine the effects of the optimization techniques proposed in Section 5. Finally, we verify the effectiveness of the algorithm FlexCS by comparing its results with a theoretical bound.

6.1 Experiment setting

Algorithms

Our FlexCS algorithm is compared with the diversified top-r cliques mining algorithm EnumKOpt [21] that finds r cliques covering the largest number of vertices and the core decomposition algorithm CORE [3] that computes all nonempty maximal k-cores. EnumKOpt uses the Update procedure (Algorithm 1) to maintain a set $\mathcal {R}$ of temporary diversified top-r cliques except that replacement only takes place if it makes $\mathcal {R}$ cover at least $\eta |\mathsf {cov}(\mathcal {R})|/r$ more vertices. When η = 1, it is exactly Procedure Update (Algorithm 1). To be consistent with [21], we set η = 0.3. In addition, since CORE returns all nonempty maximal k-cores, we only save top-r largest ones as results for ease of comparison. In the rest of this section, we use $\mathcal {R}_{f}$, $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$ to represent the outputs of FlexCS, EnumKOpt and CORE, respectively.

Parameters

The FlexCS algorithm has 4 parameters.

• r: The number of f -CCs to be found.

• α: The parameter used to tune the trade-off between randomization and greediness in Procedure FccGen (see Section 4.1).

• t: The number of threads used to execute Procedure FccGen on each maximal k-core in parallel.

• β: To attain more flexibility, we normally expect that the constraint imposed by function f is stricter on small subgraphs but looser on large subgraphs. Therefore, we tested various constraint functions with such trends in the experiments, including exponential functions in forms of f(x) = x^1/β and logarithmic functions in forms of $f(x) = \log _{\beta } (x)$, where β ≥ 1. We obtain similar results for all these functions. Therefore, we only report the results for f(x) = x^1/β in the rest of this section, where β ≥ 1.

The default values of r, α, t and β are set to 60, 0.9, 16 and 2, respectively. To avoid uninformative small clusters, we ignore cohesive subgraphs consisting of less than 5 vertices.

Datasets

Our experiments were performed on 9 real graphs obtained from the SNAP project (http://snap.stanford.edu). We regard the core number κ(G) of a graph G as an important feature because our algorithm processes each maximal k-core in G in sequence. In addition, κ(G) can reflect the density of G to some extent, which has essential impacts on most cohesive subgraph mining algorithms. Since we only consider simple graphs, we eliminated self-loops and multiple edges from all these graphs. Table 1 lists the statistics of these graphs. Note that the graph ca-GrQc is very small, which is only used for purpose of visualization in Section 6.2.

Table 1 Statistics of graphs used in experiments

Experiment setup

All the algorithms were implemented in C++ and compiled with the same optimization level. All experiments were carried out on a server with an Intel Xeon CPU (2.10GHz and 8 cores) and 220GB of RAM, running 64-bit Ubuntu 18.04. In our experiments, Procedure FccGen (Section 4.1) was implemented and executed using multi-threads.

6.2 Flexibility of the f -CC model

We first compare the flexibility of the f -CC model, the clique model and the k-core model. To evaluate the flexibility of these models, we first compare the sizes of cohesive subgraphs discovered by FlexCS, EnumKOpt and CORE. Then, we take a deeper look at the vertices covered by $\mathcal {R}_{f}$, $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$.

6.2.1 On the comparison of cohesive subgraph size

We first examine the sizes of cohesive subgraphs discovered by FlexCS, EnumKOpt and CORE. We remove the maximal 0-core and the maximal 1-core from $\mathcal {R}_{core}$ because they are nearly the entire graph. Figure 7 shows the sizes of f -CCs, cliques and k-cores in $\mathcal {R}_{f}$, $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$ in ascending order. We have the following observations: (1) The cliques found by EnumKOpt are always small, but the sizes of f -CCs discovered by FlexCS are distributed in a wide range. Both small f -CCs with tens of vertices and large f -CCs with hundreds of vertices can be characterized simultaneously. (2) Compared with f -CCs, the k-cores found by CORE are much larger. Note that the sizes of cohesive subgraphs are shown in log scale in Figure 7b. Therefore, the k-core model is not suitable for characterizing small clusters. In conclusion, the f -CC model attains more flexibility than both the clique model and the k-core model.

Fig. 7

Sizes of cohesive subgraphs discovered by FlexCS, EnumKOpt and CORE on com-DBLP. (a) f -CCs v.s. cliques; (b) f -CCs v.s. cores

6.2.2 On the comparison of cohesive subgraph coverage

In this section, we take a deeper look at the vertices covered by the cohesive subgraphs discovered under different models. Let $\mathsf {cov}(\mathcal {R}_{cli})$ and $\mathsf {cov}(\mathcal {R}_{core})$ be the coverage of $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$, respectively. For ease of comparison, we introduce two measures: precision and recall. Precision is defined as $\frac {|\mathsf {cov}(\mathcal {R}_{f}) \bigcap \mathsf {cov}(\mathcal {R}_{o})|}{|\mathsf {cov}(\mathcal {R}_{f})|}$, and recall is defined as $\frac {|\mathsf {cov}(\mathcal {R}_{f}) \bigcap \mathsf {cov}(\mathcal {R}_{o})|}{|\mathsf {cov}(\mathcal {R}_{o})|}$, where $\mathcal {R}_{o} \in \{\mathcal {R}_{cli}, \mathcal {R}_{core}\}$.

$\mathcal {R}_{f}$ v.s. $\mathcal {R}_{cli}$

When comparing the vertices covered by f -CCs found by FlexCS and cliques discovered by EnumKOpt, we vary β from 1.5 to 2.5. Table 2 shows the results. We can see that the precision is smaller than 0.5 in most cases. Actually, $\mathcal {R}_{cli}$ only contains a small proportion of vertices covered by $\mathcal {R}_{f}$ due to the strong constraint imposed by the clique model. Nevertheless, the recall is always large for most graphs, i.e., the discovered f -CCs can cover a large number of vertices in cliques. Especially, on com-DBLP, $\mathcal {R}_{f}$ covers more than 89 percent of vertices in $\mathcal {R}_{cli}$ for all β. However, for com-Amazon and gemsec-Deezer(HU) whose core numbers are relatively small, they usually contain a large number of small f -CCs and cliques. $\mathcal {R}_{cli}$ and $\mathcal {R}_{f}$ may cover different parts of the graph, and therefore the recall is small. Moreover, we can find that as β increases, the precision decreases, but the recall increases. It is consistent with our expectation that larger β leads to larger f -CCs, which will further result in a more diversified $\mathcal {R}_{f}$ that definitely contains more cliques.

Table 2 Comparison between $\mathcal {R}_{f}$ and $\mathcal {R}_{cli}$

$\mathcal {R}_{f}$ v.s. $\mathcal {R}_{core}$

When comparing vertices covered by f -CCs found by FlexCS and k-cores discovered by CORE, it is meaningless to compare $\mathcal {R}_{f}$ with some k-core since f -CCs are extracted from all maximal k-cores. Hence, we calculate the recall of $\mathcal {R}_{f}$ and each k-core for k ≤ κ(G) and then examine the variation of recall w.r.t. k to reveal the relationships between f -CCs and k-cores.

The experimental results on gemsec-Deezer (HU) and com-DBLP are shown in Figure 8. We can see that the recall increases with k, that is, $\mathcal {R}_{f}$ can basically cover k-cores for large k. Specifically, $\mathcal {R}_{f}$ covers all vertices in the 9-core on gemsec-Deezer (HU) and the 26-core on com-DBLP. However, $\mathcal {R}_{f}$ covers fewer vertices on k-cores with small k. The observation is consistent with our motivation: f -CCs can cover most vertices in cohesively connected regions but exclude those in sparse regions.

Fig. 8

Recall of $\mathcal {R}_f$ and k-core w.r.t. k on graphs gemsec-Deezer(HU) and com-DBLP. (a) Gemsec-Deezer(HU); (b) Com-DBLP

Visualization

To better illustrate the differences between cohesive subgraphs characterized by these models, we visualize $\mathcal {R}_{f}$, $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$ obtained on the smallest dataset ca-GrQc in Figure 9. The vertices in $\mathsf {cov}(\mathcal {R}_{f}) \cap \mathsf {cov}(\mathcal {R}_{o})$, $\mathsf {cov}(\mathcal {R}_{f}) - \mathsf {cov}(\mathcal {R}_{o})$ and $\mathsf {cov}(\mathcal {R}_{o}) - \mathsf {cov}(\mathcal {R}_{f})$ are colored in red, green and blue, respectively, where $\mathcal {R}_{o} = \mathcal {R}_{cli}$ or $\mathcal {R}_{core}$. Note that we eliminate all discovered cohesive subgraphs with size smaller than 6 for sake of fairness.

Fig. 9

Visualization of $\mathcal {R}_f$, $\mathcal {R}_{cli}$ and $\mathcal {R}_{core}$ on ca-GrQc. (a) $\mathcal {R}_f$ v.s. $\mathcal {R}_{cli}$; (b) $\mathcal {R}_f$ v.s. $\mathcal {R}_{core}$

Figure 9a shows the vertices covered by $\mathcal {R}_{f}$ and $\mathcal {R}_{cli}$. We can see that $\mathcal {R}_{f}$ covers a large portion of vertices in $\mathcal {R}_{cli}$. Note that the green vertices in $\mathsf {cov}(\mathcal {R}_{f})-\mathsf {cov}(\mathcal {R}_{cli})$ are also cohesively connected to each other and/or to the red vertices in $\mathsf {cov}(\mathcal {R}_{f})\bigcap \mathsf {cov}(\mathcal {R}_{cli})$, but they are excluded by $\mathcal {R}_{cli}$. Figure 9b shows the vertices covered by $\mathcal {R}_{f}$ and $\mathcal {R}_{core}$. The blue vertices in $\mathsf {cov}(\mathcal {R}_{core})-\mathsf {cov}(\mathcal {R}_{f})$ are always sparsely connected compared with the red vertices in $\mathsf {cov}(\mathcal {R}_{f})\bigcap \mathsf {cov}(\mathcal {R}_{core})$ and the green vertices in $\mathsf {cov}(\mathcal {R}_{f})-\mathsf {cov}(\mathcal {R}_{core})$, and fortunately they are excluded from the f -CCs discovered by FlexCS. The vertices in each f -CC in $\mathcal {R}_{f}$ are guaranteed to be cohesively connected.

6.3 Performance of FlexCS

Next, we evaluate the performance of the proposed FlexCS algorithm. In the experiments, we use two evaluation metrics: execution time and result coverage size (RCS) $|\mathsf {cov}(\mathcal {R}_{f})|$. For ease of presentation, let $\mathcal {R}$ denote the temporary result set at some moment of the execution of FlexCS. In the rest of this section, we only present some representative results for each experiment to save space. Note that, when evaluating the effects of a parameter, the other parameters are fixed to their default values.

Execution time and RCS w.r.t. r

Parameter r is the number of f -CCs to be found. Figure 10 shows the execution time and the RCS of FlexCS w.r.t. r on gemsec-Facebook and com-DBLP. Both RCS and execution time increase with r. This is because larger r leads to more f -CCs in $\mathcal {R}$, and therefore $\mathcal {R}_{f}$ certainly covers more vertices. While, maintaining $\mathcal {R}$ becomes more costly as r increases, and the early termination mechanism proposed in Section 5.2 becomes more difficult to take effects.

Fig. 10

Execution time and RCS w.r.t. r on graphs gemsec-Facebook and com-DBLP. (a) Gemsec-Facebook; (b) Com-DBLP

Execution time and RCS w.r.t. α

Parameter α tunes the trade-off between randomization and greediness in Procedure FccGen (see Section 4.1). Figure 11 shows the execution time and the RCS of FlexCS w.r.t. α on gemsec-Deezer (HU) and ca-AstroPh. We have the following observations: (1) In most cases, the RCS increases with α. When α becomes larger, our algorithm tends to generate an f -CC more greedily, so it is more possible to obtain f -CCs satisfying the minimum degree constraint $\mathbf {C_{1}^{\mathit {k}}}$ to fill $\mathcal {R}$. (2) The execution time decreases with α. Since larger α increases the chance to find valid f -CCs, $\mathcal {R}$ is filled with f -CCs earlier. Therefore, the early termination mechanism is more likely to take effects early.

Fig. 11

Execution time and RCS w.r.t. α on graphs gemsec-Deezer(HU) and ca-AstroPh. (a) Gemsec-Deezer(HU); (b) Ca-AstroPh

Execution time and RCS w.r.t. t

Parameter t is the number of threads used to execute Procedure FccGen on each maximal k-core in parallel. Figure 12 shows the execution time and the RCS of FlexCS w.r.t. t on musae-facebook and ca-CondMat. We have the following observations: (1) The RCS fluctuates slightly with t. It is because FlexCS is a randomized algorithm. Indeed, t has no impact on the RCS; (2) The execution time decreases as t increases, which is consistent with our expectation that executing Procedure FccGen in parallel with multiple threads can decrease the execution time to a large extent. Note that, for graph Ca-CondMat, the execution time slightly increases when using 16 threads compared with the one using 8 threads. This is because $\mathcal {R}$ can be updated by only one thread at a time. Too many threads increase the contention on updating $\mathcal {R}$.

Fig. 12

Execution time and RCS w.r.t. t on graphs musae-facebook and ca-CondMat. (a) Musae-facebook; (b) Ca-CondMat

Execution time and RCS w.r.t. f

Recall that the form of constraint function used in the experiments is f(x) = x^1/β, where β ≥ 1. Figure 13 shows the execution time and RCS w.r.t. β on com-Amazon and email-Enron. We have the following observations: (1) The RCS increases with β. Apparently, a larger β imposes a looser constraint on f -CCs, which leads to more diversified and larger f -CCs. (2) The execution time also increases with β. According to $\mathbf {C_{2}^{\mathit {k}}}$, the maximum size of f -CCs w.r.t. each minimum vertex degree increases exponentially as β increases. The number of iterations in FccGen thus increases exponentially as well, and the execution time increases significantly.

Fig. 13

Execution time and RCS w.r.t. β on graphs com-Amazon and email-Enron. (a) Com-Amazon; (b) Email-Enron

6.4 Effects of optimization techniques

We also evaluate the effects of the optimization techniques proposed in Section 5, particularly, the early termination mechanism (Section 5.2) and the CCIndex-based connected component retrieval (Section 5.3).

6.4.1 Effects of early termination mechanism

In this experiment, we evaluate the effects of the early termination mechanism (Section 5.2) on the performance of FlexCS. Table 3 shows the experimental results. We have the following observations: (1) For graphs com-Amazon and com-DBLP, the early termination mechanism can significantly decrease the execution time. For graph com-Amazon with small core number κ(G), there are lots of small f -CCs that are unable to update $\mathcal {R}$. Therefore, many ConsCS problem instances and many executions of FccGen can be eliminated. While, for graph com-DBLP whose core number κ(G) is large, $\mathcal {R}$ is filled with large f -CCs early, which helps filter out ConsCS instances on k-cores with small k. (2) For other graphs, the effects of the early termination mechanism are not so significant. This is because the number of vertices covered by $\mathcal {R}$ is not very large, so there always exist f -CCs in the graph that can update $\mathcal {R}$.

Table 3 Execution time of FlexCS without/with early termination (abbr. E.T.)

6.4.2 Effects of CCIndex

In this experiment, we evaluate the effects of the CCIndex (Section 5.3) on the performance of FlexCS. The experimental results are shown in Tables 4 and 5. We can see from Table 4 that the CCIndex brings a decrease in the execution time of FlexCS for every tested graph. The performance improvements achieved by the CCIndex seem not significant because the computation of connected components only takes a small portion of execution time of FlexCS (about 50% for com-Amazon and up to 10% for other graphs). Let us take a deeper look at the impacts of the CCIndex on the time of connected component computation and retrieval in FlexCS. From Table 5, we can see that the CCIndex helps decrease the time for component computation and retrieval by 15.1–66.7 percent on the tested graphs. These experimental results verify the effectiveness of the CCIndex.

Table 4 Execution time of FlexCS without/with the CCIndex

Table 5 Time of connected component computation and retrieval (CC-time for short) without/with the CCIndex

6.5 Effectiveness of FlexCS

To evaluate the effectiveness of FlexCS, we compare RCS with a theoretical upper bound, which is derived in the following way: We compute the maximum number of disjoint f -CCs with size g^− 1(k) for k = κ(G),…,1 and accumulate their sizes until the top-r f -CCs have been found. The correctness of such paradigm is guaranteed by Lemma 1 and the increasing monotonicity of f. Table 6 shows the results. We can see that the RCS is larger than 25 percent of the upper bound on each tested graph. Note that, the upper bound is the theoretical maximum regardless of the topological structure and connectivity of the graph, which is basically unreachable in real-world graphs.

Table 6 Comparison between RCS and its upper bound

7 Related work

7.1 Cohesive subgraph models

Different cohesive subgraph models impose constraints on different aspects of cohesive subgraphs. The existing models can be mainly categorized into three classes. The density-based models [11] impose constraints on the density of a subgraph. The distance-based models [11] impose constraints on the distance between any pair of vertices in a subgraph. The connectivity-based models [5] impose constraints on the edge/vertex connectivity of a subgraph. None of these models is flexible in characterizing multi-scale cohesive subgraphs simultaneously. We explain this with a specific model in each class. First, as a typical density-based model, a density-based γ-quasi-clique [1] with n vertices must be internally linked by at least $\gamma \left (\begin {array}{ll}{n}\\ {2} \end {array}\right )$ edges, where γ ∈ [0,1]. It is so strict that the model only fits for characterizing small cohesive subgraphs in a large graph due to the sparsity of real graphs. Second, the k-club model [14] is a typical distance-based model, in which every pair of vertices is within distance k. The size of a k-club generally grows exponentially as k increases because of the small-world nature of real graphs [18]. Therefore, the k-club model is not possible to simultaneously characterize both small and large cohesive subgraphs in a graph. Third, the k-ECC model [5] is a typical connectivity-based model. It requires that the edge connectivity of a cohesive subgraph is at least k. This model focuses on topological connectivity and is often applied to the scenarios where the edge/vertex cut size is the key consideration. Compared with these models, our f -CC model focuses on the flexibility of characterizing any relationship between the minimum degree and the number of vertices in a subgraph in various scales.

7.2 Diversified cohesive subgraph mining

Considerable work has been done on mining diversified cohesive subgraphs. An I/O-efficient approximation algorithm for mining diversified top-r cliques is proposed in [21]. Yang et al. [20] extends the notion of degree-based quasi-clique to temporal graphs and discovers diversified dense temporal subgraphs by a divide-and-conquer algorithm. Zhu et al. [22] extends the notion of k-core to multi-layer graphs and finds diversified top-r k-cores in a multi-layer graph. Recently, [19] devises a local search algorithm for the traditional diversified top-r cliques mining, which outperforms [21] on large sparse graphs. Fei et al. [9] proposes a formal concept analysis approach for diversified top-r cliques detection in Social Internet of Things. Since the models used to characterize cohesive subgraphs on these various kinds of graphs are the inflexible clique, quasi-clique or k-core models (or extended from these models), none of these algorithms fits for finding cohesive subgraphs of various scales simultaneously.

7.3 Redundancy-free cohesive subgraph mining

To discover meaningful (i.e., informative, less overlapping) cohesive subgraphs in a massive graph, one way is to maximize the diversity of the result set, which is adopted by our work and the work reviewed in Section 7.2. The other way is to reduce the redundancy of subgraphs in the result set. Boden et al. [4] defines a redundancy relationship between two cross-layer quasi-cliques in a multi-layer graph and designs algorithms to mine those cross-layer quasi-cliques that are redundancy-free and with high quality. This work provides us a new direction to investigate the problem of mining meaningful flexible cohesive subgraphs from the perspective of minimizing the redundancy in the result set. We will investigate this direction in our future work.

8 Conclusions and future work

The f -CC model is flexible in characterizing the relationship between the minimum degree of vertices and the number of vertices in a cohesive subgraph. The f -CC model is a generalization of the clique, quasi-clique and k-core models. The FlexCS problem is NP-hard and is even NP-hard to be approximated within |V |^1−𝜖 for all 𝜖 > 0. The proposed FlexCS algorithm is efficient in finding r representative f -CCs with high diversity. It outperforms the diversified top-r cliques mining algorithm and the core decomposition algorithm in discovering multi-scale cohesive subgraphs in one batch. In the future, we plan to investigate how to define and solve the problem of mining meaningful flexible cohesive subgraphs from the perspective of minimizing the redundancy of subgraphs in the result set. In addition, the problem of flexible cohesive subgraph searching given a set of query vertices is also worth to study as a further work since users often pay more attention to some specific vertices other than the entire graph in many real world applications.

Appendices

Appendix A Space and time complexity of Algorithm 2 (FlexCS)

We first analyze the space complexity of Algorithm 2. Given the input graph G = (V, E), it takes O(|V |) space to run the fast core decomposition algorithm CORE [3] on G and keep its results (line 3). By using the CCIndex proposed in Section 5.3, it takes O(|V |) space to compute and maintain the connected components of each maximal k-core of G in the CCIndex (lines 6 and 15, see Section 5.3.2). As analyzed in Section 4, Procedure ConsCS invoked in line 17 takes O(|V |) space. As mentioned in Section 3.2, the space for maintaining $\mathcal {R}$ (lines 19–20) is O(r|V |). By using the on-the-fly updating of the result set $\mathcal {R}$ (Section 5.1), the qualified f -CCs are not necessary to be stored in the main memory. Consequently, the space complexity of Algorithm 2 is O(r|V |).

Then, we analyze the time complexity of Algorithm 2. The fast core decomposition algorithm CORE [3] runs in O(|V | + |E|) time (line 3). By using the CCIndex proposed in Section 5.3, it takes O(κ(G)(|V | + |E|)) time to compute the connected components of each maximal k-core of G for 1 ≤ k ≤ κ(G) (lines 6 and 15). Moreover, the ConsCS procedure invoked in line 17 discovers an f -CC in O(|V |²) time (see Section 4). As mentioned in Section 3.2, the Update procedure invoked in line 20 runs in O(|V |) time. According to the seed selection strategies introduced in Section 4.2, at most |V | f -CCs are generated in line 9 or by ConsCS in line 17. Thus, the total time for solving all ConsCS instances and updating $\mathcal {R}$ with newly generated f -CCs are O(|V |³) and O(|V |²), respectively. Therefore, the time complexity of FlexCS is O(|V |³).

Appendix B Derivation of inequality (4)

First, let us consider the special case for $n_{0} \ge n_{1} \ge {\dots } \ge n_{\kappa (G)}$. We have

$$ \begin{array}{@{}rcl@{}} && (\kappa(G) + 1) n_{\kappa(G)} + \sum\limits_{k = 0}^{\kappa(G) - 1} (k + 1) \max\{0, (n_{k} - n_{k+1})\} \\ &= &(\kappa(G)+ 1) n_{\kappa(G)} + \sum\limits_{k = 0}^{\kappa(G) - 1} (k + 1) (n_{k} - n_{k+1}) \\ &= &\sum\limits_{k = 0}^{\kappa(G)} n_{k}. \end{array} $$

Then, we consider the cases for $n_{0} \ge n_{1} \ge {\dots } \ge n_{i}$, $n_{i + 1} \ge n_{i + 2} \ge {\dots } \ge n_{\kappa (G)}$ and n_i < n_i+ 1, where 0 ≤ i < κ(G). We have

$$ \begin{array}{@{}rcl@{}} & &(\kappa(G) + 1) n_{\kappa(G)} + \sum\limits_{k = 0}^{\kappa(G) - 1} (k + 1) \max\{0, (n_{k} - n_{k+1})\} \\ &= & (\kappa(G) + 1) n_{\kappa(G)} + \sum\limits_{k = 0}^{i - 1} (k + 1) (n_{k} - n_{k+1}) + \sum\limits_{k = i + 1}^{\kappa(G) - 1} (k + 1) (n_{k} - n_{k+1}) \\ &= & \sum\limits_{k = 0}^{i - 1} n_{k} + \sum\limits_{k = i + 2}^{\kappa(G)} n_{k} + (i + 2) n_{i + 1} - i \cdot n_{i} \\ &> &\sum\limits_{k = 0}^{\kappa(G)} n_{k}. \end{array} $$

The last inequality holds because (i + 2)n_i+ 1 − i ⋅ n_i > 2n_i+ 1 > n_i+ 1 + n_i.

For the cases where there are m > 1 integers $i_{1}, i_{2}, \dots , i_{m} \in [0, \kappa (G) - 1]$ such that $n_{i_{j}} < n_{i_{j} + 1}$ for all $j = 1, 2, \dots , m$, the proof is simply a generalization to the one given above for m = 1. The proof for the generalized cases is omitted.