MiMAG: mining coherent subgraphs in multi-layer graphs with edge labels

Abstract

Detecting dense subgraphs such as cliques or quasi-cliques is an important graph mining problem. While this task is established for simple graphs, today’s applications demand the analysis of more complex graphs: In this work, we consider a frequently observed type of graph where edges represent different types of relations. These multiple edge types can also be viewed as different “layers” of a graph, which is denoted as a “multi-layer graph”. Additionally, each edge might be annotated by a label characterizing the given relation in more detail. By simultaneously exploiting all this information, the detection of more interesting subgraphs can be supported. We introduce the multi-layer coherent subgraph model, which defines clusters of vertices that are densely connected by edges with similar labels in a subset of the graph layers. We avoid redundancy in the result by selecting only the most interesting, non-redundant subgraphs for the output. Based on this model, we introduce the best-first search algorithm MiMAG. In thorough experiments, we demonstrate the strengths of MiMAG in comparison with related approaches on synthetic as well as real-world data sets.

1 Introduction

Mining graph and network data has gained much attention in recent years. One important mining task is “dense subgraph mining” that aims at grouping the vertices of a graph into clusters (subgraphs) such that many edges between vertices of the same cluster exist, i.e. the vertices are densely connected. This can be seen as a specific form of graph clustering. Examples for dense subgraph mining approaches include the detection of cliques or quasi-cliques [26].

Besides the mere graph data, real-world data often contain additional information that can be used to improve the clustering results. An extensively studied scenario is graphs enriched by vertex labels (e.g. [15, 18, 19, 27, 35]). In this work, in contrast, we consider additional information about the edges of a graph.

In particular, we consider graphs that contain different types of edges, e.g., representing the various relations between vertices. A prominent example for this setting is the combination of multiple information sources. For example, by combining a co-author network with a citation network, we obtain two edge types: (i) “co-authorship”—authors are connected if they have common papers—(ii) “citation”—authors are connected if they cite each others papers. Furthermore, each edge might also be associated with a label, e.g. the year a co-authored paper was published.

We denote such a graph with multiple edge types as a “multi-layer graph”. It is defined as a set of graphs (called “layers”) where each graph is based on the same set of vertices and represents the edges of one certain type. Accordingly, in each layer a different edge set is given. These layers can also be viewed as “dimensions” of the graph.¹ An example multi-layer graph is depicted in Fig. 1. Apart from the author example described above, this setting can be seen in various applications: For example, in a social network the layers could represent different types of relations like “friends” or “colleagues” and the labels could represent additional information like the time when the relation has been added. In a rating network like Yelp (www.yelp.com), layers could represent information like “geographically close” and “rated by the same users”, while the labels of the edges could provide information like “how many users rated both items”. More real-world examples are described in the experimental section.

1.1 Different types of edge labels

For graphs with edge labels, we can distinguish between two possible interpretations of the labels: First, labels can be regarded as edge weights that denote the strength of the relation between the incident vertices, e.g. the number of joint papers in a co-author network. In this case, a cluster would be a set of vertices which are connected by edges with high weights. Second, edge labels can represent characteristics of the relations. For example, a co-author network might contain information about the collaboration between two authors such as their research topics or conferences/journals where the joint papers were published. In a social network, edge labels might indicate the time when a connection has been established or information about trust and distrust (see e.g. Epinions). For such characteristics, it would not make sense to treat them as edge weights. In this case, a cluster consists of a set of densely connected vertices with similar labels, e.g. a group of authors collaborating on a certain topic in a certain time range.

Both interpretations present interesting problems, and each of them has its own applications. However, while graphs with edge weights have been considered in various previous approaches, graphs with labels representing characteristics have mostly been neglected so far. In this paper, we consider the second interpretation and treat edge labels not as weights, but as characteristics of the relations.

Fig. 1

Example of a multi-layer graph. Each layer represents a different edge set

1.2 Goal of our approach

Overall, in this work, we aim at finding clusters of vertices that are densely connected by edges with similar labels in a subset of the graph layers. These clusters are denoted as (multi-layer) coherent subgraphs. It is worth mentioning that our approach is also applicable if no edge labels are given but only multiple (unlabelled) graph layers. In this case, the similarity constraint is always fulfilled and we aim to find dense subgraphs spanning across a subset of the layers.

1.3 Properties of our approach

We want to highlight that the coherent subgraphs do not need to appear across all layers, but we detect them in subsets of the layers. This is important as some of the edge types might not be relevant for finding interesting coherent subgraphs at all; other types might be relevant only for certain subgraphs. Thus, for each coherent subgraph we find an individual set of relevant layers. Since some of the edge types might be irrelevant for finding interesting coherent subgraphs, we automatically exclude such types. This principle is motivated by the field of subspace clustering [24] that aims at analysing subsets of the dimensions in a vector space and that stems from the fact that in higher-dimensional vector data it is unlikely to find objects that are similar w.r.t. all of their characteristics; each cluster is associated with an individual subspace projection.

Exploiting these observations in our model, the detected coherent subgraphs are useful in several scenarios: We might find a dense cluster of authors who started their collaboration at a similar time and co-authored papers at the same conferences. The authors in another dense cluster might have cited each others’ papers on similar research topics, but not have published joint papers. Similarly, in a co-actor graph representing the joint work of actors (cf. Sect. 5), a cluster might be a group of actors who worked together on movies with similar success.

Additionally, we consider the fact that a vertex can naturally belong to more than one cluster, e.g. an author might of course participate in several working groups. Thus, we allow our clusters to overlap. However, similar to subspace clustering, allowing overlapping clusters can lead to a huge number of clusters that mostly represent redundant information [15, 28]. Thus, we propose a clustering model that allows clusters to overlap to a certain extend, but avoids redundancy in the resulting set of clusters. This final set of clusters (“clustering”) should contain the most interesting clusters w.r.t. a quality function which can be specified by the user.

Finally, since determining the overall clustering according to our model is NP-hard (as also with most dense subgraph mining models on a single graph), we introduce the algorithm MiMAG using a best-first search [31] to find an approximate solution. Best-first search is an established search principle to explore a graph, which in our case is a search tree for enumerating subgraphs, in an informed fashion. Starting in an initial node (in our case: the root node of the search tree), best-first search algorithms iteratively expand the “most promising” node based on a given heuristic. In MiMAG, the most promising subgraphs are expanded to detect the most interesting clusters first. This concept is related to the well-known A* algorithm for finding minimum-cost paths in a graph [23].

The main contributions of this paper are the following:

• 1. We propose the new paradigm of clustering multi-layer graphs with edge labels.

• 2. We introduce the clustering model MLCS, which avoids redundancy in the result set.

• 3. We propose the best-first search algorithm MiMAG to approximate the MLCS clustering.

For repeatability and further research, our algorithm and data sets are available online at www.kdd.in.tum.de/mimag.

A preliminary version of this paper was published in Boden et al. [6]. In this extended version, we additionally provide proofs for the quality bounds used by our algorithm, we introduce additional pruning techniques and discuss them in detail, and we provide additional experimental results.²

The remainder of this paper is structured as follows: In Sect. 2, we discuss related work. We introduce our cluster model MLCS in Sect. 3 and the algorithm MiMAG in Sect. 4. In Sect. 5, we evaluate the performance of MiMAG experimentally. Section 6 concludes the paper.

2 Related work

2.1 Mining graph data

For mining graph data, there exist various mining tasks [1]. Some of the most active areas are graph clustering, graph classification and frequent subgraph mining. In this work, we concentrate on clustering graph/network data. An overview of the various existing models and techniques is given by Aggarwal and Wang [1] and Fortunato [14]. The term “graph clustering” is somewhat ambiguous as it is used (a) for the clustering of graph databases, where a cluster represents a set of graphs, and (b) for clustering in one large graph, where the clusters represent sets of vertices from the graph. The latter is the meaning that is used in this paper. Furthermore, in this work, we focus on a specific form of graph clustering often referred to as “dense subgraph mining”. For the definition of dense subgraphs, several models exist. Two of the most widely used models are cliques and $\gamma$-quasi-cliques [26, 32].

2.2 Subspace clustering

The concept of subspace clustering was developed for the task of clustering vector data. Traditionally, clustering is done by using all dimensions of the feature space. However, full-space clustering does not scale to high-dimensional data since locally irrelevant dimensions may obfuscate the clustering structure [4, 24]. As a solution, subspace clustering methods detect an individual set of relevant dimensions for each cluster [24]. For subspace clustering, several models and algorithms have been proposed. For example, cell-based subspace clustering methods obtain high-quality results and are efficiently computable [29].

2.3 Mining vertex-labelled graphs

Some clustering approaches have been proposed that consider graphs with labelled vertices (here, the vertex labels are vectors). These approaches can be seen as a combination of graph clustering with clustering approaches for vector data. However, they mostly rely on fullspace clustering on the vertex attributes (e.g. [21, 30, 35, 45]). Recently, the approaches by Moser et al. [15, 16, 18–20, 27] were introduced to deal with the combination of subspace clustering and dense subgraph mining. In these approaches, clusters are ensured to be densely connected and vertices in a cluster are similar in subsets of their attribute values. Although these cluster models are related to the model introduced in this paper, adapting these methods to handle edge labels does not lead to the desired results. Two approaches for such an adaption are discussed and evaluated in the experimental section.

2.4 Mining edge-labelled graphs

Graphs with a single edge type and labels in terms of edge weights can be considered by some graph clustering approaches like minimum cut [1] and spectral clustering [36]. In the method proposed by Qi et al. [33], labels represent “edge content”, which are feature vectors extracted from text. In this approach, the edges of the graph are clustered by a partitioning approach based on connectedness and similarity of the edge content. From these edge clusters, the method obtains overlapping communities of vertices. However, this approach considers only a single graph layer and does not consider subspaces of the edge vectors for the similarity of edges. In Araujo et al. [2], graphs with categorical edge labels are analysed using tensor decomposition. Zhou et al. [44] propose a method for finding communities of users based on the topics they communicate about. However, this method does not consider multiple edge types.

To the best of our knowledge, there are no previous approaches for clustering in multi-layer graphs with edge labels. Also in the survey by Fortunato [14], it is mentioned that such graphs have not been dealt with by any algorithm. Even though [25] mention the existence of different types of relations in a network (which they call “levels of relation”), they just summarize all the different relations between two vertices into a single edge weight.

Recently, we proposed an approach for noisy multi-layer graphs with edge labels which is based on MiMAG [7].

2.5 Mining multi-relational data

Several clustering approaches have been proposed which take a set of networks as input, where each network represents a particular kind of relationship. This type of data if often called multi-relational network [8]. Multi-relational data have often been addressed in the area of pattern mining (e.g.  [10, 37]). For example, an algorithm to extract closed patterns satisfying given (anti-)monotonic constraints has been proposed by Cerf et al. [9, 10]. Another approach by Cerf et al. [11] detects cliques that occur in subsequent time steps in a dynamic graph represented as a 3-dimensional boolean cube (i.e. a ternary relation). This approach is based on the algorithm of Cerf et al. [10]. Therefore, the desired cliques are specified by (anti-)monotonic constraints. However, an extension of this method to quasi-cliques is not possible as the quasi-clique model does not fulfil a monotonicity property.

Another approach dealing with multi-relational networks was proposed by Wu et al. [42]. In this approach, a multi-relational input network is transformed into a one-dimensional network (considering correlations between the dimensions) and a soft clustering is performed on the resulting network. Although the aim of this approach is similar to ours, due to the transformation it is not able to detect clusters in subspaces of the network. As a further difference, this approach considers edge attribute as weights, whereas our approach considers them as characteristics of the edges.

A concept which is related to these approaches is the detection of cross-graph quasi-cliques [32]. Given a database of graphs each having the same vertices, a cross-graph quasi-clique is defined as a set of vertices that forms a quasi-clique in all of the graphs. Only maximal sets having this property are output. The approaches by Wang et al. [41] and [43] also work on a graph database and mine sets of vertices that form a clique [41] or quasi-clique [43] in at least a certain percentage of the graphs in the database [which is called the “support” of the (quasi-)clique]. Both approaches aim at mining closed (quasi-)cliques. A (quasi-)clique O is closed if none of O’s supersets forms a (quasi-)clique with the same support. To adapt these approaches to our problem setting, the graphs in the graph database could be seen as the different layers of our input graph. However, edge labels are not considered by these methods. Furthermore, the existing methods do not avoid redundancy in the result set apart from simply excluding subsets of (quasi-)cliques, i.e. non-closed (quasi-)cliques. Thus, their output can often contain a large set of highly overlapping vertex sets. In our experimental section, we compare our approach to an adaption of the closed quasi-clique mining algorithm Cocain [43].

Furthermore, several partitioning clustering approaches for graphs with different layers have been proposed. The graphs considered by these approaches are annotated with edge weights, while in our problem setting the labels represent further information about the edges. Please note while for categorical edge labels one might potentially redefine the layers such that each layer represents a single categorical label, such a transformation is not reasonable for numerical labels. Furthermore, such a transformation would significantly increase the number of layers, being a further argument for finding clusters in subsets of layers—a property none of the following approaches fulfils: The approach by Dong et al. [13] combines the spectrum of the different layers and then performs spectral clustering on the joint spectrum. Berlingerio et al. [3] propose a method which first combines the different graphs to a single graph, on which then a clustering is performed. In contrast, the approach by Cheng and Zhao [12] clusters each graph separately and combines the clusterings in a post-processing step using an ensemble approach. Tang et al. [38] extend the modularity measure to networks with different types of edges. Tang et al. [40] extend this to other partitioning community detection approaches. Tang et al. [39] propose a linked matrix factorization to combine information from different graphs and use traditional clustering methods on the results. Since these approaches perform a partitioning of the data, they fail in finding overlapping clusters as our approach supports. Furthermore, none of these approaches considers clusters in subsets of the layers. Thus, applying them to our problem setting where clusters might be located in subsets of the layers fails—the irrelevant layers obfuscate the clustering structure.

3 The MLCS model

In this section, we introduce the multi-layer coherent subgraph (MLCS) model for the clustering of graphs with different types of edges. We start by providing a formal definition of the input graph. For ease of presentation, we represent the input graph as a set of graphs (called “multi-layer graph”) each having the same vertex set V; each graph contains the edges of one type with their corresponding labels. Formally, the multi-layer graph is defined as follows:

Definition 1

(Multi-Layer Graph) A multi-layer graph ${\mathcal {G}}$ for a set of dimensions $\mathrm{Dim} = \{1,\ldots ,d\}$ is a set ${\mathcal {G}}= \{G_i \mid i \in \mathrm{Dim}\}$ of graphs

$$\begin{aligned} G_i = (V,E_i,l_i), E_i \subseteq V \times V, l_i: E_i \rightarrow \mathbb {R} \end{aligned}$$

where each graph layer $G_i, i \in \mathrm{Dim}$ is an undirected graph without self-loops and $l_i$ is an edge labelling function defining the edges characteristic/label.

We can easily handle graphs with different vertex sets $V_i$ by simply considering the union $V=\bigcup V_i$. The remainder of this section is structured as follows: In Sect. 3.1, we introduce our definition for a single cluster. We define our redundancy model and selection criteria for the final clustering in Sect. 3.2. In Sect. 3.3, we introduce the cluster quality function that is used in our experiments.

3.1 Cluster model

As discussed in the introduction, an MLCS cluster is a set of vertices which are connected with a high density by edges with similar labels in a subspace of the multi-layer graph (i.e. in a subset of the graph layers).

3.1.1 Cluster property for a single graph layer

First, we consider a single graph layer $G_i$. For the density of a subgraph, we use the established quasi-clique model [26, 32, 43]. The quasi-clique model defines dense subgraphs based on their intra-cluster connectivity. Formally,

Definition 2

($\gamma$-quasi-clique) A vertex set $O \subseteq V$ in a graph $G=(V,E)$ is a $\gamma$-quasi-clique for $\gamma \in [0,1]$ if

$$\begin{aligned} \forall v \in O: \mathrm{deg}^O_G(v) \ge \lceil \gamma \cdot (|O| -1) \rceil \end{aligned}$$

where $\mathrm{deg}^O_G(v) = |\{u \in O \mid (u,v) \in E\}|$. The density of a quasi-clique O in graph layer $G_i$ is defined by

$$\begin{aligned} \gamma _{G_i}(O) = \frac{\mathrm{\min }_{v \in O}\{\mathrm{deg}^O_{G_i}(v)\}}{|O|-1} \end{aligned}$$

For our cluster model, we consider a vertex set as dense if it is a 0.5-quasi-clique, i.e. its quasi-clique density is at least 0.5. As shown by Zeng et al. [43], for $\gamma \ge 0.5$ the vertices in a $\gamma$-quasi-clique are connected “tightly and relatively evenly”. This also ensures that the subgraph is connected in the graph [43]. For the similarity of the edge labels, we use a cell-based cluster model [29]. To be considered similar, the labels of the edges in a cluster may vary at most by a threshold w. Formally, we define a cluster in a graph layer $G_i$ as follows:

Definition 3

(One-dimensional MLCS cluster) A vertex set $O \subseteq V$ with $|O|\ge 3$ is a one-dimensional MLCS cluster in a graph layer $G_i = (V,E_i,l_i)$ (w.r.t. threshold w and distance function dist) if it forms a 0.5-quasi-clique in the graph $G_i$ and

$$\begin{aligned} \forall x, y \in E_i(O): \mathrm{dist}\left( l_i(x),l_i(y)\right) \le w \end{aligned}$$

where the edge set $E_i(O)$ is defined as $E_i(O) = \{(u,v) \in E_i \mid u,v \in O\}$.

The edge set $E_i(O)$ contains exactly the edges of the induced subgraph of O. Note that the threshold w is only needed if the edge labels are continuous valued. If we have categorical labels or the layer graphs are unlabelled, we can simply set $w=0$. Since two nodes connected by a single edge trivially fulfil the definition, we only consider subgraphs with at least 3 vertices as clusters.

3.1.2 Cluster property in subspaces of the multi-layer graph

Next, we consider clusters in subspaces of the multi-layer graph. Naturally, the vertex set of a multi-dimensional cluster should fulfil the one-dimensional cluster property for all of the dimensions in the subspace. This idea leads to some important observations: If an edge (u, v) exists in one graph layer, it does not automatically exist in another layer. Thus, when we consider the same vertex set in different graph layers, the corresponding edge sets can differ from each other. If a vertex set is dense in two layers, we might observe vertices that are adjacent in the first layer but not adjacent in the second one; the whole subgraph, however, is guaranteed to be dense. This is a more useful definition than requiring the same edge set in each layer, since it is unlikely to find an edge set of high cardinality occurring in multiple layers (basically, to find such a set, the edge sets $E_i(O)$ would have to be intersected, lowering the density dramatically). Thus, in our model, we ensure the density of the subgraph for each layer individually. Formally,

Definition 4

(MLCS cluster) An MLCS cluster $C=(O,S)$ in a multi-layer graph ${\mathcal {G}}=\{G_i \mid i \in \mathrm{Dim}\}$ consists of a vertex set $O \subseteq V$ and a non-empty set of relevant layers $S \subseteq \mathrm{Dim}$ such that $\forall i \in \mathrm{Dim}: i \in S \Leftrightarrow$ O is an MLCS cluster in the graph layer $G_i$.

The density of the cluster $C=(O,S)$ is defined as

$$\begin{aligned} \gamma _S(O) = \frac{1}{|S|} \sum _{i \in S} \gamma _{G_i}(O) \end{aligned}$$

Since the edge sets per layer may differ, also the cluster’s density in each layer may vary. Thus, we define the density of the cluster as the average density over all layers in the subspace. Note that in the case of unlabelled multi-layer graphs, our cluster model resembles the definition of cross-graph quasi-cliques [32] or closed quasi-cliques [43].

Fig. 2

Example of an MLCS cluster located in layer 1 & 4

In Fig. 2, the vertex set $O = \{b,c,d,e,f\}$ forms an MLCS cluster for $w=1$ in the layers 1 and 4. In layer 2, O is not a quasi-clique, and in layer 3, the edge labels of $E_3(O)$ are not similar, and thus, O does not form a cluster in these layers.

3.2 Clustering model

In the previous section, we introduced the properties that a vertex set has to fulfil to form an MLCS  cluster. As motivated in the introduction, the clusters are allowed to overlap. However, just outputting all valid clusters can lead to a large amount of valid clusters that are possibly very similar to each other and thus contain redundant information. An example (for simplicity without edge labels) is shown in Fig. 3, where the clusters $C_2$ and $C_3$ highly overlap in layer 1. Thus, instead of reporting all clusters, the final clustering result should be a non-redundant set of the “most interesting” clusters. This result set is called the MLCS  clustering.

Fig. 3

Overlapping clusters with given qualities $Q(C_1)=2.5, Q(C_2)=5 \text { and }Q(C_3)=5.3$

As the “interestingness” of a cluster can be highly application dependent, it is defined by a quality function Q(C), which can be specified by the user. The default quality function that was used in our experiments is introduced in Sect. 3.3.

For the avoidance of redundancy, we first introduce a redundancy relation. We define a cluster C to be redundant w.r.t. a cluster $C^{\prime }$ if a significant fraction of C’s edges is also covered by $C^{\prime }$ (thus, they represent similar information) and the quality of $C^{\prime }$ is not smaller than that of C. Formally,

Definition 5

(Redundancy relation) A cluster $C=(O,S)$ is redundant w.r.t. a cluster $C^{\prime }=(O^{\prime },S^{\prime })$ (short: $C \prec _{red}C^{\prime }$) if

$$\begin{aligned} C \ne C^{\prime } \wedge Q(C) \le Q(C^{\prime }) \wedge \frac{1}{|S|} \sum _{i \in S \cap S^{\prime }} \frac{|E_i(O) \cap E_i(O^{\prime })|}{|E_i(O)|} \ge r \end{aligned}$$

for the redundancy parameter $r \in (0,1]$.

In our experiments (cf. Sect. 5.2.1), $r=0.25$ proved to be a good choice, leading to high clustering quality and manageable result sizes matching the underlying characteristics of the data. Thus, this value is used as the default redundancy parameter. In Fig. 3, the cluster $C_2$ is redundant w.r.t. the cluster $C_3$. In contrast, $C_1$ is not redundant w.r.t. $C_2$. Although its quality is lower, the edge overlap between the clusters is below the threshold. Note that two clusters with equal quality might be pairwise redundant w.r.t. each other.

Based on this redundancy relation, we now select the maximum-quality clustering Result from the set $\mathcal {A}$ of all valid clusters. This clustering should not contain clusters that are redundant w.r.t. each other, and at the same time, it should maximize the sum of the qualities of the selected clusters:

Definition 6

(MLCS clustering) Given a multi-layer graph ${\mathcal {G}}$ and the set $\mathcal {A}$ of all valid MLCS clusters, the maximum-quality clustering $\mathrm{Result} \subseteq \mathcal {A}$ fulfils:

• Redundancy freeness: $\lnot \exists C,C^{\prime } \in \mathrm{Result}: C \mathrm{\prec _{red}} C^{\prime }$

• Maximum quality sum: $\lnot \exists \mathrm{Result}^{\prime } \subseteq \mathcal {A}$: $\mathrm{Result}^{\prime }$ is redundancy-free and

  $$\begin{aligned} \sum _{C \in \mathrm{Result}^{\prime }}Q(C) > \sum _{C \in \mathrm{Result}}Q(C) \end{aligned}$$

In Fig. 3, the clustering solution would be $\{C_1, C_3\}$.

3.2.1 Complexity results

We briefly describe the main result of our complexity analysis: Given a multi-layer graph ${\mathcal {G}}$ over the vertices V, the problem of determining the MLCS clustering is NP-hard w.r.t. |V|. Here, we show that already the following decision problem is NP-hard:

Theorem 1

Given a multi-layer graph ${\mathcal {G}}$ over the vertices V, deciding if there exists a non-empty MLCS clustering is NP-hard w.r.t. |V|.

Proof

We prove this theorem by a polynomial reduction of the NP-hard clique problem (“Given a graph $G=(V,E)$ and an integer k, does G contain a clique with at least k vertices”?) to the problem described in Theorem 1.

Given a graph $G=(V,E)$ and an integer k, we can solve the clique problem as follows: Take ${\mathcal {G}}= \{G_1=(V,E,l_1)\}$ with $l_1(e)= 0$ $\forall e \in E$ as the input for the $MLCS$ clustering. As quality function for a cluster $C=(O,S)$, we choose $Q(C) = {\left\{ \begin{array}{ll} |O| &{} |O|\ge k \wedge \gamma _{G_1}(O)=1 \\ -1 &{} \mathrm{else}\end{array}\right. }$. Since an MLCS clustering has maximum quality sum, it contains only the cliques ($\gamma _{G_1}(O)=1$) of the graph G with at least k vertices. Thus, the answer to the clique problem is ’yes’, if there exists a non-empty MLCS clustering, and ’no’, else. $\square$

3.3 Instantiation of our model

In this section, we introduce a default cluster quality function for MLCS clusters. In most settings, clusters containing many vertices are considered more interesting than smaller ones. Therefore, approaches for mining quasi-cliques mostly aim at finding maximal quasi-cliques w.r.t. the number of vertices. However, just maximizing the number of vertices in a cluster can lead to the detection of low-dimensional clusters with low density. Thus, our quality function realizes a trade-off between the contradicting objective functions size, dimensionality and density. Furthermore, we are not interested in clusters that are too small (here: fewer than eight vertices) or that are only one-dimensional. Thus, the quality of a cluster $C=(O,S)$ in our instantiation is defined as

$$\begin{aligned} Q(C) = {\left\{ \begin{array}{ll} |O| \cdot |S| \cdot \gamma _S(O) &{} |O|\ge 8 \wedge |S| \ge 2\\ -1 &{} \mathrm{else}\end{array}\right. } \end{aligned}$$

Clusters that are not considered interesting are assigned a quality of -1 and will thus never be included in an MLCS clustering, as they would lower the overall quality sum of the clustering. As distance function for the edge labels we use the Manhattan distance. In all experiments in Sect. 5, these instantiations are used. However, our model and the algorithm can easily be used with other instantiations, which might be more suitable for some applications.

4 Algorithm

In this section, we introduce the mining multi-layered, attributed graphs (MiMAG) algorithm. Due to Theorem 1, we cannot expect to find an efficient algorithm computing an exact MLCS  clustering. Thus, MiMAG computes an approximate solution: Instead of determining a redundancy-free clustering with maximum quality, we compute a maximal, redundancy-free clustering with high quality. That is, we determine a clustering to which no further cluster C with $Q(C)>0$ can be added without violating the redundancy-freeness property.

4.1 Processing scheme

4.1.1 Preliminaries

MiMAG is partly based on the Quick algorithm [26] for finding quasi-cliques. In this algorithm, vertex sets $O\subseteq V$ are enumerated by a depth-first traversal in the set enumeration tree [34].³ Each set visited by the depth-first traversal is tested for the quasi-clique property. An example tree for a graph with three vertices is shown in Fig. 4 (top left). Each node O is associated with a candidate set $\mathrm{cand}_O$, which contains all vertices that are ordered behind the vertices in O ($\mathrm{cand}_O=\left\{ v_i \in V~|~\forall v_j \in O: v_j \prec v_i \right\}$) in a given order $\prec$. A child node $O^{\prime \prime }$ extends its parent node O by adding one of the vertices from $\mathrm{cand}_O$. Basically, the set enumeration tree contains all possible vertex sets $O \subseteq V$. However, the search space can be reduced/pruned: If O’s candidate set contains a vertex v that can never be part of a quasi-clique $O^{\prime } \supset O$, we can delete v from the candidate set. For example, in Fig. 4 (top left) if the vertex $v_2$ is deleted from the candidate set of O, the subtree rooted at $\{v_1, v_2\}$ is pruned from the tree. Techniques how to detect such vertices were introduced by Liu and Wong [26].

A naive approach to determine the MLCS clustering would be: (1) use the Quick algorithm on each of the graph layers individually to find all one-dimensional MLCS  clusters,⁴ (2) compose the resulting patterns to multidimensional clusters and (3) remove redundant clusters.

This naive, sequential approach is not suitable for the detection of the MLCS clustering: Too many (intermediate) patterns are generated which anyway would not be included in the final result due to their redundancy. Thus, we interweave all steps.

Fig. 4

Synchronizing set enumeration trees

4.1.2 Core aspects of the processing

The core parts of our MiMAG algorithm can be summarized as follows:

• 1. Instead of analysing the set enumeration trees for each layer independently, we perform a synchronized traversal of all set enumeration trees simultaneously (cf. Sect. 4.1.2.1). This processing—combined with special properties of our model—leads to enhanced pruning possibilities (cf. Sect. 4.3).

• 2. The synchronized tree traversal exploits an informed best-first strategy, i.e. the set enumeration tree is traversed such that high-quality clusters are detected first (cf. Section 4.1.2.2). To realize an informed search, we need to provide bounds/estimates for the quality of the clusters expected in a subtree (cf. Sect. 4.2).

• 3. Clusters (already detected; but not necessarily selected for the final result set) and subtrees (still to be traversed) are stored in a common queue and are processed according to their (estimated) quality. That is, MiMAG interweaves the construction of the result set and the traversal of the set enumeration tree (cf. Section 4.1.2.3). This step ensures the efficient generation of redundancy-free clusterings.

Synchronized Tree Traversal We propose a “synchronized traversal” of all set enumeration trees simultaneously, i.e. all instances of the tree perform the same order of traversal. Trees in which a node O was pruned temporarily pause their traversal. Another view on this synchronized traversal is that we use an extended set enumeration tree (cf. Fig. 4, bottom). In this tree, each node O has a set of active dimensions $S_O$ (which represent the set of dimensions in which the node O has not been pruned from the set enumeration tree) and candidate sets $\mathrm{cand}_{O,i}$ for each dimension $i \in S_O$. The active dimensions $S_O$ of a node O are not to be confused with the subspace S of the potential cluster $C=(O,S)$; it holds $S\subseteq S_O$, but the sets are not necessarily equal. We show in Sects. 4.2/4.3 how the set of active dimensions can be used to prune the tree and use the information about the current vertices to further prune the candidate sets $\mathrm{cand}_{O,i}$.

Informed Best-First Traversal Instead of first generating all clusters, we let the final (redundancy-free) clustering grow incrementally. Since we want to maximize the quality of the overall clustering, we aim at generating the clusters in decreasing order of their quality and adding the non-redundant clusters with highest quality to the result first. In this case, it is crucial to use a good traversal strategy for the extended set enumeration tree.⁵ Therefore, we propose an informed best-first traversal: For each node O, we compute a quality estimation that provides an upper bound for the maximal quality of any cluster that can be found in the subtree rooted at O. We start the traversal at the root node, and in each search step, we expand the node O having the highest estimated quality (i.e. MiMAG descends one step into the subtree rooted at O). The computation of the upper bounds is discussed in Sect. 4.2.

Combined Priority Queue For each set O we visit during the traversal, we check whether O forms a valid MLCS  cluster in a subset of its active dimensions. However, even if a cluster C is found at the current node, it should not be added to the result directly. Since the estimated quality provides an upper bound of the subtree’s quality only, C itself might have a lower quality. Thus, there might exist other subtrees (and potential clusters) with higher (estimated) qualities. Therefore, MiMAG maintains a priority queue which simultaneously contains the set of subtrees that are still to process, as well as the set of already detected clusters that are not added to the result so far. This queue is sorted by the (estimated) quality values of the subtrees and clusters.

If the first element of the queue is a cluster, no better clusters can exist; in this case (and if the cluster is non-redundant to previously selected clusters), we can finally add it to the result set. If the first element is a subtree, we continue with the best-first travel. During this traversal, further clusters and subtrees will be added to the queue. Note that this processing guarantees that clusters are added to the final result in monotonically decreasing order of their quality values. Since high- quality clusters can never be redundant to lower-quality clusters, a cluster selected for the result will never have to be removed from the result due to redundancy to a later generated cluster.⁶ Thus, redundancy freeness can be efficiently ensured.

4.1.3 Overall processing scheme

The processing of MiMAG is shown in Algorithm 1. Given the input multi-layer graph ${\mathcal {G}}$, MiMAG computes a redundancy-free, maximal clustering Result.

Initially, the set Result is empty (line 1); it will be iteratively filled during the processing. The combined priority queue contains initially one element which represents the root node of the extended set enumeration tree (line 2)—at the root, the traversal has to start. In general, in the queue, a subtree (short: ST) is represented by a 3-tuple $ST = (O, S_O, [\mathrm{cand}_{O,i}]_{i \in S_O})$ where O is the vertex set in the root node of ST, $S_O$ is the set of active dimensions for O and $[\mathrm{cand}_{O,i}]$ is a list representing the different candidate sets for the active dimensions. We denote with $Q_\mathrm{est}(ST)$ the upper bound for the quality of clusters of this subtree. For the root, we have $Q_\mathrm{est}(.)=\infty$ because a quality estimation has not been performed yet.

As long as the queue contains elements, the object with the highest (estimated) quality is taken from the queue. If the object is a cluster, no cluster with higher quality can be found anymore, and thus, we add it to the result set if it is not redundant to an already selected cluster (line 6). If the object is a subtree, we expand the represented set O by one neighbouring vertex u that is contained in the candidate sets; we use the vertex having the highest degree w.r.t. O since it most probably leads to dense subgraphs. This expansion step represents the resuming of the best-first traversal. Here, new clusters and subtrees will be added to the queue.

Subtree expansion The subtree expansion is illustrated in Fig. 5, where $u = v_5$. MiMAG calls the EXPAND procedure for the subtree rooted at O. In this procedure, at first the sets $O_\mathrm{next}$, $S_{O_\mathrm{next}}$ and the candidate sets $\mathrm{cand}_{O_\mathrm{next},i}$ are determined. $S_{O_\mathrm{next}}$ can only contain dimensions i for which vertex u was contained in the candidate set $\mathrm{cand}_{O,i}$ (line 13). The candidate sets are reduced using pruning techniques (cf. Sect. 4.3). These sets represent the new subtree $ST_\mathrm{next}$ rooted at $O_\mathrm{next}$, and it is added to the queue if the estimated quality is non-negative (lines 16,17).

Similar steps are done for the remaining subtree $ST_\mathrm{remain}$ rooted at O (lines 20, 21), which contains the sets $O^{\prime } \supset O$ with $u \notin O^{\prime }$ (cf. Fig 5). Note that the quality estimate for $ST_\mathrm{remain}$ is different to the one of ST since u has been removed from the candidate sets $\mathrm{cand}_{O,i}$. In the best case, the estimate becomes negative and the whole subtree can be pruned.

Finally, if $O_\mathrm{next}$ is a valid (non-redundant) cluster it is also added to the queue.

This expansion step ensures that each node in the set enumeration tree is exactly visited once. Simultaneously, the overall priority queue ensures that subtrees and clusters with a high quality are processed first.

Fig. 5

Expansion of the subtree rooted at node O to resume the tree traversal

Theorem 2

Algorithm 1 generates a redundancy-free, maximal clustering.

Proof

1. Redundancy-free clustering: Line 6 ensures that only those clusters are added to the result that do not introduce redundancy. Thus, this property is clearly fulfilled.

2. Maximality: We need to show that any further cluster we might add to the result will either introduce redundancy or will lower the quality sum. Let C be a cluster which has not been added to the result. We distinguish two cases:

• (i) C had been added to the queue during the run of the algorithm. Since C, however, is not in the result and the queue is empty after termination, line 6 of the algorithm needs to have evaluated to false $\Rightarrow$ adding C would introduce redundancy.

• (ii) C has never been added to the queue. This implies that either line 23 evaluated to false ($\Rightarrow$ C would introduce redundancy) or a subtree of the set enumeration tree containing cluster C has been discarded earlier (line 17 or 21).⁷ This case only occurs if the estimated quality of the subtree is negative. Based on the proofs of Sect. 4.2, a negative estimate means either

  • (a) there are no valid clusters in this subtree (see Sect. 4.2.1) $\Rightarrow$ this case violates the assumption that C is a valid cluster,

  • (b) all clusters in this subtree are redundant to the result (Sect. 4.2.2) $\Rightarrow$ adding C to the result would introduce redundancy,

  • (c) the estimated quality is an upper bound for C’s quality (Sec. 4.2.3) $\Rightarrow$ C would have negative quality; adding it to the result would lower the overall quality sum.

In each case, adding C is not beneficial. The result of the algorithm is maximal. $\square$

Remark

While not shown in Algorithm 1, a first reduction of the search space can be done by decomposing the input graph into its connected components and by performing the algorithm on each of the components separately (here, consider two vertices as connected if there exists a path between them using edges from any layer). As the MLCS clusters have to be connected, we do not miss any clusters by doing so.

Discussion “Complexity and Optimality”: Our algorithm follows an A*-search-like principle for enumerating the clusters with the highest quality. The A* cost function corresponds to our cluster quality function (or more precise: its inverse), while the A* heuristic corresponds to (the inverse of) the upper bounds on the quality of each subtree. Clearly, the upper bounds provide an admissible/optimistic heuristic. In this regard, our search strategy is optimal: No other admissible search algorithm using the same heuristic can expand less subtrees to find the highest quality clusters.⁸ This optimality leads to a high efficiency of our algorithm.

Clearly, the efficiency depends on the accuracy of the upper bounds. In the worst case, each node in the set enumeration tree has to be considered, leading to an exponential complexity in the number of vertices—like in the A*-search. In practice, however, the informed best-first search in combination with multiple pruning strategies analyses far less nodes. In Sect. 4.2, we introduce the various bounds we exploit in our algorithm.

Discussion “Parallelization” In the following, we will briefly discuss the opportunities for potential parallel computations within the algorithm. This discussion should act as a guideline for realizations in multi-core architectures; the actual implementation of a parallelized algorithm is beyond the scope of this work. Our algorithm can exploit parallelization at three different stages: (1) As discussed before, our method can be computed on each connected component independently, leading to an easy way of parallelization. (2) In line 4 of the algorithm, objects are extracted from the queue. As long as the extracted objects are subtrees, a parallel computation can be performed. That is, assuming multiple worker threads, each thread can independently expand one subtree, write new subtrees/clusters to the queue and extract the next object from the queue (without needing to wait for the other threads). Only if the extracted object is a cluster, the threads need to be synchronized since other threads might lead to subtrees/clusters of higher quality that need to be processed earlier. (3) Line 9+10 of the algorithm allow a further potential for parallelization. Instead of only expanding based on a single vertex u, one might expand multiple vertices $u_1,\ldots ,u_k$ in parallel. Here, it is important to note that when expanding according to vertex $u_i$, the vertices $u_1,\ldots ,u_{i-1}$ need to be removed from the corresponding candidate sets. Otherwise, the set enumeration tree would contain duplicate nodes representing the same clusters. Overall, by following these steps we can highly exploit the potential of parallel computations.

4.2 Quality bounds for subtrees

In the following, we present upper bounds for the quality of subtrees. These quality bounds are used to realize the best-first traversal using a priority queue and to prune the search space if the estimate is negative (lines 17, 21). Even by allowing arbitrary quality functions, we can derive some generally applicable bounds.

We first introduce two bounds which exploit the fact that in some cases the subtree does not contain any interesting cluster at all; the quality can be upper bounded by $-1$, and we actually do not need to add the subtree to the queue.

4.2.1 Bounds based on active dimensions

If no active dimensions are left in the node O, we know that there cannot exist any valid cluster in the subtree rooted at O. This result holds since a cluster’s subspace is a subset of the active dimensions and the active dimensions fulfil the anti-monotonicity property⁹: If a dimension i is not active for the set O (meaning that O has been pruned from the set enumeration tree in dimension i), then there cannot exist a superset $O^{\prime } \supset O$ such that i is active for $O^{\prime }$.

4.2.2 Bounds based on the redundancy model

The second bound exploits our redundancy model: If all clusters C contained in subtree ST (i.e. clusters $C=(X,S_X)$ with $S_X \subseteq S_O$ and $O \subset X \subseteq O \cup \bigcup _{i \in S_O} \mathrm{cand}_{O,i}$) would be redundant w.r.t. a cluster $C^{\prime } \in \mathrm{Result}$, we cannot add them to the final clustering. Thus, even if their quality is larger than 0, we can safely estimate the subtree’s quality with $-1$.

To check the redundancy w.r.t. a cluster $C^{\prime }=(O^{\prime },S^{\prime }) \in \mathrm{Result}$, we have to check the properties from Definition 5. The properties $C \ne C^{\prime }$ and $Q(C) \le Q(C^{\prime })$ are trivially fulfilled for every possible C due to the ordering of the queue. Thus, only the edge overlap property ($\frac{1}{|S_X|} \sum _{i \in S_X \cap S^{\prime }} \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|} \ge r$) has to be checked. Therefore, in the following we determine a lower bound $ovl_\mathrm{min}$ for the edge overlap such that $\frac{1}{|S_X|} \sum _{i \in S_X \cap S^{\prime }} \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|}\ge ovl_\mathrm{min}$ for all possible clusters C from the subtree. If $ovl_\mathrm{min}\ge r$ holds, any cluster in the subtree must be redundant, and therefore, the quality of the subtree can be estimated as $-1$.

Theorem 3

For every subtree $ST=(O,S_O, [\mathrm{cand}_{O,i}]_{i \in S_O})$, every cluster $C=(X,S_X)$ with $S_X \subseteq S_O$ and $O \subset X \subseteq O \cup \bigcup _{i \in S_O} \mathrm{cand}_{O,i}$ and every cluster $C^{\prime }=(O^{\prime },S^{\prime }) \in \mathrm{Result}$ with $S^{\prime }seteq S_O$ the following holds:

$$\begin{aligned} \frac{1}{|S_X|} \sum _{i \in S_X \cap S^{\prime }} \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|} \ge ovl_\mathrm{min} \end{aligned}$$

(1)

for

$$\begin{aligned} ovl_\mathrm{min}=\min \limits _{i\in S_O}\frac{|E_i(O\cap O^{\prime })|+\max \{\frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\}}{|E_i(O\cap O^{\prime })|+k+\max \{\frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\}} \end{aligned}$$

with $k = |E_i(O\cup \mathrm{cand}_{O,i})\backslash E_i((O\cup \mathrm{cand}_{O,i})\cap O^{\prime })|$

Note in our cluster model, an edge set $E_i(X)$ corresponds to the edges of the induced subgraph of a vertex set X. Thus, for two vertex sets X and Y it always holds that $E_i(X) \cap E_i(Y) = E_i(X \cap Y)$ and $E_i(X) \cup E_i(Y) \subseteq E_i(X \cup Y)$.

Proof

We first show a lower bound for the number of edges $|E_i(X)|$ in layer i of the cluster C. As $X \supset O$, we know $|X| \ge |O|+1$. As |X| is a 0.5-quasi-clique, we have

$$\begin{aligned} |E_i(X)|= & {} \frac{1}{2} \cdot \sum _{v \in X} \mathrm{deg}_{G_i}^X(v) \ge \frac{1}{2} \cdot \sum _{v \in X} 0.5 \cdot (|X|-1)\nonumber \\\ge & {} \frac{1}{2} \cdot (|O|+1) \cdot 0.5 \cdot (|O|) \ge \frac{1}{4} \cdot (|O|^2 + |O|) =: m_i^\mathrm{min} \end{aligned}$$

(2)

For this proof, we assume $S_X \ne \emptyset$ (else, $C=(X,S_X)$ would not be a valid cluster). As $S^{\prime } \supseteq S_O \supseteq S_X$, we get $S_X \cap S^{\prime } = S_X \ne \emptyset .$ Now we can derive for the left-hand side of Eq. 1:

$$\begin{aligned}&\frac{1}{|S_X|} \sum _{i \in S_X \cap S^{\prime }} \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|} = \frac{1}{|S_X|} \sum _{i \in S_X} \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|}\nonumber \\&\quad \ge \min _{i \in S_X} \left\{ \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|}\right\} \ge \min _{i \in S_O}\left\{ \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|}\right\} \end{aligned}$$

(3)

Next, we show a lower bound for the edge overlap $ovl_i(X) = \frac{|E_i(X) \cap E_i(O^{\prime })|}{|E_i(X)|}$ in a layer $i \in S_O$. Therefore, we construct the edge set $E_i(X)$ having the lowest possible $ovl_i(X)$. As $X \supset O$, we know that

$$\begin{aligned} E_i(X) \cap E_i(O^{\prime }) \supseteq E_i(O \cap O^{\prime }) \end{aligned}$$

(4)

To maximize the denominator of $ovl_i(X)$ without increasing the numerator, we now add to $E_i(X)$ all edges from $E_i(O \cup \mathrm{cand}_{O,i})$ that do not increase the overlap $|E_i(X) \cap E_i(O^{\prime })|$, i.e. all edges that do not belong to $E_i((O \cup \mathrm{cand}_{O,i}) \cap O^{\prime })$. The number of these edges is

$$\begin{aligned} k = |E_i(O\cup \mathrm{cand}_{O,i})\backslash E_i((O\cup \mathrm{cand}_{O,i})\cap O^{\prime })| \end{aligned}$$

(5)

Now, if $E_i(O \cap O^{\prime }) + k \ge m_i^\mathrm{min}$, we do not have to add more edges to $E_i(X)$. In this case, we can obtain the bound $ovl_i(X) \ge \frac{|E_i(O\cap O^{\prime })|}{|E_i(O\cap O^{\prime })|+k}$.

However, if $E_i(O \cap O^{\prime }) + k < m_i^\mathrm{min}$, we have to add edges from $E_i((O \cup \mathrm{cand}_{O,i}) \cap O^{\prime })$ to $E_i(X)$, which increase the overlap $|E_i(X) \cap E_i(O^{\prime })|$. In order to reach the minimum number of edges for a cluster, we have to add at least

$$\begin{aligned} m_i^\mathrm{min} - |E_i( O \cap O^{\prime })| - k \end{aligned}$$

(6)

such edges.

From (2), (4), (5) and (6), we obtain the bound

$$\begin{aligned} ovl_i(X) \ge \frac{|E_i(O\cap O^{\prime })|+\max \left\{ \frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\right\} }{|E_i(O\cap O^{\prime })|+k+\max \left\{ \frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\right\} } \end{aligned}$$

Combining this with Eq. 3, we obtain the overall bound

$$\begin{aligned} ovl_\mathrm{min}=\min \limits _{i\in S_O}\frac{|E_i(O\cap O^{\prime })|+\max \left\{ \frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\right\} }{|E_i(O\cap O^{\prime })|+k+\max \left\{ \frac{1}{4}\cdot (|O|^2+|O|)-|E_i(O\cap O^{\prime })|-k,0\right\} } \end{aligned}$$

$\square$

For example, in the case $O^{\prime } \supseteq O \cup \bigcup _{i \in S_O} \mathrm{cand}_{O,i}$ we get $ovl_\mathrm{min}=1$ and thus $Q_\mathrm{est}(ST) = -1$. However, the overlap estimation is also successful in other cases.

4.2.3 Bounds based on cluster properties

The following bounds exploit the properties of the individual clusters located in a subtree. Useful properties to incorporate in quality functions are the density and cardinality of clusters. Thus, we develop general upper bounds for these cluster properties. These bounds can later on be used for specific instantiations of the quality function (including our default quality function).

Theorem 4

Given a subtree $ST= (O,S_O,[\mathrm{cand}_{O,i}]_{i \in S_O})$, for each one-dimensional MLCS cluster X in dimension $i\in S_O$ with $O \subset X \subseteq O \cup \mathrm{cand}_{O,i}$ the following bounds apply:

• 1. $\gamma (X) \le \min \{\frac{\mathrm{min}\_\mathrm{deg}_i}{|O|},1\}=: \gamma _i^\mathrm{max}$ with $\mathrm{min}\_\mathrm{deg}_i = \min _{v \in O}\{\mathrm{deg}^{O \cup \mathrm{cand}_{O,i}}(v)\}$

• 2. $|X| \le \min \{\left\lfloor \frac{\mathrm{min}\_\mathrm{deg}_i}{0.5}\right\rfloor +1, |O \cup \mathrm{cand}_{O,i}|\} =: n_i^\mathrm{max}$

• 3. $|E_i(X)|\le |E_i(O)| + (n_i^\mathrm{max} - |O|) \cdot \max _{v \in \mathrm{cand}_O}\{\mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v)\}$

Proof

• 1. The maximal quasi-clique density of X is determined by the minimal vertex degree of the vertices of X:

  $$\begin{aligned} \gamma (X)=\frac{\min _{v \in X} \{ \mathrm{deg}^X_{G_i}(v) \}}{|X|-1} \end{aligned}$$

  It holds:

  $$\begin{aligned} \min _{v\in X} \{ \mathrm{deg}^X_{G_i}(v) \} \le \min _{v\in O} \{ \mathrm{deg}^X_{G_i}(v) \} \le \min _{v \in O}\{\mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v)\}=\mathrm{mindeg}_i \end{aligned}$$

  Furthermore, we have $X \supset O \Rightarrow |X| \ge |O|+1$. Thus, for the density of X we get:

  $$\begin{aligned} \gamma (X)=\frac{\min _{v \in X} \{ \mathrm{deg}^X_{G_i}(v) \}}{|X|-1} \le \frac{{\hbox {mindeg}}_i}{|X|-1} \le \frac{{\hbox {mindeg}}_i}{|O|} \end{aligned}$$

  For every quasi-clique, it holds $\gamma (X) \le 1$, and thus

  $$\begin{aligned} \gamma (X) \le \min \left( \frac{{\hbox {mindeg}}_i}{|O|},1\right) =: \gamma ^\mathrm{max}_i \end{aligned}$$

• 2. As X is a 0.5-Quasi-Clique, we have:

  $$\begin{aligned}&\mathrm{mindeg}_i \ge \min _{v \in X} \{ \mathrm{deg}^X_{G_i}(v) \} \ge \lceil 0.5 \cdot (|X|-1) \rceil \Leftrightarrow \lfloor \frac{{\hbox {mindeg}}_i}{0.5} \rfloor \ge |X|-1 \end{aligned}$$

  Furthermore, it holds

  $$\begin{aligned} X \subseteq O \cup \mathrm{cand}_{O,i} \Rightarrow |X| \le |O \cup \mathrm{cand}_{O,i}| \end{aligned}$$

  and thus

  $$\begin{aligned} |X| \le \min ( \lfloor \frac{{\hbox {mindeg}}_i}{0.5} \rfloor + 1, |O \cup \mathrm{cand}_{O,i}| ) =: n^\mathrm{max}_i \end{aligned}$$

• 3. As $X \supset O$, it holds $E_i(X) \supseteq E_i(O)$. We already showed $|X| \le n^\mathrm{max}_i$, and thus at most $n_i^\mathrm{max} - |O|$, vertices can be added to O to form |X|. For each vertex $v \in \mathrm{cand}_{O,i}$ it holds

  $$\begin{aligned} |E_i(O \cup \{v\})| \le |E_i(O)| + \mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v), \end{aligned}$$

  i.e. at most $\mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v)$, edges can be added to $E_i(O)$ by adding v to O. Thus, we get

  $$\begin{aligned} |E_i(X)|\le & {} |E_i(O)| + \sum _{v \in X \setminus O} \mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v)\\\le & {} |E_i(O)| + (n_i^\mathrm{max} - |O|) \cdot \max _{v \in \mathrm{cand}_O}\{\mathrm{deg}_{G_i}^{O \cup \mathrm{cand}_{O,i}}(v)\} \end{aligned}$$

$\square$

Furthermore, we have for each multi-dimensional MLCS cluster $(X,S_X)$: $|S_X| \le |S_O|$ due to the anti-monotonicity of the active dimensions.

Specific instantiation We can use the above bounds for our default instantiation of the quality function: The quality of the subtree ST is upper bounded by

$$\begin{aligned} Q_\mathrm{est}(ST) = \max _{k\in \{1,\ldots ,|S_O|\}} \big \{\mathrm{max}_k(n_i^\mathrm{max}) \cdot \sum _{m=1}^{k} \mathrm{max}_m(\gamma _i^\mathrm{max})\big \} \end{aligned}$$

where $\mathrm{max}_x(y_i)$ denotes the x-th highest value of all $\{y_i \mid i \in S_O\}$. Furthermore, if we have $\mathrm{\max }_{i \in S_O}(n_i^\mathrm{max}) < 8$ or $|S_O| < 2$, the subtree cannot contain any cluster with positive quality; in this case, the estimation is $Q_\mathrm{est}(\mathrm{ST})=-1$.

4.3 Pruning techniques

MiMAG uses multiple pruning techniques to reduce the search space. As already mentioned, MiMAG uses the quality bounds to prune whole subtrees if the estimates are negative (lines 17, 21). Additionally, MiMAG exploits pruning techniques to reduce the cardinality of the set of active dimensions and the candidate sets (lines 15, 19).

In Sect. 4.3.1, we introduce pruning techniques that aim at removing vertices from the candidate sets that cannot be contained in any valid cluster (following Definition 4). Furthermore, e.g. for our default quality function, some valid clusters may be considered as not interesting ($Q(C)=-1$) and do thus not have to be detected. Therefore, for certain quality functions we can prune even more vertices which do only lead to non-interesting clusters, which is discussed in Sect. 4.3.2.

4.3.1 Generally applicable pruning techniques

One of the generally applicable pruning techniques is the pruning by edge similarity: Due to Definition 3, a one-dimensional MLCS cluster (O, S) must only contain edges with similar labels. Thus, if the set $E_i(O)$ contains any two edges with label distance greater than w, O (and also all supersets $O^{\prime } \supset O$) cannot be a valid cluster. We use this property to prune the candidate sets $\mathrm{cand}_{O,i}$ as follows: If for a vertex $v \in \mathrm{cand}_{O,i}$ it holds that $E^{\prime } = E_i(O) \cup \{(v,o) \in E_i \mid o \in O\}$ does not fulfil the similarity property, we can remove v from $\mathrm{cand}_{O,i}$ as no set $O^{\prime } \supseteq O \cup \{v\}$ could form a valid MLCS cluster in dimension i.

Furthermore, MiMAG also uses some pruning techniques from the Quick algorithm [26], which are applicable here because each MLCS cluster also forms a quasi-clique in its relevant layers. First, we use the technique for pruning based on the degree of the vertices which has already been used by Quick [26] and Cocain [43]. In the same algorithms, also a technique for pruning based on graph diameters is used. This technique exploits the fact that the graph diameter of a $\gamma _\mathrm{min}$-quasi-clique is upper bounded by a constant k which depends only on $\gamma _\mathrm{min}$ [32]. The diameter pruning states that we can delete all vertices $v \in \mathrm{cand}_{O,i}$ from the candidate set $\mathrm{cand}_{O,i}$ for which $v \notin \bigcap _{o \in O}N^G_{k,i}(o)$ holds (where $N_{k,i}(v)$ denotes the k-neighbourhood of a vertex v in layer i). Since for MLCS clusters we have $\gamma _\mathrm{min}=0.5$, the graph diameter of an MLCS cluster is upper bounded by 2.

While we could just apply the existing diameter pruning technique in MiMAG by setting $k=2$, we can develop an even better solution: As a one-dimensional MLCS cluster may only contain edges with similar labels (deviating at most by w), we know that each possible cluster $O^{\prime } \supseteq O$ in layer i can only contain edges with labels within the range $[\mathrm{upper}_i(O) - w, \mathrm{lower}_i(O)+w]$, where $\mathrm{upper}_i(O)$ and $\mathrm{lower}_i(O)$ denote the highest and the lowest label value for the labels of edges in $E_i(O)$, respectively. Furthermore, as we know we can only add vertices from $\mathrm{cand}_{O,i}$ to O in the currently considered subtree, we only need to take the edges from the induced subgraph $E_i(O \cup \mathrm{cand}_{O,i})$ into account for the computation of the diameter. Other edges, which could lead to shorter paths and thus to a smaller diameter, do not have to be considered here. Thus, formally, we construct a reduced graph

$$\begin{aligned} \displaystyle G^{\prime }=(O\cup \mathrm{cand}_{O,i}, \{e \in E_i(O \cup \mathrm{cand}_{O,i}) \mid l_i(e) \in [\mathrm{upper}_i(O) - w, \mathrm{lower}_i(O)+w]\}) \end{aligned}$$

and perform the computation of the neighbourhoods based only on the edges of this graph. That is, we can exclude all vertices v from $\mathrm{cand}_{O,i}$ with $v \notin \bigcap _{o \in O}N^{G^{\prime }}_{k,i}(o)$. Since clearly $N^{G^{\prime }}_{k,i}(o)\subseteq N^{G}_{k,i}(o)$, this pruning is even more powerful, thus leading to less candidate vertices and fewer subtrees.

Deleting a vertex from a candidate set can change properties (e.g. the degree) of other vertices from the set. Thus, we apply the pruning techniques iteratively until no more vertices can be deleted. If after the pruning we have $\mathrm{cand}_{O,i} = \emptyset$ for a dimension i, i becomes inactive and can thus be removed from $S_{O}$.

4.3.2 Pruning techniques for specific quality functions

For certain quality functions, some clusters may not be considered as interesting $(Q(C)=-1)$. A typical example could be clusters that do not reach a certain minimum size, dimensionality or density. For example, our default quality function only considers a cluster $C=(O,S)$ as interesting if $|O|\ge 8 \wedge |S| \ge 2$. To enhance the efficiency of the algorithm, it is useful to avoid detecting these non-interesting clusters, as they will not be added to the final result set in any case. Thus, in the following, we discuss how we can prune the search space further based on such properties of the quality function.

Assume the selected quality function only considers a cluster $C=(O,S)$ as interesting if $|S|\ge s_\mathrm{min}$ for some threshold $s_\mathrm{min}$. Then, we can simply stop traversing a subtree if for its set of active dimensions $S_O$ it holds $|S_O| < s_\mathrm{min}$. Similarly, if the quality function uses a threshold $n_\mathrm{min}$ such that a cluster is considered interesting only if $|O|\ge n_\mathrm{min}$, we can remove a dimension i from the set $S_O$ if it holds $|O \cup \mathrm{cand}_{O,i}| < n_\mathrm{min}$, as the subtree cannot contain any clusters exceeding the threshold $n_\mathrm{min}$.

Furthermore, we can use $n_\mathrm{min}$ to prune the candidate set $\mathrm{cand}_{O,i}$ in a single dimension i. As the vertices of an MLCS cluster O must form a quasi-clique with a minimal density of $\gamma _\mathrm{min}=0.5$ in each relevant layer i, we can infer that each vertex in O has to reach a certain minimal degree:

$$\begin{aligned} \forall v \in O: \mathrm{deg}_i^O(v) \ge \left\lceil \gamma _\mathrm{min} \cdot (n_\mathrm{min} -1)\right\rceil =: \mathrm{min}\_\mathrm{deg} \end{aligned}$$

In the case that the quality function requires a higher-density threshold to consider a cluster as interesting, we can replace $\gamma _\mathrm{min}$ by this threshold to obtain an even higher $\mathrm{min}\_\mathrm{deg}$ value. The value of $\mathrm{min}\_\mathrm{deg}$ is used in a pre-processing step where we simply delete all vertices v with $\mathrm{deg}^V(v) < \mathrm{min}\_\mathrm{deg}$.

Forbidden edges Furthermore, we can use $\mathrm{min}\_\mathrm{deg}$ to identify edges which can never be contained in an MLCS cluster: If an edge $e=(u,v)$ is contained in an MLCS cluster O in layer i, it has to hold $\mathrm{deg}_i^V(u) \ge \mathrm{min}\_\mathrm{deg}$ and $\mathrm{deg}_i^V(v) \ge \mathrm{min}\_\mathrm{deg}$. Furthermore, the labels of all edges contained in the cluster have to lie in a range $[x_1,x_2]$ with $|x_2 - x_1| \le w$. Therefore, the vertices also have to reach the minimal degree counting only edges within such a range. Formally, an edge $e=(u,v)$ can only be part of any one-dimensional MLCS cluster in layer i if

$$\begin{aligned} \exists x_1,x_2 \in \mathbb {R}: (x_2 - x_1)\le & {} w \wedge l_i(e) \in [x_1,x_2]\\ \wedge ~\mathrm{deg}_i^{[x_1,x_2]}(u)\ge & {} \mathrm{min}\_\mathrm{deg}~\wedge ~\mathrm{deg}_i^{[x_1,x_2]}(v) \ge \mathrm{min}\_\mathrm{deg} \end{aligned}$$

with $\mathrm{deg}_i^{[x_1,x_2]}(v)=|\{(u,v) \in E_i \mid l_i((u,v)) \in [x_1,x_2]\}|$. Edges which do not meet this criterion are called forbidden edges.

In a pre-processing step, we obtain the set $F_i$ of forbidden edges for each dimension i. Even though these edges can never be contained in an MLCS cluster, we cannot simply delete the forbidden edges from the graph. Such a removal could lead to the detection of invalid clusters, since a subgraph not fulfilling Definition 3 could fulfil it after the deletion of dissimilar edges. Thus, instead of removing the forbidden edges $F_i$, we can use them for pruning subtrees: Since a forbidden edge can never be part of an MLCS cluster, we can remove all vertices $v \in \mathrm{cand}_{O,i}$ from the candidate set that are connected to a vertex $o \in O$ by a forbidden edge. Formally, we remove all vertices $v \in \mathrm{cand}_{O,i}$ if $\exists o\in O:(v,o)\in F_i$.

5 Experimental evaluation

We evaluate the clustering quality and runtime of MiMAG experimentally on synthetic and real-world data sets. All experiments were conducted on Opteron 2.3 GHz CPUs using Java 6 64bit. For the synthetic data, the clustering quality is determined by comparing the clustering results to the ground truth using the E4SC measure, which was developed for the evaluation of subspace clustering results [17]. For the real-world data sets, there is no ground truth available, which hinders an evaluation of the clustering quality. Thus, for those data sets we provide some key characteristics of the clustering results as well as example clusters to illustrate the results of MiMAG. If not specified otherwise, the redundancy parameter r is set to $r=0.25$ for all experiments.

5.1 Baseline approaches

We compare MiMAG with 3 baseline approaches: The closed quasi-clique mining algorithm Cocain [43] (cf. Sect. 2) is used on our input graph by considering each of the graph layers as a graph in a graph database. To best match our cluster model, the minimum support parameter of Cocain is set to $\mathrm{min}\_\mathrm{sup}=\frac{1}{|\mathrm{Dim}|}$ and the minimum quasi-clique density to $\gamma _\mathrm{min} = 0.5$. However, as Cocain does not consider edge labels, we cannot expect to detect the same clusters as with MiMAG.

Furthermore, we test two different ideas to adapt the GAMer algorithm [15], developed for clustering graphs with vertex labels, to our problem. Both ideas transform the multi-layer graph covering Dim layers to a graph with Dim-dimensional attribute vectors at the vertices. The resulting graph can then be clustered by GAMer. In the first idea (GAMer-avg), the transformed graph is obtained as follows: the vertices of the original graph are kept; the edges are determined by the union of the edge sets from all graph layers (i.e. $E=\bigcup E_i$; the edge labels are deleted). The ith entry of a vertex v’s attribute vector is the average label value of v’s incident edges from layer i, i.e. $v[i]=\frac{1}{|\{w|(v,w)\in E_i\}|}\sum _{(v,w)\in E_i}l_i(v,w)$ and $\bot$, if v has no incident edge in layer i (where $\bot$ is considered not similar to any value).

In the second idea (GAMer-lg), we use the well-known concept of the line graph [22]. Each vertex of a line graph represents an edge of the original graph and vice versa. In our case, a line graph vertex $v^{lg}=(v_1,v_2)$ represents all the edges $(v_1,v_2)$ from the different layers. The ith entry of $v^{lg}$’s attribute vector corresponds to the label value $l_i(v_1,v_2)$, if $(v_1,v_2) \in E_i$ and $\bot$, else. In the following experiments, we will show how the results obtained by these two approaches differ from those of MiMAG.

5.2 Evaluation on synthetic graphs

For the evaluation of MiMAG, we generated various synthetic multi-layer graphs with edge labels containing overlapping MLCS clusters as well as “noise” vertices and “noise” edges that do not belong to any cluster. The generated edge labels lie in the range [0, 1]. In our experiments, the parameter w for MiMAG (and also the corresponding parameter for GAMer) is set to $w=0.1$.

5.2.1 Results for varying redundancy parameter

Fig. 6

Number of detected clusters vs. redundancy parameter r

In Fig. 6, we analyse how the redundancy parameter r of our clustering model affects the results of MiMAG, using a graph with 10 layers and 100 hidden clusters; the cluster size varies between 10 and 15. We observe that for $r<0.5$, the correct number of clusters is found with a high clustering quality. For $r\ge 0.5$, the number of found clusters increases dramatically and the clustering quality drops. For high values for r, less clusters are considered redundant w.r.t. other clusters, which leads to a clustering that contains many low-quality clusters that would be considered redundant for lower r values. As seen, redundancy removal is essential to obtain good mining results. Thus, we propose using $r=0.25$ as a reasonable default setting for r and use this setting in all the following experiments.

5.2.2 Results for varying graph sizes

First, we analyse the behaviour of the approaches for varying graph sizes. The generated graphs consist of 10 layers, and the number of generated (“hidden”) clusters varies between 10 and 300. Each cluster contains 10 vertices and 3 relevant layers, with quasi-clique densities of 0.6; 10 % of the vertices in the graph are noise vertices, and in each layer, we have 60 noise edges.

The results are shown in Fig. 7. Although the runtimes of all approaches (cf. Fig. 7a) increase with increasing graph sizes, MiMAG constantly shows the lowest runtimes. Considering the clustering quality (cf. Fig. 7b), MiMAG reaches perfect or nearly perfect E4SC values on all data sets. The number of detected clusters (Fig. 7c) increases linearly and matches the number of hidden clusters. Cocain also achieves quite good quality values (ca. 0.8 to 0.9), as the closed quasi-clique model is closely related to our MLCS model. However, Cocain outputs a huge amount of quasi-cliques (e.g. nearly 2000 instead of the hidden 300 clusters) because it does not avoid redundancy in the result. Since the E4SC measure penalizes this redundancy only slightly, the quality values of Cocain appear relatively high; such a huge result set, however, is very hard to interpret. The high redundancy also explains Concain’s high runtimes. For GAMer-avg, the number of detected clusters approximately matches the number of hidden clusters. However, the clustering quality is significantly lower as MiMAG ’s as the averaged label values distort the cluster structure. For GAMer-lg, the number of found clusters varies very much and the clustering quality is low. This is caused by an important problem with the line graph approach: From the density of a subgraph in the line graph, it is not possible to draw conclusions about the density of the corresponding original subgraph, which hinders the detection of dense subgraphs in the original graph.

Fig. 7

Experimental evaluation on synthetic data sets with varying graph size. The number of hidden clusters in the data increases from 10 to 300. a Runtime vs. graph size, b clustering quality vs. graph size, c #detected clusters vs. graph size

5.2.3 Results for varying dimensionality

Next, we analyse the behaviour of the different approaches for varying dimensionalities (i.e. varying numbers of graph layers) of the input graph. The number of graph layers varies between 5 and 50. The generated multi-layer graphs each contain 30 clusters, each having 10 vertices and 3 relevant layers, with quasi-clique densities of 0.6. Again, we have 10 % noise vertices and 60 noise edges per layer.

The results of our experiments are shown in Fig. 8. We observe that MiMAG again achieves the lowest runtime (Fig. 8a) and highest quality (Fig. 8b). For most approaches, the runtime and the clustering quality remain relatively stable for increasing dimensionality. Just for GAMer-avg, the runtime significantly increases, while the E4SC values dramatically drop. This is caused by the graph transformation: As the edges of the transformed graph are the union of the edge sets from all graph layers, by combining an increasing number of graph layers the transformed graph gets very dense, such that for high dimensionalities GAMer-avg detects many clusters that do not exist in the original graph, which also leads to a very high number of detected clusters for GAMer-avg (Fig. 8c). Also the Cocain approach detects a large number of clusters due to its missing redundancy handling, while MiMAG detects the correct number of clusters.

Fig. 8

Experimental evaluation on synthetic data sets with varying dimensionality. a Runtime vs. dimensionality, b clustering quality vs. dimensionality, c #detected clusters vs. dimensionality

5.2.4 Results for varying degree of cluster overlap

Furthermore, we analyse the influence of the overlap between clusters on the clustering results of the different approaches. The generated multi-layer graphs each have 10 layers and consist of 30 clusters with 10 vertices each. Each cluster has 3 relevant layers and a quasi-clique density of 0.6. Furthermore, each multi-layer graph contains 10 % noise vertices and 60 noise edges per layer. We vary the amount of overlap between the clusters in the different graphs. In the results, we indicate the degree of overlap for the graphs, which represents the maximum number of different clusters in which a vertex is contained (i.e. for an overlap degree of 1, there is no overlap between the clusters).

The results of this experiment are depicted in Fig. 9. While the runtime of MiMAG remains stable for different amounts of overlap, the runtime of the other approaches increases for increasing overlap. For an overlap degree of 5, the GAMer-lg approach did not finish due to heap overflows. The clustering quality for MiMAG remains relatively stable (as well as the number of detected clusters); however, for a high overlap, it decreases slightly. This is due to the fact that for a high amount of overlap, some of the clusters are considered redundant by our redundancy model. While the GAMer-avg and the Cocain approach show good quality values if the clusters do not overlap, already for small degrees of overlap their quality decreases quickly. While Cocain detects a rapidly increasing number of clusters for high degrees of overlaps, the number of clusters detected by GAMer-avg is not as high, as the GAMer approach also excludes redundant clusters from the result. As in the previous experiments, the GAMer-lg approach obtains very low quality values.

Fig. 9

Experimental evaluation on synthetic data sets with varying degree of overlap. a Runtime vs. overlap, b clustering quality vs. overlap, c #detected clusters vs. overlap

5.3 Evaluation on real-world data

Besides synthetic graphs, we also evaluate our approach on three real-world data sets: The first one is a multi-layer graph with edge labels extracted from the IMDB movie Database.¹⁰ In this graph, the vertices represent actors; the labelled edges represent information about movies in which the actors worked together. The four layers of the graph are:

• 1. “First year of collaboration”

• 2. “Last year of collaboration”

• 3. “Rental fees” (the average earnings of all joint movies between two actors)

• 4. “Sold tickets” (the average number of sold tickets of all joint movies between two actors).

All label values were normalized to the range [0, 1], and we used $w=0.03$ for this experiment. In this special case, the same edge sets exist in all layers, but with different labelling functions. Overall, the IMDB graph contains 300 vertices (the most prolific actors) and 18368 edges. An example cluster from MiMAG ’s clustering result is shown in Fig. 10. The relevant layers of this cluster are “First year of collaboration”, “Rental fees” and “Sold tickets”. Note that the cluster does not form a clique (its quasi-clique density is 0.625), and thus, not all authors worked together in the same movie. Actually, all authors connected by an edge worked together (among other movies) in the movie “Con Air” or “The Rock” (or both).

Fig. 10

Example cluster from IMDB

In our next experiment, we evaluate the potential of our approach to handle also multi-layer graphs without edge labels. The second data set was constructed from an extract of the Arxiv publication database.¹¹ Here, each vertex represents a publication. From the abstracts of the publications, we extracted the 300 most common keywords. Each layer of the graph represents a certain keyword, and an edge of layer i represents a citation between two publications with the common topic i. Overall, the Arxiv graph contains 13396 vertices and 673800 edges. For example, the largest cluster found by MiMAG consists of 19 papers from the field of string theory. The 7 relevant layers of this cluster correspond to the keywords given in Fig. 11:

Fig. 11

Keywords for a cluster from Arxiv

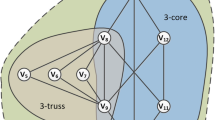
Our third real-world data set is a co-author graph extracted from the DBLP database.¹² In this graph, the vertices represent authors and the layers represent the 50 conferences in computer science having the most publications. Two authors are connected by an edge in layer i if they co-authored at least two papers that were published at the corresponding conference. Overall, the DBLP graph contains 17291 vertices and 22896 edges. As we expect co-author groups to be rather small, for this experiment we adapted our quality function to consider clusters with at least 4 vertices as interesting. Figure 12 shows three example clusters detected by MiMAG and their corresponding conferences. Note that each of the clusters has different relevant layers. While two of the clusters form cliques in both of their layers, in the top right cluster the edge sets of the layers differ.

Fig. 12

Example clusters from DBLP

5.3.1 Clustering results on real-world data sets

In Table 1, we summarize some key characteristics of the clustering results of the different approaches on the real-world data sets. Experiments that did not finish within 2 days were aborted. For each approach and data set, we provide the runtime as well as the average number of vertices, density and number of layers of the found clusters. Note that for the adaptations of GAMer, the density and subspace are determined on the corresponding transformed graphs to get a fair comparison; the clusters do not correspond to MLCS clusters in the original multi-layer graphs.

Cocain did not finish on any of the data sets within 2 days; GAMer-lg finished only on the DBLP graph, however, with a much higher runtime than the other approaches due to the size of the constructed line graph. MiMAG and GAMer-avg have similar runtimes for all data sets. On the IMDB graph, MiMAG detects clusters with a significantly higher average density and dimensionality than GAMer-avg. On Arxiv, the density of GAMer-avg’s clusters is slightly higher, which is caused by the fact that GAMer-avg unions the edge sets from all 300 layers and thus obtains a very dense graph. On DBLP, the clusters detected by MiMAG again show the highest average density, while having similar average size and dimensionality to the other approaches.

Table 1 Key characteristics of the clustering results

6 Conclusion

We proposed the new paradigm of clustering multi-layer graphs with edge labels. Besides the mere graph data, additional information about the edges is considered for finding coherent subgraphs. We introduced the clustering model MLCS, which defines clusters of vertices that are densely connected by edges with similar edge labels in a subset of the graph layers. Redundancy in the result set is avoided by selecting only the most interesting clusters. Based on this model, we introduced the efficient best-first search algorithm MiMAG. The performance and clustering quality of MiMAG were demonstrated in our experimental analysis.