On the Security of Relay Assisted Cognitive Radio Networks in the Presence of Primary Transceiver Network

Abstract

In this paper, the benefit of distinguishable diversity order within a co-operative relay system is exploited to overcome the problem of secure communication in an underlay wiretap cognitive radio network. This network is in a coexistence with a primary transceiver network and it is subjected to multiple eavesdropping attacks which employ a specific interception strategy. To improve the physical layer security, simple relay selection schemes will be proposed that aims at maximizing the minimum of the dual hop communication secrecy rates under primary network constraints. For Rayleigh fading channels, exact and asymptotic closed form expressions will be derived for the secondary system outage and secrecy rate. Furthermore, based on the network topology, tight inner and outer bounds will subsequently be derived on the system secrecy outage probability. By employing analytical and simulation results, the gain of the system diversity order is obviously investigated and emphasized.

1 Introduction

Cognitive radio network (CR) is a useful tool for solving the problem of scarcity of spectral resources and to provide a spectral efficiency by licensed/unlicensed spectrum sharing [1]. In cognitive radio networks, it is permissible to unlicensed secondary users (SUs) to access the spectrum of licensed primary users (PUs) without interfere the PUs. To preserve a certain quality of service (QoS) for unlicensed/secondary users while leveraging a limited (uninfluenced) interference to licensed/primary users, the assistance of co-operative relays in cognitive radio networks were utilized extensively [2].

Mainly, co-operative relays were proposed to promote the system performance and obtain signaling and diversity gains. This paradigm was devoted to get rid of the problem of extending the coverage of wireless networks [3,4,5,6,7,8]. Specifically, promising relay protocols had been studied to forward the secondary source message in a cognitive radio system to the destination [9,10,11,12,13,14]. However, due to wireless broadcasting, the physical layer security (PLS) is vulnerable to illegitimate benefits. Securing and protecting issues of the physical layer against eavesdroppers were extensively investigated [15,16,17,18,19,20].

In fact, cognitive radio networks may be classified with respect to spectrum sharing or access techniques into: (1) overlay CR [21], [22] and (2) underlay CR.

In an overlay CR, the SUs have to detect the spectrum holes to maintain their own communication which can be hardly performed in the dense areas due to the lack of empty resources.

Alternatively, underlay cognitive radio network is a crucial network topology for both the academicals and industrial network designers as it provides concurrent cognitive/non-cognitive communications [23, 24]. To achieve secure and reliable communication within such a network, conflict objectives of interest should be maintained:

• 1. Making the secondary network coverage as large as possible while protecting both primary and secondary networks from interference.

• 2. Satisfying adoptable (QoS) requirements for both primary and secondary users.

• 3. Preventing external attackers from overhearing secure and confidential information.

Anywhere, there exist some recent researches in the context of secure underlay CR that aims at enhancing the secrecy performance by exploiting the statistical characteristics of the wireless channels regarding interference constraint requirements [25,26,27,28,29]. For instance, in [25] the authors derived a closed form expression of some performance metrics, i.e., outage probability and secrecy outage probability, for multicasting system in the presence of multiple eavesdroppers. In [26] single and multi-relay selection schemes were investigated where security and reliability tradeoff issues were examined. In [27] the case of unknown channel state information CSI about the attackers (sub-optimal relay selection) was assumed. Regenerative multi-relay system was introduced in [28]. Reference [29] investigated licensed/unlicensed users with dual sources of interference in both directions. Unfortunately, it did not consider the security issue.

Very recently, in [30] the authors considered a secure dual-hop communication where an eavesdropper can overhear the transmission from both the direct and the relayed links. Thus, the eavesdropper performs maximal radio combining (MRC) or selection combining (SC) of the signals. Still, this has not been discussed in terms of secure underlay cognitive radio networks. In [31] the authors proposed three relay selection schemes to improve PLS in an underlay CR in the presence of multiple PUs. Unfortunately, they did not consider the effect of interference from the PUs to SUs.

To the best of our knowledge, in all of the above mentioned works (and the references therein) the mutual interference between PUs and SUs have not been highlighted especially in the presence of multiple secondary eavesdroppers. In particular, the impact of joint constraints of interference and security on the performance of both primary and secondary networks involves a tradeoff. Motivated by these considerations, a novel secure secondary communication system that incorporates cooperative diversity will be investigated. In particular, the fading characteristics will be exploited to provide useful insights regarding the main factors that regulate the secrecy performance when both direct and relayed links are overheard under all possible interference constraints. The contributions of this paper are summarized as follows:

• We propose relay selection criteria for the per-hop and the dual-hop communications to improve the PLS under the primary/secondary interference constraints.

• We evaluate the secrecy performance and derive new closed form expressions for some important metrics, i.e., achievable secrecy rate, outage probability and asymptotic outage probability.

• The impact of cooperative diversity of relay selection is characterized when perfect or statistical CSI of eavesdroppers are known.

• Thereafter, system inner and outer bounds are also derived. Those bounds become tight at high transmitted signal to interference noise ratio (SINR) in the considered system.

The rest of the paper is organized as follows. In Section II the system analysis and the optimal relay selection conditions are statistically investigated. Also, the effect of the primary user’s constraints and impact of diversity order are clarified. In Section III we evaluate the performance metrics. Simulation results are depicted in Section IV. Section V concludes the paper.

2 System and Channel Models

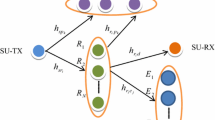
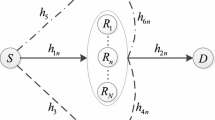
Here, we consider a wiretap cognitive radio network. It is a dual-hop decode and forward relay assisted network. It consists of the following nodes; one secondary user source, $S$, set of $N$ decode and forward (DF) relays, ($R_{i} , 1 \le i \le N$), one secondary user destination, $D$, one primary user transmitter, $P_{Tx}$, one primary user receiver, $P_{Rx}$, and multiple $M$ eavesdroppers, ($E_{j} , 1 \le j \le M$). All nodes are equipped with a single antenna.

2.1 The System Model

We rely on a worse-case model, where the secondary source transmitter transmits a confidential information to the secondary receiver in the presence of multiple eavesdroppers with the aid of $N$ trusted DF relays, while the eavesdroppers try to overhear and attack all of the communication paths between the secondary source, $S$, and destination, $D$.

Such an underlay spectrum sharing cognitive radio network in coexistence with a primary user network is shown in Fig. 1. It is assumed that the secondary network communication follows an interference power constraint condition which represents the maximum allowable transmit power of both the secondary source and relays. Thus, the interference power does not exceed a threshold limit $P$ at the primary receiver end.

Fig. 1

A class of wiretap underlay cognitive radio networks

It is further assumed that all of the receiving nodes are confirmed to know global channel state information (CSI) and either instantaneous information about eavesdroppers or statistical CSI is available at the end of the secondary user source, $S$.¹ Moreover, the secondary user destination, $D$, and relays are subjected to interference signals from the primary transmitter, $P_{Tx}$. All communication channels are quasi-static and flat fading Rayleigh channels. No direct path from $S$ to $D$ is found due to deep fading conditions. Communication takes place in a half duplex mode through two phases.

In the first phase S transmits a power constraint signal while the relays listen, type of non-colluding eavesdroppers,² i.e., multiple or co-operative eavesdroppers, try to overhear through wiretap channels.

In the second phase, the relays listen in a co-operative scheme. Then, one potential relay node is selected out of the set that successfully decodes the source message to forward the re-encoded messages toward the destination such that this relay satisfies a certain optimization condition. However, the eavesdroppers’ system tries to again overhear the second path through another dedicated wiretap channel.

A co-operative communication method based on optimal selection scheme is proposed to select the relay that has the best maximum to forward the source message to the destination.

2.2 The Communication Channels

Since it is assumed that all communication channels follow Rayleigh fading distributions, let us generally define that the fading coefficients $\gamma_{q,r} = \left| {h_{q,r} } \right|^{2} ,q,r \in \left\{ {s,i,p, j, d} \right\}$ satisfy Rayleigh fading conditions and undergo independent exponential distributions, i.e., be exponential random variables (exponential R.V.s) $with\;means\;\lambda_{q,r}$, where their cumulative density functions and probability density functions, i.e., CDF and PDF, can be expressed by

$$ F_{{\gamma_{q,r} }} \left( x \right) = 1 - exp\left( { - \frac{x}{{\lambda_{q,r} }}} \right). $$

(1)

$$ f_{{\gamma_{q,r} }} \left( x \right) = \frac{1}{{\lambda_{q,r} }}exp\left( { - \frac{x}{{\lambda_{q,r} }}} \right). $$

(2)

In the first phase, $S$ sends its message signal to $R_{i}$ with the constraint power

$$ P_{s} = \frac{P}{{\left| {h_{s,p} } \right|^{2} }}. $$

(3)

Where $h_{s,p}$ is the $S - P$ channel fading coefficient and $P$ is the constraint power at $P_{Rx}$. In the vicinity of $R_{i}$, the received signal can be expressed as

$$ y_{s,i} = \sqrt {P_{s} } h_{s,i} x_{s,i} + \sqrt {P_{p} } h_{p,i} x_{p,i} + n_{i} . $$

(4)

Where $h_{s,i}$ is the $S - R_{i}$ channel fading coefficient and $x_{s,i}$ is the $S$ transmitted symbol of the $S - R_{i}$ link, $h_{p,i}$ is the channel fading coefficient of the $P_{Tx} - R_{i}$ interference signal, $x_{p,i}$ is the corresponding transmitted interference symbol with power $P_{p}$ and $n_{i} \sim\,CN\left( {0,N_{0} } \right)$ is an additive white Gaussian noise (AWGN) signal.

In the second phase, $R_{i}$ forwards its signal to D after successful decoding³ with the constraint power

$$ P_{i} = \frac{P}{{\left| {h_{i,p} } \right|^{2} }}. $$

(5)

Where $h_{i,p}$ is the $R_{i} - P$ channel fading coefficient. The received signal at $D$ can be expressed as

$$ y_{i,d} = \sqrt {P_{i} } h_{i,d} x_{i,d} + \sqrt {P_{p} } h_{p,d} x_{p,d} + n_{d} . $$

(6)

Where $h_{i,d}$ is the $R_{i} - D$ channel fading coefficient and $x_{i,d}$ is the transmitted relay, $R_{i}$, symbol of the $R_{i} - D$ link with power $P_{i}$, $h_{p,d}$ is the channel fading coefficient of the $P_{Tx} - D$ interference signal, $P_{p}$ is the primary transmitted interference power and $n_{d} \sim\,CN\left( {0,N_{0} } \right)$ is an additive white Gaussian noise (AWGN) signal.

Considering the worst-case scenario, eavesdropper $j$ can recover the interference from the primary user and the received signals in the first and the second phases can be given by

$$ y_{\mu ,j} = \sqrt {P_{\mu } } h_{\mu ,j} x_{\mu ,j} + n_{j} , \mu \in \left\{ {s,i} \right\}. $$

(7)

Where $h_{\mu ,j} , \mu \in \left\{ {s,i} \right\}$, is the channel fading coefficient of the overheard signals from both $S$ and $R_{i}$ to $E_{j}$, $x_{\mu ,j}$ is the corresponding overheard symbol and $n_{j} \sim\,CN\left( {0,N_{0} } \right)$ is an AWGN with respect to the jth eavesdropper end.

2.3 The Secrecy Capacity

Let us first define the concept of maximum achievable secrecy rate (secrecy capacity) as [32]

$$ C_{s} = \left\{ {\begin{array}{*{20}l} {\left[ {C_{M} - C_{E} } \right]^{ + } } \hfill &\quad {if\;\gamma_{R} > \gamma_{E} } \hfill \\ 0 \hfill & \quad {if\;\gamma_{R} \le \gamma_{E} } \hfill \\ \end{array} } \right.. $$

(8)

Where $\left[ x \right]^{ + }$ represents $max\left( {0,x} \right)$, $C_{M} = \frac{1}{2}\log_{2} \left( {1 + \gamma_{M} } \right)$,⁴$C_{E} = \frac{1}{2}\log_{2} \left( {1 + \gamma_{E} } \right)$, $\gamma_{M}$, $\gamma_{E}$ are the capacity of the main channel, the capacity of the wiretap channel, the SINR of the main channel and the SINR of the wiretap channel, respectively.

Hence, the achievable transmission rate of the $S - R_{i}$ and $R_{i} - D$ channels can be given by

$$ C_{M} = \frac{1}{2}\log_{2} \left( {1 + \gamma_{M} } \right),M \in \left\{ {\left( {s,i} \right),\left( {i,d} \right)} \right\}. $$

(9)

Where $\gamma_{s,i}$ and $\gamma_{i,d}$ can be formulated as

$$ \gamma_{s,i} = \frac{{\frac{P}{{N_{0} }}\frac{{\left| {h_{s,i} } \right|^{2} }}{{\left| {h_{s,p} } \right|^{2} }}}}{{\frac{{P_{p} }}{{N_{0} }}\left| {h_{p,i} } \right|^{2} + 1}}, $$

(10)

$$ \gamma_{i,d} = \frac{{\frac{P}{{N_{0} }}\frac{{\left| {h_{i,d} } \right|^{2} }}{{\left| {h_{i,p} } \right|^{2} }}}}{{\frac{{P_{p} }}{{N_{0} }}\left| {h_{p,d} } \right|^{2} + 1}}. $$

(11)

Correspondingly, the achievable wiretap transmission rate of the $S - E$ and $R_{i} - E$ channels (intercepted by the eavesdropping system $J$) can be given by

$$ C_{{E_{J} }} = \frac{1}{2}\log_{2} \left( {1 + \gamma_{{E_{J} }} } \right), E_{J} \in \left\{ {\left( {s,J} \right),\left( {i,J} \right)} \right\}. $$

(12)

Where $\gamma_{s,j}$ and $\gamma_{i,J}$ can be formulated as

$$ \gamma_{s,J} = \frac{P}{{N_{0} }}\frac{{\left| {h_{s,J} } \right|^{2} }}{{\left| {h_{s,p} } \right|^{2} }}. $$

(13)

$$ \gamma_{i,J} = \frac{P}{{N_{0} }}\frac{{\left| {h_{i,J} } \right|^{2} }}{{\left| {h_{i,p} } \right|^{2} }}. $$

(14)

Comparatively, the achievable secrecy rate which is intercepted by the eavesdropping system $J$ can be rewritten for the two communication phases as

$$ \begin{aligned} C_{sJ,\omega } & = \frac{1}{2}\log_{2} \left( {\frac{{1 + \gamma_{M} }}{{1 + \gamma_{{E_{J} }} }}} \right) \\ & = \frac{1}{2}\log_{2} \left( {\frac{{1 + {\raise0.7ex\hbox{${\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }}}$} \!\mathord{\left/ {\vphantom {{\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }}} {Z_{4,\omega } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Z_{4,\omega } }$}}}}{{1 + {\raise0.7ex\hbox{${Z_{3,\omega } }$} \!\mathord{\left/ {\vphantom {{Z_{3,\omega } } {Z_{4,\omega } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Z_{4,\omega } }$}}}}} \right). \\ \end{aligned} $$

(15)

Where $\gamma_{{E_{J} }}$, $E_{J} \in \left\{ {\left( {s,J} \right),\left( {i,J} \right)} \right\}$, is the SINR at the eavesdropping system $J$, the superscript $\omega$, $\omega \in \left\{ 1 \right\}\;{\text{or}}\;\omega \in \left\{ 2 \right\}$, denotes the first phase or the second phase, $Z_{1,\omega } = \frac{P}{{N_{0} }}\psi_{1,\omega }$, $Z_{2,\omega } = \frac{{P_{p} }}{{N_{0} }}\psi_{2,\omega } + 1$, $Z_{3,\omega } = \frac{P}{{N_{0} }}\psi_{3,\omega }$, $Z_{4,\omega } = \psi_{4,\omega }$, $\psi_{1,1} \sim \left| {h_{s,i} } \right|^{2} , \psi_{1,2} \sim \left| {h_{i,d} } \right|^{2}$, $\psi_{2,1} \sim \left| {h_{p,i} } \right|^{2} ,\psi_{2,2} \sim \left| {h_{p,d} } \right|^{2}$, $\psi_{3,1} \sim \left| {h_{s,J} } \right|^{2} ,\psi_{3,2} \sim \left| {h_{i,J} } \right|^{2}$, $\psi_{4,1} \sim \left| {h_{s,p} } \right|^{2} \;and\;\psi_{4,2} \sim \left| {h_{i,p} } \right|^{2}$ of the first phase or the second phase, respectively.

In the following, we derive formulas for the cumulative and probability density functions, i.e., CDF and PDF, of the SINR of the two communication phases, considering the proposed selection schemes and the interception strategies, then, we use them to obtain closed form expressions for important performance metrics such as the secrecy outage probability and the non-zero achievable secrecy rate.

3 Relay Selection Schemes and Performance Metrics

Our analysis will be started with the per-hop relay selection scheme. It is remarkable that the per-hop selection may replace the dual-hop one, if perfect CSI information about the location of the eavesdropping system indicates that the eavesdroppers reside within one of the two communication phases.

3.1 Per-hop Relay Selection Schemes

In this sub-section, we propose per-hop relay selection schemes regarding one side of the secondary network transmission. If it is confirmed that the eavesdropping system reside within one of the two communication phases, it is better to derive the cooperative relay to select the one that maximizes the secrecy rate within the phase of the eavesdroppers’ residence. Let the per-hop relay selection be defined as

$$ i_{{per{ - }hop}} = \arg \mathop {\hbox{max} }\limits_{i} C_{sJ,\omega } ,\quad \omega \in \left\{ {1,2} \right\}. $$

(16)

Where $i_{per - hop}$ is the index of the selected relay.

3.1.1 Relay Selection Scheme at the First Phase Side

At this side, the selected relay depends only on the SINR of the main channel where $C_{sj,1}^{{}} = \frac{1}{2}\log_{2} \left( {\frac{{1 + \gamma_{M} }}{{1 + \gamma_{{E_{J} }} }}} \right)$, $M \in \left\{ {\left( {s,i} \right)} \right\}$, $E_{J} \in \left\{ {\left( {s,J} \right)} \right\}$, as investigated by the following theorem.

Theorem 1

The relay selection rule according to (16) is determined statistically by selecting$i$that maximizes The CDF of the achievable secrecy rate$\left( {i.e. C_{sJ,1}^{{}} } \right)$of the first communication phase as,

$$ i_{per - hop(1)} = \arg \mathop {\hbox{max} }\limits_{i} \left( {\gamma_{s,i} } \right) \Rightarrow \arg \Pr \left( {\mathop {\hbox{max} }\limits_{i} \mathop {\left( {\frac{{\tfrac{P}{{N_{0} }}\left| {h_{s,i} } \right|^{2} }}{{\tfrac{{P_{p} }}{{N_{0} }}\left| {h_{p,i} } \right|^{2} + 1}}} \right)}\limits_{{}} \le \gamma } \right) \Rightarrow \arg \left( {\prod\limits_{i = 1}^{N} {\left( {\frac{{\Omega _{s,i} \gamma \exp \left( {\Omega _{p,i} } \right)}}{{\Omega _{s,i} \gamma +\Omega _{p,i} }}} \right)} } \right) $$

(17)

where$\Omega _{p,i} = \left( {\lambda_{p,i} \frac{{P_{p} }}{{N_{0} }}} \right)^{ - 1} ,\Omega _{s,i} = \left( {\lambda_{s,i} \frac{P}{{N_{0} }}} \right)^{ - 1} ,$and$\gamma$is the threshold SINR.

Proof

Let $h_{s,i}$ and $h_{p,i}$ be Rayleigh R.V. s, then, the PDF and the CDF of $X_{s,i} = \frac{P}{{N_{0} }}\left| {h_{s,i} } \right|^{2}$ will take the forms

$$ f_{{x_{s,i} }} \left( x \right) =\Omega _{s,i} \exp \left( { -\Omega _{s,i} x} \right), $$

(18)

$$ F_{{X_{s,i} }} \left( x \right) = 1 - \exp \left( { -\Omega _{s,i} x} \right), $$

(19)

respectively, and after some algebraic manipulation the PDF of $Y_{p,i} = \frac{{P_{p} }}{{N_{0} }}\left| {h_{p,i} } \right|^{2} + 1$ can be expressed as

$$ f_{{Y_{p,i} }} \left( x \right) =\Omega _{p,i} \exp \left( {\Omega _{p,i} } \right)\exp \left( { -\Omega _{p,i} x} \right). $$

(20)

Thus, the CDF of the R.V. $Z_{i} = \frac{{{\text{X}}_{s,i} }}{{Y_{p,i} }}$ is given by

$$ F_{{Z_{i} }} \left( x \right) = \exp \left( {\Omega _{p,i} } \right)\left( {1 - \frac{{\Omega _{p,i} }}{{\Omega _{s,i} x +\Omega _{p,i} }}} \right) = \frac{{\Omega _{s,i} x\exp \left( {\Omega _{p,i} } \right)}}{{\Omega _{s,i} x +\Omega _{p,i} }}, $$

(21)

where the previous Eq. follows after applying the following integral

$$ F_{{Z_{i} }} \left( x \right) = \int\limits_{0}^{\infty } {f_{{Y_{p,i} }} \left( {z_{i} } \right)F_{{X_{s,i} }} \left( {xz_{i} } \right)dz_{i} } . $$

(22)

Consequently, (17) immediately follows after some algebraic manipulations by using

$$ F_{{Z_{i} }} \left( \gamma \right) = \Pr \left( {\mathop {\hbox{max} }\limits_{i} } \right.\left( {F_{{Z_{1} }} \left( \gamma \right), \ldots F_{{Z_{N} }} \left( \gamma \right)} \right) \le \left. \gamma \right) = \prod\limits_{i = 1}^{N} {\left( {F_{{Z_{i} }} \left( \gamma \right)} \right)} . $$

(23)

It can be concluded that, this relay selection is briefly a conventional selection rule.□

3.1.2 Relay Selection Scheme at the Second Phase Side

At the second phase side, the selected relay depends on $C_{sJ,2}^{{}} = \frac{1}{2}\log_{2} \left( {\frac{{1 + \gamma_{M} }}{{1 + \gamma_{{E_{J} }} }}} \right)$, $M \in \left\{ {\left( {i,d} \right)} \right\}$, $E_{J} \in \left\{ {\left( {i,J} \right)} \right\}$, where the $R_{i} - E_{J}$ channel fading coefficient has a great impact on the decision of the relay selection. Thus, two applicable cases of eavesdropping are adopted and investigated as follows.

Case 1: Maximum of the eavesdroppers:

In this case, the strongest attacker is picked up. Thus, the group SINR is considered by the one that has the highest SINR and is given by,

$$ \gamma_{i,J} = \mathop {\hbox{max} }\limits_{j} \gamma_{i,j} \Rightarrow \left| {h_{i,J} } \right|^{2} = \mathop {\hbox{max} }\limits_{j} \left| {h_{i,j} } \right|^{2} . $$

(24)

Let $\left| {h_{i,j} } \right|^{2}$ be an exponential R.V., then, the CDF of $Z_{3,2} = \frac{P}{{N_{0} }}\left| {h_{i,J} } \right|^{2}$ can be denoted as follows

$$ F_{{\left| {h_{i,j} } \right|^{2} }} \left( x \right) = 1 - \exp \left( { - \Omega_{i,j} x} \right). $$

(25)

Where $\Omega_{i,j} = \left( {\lambda_{i,j} \frac{P}{{N_{0} }}} \right)^{ - 1}$. By using (23) the CDF of $Z_{3,2}$ will take the form

$$ F_{{Z_{3,2} }} \left( x \right) = \prod\limits_{j = 1}^{M} {\left( {1 - \exp \left( { -\Omega _{i,j} x} \right)} \right)} = 1 + \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j} \sum\limits_{{l_{1} \prec l_{2} \prec \cdots l_{M} }} {\exp \left( { - \sum\limits_{k = 1}^{j} {\Omega _{{i,l_{k} }} } x} \right)} } . $$

(26)

By applying following relation

$$ \begin{aligned} & \prod\limits_{j = 1}^{M} {\left( {1 - \theta_{j} } \right)} = 1 + \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j} \sum\limits_{{l_{1} \prec l_{2} \prec \ldots l_{M} }} {\prod\limits_{k = 1}^{j} {\theta_{{l_{k} }} } } } \\ & where\;\sum\limits_{{l_{1} \prec l_{2} \prec \cdots l_{M} }} {} \equiv \sum\limits_{{l_{1} = 1}}^{M - j + 1} {\sum\limits_{{l_{2} = l_{1} + 1}}^{M - j + 2} { \cdots \sum\limits_{{l_{j} = l_{j - 1} + 1}}^{M} {} } } . \\ \end{aligned} $$

(27)

Then, the PDF of can be expressed as

$$ f_{{Z_{3,2} }} \left( x \right) = \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \prec \cdots l_{M} }} {\exp \left( { - \sum\limits_{k = 1}^{j} {\left( {\Omega _{{i,l_{k} }} - \ln \left( {\Omega _{{i,l_{k} }} } \right)} \right)} x} \right)} } . $$

(28)

Theorem 2

The relay selection rule according to (16) is determined statistically by selecting$i$that maximizes The CDF of the achievable secrecy rate$\left( {i.e. C_{sJ,2}^{{}} } \right)$of the second communication phase can be derived as,

$$ i_{per - hop(2)} = \arg \mathop {\hbox{max} }\limits_{i} \left( {C_{sJ,2}^{{}} } \right) \Rightarrow \arg \Pr (\mathop {\hbox{max} }\limits_{i} \mathop {\left( {\frac{{\tfrac{{Z_{1,2} }}{{Z_{4,2} }} + 1}}{{\tfrac{{Z_{3,2} }}{{Z_{4,2} }} + 1}}} \right)}\limits_{{}} \le \gamma ) \Rightarrow \arg \left( {\prod\limits_{i = 1}^{N} {F_{{\sigma_{i} }} \left( \gamma \right)} } \right), $$

where

$$ F_{{\sigma_{i} }} \left( \sigma \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne r \end{subarray} }^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \cdots l_{M} }} {\frac{{\tfrac{{\zeta_{i,j} }}{\sigma }\tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\tfrac{{\zeta_{i,j} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}} } \left( {\frac{1}{{\tfrac{{\Omega_{i,p} }}{\sigma - 1} + \Omega_{i,d} }} - \frac{1}{{\tfrac{{\zeta_{i,j} }}{\sigma } + \Omega_{i,d} }}} \right) + \left( { - 1} \right)^{r} \left( {\frac{{\lambda_{i} }}{{\lambda_{i} + \Omega_{i,d} }}} \right)^{2} } \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{i,r} }}{\sigma }} \right|_{{r \in \left\{ {1,2, \ldots M} \right\}}} } \hfill \\ {1 - \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \cdots l_{M} }} {\frac{{\tfrac{{\zeta_{i,j} }}{\sigma }\tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\tfrac{{\zeta_{i,j} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}} \left( {\frac{1}{{\tfrac{{\Omega_{i,p} }}{\sigma - 1} + \Omega_{i,d} }} - \frac{1}{{\tfrac{{\zeta_{i,j} }}{\sigma } + \Omega_{i,d} }}} \right)} } \hfill & {otherwise} \hfill \\ \end{array} } \right., $$

(29)

where$\Omega _{\text{i,p}} = \left( {\uplambda_{\text{i,p}} } \right)^{ - 1} ,\Omega _{\text{i,d}} = \left( {\uplambda_{\text{i,d}} \frac{{{\text{P}}_{{{\text{R}}_{\text{p}} }} }}{{{\text{N}}_{0} }}} \right)^{ - 1}$and$\upgamma$is the threshold SINR.

Proof

For the second communication phase, one can innovate in (15) that the relay selection relies again only on $i$ which is independent of $Z_{2,2}$.

Firstly, the CDF of the R.V. $\sigma_{i} = \frac{{1 + Z_{1,2} \text{ / }Z_{4,2} }}{{1 + Z_{3,2} \text{ / }Z_{4,2} }} \to F_{{\sigma_{i} }} \left( \sigma \right) = Pr\left( {\sigma_{i} \le \sigma } \right)$ can be derived as follows

$$ F_{{\sigma_{i} }} \left( \sigma \right) = \Pr \left( {Z_{1,2} \le \left( {\sigma Z_{3,2} + \left( {\sigma - 1} \right)Z_{4,2} } \right)} \right) $$

(30)

Let the CDF of $Z_{1,2}$ takes the forms

$$ F_{{Z_{1} }} \left( x \right) = 1 - \exp \left( { - \Omega_{i,d} x} \right). $$

(31)

By using (28) and after some algebraic manipulations, the PDF $\sigma Z_{3,2}$ of can be expressed as

$$ f_{{\sigma Z_{3,2} }} \left( x \right) = \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \prec \cdots l_{M} }} {\exp \left( { - \sum\limits_{k = 1}^{j} {\left( {\frac{{\Omega_{{i,l_{k} }} }}{\sigma } - \ln \left( {\frac{{\Omega_{{i,l_{k} }} }}{\sigma }} \right)} \right)x} } \right)} } $$

(32)

For simplicity, a decomposed form can be denoted as

$$ \begin{aligned} & f_{{\sigma Z_{3,2} }} \left( x \right) = \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \prec \cdots l_{M} }} {\frac{{\zeta_{i,j} }}{\sigma }\exp \left( { - \frac{{\zeta_{i,j} }}{\sigma }x} \right)} } \\ & where\;\zeta_{i,j} = \sum\limits_{k = 1}^{j} {\Omega_{{i,l_{k} }} } . \\ \end{aligned} $$

(33)

The PDF of the R.V. $\left( {\sigma - 1} \right)Z_{4,2}$ is given by

$$ f_{{\left( {\sigma - 1} \right)Z_{4,2} }} \left( x \right) = \frac{{\Omega_{i,p} }}{\sigma - 1}\exp \left( { - \frac{{\Omega_{i,p} }}{\sigma - 1}x} \right). $$

(34)

Then, the PDF of $Y_{i} = \sigma Z_{3,2} + \left( {\sigma - 1} \right)Z_{4,2}$ can be computed as

$$ f_{{Y_{i} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} > - l_{M} }} {\frac{{\tfrac{{\zeta_{i,j} }}{\sigma }\tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\tfrac{{\zeta_{i,j} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}} } \left( {\exp \left( { - \tfrac{{\Omega_{i,p} }}{\sigma - 1}x} \right) - \exp \left( { - \tfrac{{\zeta_{i,j} }}{\sigma }x} \right)} \right)} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} \ne \tfrac{{\zeta_{i,j} }}{\sigma }\forall j \in \left\{ {1,2, \ldots M} \right\}} \hfill \\ {\lambda_{i}^{2} x\exp \left( { - \lambda_{i} x} \right)} \hfill & {for\;\lambda_{i} = \tfrac{{\Omega_{i,p} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{i,j} }}{\sigma }} \right|_{j = 1,2, \ldots M} } \hfill \\ \end{array} } \right.. $$

(35)

By applying the integral

$$ f_{{Y_{i} }} \left( x \right) = \int\limits_{0}^{x} {f_{{\sigma Z_{3} }} \left( \tau \right)f_{{\left( {\sigma - 1} \right)Z_{4} }} \left( {x - \tau } \right)d\tau } , $$

(36)

Hence, $F_{{\sigma_{i} }} \left( \sigma \right)$ can be given by

$$ F_{{\sigma_{i} }} \left( \sigma \right) = \left\{ {\begin{array}{*{20}l} {1 - \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\frac{{\tfrac{{\zeta_{i,j} }}{\sigma }\tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\tfrac{{\zeta_{i,j} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}} } \left( {\frac{1}{{\tfrac{{\Omega_{i,p} }}{\sigma - 1} + \Omega_{i,d} }} - \frac{1}{{\tfrac{{\zeta_{i,j} }}{\sigma } + \Omega_{i,d} }}} \right)} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} \ne \tfrac{{\zeta_{i,j} }}{\sigma }\forall j \in \left\{ {1,2, \ldots M} \right\}} \hfill \\ {1 - \left( {\frac{{\lambda_{i} }}{{\lambda_{i} + \Omega_{i,d} }}} \right)^{2} } \hfill & {for\;\lambda_{i} = \tfrac{{\Omega_{i,p} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{i,j} }}{\sigma }} \right|_{j = 1,2, \ldots M} } \hfill \\ \end{array} } \right.. $$

(37)

Where the following integral is solved for $x = 1$ as

$$ F_{{\sigma_{i} }} \left( {x,\sigma } \right) = \int\limits_{0}^{\infty } {f_{{Y_{i} }} \left( {z_{i} } \right)F_{{Z_{1} }} \left( {xz_{i} } \right)dz_{i} } . $$

(38)

Consequently, (29) immediately follows after some algebraic manipulations by using a similar form as (23).□

Case 2: Co-operative eavesdroppers:

In this case, the group SINR is given by,

$$ \gamma_{i,J} = \sum\limits_{j = 1}^{M} {\gamma_{i,j} } \Rightarrow \left| {h_{i,J} } \right|^{2} = \sum\limits_{j = 1}^{M} {\left| {h_{i,j} } \right|^{2} } , $$

(39)

where the eavesdroppers cooperate the MRC reception. Thus, the CDF of the R.V. $Z_{3,2}$ can be computed as follows

$$ F_{{\left| {h_{i,J} } \right|^{2} }} \left( x \right) = \Pr \left( {\sum\limits_{j = 1}^{M} {\left| {h_{i,j} } \right|^{2} } \le x} \right) = \mathop E\limits_{{\sum\limits_{j = 1}^{M - 1} {\left| {h_{i,j} } \right|^{2} } }} \left( {\mathop E\limits_{{\sum\limits_{j = 1}^{M - 2} {\left| {h_{i,j} } \right|^{2} } }} \left( { \cdots \left( {\mathop E\limits_{{\left| {h_{i,j} } \right|^{2} }} \left( {F_{{\left| {h_{i,j} } \right|^{2} }} \left( {x - \sum\limits_{j = 1}^{M - 1} {\left| {h_{i,j} } \right|^{2} } } \right)} \right)} \right)} \right)} \right), $$

(40)

where the subscripts $\sum\nolimits_{j = 1}^{\epsilon } {\left| {h_{i,j} } \right|^{2} }$ of E represent the computation of the mean under the PDF of the R.V. $\sum\nolimits_{j = 1}^{\epsilon } {\left| {h_{i,j} } \right|^{2} } , \in is\;an\;integer.$

Applying recursive calculus, the CDF of $Z_{3,2}$ will take the form,

$$ F_{{Z_{3,2} }} \left( x \right) = \frac{1}{{\left( {M - 1} \right)!}}\int\limits_{0}^{{\Omega_{iJ} x}} {t^{M - 1} \exp \left( { - t} \right)} dt, $$

(41)

where $\Omega_{\text{iJ}} = {\text{aver}}_{j} \Omega_{i,j}$, the PDF (Chi square distribution) of the R.V. $Z_{3,2}$ is determined directly by differentiating (41) by $x$ as follows,

$$ f_{{Z_{3,2} }} \left( x \right) = \frac{{\left( {\Omega_{iJ} } \right)^{M} }}{{\left( {M - 1} \right)!}}x^{M - 1} \exp \left( { - \Omega_{iJ} x} \right). $$

(42)

Theorem 3

The relay selection rule according to (16) and (42) is determined statistically by selecting$i$that maximizes the CDF of the achievable secrecy rate$\left( {i.e. C_{sJ,2}^{{}} } \right)$whose CDF can be derived as,

$$ F_{{\sigma_{i} }} \left( \sigma \right) = \left\{ {\begin{array}{ll} \begin{aligned} &\frac{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{M} \Omega_{i,d} }}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{M} \left( {\tfrac{{\Omega_{i,p} }}{\sigma - 1} + \Omega_{i,d} } \right)}} - \frac{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{M} \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{M} }} \hfill \\& \left( {\left( {\sum\limits_{\delta = 0}^{M - 1} {\left( {\frac{1}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{\delta + 1} }} - \frac{1}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } + \Omega_{i,d} } \right)^{\delta + 1} }}} \right)\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{\delta } } } \right)} \right) \hfill \\ \end{aligned} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} \ne \tfrac{{\Omega_{iJ} }}{\sigma }} \hfill \\ {1 - \left( {\frac{{\lambda_{i} }}{{\lambda_{i} + \Omega_{i,d} }}} \right)^{M + 1} } \hfill & {for\tfrac{{\Omega_{i,p} }}{\sigma - 1} = \tfrac{{\Omega_{iJ} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right.. $$

(43)

Proof

Applying similar steps as Theorem 2, it is necessary to compute the PDF of $Y_{i} = \sigma Z_{3,2} + \left( {\sigma - 1} \right)Z_{4,2}$, in this case, which is given by

$$ f_{{Y_{i} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{M} \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{M} }}\left( {\exp \left( { - \tfrac{{\Omega_{i,p} }}{\sigma - 1}x} \right) - \left( {\exp \left( { - \tfrac{{\Omega_{iJ} }}{\sigma }x} \right)\sum\limits_{\delta = 0}^{M - 1} {\tfrac{{x^{\delta } }}{\delta !}\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{\delta } } } \right)} \right)} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} \ne \tfrac{{\Omega_{iJ} }}{\sigma }} \hfill \\ {\lambda_{i}^{M + 1} \frac{{x^{M} }}{M!}\exp \left( { - \lambda_{i} x} \right)} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} = \tfrac{{\Omega_{i,J} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right., $$

(44)

where the integral (36) is utilized. Consequently, $F_{{\sigma_{i} }} \left( \sigma \right)$ is given by,

$$ F_{{\sigma_{i} }} \left( \sigma \right) = \left\{ {\begin{array}{*{20}l} \begin{aligned} \frac{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{M} \tfrac{{\Omega_{i,p} }}{\sigma - 1}}}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{M} }}\left( {\left( {\frac{1}{{\tfrac{{\Omega_{i,p} }}{\sigma - 1}}} - \frac{1}{{\left( {\tfrac{{\Omega_{i,p} }}{\sigma - 1} + \Omega_{i,d} } \right)}}} \right)} \right. \hfill \\ \left. { - \left( {\sum\limits_{\delta = 0}^{M - 1} {\left( {\frac{1}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma }} \right)^{\delta + 1} }} - \frac{1}{{\left( {\tfrac{{\Omega_{iJ} }}{\sigma } + \Omega_{i,d} } \right)^{\delta + 1} }}} \right)\left( {\tfrac{{\Omega_{iJ} }}{\sigma } - \tfrac{{\Omega_{i,p} }}{\sigma - 1}} \right)^{\delta } } } \right)} \right) \hfill \\ \end{aligned} \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} \ne \tfrac{{\Omega_{iJ} }}{\sigma }} \hfill \\ {1 - \left( {\frac{{\lambda_{i} }}{{\lambda_{i} + \Omega_{i,d} }}} \right)^{M + 1} } \hfill & {for\;\tfrac{{\Omega_{i,p} }}{\sigma - 1} = \tfrac{{\Omega_{iJ} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right., $$

(45)

where the integral (38) is solved for $x = 1$ (see [ [33], Eq. (3.351.1)]). Then, (43) follows after some algebraic manipulations by using a similar form as (23).□

3.2 The Optimal Relay Selection Schemes

In the previous analysis, we state the statistical conditions of relay selection schemes for the two per-hop communication, individually. However, the relay selected to achieve maximum secrecy rate at one hop, can severely interrupt the reception security at the other.

To investigate the corresponding diversity analysis and propose a relay selection scheme to maintain secure and reliable communication, it suffices to check in and deal with the relay index dependent coefficients of dual hop communication phases.

Thus, in order to guarantee that neither of the separate secrecy rates falls down to a low level (i.e., which implies a security degradation), a low complexity overall relay selection scheme is adopted to select a relay, i.e., or more, out of N relays in the co-operative system that maximizes the minimum of the dual secrecy rates as follows.

3.2.1 Optimal Relay Selection in Global CSI Availability

Let $C_{sJ,\omega }^{{}} , \omega \in \left\{ {1,2} \right\}$ denote the achievable secrecy rates at the first and the second communication phases, respectively. The optimal relay $R_{i}^{*}$ can be formulated by maximizing the relation

$$ i^{ * } = \arg \mathop {\hbox{max} }\limits_{i} C_{sJ,1,2}^{{}} . $$

(46)

Where $C_{sJ,1,2}^{{}} = min\left( {C_{sJ,1}^{{}} , C_{sJ,2}^{{}} } \right)$. Therefore, the CDF of $C_{sJ,1,2}$ leads directly to

$$ F_{{C_{sJ,1,2}^{{}} }} \left( \gamma \right) = \Pr \left( {\hbox{min} \left( {C_{sJ,1}^{{}} ,C_{sJ,2}^{{}} } \right) \le \tau } \right) = F_{{C_{sJ,1}^{{}} }} \left( \tau \right) + F_{{C_{sJ,2}^{{}} }} \left( \tau \right) - F_{{C_{sJ,1}^{{}} }} \left( \tau \right)F_{{C_{sJ,2}^{{}} }} \left( \tau \right). $$

(47)

Where $\gamma = 2^{\tau } - 1$ is the threshold capacity, $F_{{C_{sJ,1} }} \left( \tau \right) and F_{{C_{sJ,2} }} \left( \tau \right)$ are the CDFs of $C_{sJ,1} and C_{sJ,2}$. The CDF of $C_{sJ,1}$ is sufficiently given by (17) and the CDF of $C_{sJ,2}$ can be given by $F_{{\sigma_{i} }} \left( \gamma \right)$ in (29) and (43), respectively.

The assumption of spatial independence can be exclusively deduced from the uncorrelated ordering concept where the CDF of the selected ith relay for each path satisfies

$$ F_{{C_{sJ,1,2} \left( i \right)}} \left( \gamma \right) = N\int_{0}^{\tau } {\Pr \left( {i = k\left| {C_{k} = x} \right.} \right)f_{{C_{k} }} \left( x \right)dx} . $$

(48)

Where $C_{sJ,1,2} \left( i \right)$ denote the achievable secrecy R.V.s of the ith relay index. For simplicity, it is assumed that for each communication phase, the order statistics of the best relay selection in (48) is independent of $\tau$, the threshold capacity as

$$ \Pr \left( {i = k\left| {C_{k} = \tau } \right.} \right) = \Pr \left( {i = k} \right) = \frac{1}{N}. $$

(49)

Thus, to evaluate (48), we have exclusively to determine $C_{sJ,1,2} \left( i \right)$ and the diversity order statistics of the best relay selection for the system relies only on the joint order statistics of the two combined communication phases, as it will be investigated.

Let us consider that the cooperative relay system will select the same relay to interconnect the secondary source, $S$, to the destination, $D$, for a certain, $r \triangleq number of selected relays$, an optimal relay selection expression can be derived from the equivalent permanent order statistics (see [34]) represented by

$$ \begin{aligned} & F_{{C_{r:N} }} \left( \gamma \right) = \Pr \left( {C_{r:N} \le \tau } \right) = \\ & \sum\limits_{l = r}^{N} {\Pr \left( {exactly(l)outof(N):\hbox{max} F_{{C_{{i_{l} }} }} \left( x \right) \le \tau } \right) = \sum\limits_{l = r}^{N} {\frac{1}{{l!\left( {N - l} \right)!}}\sum\limits_{\Im } {F_{{C_{{i_{1} }} }} \left( \tau \right) \cdots F_{{C_{{i_{l} }} }} \left( \tau \right)\left( {1 - F_{{C_{{i_{l + 1} }} }} \left( \tau \right)} \right) \cdots \left( {1 - F_{{C_{{i_{N} }} }} \left( \tau \right)} \right)} } } . \\ \end{aligned} $$

(50)

Where $\sum\nolimits_{{\Im }} \triangleq$ represents the sum over all $N!$ permutations $\left( {i_{1} ,i_{2} ,i_{3} , \ldots i_{N} } \right)\;of\;\left( {1,2,3, \ldots N} \right)$. Let $\gamma_{i\omega } ,\omega \in \left\{ {1,2} \right\}$, represent the SINR within the first and the second phases, respectively, where $\gamma_{i1} = \frac{{1 + \gamma_{M} }}{{1 + \gamma_{{E_{J} }} }}$, $M \in \left\{ {\left( {s,i} \right)} \right\}$, $E_{J} \in \left\{ {\left( {s,J} \right)} \right\}$, $\gamma_{i2} = \frac{{1 + \gamma_{M} }}{{1 + \gamma_{{E_{J} }} }}$, $M \in \left\{ {\left( {i,d} \right)} \right\}$, $E_{J} \in \left\{ {\left( {i,J} \right)} \right\}$ and $\gamma_{i} = \mathop {\hbox{min} }\limits_{{}} \left( {\gamma_{i1} ,\gamma_{i2} } \right)$, then, $C_{sJ,1,2} \left( i \right)$ can be replaced by $\gamma_{i}$, by substituting $F_{{C_{{i_{l} }} }} \left( \tau \right) = F_{{\gamma_{i} \left| {i = i_{l} } \right.}} \left( \gamma \right)\,in\,\left( {47} \right), i_{1} < i_{2} \ldots i_{N}$, the CDF of the achievable rate of the ith selected relay that has the order $l$ can be formulated.

Finally, the optimal relay, i.e., $R_{{i|i = i^{*} }}^{*} ,\,r = 1$, is selected based on a robust form of (50) as

$$ F_{{C_{1:N} }} \left( \gamma \right) = \Pr \left( {\max_{{i_{l} }} \left( {\gamma_{{i_{l} }} } \right) \le \gamma ,l_{1} \prec l_{2} \prec \ldots l_{N} } \right) = \sum\limits_{l = 1}^{N} {\sum\limits_{{\Im_{L} }} {\left( {\prod\limits_{s = 1}^{l} {F_{{\gamma_{{i_{s} }} }} \left( \gamma \right)} } \right)\left( {\prod\limits_{s = l + 1}^{N} {1 - F_{{\gamma_{{i_{s} }} }} \left( \gamma \right)} } \right)} } . $$

(51)

$where\;\sum\nolimits_{{{\Im }_{l} }} \triangleq \;represents\;the\;sum\;over\;all\;permutations\;\left( {i_{1} ,i_{2} ,i_{3} , \ldots i_{N} } \right)\;of\;\left( {1,2,3, \ldots N} \right)\;that\;includes\;\left( {\begin{array}{*{20}c} N \\ l \\ \end{array} } \right)\;terms\;instade\;of\;N!terms\;in\;\left( {50} \right),\,i_{1} < i_{2} \ldots i_{N} .$

3.2.2 Optimal Relay Selection in Statistical CSI Availability

In this subsection, we rely on the statistical data of the global CSI of all links where it is confirmed that the small and large scale computations of the channels’ characteristics do not vary drastically over a long period of time. Thus, it is sufficient to compute and test a specific performance metric such as the secrecy outage probability to decide which relay will be selected.

The secrecy outage probability is defined as the probability that the achievable secrecy rate (e.g., correspondingly SINR) falls below a desired secrecy rate (e.g., correspondingly a desired level).

Let the desired threshold levels $\gamma_{out1}$ and $\gamma_{out2}$ for the first and the second phases, respectively. The secrecy outage probability may be computed equivalently as

$$ \begin{aligned} & P_{{out_{i} }} = 1 - \underbrace {{\Pr \left( {\gamma_{i1}^{{}} \succ \gamma_{out1} ,\gamma_{i2}^{{}} \succ \gamma_{out2} } \right)}}_{\alpha } = 1 - \Pr \left( {\gamma_{i1}^{{}} \succ \gamma_{out1} } \right) \times \Pr \left( {\gamma_{i2}^{{}} \succ \gamma_{out2} } \right) \\ & = 1 - \left( {1 - \Pr \left( {\gamma_{i1}^{{}} \le \gamma_{out1} } \right)} \right)\left( {1 - \Pr \left( {\gamma_{i2}^{{}} \le \gamma_{out2} } \right)} \right) = 1 - \left( {\left( {1 - F_{{\gamma_{i1}^{{}} }} \left( {\gamma_{out1} } \right)} \right)\left( {1 - F_{{\gamma_{i2}^{{}} }} \left( {\gamma_{out2} } \right)} \right)} \right), \\ \end{aligned} $$

(52)

where $\alpha$ indicates the joint probability and the last two terms follow from the fact that they are two disjoint events.

Hence, the optimal relay selection can be formulated by selecting $R_{i}^{*}$ that minimizing the statistical secrecy outage probability by satisfying

$$ i^{*} = \arg \mathop {\hbox{min} }\limits_{i} P_{{out_{i} }} \left( \gamma \right). $$

(53)

In the next section, we are going to derive expressions for the secrecy outage probability and some other performance metrics such as non-zero achievable secrecy rate and asymptotic secrecy outage probability.

3.3 Performance Metrics

In the concerned system, one feasible method to ensure a confidential data security and reliability against eavesdropping is to transmit the data with a rate that is less than its dedicated channel capacity (i.e., from the source to destination) while maintain the difference between the transmitted and the confidential data rates larger than the channel capacity dedicated for the eavesdropping system. This guarantees that any transmitted data rate will become beyond the reliable illegal interception.

3.3.1 The Exact Secrecy Outage Probability

A special case of (52) when the communication channel requires one desired or predefined SINR level, $\gamma$. In such a case, $P_{{out_{i} }} \left( \gamma \right)$ of the ith relay is given by

$$ P_{{out_{i} }} \left( \gamma \right) = 1 - \Pr \left( {\hbox{min} \left( {\gamma_{i1}^{{}} ,\gamma_{i2}^{{}} } \right) \succ \gamma } \right) = F_{{\gamma_{i1}^{{}} }} \left( \gamma \right) + F_{{\gamma_{i2}^{{}} }} \left( \gamma \right) - F_{{\gamma_{i1}^{{}} }} \left( \gamma \right)F_{{\gamma_{i2}^{{}} }} \left( \gamma \right). $$

(54)

Unlike the relay selection scheme, closed form expressions for $P_{{out_{i} }} \left( \gamma \right)$ can be derived in terms of $\gamma_{i1}^{{}}$ and $\gamma_{i2}^{{}}$ as shown in the following theorems.

Let $\upgamma_{{{\text{i}}\upomega}} = \frac{{1 + {\raise0.7ex\hbox{${\frac{{Z_{{1,\upomega}} }}{{Z_{{2,\upomega}} }}}$} \!\mathord{\left/ {\vphantom {{\frac{{Z_{{1,\upomega}} }}{{Z_{{2,\upomega}} }}} {Z_{{4,\upomega}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Z_{{4,\upomega}} }$}}}}{{1 + {\raise0.7ex\hbox{${Z_{{3,\upomega}} }$} \!\mathord{\left/ {\vphantom {{Z_{{3,\upomega}} } {Z_{{4,\upomega}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Z_{{4,\upomega}} }$}}}}$, $\omega \in \left\{ {1,2} \right\}$, be the SINRs of the first and the second communication phases, then, we have the following cases.

Case 1: Maximum of the eavesdroppers:

Theorem 4

The CDF of the SINR $\upgamma_{{{\text{i}}\upomega}}$, $\upomega \in \left\{ {1,2} \right\}$, according to (28) can be derived statistically as

$$ F_{{\gamma_{i\omega } }} \left( \gamma \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne r \end{subarray} }^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\aleph_{j} \left( \gamma \right)} } + \left( { - 1} \right)^{r - 1} \ell_{r} \left( \gamma \right)} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\gamma - 1} = \left. {\tfrac{{\zeta_{\omega ,r} }}{\gamma }} \right|_{{r \in \left\{ {1,2, \ldots M} \right\}}} } \hfill \\ {\sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\aleph_{j} \left( \gamma \right)} } } \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

where

$$ \left\{ {\begin{array}{*{20}l} {\aleph_{j} \left( \sigma \right) = \exp \left( {\Omega_{{Z_{2,\omega } }} } \right)\left( {1 + \frac{{\tfrac{{\alpha_{j} }}{\sigma }\tfrac{{\Omega_{{Z_{4} ,\omega }} }}{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } - \tfrac{{\Omega_{{Z_{4} ,\omega }} }}{\sigma - 1}}}\left( {\exp \left( {\tfrac{{\alpha_{j} }}{\sigma }} \right)Ei\left( { - \tfrac{{\alpha_{j} }}{\sigma }} \right)} \right) - \frac{{\tfrac{{\zeta_{\omega ,j} }}{\sigma }\tfrac{\beta }{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } - \tfrac{{\Omega_{{Z_{4} ,\omega }} }}{\sigma - 1}}}\left( {\exp \left( {\tfrac{\beta }{\sigma - 1}} \right)Ei\left( { - \tfrac{\beta }{\sigma - 1}} \right)} \right)} \right)} \hfill \\ {\ell_{j} \left( \sigma \right) = 1 - \frac{{\Omega_{{Z_{2,\omega } }} }}{{\Omega_{{Z_{1,\omega } }} }}\lambda_{i} - \left( {\frac{{\Omega_{{Z_{2,\omega } }} }}{{\Omega_{{Z_{1,\omega } }} }}\lambda_{i} } \right)^{2} \exp \left( {\frac{{\Omega_{{Z_{2,\omega } }} }}{{\Omega_{{Z_{1} ,\omega }} }}\lambda_{i} } \right)Ei\left( { - \frac{{\Omega_{{Z_{2,\omega } }} }}{{\Omega_{{Z_{1,\omega } }} }}\lambda_{i} } \right),\lambda_{i} = \tfrac{{\zeta_{\omega ,j} }}{\sigma } = \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \hfill \\ \end{array} } \right. $$

(55)

where$\upzeta_{{1,{\text{j}}}} \in \left\{ {\upzeta_{{{\text{s}},{\text{j}}}} } \right\},\upzeta_{{2,{\text{j}}}} \in \left\{ {\upzeta_{{{\text{i}},{\text{j}}}} } \right\}$, $\upalpha_{\text{j}} = \frac{{\Omega_{{{\text{Z}}_{{2,\upomega}} }}\upzeta_{{\upomega,{\text{j}}}} }}{{\Omega_{{{\text{Z}}_{{1,\upomega}} }} }},\quad \forall {\text{j}} = 1, \ldots {\text{M}},\quad\upbeta = \frac{{\Omega_{{{\text{Z}}_{{2,\upomega}} }} \Omega_{{{\text{Z}}_{{4,\upomega}} }} }}{{\Omega_{{{\text{Z}}_{{1,\upomega}} }} }}$, $\left| {{ \arg }\left( {\frac{{ \Omega_{{{\text{Z}}_{{2,\upomega}} }} }}{{\Omega_{{{\text{Z}}_{{1,\upomega}} }} }}} \right)} \right| \le\uppi$and$\upgamma$is the SINR threshold.

Proof

Applying similar steps as Theorem 2, the CDF of the R.V. $\gamma_{i\omega }$ can be derived as follows

$$ F_{{\gamma_{i\omega } }} \left( \sigma \right) = \Pr \left( {\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }} \le \left( {\sigma Z_{3,\omega } + \left( {\sigma - 1} \right)Z_{4,\omega } } \right)} \right),\hbox{max} .of(eaves.). $$

(56)

First, we have to compute the CDF of $Z_{i\omega } = \frac{{Z_{1,\omega } }}{{Z_{2,\omega } }}$, which can be computed in a similar form as (21) using (22) as

$$ F_{{Z_{i\omega } }} \left( x \right) = \frac{{\Omega_{{Z_{1,\omega } }} x\exp \left( {\Omega_{{Z_{2,\omega } }} } \right)}}{{\Omega_{{Z_{1,\omega } }} x + \Omega_{{Z_{2,\omega } }} }}. $$

(57)

Then, it is necessary to compute the PDF of $Y_{i\omega } = \sigma Z_{3,\omega } + \left( {\sigma - 1} \right)Z_{4,\omega }$ in that case, in a similar way to (36)

$$ f_{{Y_{i\omega } }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\frac{{\tfrac{{\zeta_{\omega ,j} }}{\sigma }\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}} } \left( {\exp \left( { - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}x} \right) - \exp \left( { - \tfrac{{\zeta_{\omega ,j} }}{\sigma }x} \right)} \right)} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\zeta_{\omega ,j} }}{\sigma }\forall j \in \left\{ {1,2, \ldots M} \right\}} \hfill \\ {\lambda_{i}^{2} x\exp \left( { - \lambda_{i} x} \right)} \hfill & {for\;\lambda_{i} = \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{\omega ,j} }}{\sigma }} \right|_{j = 1,2, \ldots M} } \hfill \\ \end{array} } \right.. $$

(58)

Utilizing a similar integral as (38) (see [33, Eq. (3.353.5)]) and some algebraic manipulations the CDF of the R.V. $\gamma_{i\omega }$ can be derived in part as

$$ F_{{\gamma_{i\omega } }} \left( \sigma \right) = \left\{ {\begin{array}{*{20}l} \begin{aligned} \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\exp \left( {\varOmega_{{Z_{2,\omega } }} } \right)\left( 1 \right. + \frac{{\tfrac{{\alpha_{j} }}{\sigma }\tfrac{{\varOmega_{{Z_{4,\omega } }} }}{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } - \tfrac{{\varOmega_{{Z_{4,\omega } }} }}{\sigma - 1}}}} } \left( {\exp \left( {\tfrac{{\alpha_{j} }}{\sigma }} \right)Ei\left( { - \tfrac{{\alpha_{j} }}{\sigma }} \right)} \right) \hfill \\ - \frac{{\tfrac{{\zeta_{\omega ,j} }}{\sigma }\tfrac{\beta }{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } - \tfrac{{\varOmega_{{Z_{4,\omega } }} }}{\sigma - 1}}}\left. {\left( {\exp \left( {\tfrac{\beta }{\sigma - 1}} \right)Ei\left( { - \tfrac{\beta }{\sigma - 1}} \right)} \right)} \right) \hfill \\ \end{aligned} \hfill & {for\tfrac{{\varOmega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\zeta_{\omega ,j} }}{\sigma }\forall j \in \left\{ {1,2, \ldots M} \right\}} \hfill \\ {1 - \frac{{\varOmega_{{Z_{2,\omega } }} }}{{\varOmega_{{Z_{1,\omega } }} }}\lambda_{i} - \left( {\frac{{\varOmega_{{Z_{2,\omega } }} }}{{\varOmega_{{Z_{1,\omega } }} }}\lambda_{i} } \right)^{2} \exp \left( {\frac{{\varOmega_{{Z_{2,\omega } }} }}{{\varOmega_{{Z_{1,\omega } }} }}\lambda_{i} } \right)Ei\left( { - \frac{{\varOmega_{{Z_{2,\omega } }} }}{{\varOmega_{{Z_{1,\omega } }} }}\lambda_{i} } \right)} \hfill & {for\lambda_{i} = \tfrac{{\varOmega_{{Z_{4,\omega } }} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{\omega ,j} }}{\sigma }} \right|_{j = 1,2, \ldots M} } \hfill \\ \end{array} } \right. $$

(59)

and (55) follows after rearranging the terms.□

Case 2: Co-operative eavesdroppers:

Theorem 5

The CDF of the SINR$\gamma_{i\omega }$ (42), $\upomega \in \left\{ {1,2} \right\}$, can be derived statistically as

$$ F_{{\gamma_{i\omega } }} \left( \sigma \right) = \left\{ {\begin{array}{*{20}l} \begin{aligned} \frac{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \right)^{M} \exp \left( {\Omega_{{Z_{2,\omega } }} } \right)}}{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{M} }}\left( {1 + \tfrac{\beta }{\sigma - 1}\exp \left( {\tfrac{\beta }{\sigma - 1}} \right)Ei\left( { - \tfrac{\beta }{\sigma - 1}} \right) - \tfrac{\beta }{\sigma - 1}\sum\limits_{w = 0}^{M} {\tfrac{{\left( { - 1} \right)^{w} }}{w!}\left( {\alpha - \beta } \right)} } \right. \hfill \\ \left. {\left( {\exp \left( {\tfrac{\alpha }{\sigma }} \right)Ei\left( { - \tfrac{\alpha }{\sigma }} \right) + \sum\limits_{\delta = 0}^{w} {\left( { - 1} \right)^{\delta } \delta !\left( {\tfrac{\alpha }{\sigma }} \right)^{{ - \left( {\delta + 1} \right)}} } } \right)} \right) \hfill \\ \end{aligned} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\Omega_{{Z_{3} ,\omega }} }}{\sigma }} \hfill \\ {\frac{{\left( { - 1} \right)^{M} }}{M!}\left( {\Omega_{\alpha \beta } } \right)^{M + 1} \exp \left( {\Omega_{{Z_{2} }} } \right)\left( {\exp \left( {\Omega_{\alpha \beta } } \right)Ei\left( { - \Omega_{\alpha \beta } } \right) + \sum\limits_{w = 0}^{M} {\left( { - 1} \right)^{w} w!\left( {\Omega_{\alpha \beta } } \right)^{{ - \left( {w + 1} \right)}} } } \right)} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right. $$

(60)

Where$\Omega _{{{\text{Z}}_{3,1} }} \in \left\{ {\Omega _{\text{sJ}} \triangleq {\text{aver}}_{\text{j}} \left( {\Omega _{{{\text{s}},{\text{j}}}} } \right)} \right\}$, $\Omega _{{{\text{Z}}_{3,2} }} \in \left\{ {\Omega _{\text{iJ}} \triangleq {\text{aver}}_{\text{j}} \left( {\Omega _{{{\text{i}},{\text{j}}}} } \right)} \right\},\;\forall {\text{j}} = 1, \ldots {\text{M}}$, $\upalpha = \frac{{\Omega _{{{\text{Z}}_{{2,\upomega}} }}\Omega _{{{\text{Z}}_{{3,\upomega}} }} }}{{\Omega _{{{\text{Z}}_{{1,\upomega}} }} }}$, $\upbeta = \frac{{\Omega _{{{\text{Z}}_{{2,\upomega}} }}\Omega _{{{\text{Z}}_{{4,\upomega}} }} }}{{\Omega _{{{\text{Z}}_{{1,\upomega}} }} }}$, $\Omega _{{\upalpha \upbeta }} =\uplambda_{\text{i}} \frac{{\Omega _{{{\text{Z}}_{{2,\upomega}} }} }}{{\Omega _{{{\text{Z}}_{{1,\upomega}} }} }}$, $\left| {{ \arg }\left( {\frac{{ \Omega _{{{\text{Z}}_{{2,\upomega}} }} }}{{\Omega _{{{\text{Z}}_{{1,\upomega}} }} }}} \right)} \right| \le\uppi\;{\text{and}}\;\upsigma$is the SINR threshold.

Proof

Applying similar steps as Theorem 3, the CDF of the R.V. $\gamma_{i\omega }$ can be derived as follows

$$ F_{{\gamma_{i\omega } }} \left( \sigma \right) = \Pr \left( {\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }} \le \left( {\sigma Z_{3,\omega } + \left( {\sigma - 1} \right)Z_{4,\omega } } \right)} \right),Cooperative(eaves.). $$

(61)

The CDF of $Z_{i\omega } = \frac{{Z_{1,\omega } }}{{Z_{2,\omega } }}$ is given by (57). Then, the PDF of $Y_{i\omega } = \sigma Z_{3,\omega } + \left( {\sigma - 1} \right)Z_{4,\omega }$ in that case, which is directly given as (36) by

$$ f_{{Y_{i\omega } }} \left( x \right) = \left\{ {\begin{array}{*{20}l} \begin{aligned} \frac{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \right)^{M} \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{M} }}\left( {\exp \left( { - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}x} \right)} \right. \hfill \\ \left. { - \left( {\exp \left( { - \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }x} \right)\sum\limits_{\delta = 0}^{M - 1} {\tfrac{{x^{\delta } }}{\delta !}\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{\delta } } } \right)} \right) \hfill \\ \end{aligned} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \hfill \\ {\lambda_{i}^{M + 1} \frac{{x^{M} }}{M!}\exp \left( { - \lambda_{i} x} \right)} \hfill & {for\;\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right.. $$

(62)

Utilizing a similar integral as (38) (see [33, Eq. (3.353.5)]) and some algebraic manipulations the CDF of the R.V. $\gamma_{i\omega }$ or (60) follow after rearranging the terms.□

Hence, the secrecy outage probability can be expressed by substituting in (54) and its related form of the optimal relay selection which can be likely written without order statistics as

$$ P_{{out_{optimal} }} = \prod\limits_{i = 1}^{N} {P_{{out_{i} }} } . $$

(63)

3.3.2 The Non-zero Achievable Secrecy Rate

By employing the fact that $\forall \epsilon \in \Re , \left( {\log_{2} \epsilon } \right) > 0\mathop \to \limits^{yields} \epsilon > 1$, it is obtained from (56) and (61) by substituting for $\sigma = 1$ as in the following forms.

Let $P_{secrecy}$ be the optimal achievable non-zero secrecy probability which occurs when there exists a non-zero secrecy capacity for the secondary communication network, namely

$$ P_{secrecy} = \Pr \left( {C_{{i^{ * } }} \succ 0} \right) = \Pr \left( {\gamma_{{i^{ * } }} \succ 1} \right) = \prod\limits_{i = 1}^{N} {\left( {1 - P_{{out_{i} }} \left( 1 \right)} \right)} . $$

(64)

Where $i^{*}$ represents the optimal relay, by considering the cases of eavesdropping $P_{{out_{i} }} \left( 1 \right)$ can be determined as follows:

Case 1: Maximum of the eavesdroppers:

Plugging (33) and (57) into (56), solving for $\sigma = 1$ and using a similar integral as (36), $F_{{\gamma_{i\omega } }} \left( 1 \right)$ is given by,

$$ F_{{\gamma_{i\omega } }} \left( 1 \right) = \Pr \left( {\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }} \le Z_{3,\omega } } \right),\hbox{max} .of(eaves.) = 1 + \sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \prec \ldots l_{M} }} {\alpha_{j} \exp \left( {\alpha_{j} } \right)Ei\left( { - \alpha_{j} } \right)} } . $$

(65)

Where $\alpha_{j} = \frac{{\Omega _{{{\text{Z}}_{{2,\upomega}} }}\upzeta_{{\upomega,{\text{j}}}} }}{{\Omega _{{{\text{Z}}_{{1,\upomega}} }} }}, \forall j = 1, \ldots M\;and\;\left| {arg\left( {\frac{{ \Omega _{{Z_{{2,\upomega}} }} }}{{\Omega _{{Z_{{1,\upomega}} }} }}} \right)} \right| \le \pi$, by substituting in (54) for $\omega = 1\;{\text{or}}\;2$, $P_{{out_{i} }} \left( 1 \right)$ follows directly.

Case 2: Co-operative eavesdroppers:

Plugging (42) and (57) into (61), solving for $\sigma = 1$ and using a similar integral as (36), $F_{{\gamma_{i\omega } }} \left( 1 \right)$ is given by

$$ F_{{\gamma_{i\omega } }} \left( 1 \right) = \Pr \left( {\frac{{Z_{1,\omega } }}{{Z_{2,\omega } }} \le Z_{3,\omega } } \right),Cooperative(eaves.) = \frac{{\left( { - 1} \right)^{M - 1} \alpha^{M} }}{{\left( {M - 1} \right)!}}\exp \left( {\Omega_{{Z_{2,\omega } }} } \right)\left( {\exp \left( \alpha \right)Ei\left( { - \alpha } \right) + \sum\limits_{\delta = 1}^{M} {\tfrac{{\left( { - 1} \right)^{\delta } \left( {\delta - 1} \right)!}}{{\alpha^{\delta } }}} } \right). $$

(66)

Where $\left| {arg\left( {\frac{{ \Omega _{{Z_{2,\omega } }} }}{{\Omega _{{Z_{1,\omega } }} }}} \right)} \right| \le \pi$, by substituting in (54) for $\omega = 1\;{\text{or}}\;2$, $P_{{out_{i} }} \left( 1 \right)$ follows directly.

3.3.3 Inner and Outer System Bounds for the Secrecy Outage Probability

As a reference relay selection scheme, system bounds can be considered by assuming that the cooperative system can possess the buffering capability [37] at the relay nodes. Therefore, the cooperative system has the option to store data for the next phase and select the two relays of the strongest secrecy rates for the two phases yielding the lowest secrecy outage probability. Thus, we can define an inner (lower) bound for the secrecy outage probability when the minimum secrecy outage probability of a dual-hop communication itself for a certain selected relay is indeed the minimum outage amongst the entire relays, namely

$$ P_{out}^{\hbox{min} } = \Pr \left( {\max_{i} \left( {\hbox{max} \left( {\gamma_{i1} ,\gamma_{i2} } \right) \le \gamma } \right)} \right) = F_{{\gamma_{{i^{ * } }} }} \left( \gamma \right) = \prod\limits_{i = 1}^{N} {} \left( {F_{{\gamma_{i1} }} \left( \gamma \right)F_{{\gamma_{i2} }} \left( \gamma \right)} \right). $$

(67)

In contrary, the system outer (upper) bound is defined by

$$ P_{out}^{\hbox{max} } = \Pr \left( {\max_{i} \left( {P_{{out_{i} }} } \right) \le \gamma } \right) = 1 - \prod\limits_{i = 1}^{N} {\left( {1 - P_{{out_{i} }} } \right)} . $$

(68)

In this case, the maximum secrecy outage probability of a dual-hop communication itself for a certain selected relay is indeed the maximum outage amongst the entire relays.

3.4 The Asymptotic Outage Probability

Exact expressions are too complicated to interpret conceptually the impact of interference and eavesdropping for high SINR regime which represents the main agent that identifies and controls the network behavior. In the following, the effect of increasing the SINR statistically on all network parameters will be studied.

If the transmit SINR is abruptly increased toward the received nodes to enhance the system performance within the secondary network, the CDF of $Z_{1,\omega }$ can be approximated to its first order term, simply

$$ F_{{Z_{1,\omega } }} \left( x \right) = \Omega_{{Z_{1,\omega } }} x. $$

(69)

Upon this fact, let the other R.V. s be dependently unchanged, then, by applying similar statistical analysis the system asymptotic optimal secrecy outage probability can be expressed in a generalized form as

$$ P_{{out_{{i^{ * } }} }}^{\infty } = \left( {\kappa \times SINR_{system} } \right)^{ - \eta } . $$

(70)

Where the impact of diversity order (gain) $\eta$ will be emphasized here,⁵ (e.g., it can be enhanced by using relays with distinguishable parameters). The diversity gain can be defined as the negative exponent of the average symbol error probability SEP in a log–log scale when SINR goes to infinity [35, 36] and related to the secrecy outage probability by (70), $\kappa$ is the coding gain parameter, $i^{*}$ is the optimal relay and $SINR_{system}$ is the overall system SINR.

To investigate the impact of the diversity order, system high SINR and coding gain, $P_{{out_{{i^{*} }} }}^{\infty }$ should be computed and coincided with (70), then, by extracting comparative relations for $\kappa , SINR_{system} \;{\text{and}}\;\eta$, one can study a unified framework for the effect of those system communication metrics and build up relay selection strategies.

Accordingly, we have to compute $P_{{out_{i} }}^{\infty } \;{\text{of}}\;{\text{relay}}\;R_{i}$ in terms of the CDF of the corresponding SINR as in (54).

Theorem 6

By considering (70) the CDF of$\gamma_{i\omega }$may be generally derived as

$$ F_{{\gamma_{i\omega } }} \left( \gamma \right) = \varphi_{i\omega } \gamma . $$

(71)

Where $\phi_{i\omega }$ is expressed as follows:

Case of max. of eavesdroppers

$$ \varphi_{i\omega } = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne r \end{subarray} }^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\varXi_{j} } } + \left( { - 1} \right)^{r - 1} \varTheta_{r} } \hfill & {for\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{\omega ,r} }}{\sigma }} \right|_{{r \in \left\{ {1,2, \ldots M} \right\}}} } \hfill \\ {\sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\varXi_{j} } } } \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

where

$$ \left\{ {\begin{array}{*{20}l} {\varXi_{j} \left( \sigma \right) = \frac{{\Omega_{{Z_{1,\omega } }} }}{{\Omega_{{Z_{2,\omega } }} }}\exp \left( {\Omega_{{Z_{2,\omega } }} } \right)\sum\limits_{j = 1}^{M} {\left( { - 1} \right)^{j - 1} \sum\limits_{{l_{1} \prec l_{2} \ldots l_{M} }} {\frac{{\tfrac{{\zeta_{\omega ,j} }}{\sigma } + \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}{{\tfrac{{\zeta_{\omega ,j} }}{\sigma }\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}} } } \hfill & {for\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\zeta_{\omega ,j} }}{\sigma }\forall j \in \left\{ {1,2, \ldots M} \right\}} \hfill \\ {\varTheta_{j} \left( \sigma \right) = \frac{{2\Omega_{{Z_{1,\omega } }} }}{{\lambda_{i} \Omega_{{Z_{2,\omega } }} }}\exp \left( {\Omega_{{Z_{2,\omega } }} } \right)} \hfill & {for\lambda_{i} = \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \left. {\tfrac{{\zeta_{\omega ,j} }}{\sigma }} \right|_{j = 1,2, \ldots M} } \hfill \\ \end{array} } \right.. $$

(72)

Case of cooperative eavesdroppers

$$ \phi_{i\omega } = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \right)^{M} \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}}}{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{M} }}\left( {\frac{1}{{\left( {\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{2} }} - \left( {\sum\limits_{\delta = 0}^{M - 1} {\frac{{\left( {\delta + 1} \right)}}{{\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \right)^{\delta + 2} }}\left( {\tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } - \tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1}} \right)^{\delta } } } \right)} \right)} \hfill & {for\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} \ne \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma }} \hfill \\ {\frac{{\left( {M + 1} \right)\Omega_{{Z_{1,\omega } }} }}{{\lambda_{i} \Omega_{{Z_{2,\omega } }} }}\exp \left( {\Omega_{{Z_{2,\omega } }} } \right)} \hfill & {for\tfrac{{\Omega_{{Z_{4,\omega } }} }}{\sigma - 1} = \tfrac{{\Omega_{{Z_{3,\omega } }} }}{\sigma } = \lambda_{i} } \hfill \\ \end{array} } \right. $$

(73)

Proof

From (70), the CDF of $Z_{i\omega } = \frac{{Z_{1,\omega } }}{{Z_{2,\omega } }}$ is given easily by

$$ F_{{Z_{iw} }} \left( x \right) = \frac{{\Omega_{{Z_{1,\omega } }} \exp \left( {\Omega_{{Z_{2,\omega } }} } \right)}}{{\Omega_{{Z_{2,\omega } }} }}x. $$

(74)

The CDF of the R.V. $\gamma_{i\omega }$ which is given by (56) and (61) of the considerable cases can be derived here after computing the PDF of $Y_{i\omega }$ in these cases, which are directly given by (58) and (62), respectively.

Applying similar steps as the above theorems, after utilizing a similar integral as (38) (see [33, Eq. (3.351.1–3)]), some algebraic manipulations and rearranging the terms, the CDF of the R.V. $\gamma_{i\omega }$ (71) follows.□

Therefore, $P_{{out_{i} }}^{\infty } of relay R_{i}$ can be expressed by substituting in (54) which leads to

$$ P_{{out_{i} }}^{\infty } = \phi_{i1} \gamma + \phi_{i2} \gamma - \phi_{i1} \phi_{i2} \gamma^{2} , $$

(75)

By inserting (75) into a similar form of (51), it can be found that it perfectly matches (70) to the extent of

$$ P_{{out_{{r^{ * } :N}} }}^{\infty } \left( \gamma \right) = \sum\limits_{l = r}^{N} {\sum\limits_{{\Im_{L} }} {\left( {\prod\limits_{s = 1}^{l} {P_{{out_{{i_{s} }} }} \left( \gamma \right)} } \right)\left( {\prod\limits_{s = l + 1}^{N} {1 - P_{{out_{{i_{s} }} }} \left( \gamma \right)} } \right)\mathop = \limits^{\left( a \right)} } } \left( {C\gamma } \right)^{N - r + 1} + {\rm O}\left( \gamma \right). $$

(76)

Where $P_{{out_{{r^{*} :N}} }}^{\infty }$ represents the asymptotic secrecy outage probability of optimal rth out of $N$ relays, C is an arbitrary constant, $C \triangleq f\left( {\phi_{i1} ,\phi_{i2} } \right),{\rm O}\left( \gamma \right)$ are the higher order terms of $\gamma$ and (a): follows after algebraic manipulations, equating powers and inserting

$$ \begin{aligned} & \prod\limits_{s = l + 1}^{M} {\left( {1 - P_{{outi_{s} }} } \right)} = 1 + \sum\limits_{s = l + 1}^{M} {\left( { - 1} \right)^{s} \sum\limits_{{l_{1} \prec l_{2} \prec \ldots l_{M} }} {\prod\limits_{k = 1}^{s} {P_{{outi_{{l_{k} }} }} } } } \\ & where\;\sum\limits_{{l_{1} \prec l_{2} \prec \ldots l_{M} }} {} \equiv \sum\limits_{{l_{1} = 1}}^{M - j + 1} {\sum\limits_{{l_{2} = l_{1} + 1}}^{M - j + 2} { \cdots \sum\limits_{{l_{j} = l_{j - 1} + 1}}^{M} {} } } . \\ \end{aligned} $$

(77)

The diversity order of the system can be extracted by equating lowest order exponent of SINR to (70), this shows that the achievable diversity can be of the order of $N - r + 1$.

4 Simulation Results

In this section, the analytical derivations are verified to be in consistent with simulation results as well as the impact of the system parameters on the security performance will be studied. This is confirmed by performing Monte Carlo simulations with $10^{6}$ experimental trials.

From the previous analysis, one can find that the impact of relay interference is more severe with respect to the primary network than the source and destination and consequently, it dominates. However, we are interested in the impact of diversity gain that can be enhanced to approach $N,N \triangleq number\;of\;relays,$ in optimal relay selection. In general, the simulation is carried assuming equal values of fading coefficients ($\Omega_{q,r} = \Omega = 0.3\;{\text{dB}},q,r \in \left\{ {s,i,p, j, d} \right\}$).

Figure 2 illustrates the exact curves between the outage probability and a relay transmit power while fixing the source power, i.e., relay transmitters are the dominant interfere sources of power, with different number of co-operative relays. This figure indicates a local minimum value of outage which represents the optimal value of the relay power for security interference trade off. This value can be verified by plugging the inequality of arithmetic and geometric means together, i.e., $\prod\nolimits_{i = 1}^{N} {P_{{out_{i} }} \le \left( {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {P_{{out_{i} }} } } \right)^{N} }$, into (63) and solving for the equality. This figure also compares our exposed eavesdropping models. It is obvious that the co-operative eavesdropping scheme exhibits worse performance than the maximum of eavesdroppers scheme due to its robust overhearing procedure. Increasing the number of relays adds a quite degree of freedom that improves the system performance.

Fig. 2

Outage probability versus relay transmit power for target secrecy rate of 0.8, with N = 1, 2, 10

For low transmitted power the outage probability begins to deteriorate until it reaches its minimum value, then, it again begins to increase by increasing the transmitted power due to primary network constraints.

In Fig. 3 a statistical CSI knowledge about the primary network i.e., $\Omega _{p,i} ,\Omega _{i,p} ,\Omega _{s,p} \;{\text{and}}\;\Omega _{p,d}$ is considered where constraint sources of power are maintained. The performance of the secrecy outage probability against the increasing in SINR is highlighted, i.e., when $\Omega _{s,i} =\Omega _{i,d}$. Moreover, the impact of increasing the number of relays, the inner and outer bounds are included in this figure. It is cleared that case of the maximum of eavesdroppers scheme outperforms the case of co-operative eavesdropping scheme. It is notable that the outage probability drops down when the SINR increases. The asymptotic responses and bounds approximate the exact ones to the extent that asymptotic, outer bound and exact curves are tightly compromised at high SINR. Finally, parallel slops for different values of $N,N \triangleq number\;of\;relays$, reflect the equality of the diversity gain.⁶ There exists a successful agreement between the theoretical and simulation results which justifies our derivations.

Fig. 3

Secrecy Outage probability versus SINR for relaxed target secrecy rate of 0.5

In Fig. 4, it is anticipated that the secrecy outage probability increases when moving towards the decreased order statistics of the optimal relay selection, i.e., towards the optimal rth order relay selection, given the number of active relays in the co-operative relay system. It is also worthwhile to see that the asymptotic curve exhibits wider divergence from the exact curve at low SINR, when higher order statistics relay is selected. This verifies the impact of diversity order on the system performance. However, at high SINR the asymptotic curve perfectly fits the exact one. Moreover, it is evident that the asymptotic curve is plotted using (76) by substituting $C \triangleq f\left( {\gamma_{i1} ,\gamma_{i2} } \right) = \gamma_{i1} + \gamma_{i2}$ and neglecting the higher order terms.

Fig. 4

Secrecy Outage Probability versus average SINR

An illustration for the maximum achievable secrecy rate versus the average SINR ($\Omega_{s,i} = \Omega_{i,d} = \Omega$) is shown in Fig. 5. Using the proposed optimal selection and constraint power sources, one can observe that there is a limited maximum capacity values “upper floor” [25] after which the secrecy rate will collapse unless the constraints are preserved. This means that at high SINR the secrecy rate is approximately fixed.

Fig. 5

Achievable capacity versus average SINR

As depicted in Fig. 6, the secrecy rate decreases when the overhearing nodes “$M$” increase. With a target rate of the secondary network of 0.5 bits/s/Hz, $P_{Tx}$ power of 6 dB and $S$ power of 2 dB, it can be shown that, increasing the number of eavesdroppers causes significant degradation in the secrecy rate. For $M \gg 1$, the performance curve over the co-operative eavesdropping scheme or the maximum of eavesdroppers scheme is asymptotically the same.

Fig. 6

The impact of the number of eavesdroppers on the secrecy rate

For a selected optimal relay $i^{*}$, our results are compared with [38, Fig. 3] where we use the same system parameters, i.e., the channel coefficients are modeled as $\Omega_{q,r} = \left( {\frac{1}{{d_{q,r} }}} \right)^{\updelta}$,  = 3, where is the path loss exponent and $d_{q,r}$ is the distance between the node and the node . Thus, the following parameters are assumed: $d_{{s,i^{*} }} = d_{{i^{*} ,d}} = 1$, $d_{s,J} = d_{s,p} = d_{{i^{*} ,p}} = 6$, $d_{{i^{*} ,J}} = 4$, $P = \vartheta P_{p}$; where $0 \le \vartheta < 1$ is an arbitrary constant, $N_{0} = 1$ and a target secrecy rate of 0.5 bits/s/Hz. The secrecy outage probability is plotted against the secondary constraint power $\frac{P}{{\left| {h_{s,p} } \right|^{2} }}$ as shown in Fig. 7, where for the comparison we consider MRC at the eavesdropping system (e.g., as in [38] and our cooperative eavesdropper scheme with two eavesdroppers). Different from the results in [38], it is observed that the relaxation of the constraint power by increasing the $P_{Tx}$ transmit power can cause severe interference at the secondary networks. In [38], the secrecy outage first decreases with increase in the constraint power and later exhibits a floor because of increasing in parallel the ability of overhearing by the eavesdropping system. However, in our case, the interference of the primary network increases significantly the secrecy outage probability.

Fig. 7

The impact of increasing the constraint power P on the secrecy outage probability

5 Conclusions

In this paper, relay selection schemes have been proposed and investigated to maintain secure communications in relay assisted underlay cognitive radio networks in the presence of multiple eavesdroppers. To evaluate the system performance, some important metrics have been computed such as secrecy outage probability and achievable secrecy rate to give an account on security and reliability trade-off parameters. Analytical expressions have been derived upon the exposed model to verify the impact of mutual interferences, sources of power and target rates of both the primary and the secondary networks in order to optimize the communication quality. Some system bounds have also been derived where the impact of their tightness at high SINR was demonstrated. Co-operative diversity adds another degree of freedom especially when the instantaneous CSI of the eavesdroppers is known. It is worth mentioning that the dual-hop secrecy optimization has replaced the per-hop one in order to jointly enhance the secrecy performance via exploiting the diversity gain. Simulation results were in accordance with the analytical ones. In the future work, we will examine the situation when the eavesdropping system realizes the same benefit of diversity order.