1 Introduction

Privacy and security issues caused by the broadcast nature of wireless media have attracted considerable attention. Conventionally, confidential messages are protected by using a key, as was introduced by Shannon [1], or by using cryptographic methods [2]. More recently, physical layer security (PLS) was proposed by Whyner with the basic idea that secure communication is guaranteed if the eavesdropper channel is a degraded version of the main channel [3]. PLS has been considered in Gaussian wiretap channels [4] and has also been extended to broadcast channels [5], fading channels [6], and in the presence of an eavesdropper in the communication between two legitimate users [7, 8].

To combat multipath fading in wireless communication, cooperative communication is an effective solution that increases the diversity capacity [9, 10]. Decode-and-forward (DF) and amplify-and-forward (AF) are the two main strategies applied at relay nodes in cooperative networks. In DF mode, the relay node detects information from the received signal and then re-encodes and forwards it in the following hop. In AF mode, the relay only amplifies the received signal and forwards it; this is simpler than DF but has the drawback that it contains additional noise.

To deal with attack from an eavesdropper, numerous studies have focused on PLS in cooperative communication (e.g., [11,12,13,14,15] and the references therein). In [11], three relay strategies [AF, DF, and cooperative jamming (CJ)] were employed to improve the security of wireless communications. In [12], the exact and asymptotic ergodic secrecy rate was studied in cooperative single-carrier systems under the affecting by multiple eavesdroppers. The authors in [13] investigate two best relay and user pair selection strategies to enhance the physical layer security of a multiuser cooperative relaying network in term of the secrecy outage probability (SOP). In [14], the authors design relay beamforming weights to enhance the secrecy rate under total and individual power constraint for relaying network. In [15], the authors proposed two user and relay pair selection criterions for multi-user multi-relay networks under considering the communication between multi-user and the base station is assisted by direct links and by multi-relay.

Cognitive radio has considered as an efficient technique to improve the spectrum efficiency in wireless communication systems [16]. It allows secondary users to access the spectrum bands of primary users without interfering with primary users communications by intelligently sensing to the environment. In the underlay mode of cognitive radio, secondary users transmit simultaneously with primary users over the same spectrum without degrading the quality of the primary transmission by keeping the interference to the primary users under a predefined threshold [17]. In [18], the authors investigate the performance of cognitive multi-hop DF and AF relay networks over independent but not necessarily identically distributed (i.n.i.d) Rayleigh fading channels. In [19], the optimal power allocation and relay selection strategies are proposed to enhance the transmission quality between source and destination in both dual-hop and multi-hop scenarios. Some relay-selection schemes [20] as well as assistance from a cooperative friendly jammer [21] have been shown to enhance the secrecy outage performance in cooperative cognitive radio networks.

To the best of our knowledge, there have been no studies investigating the effect of an active eavesdropper in cognitive radio networks under wiretapping by eavesdroppers. Therefore, we were motivated to analyze the exact secrecy outage probability of secure communication conducted via underlay cognitive relaying networks. In this model, we consider the communication between a secondary source and a secondary destination by means of assistance from multiple intermediate secondary relays (taking place in the presence of multiple primary users and eavesdroppers). To allow for performance evaluation and comparison, exact expressions are derived for the secrecy outage probability of four partial relay selection schemes. Four relay selection schemes are presented in order to select the one with the best relay to decode the information from the received signal and forward it to the destination: 1) a scheme for maximizing the channel gain from the source to the relays (MaSR), 2) a scheme for minimizing the channel gain from the relays to the primary users (MiRP), 3) a scheme for minimizing the channel gain from the relays to the eavesdroppers (MiRE), and 4) the optimal relay selection (ORS). Monte Carlo simulations are used to verify our theoretical analysis.

The rest of the paper is organized as follows. Section 2 presents the system model. Section 3 presents the secrecy outage probability analyses for the four schemes that were studied. Section 4 presents the numerical results from the simulations and theoretical analyses. Finally, Section 5 presents our conclusions.

Notation The functions \({f_X}\left( . \right)\) and \({F_X}\left( . \right)\) present the probability density function (PDF) and cumulative distribution function (CDF) of RV X. \({\left[ x \right] ^ + }\) returns x if \(x \ge 0\) and 0 if \(x < 0\). \(\mathcal {E}\left\{ . \right\}\) denotes mathematical expectation. \(\Pr [.]\) returns the probability. \(C_b^a = \frac{{b!}}{{a!\left( {b - a} \right) !}}\). The function \(\Gamma \left( {x,y} \right)\) is an incomplete Gamma function [22, Eq. (8.350.2)]. The function \(_2{F_1}\left( . \right)\) represents Gausss hypergeometric function [22].

2 System Model and the Principle Operation of Three Protocols

Fig. 1
figure 1

System model

Full size image

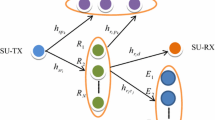
As shown in Fig. 1, we consider a dual-hop spectrum sharing network under physical layer security. This consists of a secondary source (S), a secondary destination (D), N secondary relays (\({R_n}\), \(n \in \left\{ {1,2,\ldots ,N} \right\}\), where \({R_n}\) indicates the nth relay node among N relays located in a cluster), a primary receiver (P), and an eavesdropper (E). In the network, all nodes are equipped with a single antenna operating in a half-duplex mode [15]. We assume that the primary transmitter is far enough away from the secondary receiver such that interference to the secondary receivers (i.e., \({R_n}\), D, and E) can be ignored. We denote \(\left( {{h_{1n}},{d_{1n}}} \right)\), \(\left( {{h_{2n}},{d_{2n}}} \right)\), \(\left( {{h_3},{d_3}} \right)\), \(\left( {{h_{4n}},{d_{4n}}} \right)\), \(\left( {{h_5},{d_5}} \right)\), and \(\left( {{h_{6n}},{d_{6n}}} \right)\) as the Rayleigh fading channel coefficients and distances of the links \(S - {R_n}\), \({R_n} - D\), \(S - E\), \({R_n} - E\), \(S - PR\), and \({R_n} - PR\), respectively. Thus, the corresponding channels \({g_\Omega } = {\left| {{h_\Omega }} \right| ^2}\), with \(\Omega \in \left\{ {1n,2n,3,4n,5,6n} \right\}\), are exponentially distributed independent random variables (RVs) with parameters \({\lambda _\Omega } = {\left( {{d_\Omega }} \right) ^\beta }\), where \(\beta\) denotes the path loss exponent (typically between 2 and 6). The corresponding cumulative distribution functions (CDFs) and probability density functions (PDFs) of the RVs \({g_\Omega }\) are expressed as \({F_{{g_\Omega }}}\left( x \right) = {\lambda _\Omega }{e^{ - {\lambda _\Omega }x}}\) and \({f_{{g_\Omega }}}\left( x \right) = 1 - {e^{ - {\lambda _\Omega }x}}\), respectively. The distances between two relay nodes in a cluster are insignificant compared to the distances between a relay node in a cluster and a node outside. Thus, we denote \({d_{\Phi n}} = {d_\Phi }\) and \({\lambda _{\Phi n}} = {\lambda _\Phi }\) with \(\Phi \in \left\{ {1,2,4,6} \right\}\). Let us assume that there is no direct link from to (due to deep shadowing). Additionally, the global channel state information (CSI) is assumed to be available [11].

In this underlay network, the secondary transmitters S and \({R_n}\) are adapted from their transmit powers as \({P_S}\) and \({P_R}\), respectively, such that the interference caused at the PR does not exceed the maximum allowable interference power limit I.

$$\begin{aligned} {P_S} = \frac{I}{{{{\left| {{h_5}} \right| }^2}}} = \frac{I}{{{g_5}}}\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{P_{{R_n}}} = \frac{I}{{{{\left| {{h_{6n}}} \right| }^2}}} = \frac{I}{{{g_{6n}}}} \end{aligned}$$
(1)

There are two phases of total communication. In the first phase, S broadcasts its signal \(x\left( t \right)\), with \(\mathcal {E}\left\{ {{{\left| {x\left( t \right) } \right| }^2}} \right\} = 1\), by the transmit power \({P_S}\) to all relays under the overhearing of an eavesdropper. The best relay (\({R_b}\)), which was selected from available relay nodes [from the four relay selection schemes presented in Eqs. (14), (19), (23), and (28)], decodes the information from the received signal. Based on this, the received instantaneous signal-to-noise ratios (SNRs) at \({R_b}\) and E are given by:

$$\begin{aligned} {\gamma _{S{R_b}}} = \frac{{{P_S}}}{{{N_0}}}{\left| {{h_{1b}}} \right| ^2} = \gamma \frac{{{g_{1b}}}}{{{g_5}}}\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\gamma _{SE}} = \frac{{{P_S}}}{{{N_0}}}{\left| {{h_3}} \right| ^2} = \gamma \frac{{{g_3}}}{{{g_5}}} \end{aligned}$$
(2)

where, \({N_0}\) is the noise variance at all receivers, and we denote \(\gamma \buildrel \Delta \over = \frac{I}{{{N_0}}}\).

The secrecy capacity for the first hop is defined as follows:

$$\begin{aligned} {\psi _{1b}} = {\left[ {{\psi _{S{R_b}}} - {\psi _{SE}}} \right] ^ + } = {\left[ {\frac{1}{2}{{\log }_2}\left( {\frac{{1 + {\gamma _{S{R_b}}}}}{{1 + {\gamma _{SE}}}}} \right) } \right] ^ + } \end{aligned}$$
(3)

where \({\psi _{S{R_b}}} = \frac{1}{2}{\log _2}\left( {1 + {\gamma _{S{R_b}}}} \right)\) and \({\psi _{SE}} = \frac{1}{2}{\log _2}\left( {1 + {\gamma _{SE}}} \right)\) denote the capacity of the links \(S - {R_b}\) and \(S - E\), respectively.

In the second phase, after successful decoding, \({R_b}\) re-encodes and forwards the signal to D with the transmit power \({P_{Rb}}\) under the eavesdropping of E. The received instantaneous SNRs at D and E in this phase are expressed as:

$$\begin{aligned} {\gamma _{{R_b}D}} = \frac{{{P_{{R_b}}}}}{{{N_0}}}{\left| {{h_{2b}}} \right| ^2} = \gamma \frac{{{g_{2b}}}}{{{g_{6b}}}}\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\gamma _{{R_b}E}} = \frac{{{P_{{R_b}}}}}{{{N_0}}}{\left| {{h_{4b}}} \right| ^2} = \gamma \frac{{{g_{4b}}}}{{{g_{6b}}}} \end{aligned}$$
(4)

The capacity of the link \({R_b} - D\) is given as \({\psi _{{R_b}D}} = \frac{1}{2}{\log _2}\left( {1 + {\gamma _{{R_b}D}}} \right)\). Since eavesdropper E receives two independent copies of the source signal, the worst case is considered, i.e., E adopts the MRC scheme: \({\gamma _E} = {\gamma _{SE}} + {\gamma _{{R_b}E}}\). Additionally, the capacity at \({\psi _E} = \frac{1}{2}{\log _2}\left( {1 + {\gamma _E}} \right)\) is expressed as . Therefore, the secrecy capacity for this second hop can be obtained as:

$$\begin{aligned} {\psi _{2b}} = {\left[ {{\psi _{{R_b}D}} - {\psi _E}} \right] ^ + } = {\left[ {\frac{1}{2}{{\log }_2}\left( {\frac{{1 + {\gamma _{{R_b}D}}}}{{1 + {\gamma _{SE}} + {\gamma _{{R_b}E}}}}} \right) } \right] ^ + } \end{aligned}$$
(5)

3 Secrecy Outage Probability Analyses

In this section, we analyze the secrecy outage probability of four relay selection schemes. The best relay is selected to have the maximum channel gain to S (MaSR) and to D (MaRD), the minimum channel gain to E (MiRE), or the optimal relay selection criteria (ORS). The exact SOP expressions are derived without using the assumption of a high SNR (as was done in previous works). The SOP is defined as the probability that the secrecy capacity \({\psi _s} = \min \left( {{\psi _{1b}},{\psi _{2b}}} \right)\) will be less than the desired threshold secrecy rate \({\psi _{th}}\). By denoting \({X_3} \buildrel \Delta \over = {g_3}\) and \({X_5} \buildrel \Delta \over = {g_5}\), the SOP can be given by:

$$\begin{aligned} {P_{out}} = \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {{F_{{\psi _s}}}\left( {{\psi _t}} \right) {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5} \end{aligned}$$
(6)

The term \({F_{{\psi _s}}}\left( {{\psi _t}} \right)\) is computed by:

$$\begin{aligned} {F_{{\psi _s}}}\left( {{\psi _t}} \right)= & {} \Pr \left\{ {\min \left[ {\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{1b}}}}{{{X_5}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}}}}} \right) ,\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{2b}}}}{{{g_{6b}}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}} + \gamma \frac{{{g_{4b}}}}{{{g_{6b}}}}}}} \right) } \right] < {\psi _{th}}} \right\} \nonumber \\= & {} 1 - \Pr \left[ {\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{1b}}}}{{{X_5}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}}}}} \right) \ge {\psi _{th}},\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{2b}}}}{{{g_{6b}}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}} + \gamma \frac{{{g_{4b}}}}{{{g_{6b}}}}}}} \right) \ge {\psi _{th}}} \right] \nonumber \\= & {} 1 - \Pr \left[ {{g_{1b}} \ge \frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3},{g_{2b}} \ge \left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {g_{6b}} + \theta {g_{4b}}} \right] \nonumber \\= & {} 1 - \int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) \int _0^\infty {{f_{{g_{6b}}}}\left( {{x_6}} \right) \int _0^\infty {{f_{{g_{4b}}}}\left( {{x_4}} \right) \int _{\left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {x_6} + \theta {x_4}}^\infty {{f_{{g_{2b}}}}\left( {{x_2}} \right) } } } } d{x_2}d{x_4}d{x_6}d{x_1} \end{aligned}$$
(7)

where \(\theta \buildrel \Delta \over = {2^{2{\psi _{th}}}}\). The next five subsections present the SOP derivations for the case of single-relay and four-relay selection schemes.

3.1 Single Relay

We first consider the system model with one relay, i.e., \(N = 1\). Thus, there is no relay selection scheme. The PDFs of RVs \({g_{1b}}\), \({g_{2b}}\), \({g_{4b}}\), and \({g_{6b}}\) are expressed by \({f_{{g_{1b}}}}\left( {{x_1}} \right) = {\lambda _1}{e^{ - {\lambda _1}{x_1}}}\), \({f_{{g_{2b}}}}\left( {{x_2}} \right) = {\lambda _2}{e^{ - {\lambda _2}{x_2}}}\), \({f_{{g_{4b}}}}\left( {{x_4}} \right) = {\lambda _4}{e^{ - {\lambda _4}{x_4}}}\), and \({f_{{g_{6b}}}}\left( {{x_6}} \right) = {\lambda _6}{e^{ - {\lambda _6}{x_6}}}\), respectively. Substituting these PDFs into (7), we obtain:

$$\begin{aligned} {F_{{\psi _s}}}\left( {{\psi _t}} \right)= & {} 1 - \int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) } \int _0^\infty {{f_{{g_{6b}}}}\left( {{x_6}} \right) } {e^{ - {\lambda _2}\left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {x_6}}}\nonumber \\&\quad \int _0^\infty {{f_{{g_{4b}}}}\left( {{x_4}} \right) } {e^{ - {\lambda _2}\theta {x_4}}}d{x_4}d{x_6}d{x_1}\nonumber \\= & {} 1 - \frac{{{\lambda _4}}}{{{\lambda _4} + {\lambda _2}\theta }}\frac{{{\lambda _6}}}{{{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}}}\int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) } d{x_1}\nonumber \\= & {} 1 - \frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\theta {X_3}}} \end{aligned}$$
(8)

Then, the SOP for this case is expressed by:

$$\begin{aligned} P_{out}^{\mathrm{{1}}\,\mathrm{{relay}}}= & {} \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {\left[ {1 - \frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{x_5}}}{e^{ - {\lambda _1}\theta {x_3}}}} \right] {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5}\nonumber \\= & {} 1 - \frac{{{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{{\lambda _4} + {\lambda _2}\theta }}\int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \underbrace{\int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}}_{{I_1}}d{x_5} \end{aligned}$$
(9)

Lemma 1

The following expression is valid for the integral \({I_1}\).

$$\begin{aligned} {I_1} = \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3} = \frac{{{x_5}}}{{{\lambda _2}\theta }}{e^{{\omega _1}{x_5}}}\Gamma \left( {0,{\omega _1}{x_5}} \right) \end{aligned}$$
(10)

where

$$\begin{aligned} {\omega _1} \buildrel \Delta \over = \left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\theta }}} \right) \end{aligned}$$

Proof

Given in “Appendix 1”. \(\square\)

Using Eq. (6.455.1) of [22]: \(\int _0^\infty {{x^{\mu - 1}}{e^{ - \beta x}}\Gamma \left( {v,\alpha x} \right) dx} = \frac{{{\alpha ^v}\Gamma \left( {\mu + v} \right) }}{{\mu {{\left( {\alpha + \beta } \right) }^{\mu + v}}}}{\,_2}{F_1}\left( {1,\mu + v;\mu + 1;\frac{\beta }{{\alpha + \beta }}} \right)\) with \(\mu = 2\), \(\beta = {\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma } - {\omega _1}\), \(v = 0\), and \(\alpha = {\omega _1}\), we obtain:

$$\begin{aligned}&\int _0^\infty {{x_5}} {e^{ - \left[ {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma } - {\omega _1}} \right] {x_5}}}\Gamma \left( {0,{\omega _1}{x_5}} \right) d{x_5}\nonumber \\&\qquad = \frac{1}{{2{{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;\frac{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma } - {\omega _1}}}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(11)

Combining (10) and (11), we have:

$$\begin{aligned}&\int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}d{x_5}\nonumber \\&\qquad = \frac{1}{{{\lambda _2}\theta }}\frac{1}{{2{{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(12)

Substituting (12) into (9), the exact expression for the SOP with a single relay is given by:

$$\begin{aligned} P_{out}^{\mathrm{{1}}\,\mathrm{{relay}}} = 1 - \frac{{{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{2{\lambda _2}\theta \left( {{\lambda _4} + {\lambda _2}\theta } \right) {{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(13)

3.2 The MaSR Scheme

This subsection considered the MaSR relay selection scheme is applied. This is formulated by:

$$\begin{aligned} {R_b} = \arg \mathop {\max }\limits _{n = 1,2,\ldots ,N} {g_{1n}} \end{aligned}$$
(14)

The CDF of RV \({g_{1b}}\) is different compared to what was shown in Sect. 3.1; the new value is given by:

$$\begin{aligned} {F_{{g_{1b}}}}\left( {{x_1}} \right)= & {} \Pr \left[ {{g_{1b}}< {x_1}} \right] = \Pr \left[ {\mathop {\max }\limits _{n = 1,2,\ldots ,N} {g_{1n}}< {x_1}} \right] \nonumber \\= & {} \prod \limits _{n = 1}^N {\Pr \left[ {{g_{1n}} < {x_1}} \right] } = {\left( {1 - {e^{ - {\lambda _1}{x_1}}}} \right) ^N} \end{aligned}$$
(15)

Taking the derivative of \({F_{{g_{1b}}}}\) with respect to \({x_1}\), we obtain the PDF of RV \({g_{1b}}\):

$$\begin{aligned} {f_{{g_{1b}}}}\left( {{x_1}} \right) = N{\lambda _1}{e^{ - {\lambda _1}{x_1}}}{\left( {1 - {e^{ - {\lambda _1}{x_1}}}} \right) ^{N - 1}} = N{\lambda _1}\sum \limits _{n = 0}^{N - 1} {C_{N - 1}^n{{\left( { - 1} \right) }^n}{e^{ - {\lambda _1}\left( {n + 1} \right) {x_1}}}} \end{aligned}$$
(16)

Substituting the PDFs \({f_{{g_{1b}}}}\left( {{x_1}} \right)\), \({f_{{g_{2b}}}}\left( {{x_2}} \right)\), \({f_{{g_{4b}}}}\left( {{x_4}} \right)\), and \({f_{{g_{6b}}}}\left( {{x_6}} \right)\) into (7), we obtain the term \({F_{{\psi _s}}}\left( {{\psi _t}} \right)\) for this protocol after some mathematical manipulations as

$$\begin{aligned} {F_{{\psi _s}}}\left( {{\psi _t}} \right)= & {} 1 - \frac{{{\lambda _4}}}{{{\lambda _4} + {\lambda _2}\theta }}\frac{{{\lambda _6}}}{{{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}}}\int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {N{\lambda _1}\sum \limits _{n = 0}^{N - 1} {C_{N - 1}^n{{\left( { - 1} \right) }^n}{e^{ - {\lambda _1}\left( {n + 1} \right) {x_1}}}} } d{x_1}\nonumber \\= & {} 1 - \frac{{N{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ -1}}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}{e^{ - {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\left( {n + 1} \right) \theta {X_3}}}} \end{aligned}$$
(17)

Substituting (17) into (6), we can obtain the SOP for this protocol:

$$\begin{aligned}&P_{out}^{\mathrm{{MaSR}}}\mathop = \limits ^{\left( {18.1} \right) } \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {\left[ \begin{array}{l} 1 - \frac{{N{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) ^{ - 1}}\\ \sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}{e^{ - {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }{x_5}}}{e^{ - {\lambda _1}\left( {n + 1} \right) \theta {x_3}}}} \end{array} \right] {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5}\nonumber \\&\quad \mathop = \limits ^{\left( {18.2} \right) } 1 - \frac{{N{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{{\lambda _4} + {\lambda _2}\theta }}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}} \nonumber \\&\qquad \int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left[ {{\lambda _3} + {\lambda _1}\left( {n + 1} \right) \theta } \right] {x_3}}}} d{x_3}d{x_5}\nonumber \\&\quad \mathop = \limits ^{\left( {18.3} \right) } 1 - \frac{{N{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{2{\lambda _2}\theta \left( {{\lambda _4} + {\lambda _2}\theta } \right) }}\nonumber \\&\qquad \sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}} \frac{1}{{{{\left( {{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _1}\left( {n + 1} \right) \theta + {\lambda _3}}}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(18)

where (18.3) is obtained from (18.2) by using the result of Eq. (12):

$$\begin{aligned}&\int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left[ {{\lambda _3} + {\lambda _1}\left( {n + 1} \right) \theta } \right] {x_3}}}} d{x_3}d{x_5}\\&\quad = \frac{1}{{{\lambda _2}\theta }}\frac{1}{{2{{\left( {{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _1}\left( {n + 1} \right) \theta + {\lambda _3}}}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$

3.3 The MaRD Scheme

The best relay \({R_b}\) is selected based on the MaRD relay selection scheme as follows:

$$\begin{aligned} {R_b} = \arg \mathop {\max }\limits _{n = 1,2,\ldots ,N} {g_{2n}} \end{aligned}$$
(19)

Then, the PDF of RV \({g_{2b}}\) is changed and given by:

$$\begin{aligned} {f_{{g_{2b}}}}\left( {{x_2}} \right) = N{\lambda _2}{e^{ - {\lambda _2}{x_2}}}{\left( {1 - {e^{ - {\lambda _2}{x_2}}}} \right) ^{N - 1}} = N{\lambda _2}\sum \limits _{n = 0}^{N - 1} {C_{N - 1}^n{{\left( { - 1} \right) }^n}{e^{ - {\lambda _2}\left( {n + 1} \right) {x_2}}}} \end{aligned}$$
(20)

Similarly, we also \({F_{{\psi _s}}}\left( {{\psi _t}} \right)\) from (7) for this protocol as

$$\begin{aligned} {F_{{\psi _s}}}\left( {{\psi _t}} \right)= & {} 1 - \int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) } \int _0^\infty {{f_{{g_{6b}}}}\left( {{x_6}} \right) } \int _0^\infty {{f_{{g_{4b}}}}\left( {{x_4}} \right) } \nonumber \\&\quad \int _{\left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {x_6} + \theta {x_4}}^\infty {{f_{{g_{2b}}}}\left( {{x_2}} \right) } d{x_2}d{x_4}d{x_6}d{x_1}\nonumber \\= & {} 1 - \int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) } \nonumber \\&\quad \int _0^\infty {N\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}\frac{{{\lambda _4}}}{{{\lambda _4} + {\lambda _2}\left( {n + 1} \right) \theta }}{e^{ - {\lambda _2}\left( {n + 1} \right) \left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {x_6}}}} {f_{{g_{6b}}}}\left( {{x_6}} \right) } d{x_6}d{x_1}\nonumber \\= & {} 1 - N{\lambda _4}{\lambda _6}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}\frac{1}{{\left[ {{\lambda _4} + {\lambda _2}\left( {n + 1} \right) \theta } \right] }}} \nonumber \\&\quad {\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma } + {\lambda _2}\left( {n + 1} \right) \theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\theta {X_3}}} \end{aligned}$$
(21)

The SOP for this protocol can be obtained by substituting (21) into (6) as

$$\begin{aligned}&P_{out}^{\mathrm{{MARD}}}\mathop = \limits ^{\left( {22.1} \right) } \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \nonumber \\&\int _0^\infty {\left[ \begin{array}{l} 1 - N{\lambda _4}{\lambda _6}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}\frac{1}{{\left[ {{\lambda _4} + {\lambda _2}\left( {n + 1} \right) \theta } \right] }}} \\ {\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma } + {\lambda _2}\left( {n + 1} \right) \theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{x_5}}}{e^{ - {\lambda _1}\theta {x_3}}} \end{array}\right] {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5}\nonumber \\&\mathop = \limits ^{\left( {22.2} \right) } 1 - N{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}\frac{1}{{{\lambda _4} + {\lambda _2}\left( {n + 1} \right) \theta }}} \nonumber \\&\int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma } + {\lambda _2}\left( {n + 1} \right) \theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}d{x_5}\nonumber \\&\mathop = \limits ^{\left( {22.3} \right) } 1 - \frac{{N{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{2{{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}\sum \limits _{n = 0}^{N - 1} {\frac{{C_{N - 1}^n{{\left( { - 1} \right) }^n}}}{{n + 1}}} \nonumber \\&\frac{1}{{\left[ {{\lambda _4} + {\lambda _2}\left( {n + 1} \right) \theta } \right] \left[ {{\lambda _2}\left( {n + 1} \right) \theta } \right] }}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\left( {n + 1} \right) \theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(22)

where (22.3) is obtained from (22.2) by using the result of Eq. (12):

$$\begin{aligned}&\int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma } + {\lambda _2}\left( {n + 1} \right) \theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}d{x_5}\\&\qquad = \frac{1}{{{\lambda _2}\left( {n + 1} \right) \theta }}\frac{1}{{2{{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\left( {n + 1} \right) \frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\left( {n + 1} \right) \theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$

3.4 The MiRE Scheme

The MiRE relay selection scheme is expressed by (23), and the CDF of RV \({g_{4b}}\) is changed compared to the case of Sect. 3.1 and given by (24) as follows

$$\begin{aligned} {R_b}= & {} \arg \mathop {\min }\limits _{n = 1,2,\ldots ,N} {g_{4n}} \end{aligned}$$
(23)
$$\begin{aligned} {F_{{g_{4b}}}}\left( {{x_4}} \right)= & {} \Pr \left[ {\mathop {\min }\limits _{n = 1,2,\ldots ,N} {g_{4n}} < {x_4}} \right] \nonumber \\= & {} 1 - \prod \limits _{n = 1}^N {\Pr \left[ {{g_{4n}} \ge {x_4}} \right] } = 1 - {e^{ - {\lambda _4}N{x_4}}} \end{aligned}$$
(24)

The PDF of RV \({g_{4b}}\) is obtained by taking the derivative of \({F_{{g_{4b}}}}\left( {{x_4}} \right)\):

$$\begin{aligned} {f_{{g_{4b}}}}\left( {{x_4}} \right) = \frac{{d\left\{ {{F_{{g_{4b}}}}\left( {{x_4}} \right) } \right\} }}{{d{x_4}}} = N{\lambda _4}{e^{ - {\lambda _4}N{x_4}}} \end{aligned}$$
(25)

We also obtain \({F_{{\psi _s}}}\left( {{\psi _t}} \right)\) from (7) as

$$\begin{aligned} {F_{{\psi _s}}}\left( {{\psi _t}} \right)= & {} 1 - \int _{\frac{{\theta - 1}}{\gamma }{X_5} + \theta {X_3}}^\infty {{f_{{g_{1b}}}}\left( {{x_1}} \right) } \int _0^\infty {{f_{{g_{6b}}}}\left( {{x_6}} \right) {e^{ - {\lambda _2}\left( {\frac{{\theta - 1}}{\gamma } + \theta \frac{{{X_3}}}{{{X_5}}}} \right) {x_6}}}} \nonumber \\&\qquad \int _0^\infty {{\lambda _4}N{e^{ - \left( {N{\lambda _4} + {\lambda _2}\theta } \right) {x_4}}}} d{x_4}d{x_6}d{x_1}\nonumber \\= & {} 1 - \frac{{N{\lambda _4}{\lambda _6}}}{{N{\lambda _4} + {\lambda _2}\theta }}{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\theta {X_3}}} \end{aligned}$$
(26)

Then, substituting (25) into (6), we can obtain the SOP for this protocol:

$$\begin{aligned}&P_{out}^{\mathrm{{MIRE}}}\mathop = \limits ^{\left( {26.1} \right) } \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \nonumber \\&\int _0^\infty {\left[ {1 - \frac{{N{\lambda _4}{\lambda _6}}}{{N{\lambda _4} + {\lambda _2}\theta }}{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) }^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{x_5}}}{e^{ - {\lambda _1}\theta {x_3}}}} \right] {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}dx\nonumber \\&\mathop = \limits ^{\left( {26.2} \right) } 1 - \frac{{N{\lambda _4}{\lambda _6}{\lambda _3}{\lambda _5}}}{{{\lambda _4}N + {\lambda _2}\theta }}\int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) {e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) {x_5}}}} \nonumber \\&\quad \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}d{x_5}\nonumber \\&\mathop = \limits ^{\left( {26.3} \right) } 1 - \frac{{N{\lambda _4}{\lambda _6}{\lambda _3}}}{{2{\lambda _2}\theta \left( {{\lambda _4}N + {\lambda _2}\theta } \right) {{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) \end{aligned}$$
(27)

where (26.3) is obtained by using the result in (12):

$$\begin{aligned}&\int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) {e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{x_5}}}} \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) }^{ - 1}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta } \right) {x_3}}}} d{x_3}d{x_5}\\&\qquad = \frac{1}{{{\lambda _2}\theta }}\frac{1}{{2{{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }} \right) }^2}}}{\,_2}{F_1}\left( {1,2;3;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta }}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }}}} \right) . \end{aligned}$$

3.5 The Optimal Relay Selection Scheme

The best relay is selected optimally by using the following strategy:

$$\begin{aligned} {R_b} = arg\mathop {max}\limits _{n = 1,2,\ldots ,N} \min \left( {{\psi _{1n}},{\psi _{2n}}} \right) \end{aligned}$$
(28)

Then, th

$$\begin{aligned} P_{out}^{\mathrm{{ORS}}}= & {} \Pr \left[ {\min \left( {{\psi _{1b}}{\psi _{2b}}} \right)< {\psi _t}} \right] \\= & {} \Pr \left[ {\mathop {max}\limits _{n = 1,2,\ldots ,N} \left\{ {\min \left( {{\psi _{1n}},{\psi _{2n}}} \right) } \right\}< {\psi _t}} \right] \\= & {} \Pr \left\{ {\mathop {\max }\limits _{n = 1,2,\ldots ,N} \min \left[ {\underbrace{\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{1n}}}}{{{g_5}}}}}{{1 + \gamma \frac{{{g_3}}}{{{g_5}}}}}} \right) }_{{\psi _{1n}}},\underbrace{\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{2n}}}}{{{g_{6n}}}}}}{{1 + \gamma \frac{{{g_3}}}{{{g_5}}} + \gamma \frac{{{g_{4n}}}}{{{g_{6n}}}}}}} \right) }_{{\psi _{2n}}}} \right]< {\psi _t}} \right\} \\= & {} \Pr \left\{ {\mathop {\max }\limits _{n = 1,2,\ldots ,N} \min \left[ {\underbrace{\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{1n}}}}{{{X_5}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}}}}} \right) }_{{\psi _{1n}}},\underbrace{\frac{1}{2}{{\log }_2}\left( {\frac{{1 + \gamma \frac{{{g_{2n}}}}{{{g_{6n}}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}} + \gamma \frac{{{g_{4n}}}}{{{g_{6n}}}}}}} \right) }_{{\psi _{2n}}}} \right]< {\psi _t}} \right\} \\= & {} \Pr \left\{ {\mathop {\max }\limits _{n = 1,2,\ldots ,N} \underbrace{\min \left[ {\frac{{1 + \gamma \frac{{{g_{1n}}}}{{{X_5}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}}}},\frac{{1 + \gamma \frac{{{g_{2n}}}}{{{g_{6n}}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}} + \gamma \frac{{{g_{4n}}}}{{{g_{6n}}}}}}} \right] }_{{\psi _n}} < \theta } \right\} \\= & {} \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {\prod \limits _{n = 1}^N {{F_{{\psi _n}}}\left( \theta \right) } {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5} \end{aligned}$$
(29)

e secrecy outage probability for this protocol can be expressed by:Using the result in (8), the CDF of , where the term \({\psi _n}\) is defined by \({\psi _n} = \min \left[ {\frac{{1 + \gamma \frac{{{g_{1n}}}}{{{X_5}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}}}},\frac{{1 + \gamma \frac{{{g_{2n}}}}{{{g_{6n}}}}}}{{1 + \gamma \frac{{{X_3}}}{{{X_5}}} + \gamma \frac{{{g_{4n}}}}{{{g_{6n}}}}}}} \right]\), is obtained by

$$\begin{aligned} {F_{{\psi _n}}}\left( \theta \right) = 1 - \frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) ^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\theta {X_3}}} \end{aligned}$$
(30)

The term \({\psi _n}\) with \(n \in \left\{ {1,2,\ldots ,N} \right\}\) are independent of each other, thus we have

$$\begin{aligned} \prod \limits _{n = 1}^N {{F_{{\psi _n}}}\left( \theta \right) }= & {} {\left[ {{F_{{\psi _n}}}\left( \theta \right) } \right] ^N}\nonumber \\= & {} {\left[ {1 - \frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) }^{ - 1}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}}}{e^{ - {\lambda _1}\theta {X_3}}}} \right] ^N}\nonumber \\= & {} \sum \limits _{n = 0}^N {C_N^n{{\left( { - 1} \right) }^n}{{\left( {\frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}} \right) }^n}{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{X_3}}}{{{X_5}}}} \right) }^{ - n}}{e^{ - {\lambda _1}\frac{{\theta - 1}}{\gamma }{X_5}n}}{e^{ - {\lambda _1}\theta {X_3}n}}} \end{aligned}$$
(31)

Then, by substituting (31) into (29), we obtain:

$$\begin{aligned} P_{out}^{\mathrm{{ORS}}}&= \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {\prod \limits _{n = 1}^N {{F_{{\psi _n}}}\left( \theta \right) } {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5}\nonumber \\ &= {\lambda _3}{\lambda _5}\sum \limits _{n = 0}^N {C_N^n{{\left( { - 1} \right) }^n}{{\left( {\frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}} \right) }^n}} \int _0^\infty {{e^{ - \left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n} \right) {x_5}}}} \nonumber \\&\quad \int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - n}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta n} \right) {x_3}}}} d{x_3}d{x_5} \end{aligned}$$
(32)

By setting \(u = {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}\), we obtain (33.1). Using equation 3.382.4 of [22], we obtain (33.2) as follows:

$$\begin{aligned}&\int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + {\lambda _2}\theta \frac{{{x_3}}}{{{x_5}}}} \right) }^{ - n}}{e^{ - \left( {{\lambda _3} + {\lambda _1}\theta n} \right) {x_3}}}} d{x_3}\nonumber \\&\mathop = \limits ^{\left( {33.1} \right) } \frac{{{x_5}}}{{{\lambda _2}\theta }}\int _0^\infty {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma } + u} \right) }^{ - n}}{e^{ - \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}u}}du} \nonumber \\&\mathop = \limits ^{\left( {33.2} \right) } \frac{{{x_5}}}{{{\lambda _2}\theta }}{\left[ {\left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}} \right] ^{n - 1}}{e^{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}}}\nonumber \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Gamma \left[ {1 - n,\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}} \right] \end{aligned}$$
(33)

Using equation 6.455.1 of [22], we obtain:

$$\begin{aligned}&\int _0^\infty {{e^{ - \left[ {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n - \left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) } \right] {x_5}}}} {\left( {{x_5}} \right) ^n}\Gamma \left[ {1 - n,\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}} \right] d{x_5}\nonumber \\&\quad = \frac{{\left( {{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) }^{1 - n}}{{\left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) }^{1 - n}}} \right) }}{{\left( {n + 1} \right) {{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n} \right) }^2}}}{\,_2}{F_1}\left( {1,2;n + 2;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n}}} \right) \end{aligned}$$
(34)

Finally, by substituting (33) and (34) into (32), we obtain:

$$\begin{aligned} P_{out}^{\mathrm{{ORS}}}&= \int _0^\infty {{f_{{X_5}}}\left( {{x_5}} \right) } \int _0^\infty {\prod \limits _{n = 1}^N {{F_{{\psi _n}}}\left( {{\psi _t}} \right) } {f_{{X_3}}}\left( {{x_3}} \right) } d{x_3}d{x_5}\nonumber \\&= {\lambda _3}{\lambda _5}\sum \limits _{n = 0}^N {C_N^n{{\left( { - 1} \right) }^n}{{\left( {\frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}} \right) }^n}{{\left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) }^{n - 1}}\frac{1}{{{\lambda _2}\theta }}} \nonumber \\&\quad \int _0^\infty {{e^{ - \left[ {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n - \left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) } \right] {x_5}}}} {\left( {{x_5}} \right) ^n}\Gamma \left[ {1 - n,\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) {x_5}} \right] d{x_5}\nonumber \\ &= \frac{{{\lambda _3}{\lambda _5}}}{{{\lambda _2}\theta }}\sum \limits _{n = 0}^N {C_N^n{{\left( { - 1} \right) }^n}{{\left( {\frac{{{\lambda _4}{\lambda _6}}}{{{\lambda _4} + {\lambda _2}\theta }}} \right) }^n}\frac{{{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) }^{1 - n}}}}{{\left( {n + 1} \right) {{\left( {{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n} \right) }^2}}}\,} \,\nonumber \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\,_2}{F_1}\left( {1,2;n + 2;1 - \frac{{\left( {{\lambda _6} + {\lambda _2}\frac{{\theta - 1}}{\gamma }} \right) \left( {\frac{{{\lambda _3} + {\lambda _1}\theta n}}{{{\lambda _2}\theta }}} \right) }}{{{\lambda _5} + {\lambda _1}\frac{{\theta - 1}}{\gamma }n}}} \right) \end{aligned}$$
(35)

4 Numerical Results

This section presents the numerical results used to verify the analytical results of the four relay selection schemes that we considered for use in the underlay cognitive cooperative network under physical layer security; these were the results derived in the previous section.

The analyses considered a network in a two-dimensional plane with the following coordinates for the source S, the destination D, the relay cluster, the primary user PR, and the eavesdropper E: \(\left( {0,0} \right)\), \(\left( {1,0} \right)\), \(\left( {{x_R},0} \right)\), \(\left( {0.5,{y_P}} \right)\), and \(\left( {0.5,{y_E}} \right)\), respectively. Hence, we have distances \({d_{SD}} = 1\), \({d_{SR}} = \left| {{x_R}} \right|\), \({d_{SP}} = \sqrt{{{0.5}^2} + {{\left( {{y_P}} \right) }^2}}\), \({d_{RD}} = \sqrt{{{\left( {1 - {x_R}} \right) }^2}}\), and \({d_{RE}} = \sqrt{{{\left( {{x_R} - 0.5} \right) }^2} + {{\left( {{y_E}} \right) }^2}}\). In all simulation scenarios, we assumed the path loss to be \(\beta = 3\).

Fig. 2
figure 2

Secrecy outage probability versus \({x_R}\) for the four protocols studied. N = 1, 3, and 5 with \(\gamma = 20\) dB, \({y_P} = 0.5\), \({y_E} = - 0.8\), and \({\psi _t} = 0.5\) bits/s/Hz

Full size image

First, in Fig. 2, we compare and discuss the exact and approximate secrecy outage probability expressions for each scheme with Monte Carlo simulations. The simulated and theoretical results matched perfectly, demonstrating the accuracy of our analysis. When \(N = 1\), no relay selection process is used; thus, the four protocols all achieved the same performance. Their performances were improved when the number of relays was increased, i.e., the performances when \(N = 3\) were higher than those when \(N = 1\), and the performances were further improved when \(N = 5\). When \(N = 3\) and \(N = 5\), the four protocols yield their best performance at the optimal value of \({x_R}\) for each protocol, i.e., the MaSR, MaRD, MiRE, and ORS protocols achieved the highest performance compared to themselves when \({x_R} \approx 0.8\), \({x_R} \approx 0.6\), \({x_R} \approx 0.65\), and \({x_R} \approx 0.7\), respectively. In addition, the performance of MaRD is higher than that of MiRE for all values of \({x_R}\), and their performances are equal when \(0.9<x_R< 1\). The performance of MaSR is the worst, compared to the other three protocols, when \(0<x_R< 0.55\). This is the case because the MaSR relay selection scheme is not effective when the relays are located close to the source. However, its performance is increased and superior to those of the MaRD and MiRE protocols when the relays move closer to the destination, i.e., \({x_R} > 0.55\). As expected, ORS achieved the highest secrecy outage performance for all values of \({x_R}\). Interestingly, MaRS can perform similarly to the ORS protocol when the relays are very close to the destination (\(0.9< {x_R} < 1\)).

Fig. 3
figure 3

Secrecy outage probability versus \(\gamma\) (in dB) for the four protocols studied. \({\psi _t}\) of 0.1 and 0.5 bits/s/Hz, \(N = 3\), \({x_R} = 0.5\), \({y_P} = 0.5\), and \({y_E} = - 0.8\)

Full size image

Figure 3 illustrates the secrecy outage probability for the four relay selection schemes as a function of \(\gamma = \frac{I}{{{N_0}}}\) for two secrecy target values, \({\psi _t} = 0.1\) and \({\psi _t} = 0.5\). The outage performances of all four schemes were degraded with increasing \({\psi _t}\) (e.g., from \({\psi _t} = 0.1\) to \({\psi _t} = 0.5\)) due to the increasing quality requirement of the system. Their performances were all improved when \(\gamma\) increased because more transmitted power is allowed at the source S and the best relay \({R_b}\); this helps the decoding process at the receiver nodes. This trend is stable in the approximation form when \(\gamma\) is sufficiently high (\(\gamma > 15\) dB) due to the effect of the eavesdropper. The MaSR protocol has the worst performance (compared to the other three protocols) except when \(\gamma\) is low, i.e., \(\gamma < 7\) dB with \({\psi _t} = 0.5\) and \(\gamma < 1\) dB with \({\psi _t} = 0.1\), when its performance is superior to that of MiRE.

Fig. 4
figure 4

Secrecy outage probability versus \({y_P}\) (in dB) for the four protocols studied. N = 3 and 5, \(\gamma = 20\), \({x_R} = 0.5\), \({y_E} = - 0.8\), and \({\psi _t} = 0.5\) bits/s/Hz

Full size image
Fig. 5
figure 5

Secrecy outage probability versus \({y_E}\) (in dB) for the four protocols studied. N = 3 and 5, \(\gamma = 20\), \({x_R} = 0.5\), \({y_P} = 0.5\), and \({\psi _t} = 0.5\) bits/s/Hz

Full size image

Figures 4 and 5 show the effects of the primary user and eavesdropper positions, i.e., \({y_P} \in \left( {0.1,1} \right)\) and \({y_E} \in \left( { - 1, - 0.1} \right)\), respectively. The secrecy outage performances of all four protocols are increased when the primary user and eavesdropper are located far away from the source and the relays; this is due to the decreasing impact of the primary user and eavesdropper on the two-hop transmission. The outage performances are also improved when the number of relays is increased because relay selection schemes are used. As expected, the ORS protocol achieved the highest performance. In this network, the MRC technique is used at the eavesdropper; thus, the impact of the eavesdropper on the second hop is greater than that of the first hop. Consequently, the MaRD relay selection scheme, which increases the secrecy capacity of the second hop, is more suitable than the MaSR and MiRE relay selection schemes. Therefore, as can be seen in Figs.  3 and 5, the performance of the MaRD protocol is better than those of the MaSR and MiRE protocols.

In this network, the MRC technique is used at the eavesdropper; thus, the impact of the eavesdropper on the second hop \(\left( {R - D} \right)\) is greater than that of the first hop \(\left( {S - R} \right)\). Consequently, the MaRD relay selection scheme, which increases the secrecy capacity of the second hop, is more suitable than the MaSR and MiRE relay selection schemes. Therefore, as can be seen in Figs. 3 and 5, the performance of the MaRD protocol is better than those of the MaSR and MiRE protocols.

5 Conclusions

We have proposed and analyzed an underlay cognitive cooperative energy network under physical layer security. For comparison purposes, we presented four relay selection schemes for this model: MaSR, MaRD, MiRE, and ORS. Monte Carlo simulations were used to verify the theoretical expressions. The exact secrecy outage probability expressions agreed very well with the simulated curves for all scenarios. By analyzing the simulation and theoretical results, it was discovered that 1) when the number of relay nodes is increased, the power threshold is increased, or the target rate is decreased, the outage performances of all protocols are improved; 2) the outage performance of the system is enhanced when the relays are located close to the destination or the primary user and eavesdropper are located far from the source; 3) when the best relay is at the optimal location, the secrecy outage probability of all four schemes are at their lowest; 4) the MaSR scheme yields the worst performance in some cases; and 5) the ORS scheme achieves the best performance in all scenarios.