1 Introduction

Multipath propagation in wireless channel will results in intersymbol interference, equalization is an effective way to reduce or remove this type of interference. In resource limited or non-cooperative communication system, the blind equalization technique is the first choice [1,2,3,4]. Different channels have different impacts on the transmitted signal, the corresponding blind equalization algorithm should also be different if we take into account the balance of the performance and computational cost of the algorithm [5]. Eigenvalue spread can reflect the influence of the channel on the transmitted signal [6]. When the eigenvalue spread of the channel is high, the received signal will much more concentrate on the direction of eigenvectors corresponding to the relatively bigger eigenvalues, which results in the strong correlation of the signal. The transmitted symbols are usually uniformly distributed and uncorrelated, however, they become strong correlation through this kind of channel, and the serious ISI results. On the contrary if the eigenvalue spread of the channel is small, the channel has less effect on the symbols, and the ISI can also be small, which means that a simple equalizer can be competent.

For blind equalization there is no training sequence, only the statistical information of the sending signal is available. In order to achieve the purpose of equalization, an equalizer usually constrains the statistical property of the output signal to be as same as that of the input signal [1, 2]. For example, using the second order and four-order statistics of both input signal and out signal a nonminimum-phase system can be completely equalized. Commonly used algorithms for blind equalization are Bussgang class algorithm [7], such as Sato algorithm and Godard algorithm [8,9,10]. CMA and MCMA, which belong to the Godard algorithm, are widely used because of its low complexity, however their convergence speed is relatively slow [4, 11,12,13,14], especially for high order modulation signal. In [15] a super-exponential convergence algorithm is presented, this algorithm uses the high-order statistics of the equalizer output signal to realize the equalization under the condition of the input signal with non-Gauss distribution. Although the algorithm converges faster, its complexity is high [5]. From the point of computation complexity and performance CMA (or MCMA) and SWA resemble the adaptive algorithm LMS and RLS [5, 16]. Generally speaking, the former has low computational complexity at the expense of worse performance, and the latter is just the inverse. In [6] it is shown that with the increase of the eigenvalue spread LMS algorithm will slow down the convergence rate and increase the steady-state error. On the contrary, RLS algorithm is relatively not sensitive to the eigenvalue spread. Therefore, according to the analogy of adaptive filter algorithm and blind equalization algorithm, we need to select different blind equalization algorithms with regard to the different eigenvalue spread of the channel.

In this paper, the eigenvalue spread of the channel is described, channel is distinguished by the value of the eigenvalue spread. As the calculation of eigenvalue spread involves the matrix decomposition which has high complexity, the paper proposes a way to substitute the matrix decomposition according to the correlation coefficient of the input signal vector. We show that value of the correlation coefficient can reflect the difference of the eigenvalue spread. On the basis of this, with the consideration of the performance and computational complexity the different equalization algorithms are selected. When the eigenvalue spread is small MCMA algorithm is used, on the contrary when the eigenvalue spread is high SWA algorithm is selected. If the eigenvalue spread is moderate, one of them or other improved algorithms can be chosen according to the consideration of performance and complexity. A new MCMA algorithm based on the decorrelation is proposed whose performance and complexity is between those of MCMA and SWA.

The paper is organized as follows. In Sect. 2 the system model and the classic algorithm is introduced. The proposed algorithm is presented in Sect. 3. In Sect. 4 simulations are given to certify the effectiveness of the proposed algorithm. Finally conclusion is given in Sect. 5.

2 System Model and Classic Algorithms

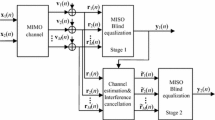
A simplified blind equalization diagram is shown in Fig. 1. The signal u(n), assumed independent and identically distributed, is transmitted through an unknown channel. The symbol h a denotes the total channel response (including transmitting filter receiving filter and wireless channel), The symbol v(n) represents the channel noise which is supposed to be white and Gaussian distribution. The input and output of the equalizer are denoted by x(n) and y(n) respectively. w(n) represents the weight of the equalizer. The decision signal is given by the symbol \(\hat{u}\left( n \right)\). The error signal is denoted by the symbol e(n).

Fig. 1
figure 1

Diagram of the blind equalization

Full size image

The received signal at time n is

$$x\left( n \right) = h_{a} \otimes u\left( n \right) + v\left( n \right)$$
(1)

where the symbol “⊗” denotes a convolution process.

Assuming the ideal equalizer tap coefficient vector is W opt , the following formula should be satisfied.

$$W^{*} \otimes h_{a} = \delta_{n}$$
(2)

where δ n denotes the impulse signal. In practice the equalizer is commonly implemented by a finite-length filter, the equalizer with truncated length can produce error, which results in the residual ISI.

2.1 CMA Algorithm

The most typical blind equalization algorithm is Godard type algorithm whose cost function is as follows [17]

$$J\left( n \right) = E\left[ {\left( {\left| {y\left( n \right)} \right|^{p} - R_{p} } \right)^{2} } \right]$$
(3)

where \(R_{p} = \frac{{E\left[ {\left| {s\left( n \right)} \right|^{2p} } \right]}}{{E\left[ {\left| {s\left( n \right)} \right|^{p} } \right]}}\), p is a positive integer, s(n) is the transmitted symbol. The symbol E[·] denotes the expectation operation.

$$y\left( n \right) = W^{H} \left( {n - 1} \right)X\left( n \right)$$
(4)

where \(X\left( n \right) = \left[ {x\left( n \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x\left( {n - 1} \right)\, \cdots \,x\left( {n - N + 1} \right)} \right]^{T}\) is the equalizer input vector, N represents the length of the equalizer.

Assume p = 2, we get the constant modulus algorithm [18, 19], the cost function of CMA is

$$J_{C} \left( n \right) = E\left[ {\left( {\left| {y\left( n \right)} \right|^{2} - R_{c} } \right)^{2} } \right]$$
(5)
$$R_{c} = \frac{{E\left[ {\left| {s\left( n \right)} \right|^{4} } \right]}}{{E\left[ {\left| {s\left( n \right)} \right|^{2} } \right]}}$$
(6)

The stochastic gradient-descent minimization of (5) yields the following algorithm.

$$W\left( n \right) = W\left( {n - 1} \right) + \mu * e\left( n \right)X^{*} \left( n \right)$$
(7)
$$e\left( n \right) = \left( {R_{c} - \left| {y\left( n \right)} \right|^{2} } \right) * y\left( n \right)$$
(8)

From (5) we see that the purpose of the CMA is to minimize the distance between the modulus square of the equalizer output and the constant R c . From another point of view the equalizer restricts the constellation of output symbol located on the circle with the radius yR c . The CMA algorithm is simple and easy to implement, but its cost function contains only the amplitude information of the signals. Therefore the CMA is not sensitive to the phase deflection. To solve the phase ambiguity a phase correction algorithm is required.

MCMA algorithm is one of the improved CMAs [20], also known as MMA, and it restricts the amplitude square of the real and the imaginary parts of the equalizer output separately. Similar to the CMA we can get the error function of the MCMA.

$$e\left( n \right) = y_{\text{R}} \left( n \right)\left( {R_{2,R} - y_{R}^{2} \left( n \right)} \right) + j * y_{I} \left( n \right)\left( {R_{2,I} - y_{I}^{2} \left( n \right)} \right)$$
(9)

where y R (n) is the real part of y(n) and y I (n) is the imaginary part. The constant value of real and imaginary parts of MCMA are given by

$$R_{2,R} = \frac{{E\left[ {s_{R}^{4} \left( n \right)} \right]}}{{E\left[ {s_{R}^{2} \left( n \right)} \right]}}$$
(10)
$$R_{2,I} = \frac{{E\left[ {s_{I}^{4} \left( n \right)} \right]}}{{E\left[ {s_{I}^{2} \left( n \right)} \right]}}$$
(11)

where s R (n) and s I (n) are real and imaginary parts of the symbol s(n) respectively. MCMA cost function includes not only the amplitude information of output signal, but also the phase information. Compared with CMA, MCMA has not phase ambiguity problem and generally has a faster convergence rate.

2.2 SWA Algorithm

Although the MCMA is better than CMA from the convergence point it still converges much slower under some channels, especially seriously distorted channels.

The cost function of the SWA is given by [3].

$$J\left( n \right) = \sum\limits_{k = 0}^{n} {\lambda^{n - k} \left( {\left| {y_{n,k} } \right|^{2} - R_{c} } \right)^{2} }$$
(12)

A robust algorithm is derived in [5] as follows

$$W\left( n \right) = W\left( {n - 1} \right) + \frac{{e^{*} \left( n \right)R_{xx}^{ - 1} \left( n \right)X\left( n \right)}}{{R_{c} - \alpha_{SWA} * C_{1,1}^{s} }}$$
(13)
$$e\left( n \right) = \left( {\left| {y\left( n \right)} \right|^{2} - R_{c} } \right) * y\left( n \right)$$
(14)

where R xx (n) is the autocorrelation matrix of X(n), α SWA is a constant parameter.

The inverse matrix of the R xx (n) can be calculated by iteration

$$R_{xx}^{ - 1} \left( n \right) = \frac{1}{\lambda }\left[ {R_{xx}^{ - 1} \left( {n - 1} \right) - \frac{{R_{xx}^{ - 1} \left( {n - 1} \right)X\left( n \right)X^{H} \left( n \right)R_{xx}^{ - 1} \left( {n - 1} \right)}}{{\lambda + X^{H} \left( n \right)R_{xx}^{ - 1} \left( {n - 1} \right)X\left( n \right)}}} \right]$$
(15)

where λ is the adjustment factor, C s1,1  = E[|s(n)|2],for complex data α SWA  = 2 [5].

3 Principle of the Proposed Algorithm

3.1 Eigenvalue Spread of the Channel

If the channel length is Lh, (1) can be rewritten as

$$x\left( n \right) = \sum\limits_{k = 1}^{Lh} {h_{a,k} u\left( {n - k} \right)} + v\left( n \right)$$
(16)

Suppose the length of the equalizer satisfies N > Lh, ignoring the channel noise the input signal vector of the equalizer at time n can be written as follows

$$\begin{aligned} X\left( n \right) = & \left( {\begin{array}{*{20}c} {x\left( n \right)} \\ {x\left( {n - 1} \right)} \\ {{\kern 1pt} \vdots } \\ {x\left( {n - N + 1} \right)} \\ \end{array} } \right) \\ {\kern 1pt} \, = & \left( {\begin{array}{*{20}l} {h_{a,1} {\kern 1pt} } \hfill & {h_{a,2} } \hfill & {h_{a,3} } \hfill & {{\kern 1pt} \cdots } \hfill & {h_{a,Lh} } \hfill & 0 \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ 0 \hfill & {h_{a,1} } \hfill & {h_{a,2} } \hfill & \cdots \hfill & {h_{a,Lh - 1} } \hfill & {h_{a,Lh} } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & \cdots \hfill & 0 \hfill & {h_{a,1} {\kern 1pt} } \hfill & {h_{a,2} } \hfill & \cdots \hfill & {h_{a,Lh} } \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {u\left( {n - 1} \right)} \\ {u\left( {n - 2} \right)} \\ {{\kern 1pt} \vdots } \\ {u\left( {n - N - Lh + 1} \right)} \\ \end{array} } \right) \\ {\kern 1pt} {\kern 1pt} \, =\, & H_{a} U \\ \end{aligned}$$
(17)

The autocorrelation matrix of X(n) is given by

$$\begin{aligned} R_{xx} =\, & E\left[ {XX^{H} } \right] \\ {\kern 1pt} \, =\, & E\left[ {H_{a} UU^{H} H_{a}^{H} } \right] \\ \, {\kern 1pt} =\, & H_{a} E\left[ {UU^{H} } \right]H_{a}^{H} \\ \, {\kern 1pt} =\, & E\left[ {UU^{H} } \right]H_{a} H_{a}^{H} \\ {\kern 1pt} \, {\kern 1pt} =\, & E\left[ {UU^{H} } \right]\left( {\begin{array}{*{20}l} {r\left( 0 \right)} \hfill & {r\left( 1 \right)} \hfill & \cdots \hfill & {r\left( {Lh - 1} \right)} \hfill & {0{\kern 1pt} } \hfill & \cdots \hfill & 0 \hfill \\ {r\left( 1 \right)} \hfill & {r\left( 0 \right)} \hfill & { \cdots {\kern 1pt} } \hfill & {r\left( {Lh - 2} \right)} \hfill & {r\left( {Lh - 1} \right)} \hfill & {{\kern 1pt} \cdots } \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & 0 \hfill & 0 \hfill & \cdots \hfill & {r\left( 0 \right)} \hfill \\ \end{array} } \right) \\ {\kern 1pt} {\kern 1pt} \, =\, & \sigma_{u}^{2} R_{r} \\ \end{aligned}$$
(18)

In (18), R xx is a symmetric matrix of N × N, E[UUH] = σ 2 u is the variance of input signal, r(τ) = ∑  Lh−τk=1 h *a,k  * ha,k+τ, τ ∊ [0, Lh − 1], is the autocorrelation function of the channel.

Using eigenvalue decomposition for matrix R r we get

$$R_{r} = Q_{r} \Lambda Q_{r}^{ - 1} = Q_{r} \left( {\begin{array}{*{20}l} {\lambda_{{R_{r} ,{\kern 1pt} 1}} {\kern 1pt} } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ 0 \hfill & {\lambda_{{R_{r} ,{\kern 1pt} 2}} } \hfill & \cdots \hfill & 0 \hfill \\ { \vdots {\kern 1pt} } \hfill & { \vdots {\kern 1pt} } \hfill & \ddots \hfill & { \vdots {\kern 1pt} } \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & {\lambda_{{R_{r} ,{\kern 1pt} {\kern 1pt} N}} } \hfill \\ \end{array} } \right)Q_{r}^{ - 1}$$
(19)

where Q r is the eigenvalue vector matrix, \(\lambda_{{R_{r} ,i}} {\kern 1pt} ,\quad {\kern 1pt} i = 1,2, \ldots ,{\kern 1pt} N\) are the eigenvalues of R r which satisfy \(\lambda_{{R_{r} ,1}} {\kern 1pt} \le \lambda_{{R_{r} ,2}} {\kern 1pt} \le \cdots \le \lambda_{{R_{r} ,N}} {\kern 1pt}\), the minimal eigenvalue of R r is \(\lambda_{\hbox{min} } = \lambda_{{R_{r} ,1}}\), the maximal eigenvalue is \(\lambda_{\hbox{max} } = \lambda_{{R_{r} ,N}}\),we get the eigenvalue spread.

$$\chi \left( {R_{r} } \right) = \frac{{\lambda_{\hbox{max} } }}{{\lambda_{\hbox{min} } }}$$
(20)

From (18) and (19), as σ 2 u is a positive constant, the eigenvalue relationship between matrix R xx and matrix R r is given by

$$\lambda_{{R_{xx} ,i}} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sigma_{u}^{2} * \lambda_{{R_{r} ,i}} ,\quad i = 1,2, \ldots ,{\kern 1pt} {\kern 1pt} N$$
(21)

From (20) and (21) we see that the eigenvalue spread of R r and R xx is same, and it is independent of the input signal.

Using the raised cosine channel [6] as an example, the length of channel is 3, and the impulse response is given by

$$h_{n} = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left[ {1 + \cos \left( {\frac{2\pi }{C}\left( {n - 2} \right)} \right)} \right]} \hfill & {n = 1,2,3} \hfill \\ 0 \hfill & {others} \hfill \\ \end{array} } \right.$$
(22)

The minimax eigenvalue spread of the channel for different channel parameter C is given in Table 1.

Table 1 Eigenvalue spread for different parameter C
Full size table

It can be seen from Table 1 that the larger the parameter C is, the higher the eigenvalue spread is. When the signal is transmitted through the channel with higher eigenvalue spread the output signal will concentrate the eigenvectors corresponding to the larger eigenvalues, which results in the serious ISI comparatively. Under this condition different equalization algorithms should be chosen according to the eigenvalue spread with the consideration of the balance of the complexity and performance.

3.2 Algorithm to Identify the Eigenvalue Spread of the Channel

The eigenvalue spread of the channel reflects the influence of the channel to the input signal. According to (19) and (20) computing the eigenvalue spread of the channel involves the computation of the correlation matrix and eigenvalue decomposition, and this means a high computation complexity. The paper presents a method by calculating the correlation value of the equalizer input to distinguish different channels.

At time n − 1 and n the input signal vector is

$$X\left( {n - 1} \right) = \left[ {x\left( {n - 1} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x\left( {n - 2} \right)\; \cdots \;x\left( {n - N} \right)} \right]^{T}$$
(23)
$$X\left( n \right) = \left[ {x\left( n \right){\kern 1pt} {\kern 1pt} {\kern 1pt} x\left( {n - 1} \right)\; \cdots \;x\left( {n - N + 1} \right)} \right]^{T}$$
(24)

The correlation coefficient between X(n) and X(n − 1) is as follows

$$corr\left( n \right) = \frac{{X^{\text{H}} \left( n \right)X\left( {n - 1} \right)}}{{\sqrt {X^{H} \left( n \right)X\left( n \right)} \sqrt {X^{H} \left( {n - 1} \right)X\left( {n - 1} \right)} }}$$
(25)

Taking the sliding average of correlation coefficient instead of its instantaneous value we get a smoothing version of the correlation coefficient.

$$c\left( n \right) = \frac{{c\left( {n - 1} \right) + corr\left( n \right)}}{2}$$
(26)

For the raised cosine channel with different C the corresponding correlation coefficient of the equalizer input signal is shown in Fig. 2. The transmitted signal is 16QAM. The length of the input vector is 11.

Fig. 2
figure 2

Correlation for raised cosine channel with different C

Full size image

Combining Table 1 and Fig. 2, it is clear that for channels with different eigenvalue spread the correlation coefficient of the equalizer input vector can reflect this difference. Therefore we can use correlation rather than matrix decomposition to estimate the eigenvalue spread of the channel.

3.3 Algorithm Selection for Different Channels

It is shown that, compared with LMS algorithm, the RLS algorithm has better performance (low steady-state error or fast convergence speed) in the high eigenvalue spread channel [11]. The RLS algorithm, however, is complex because of calculation of the inverse matrix, whose complexity is about O(N2). The LMS algorithm, on the contrary, has a small computation complexity, which is about O(N), and performs well in small eigenvalue spread channel. From the analogy of blind equalization (CMA and SWA) and adaptive algorithm (LMS and RLS) we draw the conclusion that with the consideration of complexity and performance CMA is more suitable for the small eigenvalue spread channel and SWA is on the contrary. Compared with the CMA, the MCMA algorithm, with the same order of magnitude complexity, corrects phase ambiguity problem and performs better under the same channel, so it is more widely used [13]. Table 2 lists the computation complexity of SWA and MCMA.

Table 2 Calculation complexity of SWA and MCMA
Full size table

Compared with MCMA, SWA involves the matrix inversion, which whitens the input signal, resulting in O(N2) order of complex multiplication in exchange for the improved performance especially under the high eigenvalue spread channel.

Using the algorithm proposed in this paper, we can distinguish the different eigenvalue spread of the channel by calculating the correlation coefficient of the input vector. Therefore a corresponding threshold can be given, according the threshold different blind equalization algorithm will be selected. The diagram of the algorithm is shown in Fig. 3. If the eigenvalue spread is relatively small, for example c(n) < Th, where Th represents the threshold, MCMA is chosen. On the contrary if c(n) > Th SWA will be chosen. We can also set two thresholds, Th1 and Th2, Th1 < Th2, if c(n) < Th1 MCMA is selected, if c(n) > Th2 SWA is selected, in other conditions one modified algorithm, whose complexity and performance lies between that of SWA and MCMA, can be selected.

Fig. 3
figure 3

Diagram of the proposed algorithm

Full size image

When the eigenvalue spread is moderate, such as Th2 < c(n) < Th1, an improved MCMA is proposed in the following section.

3.4 Decorrelation MCMA (DMCMA)

From the previous analysis, the correlation of signal will be enhanced through the high eigenvalue spread channel, which will lead to the slow convergence of MCMA. The SWA converges faster, mainly due to the input signal is whitened by the inverse autocorrelation matrix. Therefore the convergence rate can be improved by decorrelation of the equalizer input.

At time n, the correlation coefficient of equalizer input vector X(n) and X(n − 1) can be defined as [21]

$$a(n) = \frac{{X^{H} (n)X(n - 1)}}{{X^{H} (n - 1)X(n - 1)}}$$
(27)

here a(n)X(n − 1) denotes the correlation part of X(n) and X(n − 1). Decorrelation is to reduce the correlation between the adjacent input vector. After decorrelation we get the new equalizer input.

$$X_{decorr} (n) = X(n) - a(n)X(n - 1)$$
(28)

The flowchart of DMCMA algorithm is shown in Table 3.

Table 3 The flow chart of the decorrelation MCMA algorithm
Full size table

For each iteration, the complex and real multiplication of DMCMA algorithm is 5 N and 6 respectively, the addition of complex and real numbers is 5 N − 3 and 3 respectively, floating division is 2. The computational complexity of decorrelation MCMA algorithm is between that of SWA and MCMA. Due to the decorrelation, its convergence is faster than MCMA, but will be slower than SWA.

4 Simulation and Performance Analysis

This section uses the raised cosine channel for simulation, the transmitted signal is 16QAM. The length of equalizer is 11. Th1 = 0.4, Th2 = 0.45, which corresponds to the eigenvalue spread approximately equaling to 8 and 15 respectively.

Performance is evaluated by the mean square error (MSE) and residual intersymbol interference (ISI) [9,10,11,12,13,14]. The MSE and ISI are defined as follows.

  1. (1)

    Mean square error

    $$MSE\left( n \right) = \theta * MSE\left( {n - 1} \right) + \left( {1 - \theta } \right) * \left| {\hat{u}\left( n \right) - y\left( n \right)} \right|^{2}$$
    (29)

    where θ is forgetting factor, usually θ = 0.99.

  2. (2)

    Intersymbol interference

    $$ISI\left( n \right) = \frac{{\sum {\left| {h_{a,w} \left( n \right)} \right|^{2} } - \hbox{max} \left| {h_{a,w} \left( n \right)} \right|^{2} }}{{\hbox{max} \left| {h_{a,w} \left( n \right)} \right|^{2} }}$$
    (30)

    where ha,w(n) = h a  ⊗ W(n).

Case 1

Channel with C = 3.0

The step size for MCMA and DMCMA is set to 2.5 × 10−5 and 2.8 × 10−5 respectively. The parameter λ for SWA is set to 0.9995.

The result is shown in Fig. 4. We can see that the three algorithms perform relatively same. It is obvious that under this channel MCMA should be selected if the algorithm complexity and performance are taken into account. According Table 1 the eigenvalue spread of this channel is 4.5866.

Fig. 4
figure 4

Performance curve for channel C = 3.0

Full size image

Case 2

Channel with C = 3.1

The step size of MCMA and DMCMA is set to 2.5 × 10−5 and 2.8 × 10−5 respectively, λ = 0.9995. Figure 5 shows the simulation result.

Fig. 5
figure 5

Performance curve for channel C = 3.1

Full size image

From the Fig. 5 it is clear that the MCMA converges relatively slow compared the other two. SWA converges almost as same as DMCMA finally even though it performs better before convergence. According Table 2 the eigenvalue spread of this channel is 11.1238. Under this channel the DMCMA should be selected.

Case 3

Channel with C = 3.2

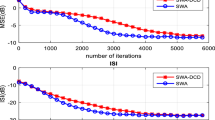
The parameters for SWA is λ = 0.9995. The step size for MCMA and DMCMA is 2.5 × 10−5 and 2.8 × 10−5 respectively. The result is shown in Fig. 6. Different from Case 2 in this case the performance of the three algorithms has relatively obvious difference. The eigenvalue spread of this channel is 15.4082, this will results in a relatively strong correlation of the input signal. That is why both SWA and DMCMA converge faster than MCMA. Compared with DMCMA SWA performs relatively better but not remarkably. In this case if complexity is more important than performance, DMCMA should be selected, otherwise SWA is chosen.

Fig. 6
figure 6

Performance curve for channel C = 3.2

Full size image

Case 4

Channel with C = 3.3

The parameters for SWA is λ = 0.9996. The step size for MCMA and DMCMA is 2.0 × 10−5 respectively. The result is shown in Fig. 7. It is clear that SWA obviously converges faster than the other two. The eigenvalue spread of this channel is 21.7321. The result shows that SWA is more suitable for large eigenvalue spread channel.

Fig. 7
figure 7

Performance curve for channel C = 3.3

Full size image

Case 5

Channel with C = 3.6

The parameters for SWA is λ = 0.9982. The step size for MCMA and DMCMA is 6 × 10−5 and 8.5 × 10−5 respectively. The result is shown in Fig. 8.

Fig. 8
figure 8

Performance curve for channel C = 3.6

Full size image

From Table 1 we see that the eigenvalue spread of the channel with c = 3.6 is larger than 74. It is obvious a relatively big number, and which means the received signal will become strong correlation. This also explains why the three algorithms perform differently with a significant level. Among them SWA converges fast, and MCMA is worst. Under this channel SWA is selected with priority.

Through simulations we can see that with the consideration of complexity and performance MCMA should be used under small eigenvalue spread channel, for example χ < 10. When the eigenvalue spread become relatively high, such as χ > 20, SWA should be used. When the eigenvalue spread is moderate, some modified MCMA should be selected. For different channels the eigenvalue spread can be estimated by the calculating the correlation coefficient of the input vector. By comparing with the threshold different algorithms will be selected for different eigenvalue spread channels.

5 Conclusion

The performance of the different blind algorithms are not only related to the algorithm themselves but also the channel characteristics. The eigenvalue spread of the channel can reflect the impact degree of the channel on the transmitted signal. The calculation of the eigenvalue spread of the channel, however, has high complexity because of matrix decomposition involved. This paper presents a method to distinguish different eigenvalue spread channel by calculating the correlation value of the equalizer input vector. On this basis, for different eigenvalue spread channel, considering the performance and computational complexity the corresponding blind equalization algorithm is selected. Besides the commonly used algorithm the new algorithm based on decorrelation is presented whose complexity and performance lie between the SWA and MCMA. Simulations verify the applicability of the proposed algorithm.