1 Introduction

With the increasing data rate of wireless communication, the intersymbol interference (ISI) caused by multipath propagation becomes more serious. Adaptive equalizers are widely used to remove the ISI. When there is no training sequence the blind equalization algorithms are generally chosen [1, 2]. The typical blind equalization algorithms include constant modulus algorithm (CMA) [3], Shalvi-Weinstein algorithm (SWA) [4, 5] and the corresponding modified versions [6, 7]. In [4], an improved SWA, which avoids divergence, is given. CMA has slow convergence rate but low computation complexity. On the contrary, SWA converges faster at the expense of higher computation complexity because of the computation of the matrix inversion involved. Generally, the computation of the inverse matrix may also lead to numerical calculation error.

In practical application, the computational complexity is one of the most important indexes to evaluate an algorithm. It is worth studying an algorithm with low complexity and a guaranteed performance. For solving the problem of the norm equation, the dichotomous coordinate descent (DCD) algorithm [8, 9] does not need the computation of the inverse matrix. Compared with LS algorithm for solving the same problem, the complexity of the DCD algorithm is changed from \(O(N^{2} )\) to \(O(N)\). By quantization of some parameters, the DCD algorithm has only addition and bit shift operation for hardware implementation [10, 11].

Although the SWA has relatively good equalization performance, it has high computational complexity because it involves matrix inversion. Based on the DCD and the algorithm presented in [4], a low complexity SWA is presented. The total computation complexity of the proposed algorithm is comparable to that of the CMA.

For blind equalization, when output symbols have relatively low error probability, switching to a decision-directed (DD) mode can further improve the equalization performance [12, 13]. Therefore, a low complexity dual-mode algorithm with RLS used at the second stage is also presented.

The paper is organized as follows. In Sect. 2 the system model and the classic algorithms are introduced. The proposed algorithm is presented in Sect. 3. In Sect. 4 simulations are given to verify the effectiveness of the proposed algorithm. Conclusion is given in Sect. 5.

2 Algorithm Description

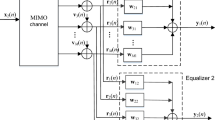
The received signal \(x\left( n \right)\) in multipath channel is given by

$$x\left( n \right) = h \otimes s\left( n \right) + v\left( n \right)$$
(1)

where \(s(n)\) is transmitted symbols through the channel \(h\), and \(\otimes\) represents the convolution operation.\(v\left( n \right)\) is the white Gaussian noise. At time n the input vector of the equalizer is \({\mathbf{x}}\left( n \right) = \left[ {x\left( n \right){\kern 1pt} ,x\left( {n - 1} \right),{\kern 1pt} \ldots ,x\left( {n - N + 1} \right)} \right]^{H}\), where \(N\) is the length of the equalizer weights, the superscript \(H\) denotes the complex conjugate transpose. The output of the equalizer is

$$y\left( n \right) = {\mathbf{w}}(n)^{H} {\mathbf{x}}(n)$$
(2)

where \({\mathbf{w}}\left( n \right)\) is the weight vector of the equalizer.

2.1 Introduction of SWA [4]

The cost function of the SWA is

$$J\left( n \right) = \sum\limits_{{l = 0}}^{n} {\lambda ^{{n - l}} \left( {\left| {y_{{n,l}} } \right|^{2} - \beta } \right)^{2} }$$
(3)

where \(\beta = E\left[ {\left| {s\left( n \right)} \right|^{4} } \right]/E\left[ {\left| {s\left( n \right)} \right|^{2} } \right]\) is a statistical constant. \(0 \le \lambda < 1\) is the forgetting factor, \(y_{{n,l}} = {\mathbf{w}}(n)^{H} {\mathbf{x}}(l)\).

According to [4], the procedure of SWA is as follows.

$${\mathbf{w}}\left( n \right) = {\mathbf{w}}\left( {n - 1} \right) + \mu e_{{SWA}}^{*} \left( n \right){\mathbf{R}}_{{}}^{{ - 1}} \left( n \right){\mathbf{x}}\left( n \right)$$
(4)
$$e_{{SWA}} \left( n \right) = \left\{ {\begin{array}{*{20}l} {\left( {\left| {y\left( n \right)} \right|^{2} - \beta } \right)y\left( n \right),} \hfill & {\left| {y\left( n \right)} \right|^{2} \ge \beta C_{{1,1}}^{s} } \hfill \\ { - y(n),} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(5)
$${\mathbf{R}}\left( n \right) = \sum\limits_{{l = 1}}^{n} {\lambda ^{{n - l}} {\mathbf{x}}\left( l \right){\mathbf{x}}^{H} \left( l \right)}$$
(6)
$$\mu = 1/(\beta - \alpha C_{{1,1}}^{s} )$$
(7)

where \(e_{{SWA}} \left( n \right)\) and \(\mu\) denote the error and step size of the equalizer respectively, and * stands for complex conjugate. \(\alpha\) is a constant,\({\mathbf{R}}\left( n \right)\) is the autocorrelation matrix. \(C_{{1,1}}^{s} = E\{ |s(n)|^{2} \}\).

2.2 DCD Algorithm [8,9,10]

For solving the normal equation \({\mathbf{Qx}} = {\mathbf{p}}\), it is equivalent to minimize the following quadratic equation.

$$f\left( {\mathbf{x}} \right) = \frac{1}{2}{\mathbf{x}}^{T} {\mathbf{Qx}} - {\mathbf{x}}^{T} {\mathbf{p}}$$
(8)

where the superscript T denotes the transpose operation.

Standard linear iterative search uses the formula

$$f\left( {{\mathbf{x}} + \varsigma \user2{d}} \right) = f\left( {\mathbf{x}} \right) - \frac{1}{2}\frac{{\left( {\user2{d}^{T} {\mathbf{r}}} \right)^{2} }}{{\user2{d}^{T} {\mathbf{Q}}\user2{d}}}$$
(9)

where \(\varsigma\) is the searching step size, which is equal to \(\user2{d}^{T} {\mathbf{r}}/\user2{d}^{T} {\mathbf{Q}}\user2{d}\), r is the residual vector,\(\user2{d}\) is the search direction vector, which is non-orthogonal to r, i.e.\(\user2{d}^{\user2{T}} {\mathbf{r}} \ne 0\).

If the search direction is a Euclidean space coordinate, the formula (9) is the coordinate descent algorithm, and \({\mathbf{Q}}\user2{d} = {\mathbf{Q}}^{{\left( p \right)}}\), where \({\mathbf{Q}}^{{\left( p \right)}}\) denotes the pth column of the matrix Q, thereby removing the multiplication of the matrix and the vector.

$$f\left( {{\mathbf{x}} + \varsigma \user2{e}_{\user2{p}} } \right) = f\left( {\mathbf{x}} \right) - \frac{1}{2}\frac{{{\mathbf{r}}_{p}^{2} }}{{{\mathbf{Q}}_{{p,p}} }}$$
(10)

where \(\user2{e}_{\user2{p}}\) is the searching direction in Euclidean space and the step size is \(\varsigma = {\mathbf{r}}_{p} /{\mathbf{Q}}_{{p,p}}\).

According to the principle of the descent method, for the kth iteration the incremental of the quadratic formula should meet the following condition.

$$\Delta f\left( {{\mathbf{x}}_{k} } \right) = f\left( {{\mathbf{x}}_{{k + 1}} } \right) - f\left( {{\mathbf{x}}_{k} } \right) < 0$$
(11)

where \({\mathbf{x}}_{k}\) represents the corresponding kth iteration value of \({\mathbf{x}}\). Based on (11), the following iteration formula is obtained.

$${\mathbf{x}}_{{k + 1}} = \left\{ {\begin{array}{*{20}l} {{\mathbf{x}}_{k} } \hfill & {\Delta f\left( {{\mathbf{x}}_{k} } \right) \ge 0} \hfill \\ {{\mathbf{x}}_{k} + \varsigma _{k} \cdot e_{p} } \hfill & {\Delta f\left( {{\mathbf{x}}_{k} } \right) < 0} \hfill \\ \end{array} } \right.$$
(12)

where \(\varsigma _{k}\) denotes the step size of the kth iteration, and the symbol · denotes the dot product.

The iteration formula of the step size is as follows.

$$\varsigma _{{k + 1}} = \left\{ {\begin{array}{*{20}l} {\varsigma _{k} } \hfill & {others} \hfill \\ {c \cdot \varsigma _{k} } \hfill & {n = N\;{\text{and}}\;{\mathbf{x}}_{{\text{k}}} = {\mathbf{x}}_{{k - N + 1}} } \hfill \\ \end{array} } \right.$$
(13)

where \({\text{0 < }}c{\text{ < 1}}\) is a constant.

For DCD algorithm, the iterative direction is still the Euclidean coordinate direction, but the selections of the step size \(\varsigma\) and the constant c are different with the exact line search method. Suppose that each element of the vector \({\mathbf{x}}\) is limited, i.e.\(|{\mathbf{x}}_{n} | \le A\), and A is known. A can be expressed as \(A = 2^{{N_{b} + p}}\), where p is an arbitrary integer, and Nb is a positive integer. In order to reduce the complexity of hardware implementation, the corresponding parameters in (13) are set to \(c = 1/2\) and \(\varsigma _{0} = A/2\) respectively. In such a way, the multiplication is substituted by shift operation for hardware implementation.

3 Low Complexity SWA Based on DCD

The main idea of the low complexity SWA based on DCD (SWA-DCD) algorithm is as follows. The solution of the cost function (3) is equivalent to the solution of the normal equation. Moreover, the weight increment can be derived from the weight incremental canonical equation, which will be transformed to the normal equation form and solved by DCD algorithm. In the following, we will explain this idea in details.

3.1 The SWA-DCD Algorithm

Let the derivative of the cost function (3) to \({\mathbf{w}}\left( n \right)\) equal to zero, we get the following canonical equation.

$${\mathbf{R}}\left( n \right){\mathbf{w}}\left( n \right) = {\mathbf{q}}\left( n \right)$$
(14)

where \({\mathbf{q}}\left( n \right) = \frac{1}{\beta }\sum\nolimits_{{l = 1}}^{n} {\lambda ^{{n - l}} \left| {y_{{n,l}} } \right|^{2} y_{{n,l}}^{*} {\mathbf{x}}\left( l \right)}\).

The \({\mathbf{R}}\left( n \right)\) can be obtained by the iteration form.

$${\mathbf{R}}\left( n \right) = \lambda {\mathbf{R}}\left( {n - 1} \right) + {\mathbf{x}}\left( n \right){\mathbf{x}}^{H} \left( n \right)$$
(15)

It is noted that unlike [4] we leave the parameter \(\beta\) on the right side of (14). In the following, we derive the weight incremental canonical equation of the equalizer coefficients.

We denote \(\Delta {\mathbf{R}}\left( n \right)\),\(\Delta {\mathbf{w}}\left( n \right)\) and \(\Delta {\mathbf{q}}\left( n \right)\) as follows.

$$\Delta {\mathbf{R}}\left( n \right) = {\mathbf{R}}\left( n \right) - {\mathbf{R}}\left( {n - 1} \right)$$
(16)
$$\Delta {\mathbf{w}}\left( n \right) = {\mathbf{w}}\left( n \right) - {\mathbf{w}}\left( {n - 1} \right)$$
(17)
$$\Delta {\mathbf{q}}\left( n \right) = {\mathbf{q}}(n) - {\mathbf{q}}(n - 1)$$
(18)

According to Ref. [4], we have

$${\mathbf{R}}\left( n \right)\Delta {\mathbf{w}}\left( n \right){\kern 1pt} = {\kern 1pt} \text{e} _{{SWA}}^{*} \left( n \right){\mathbf{x}}\left( n \right)/\beta + {\mathbf{\rho }}\left( n \right)/\beta$$
(19)
$${\mathbf{\rho }}\left( n \right) \approx \alpha C_{{1,1}}^{{\text{s}}} {\kern 1pt} {\mathbf{R}}\left( n \right)\Delta {\mathbf{w}}\left( n \right){\kern 1pt}$$
(20)

Substitute (19) into (20), we get

$${\mathbf{\rho }}\left( n \right) = c_{{SWA}} e_{{SWA}}^{*} \left( n \right){\mathbf{x}}\left( n \right)$$
(21)

where \(c_{{SWA}} = \alpha \cdot C_{{1,1}}^{s} /(\beta - \alpha \cdot C_{{1,1}}^{s} )\).

\({\mathbf{q}}\left( n \right)\) is updated in the following rule [4].

$${\mathbf{q}}\left( n \right) = \lambda {\mathbf{q}}\left( {n - 1} \right) + \left| {y\left( n \right)} \right|^{2} y^{*} \left( n \right){\mathbf{x}}\left( n \right)/\beta + {\mathbf{\rho }}\left( n \right)/\beta {\kern 1pt} {\kern 1pt}$$
(22)

Substituting (21) into (22), we get the iteration formula of \({\mathbf{q}}\left( n \right)\).

$${\mathbf{q}}\left( n \right) = \lambda {\mathbf{q}}\left( {n - 1} \right) + z^{*} (n){\mathbf{x}}\left( n \right)$$
(23)

where \(z(n) = \left( {\left| {y\left( n \right)} \right|^{2} y\left( n \right) + c_{{SWA}} \cdot e_{{SWA}}^{{}} \left( n \right)} \right)/\beta\).

Define the residual vector \({\mathbf{r}}\left( n \right)\)

$${\mathbf{r}}\left( n \right) = {\mathbf{q}}\left( n \right) - {\mathbf{R}}\left( n \right){\mathbf{w}}\left( n \right)$$
(24)

Substitute (17) into (14), we obtain

$${\mathbf{R}}\left( n \right)\left[ {\Delta {\mathbf{w}}\left( n \right) + {\mathbf{w}}\left( {n - 1} \right)} \right] = {\mathbf{q}}\left( n \right)$$
(25)

Combining (16), (18) and (24), we get

$$\begin{aligned} {\mathbf{R}}\left( n \right)\Delta {\mathbf{w}}\left( n \right) = & {\mathbf{q}}\left( n \right) - {\mathbf{R}}\left( n \right){\mathbf{w}}\left( {n - 1} \right) \\ = & {\mathbf{q}}\left( n \right) - \left[ {{\mathbf{R}}\left( {n - 1} \right) + \Delta {\mathbf{R}}\left( n \right)} \right]{\mathbf{w}}\left( {n - 1} \right) \\ = & {\mathbf{q}}\left( n \right) - {\mathbf{R}}\left( {n - 1} \right){\mathbf{w}}\left( {n - 1} \right) - \Delta {\mathbf{R}}\left( n \right){\mathbf{w}}\left( {n - 1} \right) \\ = & \Delta {\mathbf{q}}\left( n \right) + \left[ {{\mathbf{q}}\left( {n - 1} \right) - {\mathbf{R}}\left( {n - 1} \right){\mathbf{w}}\left( {n - 1} \right)} \right] - \Delta {\mathbf{R}}\left( n \right){\mathbf{w}}\left( {n - 1} \right) \\ = & \Delta {\mathbf{q}}\left( n \right) + {\mathbf{r}}\left( {n - 1} \right) - \Delta {\mathbf{R}}\left( n \right){\mathbf{w}}\left( {n - 1} \right) \\ \end{aligned}$$
(26)

Let \({\mathbf{q}}_{0} \left( n \right){\kern 1pt} {\kern 1pt} {\kern 1pt}\) represent the right side of (26) and we get the weight incremental canonical equation.

$${\mathbf{R}}\left( n \right)\Delta {\mathbf{w}}\left( n \right) = {\mathbf{q}}_{0} \left( n \right)$$
(27)

where \({\mathbf{q}}_{0} (n) = \lambda {\mathbf{r}}\left( {n - 1} \right) + \gamma e_{{SWA}}^{*} \left( n \right){\mathbf{x}}\left( n \right)\) (The derivation process is shown in the appendix),\(\gamma = (1 + c_{{{\text{SWA}}}} )/\beta\).

The solution of (14) is transformed into solving (27), and (27) has similar form as the normal equation. It is clear that the solution of (27) can be achieved by the DCD algorithm. After we get the \(\Delta {\mathbf{w}}\left( n \right){\kern 1pt}\), the weight vector can be calculated by \({\mathbf{w}}(n) = {\mathbf{w}}(n - 1) + \Delta {\mathbf{w}}\left( n \right){\kern 1pt}\).

We solve (14) iteratively way rather than directly, mainly based on the following two points. First, the calculation of \({\mathbf{q}}_{0} \left( n \right)\) involves less computation compared with that of \({\mathbf{q}}\left( n \right)\), and the calculation of \({\mathbf{q}}\left( n \right)\) will further enlarge the nonlinear effect involved in the algorithm. Second, with the same accuracy of calculating the weight vector, the iterative way will require a smaller number of iterations [8].

For the original SWA, the instability mainly comes from the nonlinear feedback of the filter output and finite arithmetic problems [4]. For the latter problem, it comes from the update of matrix inversion. For SWA-DCD algorithm, however, there is no need to calculate the inverse matrix, so this problem will not happen. In [4], a region of interest, which is determined by \({\text{|}}{\kern 1pt} {\kern 1pt} y{\text{(n)|}}^{{\text{2}}} \le \alpha \cdot \;C_{{1,1}}^{s}\), is provided to avoid the divergence caused by nonlinear feedback. In this paper, we take the same way to deal with the instability problem.

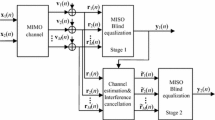
3.2 A Low Complexity Dual-mode Algorithm

When the output symbols have relatively low errors, using decision directed mode can further improve the performance of equalizer [13]. Here a dual-mode algorithm is presented. At the first stage the SWA-DCD algorithm is used, and low complexity RLS based on DCD (RLS-DCD) is taken at the second state. This dual-mode algorithm is named as SWA-RLS-DCD. The total complexity of the SWA-RLS-DCD algorithm is \(O\left( N \right)\) order of magnitude.

The main difference between SWA-DCD and RLS-DCD is the calculation \({\mathbf{q}}_{0} (n)\) in (27), which is shown as follows.

$${\mathbf{q}}_{0} (n) = \lambda {\mathbf{q}}_{0} \left( {n - 1} \right) + e_{{RLS}}^{*} \left( n \right){\mathbf{x}}\left( n \right)$$
(28)

where \({\kern 1pt} e_{{RLS}} (n) = \hat{u}(n) - y(n){\kern 1pt} {\kern 1pt}\) and \(\hat{u}(n)\) is the estimated symbol.

For dual-mode the switching point is a key factor, here we use a threshold to switch the different algorithms, which is determined by the following function.

$$g\left( y \right) = \cos ^{2} (y\pi /2d)$$
(29)

where 2d stands for the minimum distance between any two symbols in a standard constellation.

The closer the output signal is to the constellation point of the transmitted signal, the smaller the value \(g\left( y \right)\) is, and when it coincides with the signal constellation, the value is 0. Therefore the algorithm will switches to the DD mode when the following condition is reached.

$$g\left( {y_{{\text{Re} }} \left( n \right)} \right) < Th and g\left( {y_{{\text{Im} }} \left( n \right)} \right) < Th$$
(30)

where \(Th\) is the threshold, and yRe, yIm are real and imaginary parts of y(n) respectively.

The computation complexity of different algorithms is given in Table 1, where \(P_{a} \le (2N + 1)N_{u} + N_{b}\). From Table 1, it can be seen that the computation complexity of both SWA-DCD and RLS-DCD is comparable to that of CMA and LMS.

Table 1 Computation Complexity of different algorithms
Full size table

4 Simulation and Performance Anslysis

For all simulations the transmitted signal is 64QAM.Two typical channels are used.

Channel 1 [14]: \(\begin{array}{l} [ - 0.005 - 0.004{\rm{j}}\;\;0.009 + 0.03{\rm{j}}\;\; - 0.024 - 0.104{\rm{j}}\\ \quad 0.854 + 0.52{\rm{j}}\;\; - 0.218 + 0.273{\rm{j}}\;\;0.049 - 0.074{\rm{j}}\\ \; - 0.016 + 0.02{\rm{j}}]; \end{array}\)

Channel 2 [15]: \(h_{n} = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left[ {1 + \cos \left( {\frac{{2\pi }}{C}\left( {n - 2} \right)} \right)} \right]} \hfill & {n = 1,2,3} \hfill \\ 0 \hfill & {others} \hfill \\ \end{array} } \right.\)

Two evaluation indicators, MSE and residual ISI, are used for performance comparison.

Case 1 Comparison of SWA and SWA-DCD.

Here channel 1 is used. The length of the equalizer is 11. The SNR is set to 30 dB. The parameters \(\lambda\),\(N_{{\text{b}}}\) and \(N_{s}\) are set to be 0.999, 16 and 12 respectively, \(\beta\) is 2.

The result is shown in Fig. 1.We can see that SWA-DCD converges relatively slower than SWA and they reach the same results when the algorithms converge. However, the computation complexity of SWA-DCD is much smaller than that of SWA, which is very obvious when we compare the complex addition and multiplication. The results verify that the proposed algorithm can greatly reduce the implementation complexity while ensuring the equalization performance.

Fig. 1
figure 1

Performance of SWA and SWA-DCD

Full size image

Case 2 Comparison of dual-mode algorithm.

First the channel 1 is chosen. The parameters \(\lambda\) for SWA-RLS-DCD, SWA-DCD and SWA-DCD-LMS (at the second stage the LMS is used) are 0.995, 0.999 and 0.99 respectively. For DD mode the step size of LMS is 6 × 10–4,\(N_{b}\) and \(N_{s}\) are equal to 16 and 12 respectively, the switching threshold Th is 0.9, The SNR is 30 dB.

The results are shown in Fig. 2. It is clear that dual-mode algorithm has faster convergence speed and lower MSE and residual ISI compared with the single mode. Comparing the two dual-mode algorithms, SWA-RLS-DCD has relatively lower steady state error and residual ISI but with almost the same convergence speed. However, the computation complexity of the two algorithms are almost on the same order, and SWA-RLS-DCD performs better than SWA-DCD-LMS with regard to both MSE and residual ISI.

Fig. 2
figure 2

Performance of dual-mode algorithm with channel 1

Full size image

Then we take channel 2 for simulation. The channel parameter C is set to 3.3, which corresponds a channel with eigenvalue spread more than 21. The length of the channel is 11. The parameter \(\lambda\) for SWA-RLS-DCD, SWA-DCD and SWA-DCD-LMS are 0.994, 0.9995 and 0.996 respectively. The step size of LMS is 3 × 10–4, \(N_{b}\) and \(N_{s}\) are equal to 8 and 2 respectively. The SNR is 30 dB.

The results are shown in Fig. 3. From the results we see that SWA-RLS-DCD also has relatively faster convergence speed compared with that of SWA-DCD-LMS.

Fig. 3
figure 3

Performance of dual-mode algorithm with channel 2

Full size image

Both the results in Figs. 2 and 3 show that the dual-mode algorithm can achieve better performance compared with the single mode algorithm. Since the compuation complexity does not increase much, SWA-RLS-DCD is much more prefered.

The proposed algorithm solves the weight incremental norm equation rather than SWA problem directly, which avoids the computation of the matrix inversion and reduces the computation complexity with a great amount. Moreover, in the case of a small increase in computation complexity, the convergence speed of the dual-mode algorithm is obviously accelerated compared with the single mode algorithm, and the steady-state error and the residual ISI are smaller.

5 Conclusions

In this paper the DCD algorithm is introduced to lower the complexity of the SWA. At the same time a low complexity dual-mode algorithm is also presented. Simulations verify effectiveness of the proposed algorithm, especially for dual mode algorithm the proposed algorithm has not only low computation complexity but also better performance with regard to the MSE and residual ISI.