1 Introduction

A wireless sensor network (WSN) is made up of a mass of distributed autonomous sensors, which monitor the environmental conditions, such as temperature, sound, vibration, pressure, motion and pollutants [1]. WSNs have been applied to many different domains, such as environmental monitoring, hospital-tracking systems, military applications, traffic control, intelligent buildings (or bridges) and other commercial applications. The characteristics of WSNs inevitably cause a sensor node be extremely restricted by resources, including energy, memory, computing, bandwidth, and transmission range. Also due to the nature of the sensor networks, they are vulnerable to security threats, both external and internal [1–3]. Most of the security techniques devised for traditional wired networks are not directly applicable to a WSN environment [4]. Hence, security in WSNs is a very big challenge especially in critical environments.

In a security system, intrusion prevention presents the first line of defense to reduce possible intrusions but it cannot eliminate them. On the other hand, intrusion detection and response system can be used as a second line of defense to detect any suspicious behavior in network traffic [4]. Intrusion detection is defined as the process of monitoring the events occurring in a computer system or network, and analyzing them for any sign of possible incidents; which are violations (or imminent threats of violation) of computer policies, acceptable use policies, or standard practices [5]. Despite the fact that intrusion detection systems are well-implemented technologies in wired networks, there are still many open areas in intrusion detection of WSNs [6]. There are two general approaches to intrusion detection: misuse intrusion detection (MID) and anomaly intrusion detection (AID) [7–9]. Anomaly detection is best suited to WSN because its methodology is flexible and resource-friendly in general [1]. Anomaly detection is defined as the process of comparing definitions of normal activity against observed events in order to identify significant deviations. Anomaly may be caused by not only security threats, but also faulty sensor nodes in the network, or unusual phenomena in the monitoring zone [10].

Several approaches have been proposed for anomaly detection in wired/wireless networks, but they cannot be applied to WSN, as they are too computationally complex to be executed in sensor nodes. Anomaly detection techniques could be categorized as [1]: rule based methods, statistical techniques, machine learning and data mining approaches. Among them, machine learning and data mining schemes are characterized by effective detection of anomalies [11–13]. Classification methods are important systematic approaches in the data mining and machine learning community. They learn a classification model using a set of data instances (training) and classify a new incoming instance into one of the learned (normal/outlier) class (testing) [14].

The one-class classifier is a kind of classification approach that learns the boundary around the normal instances and declares any new instance falling outside this boundary as an outlier. In this kind of classification, we assume one class of data as the target class, and the remaining data is then classified as outliers. One-class classification is particularly significant in applications where only a single class of data-objects is applicable and easy to obtain. Objects from the other classes might be too difficult or expensive to be made available. Accordingly, we would only describe the target class to separate it from the outlier class. However, it is not appropriate to directly apply these kinds of anomaly detection methods which are usually used for wired networks into sensor networks, because of unique properties of sensor networks [15].

The SVDD is a kind of one-class classification approach based on support vector machine [16]. It tries to construct a boundary around the target data by enclosing the target data within a minimum hyper-sphere. Inspired by the support vector machines (SVMs), the SVDD decision-boundary is described by a few target objects, known as support vectors (SVs). A more flexible boundary can be obtained with the introduction of kernel functions, by which data is mapped into a high-dimensional feature-space. The most commonly used kernel function is Gaussian kernel [17]. The SVDD method has two major disadvantages: (1) it could sometimes generate loose decision boundaries when some noisy samples (outliers) exist in the training set, and (2) it requires the solution of a computationally-intensive quadratic programming approach, which is not applicable in WSNs.

In this paper, our goal is to propose a light-weight data mining approach for anomaly detection in WSNs and present a foresight response strategy to resist any kind of anomaly. The main contributions of this paper are as follows:

  • We introduce a new one-class classification approach for anomaly detection in WSNs based on support vector data description (SVDD).

  • We modify the standard version of SVDD, and propose a Linear Programming based Fuzzy-Constraint SVDD (LP-FCSVDD) method which is a linear optimization problem and can be solved by using the linear programming methods.

  • By defining the fuzzy constraints, the LP-FCSVDD method can identify outliers in the training set and also tolerate the sensor failure.

  • We present a foresight response strategy to resist the intentional, unintentional and false anomalies in WSNs.

The rest of the paper is organized as follows. In the next section, we summarize related work in this field. The proposed anomaly detection and foresight response strategy are explained in Sect. 3. Simulation results and performance evaluation of our approach are reported in Sect. 4. Finally, conclusions are given in Sect. 5.

2 Related work

In this section, we review related work using similar methods in the field of anomaly intrusion detection in wireless networks. In general, the anomaly detection techniques can be divided into four categories: rule based methods, statistical techniques, machine learning and data mining approaches.

In rule-based anomaly detection, the detector uses predefined rules to classify traffic as normal or anomalies. Silva et al. [18] have proposed a flexible rule-based detection scheme, in which a wide range of rules are available for a variety of application scenarios. Their approach is able to against attacks including message delay, repetition, wormhole, data alteration, jamming, message negligence, black-hole and selective forwarding. Another rule-based detection scheme is developed by Ioannis et al. [19] that concerned with the packet dropping rate. They used a cooperative decision making approach to detect black-hole and selective forwarding attacks, requiring only small amounts of communication and computational resources. Karapistoli et al. [20] proposed a rule-based detection engine that accurately analyzes data packets to detect signs of sensor network anomalies. Their presented algorithm, named ADLU, has dedicated procedures for secure cluster formation, periodic re-clustering, and efficient cluster member monitoring. Since a lot of rules are available, the rule-based anomaly detection schemes are effective against many security issues if appropriate rules are running. But, without a security expert to suggest the appropriate use of rules, these schemes can be inefficient.

In statistical techniques used for anomaly detection in WSNs, the underlying assumption is that the density distribution of the data points being analyzed for anomalies is known a priori (e.g., a Gaussian distribution). The parameters of the distribution are first estimated, and then anomalies are flagged as those data points with low likelihood given that distribution [10]. Palpanas et al. [21] have proposed a statistical technique for distributed deviation detection in the environment of sensor networks. They tried to find those values that deviate significantly from the norm to identify faulty sensors, and to filter spurious reports from different sensors. Ngai et al. [22] have presented a multivariate statistical technique based on a Chi square test to detect sinkhole attacks in a wireless sensor network. Their algorithm consists of two steps. At first, it locates a list of suspected nodes by checking data consistency, and then identifies the intruder in the list through analyzing the network flow information. The nodes affected by the intrusion are detected by testing for anomalies in the data received at the base station using the proposed test statistic. Depending on the packet arrival process, another anomaly detection scheme is proposed by Onat and Miri [23]. In their approach the standard deviation of packet arrival intervals during a specified time period is trained as the normal profile for identifying anomaly. Each sensor node maintains the normal traffic profile on its one-hop neighbor nodes. Li et al. [24] proposed a statistical distribution-based scheme for intrusion detection in wireless sensor networks. They first partitioned the sensor nodes in a network into a number of groups such that the nodes in a group are physically close to each other and sense the similar observation. And then they adopted the Mahalanobis distance measurement and the OGK estimators in the intrusion detection algorithm to take into account the inter-attribute dependencies of multidimensional observed values and ensure a high breakdown with some missing data at a lower computational cost. The statistical techniques are just suitable when the underlying type of distribution of the data is well known [10].

Recently there has been much interest in applying machine learning and data mining approaches for anomaly detection problem in WSN [25–34]. Wang et al. [34] proposed a multi-agents-based detection scheme, by combination of self-organizing map (SOM) neural network algorithm and K-means clustering algorithm. Four kinds of agents including sentry, analysis, response, and management are attached to each node over the network. Each node executes different operations of detection due to its role. In this scheme, the cluster headers are responsible for monitoring all common member nodes in the cluster, while the common member nodes are responsible for monitoring the cluster headers. Ahmadi and Abadi [33] have presented a PCA-based centralized approach, called PCACID, for anomaly detection in WSNs. They partition a WSN into groups of sensor nodes. In each group, some nodes are selected as monitor nodes. In PCACID, every monitor node independently establishes a profile of its own normal network traffic using PCA and uses it to detect anomalous network traffic. Rajasegarar et al. [35] proposed a distributed, non-parametric anomaly detection algorithm that identifies anomalous measurements at nodes based on the data clustering. They use a hyper-spherical clustering algorithm and k-nearest neighbor scheme to collaboratively detect anomalies in wireless sensor network data. In another paper, Rajasegarar et al. [36, 37] proposed a distributed anomaly detection approach based on a one-class SVM, for wireless sensor networks. They have formulated a centered hyper-ellipsoidal SVM (CESVM) scheme to achieve high detection accuracy. The CESVM has limited scope for distributed implementation in sensor networks. Also they have proposed a quarter-sphere SVM (QSSVM), as a special case of the CESVM to perform distributed anomaly detection. In general, machine learning and data mining schemes can provide high detection accuracy through the other approaches. However, the high computational complexity and the lack of applying a proper response strategy to resist any kind of anomaly, are the main shortcomings of the mentioned methods.

Therefore, in this paper, we propose a light-weight data mining approach for anomaly detection in WSNs. For this purpose, we modify the SVDD method, as a well-known one-class classification approach, to increase its accuracy and reduce its computational complexity. After detecting the anomalies, the next goal is to eliminate the effects of anomalies as much as possible in order to increasing the lifetime of WSNs. So, we present a foresight response strategy to resist the intentional, unintentional and false anomalies in WSNs.

3 Proposed methods

The support vector data description was presented by Tax and Duin [16, 38] and again in Tax and Duin [39] with extensions and a more thorough treatment. The SVDD is a one-class classification method that estimates the distributional support of a dataset. A flexible closed boundary function is used to separate trustworthy data on the inside from outliers on the outside. The basic idea of SVDD is to find a minimum hyper-sphere containing all the objective samples and none of the nonobjective samples. However, one of the major disadvantages of the SVDD method is that it cannot tolerate the outliers existed in the training set. For example, Fig. 1 shows a synthetic dataset with two noisy samples. Even with proper parameters, the SVDD cannot relinquish the outliers and they destroy the actual boundary of target object. In the following section, we propose a modified version of the SVDD to identify outliers in the training set.

Fig. 1
figure 1

SVDD boundary for a synthetic dataset with two outliers in the training set

Full size image

3.1 Fuzzy constraint SVDD (FCSVDD)

The basic idea of FCSVDD is to find a minimum hyper-sphere with fuzzy constrains. The hyper-sphere is specified by its center a and its radius R. The data description is achieved by minimizing the error function:

$$F\left( {R,a} \right) = R^{2} ,$$
(1)
$$s.t.\quad \, \left\| {x_{i} - a} \right\|^{2}\, { \lesssim }\,R^{2} ,\quad\forall i.$$
(2)

The symbol \({ \lesssim }\) means that we like to permit some violations in the satisfaction of the constraints. In order to the flexibility of the FCSVDD method, the distance of each training sample xi to the center of the sphere should not be strictly smaller than R2. However, large distances should be penalized. Therefore, after introducing slack variables \(\upxi_{\text{i}} \ge 0\) the minimization problem becomes:

$$F\left( {R,a} \right) = R^{2} + {\text{C}}\mathop \sum \limits_{\text{i}}\upxi_{\text{i}} ,$$
(3)
$$s.t.\quad \left\| {x_{i} - a} \right\|^{2} \,{ \lesssim }\,R^{2} + \,\upxi_{\text{i}} , \quad \forall i.$$
(4)

The parameter C gives the tradeoff between the volume of the description and the errors. Note that the slack variables and C cannot tolerate noisy samples. They are tuned by system without any information about importance of samples. Therefore, we need a data description method which considers this aspect.

We can easily show that each fuzzy inequality can transform to a non-fuzzy inequality. According to Fig. 2, if A is fuzzy less than B then:

$$A\,{ \lesssim }\,B \Rightarrow A \le B + d\left( {1 -\upalpha} \right).$$
(5)
Fig. 2
figure 2

Presentation of a fuzzy inequality (A≲B)

Full size image

Now we transform the fuzzy constraints in Eq. (4) to a non-fuzzy inequality.

$$\left\| {x_{i} - a^{2} } \right\|\,{ \lesssim }\,R^{2} + {\upxi}_{\text{i }} ,\quad \forall i.$$
(6)
$$\left\| {x_{i} - a^{2} } \right\| \le \left( {R^{2} + {{\upxi }}_{\text{i}} } \right) + {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right),\quad\forall i.$$
(7)

We have two new concepts in Eq. (7). They are user defined parameters which indicate the importance of samples. The weight of each sample is defined by \({\text{d}}_{\text{i}}\) and the uncertainty of this weight is shown by α. The value of \({\text{d}}_{\text{i}}\) can be defined by user or some automatic methods (such as inverse of distance of each sample to the center of training set). So we have the following error function:

$$F\left( {R,a} \right) = R^{2} + {\text{C}}\mathop \sum \limits_{\text{i}}\upxi_{\text{i}} ,$$
(8)
$$s.t.\quad \, \left\| {x_{{{\text{i}} - a}} } \right\|^{2} \le (R^{2} +\upxi_{\text{i}} ) + {\text{d}}_{\text{i}} \left( {1 -\upalpha} \right),\quad \forall i.$$
(9)

In order to solve this problem the constraints should be incorporated into the error function by introducing Lagrange multipliers and constructing the Lagrangian function.

$${\text{L}}\left( {{\text{R}}, {\text{a}},\upalpha_{\text{i}} ,\upgamma_{\text{i}} ,\upxi_{\text{i}} } \right) = {\text{R}}^{2} + {\text{C}}\mathop \sum \limits_{\text{i}}\upxi_{\text{i}} - \mathop \sum \limits_{\text{i}} \lambda_{\text{i}} \left\{ {\left( {{\text{R}}^{2} +\upxi_{\text{i}} } \right) + {\text{d}}_{\text{i}} \left( {1 -\upalpha } \right) - \left( {\left\| {{\text{x}}_{\text{i}} } \right\|^{2}- 2a.{\text{x}}_{\text{i}} + \left\| {\text{a}} \right\|^{2} } \right)} \right\} - \mathop \sum \limits_{\text{i}}\upgamma_{\text{i}}\upxi_{\text{i}} ,$$
(10)

with the Lagrange multipliers \({\uplambda}_{\text{i}} \ge 0\) and \({\upgamma}_{\text{i}} \ge 0\). Setting partial derivatives to 0 gives these constraints:

$$\frac{{\partial {\text{L}}}}{{\partial {\text{R}}}} = 0: \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} = 1,$$
(11)
$$\frac{{\partial {\text{L}}}}{\partial a} = 0 :a = \frac{{\mathop \sum \nolimits_{\text{i}} {\uplambda}_{\text{i}} {\text{x}}_{\text{i}} }}{{\mathop \sum \nolimits_{\text{i}} {\uplambda}_{\text{i}} }} = \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{x}}_{\text{i}} ,$$
(12)
$$\frac{{\partial {\text{L}}}}{{\partial {\upxi}_{\text{i}} }} = 0:{\text{C}} - {\uplambda}_{\text{i}} - {\upgamma}_{\text{i}} = 0.$$
(13)

From the above equations and the fact that the Lagrange multipliers are not all negative, when we add the condition \(0 < \lambda_{\text{i}} < {\text{C}},\) Lagrange multipliers \({\upgamma}_{\text{i}}\), can be safely removed. So the problem can be transformed into maximizing the following function L with respect to the Lagrange multipliers \({\uplambda}_{\text{i}} :\)

$$\hbox{max} \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right) - \mathop \sum \limits_{{{\text{i}},{\text{j}}}} {\uplambda}_{\text{i}} {\uplambda}_{\text{j}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right) - \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right),$$
(14)
$${\text{s}}.{\text{t}} .\quad 0 < {\uplambda}_{\text{i}} < {\text{C}}.$$
(15)

Similar to the SVDD method, for more flexible boundaries, inner products of samples \(\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right)\) can be replaced by a kernel function \({\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right)\), where \({\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right)\) satisfies Mercer’s theorem [40]. This implicitly, maps samples into a nonlinear space to obtain a more tight and nonlinear boundary. In this context, the FCSVDD problem can be expressed as:

$$\hbox{max} \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right) - \mathop \sum \limits_{{{\text{i}},{\text{j}}}} {\uplambda}_{\text{i}} {\uplambda}_{\text{j}} {\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right) - \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right),$$
(16)
$${\text{s}}.{\text{t}}\quad 0 < {\uplambda}_{\text{i}} < C.$$
(17)

Note that from Eq. (12), the center of the sphere is a linear combination of the training samples. Only those training samples xi which satisfy Eq. (7) by equality are needed to generate the description since their coefficients are not zero. Therefore these samples are called Support Vectors. The radius can be computed using any of the support vectors:

$${\text{R}}^{2} = \left( {{\text{x}}_{\text{k}} \cdot {\text{x}}_{\text{k}} } \right) - 2\mathop \sum \limits_{\text{i}} \lambda_{\text{i}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{k}} } \right) + \mathop \sum \limits_{\text{i,j}} \lambda_{\text{i}} \lambda_{\text{j}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right) - {\text{d}}_{\text{k}} \left( {1 -\upalpha } \right).$$
(18)

To judge whether a test sample \({\text{x}}_{\text{z}}\) is in the target class or not, its distance to the center of sphere is computed and compared with R, if satisfies Eq. (9), it will be accepted, and otherwise, rejected.

$$\left\| {{\text{x}}_{\text{z}} - {\text{a}}^{2} } \right\| = \left( {{\text{x}}_{\text{z}} \cdot {\text{x}}_{\text{z}} } \right) - 2\mathop \sum \limits_{\text{i}} \lambda_{\text{i}} \left( {{\text{x}}_{\text{z}} \cdot {\text{x}}_{\text{i}} } \right) - \mathop \sum \limits_{\text{i,j}} \lambda_{\text{i}} \lambda_{\text{j}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{j}} } \right) \le {\text{R}}^{2} + {\text{d}}_{\text{z}} \left( {1 -\upalpha } \right).$$
(19)

Several kernel functions have been proposed for the support vector classifiers. Not all kernel functions are equally useful for the FCSVDD. It has been demonstrated that using the Gaussian kernel results in tighter description. The results of FCSVDD for different value of α are shown in Fig. 3. We assume that the weights of outlier samples are half of the other samples. If α = 1 or all of the samples have the same weights, the results of FCSVDD is the same as SVDD method.

Fig. 3
figure 3

FCSVDD boundaries for a synthetic dataset with two outliers in the training set. The effect of outlier samples will be eliminated by decreasing the uncertainty value (α). If α = 1 the results of FCSVDD is the same as SVDD. a α = 1, b α = 0.9, c α = 0.7, d α = 0.5, e α = 0.3, f α = 0.1

Full size image

3.2 Linear Programming based FCSVDD (LP-FCSVDD)

Here we address the computational challenge of FCSVDD for using in WSN. FCSVDD requires the solution of a computationally intensive quadratic programming approach which is not applicable in WSN. We solved this problem by formulating a centered hyper-spherical scheme, which enables us to use a linear programming approach. Consider the following minimization problem:

$$F\left( {R,a} \right) = R^{2} + {\text{C}}\mathop \sum \limits_{\text{i}} {\upxi}_{\text{i}} ,$$
(20)
$$\begin{aligned} s.t. \left\|x_{i}\right\|^{2} \,{ \lesssim }\,R^{2} + {\upxi}_{\text{i}},\;\;\forall i . \hfill \\ {\upxi}_{\text{i}} \ge 0,\;\; \forall i . \hfill \\ \end{aligned}$$
(21)

As mentioned above, we can transform the fuzzy constraints in Eq. (21) to a non-fuzzy inequality. Hence the minimization problem becomes:

$$F\left( {R,a} \right) = R^{2} + {\text{C}}\mathop \sum \limits_{\text{i}} {\upxi}_{\text{i}} ,$$
(22)
$$\begin{aligned} s.t. \quad \left\|x_{i}\right\|^{2} \le \left( {R^{2} + {\upxi}_{\text{i}} } \right) + {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right),\quad \forall i. \hfill \\ {\upxi}_{\text{i}} \ge 0,\quad \forall i . \hfill \\ \end{aligned}$$
(23)

The constraints can be incorporated into the error function by introducing Lagrange multipliers and constructing the Lagrangian.

$${\text{L}}\left( {{\text{R}},{{ \lambda }}_{\text{i}} ,{\upgamma}_{\text{i}} ,{{ \xi }}_{\text{i}} } \right) = {\text{R}}^{2} + {\text{C}}\mathop \sum \limits_{\text{i}} {\upxi}_{\text{i}} - \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} \left\{ {\left( {{\text{R}}^{2} + {\upxi}_{\text{i}} } \right) + {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right) - \left\| {{\text{x}}_{\text{i}}^{2} } \right\|} \right\} - \mathop \sum \limits_{\text{i}} {\upgamma}_{\text{i}} {\upxi}_{\text{i}} ,$$
(24)

With the Lagrange multipliers \({\uplambda}_{\text{i}} \ge 0\) and \({\upgamma}_{\text{i}} \ge 0\). Setting partial derivatives to 0 gives these constraints:

$$\frac{{\partial {\text{L}}}}{{\partial {\text{R}}}} = 0 : \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} = 1 ,$$
(25)
$$\frac{{\partial {\text{L}}}}{{\partial {\upxi}_{\text{i}} }} = 0 :{\text{C}} - {\uplambda}_{\text{i}} - {\upgamma}_{\text{i}} = 0 .$$
(26)

Therefore, the problem can be transformed into maximizing the following programming problem:

$$\hbox{max} \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} \left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right) - \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right) ,$$
(27)
$$\begin{gathered} {\text{s}}.{\text{t }}\mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} = 1 , \hfill \\ 0 < {\uplambda}_{\text{i}} < C. \hfill \\ \end{gathered}$$
(28)

Using the kernel trick, the inner product can be replaced by a kernel function \({\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right)\), and the following optimization problem is obtained:

$$\hbox{max} \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right) - \mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} {\text{d}}_{\text{i}} \left( {1 - {\upalpha}} \right)$$
(29)
$$\begin{gathered} {\text{s}}.{\text{t}} .\mathop \sum \limits_{\text{i}} {\uplambda}_{\text{i}} = 1 , \hfill \\ 0 < {\uplambda}_{\text{i}} < C. \hfill \\ \end{gathered}$$
(30)

This dual problem is a linear optimization problem, so the \({\uplambda}_{\text{i}}\) can be obtained using widely available linear optimization techniques. Compared to the SVDD and FCSVDD formulations, which require solving a quadratic optimization problem, this formulation with linear optimization is advantageous in terms of its computations.

Further, in Eq. (29) the solution is affected only by the norms of the non-linear mapping of data vectors using the kernel \({\text{K}}\left( {{\text{x}}_{\text{i}} \cdot {\text{x}}_{\text{i}} } \right)\). This creates a problem for the application of this approach with distance-based kernels such as the RBF kernel, as the norms of the kernels are now equal for all data vectors [36, 41]. In order to solve this problem, the centered image vectors can be computed by:

$$\tilde{\varPhi }\left( {x_{i} } \right) = {\Phi }\left( {x_{i} } \right) - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} {\Phi }(x_{i} )$$
(31)

In other words, the mapped vectors are subtracted from the mean in the feature space. The dot product \(\tilde{K} = \left( {\tilde{\varPhi }\left( {{\text{x}}_{\text{i}} } \right) \cdot \tilde{\varPhi }\left( {{\text{x}}_{\text{i}} } \right)} \right)\) of the centered image vectors can be obtained in terms of kernel \({\text{K}} = \left( {{\Phi }\left( {{\text{x}}_{\text{i}} } \right) \cdot {\Phi }\left( {{\text{x}}_{\text{i}} } \right)} \right)\) as follows:

$$\tilde{K} = K - 1_{n} K - K1_{n} + 1_{n} K1_{n} ,$$
(32)

where \(1_{\text{n}}\) is an \({\text{n}} \times {\text{n}}\) matrix with all values equal to \(1/{\text{n}}\). \(\tilde{K}\) is called the centered kernel matrix [40]. Once the image vectors are centered, the norms of the kernels are no longer equal. Hence the dual problem might be solved now. Figure 4 shows the decision boundary which is generated by LP-FCSVDD method around the target class with cross markers. The LP-FCSVDD method can produce a very tight description for the target class similar to a quadratic one-class classifier. Moreover, it can detect the outliers and eliminate them from the target class boundaries.

Fig. 4
figure 4

LP-FCSVDD in comparison with the standard SVDD. a SVDD could sometimes generate such a loose decision boundary, when some noisy samples exist in the training set. b The LP-FCSVDD method detects the outliers exist in the training set and generates much better decision boundaries

Full size image

3.3 Distributed anomaly detection and foresight response strategy in WSN

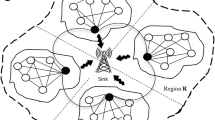
In this section, the LP-FCSVDD method is applied to resist anomalies in WSN. The sensor nodes can be organized as a flat network or a clustered network. In the flat architecture, all sensor nodes transmit their own data and relay data for other nodes to the sink. In the clustered architecture, adjacent nodes are organized as a cluster; a head is elected for each cluster. Sensor nodes that belong to the same cluster can only send or relay data to their cluster head. The cluster head then relays the data to the sink via a long-haul communication link [42].

Here we want to find local and global anomalies in the data measurements collected by each node in the network. Local anomalies are anomalous measurements in a sensor node’s own (local) data measurements, where only the measurements at the same node are used as a basis for comparison. However, we are also interested in cases where the majority of measurements at a sensor node are anomalous in comparison to other nodes in the network. These global anomalies are anomalous measurements in the union of the measurements collected from multiple sensor nodes in the network. Local anomalies can be detected by considering local measurements of a sensor node without incurring any energy intensive communication overhead in the network. However, detecting global anomalies requires all the measurements from multiple nodes to be considered. Centralized schemes perform this by communicating all the sensor measurements to a central node to detect global anomalies. However, communicating all the measurements in the network is an energy-intensive operation, which affects the lifetime of the network. Hence, we require energy efficient distributed approaches to detect these anomalies in sensor networks. This motivates us to propose a distributed anomaly detection approach using LP-FCSVDD that can efficiently and effectively detect anomalies (local and global) in data measurements collected by sensor nodes in wireless sensor networks [37].

After detecting anomalies, a proper response strategy should be trigger to resist the anomaly effects. Here, we introduce a foresight response model for intentional, unintentional and false anomalies (see Fig. 5). If the anomaly is caused by a faulty sensor, we can estimate the sensor error to eliminate the negative impact in global radius computation. But when the error is intentional, ignoring the compromised sensor outcomes is the best solution for response. Also, when the detection process leads to false anomalies, we should improve the detection parameters and use the sensor outcomes. Hence, selecting the proper response in each situation minimizes the cost of response in future.

Fig. 5
figure 5

The possible future and foresight response strategy, when an anomaly is detected

Full size image

First, we consider a clustered based wireless sensor network, deployed to monitor an area of interest. In the distributed anomaly detection process, each sensor \(({\text{S}}_{\text{j}} )\) runs the LP-FCSVDD method on its own data to find the local radius (\({\text{R}}_{\text{j}}^{{({\text{t}})}}\)) as a decision boundary in time-window (t). The cluster head \(({\text{S}}_{0} )\) collects these obtained local radii from all sensors in the cluster and computes the mean of them as the global radius (R (t) g ). The cluster head sends the global radius to each sensor node in its cluster except the compromised nodes. After detecting the anomalies, we should trigger the foresight response strategy to mitigate the intentional, unintentional and false anomalies. For this purpose, we compute a trust value between 0 (untrusted) and 1 (fully trusted) for each sensor node.

According to the given trust value, we should apply one of the following response strategies:

  • The sensor’s trust value is very low (its value is close to zero): we should ignore the sensor outcomes.

  • The sensor’s trust value is very high (its value is close to one): we should improve the detection parameters and use the sensor outcomes.

  • The sensor’s trust value is medium (its value is around 0.5): we should estimate the sensor error to eliminate the negative impact in global radius computation.

Algorithm 1 presents the distributed anomaly detection and foresight response strategy using LP-FCSVDD to resist the local and global anomalies in a clustered based WSN. We use a similar method for a wireless sensor network with flat topology. Each sensor runs the LP-FCSVDD method on its own data to find the local radius and broadcast it to its neighbors. When a sensor receives the all of the neighbor’s radii, computes the global radius, the trust value of its neighbors and its own trust value. The neighbors which have very low trust value are tagged as compromised nodes and ignored in global radius computation. Also, we can compute the weight of each sensor according to its own trust value. Then each sensor runs the LP-FCSVDD method again with the new samples weight. Algorithm 2 presents the distributed anomaly detection and foresight response strategy using LP-FCSVDD to resist the local and global anomalies in a flat WSN. Figure 6 shows the process of scheme according to the mentioned algorithms for distributed anomaly detection and foresight response strategy in a clustered and flat WSN.

figure e
figure f
Fig. 6
figure 6

Distributed anomaly detection and response process using LP-FCSVDD method in a clustered WSN b flat WSN

Full size image

3.4 Complexity analysis

This section analyzes the complexity of the proposed anomaly detection and response strategy. Suppose that \({\text{s}}\) is the number of sensor nodes in the network, \({\text{n}}\) is the number of data vectors at a sensor node, and \({\text{p}}\) is the number of dimensions in a data vector. The LP-FCSVDD method involves the computation of a kernel matrix \({\text{K}}\) with a computational complexity of \({\text{O}}({\text{n}}^{2} )\) and solving a linear optimization problem. Several approaches have been proposed for the linear programming in the literature. Khachiyan [43] was the first to show that the linear programming problem could be solved in time polynomial in the length of the binary encoding of the input. Karmarkar’s original method requires a total complexity of \({\text{O}}({\text{n}}^{4} {\text{L}})\) arithmetic operations where \({\text{n}}\) is the number of variables and \({\text{L}}\) is the length of the input data. Subsequent results have reduced this to a total complexity of \({\text{O}}({\text{n}}^{3} {\text{L}})\) [44]. On the other hand, it is demonstrated that the linear programming problem with \({\text{d}}\) variables and \({\text{m}}\) constraints can be solved in \({\text{O}}({\text{m}})\) time when \({\text{d}}\) is fixed [45]. According to Eq. (21), in our proposed linear programing model the number of constraints \(({\text{m}})\) is equal to the number of data vectors at a sensor node \(({\text{n}})\), so the total computational complexity of LP-FCSVDD is \({\text{O}}\left( {\text{n}} \right) + {\text{O}}({\text{n}}^{2} )\).

In the proposed distributed scheme, each sensor node runs LP-FCSVDD on its own data with time complexity \({\text{O}}\left( {\text{n}} \right) + {\text{O}}({\text{n}}^{2} )\) and the memory complexity of \({\text{O}}({\text{np}})\). Furthermore, in the foresight response strategy, the trust value of each sensor is computed by time complexity \({\text{O}}({\text{n}})\) and the memory complexity of \({\text{O}}({\text{n}})\). So the total time complexity of proposed approach is \(2{\text{O}}\left( {\text{n}} \right) + {\text{O}}({\text{n}}^{2} )\) and the total memory complexity is \({\text{O}}\left( {\text{np}} \right) + {\text{O}}({\text{n}})\). It also requires communication of the radius information and the sensor weights with a communication complexity of \({\text{O}}\left( 1 \right)\). In the centralized approach, each sensor node sends its local data into the central node (i.e., base station). So, the communication of the whole set of data measurements to a central node with a communication complexity of \({\text{O}}\left( {\text{np}} \right)\) per link leads to a total complexity of \({\text{O}}({\text{snp}})\). The central node runs LP-FCSVDD on the collected data with a maximum computational complexity of \({\text{O}}({\text{s}}^{2} {\text{n}}^{2} )\), and also the trust value of each sensor is computed by time complexity \({\text{O}}({\text{sn}})\). The memory complexity at the central node is \({\text{O}}\left( {\text{snp}} \right) + {\text{O}}({\text{sn}})\), which includes the memory complexity required to keep data vectors and the trust value of sensors. In Table 1 the complexity of proposed anomaly detection and foresight response strategy is summarized in both centralized and distributed schemes.

Table 1 Comparison of various complexities for the distributed and centralized anomaly detection schemes using LP-FCSVDD
Full size table

4 Experiments

In this section, we want to evaluate the performance of our proposed methods by applying them to real and synthetic datasets. The synthetic dataset is similar to that used by Rajasegarar et al. [37]. It has two features, each generated from a normal distribution with mean 1 and standard deviation 3. Noise samples are generated by uniformly distributed data around the normal samples. The synthetic dataset consists of 15 sensor nodes and comprises 1,575 data vectors of two features, including 75 outliers.

In the first experiment, we apply the proposed methods to the synthetic dataset. Figure 7 shows the area under the ROC curve (AUC) for LP-FCSVDD and FCSVDD, which have linear and quadratic complexities respectively. Here, we use the RBF kernel with different value for the \({{ \sigma }}\) parameter in the range 2−10–240, in exponential intervals. This experiment shows that the proposed linear method has the same performance, compared to the quadratic one.

Fig. 7
figure 7

AUC for LP-FCSVDD and FCSVDD methods in the synthetic dataset by using the RBF kernel (\({\varvec{\upsigma}}\) is the kernel parameter)

Full size image

In the second experiment, we applied SVDD and LP-FCSVDD methods for the synthetic dataset in centralized scheme. The false positive rate (FPR) is then computed as the percentage ratio between the false positives and the actual normal measurements. Also, the true positive rate (TPR) is computed as the percentage ratio between the true positives and the actual anomalous measurements. Table 2 and Fig. 8 show the obtained results for SVDD and LP-FCSVDD methods in the synthetic dataset. In this experiment, we get the AUC value of 0.9964 and 0.9742 for LP-FCSVDD and SVDD methods respectively.

Table 2 SVDD and LP-FCSVDD results for the synthetic dataset in centeralized scheme
Full size table
Fig. 8
figure 8

ROC curves for SVDD and LP-FCSVDD methods in the synthetic dataset in centralized scheme

Full size image

Now, we evaluate the proposed methods with two real WSN datasets namely the IBRL and GDI datasets. The IBRL dataset contains information about data collected from 54 sensors deployed in the Intel Berkeley Research Lab, between February 28th and April 5th, 2004. Mica2Dot sensors with weather-boards collected time-stamped topology information, along with humidity, temperature, light and voltage values once every 31 s. The data was collected using the TinyDB in-network query processing system, built on the TinyOS platform [46]. The sensors were arranged in the lab, according to the diagram shown in Fig. 9. We considered a part of this dataset formed from measurements collected by 5 sensor nodes, namely, the nodes 1, 2, 3, 33 and 35 which are closed to each other. A 24-h period of data, recorded on March 6, 2004, was used in our evaluation. The sensor’s data is divided into 41 time-windows and three attributes are used for each data vector including humidity, temperature, and light measurements.

Fig. 9
figure 9

The sensors position in the IBRL dataset

Full size image

The other real dataset that we used was the sensor measurements gathered from a deployment of wireless sensors in the Great Duck Island (GDI), Maine, USA [31, 47]. The network monitors the habitat of a sea bird called the Leach’s Storm Petrel. This is an example of an outdoor environmental monitoring deployment. Each sensor recorded temperature, humidity, and barometric pressure at 5-min intervals. Five sensor nodes are selected for the evaluation, namely nodes 101, 103, 110, 111 and 129 that are physically close to each other and sense the similar observation. A 24-h period of data recorded on June 18, 2003, was used in our evaluation. Each data vector has three features: humidity, temperature and pressure.

We define two scenarios to evaluate the proposed anomaly detection and foresight response strategies. In the first scenario, some noisy samples are generated randomly and added to the normal data in each time-window. Then, the mentioned anomaly detection approach runs on each time-window. Tables 3 and 4 present the summary results of simulation for each sensor node in the IBRL and GDI datasets respectively. The average of each measure for all time-windows is displayed in the results. The detailed results for applying LP-FCSVDD method on sensor node 1 in the IBRL dataset and sensor node 101 in the GDI dataset is described in Tables 7 and 8 of appendix. Figure 10 shows ROC curves for these experiments in both centralized and distributed schemes.

Table 3 SVDD and LP-FCSVDD results for the sensor nodes 1, 2, 3, 33 and 35in the IBRL dataset
Full size table
Table 4 SVDD and LP-FCSVDD results for the sensor nodes 101, 103, 110, 111 and 129 in the GDI dataset
Full size table
Fig. 10
figure 10

ROC curves for SVDD and LP-FCSVDD methods a in the IBRL dataset b in the GDI dataset

Full size image

In the second scenario, in addition to injecting some noisy samples, we suppose that there is a compromised sensor which generates intentional anomalies. In this situation we should ignore the compromised sensor outcomes because it has negative impact in global radius computation. Suppose that node 1 is a compromised sensor and generates intentional anomalies in the IBRL dataset. Without applying the foresight response strategy, the accuracy of detection is severely decreased over the time. Table 5 and Fig. 11 show the LP-FCSVDD results with/without response strategy for the centralized and distributed schemes in the IBRL dataset. Similar results were obtained by repeating the experiment for the GDI dataset (see Table 6, Fig. 12).

Table 5 LP-FCSVDD results with/without applying the foresight response strategy in the IBRL dataset. Suppose that node 1 is a compromised sensor and generates intentional anomalies
Full size table
Fig. 11
figure 11

ROC curves for LP-FCSVDD with/without applying the foresight response strategy in the IBRL dataset. Suppose that node 1 is a compromised sensor and generates intentional anomalies

Full size image
Table 6 LP-FCSVDD results with/without applying the foresight response strategy in the GDI dataset. Suppose that node 101 is a compromised sensor and generates intentional anomalies
Full size table
Fig. 12
figure 12

ROC curves for LP-FCSVDD with/without applying the foresight response strategy in the GDI dataset. Suppose that node 101 is a compromised sensor and generates intentional anomalies

Full size image

The proposed anomaly detection and foresight response strategy has the following advantages: (1) it can detect the anomalies with high accuracy in polynomial time, (2) it can be used in a distributed scheme with minimal communication overhead, and (3) it can offer a proper response strategy to eliminate the effect of intentional anomalies. Accordingly, we can apply the LP-FCSVDD as a robust distributed anomaly detection method in WSNs which resist the intentional, unintentional and false anomalies.

5 Conclusion

In this paper, we have presented a new approach to address the problem of anomaly detection and response strategy in wireless sensor networks. The proposed approach is based on support vector data description (SVDD) as a popular one-class classifier. The SVDD method has two major disadvantages: (1) It could sometimes generate such a loose decision boundary when some noisy samples (outliers) exist in the training-set, and (2) It requires the solution of a computationally intensive quadratic programming approach, which is not applicable in WSN. We present the FCSVDD method to solve the first problem. The basic idea of FCSVDD method is to find a minimum hyper-sphere around the target class by using the fuzzy constrains. Unfortunately, the FCSVDD method requires a quadratic programming approach to find the decision boundaries. We solved this problem by formulating a centered hyper-spherical scheme, which enables us to use a linear programming approach and proposed the Linear-Programming based Fuzzy-Constraint SVDD (LP-FCSVDD) method. The using of fuzzy constraints leads to additional abilities that can be used in the response process to tolerate the sensor failure. Accordingly, we present a foresight response strategy to mitigate the intentional, unintentional and false anomalies. In order to evaluate our proposed approach, we use a synthetic dataset and two real WSN datasets namely the IBRL and GDI. The results show the prominence of the LP-FCSVDD method to detect local and global anomalies in WSNs.