An Explicit Solution for Image Restoration using Markov Random Fields

Abstract

Image restoration and denoising is an essential preprocessing step for almost every subsequent task in computer vision. Markov Random Fields offer a well-founded, sophisticated approach for this purpose, but unfortunately the associated computation procedures are not sufficiently fast, due to a high-dimensional optimization problem. While the increase of computing power could not solve this runtime issue appropriately, we address it in a mathematical way: we suggest an analytical solution for the optimum of the inference problem, which provides desirable mathematical properties. In practice, our new method accelerates the runtime via reducing the computational complexity of the image restoration task by orders of magnitude, independent from the smoothing intensity. As a result, Markov Random Fields can be considered for modern big data problems in computer vision, especially if numerous images with equal sizes are processed.

1 Introduction

Among other areas in computer science, image processing and computer vision are nowadays facing an increasing number of big data applications. Hence, huge datasets consisting of a multitude of images need to be processed in parallel. In order to deal with this new requirement, the efficiency of algorithms has become crucial. Regarding the tasks of image restoration, pattern enhancement and noise reduction, faster tools (such as e.g. convolution) increased in popularity compared to slower, model-based approaches.

Markov Random Fields (MRF) provide an image restoration procedure, first suggested by Geman and Geman [6], with a strong theoretical background, based on Bayesian inference for a spatial stochastic model. In contrast to convolution-based methods, the MRF procedure can be proven to reach an optimal and mathematically tractable result for image restoration. Unfortunately, in spite of their promising model and properties, performing Bayesian inference requires a continuous optimization by an iterative scheme for each single image in a high-dimensional space, such as Gradient Descent (GD). Furthermore, the runtime of the optimization (which is proportional to the number of iterations) highly depends on a smoothing parameter, indicating the degree of noise reduction. Therefore, a higher level of noise on the image will result in a longer runtime of the denoising procedure.

From a mathematical perspective, gradient-based optimization methods are known to converge towards the optimum for real-valued, differentiable, convex target functions [4]. Nevertheless, the speed of convergence might be very low. Even though improvements for this method increase the convergence rate by e.g. employing conjugate gradients instead of the steepest descent direction [7], they do not sufficiently solve the issue for a high number of independent optimization problems.

We propose to solve the runtime issue of the MRF model for image restoration in a different way: due to the quadratic structure of the target function, we solve the optimization problem explicitly and thereby solve a linear equation system. By investigating the properties of the resulting matrix, we detect that solving the system can be achieved via a Block Cholesky Decomposition [5], which saves valuable computation time. Additionally, the method shows the benefit that the resulting matrix only depends on the neighborhood structure, the image size and the smoothing parameter and not on the image content - hence, multiple images can be processed by forward and backward substitution using one constant matrix decomposition.

We apply the MRF image restoration procedure to three different images, comparing GD and the analytical optimization method for different smoothing intensities. The results provide evidence for two desired properties of our suggested method: firstly, the quality of noise reduction is improved as the exact optimum is returned instead of an approximation. Secondly, the computational complexity, indicated by the runtime comparison of the algorithms, is significantly reduced, especially if multiple equally-sized images are processed successively. In summary, our proposed method is able to enhance the usability of MRFs for image restoration significantly.

2 Markov Random Fields for Image Restoration

According to [1], a MRF is a multivariate stochastic process, which describes a field of random variables by their local, spatial dependencies. In contrast to Markov chains, i.e. a category of univariate stochastic processes, a random field consists of multiple dimensions, usually interpreted as space or space-time components. The so-called Markov property, which is frequently investigated in applications of time series, is extended to a local neighborhood of nodes in the corresponding undirected graph.

Applications of MRF models include image processing, computer vision and geostatistics. In the context of image analysis, MRFs can be used for low-level image transformation and filtering, as well as for higher-level tasks, such as object or texture classification, see e.g. [2].

2.1 Theory of Markov Random Fields

In general, an MRF model consists of a graph G = (V, E), which defines spatial neighborhoods by the edges E between the nodes in V. Each node v ∈ V is considered as a random variable, with n = |V |, i.e. n is the number of nodes in V. As the joint probability distribution $\mathcal {P}$ over all nodes in V is n-dimensional, it is rarely possible to estimate it in any practical model. To resolve this issue, each node v ∈ V is assumed to fulfill the Markov property, i.e.

$$ \mathcal{P}(v|w \in V) = \mathcal{P}(v|w \in \mathcal{N}(v)), $$

(1)

where $\mathcal {N}(v) \subset V$ is defined as the set of neighbors of node v in the graph G. This property implies that each node exclusively depends on its neighbors, but is conditionally independent from all other nodes in G, provided that the neighbors are known.

Under the assumption that the Markov property holds, the joint probability distribution $\mathcal {P}$ can be decomposed into the product of the probability distribution over the complete subgraphs in G, i.e. the so-called cliques C_l of G, where $l\in \mathbb {N}$ denotes the clique size. This can be explained by the Hammersley-Clifford theorem [3], which characterizes the joint probability distribution of an MRF explicitly: a random field fulfills the Markov property if and only if its joint probability distribution is a so-called Gibbs distribution. The Gibbs distribution is characterized by the probability density function $f_{\text {Gibbs}}:\mathbb {R}^{n}\rightarrow \mathbb {R}$,

$$ f_{\text{Gibbs}}(\mathbf{x}) = Z(\beta)^{-1}e^{-\beta E(\mathbf{x})}, $$

(2)

where $\beta \in \mathbb {R}$ is the distribution parameter, Z(β) is a normalizing constant and $E:\mathbb {R}^{n}\rightarrow \mathbb {R}$ is called the energy function. The latter is required to be decomposable into clique potentials $V_{l}:\mathbb {R}^{l}\rightarrow \mathbb {R}$, introducing the impact of each clique in C_l. In summary, it follows that the (global) joint density function f_Gibbs is decomposed into (local) marginal densities. Consequently, Eq. 2 can be decomposed as well:

$$ f_{\text{Gibbs}}(\mathbf{x}) \propto \prod\limits_{\{i\}\in C_{1}} e^{-\beta V_{1}(x_{i})} \cdot \underset{\{i,j\}\in C_{2}}{\prod\prod} e^{-\beta V_{2}(x_{i},x_{j})} \cdot {\dots} \\ $$

(3)

This result renders unnecessary to determine the joint (global) distribution $\mathcal {P}$ over all nodes in V - instead, the marginal (local) distribution over each clique is sufficient to specify the MRF model.

In low-level image analysis, each node v ∈ V usually refers to one pixel in the image. The edges in the graph are commonly defined as a regular 4-, 8-, 12- or 24-neighborhood structure, see Fig. 1. Such models are highly complex due to the high number of nodes, especially in high-resolution images containing up to several millions of image pixels. This results in the need for fast algorithms and high computing power to process the model in a reasonable period of time.

Figure 1

Regular 4-, 8-, 12- or 24- neighborhood structures are usually used for low-level MRF models for image analysis.

In the following, we will restrict to the task of image denoising and pattern enhancement using a MRF model. This task is categorized as a low-level problem in image processing literature and will be tackled by a well-known Bayesian inference procedure.

2.2 The Model for Image Restoration

Li [2] presented a Bayesian image restoration approach, based on the assumption that a denoised image corresponds to a continuous, 2-dimensional surface. In MRF models for computer vision, the maximum a posteriori (MAP) probability in combination with decision theory is the most popular approach to derive statistical models. For a given grayscale image, let S be a set of image pixels (given by their x- and y-coordinates) and n = |S| is the number of pixels in the image. For reasons of simplicity, the 2-dimensional index set S will be reduced to 1 dimension in the following, assuming a column-wise numbering of the image pixels. Models for image restoration and image denoising commonly consist of the real (noisy) pixel intensities $\mathbf {d} \in \mathbb {R}^{n}$, the underlying true pixel values $\mathbf {x} \in \mathbb {R}^{n}$ and an error term $\mathbf {\varepsilon } \in \mathbb {R}^{n}$. Hence, we define the observation model as

$$ \mathbf{d}=\mathbf{x}+\mathbf{\varepsilon}, $$

(4)

where ε is assumed as homogenous Gaussian white noise, i.e. $\varepsilon _{i}\underset {\text {i.i.d.}}{\sim }\text {N}(0,\sigma ^{2})$. Note that the restriction of variance homogeneity, i.e. $\sigma _{i} \equiv \sigma , ~\forall i\in \{1,\dots ,n\}$, is not mandatory for the model, but will be assumed in this paper. With this setup the likelihood function L of the restored image values x (which is defined as the probability density function of d given x) is given as

$$ L(\mathbf{d}|\mathbf{x})=\left( 2\pi\sigma^{2}\right)^{-\frac{n}{2}}e^{-U(\mathbf{d}|\mathbf{x})}, $$

(5)

where

$$ U(\mathbf{d}|\mathbf{x})=\sum\limits_{i\in S}\frac{(x_{i}-d_{i})^{2}}{2\sigma^{2}} $$

(6)

is the so-called likelihood energy. Notice, that Eq. 5 is a special case of a Gibbs distribution (2), where only single-site clique potentials, i.e. corresponding to cliques of size 1, are considered for the energy function.

For the definition of a prior distribution we deploy the Hammersley-Clifford-theorem (see Section 2.1). Hence, to specify the prior distribution of an MRF we have to define the clique potential functions V_l in the related Gibbs prior distribution. For continuous, bounded surfaces usually only pair-site clique potentials, i.e. cliques of size 2, are used (Li [2]). For this purpose, we can define a function $g:\mathbb {R}\rightarrow \mathbb {R}$ as follows:

$$ V_{2}(x_{i},x_{j})=g(x_{i}-x_{j}). $$

(7)

This function g penalizes the deviation from a continuous surface, effected by the difference x_i − x_j. In case of image denoising and restoration it is required that g fulfills the following properties:

$$ g(\zeta)=g(-\zeta) \text{ (even)} $$

(8)

$$ g^{\prime}(\zeta)\geq 0\text{, for }\zeta\in[0,\infty) \text{ (non-decreasing)} $$

(9)

Various choices exist for g, related to smoothness assumptions, continuity properties, or labeling problems (Geman and Geman [6], Li [2], Blake and Zisserman [8]). In this paper we use a simple quadratic function

$$ g(x_{i}-x_{j})=(x_{i}-x_{j})^{2}. $$

(10)

In case of discontinuities, this approach leads to an oversmoothed result after energy minimization, i.e. the right-hand side of Eq. 10 explodes numerically and entails a large smoothing power. In order to avoid this phenomenon, the user can choose a suitable smoothing function g.

According to the presented setup we can define the Gibbs prior distribution via the potential functions as follows:

$$ p(\mathbf{x})\propto \underset{\{i,j\}\in C_{2}}{\prod\prod}e^{-\beta V_{2}(x_{i},x_{j})}=\underset{\{i,j\}\in C_{2}}{\prod\prod} e^{-\beta g(x_{i}-x_{j})}, $$

(11)

where C₂ denotes the set of cliques of size 2. Consequently, the so-called prior energy is the sum of all clique potentials

$$ U(\mathbf{x})=\sum\limits_{i\in S}\sum\limits_{j\in \mathcal{N}_{i}}g(x_{i}-x_{j})=\sum\limits_{i\in S}\sum\limits_{j\in \mathcal{N}_{i}} (x_{i}-x_{j})^{2}, $$

(12)

where $\mathcal {N}_{i}$ is the set of neighbors of site (position) i. The common neighborhood structures are 4, 8, 12, or 24 (see Fig. 1), and the selection mainly depends on the desired smoothing intensity.

Now we can apply Bayes’ theorem to merge the likelihood energy (6) and the prior energy (12). Li [2] derives the so-called posterior energy E(x|d) as follows:

$$ \begin{array}{@{}rcl@{}} E(\mathbf{x}|\mathbf{d}) &=& U(\mathbf{d}|\mathbf{x})+ U(\mathbf{x})\\ &=& \sum\limits_{i\in S}\frac{(x_{i}-d_{i})^{2}}{2\sigma^{2}}+\sum\limits_{i\in S}\sum\limits_{j\in \mathcal{N}_{i}}(x_{i}-x_{j})^{2}. \end{array} $$

(13)

In order to determine the optimal restored image, the MAP solution is defined as

$$ \hat{\mathbf{x}}_{\text{MAP}} =\underset{\mathbf{x} \in \mathbb{R}^{n}}{\text{arg min }} \sum\limits_{i\in S}(x_{i}-d_{i})^{2}+\vartheta\sum\limits_{i\in S}\sum\limits_{j\in \mathcal{N}_{i}}(x_{i}-x_{j})^{2}, $$

(14)

where 𝜗 = 2σ². Obviously, if 𝜗 = 0, i.e. no noise occurs, only the likelihood energy effects the posterior and the MAP solution is equal to the input. However, the more 𝜗 increases, the more impact on the MAP solution is given on the prior energy term (i.e. the smoothness term).

Due to the fact that the minimization problem (14) is a quadratic optimization problem over a continuous surface, it is convex and possesses a global minimum. This fact allows to apply any known optimization procedure. The most common choice is to apply the GD algorithm starting with an initial configuration x⁽⁰⁾. The update step for the iteration is given as

$$ \mathbf{x}^{(t+1)} \longleftarrow \mathbf{x}^{(t)} - \mu \nabla_{\mathbf{x}}E\left( \mathbf{x}^{(t)}|\mathbf{d}\right), $$

(15)

where μ is the step size and ∇_x is the gradient with respect to x. Each component of the gradient, i.e. the partial derivatives of E(x|d) w.r.t. x_i, has the following structure:

$$ \frac{\partial E(\mathbf{x}|\mathbf{d})}{\partial x_{i}}=2(x_{i}-d_{i})+2\vartheta\sum\limits_{j\in \mathcal{N}_{i}}(x_{i}-x_{j}). $$

(16)

This iteration converges towards the optimum point $\hat {\mathbf {x}}$, where $\nabla _{\mathbf {x}}E(\hat {\mathbf {x}}|\mathbf {d})=0$.

One big disadvantage of this procedure is the runtime of the GD algorithm. To minimize the number of iterations, one could extend or change the algorithm (e.g. Geman et al. [6] suggest a simulated annealing algorithm), but our experiments showed that a higher smoothing parameter increases the number of iteration steps, which are needed to reach the optimum. In Section 4, exact results on the runtime and the concrete number of iterations will be shown and compared to our suggested approach.

2.3 Related Work

Apart from the MRF approach for image restoration presented in this work, various other methods for image noise removal exist in literature. A short survey on those methods can be found e.g. in the papers of Motwani et al. [10] and Buades et al. [11], where several state-of-the-art approaches are listed. In [10], the authors present two categories of approaches for noise removal in images: Spatial Filtering and Transform Domain Filtering. They further introduce several subcategories for each of them.

While Spatial Filtering methods directly apply a filter to a local group of pixels, Transform Domain methods focus on suitable transformations of the image to separate signal from noise. Popular examples for transformations are e.g. the Fourier or the Wavelet transform. According to its definition, the Markov Random Field model used in our work [6], is a typical example for the Spatial Domain category. Also other possibilities to apply MRF structures to images exist, e.g. Markov models for modelling Wavelet coefficients (cf. [12] or [13]).

Talebi and Milanfar [14] present an approach to achieve fast noise filtering using Spatial Filtering. They state the general image restoration model form in the same way as we do in this paper (4), but provide a more general form of the restoration framework by

$$ \hat{x_{i}} =\underset{x_{i} \in \mathbb{R}}{\text{arg min }} \sum\limits_{j\in S}K_{i,j} \cdot (x_{i}-d_{j})^{2}, $$

(17)

where i ∈ S and K_{i, j} is an arbitrary kernel function, measuring the similarity between x_i and d_j. The authors suggest to solve the problem by performing an eigen-decomposition of the model matrix. They point out that the computational costs are high due to the high dimension of the matrix, to solve this problem they use approximators for the decomposition. Then, they analyze the MSE and apply iterative approximations of image filters based on their eigenvalues.

Instead of assuming normally distributed noise (which is common in image processing), Le et al. [15] suggest a variational, edge-preserving approach in order to reconstruct images with Poisson noise.

A distinct approach towards image restoration is presented by Dabov et al. [16]. In their work, the authors suggested a method to remove noise from single image fragments in a transformed domain, conserving major characteristics within similar blocks. The deployed similarity of fragments is obtained from a collaborative filtering method, resulting in edge-preserving behavior.

The idea of using different MRF models for image restoration is also investigated in other settings: for example, a different MRF model to restore the image and, in parallel, detect edges in the image in a robust way is employed by Figueiredo and Leitao [17]. Babacan et al. [18] suggest a generalized Gaussian prior model for MRF. Numerous other models applying MRFs for image restoration exist. They have in common the fundamental usage of Bayesian inference to optimize the a-posteriori estimate of the image.

3 Proposed Solution

The main contribution to global image reconstruction and denoising procedures of this paper is the development of a closed analytical solution for the MAP-MRF estimator (14) using a quadratic smoothness function g(⋅) (10). In this section the theory behind the analytical solution and the solution itself is presented.

3.1 Analytical Solution

Resuming to the definition of the MAP estimator for x given a noisy image d, we investigate the mathematical structure of the problem in more detail in the following. Therefore, we divide the formula in two separate parts:

$$ {\hat{\mathbf{x}}}_{\text{MAP}} =\underset{\mathbf{x} \in \mathbb{R}^{n}}{\text{arg min }} \underbrace{\sum\limits_{i=1}^{n}(x_{i}-d_{i})^{2}}_{(\text I)}+\underbrace{\vartheta\sum\limits_{i=1}^{n}\sum\limits_{j\in \mathcal{N}_{i}}(x_{i}-x_{j})^{2}}_{(\text{II})}. $$

(18)

We can now rewrite the right-hand side into matrix/vector notation in order to derive a more compact representation. The likelihood energy (I) can be converted to a simple vector notation without extra effort

$$ (\text I)=(\mathbf{x}-\mathbf{d})^{T}(\mathbf{x}-\mathbf{d}). $$

(19)

For the prior energy (II) some algebraic manipulations are needed to achieve the desired matrix structure:

$$ \begin{array}{@{}rcl@{}} (\text{II})&=&\vartheta\sum\limits_{i=1}^{n}\sum\limits_{j\in\mathcal{N}_{i}}(x_{i}-x_{j})^{2}\\ &=& \vartheta\sum\limits_{i=1}^{n}(x_{i}\mathbf{1}-\mathbf{x})^{T} \mathbf{B}_{i}(x_{i}\mathbf{1}-\mathbf{x})\text{,}\\ &&\text{where }\left( \mathbf{B}_{i}\right)_{j,k}= \left\{\begin{array}{ll} 1 & j=k\in \mathcal{N}_{i}\\ 0 & \text{else,} \end{array}\right. \end{array} $$

and 1 denotes a vector of n ones. Multiplying and collecting terms we further obtain

$$ \begin{array}{@{}rcl@{}} (\text{II})&=& \vartheta\sum\limits_{i=1}^{n}\left[ {x_{i}^{2}}\mathbf{1}^{T} \mathbf{B}_{i}\mathbf{1} - 2x_{i}\mathbf{1}^{T}\mathbf{B}_{i}\mathbf{x}+\mathbf{x}^{T}\mathbf{B}_{i}\mathbf{x}\right]\\ &=& \vartheta\left( \sum\limits_{i=1}^{n} {x_{i}^{2}}\mathbf{1}^{T} \mathbf{B}_{i}\mathbf{1} - 2\sum\limits_{i=1}^{n}x_{i}\mathbf{1}^{T}\mathbf{B}_{i} \mathbf{x}+\sum\limits_{i=1}^{n}\mathbf{x}^{T}\mathbf{B}_{i}\mathbf{x}\right). \end{array} $$

Observing that $\mathbf {1}^{T}\mathbf {B}_{i}\mathbf {1}=|\mathcal {N}_{i}|=N_{i}$, say, where N_i stands for the number of neighbors of pixel i, and denoting $\mathbf {1}^{T}\mathbf {B}_{i}=:{\gamma _{i}^{T}}$, we arrive that

$$ (\text{II})=\vartheta\left( \mathbf{x}^{T}\underbrace{\text{diag}(\tilde{\mathbf{N}})}_{=:\tilde{\mathbf{B}}}\mathbf{x}-2\mathbf{x}^{T}\underbrace{\left( \begin{array}{l} \mathbf{\gamma}_{1}^{T}\\ \vdots\\ \mathbf{\gamma}_{n}^{T} \end{array}\right)}_{=:\boldsymbol{\Gamma}}\mathbf{x}+\mathbf{x}^{T}\underbrace{\sum\limits_{i=1}^{n}\mathbf{B}_{i}}_{=\tilde{\mathbf{B}}}\mathbf{x}\right), $$

where $\tilde {\mathbf {N}}=(N_{1},...,N_{n})$, $\tilde {\mathbf {B}}\in \mathbb {R}^{n\times n}$ is a diagonal matrix with diagonal entries N_i and $\mathbf {\Gamma }\in \mathbb {R}^{n\times n}$ is the adjacency matrix of the whole image. The value 1 occurs at the j th diagonal entry of the diagonal matrix B_i, if and only if i and j are adjacent in the neighborhood graph. Hence, the sum over the B_i’s exactly results in the number of neighbors for each node, i.e. $\tilde {\mathbf {B}}= {\sum }_{i=1}^{n} \mathbf {B}_{i} = diag(\tilde {\mathbf {N}})$. Finally,

$$ \begin{array}{@{}rcl@{}} \text{(II)}&=& 2\vartheta\mathbf{x}^{T}\left( \underbrace{\tilde{\mathbf{B}}-\boldsymbol{\Gamma}}_{=:\mathbf{G}}\right)\mathbf{x}\\ &=&2\vartheta\mathbf{x}^{T}\mathbf{G}\mathbf{x}. \end{array} $$

(20)

Combining the compact representations of the likelihood energy and the prior energy, we can rewrite the MAP optimization problem from Eq. 18 as

$$ \hat{\mathbf{x}}_{\text{MAP}} =\underset{\mathbf{x} \in \mathbb{R}^{n}}{\text{arg min }} \left[(\mathbf{x}-\mathbf{d})^{T}(\mathbf{x}-\mathbf{d})+2\vartheta\mathbf{x}^{T}\mathbf{G}\mathbf{x}\right]. $$

(21)

Due to the positive quadratic structure of the target function, the optimization problem is convex and we can retrieve the optimum by the gradient:

$$ (21)\Longleftrightarrow\mathbf{0}=\nabla_{\mathbf{x}}\left[(\mathbf{x}-\mathbf{d})^{T}(\mathbf{x}-\mathbf{d})+2\vartheta\mathbf{x}^{T}\mathbf{G}\mathbf{x}\right]. $$

(22)

Since Γ is an adjacency matrix and $\tilde {\mathbf {B}}$ is diagonal, G must be a symmetric matrix and, as a consequence,

$$ (21)\Longleftrightarrow\mathbf{x}=(\underbrace{\mathtt{I}+2\vartheta\mathbf{G}}_{=:\mathbf{M}})^{-1}\mathbf{d}, $$

(23)

where $\mathtt {I}\in \mathbb {R}^{n\times n}$ is the identity matrix. In order to solve the equation system (23), we emphasize some important matrix properties. Since all columns and rows of G sum up to zero

$$ \begin{array}{@{}rcl@{}} \sum\limits_{j} \mathbf{G}_{ij}&=&\mathbf{G}_{ii}+\sum\limits_{i\neq j}\mathbf{G}_{ij}=2\tilde{\mathbf{B}}_{ii}-2\sum\limits_{i\neq j}\mathbf{\Gamma}_{ij}\\ &=&2(\tilde{\mathbf{B}}_{ii}-\tilde{\mathbf{B}}_{ii})=0~\forall i, \end{array} $$

(24)

the column space is linear dependent, i.e.

$$ \sum\limits_{i}\mathbf{g}_{i}=\mathbf{0}, $$

(25)

where g_i denotes the i th column of G. Therefore, G is rank deficient and not invertible. While G fulfills the property of weak diagonal dominance, i.e.

$$ \sum\limits_{i\neq j}|\mathbf{G}_{ij}|\leq |\mathbf{G}_{ii}|~\forall i, $$

(26)

the matrix M is strictly diagonal dominant, as it holds for all i that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i\neq j}|\mathbf{M}_{ij}|&=&2\vartheta\sum\limits_{i\neq j}|\mathbf{G}_{ij}|\leq 2\vartheta|\mathbf{G}_{ii}|\\ &&< 1+2\vartheta|\mathbf{G}_{ii}|=|1+2\vartheta\mathbf{G}_{ii}|=|\mathbf{M}_{ii}|. \end{array} $$

(27)

An important result from linear algebra (Garcia and Horn [9]) implies that a matrix A is positiv definite, if it fulfills the following properties:

• A is Hermitian (equivalent to symmetry in case of real entries),

• all main diagonal elements of A are positive and real,

• and A is strictly diagonal dominant.

Positive definiteness implies invertibility according to basic results from linear algebra, Garcia and Horn [9]. The matrix M satisfies all three conditions, therefore the inverse M^− 1 exists, as well as a unique solution of the equation system (23) for arbitrary right side $\tilde {\mathbf {d}}$.

A strong computational limitation is the large size of the matrix M. In case of common image sizes with e.g. 500 × 700 pixels, the order of magnitude of matrix entries is 10¹¹. Computing the inverse of this matrix is expensive w.r.t. storage space and, even worse, w.r.t. computation time, as standard inversion algorithms require $\mathcal {O}(n^{3})$ operations. Fortunately, the matrix properties of M permit to define a more efficient procedure.

Firstly, the matrix M has a sparse structure, i.e. only few entries differ from 0. Depending on the neighborhood structure defined for the MRF, M has at most $n\cdot (|\mathcal {N}|+1)$ entries unequal to 0, where n is the number of pixels and $|\mathcal {N}|$ is the number of neighbors for each pixel. For instance, for an image of size 500 × 700 together with an 8-neighborhood structure, the number of matrix entries is approximately 10¹¹, while only about 3 ⋅ 10⁶ thereof are unequal to 0. Secondly, M has a band structure, whose bandwidth only depends on the image size and the neighborhood structure. Figure 2 shows the structure of the sparse band matrix M of an image with an 8-neighborhood structure and with 𝜗 = 1. In the subpictures you can see the exact matrix entries of the main- and the minor diagonal, respectively. The subpicture of the main diagonal (upper right) further shows the transition from the first to the second pixel column.

Figure 2

The sparse band matrix M calculated from the first three pixel columns of an example image (500 × 700) with an 8-neighborhood structure, with 𝜗 = 1, and a bandwidth of 2 ⋅ (k + 2), where k is the number of the image rows.

Nevertheless, M^− 1 is not a sparse matrix. Hence, it is hardly possible to solve the equation system in a reasonable amount of time. However, we can use an additional property of M, the block-band structure. This offers the possibility to apply a Block Cholesky Decomposition without explicitly calculating the inverse M^− 1.

3.2 Block Cholesky Decomposition

In general, the Cholesky Decomposition [5] of a Hermitian positive definite matrix $\mathbf {A}\in \mathbb {C}^{n\times n}$ can be converted into the form

$$ \mathbf A=\mathbf{L}\mathbf{L}^{\star}, $$

(28)

where $\mathbf {L}\in \mathbb {C}^{n\times n}$ is a lower triangular matrix with real positive diagonal elements and $\mathbf {L}^{\star }\in \mathbb {C}^{n\times n}$ is the conjugate transpose of L. In the real-valued case, $\mathbf {A}\in \mathbb {R}^{n\times n}$ must be symmetric and positive definite,then the conjugate transpose L^⋆ reduces to L^⋆ = L^T, $\mathbf {L}\in \mathbb {R}^{n\times n}$. Given a linear equation system

$$ \mathbf{A}\mathbf{x}=\mathbf{b}, $$

(29)

with $\mathbf {x},\mathbf {b}\in \mathbb {R}^{n}$, we can obtain x by solving the equations

$$ \mathbf{L}\mathbf{y}=\mathbf{b}\quad\text{(forward substitution)} $$

(30)

and

$$ \mathbf{L}^{T}\mathbf{x}=\mathbf{y}\quad\text{(backward substitution)}, $$

(31)

with $\mathbf {y}\in \mathbb {R}^{n}$, without calculating the inverse of A.

The Cholesky Decomposition can also be applied for blocks instead of scalar matrix entries. Hence, in order to exploit the efficient decomposition to solve equation systems, we divide the matrix M into blocks and obtain the so-called block tridiagonal structure:

$$ \left( \begin{array}{lllll} \mathbf A_{1} & \mathbf{B}_{1}^{T} & & & \\ \mathbf{B}_{1} & \mathbf A_{2} & \mathbf{B}_{2}^{T} & & \\ & {\ddots} & {\ddots} & {\ddots} & \\ & & \mathbf{B}_{N-2} & \mathbf{A}_{N-1} & \mathbf{B}_{N-1}^{T}\\ & & & \mathbf{B}_{N-1} & \mathbf{A}_{N} \end{array}\right), $$

(32)

with $N\in \mathbb {N}$. Analogously to the scalar case of the Cholesky Decomposition, this block matrix can be decomposed into

$$ \left( \begin{array}{lllll} \mathbf L_{1} & & & & \\ \mathbf C_{1} & \mathbf L_{2} & & & \\ & {\ddots} & {\ddots} & & \\ & & \mathbf{C}_{N-2} & \mathbf{L}_{N-1} & \\ & & & \mathbf{C}_{N-1} & \mathbf{L}_{N} \end{array}\right)\cdot\left( \begin{array}{lllll} \mathbf{L_{1}^{T}} &\mathbf{C_{1}^{T}} & & & \\ & \mathbf{L_{2}^{T}} & \mathbf{C_{2}^{T}} & & \\ & & {\ddots} & {\ddots} & \\ & & & \mathbf{L}_{N-1}^{T} &\mathbf{C}_{N-1}^{T} \\ & & & & \mathbf{L}_{N}^{T} \end{array}\right). $$

(33)

Figure 3

The tridiagonal block band structure of our matrix M in the case of an 8-neighborhood structure.

By comparing the elements of the original tridiagonal block matrix (32) to the elements of the multiplied right hand side of Eq. 33, we can solve the block equations for C_i and $\mathbf {L}_{i}\mathbf {L}_{i}^{T}$ and obtain the iterative block equation system as follows:

$$ \begin{array}{@{}rcl@{}} \mathbf{L}_{1}\mathbf{L}_{1}^{T} &=& \mathbf{A}_{1}\\ \mathbf{C}_{1} &=& \mathbf{B}_{1}\mathbf{L}_{1}^{-T}\\ \mathbf{L}_{2}\mathbf{L}_{2}^{T} &=& \mathbf{A}_{2}-\mathbf{C}_{1}\mathbf{C}_{1}^{T}\\ \mathbf{C}_{2} &= &\mathbf{B}_{2}\mathbf{L}_{2}^{-T}\\ &~~\vdots&\\ \mathbf{L}_{N-1}\mathbf{L}_{N-1}^{-T} &=& \mathbf{A}_{N-1}-\mathbf{C}_{N-2}\mathbf{C}_{N-2}^{T}\\ \mathbf{C}_{N-1} &=& \mathbf{B}_{N-1}\mathbf{L}_{N-1}^{-T}\\ \mathbf{L}_{N}\mathbf{L}_{N}^{T} &=& \mathbf{A}_{N}-\mathbf{C}_{N-1}\mathbf{C}_{N-1}^{T}. \end{array} $$

In our case, the matrix M follows the required tridiagonal block structure and furthermore, each block is a sparse matrix. Figure 3 depicts the general block structure of M for an 8-neighborhood structure, where A₁, A and B are symmetric blocks of size k × k and k is the number of image rows. We can observe that the blocks of the minor diagonal, B, are constant and only the first and the last block on the main diagonal, A₁, differs from all the remaining ones, A. This useful property depends on the neighborhood structure, the image size and the parameter 𝜗. Hence, more neighbors in the neighborhood structure imply a larger block size and a higher number of distinct blocks occuring in the matrix M.

Matrix inversion by standard methods requires $\mathcal {O}(n^{3})$ operations and $\mathcal O(n\cdot k)$ units of storage, where n is the number of pixels. By exploiting the matrix properties of M (sparse structure, tridiagonality, band-block structure) and using the Block Cholesky Decomposition we reach a complexity of $(\frac {n}{k})\cdot \mathcal {O}(k^{3})=\mathcal {O}(n\cdot k^{2})$ operations and $\left (\frac {n}{k}\right )\cdot \mathcal {O}\left (k^{2}\right )=\mathcal {O}(n\cdot k)$ units of storage, where k is the block size.

4 Experiments & Results

For the demonstration and evaluation of our method, we use three famous test images in grayscale [22]. For the computation, we use an Intel Core i5 processor with 2.4 GHz on a 64-bit operating system and implementations in the statistical software R [21] (version 3.3.3; 2017-03-06). We deploy this software for both compared algorithms, which guarantees comparable results, although R is known to introduce some computational overhead compared to other programming languages. However the main focus of our evaluation is the proportion of improvement rather than the absolute values.

We aim to point out that our algorithm is able to retrieve an original image after homogenous Gaussian white noise was added and that we can restrict the choice of 𝜗 in an empirical way. Furthermore, we show the large improvements in runtime compared to the conventional GD algorithm.

To compare the results of the presented method dependent on the input parameters, we deploy two measures for noise quantification: the peak-noise-to-signal-ratio (PSNR) and the structural-similarity (SSIM) [19]. The PSNR is defined as

$$ \begin{array}{@{}rcl@{}} \text{PSNR}&=&10\cdot{\log}_{10}\frac{\text{MAX}_{I}^{2}}{\text{MSE}}\\ &=&20\cdot{\log}_{10}(\text{MAX}_{I})-10\cdot{\log}_{10}(\text{MSE}), \end{array} $$

(34)

where MAX_I is the maximum possible pixel value (in case of images, MAX_I = 255) and the MSE is the typical mean squared error. Typically, the PSNR is measured in decibel (dB). The SSIM is a more complex measure and combines the loss of correlation, the luminance distortion and the contrast distortion by

$$ \text{SSIM}\left( \mathbf{x},\mathbf{y}\right)=\frac{\text{cov}\left( \mathbf{x},\mathbf{y}\right)}{\sigma_{\mathbf{x}}\sigma_{\mathbf{y}}}\cdot\frac{2\mathbf{\overline{x}}\mathbf{\overline{y}}}{\mathbf{\overline{x}}^{2}+\mathbf{\overline{y}}^{2}}\cdot\frac{2\sigma_{\mathbf{x}}\sigma_{\mathbf{y}}}{\sigma_{\mathbf{x}}^{2}+\sigma_{\mathbf{y}}^{2}}. $$

(35)

In Eq. 35, σ_⋅ denotes the standard deviation and $\sigma ^{2}_{\cdot }$ the variance of the images and $\mathbf {\overline {x}}$, $\mathbf {\overline {y}}$ are the means of the noisy and the restored image. The SSIM ranges in [0,1] and is robust.

As mentioned in Section 2, the higher 𝜗, the more smoothing power will be reached. The optimization is a function of 𝜗 and has no optimum, i.e. this is an unbounded problem. Therefore, the choice of the parameter 𝜗 is left to the user based on practical considerations.

To demonstrate the impact of the smoothing parameter 𝜗, examples with different values of 𝜗 are analyzed and shown in Figs. 4 and 5. We add a homogenous Gaussian white noise with a standard deviation of σ = 20 to produce noise on an image. To compare these results to results with a “real” noisy image, we use the test image kennedy (see Fig. 6). The choice of 𝜗 = 0.07 for the smoothness parameter is made empirically, resulting from the best solution to the human eye. A noticeable fact (last images of Figs. 4–6) is that our proposed global denoising method is not edge-preserving.

Figure 4

Test image cameraman (256 × 256); a the original image [22], b the noisy image with σ = 20, c-e the restored images with the exact solution for 𝜗 = 0.01, 𝜗 = 0.05 and 𝜗 = 1.

Figure 5

Test image flower (766 × 500); a the original image [22], b the noisy image with σ = 20, c-e the restored images with the exact solution for 𝜗 = 0.01, 𝜗 = 0.05 and 𝜗 = 1.

Figure 6

Test image kennedy (343 × 367); a the original (noisy) image [22], b-c the restored images with the exact solution for 𝜗 = 0.07 and 𝜗 = 1.

In order to choose an “optimal” parameter we want to point out the dependence of the PSNR and the SSIM measurements from the smoothness parameter 𝜗. Although the optimal choice of 𝜗 is an unbounded problem, the range of an adequate 𝜗 can be restricted by investigating PSNR and SSIM. In Fig. 7 the PSNR and in Fig. 8 the SSIM for a varying smoothness parameter are visualized. The red lines indicate the values for the noisy image flower, whereas the black circles are the values of the image after the application of MRF with a given 𝜗. We can see that in general for higher 𝜗 the PSNR and the SSIM are worse, but empirically an optimal value for 𝜗 can be detected.

Figure 7

Test image flower; PSNR for different 𝜗 values (circles) and the PSNR for the noisy (σ = 20) image (red line).

Figure 8

Test image flower; SSIM for different 𝜗 values (circles) and the SSIM for the noisy (σ = 20) image (red line).

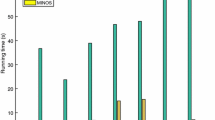
A central benefit of the proposed analytical method based on the block Cholesky decomposition is the improvement w.r.t. computational complexity, which is indicated by a reduced runtime. In Table 1 the runtimes for several smoothness parameters for the different test images are presented; values for 𝜗 (first column), runtime of the GD algorithm using integrated linesearch and the number of iterations to reach the optimum (Runtime (GD), Number of iterations), the runtime of our exact solution (Runtime (CholDecomp)) and the relativ runtime improvement (last column). Although computational overhead might result from the choice of the programming language and contribute to the absolute values, the relative improvement factors clearly demonstrate a reduction of computational complexity of the analytical solution compared to the GD algorithm for all images. In detail, the factor is larger than 85%, in some cases it even reaches 98%. Thus, a significant reduction of the complexity, indicated by the runtime is achieved. Furthermore, the GD algorithm with integrated linesearch needs a higher number of iterations for larger values of 𝜗 to reach the optimum, whereas in our proposed solution this parameter acts like a constant and does not affect the runtime - hence, scalability w.r.t. to this parameter can be guaranteed independently from the implementation.

Table 1 Runtime comparison with the test images cameraman, flower and kennedy.

5 Discussion

The complexity reduction of the suggested solution compared to the GD procedure is clearly visible from the experimental results. Most of the runtime is used for the Cholesky Decomposition, whereas the forward and backward substitution is done very quickly. Therefore, the worst case for our algorithm is to restore only one image using a given smoothness parameter 𝜗. In concrete terms, for the test image cameraman the entire runtime is about 7 seconds (see Table 1), out of these 7 seconds it takes about 5.7 seconds to calculate the decomposition and only 1.3 seconds for the forward and backward substitution. In case that several images with the same size, neighborhood structure and 𝜗 are processed at once, the Cholesky Decomposition is constant. Hence, if one has several equally sized images, which require the same smoothing power (i.e. the same degree of denoising), the runtime improvement of the presented method compared to the GD approach will be even larger. Given this fact, several further fields of application are accessible for our suggested method: For instance, in manufacturing environments, where image sizes and noise rates might not change due to constant measurement equipment or in case of video processing, where constantly the same image sizes are provided.

As mentioned in Section 3.2, the complexity of our proposed denoising method is $\mathcal {O}(n\times k^{2})$ (operations) and $\mathcal {O}(n\times k)$ (storage). Both of these quantities depend on the number of pixels n, as well as the block size k. In order to save time and storage space, the blocks should be chosen as small as possible. Given an 8-neighborhood structure and a column-wise numbering of the image pixels, the lower bound of the block size equals to the number of rows in the image, otherwise the block tridiagonal structure is violated. W.l.o.g. we can rotate vertical images by 90^∘ to reduce the block size. Quadratic images therefore represent the worst case w.r.t. complexity, as $k = \sqrt {n}$ implies that $\mathcal {O}(n^{3})$ operations and $\mathcal {O}(n^{2})$ storage units are required.

The scalability of our method w.r.t. image size is good, since the complexity grows linearly for an increasing number of image pixels at a constant block size. Storage and runtime issues are therefore significantly reduced by our suggested procedure, compared to classical approaches using the same MRF model. Further improvements are possible by selecting a faster programming language. Image processing for large images (e.g. HD images) is nonetheless challenging for any utilized algorithm and hardware.

For applications, where edge-preservation is important, our presented method is not adequate since with the quadratic smoothness function g(⋅) sharp edges are over-smoothed. Hence, it is sensitive to outliers. Lee [2] suggests to correct this issue by using other smoothness functions and varying the setting according to the specific application. There is a wide range of smoothing functions to handle distinct image types and requirements.

At the end, the choice of the adequate smoothness parameter 𝜗 has a high influence on the result, but needs to be left to the user in order to reach satisfying results for a specific use-case.

6 Conclusion

In this paper, we provided a mathematical approach to solve the issue of high computational complexity of the Markov Random Field approach for image restoration. By analytically deriving the optimal posterior Markov Random Field over all image pixels given a continuous prior function, we obtained an explicit representation of the underlying surface. The matrix properties of this linear equation system were exploited to prove the invertibility of the system matrix and to compute the solution efficiently by using Block Cholesky Decomposition.

Further, we showed a comparison of the results for different images with respect to runtime and restoration quality. In the presented cases, a runtime improvement of more than 85% has been achieved in the current implementation, compared to state-of-the-art approaches for the same image restoration model (e.g. using Gradient Descent optimization). The speed-up is even higher if multiple images of equal size and noise intensity are processed due to the constant decomposition of the equation system, which launches new possibilities of application, e.g. video processing or industrial image applications [20]. Regarding the quality of the presented analytical solution of MRFs, the mathematical optimum of the restoration is reached exactly and cannot be beaten by any other approach for the same model. Unfortunately, due to the formulation of the prior distribution, the procedure is not edge-preserving, which might be a disadvantage for certain applications.

In order to improve the properties of the Markov Random Field model with respect to edges and contours, other prior functions could be introduced, e.g. truncated quadratic or exponential types. For the presented analytical approach, this would result in a nonlinear (or even non-continuous) instead of a linear equation system. Hence, numerical optimization algorithms would be required and a solution would not be feasible in a reasonable amount of time, due to the high dimensionality. Instead, an adjustment of the neighborhood graph of the Markov Random Field (e.g. deleting edges in the neighborhood graph, which correspond to very large image gradients) could possibly solve the problem and preserve the mathematical structure in an empirical way.