Tree-based iterated local search for Markov random fields with applications in image analysis

Abstract

The maximum a posteriori assignment for general structure Markov random fields is computationally intractable. In this paper, we exploit tree-based methods to efficiently address this problem. Our novel method, named Tree-based Iterated Local Search (T-ILS), takes advantage of the tractability of tree-structures embedded within MRFs to derive strong local search in an ILS framework. The method efficiently explores exponentially large neighborhoods using a limited memory without any requirement on the cost functions. We evaluate the T-ILS on a simulated Ising model and two real-world vision problems: stereo matching and image denoising. Experimental results demonstrate that our methods are competitive against state-of-the-art rivals with significant computational gain.

1 Introduction

Markov random fields (MRFs) (Besag 1974; Geman and Geman 1984; Lauritzen 1996) are popular probabilistic representations of structured objects. For example, grid MRF is a powerful image representation for pixels, where each site represents a pixel state (e.g., intensity) and each edge represents local relations between neighboring pixels (e.g., smoothness). One of the most important MRF inference problems is maximum a posteriori (MAP) assignment. The goal is to search for the most probable state configuration of all objects, or equivalently, the lowest energy of the model. The problem is known to be NP-complete (Boykov et al. 2001). Given a MRF of $N$ objects, each of which has $S$ states, a brute-force search must explore $S^{N}$ state configurations. In image denoising, for example, $N$ is the number of pixels, which ranges from $10^{4}-10^{7}$, and $S$ is the number of pixel intensity levels, which are in the order of $2^{8}-2^{32}$. This calls for heuristic methods that find reasonable solutions in practical time.

There have been numerous attempts to solve this problem. An early approach was based on simulated annealing (SA) whose convergence is guaranteed (Geman and Geman 1984). The main drawback of SA is low speed—it takes a long time to achieve reasonably good solutions. Another strategy was local greedy search where the iterated conditional mode (ICM) (Besag 1986) was the most well-known method. The ICM climbs down local valleys by iteratively exploring small neighborhoods of size $S$—the number of possible states per object. Not surprisingly, this method is prone to getting stuck at poor local minima.

A more successful approach is belief-propagation (BP) (Pearl 1988) which exploits the problem structure better than the ICM does. The BP maintains a set of messages sending simultaneously along all edges of the MRF. A message carries the state information of the source site. Any update of a target site is informed by messages from all nearby sites. However, this method can only be guaranteed to work for a limited class of network structures—when the network reduces to a tree. Another drawback is that the memory requirement for the BP is high: It is proportional to the number of edges in the network. More recently, efficient algorithms with theoretical guarantees have been introduced based on the theory of graph cuts (Boykov et al. 2001). This class of algorithms, while being useful in certain computer vision problems, has a limitation in the range of problems it can solve—the energy formulation must admit a certain metric form (Boykov et al. 2001; Szeliski et al. 2008). In effect, these algorithms are not applicable to problems where energy functions are not known a priori.

Given this ground, it is desirable to have an approximate algorithm that is fast, consumes little memory and does not have any specific requirements of network structures or energy functions. We explore a metaheuristic known as Iterated Local Search (ILS) (e.g. see Lourenco et al. 2003). The ILS encourages jumping between local minima, which can be found by local search methods such as the ICM. This algorithm, however, does not exploit any problem structure. To this end, we propose a novel algorithm called Tree-based Iterated Local Search (T-ILS), which combines strength of the BP and the ILS. The T-ILS exploits the fact that the BP works efficiently on trees, and thus can be effective at locating good local minima. The main difference from the standard tree-based BP is that our trees are conditional on states of neighbor leaves. When combined with the ILS, we have a heuristic algorithm that is less likely to get stuck in poor local minima, and has better chance to reach high quality solutions.

We evaluate the T-ILS on three benchmark problems: finding the ground state of an Ising model, stereo correspondence and image denoising. We empirically demonstrate that the T-ILS finds good solutions, while requiring less training time and memory than the loopy BP, which is one the state-of-the-arts for these problems.

To summarize, our main contributions are the proposal and evaluation of fast and lightweight tree-based inference methods in MRFs. Our choice of trees on $N=W\times H$ images requires only $\mathcal {O}\left( 2\max \{W,H\}\right)$ memory and two passes over all sites in the MRF per iteration. These are much more economical than the $\mathcal {O}(4WH)$ memory and many passes needed by the traditional loopy BP.

This paper is organized as follows. Section 3 describes MRFs, the MAP assignment problem, and the belief propagation algorithm on trees. In Sect. 4, conditional trees are defined, followed by two algorithms: the strong local search T-ICM and the global search T-ILS. Section 5 provides empirical support for the performance of the T-ICM and T-ILS. Sect. 6 concludes the paper.

2 Related work

The MAP assignment for MRFs as a combinatorial search problem has attracted a great amount of research in the past decades, especially in computer vision (Li 1995) and probabilistic artificial intelligence (Pearl 1988). The problem is NP-hard (Shimony 1994). For example, in labeling of an image of size $W\times H$, the problem space is $S^{WH}$ large, where $S$ is the number of possible labels per pixel.

Techniques for the MAP assignment can be broadly classified into stochastic and deterministic classes. In early days, stochastic algorithms were based on simulated annealing (SA) (Kirkpatrick et al. 1983). The first application of SA to MRFs with provable convergence was the work of Geman and Geman (1984). The main drawback of this method is slow convergence toward good solutions (Szeliski et al. 2008). Nature-inspired algorithms were also suggested, especially the family of genetic algorithms (Brown et al. 2002; Kim et al. 1998; Kim and Lee 2009; Maulik 2009; Tseng and Lai 1999). Some attempts using ant colony optimization and tabu-search have also been made (Ouadfel and Batouche 2003; Yousefi et al. 2012).

Deterministic algorithms started in parallel with ICM (Besag 1986). The ICM is a simple greedy search method that updates one label at a time. Thus it is slow and sensitive to initialization. A more successful approach is based on Pearl’s loopy BP (Pearl 1988). Due to its nature of using local information (called “messages”) to update “belief” about the optimal solution, the loopy BP is also called message passing algorithm. Although the loopy BP is not guaranteed to converge, empirical evidences so far have indicated that it is competitive against the state-of-the-arts in a variety of image analysis problems (Felzenszwalb and Huttenlocher 2006; Szeliski et al. 2008). Research on improving the loopy BP is currently an active topic in artificial intelligence, statistical physics, computer visions and social network analysis (Duchi et al. 2007; Felzenszwalb and Huttenlocher 2006; Hazan and Shashua 2010; Kolmogorov 2006; Meltzer et al. 2009). The most recent development centers around convex analysis (Johnson et al. 2007; Kumar et al. 2009; Ravikumar and Lafferty 2006; Wainwright et al. 2005; Werner 2007). In particular, the MAP is converted into linear programming with relaxed constraints from which a mixture of convex optimization and message passing can be used.

Another powerful class of algorithms is graph cuts (Boykov et al. 2001; Szeliski et al. 2008). They are, nevertheless, designed with specific cost functions in mind (i.e., metric and semi-metric) (Kolmogorov and Zabih 2004), and therefore inapplicable for generic cost functions. Interestingly, it has been recently proved that graph cuts are in fact loop BP (Tarlow et al. 2011).

It is fair to say that the deterministic approach has become dominant due to their performance and theoretical guarantee for certain classes of problems (Kappes et al. 2014). However, the problem is still unsolved for general settings. Our approach, the T-ILS, has both deterministic and heuristic components. It relies on the concept of strong local search using the deterministic method of BP. The local search is strong because it covers a significant number of sites, rather than just one, which is often found in other local search methods such as the ICM (Besag 1986). The neighborhood size in our method is very large (Ahuja et al. 2002). For typical image labeling problems, the size is $S^{0.5WH}$ for an image of height $H$, width $W$ and label size $S$. Standard local search like the ICM, in contrast, only explores a neighborhood of size $S$ at a time. For the T-ILS, once a strong local minimum is found, a stochastic procedure based on iterated local search (Lourenco et al. 2003) is applied to escape from the local valley and explores a better local minimum.

The idea of exploiting trees in MRFs is not entirely new. In early days, spanning trees were used to approximate the entire MRF (Chow and Liu 1968; Wu and Doerschuk 1995). This method is efficient but may hurt the approximation quality because the number of edges in a tree is far less than that in the original MRF. Another way was to build a hierarchical MRF with multiple resolutions (Willsky 2002), but this is less applicable to flat image labeling problems. Our method differs from these efforts in that we use trees embedded in the original graph rather than building an approximate tree. Second, our trees are conditional—they are defined on the values of its leaves. Third, trees are selected as the search progresses.

More recently, trees have been used in variants of loop BP to specify the orders which messages are scheduled (Wainwright et al. 2005; Sontag and Jaakkola 2009). Our method can also be viewed along this line but differs in the way trees are built and messages are updated. In particular, our trees are conditional on neighbor labeling, which is equivalent to collapsing an associated message to a single value.

Iterated Local Search, also known as basin hopping (David 1997), has been used in related applications such as image registration (Cordón and Damas 2006) and structure learning (Biba et al. 2008). The success of the ILS depends critically on the local search and the perturbation strategy (Lourenço et al. 2010). In David (1997), for example, a powerful local search based on conjugate gradients is essential for the Lennard–Jones clusters problem. Our work builds strong local search using the tree-based BP on the discrete spaces rather than continuous ones.

3 Markov random fields for image labeling

In this section we introduce MRFs and the MAP assignment problem with application to image labeling. MRF is a probabilistic way to represent a discrete system of many interacting variables (Pearl 1988). In what follows, we briefly describe the MRF and its MAP assignment problem and focus on the minimization of model energy.

Formally, a MRF specifies a random field $\mathbf {x}=\{x_{i}\}_{i=1}^{N}$ over a graph $\mathcal {G}=(\mathcal {V},\mathcal {E})$, where $\mathcal {V}$ is the collection of $N$ sites $\{i\}$, $\mathcal {E}$ is the collection of edges $\{(i,j)\}$ between sites, and $x_{i}\in L$ represents states at site $i$. One of the main objectives is to compute the most probable specification, also known as MAP assignment, which is the main focus of this paper.

3.1 Image labeling as energy minimization and MAP assignment

In image labeling, an image $\mathbf {y}$ is a collection of pixels arranged in a particular geometrical way, as defined by the graph $\mathcal {G}$. Typically, we assume the grid structure over pixels, where every inner pixel has exactly four nearby pixels. A labeling $\mathbf {x}$ is the assignment of each pixel $y_{i}$ to a corresponding label $x_{i}$ for all $i=1,2,\ldots ,N$.

A full specification of a MRF over the labeling $\mathbf {x}$ can be characterized by its energy. Assuming pairwise interaction between connected sites, the energy is the sum of local energies as follows:

$$\begin{aligned} E(\mathbf {x},\mathbf {y})&= \sum _{i\in \mathcal {V}}E_{i}(x_{i},\mathbf {y})+\sum _{(i,j)\in \mathcal {E}}E_{ij}(x_{i},x_{j}) \end{aligned}$$

(1)

The singleton energy $E_{i}(x_{i},\mathbf {y})$ encodes the disassociation between the label $x_{i}$ and descriptors of image $\mathbf {y}$ at site $i$. In image denoising, for example, where $y_{i}$ is a corrupted pixel and $x_{i}$ is a true pixel we may use $E_{i}(x_{i},\mathbf {y})=\left| x_{i}-y_{i}\right|$ as the corruption cost. The pairwise energy $E_{ij}(x_{i},x_{j})$ captures spatial smoothness, i.e., the tendency for two nearby pixels to be similar. For example, $E_{ij}(x_{i},x_{j})=\lambda \left| x_{i}-x_{j}\right|$ is a cost of difference between two labels, where $\lambda >0$ is a problem-specific parameter.

The task is to find the optimal $\mathbf {x}^{map}$ that minimizes the energy $E(\mathbf {x},\mathbf {y})$, which now plays the role of a cost function:

$$\begin{aligned} \mathbf {x}^{map}&= \arg \min _{\mathbf {x}}E(\mathbf {x},\mathbf {y}) \end{aligned}$$

(2)

For example, in image denoising, this translates to finding a map of intensity that admits both the low cost of corruption and high degree of smoothness.

The formal justification for energy minimization in MRF can be found through the probability of the labeling defined as:

$$\begin{aligned} P(\mathbf {x}\mid \mathbf {y})\propto e^{-E(\mathbf {x},\mathbf {y})} \end{aligned}$$

(3)

Thus minimizing the energy is equivalent to finding the most probable labeling $\mathbf {x}^{map}$. As $P(\mathbf {x}\mid \mathbf {y})$ is often called the posterior distribution in computer vision,¹ the energy minimization problem is also referred to as MAP assignment.

3.2 Local search: iterated conditional mode

Iterated conditional mode (Besag 1986) is a simple local search algorithm. It iteratively finds the local optimal labeling for each site $i$ as follows

$$\begin{aligned} x_{i}^{*}&=\arg \min \nolimits _{x_{i}}&\left\{ E_{i}(x_{i},\mathbf {y})+\sum _{j\in \mathcal {N}(i)}E_{ij}(x_{i},x_{j})\right\} \end{aligned}$$

(4)

where $\mathcal {N}(i)$ is the set of sites connected to the site $i$, often referred to as Markov blanket. The Markov blanket shields a site from the long-range interactions, a phenomenon known as Markov property, which states that probability of a label assignment at site $i$ depends only on the nearby assignments (Hammersley and Clifford 1971; Lauritzen 1996). The probabilistic interpretation of Eq. (4) is

$$\begin{aligned} x_{i}^{*}=\arg \max _{x_{i}}P\left( x_{i}\mid \{x_{j}\}_{j\in \mathcal {N}(i)},\mathbf {y}\right) \end{aligned}$$

The local update in Eq. (4) is repeated for all sites until no more improvement can be made. This procedure is guaranteed to find a local minimum energy in a finite number of steps. However, the solutions found by the ICM are sensitive to initialization and often unsatisfactory for image labeling (Szeliski et al. 2008).

3.3 Exact global search on trees: belief-propagation

Belief-propagation was first proposed as an inference method on MRFs with tree-like structures (Pearl 1988). The BP operates by sending messages between connecting sites. For this reason, it is also called message passing algorithm. The BP is efficient because instead of dealing with all the sites simultaneously, we only need to compute messages passing between two local sites at a time. At each site, local information modifies the incoming messages before sending out to neighbor sites.

3.3.1 General BP

The message sent from site $j$ to site $i$ is computed as follows

$$\begin{aligned} \mu _{j\rightarrow i}(x_{i})&= \min _{x_{j}}\left( E_{j}(x_{j},\mathbf {y})+E_{ij}(x_{i},x_{j})+\sum _{k\in \mathcal {N}(j),k\ne i}\mu _{k\rightarrow j}(x_{j})\right) \end{aligned}$$

(5)

i.e., the outgoing message is aggregated from all incoming messages, except for the one in the opposite direction. Messages can be initialized arbitrarily, and the procedure is guaranteed to converge after finite steps on trees (Pearl 1988). At convergence, the optimal labeling is obtained by:

$$\begin{aligned} x_{i}^{map}=\arg \min _{x_{i}}\left( E_{i}(x_{i},\mathbf {y})+\sum _{k\in \mathcal {N}(i)}\mu _{k\rightarrow i}(x_{i})\right) \end{aligned}$$

(6)

3.3.2 2-pass BP

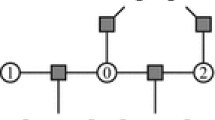
A more efficient variant of BP is a 2-pass procedure, as summarized in Fig. 1. First we pick one particular site as root. Since the tree has no loops, there is a single path from a site to any other site. Each site, except for the root, has exactly one parent. The procedure consists of two passes:

• Upward pass Messages are first initiated at the leaves, and are set to $0$. Then all messages are sent upward and updated as messages converging at common parents along the paths from leaves to the root. The pass stops when all the messages reach the root.

• Downward pass Messages are combined and re-distributed downward from the root back to leaves. Messages are then terminated at leaves.

The 2-pass BP procedure is a remarkable algorithm: It searches through a combinatorial space of $S^{N}$ using only $\mathcal {O}\left( 2NS^{2}\right)$ operations and $\mathcal {O}\left( 2NS\right)$ memory.

Fig. 1

Belief propagation on trees: the two-pass procedure

Remark

We note in passing that this procedure may be also known as min-sum or max-product. The term max-product comes from the use of exponentials of negative energies in Eqs. (5, 6), and turning mins into maxes and sums into products.

3.4 Approximate global search on general graphs: loopy belief-propagation

Standard MRFs in image analysis are usually not tree-structured. A common topology is a grid in which each site represents a pixel and has four neighbors. Thus the resulting graph has many cycles, rendering the 2-pass BP algorithm useless.

However, an approximation to the exact BP has been suggested. Using the general BP described above, messages are sent across all edges without worrying about the order (Pearl 1988). At each step, messages are updated using Eq. (5). After some stopping criteria are met, we still use Eq. (6) to find the best labeling. This procedure is often called loopy BP due to the presence of loops in the graph. The heuristic has been shown to be useful in several applications (Murphy et al. 1999) and this has triggered much research on improving it (Duchi et al. 2007; Felzenszwalb and Huttenlocher 2006; Wainwright et al. 2005; Weiss and Freeman 2001; Yanover et al. 2006).

The main drawback of the loopy BP is lack of convergence guarantee. In our simulation of Ising models (Sect. 5.1), the loop BP clearly fails in the cases where interaction energies dominate singleton energies, that is $\left| E_{ij}(x_{i},x_{j})\right| \gg \left| E_{i}(x_{i},\mathbf {y})\right|$ for all $i,j$ (see Fig. 4). Another drawback is that the memory will be very demanding for large images. For grid-image, the memory needed is $\mathcal {O}\left( 4HWS\right)$.

4 Iterated strong local search

In this section we present a method to exploit the efficiency of the BP on trees to build strong local search. By ‘strong’, we mean the quality of the local solution found by the procedure is often much better than the standard greedy local search. Although a typical MRF in computer vision is not a tree, we observe that any graph is a super-imposition of trees. Second, due to the Markov property, described in Sect. 3.2, variables in a tree can be shielded from other variables through the Markov blanket of the tree. This gives rise to the concept of conditional trees, which we present subsequently.

4.1 Conditional trees

Fig. 2

Examples of conditional trees on grid (connecting empty sites). Filled nodes are labeled sites. Arrows indicate absorbing direction, dashes represent unused interactions. Dotted lines in (c,d) are dummy edge (with zeros interacting energy) that connects separate sub-trees together to form a full tree

For concreteness, let us consider grid-structured MRFs. There are multiple ways to extract a tree out of a grid, as shown in Fig. 2. In particular, we fix the labeling to some sites, leaving the rest to form a tree. Consider a tree $\tau$ and let $\mathbf {x}_{\tau }=\{x_{i}\mid i\in \tau \}$, and $\mathbf {x}_{\lnot \tau }=\{x_{i}\mid i\notin \tau \}$. Denote by $\mathcal {N}(\tau )$ the set of sites connecting to $\tau$ but do not belong to $\tau$, i.e., the Markov blanket of $\tau$. The collection of sites $\left( \tau ,\mathcal {N}(\tau )\right)$ and the partial labeling of the neighbor sites $\mathbf {x}_{\mathcal {N}(\tau ),}$ form a conditional tree. The energy of the conditional tree can be written as:

$$\begin{aligned} E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right)&= \sum _{i\in \tau }E_{i}^{*}(x_{i},\mathbf {y})+\sum _{i,j\in \tau }E_{ij}(x_{i},x_{j}) \end{aligned}$$

(7)

where

$$\begin{aligned} E_{i}^{*}(x_{i},\mathbf {y})=E_{i}(x_{i},\mathbf {y})+\sum _{(i,j)\in \mathcal {E}, j\in \mathcal {N}(\tau )}E_{ij}(x_{i},x_{j}) \end{aligned}$$

(8)

In other words, the interacting energies at the tree border are absorbed into the singleton energy of the leaves. In Fig. 2, the absorbing direction is represented by an arrow.

The minimizer of this conditional tree energy can be found efficiently using the BP:

$$\begin{aligned} \hat{\mathbf {x}}_{\tau }=\arg \min _{\mathbf {x}_{\tau }}E_{\tau }\left( \mathbf {x}_{\tau }, \mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) \end{aligned}$$

(9)

This is because that Eq. (7) has the form of Eq. (1).

One may wonder how the minima of the energy of conditional trees $E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right)$ relate to the minima of the entire network $E\left( \mathbf {x},\mathbf {y}\right)$. We present here two theoretical results. First, the local minimum found by Eq. (9) is also a local minimum of $E\left( \mathbf {x},\mathbf {y}\right)$:

Proposition 1

Finding the mode $\hat{\mathbf {x}}_{\tau }$ as in Eq. (9) guarantees a local minimization of model energy over all possible tree labelings. That is

$$\begin{aligned} E(\hat{\mathbf {x}}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})\le E(\mathbf {x}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y}) \end{aligned}$$

for all $\mathbf {x}_{\tau }\ne \hat{\mathbf {x}}_{\tau }$.

Proof

The proof is presented in Appendix 7.2.

The second theoretical result is that the local minimum found by Eq. (9) is indeed the global minimum of the entire system if all other labels outside the tree happen to be part of the optimal labeling:

Proposition 2

If $\mathbf {x}_{\lnot \tau }\in \mathbf {x}^{map}$ then $\hat{\mathbf {x}}{}_{\tau }\in \mathbf {x}^{map}$.

Proof

We first observe that since $E(\mathbf {x}^{map},\mathbf {y})$ is the lowest energy then

$$\begin{aligned} E(\mathbf {x}^{map},\mathbf {y})&\le E(\hat{\mathbf {x}}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y}) \end{aligned}$$

(10)

Now assume that $\hat{\mathbf {x}}_{\tau }\notin \mathbf {x}^{map}$, so there must exist $\mathbf {x}'_{\tau }\in \mathbf {x}^{map}$ that $\hat{\mathbf {x}}_{\tau }\ne \mathbf {x}'_{\tau }$ and $E(\mathbf {x}'_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})>E(\hat{\mathbf {x}}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})$, or equivalently $E(\mathbf {x}^{map},\mathbf {y})>E(\hat{\mathbf {x}}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})$, which contradicts with Eq. (10) $\square$

The derivation in Eq. (7) from the probabilistic formulation is presented in Appendix 7.1.

4.2 Tree-based ICM (T-ICM): conditional trees for strong local search

As conditional trees can be efficient to estimate the optimal labeling, we propose a method in the spirit of the simple local search ICM (Besag 1986) (Sect. 3.2). First of all, a set of conditional trees $\mathcal {T}$ is constructed. At each step, a tree $\tau \in \mathcal {T}$ is picked according to a predefined update schedule. Using the 2-step BP, we find the optimal labeling for $\tau$ using Eq. (9). As this method includes the ICM as a special case when the tree is reduced to a single site, we call it the tree-based ICM (T-ICM) algorithm, which is presented in pseudo-code in Algorithm 1.

4.2.1 Specification of T-ICM

Tree set and update schedule For a given graph, there are exponentially many ways to build conditional trees, and thus defining the tree set is itself a nontrivial task. However, for grids used in image labeling with height $H$ and width $W$, we suggest two simple ways:

• The set of $H$ rows and $W$ columns. The neighborhood size is $HS^{W}+WS^{H}$.

• The set of $2$ alternative rows and $2$ alternative columns (Fig. 2c, d). Since alternative rows (or columns) are separated, they can be connected by dummy edges to form a tree (e.g., see Fig. 2c, d). A dummy edge has the interacting energy of zero, thus does not affect search operations on individual components. The neighborhood size is $4S^{0.5HW}$.

These two sets lead to an efficient T-ICM compared to the standard ICM which only covers the neighborhood of size $SHW$ using the same running time. Once the set has been defined, the update order for trees can be a fixed sequence (e.g., rows from-top-to-bottom then columns from-left-to-right), or entirely random.

4.2.2 Properties of T-ICM

Due to Proposition 1, at each step of Algorithm 1, either the total energy $E(\mathbf {x},\mathbf {y})$ will be reduced or the algorithm will terminate. Since the model is finite and the energy reduction is discrete (hence non-vanishing), the algorithm is guaranteed to reach a local minimum after finite steps.

Although the T-ICM only finds local minima, we expect the quality to be better than those found by the original ICM because each tree covers many sites. For example, as shown in Fig. 2a, b, a tree in the grid can account for a half of all the sites, which is overwhelmingly large compared to a single site used by the ICM. The number of configurations of the tree $\tau$, or equivalently the neighborhood size, is $S^{N_{\tau }}$, where $N_{\tau }$ is the number of sites on the tree $\tau$. The neighborhood size of the ICM, on the other hands, is just $S$.

For the commonly used $4$-neighbor grid MRF in image labeling, and the tree set of alternative rows and columns, the BP takes $\mathcal {O}(4HW)$ time to pass messages, each of which costs $3S^{2}$ time to compute. Thus, the time complexity per iteration of the T-ICM is only $S$ times higher than that of the ICM and about the same as that of the loop BP (Sect. 3.4). However, the memory in our case is still $\mathcal {O}\left( 2\times \max \{H,W\}\right)$, which is much smaller than the $\mathcal {O}(4HW)$ memory required by the loopy BP. In addition, each step in the T-ICM takes exactly 2 passes, while the number of iterations of the loopy BP, if the method does converge at all, is unknown and parameter dependent.

4.3 Tree-based ILS: global search

As the T-ICM is still a local search procedure, inherent drawbacks remain: (i) it is sensitive to initialization, and (ii) it can get stuck in suboptimal solutions. To escape from the local minima, global search strategies must be employed. We can consider the entire T-ICM as a single super-move in an exponentially large neighborhood.

Fig. 3

Search behavior of T-ICM and T-ILS. The use of T-ICM creates a smoother energy landscape for T-ILS (the surrogate dotted curve). ICM gets stuck on the first local minimum it finds, but T-ICM could find a much better solution by operating on an exponentially large neighborhood

Since it is not our intention to create a totally new escaping heuristic, we draw from the rich pool of metaheuristics in the literature and adapt to the domain of image labeling. In particular, we choose an effective heuristic, commonly known as ILS (Lourenco et al. 2003) for escaping from the local minima. The ILS advocates jumps from one local minimum to another. If a jump fails to lead to a better solution, it can still be accepted according to an acceptance scheme, following the spirit of simulated annealing (SA). However, we do not decrease the temperature as in the SA, but rather, the temperature is adjusted so that on average the acceptance probability is roughly $0.5$. The process is repeated until the stopping criteria are met. We term the resulting metaheuristic the Tree-based Iterated Local Search (T-ILS) whose pseudo-code is presented in Algorithm 2, and behavior is illustrated in Fig. 3. In what follows we specify the algorithm in more details.

4.3.1 Specification of T-ILS

Jump The jump step-size has to be large enough to successfully escape from the basin that traps the local search. In this study, we design a simple jump by randomly changing labels of $\rho \%$ of sites. The step-size $\rho$ is drawn randomly in the range $(0,\rho _{max})$, i.e., $\rho \sim \mathcal {U}\left( 0,\rho _{max}\right)$, where $\rho _{max}$ is an user-specified parameter.

Acceptance After a jump, the local search is invoked, followed by an acceptance decision to accept or reject the jump. We consider the following acceptance probability:

$$\begin{aligned} a=\min \left\{ 1,\exp (-\beta \varDelta E)\right\} \end{aligned}$$

where $\varDelta E=E(\hat{\mathbf {x}}^{t+1},\mathbf {y})-E(\mathbf {x}^{t},\mathbf {y})$ is the change in energy between two consecutive minima, and $\beta >0$ is the adjustable “inverse temperature”. A large $\beta$ lowers the acceptance rate but a small $\beta$ increases it. This fact will be used to adjust the acceptance rate, as detailed below.

Adjusting inverse temperature We wish to maintain an average acceptance probability of $0.5$, following the success of David (1997). However, unlike the work in David (1997), we do not change the step-size, but rather adjusting the inverse temperature. The estimation of acceptance rate is $r\leftarrow r/t$, where $n$ is the total number of accepted jumps up to step $t$. To introduce short-term effect, we use the last event:

$$\begin{aligned} r\leftarrow 0.9r+0.1\mathbb {I}\left[ \mathbf {x}^{t+1}=\hat{\mathbf {x}}^{t+1}\right] \end{aligned}$$

If the acceptance rate is within the range $[0.45,0.55]$ we do nothing. A rate below $0.45$ will decrease of the inverse temperature: $\beta \leftarrow 0.8\beta$, and a rate above $0.55$ will increase it: $\beta \leftarrow \beta /0.8$.

4.3.2 Properties of T-ILS

Figure 3 illustrates the behavior of the T-ILS. Through the T-ICM component, the energy landscape is smoothed out, helping the T-ICM to locate good local minima. When the jump is not large, the search trajectory can be tracked to avoid self-crossing walks. If the jump is far enough (with large $\rho _{max}$), the resulting algorithm will behave like multistart procedures.

When the inverse temperature $\beta$ is set to $0$, the acceptance behavior becomes deterministic, that is, we only accept the jump if it improves the current solution. In other words, the T-ILS becomes a greedy algorithm. Alternatively, when $\beta$ is sufficiently large, we would accept all the jumps, allowing a memoryless foraging behavior.

5 Experiments

In this section, we evaluate our proposed algorithms on a simulated Ising model and two benchmark vision labeling problems: stereo correspondence and image denoising. In all settings, we employ MRFs with the grid-structure (e.g., each inner pixel is connected to exactly 4 nearby pixels). Trees are composed of rows and columns as specified in Sect. 4.2.1. The tree update schedule starts with rows (top to bottom) followed by columns (left to right). Unless specified otherwise, the initial labeling is randomly assigned. The max step-size is $\rho _{max}=10\,\%$ (Sect. 4.3.1). For the T-ILS, the inner loop has $T_{inner}=1$, i.e., full local minima may not be reached by the T-ICM, as this setting does not seem to hurt the final performance. The outer loop has $T_{outer}=1,000$ and $T_{backtrack}=1,000$.

5.1 Simulated Ising model

In this subsection, we validate the robustness of our proposed algorithms on Ising models, which have wide applications in magnetism, lattice gases, and neuroscience (McCoy and Wu 1973). Within the MRF literature, Ising lattices are often used as a benchmark to test inference algorithms (e.g., see Wainwright et al. 2005). Following Wainwright et al. (2005), we simulate a 500$\times$500 grid Ising model where labels are binary spin orientations (up or down): $x_{i}\in \pm 1$, and local energy functions are: $E_{i}(x_{i})=\theta _{i}x_{i}$; $E_{ij}(x_{i},x_{j})=\lambda \theta _{ij}x_{i}x_{j}$. The parameter $\theta _{i}$ specifies the influence of external field on the spin orientation and $\theta _{ij}$ specifies the interaction strength and direction (attractive or repulsive) between sites. The parameters $\left\{ \theta _{i},\theta _{ij}\right\}$ are set as follows

$$\begin{aligned} \theta _{i},\theta _{ij}&\sim \mathcal {U}(-1,1) \end{aligned}$$

where $\mathcal {U}(-1,1)$ denotes the uniform distribution in the range $(-1,1)$. The parameter $\lambda >0$ specifies the interaction strength. When $\lambda$ is small, the interaction is weak, and thus the external field has more effect on the spin arrangement. However, when $\lambda$ is large, the spin arrangement depends more on the interacting nature. A stable arrangement would be of the minimum energy.

The result of minimizing energy is shown in Fig. 4. When the interaction is weak (e.g., $\lambda =0.5$), the loopy BP performs well, but when the interaction is strong (e.g., $\lambda =1.0$), the T-ILS has a clear advantage. Thus the T-ILS is more robust since it is less sensitive to $\lambda$.

Fig. 4

Performance of T-ILS and loopy BP algorithm in minimizing Ising energy with $\lambda =0.5$ (left) and $\lambda =1.0$ (right).

5.2 Stereo correspondence

Stereo correspondence is to estimate the depth of field (DoF) given two or more 2D images of the same scene taken from two or more cameras arranged horizontally. This is used in 3D reconstruction of a scene using standard 2D cameras. The problem is often translated into estimating the disparity between images—how much two images differ and this reflects the depth at any pixel locations. For simplicity, we only investigate the two-cameras setting. In the MRF-based stereo framework, a configuration of $\mathbf {x}\in \mathbb {N}^{W\times H}$ realizes the disparity map. The disparity set (or the label set) is predefined. For example, of the two benchmark datasets ² used in this experiment, the Tsukuba has $16$ labels (Fig. 5), and the Venus has $20$ (Fig. 6).

Fig. 5

Stereo results on the Tsukuba dataset. (Top-left) left image, (top-middle) right image, (top-right) groundtruth; (bottom-left) scan-line, (bottom-middle) loop BP, and (bottom-right) T-ILS (initialized from scan-line)

Fig. 6

Stereo results on the Venus dataset. (Top-left) left image, (top-middle) right image, (top-right) groundtruth; (bottom-left) scan-line, (bottom-middle) loop BP, and (bottom-right) T-ILS (initialized from scan-line)

The singleton energy $E_{i}(x_{i},\mathbf {y})$ at each pixel location measures the dissimilarity in pixel intensity between the left/right images, and the interaction energy $E_{ij}(x_{i},x_{j})$ measures the discontinuity in the disparity map. We use a simple linear Potts cost model as in Scharstein and Szeliski (2002). Let $\mathbf {y}=(I^{l},I^{r})$ where $I^{l}$ and $I^{r}$ are intensities of the left and right images respectively, and $i=(i_{X},i_{Y})$ where $i_{X}$ and $i_{Y}$ are horizontal and vertical coordinates of pixel $i$. The local energies are defined as (Scharstein and Szeliski 2002):

$$\begin{aligned} E_{i}(x_{i},\mathbf {y})&= \varDelta I(i,x_{i})\\ E_{ij}(x_{i},x_{j})&= \lambda \times \mathbb {I}[x_{i}\ne x_{j}] \end{aligned}$$

where $\mathbb {I}[\cdot ]$ is the indicator function, $\lambda >0$ is the smoothness parameter, and $\varDelta I(i,x_{i})=\left| I^{l}(i_{X},i_{Y})-I^{r}(i_{X}-x_{i},i_{Y})\right|$ is the difference in pixel intensity in two images when pixel positions are $x_{i}$ pixels apart in the horizontal direction. A small $x_{i}$ would result in large $\varDelta I(i,x_{i})$ if the true DoF is small. Thus by minimizing the singleton energy with respect to $x_{i}$, a small DoF leads to stronger reduction of $x_{i}$ than a large DoF does. We choose $\lambda =20$ following Scharstein and Szeliski (2002) and implement algorithms based on the software framework of Szeliski et al. (2008). ³

There is a wide range of techniques available for stereo estimation, and the loopy BP is one of the winning methods (Scharstein and Szeliski 2002; Szeliski et al. 2008). Fast methods like scan-line (SL) optimization are widely used for real-time implementation. The scan-line is equivalent to taking independent 1D rows and running the chain BP. Since the SL does not admit the original 2D structure, we need to adapt the singleton energy as $\bar{E}_{i}(x_{i},\mathbf {y})=\nu E_{i}(x_{i},y)$, where $\nu \in [0,1]$, to account for the lack of inter-row interactions.

Table 1 Stereo energy found by algorithms (SL = Scan-line)

Table 1 shows the effect of changing from $\nu =1.0$ to $\nu =0.4$ in term of reducing 2D energy. The result, however, has the inherent horizontal ‘streaking’ effect since no 2D constraints are ensured (Figs. 5, 6, bottom-left). The randomly initialized T-ICM with one iteration ($T=1$ in Algorithm 1) performs comparably with the best of SL ($\nu =0.4$). The performance of the T-ICM improves significantly by initializing from the result of SL. The T-ILS initialized from the SL finds a better energy than the loopy BP given the same number of iterations, as shown in Fig. 7.

5.3 Image denoising

In image denoising, the task is to reconstruct the original image from a corrupted source. We use the $122\times 179$ noisy gray Penguin image ⁴ (Fig. 8). The labels of the MRF correspond to $S=256$ intensity levels ($8$ bits depth). Similar to the stereo correspondence problem, we use a simple truncated Potts model as follows

$$\begin{aligned} E_{i}(x_{i},\mathbf {y})&= \min \left\{ |x_{i}-y_{i}|,\tau \right\} \\ E_{ij}(x_{i},x_{j})&= \lambda \times \delta [x_{i}\ne x_{j}] \end{aligned}$$

where the truncation at $\tau =100$ prevents the effect of extreme noise, and $\lambda =25$ is the smoothness parameter, following Szeliski et al. (2008). In addition, the optimized loopy BP for Potts models from Felzenszwalb and Huttenlocher (2006) is used. Fig. 8b, c demonstrates that the T-ILS runs faster than the optimized loopy BP, yielding a lower energy and a smoother restoration.

Fig. 7

Stereo energy minimization by Loopy BP (dashed line) and T-ILS (line) on Tsukuba (left) and Venus (right) images

Fig. 8

Penguin images a noisy, b restored with T-ILS, c restored with loopy BP; d running time. Algorithms stop after $5$ unsuccessful iterations

6 Discussion

We have proposed a fast method for inference in Markov random fields by exploiting conditional trees embedded in the network. We introduced a strong local search operator (T-ICM) based on Belief-Propagation and a global stochastic search operator T-ILS based on the iterated local search framework. We have shown in both simulation and two real-world image analysis tasks (stereo correspondence and image denoising) that the T-ILS is competitive against state-of-the-art algorithms. We have demonstrated that by exploiting the structure of the domains, we can derive strong local search operators which can be exploited in a metaheuristic strategy such as the ILS.

6.1 Future work

The line of the current work could be extended in several directions. First, we could adapt the T-ILS for certain cost functions. Currently, the T-ILS is designed as a generic optimization method, making no assumptions about the nature of the optimal solution. In contrast, label maps in vision are often smooth almost everywhere except for sharp boundaries. Second, Markov random fields may offer a more informative way to perform the jump steps, e.g., by relaxing the messages in the local edges or by keeping track of the hopping trajectories. Third, we have limited the T-ILS to uniform distribution of step-sizes, but it needs not be the case. One useful heuristic is Lévy flights (Tran et al. 2004) in which the step-size $\rho$ is drawn from the power-law distribution: $\rho ^{-\alpha }$ for $\alpha >0$. This distribution allows occasional big jumps (which might behave like a total restart). Fourth, other metaheuristics are applicable. For example, we can use genetic algorithms in conjunction with the conditional trees as follows. Each individual in the population can be represented by a string of $N$ characters, each of which has one of $S$ values in the label alphabet. For each individual, we run the 2-pass BP to obtain a strong local solution. Then the crossover operator can be applied character-wise on a selected subset to generate a new population. Finally, although we have limited ourselves to applications in image analysis, the proposed algorithm is generic to any problems where MRFs are applicable.

Appendix: Distribution over conditional trees

We provide the derivation of Eq. (7) from a probabilistic argument. Recall that $\mathcal {N}(\tau )$ is the Markov blanket of the tree $\tau$, that is, the set of sites connecting to $\tau$. Due to the Markov property

$$\begin{aligned} P\left( \mathbf {x}_{\tau }\mid \mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right)&= P\left( \mathbf {x}_{\tau }\mid \mathbf {x}_{\lnot \tau },\mathbf {y}\right) \\&\propto \exp \left\{ -E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) \right\} \end{aligned}$$

where

$$\begin{aligned} E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right)&= \sum _{i\in \tau }E_{i}(x_{i},\mathbf {y})+\sum _{(i,j)\in \mathcal {E}\mid i,j\in \tau }E_{ij}(x_{i},x_{j})\nonumber \\&+\sum _{(i,j)\in \mathcal {E}\mid i\in \tau ,j\in \mathcal {N}(\tau )}E_{ij}(x_{i},x_{j}) \end{aligned}$$

(11)

Equation (7) can be derived from the energy above by letting:

$$\begin{aligned} E_{i}^{*}(x_{i},\mathbf {y})=E_{i}(x_{i},\mathbf {y})+\sum _{(i,j) \in \mathcal {E},j\in \mathcal {N}(\tau )}E_{ij}(x_{i},x_{j}) \end{aligned}$$

(12)

Thus finding the most probable labeling of the tree $\tau$ conditioned on its neighborhood is equivalent to minimizing the conditional energy in Eq. (9):

$$\begin{aligned} \hat{\mathbf {x}}_{\tau }=\arg \max _{\mathbf {x}_{\tau }}P\left( \mathbf {x}_{\tau }\mid \mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) \end{aligned}$$

(13)

The equivalence can also be seen intuitively by considering the tree $\tau$ as a mega-site, so the update in Eq. (9) is analogous to that in Eq. (4).

1.1 Proof of Proposition 1

Recall that the energy can be decomposed into singleton and pairwise local energies (see Eq. 1)

$$\begin{aligned} E(\mathbf {x}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})&= \sum _{i\in \tau }E_{i}(x_{i},\mathbf {y})+\sum _{i\notin \tau }E_{i}(x_{i},\mathbf {y})+\sum _{(i,j)\in \mathcal {E}|i,j\in \tau }E_{ij}(x_{i},x_{j})+\\&\quad +\sum _{j\in \mathcal {N}(\tau )|(i,j)\in \mathcal {E}}E_{ij}(x_{i},x_{j})+\sum _{(i,j)\in \mathcal {E}|i,j\notin \tau }E_{ij}(x_{i},x_{j}) \end{aligned}$$

where:

• $\sum _{i\in \tau }E_{i}(x_{i},\mathbf {y})$ is the data energy belonging to the tree $\tau$,

• $\sum _{i\notin \tau }E_{i}(x_{i},\mathbf {y})$ is the data energy outside $\tau$,

• $\sum _{(i,j)\in \mathcal {E}|i,j\in \tau }E_{ij}(x_{i},x_{j})$ is the interaction energy within the tree,

• $\sum _{j\in \mathcal {N}(\tau )|(i,j)\in \mathcal {E}}E_{ij}(x_{i},x_{j})$ is the interaction energy between the tree and its boundary, and

• $\sum _{(i,j)\in \mathcal {E}|i,j\notin \tau }E_{ij}(x_{i},x_{j})$ is the interaction energy outside the tree.

By grouping energies related to the tree and the rest, we have

$$\begin{aligned} E(\mathbf {x}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})&= E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) +\sum _{(i,j)\in \mathcal {E}|i,j\notin \tau }E_{ij}(x_{i},x_{j}) \end{aligned}$$

where $E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right)$ is given in Eq. (11) for all $i\in \tau$. This leads to:

$$\begin{aligned} E(\hat{\mathbf {x}}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y})&= E_{\tau }\left( \hat{\mathbf {x}}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) +\sum _{(i,j)\in \mathcal {E}|i,j\notin \tau }E_{ij}(x_{i},x_{j})\\&\le E_{\tau }\left( \mathbf {x}_{\tau },\mathbf {x}_{\mathcal {N}(\tau )},\mathbf {y}\right) +\sum _{(i,j)\in \mathcal {E}|i,j\notin \tau }E_{ij}(x_{i},x_{j})\\&= E(\mathbf {x}_{\tau },\mathbf {x}_{\lnot \tau },\mathbf {y}) \end{aligned}$$

This completes the proof $\square$