1 Introduction

Static friction force is an important factor for determining the capabilities of sliding systems. A large static friction force is effective to prevent unnecessary slippage. On the other hand, in some cases, a low static friction force is required to achieve a smooth start motion without unstable slippage because large static friction sometimes causes an unstable sliding motion, such as stick–slip vibration [1, 2]. For the above reasons, designing static friction force has been an important issue in the study of friction, especially in mechanical engineering.

One of the methods for designing static friction force is based on the use of surface textures, which includes artificial surface structures ranging from μm to mm scales. For example, as experimentally and theoretically demonstrated, the use of a split contact interface is an effective method to reduce the level of static friction force [3–9]. When a split contact interface slides on a rigid smooth plane, the transition from static to kinetic friction at each contact region occurs independently at different times because the local stiffness and normal load at each contact region are not perfectly equal to each other. Therefore, the local static friction force that appears in the local scale is canceled at the macroscopic scale. When a time change in macroscopic friction force is focused on, a smooth start motion is often observed, even if a local stick–slip motion occurs at each contact point.

In the previous report by Maegawa et al. [10], it was pointed out that the existence of the stop–restart (SR) motion works to increase macroscopic static friction force, based on numerical and experimental results focusing on the sliding friction of a rubber slider with a split contact interface. In this study, the effect of SR motion on static friction force is reported again with some additional discussions. In addition, as a new insight, the effect of stop–inversion (SI) motion on static friction force is discussed. From numerical simulations, it was found that SI motion reduces static friction force, in contrast to the case for SR motion. Furthermore, the mechanism of this tangential loading history dependence of static friction force is also discussed.

2 Analytical Model

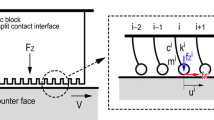
Figure 1 shows a schematic illustration of the analytical model used in this study, which was already developed in the previous study by Maegawa et al. [10]. The model is based on a simplified analytical model developed by Kligerman and Varenberg [7], which suggested treating dynamic stick–slip phenomena in terms of massless quasi-static approach based on the difference between static and kinetic friction. In order to facilitate discussion, the details of this model are described again. This model represents the sliding friction between an elastic split surface with multiple contact points and a rigid smooth plane that moves in the x direction with a driving speed of V. The contact interface is divided into N contact points, and the ith contact point is connected to the bulk region via a spring with a stiffness of k i. It should be noted that to simplify the analysis, the mass of the contact point, m i, and the viscosity at the connection, c i, were set to zero values: m i = 0 and c i = 0. In addition, the interaction between neighboring contacts points was not considered; all of the contact points were connected to the bulk region independently. Therefore, dynamic behaviors, such as crack propagation [11–13], were not considered in this study. At each contact point, a local normal load, f i z , was applied on the contact interface, and a local tangential force, f i x , also acts along the tangential direction.

Fig. 1
figure 1

Schematic diagram of the analytical model

Full size image

As discussed by Farkas et al. [14], the coherence of the contact interface, which is the magnitude of the dispersion in the distribution of threshold lengths for the onset of slip at each contact point, is an important factor for characterizing the level of macroscopic static friction force in a split (or rough) contact interface. Similarly, Kligerman and Varenberg [7] numerically analyzed the effect of the distributions on the local stiffness of k i and the effects of the local normal load, f i z , on macroscopic static friction force.

In this study, based on the description by Kligerman and Varenberg, the stiffness of the spring, k i, and the local normal load, f i z , are statistically scattered as:

$$\begin{aligned} & k^{i} = K/N + \delta k^{i} \\ & f_{z}^{i} = F_{z} /N + \delta f_{z}^{i} , \\ \end{aligned}$$
(1)

where K and F z are the total tangential stiffness and the normal load, respectively. Here, the dispersions of stiffness and normal load distributions are characterized by δk i and δf i z , which represent small statistical deviations (positive or negative) of those parameters from their average values. The random values of δk i and δf i z are chosen using a random number generator with a Gaussian distribution. Here, the mean values of the distributions of k i and f i z correspond to K/N and F z /N, respectively. In addition, the standard deviations of these distributions are formulated as λ K K/N and λ Fz F z /N, respectively. Therefore, the level of their variation is characterized by the values of λ K and λ Fz .

The motion of each contact point is governed by the force balance between the spring force and friction force; thus, k i u i = f i x . Here, u i, which is denoted in Fig. 1b, is the displacement that originates from the position under the natural length of the spring of the ith contact point, and f i x is the local friction force that acts on the contact between the ith contact point and the counter face. The relationship between f i x and u i is illustrated in Fig. 1c, where l i is the threshold displacement for the onset of the transition from static to kinetic friction at each contact point. Considering that the maximum static friction force is described as f ismax  = μ s f i z , where μ s is the static friction coefficient, l i can be formulated as μ s f i z /k i. Thus, f i x is described by:

$$f_{x}^{i} = \left\{ {\begin{array}{*{20}l} {f_{\text{s}}^{i} = k^{i} u^{i} } \hfill & {{\text{when}}\,{\text{in}}\,{\text{the}}\,{\text{stick}}\,{\text{state}},\,{\text{i}}.{\text{e}}.,\, u^{i} < l^{i} } \hfill \\ {f_{\text{k}}^{i} } \hfill & {{\text{when}}\,{\text{in}}\,{\text{the}}\,{\text{slip}}\,{\text{state}}, \,{\text{i}}.{\text{e}}.,\,u^{i} \ge l^{i} } \hfill \\ \end{array} } \right..$$
(2)

Here, l i = μ s f i z /k i. On the other hand, in the slip state, the local kinetic friction force f ik is described as f ik  = μ k f i z , where μ k is the kinetic friction coefficient. This study does not consider the velocity dependence of the kinetic friction coefficient and assumes that μ s > μ k. Here, the total tangential force, F x , was determined by the sum of the local friction forces; thus,

$$F_{x} = \sum f_{x}^{i} = \bar{f}_{\text{s}} N_{\text{stick}} + \bar{f}_{\text{k}} N_{\text{slip}} ,$$
(3)

where \(\bar{f}_{\text{s}}\) and \(\bar{f}_{\text{k}}\) are the averaged values of f is and f ik of the contact points under stick and slip states, respectively. In addition, N stick and N slip are the number of masses under stick or slip states, respectively. Here, N stick + N slip = N. It should be noted that in this study, for a simple description, the term “static friction force” is used in referring to “maximum static friction force.”

The four types of tangential loading sequences focused on in this study are illustrated in Fig. 2, in which time changes in the driving velocity V of the moving counter face are shown. In all cases, the loading sequence includes three loading periods (LPs), 1st LP, 2nd LP, and 3rd LP, and two stopping periods (SPs). During the SP, V = 0. For example, in the SR–SR motion (Fig. 2a), during all LPs, V has a positive value. In contrast, in the SR–SI motion (Fig. 2b), in the first and second LPs, V is positive; while in the third LP, V is negative. In addition, in Fig. 2, two different types of basic motions (SI motion and SR motion) are included in the four loading sequences and are represented using large color arrows. Here, “SR motion” refers to the stop–restart motion, in which the sign of V does not change before or after the SP. In contrast, “SI motion” refers to the stop-inversion motion, in which the sign of V changes before and after the SP. Therefore, for example, the SR–SR motion includes two SR motions, and the SI–SI motion includes two SI motions, as illustrated in Fig. 2.

Fig. 2
figure 2

Schematic illustration of the four types of tangential loading sequences considered in this study

Full size image

3 Results

Figure 3 shows calculation results under four types of loading sequences: (a) SR–SR, (b) SR–SI, (c) SI–SR, and (d) SI–SI motions. Based on the above descriptions, time changes in driving velocity (V), total tangential force (F x ) calculated by Eq. (3), and the ratio of the mass number under stick condition N stick on the total mass number (N) are presented. The gray bands between the first and second LPs and between the second and third LPs depict the SP, where V = 0 mm/s. The top graphs in Fig. 3 correspond to the illustration in Fig. 2. The calculation conditions are as follows: F z  = 10 N, K = 1 N/µm, V = 0.1 mm/s, μ s = 1.0, μ k = 0.5, N = 1000, λ K  = 0.1, and λ Fz  = 0.1.

Fig. 3
figure 3

Time changes in V (top), F X (middle), and N stick/N (bottom) under the SR–SR, SR–SI, SI–SR, and SI–SI motions: F z  = 10 N, K = 1 N/µm, μ s = 1.0, μ k = 0.5, N = 1000, λ K  = 0.1, and λ Fz  = 0.1

Full size image

From the middle graph in Fig. 3a, it was found that in the SR–SR motion, the first static friction force F 1stsmax , which is defined as the maximum value of F x during the first LP, is lower than F 2ndsmax and F 3rdsmax ; thus, F 1stsmax  < F 2ndsmax  = F 3rdsmax . Similarly, in the other three loading sequences, depicted in Fig. 3b–d, F 2ndsmax and F 3rdsmax do not equal F 1stsmax . The changes in F smax due to the change in the tangential loading sequence are summarized in Fig. 4. It should be noted that the vertical axis in Fig. 4 represents the absolute values of static friction force, i.e., |F smax|. It is clear that after the SR motion, |F smax| increases from its value at the first LP; while after the SI motion, it decreases from its value at the first LP. Therefore, it was determined that F smax depends on the type of tangential loading sequence. The mechanism of the effect of the tangential loading history on static friction force will be discussed in the following section.

Fig. 4
figure 4

Changes in static friction force during three loading periods in the SR–SR, SR–SI, SI–SR, and SI–SI motions: F z  = 10 N, K = 1 N/µm, μ s = 1.0, μ k = 0.5, N = 1000, λ K  = 0.1, and λ Fz  = 0.1

Full size image

The bottom graphs in Fig. 3 show the changes in N stick/N. At the initial condition when time is 0 s, N stick/N is unity because all of the contact points are under the stick state. After the onset of the driving motion, N stick/N decreases with time, and then, reaches a zero value when global slip is established. The values of N stick/N when F x  = F 1stsmax , F x  = F 2ndsmax , and F x  = F 3rdsmax are also depicted in Fig. 3. Comparing with each of the loading sequences, it was found that during the SR motion, N stick/N at F x  = F 2ndsmax , or F x  = F 3rdsmax increases from the value at F x  = F 1stsmax ; while during the SI motion, they decrease from the values at F x  = F 1stsmax . For example, in the SR–SI motion (Fig. 3b), during the SR motion, N stick/N at F x  = F 2ndsmax is 0.95, but during the SI motion, N stick/N at F x  = F 2rdsmax is 0.78. As formulated in Eq. (3), the value of the macroscopic tangential force, F x , is characterized by N stick and N slip, where N slip = N − N stick. Here, N stick is described using a probability distribution function of the threshold length, l, i.e., P(l),

$$N_{\text{stick}} = N\mathop \int \limits_{U}^{\infty } P(l){\text{d}}l,$$
(4)

where U is the macroscopic sliding distance (displacement), and \(\mathop \int \nolimits_{0}^{\infty } P(l){\text{d}}l = 1.\) From Eq. (4), it is obvious that the magnitude of the dispersion of the threshold length distribution characterizes the value of N stick at the macroscopic sliding distance U, and it determines the value of F x . Therefore, considering that the magnitude of static friction force is characterized by the value of N stick/N, as shown in Fig. 3, it was found that the coherence of the threshold length, l, is an important factor for determining the macroscopic static friction force. The role of the coherence on friction has been already pointed out in the reference in [14], based on the theoretical analysis. Thus, the static friction force of the slider with a relatively high coherence of the threshold length is larger than that with a low coherence slider.

4 Discussion

We considered the mechanism of the effect of tangential loading history on static friction force. From the above discussion, it was found that the threshold length distribution, i.e., P(l), affects the magnitude of the static friction force. Therefore, in this section, we focused on the changes in P(l) during the tangential loading sequences. Here, we again define the threshold length for the onset of the transition from static to kinetic friction. When the spring k i is perfectly relaxed before applying tangential loading, l i can be described by μ s f i z /k i, as denoted in Fig. 1. However, in many cases, a certain strain is stored in the contact interface before tangential loading, i.e., l iresidual  ≠ 0 and l i ≠ μ s f i z /k i. Therefore, the effective threshold length, l ieffective , which varies with time during tangential loading sequence, should be defined as

$$l_{\text{effective}}^{i} = \mu_{\text{s}} f_{z}^{i} /k^{i} - l_{\text{residual}}^{i} .$$
(5)

Here, it is clear that the value of l iresidual at the jth loading period (LP) is determined by the kinetic friction force at the j − 1th LP because during the SP, the strain of the ith spring for the kinetic friction that is applied during the j − 1th LP is stored for the jth LP. Thus, l iresidual at the second LP is determined by the value of f ik at the first LP, and l iresidual at the third LP is determined by the value of f ik at the second LP. On the other hand, l iresidual at the first LP is zero value because no residual strain is stored before the start of the first tangential loading. Consider that after the SR motion the sign of f ik does not change; while after the SI motion, f ik after the SP is the opposite sign as before the SP,

$$\left| {l_{\text{effective}}^{i} } \right| = \left\{ {\begin{array}{*{20}l} {\frac{{\mu_{\text{s}} f_{z}^{i} }}{{k^{i} }}} \hfill & {{\text{at}}\,1{\text{st}}\,{\text{LP}}} \hfill \\ {\frac{{\mu_{\text{s}} f_{z}^{i} }}{{k^{i} }} - \frac{{\mu_{\text{k}} f_{z}^{i} }}{{k^{i} }}} \hfill & {{\text{at}}\,{\text{SR}}\,{\text{motion}}} \hfill \\ {\frac{{\mu_{\text{s}} f_{z}^{i} }}{{k^{i} }} + \frac{{\mu_{\text{k}} f_{z}^{i} }}{{k^{i} }}} \hfill & {{\text{at}}\,{\text{SI}}\,{\text{motion}}} \hfill \\ \end{array} } \right..$$
(6)

Using the following relationship:

$$l_{\text{ini}}^{i} = \frac{{\mu_{\text{s}} f_{z}^{i} }}{{k^{i} }},$$
(7)

Equation (6) can be written as

$$\left| {l_{\text{effective}}^{i} } \right| = \left\{ {\begin{array}{*{20}l} {l_{\text{ini}}^{i} } \hfill & {{\text{at}}\,1{\text{st}}\,{\text{LP}}} \hfill \\ {l_{\text{SR}}^{i} = l_{\text{ini}}^{i} \left( {1 - \frac{{\mu_{\text{k}} }}{{\mu_{\text{s}} }}} \right)} \hfill & {{\text{at}}\,{\text{SR}}\,{\text{motion}}} \hfill \\ {l_{\text{SI}}^{i} = l_{\text{ini}}^{i} \left( {1 + \frac{{\mu_{\text{k}} }}{{\mu_{\text{s}} }}} \right)} \hfill & {{\text{at}}\,{\text{SI}}\,{\text{motion}}} \hfill \\ \end{array} } \right..$$
(8)

From Eq. (8), the changes in the effective threshold length, l ieffective , during the tangential loading sequence were quantified. Thus, the changes in the distribution of l ieffective during the changes in tangential loading sequence are characterized by the factor μ k/μ s.

Figure 5 shows histograms of the distributions of l ieffective , which were calculated using Eq. (6). The black, dark gray, and gray bars represent l ieffective distributions for the SR, initial, and SI motions, respectively. It is obvious that the dispersion of l ieffective for the SR motion is smaller than that at the initial motion. In contrast, the dispersion for the SI motion is larger than that at the initial motion. In this study, it is assumed that a probability distribution function at the initial motion P ini(l effective) can be described by using the Gaussian function. Therefore, P ini(l effective) is determined by a fitting process as

$$\begin{aligned} P_{\text{ini}} \left( {l_{\text{effective}} } \right) & = \frac{A}{{\sqrt {2\pi \sigma_{\text{effective}}^{2} } }}{ \exp }\left( { - \frac{{\left( {l_{\text{effective}} - l_{{{\text{effective}}\_{\text{c}}}} } \right)^{2} }}{{2\sigma_{\text{effective}}^{2} }}} \right) \\ & = \frac{A}{{\sqrt {2\pi \sigma_{\text{ini}}^{2} } }}{ \exp }\left( { - \frac{{\left( {l_{\text{ini}} - l_{{{\text{ini}}\_{\text{c}}}} } \right)^{2} }}{{2\sigma_{\text{ini}}^{2} }}} \right), \\ \end{aligned}$$
(9)

where A and σ ini are fitting parameters, which were determined to be A = 512, and σ initial = 1.45 µm. In addition, it is assumed that the center value of the distribution l ini_c is l ini_c = μ k Fz/K. Here, from Eq. (8), the following relationships are obtained: l iSR  = l iini (1 − μ k/μ s), l SR_c = l ini_c(1 − μ k/μ s), l iSI  = l iini (1 + μ k/μ s), and l SI_c = l ini_c (1 + μ k/μ s). Therefore, the probability distribution functions at the SR and SI motions, i.e., P SR(l effective) and P SI(l effective), are described as

$$P_{\text{SR}} \left( {l_{\text{effective}} } \right) = \frac{A}{{\sqrt {2\pi \sigma_{\text{SR}}^{2} } }}\exp \left( { - \frac{{\left( {{\text{l}}_{\text{SR}} - l_{{{\text{SR}}\_{\text{c}}}} } \right)^{2} }}{{2\sigma_{\text{SR}}^{2} }}} \right)$$
(10)

and

$$P_{\text{SI}} \left( {l_{\text{effective}} } \right) = \frac{A}{{\sqrt {2\pi \sigma_{\text{SI}}^{2} } }}{ \exp }\left( { - \frac{{\left( {l_{\text{SI}} - l_{{{\text{SI}}\_{\text{c}}}} } \right)^{2} }}{{2\sigma_{\text{SI}}^{2} }}} \right),$$
(11)

where σ SR = σ ini(1 − μ k/μ s) and σ SI = σ ini(1 + μ k/μ s). The black and gray curves for the SR and SI motions in Fig. 7 are based on Eqs. (10) and (11), respectively. Considering that the magnitude of the static friction force is determined by the coherence of the threshold length distribution, which is characterized by σ ini, σ SR(=σ ini(1 − μ k/μ s)), and σ SR(=σ ini(1 + μ k/μ s)), it was determined that the factor μ k/μ s is an important factor for determining the magnitude of the changes in static friction force due to the existence of SR or SI motions.

Fig. 5
figure 5

Histograms for threshold length. Black bars SR motion, dark gray bars initial motion, and gray bars SI motion

Full size image

In order to quantify the magnitude of the tangential loading history dependence of static friction force, the following parameters are defined:

$$\chi_{\text{SR}} = \frac{{\Delta F_{{x\_{\text{SR}}}} }}{{\Delta F_{{x\_{\text{ini}}}} }}$$
(12)

and

$$\chi_{\text{SI}} = \frac{{\Delta F_{{x\_{\text{SI}}}} }}{{\Delta F_{{x\_{\text{ini}}}} }},$$
(13)

where the meanings of ΔF x_ini, ΔF x_SR, and ΔF x_SI are illustrated in Fig. 6. Here, it should be noted that the vertical axis of Fig. 6 represents the absolute value of F x . When χ SR has a large value, the static friction force largely increases because of the SR motion. On the other hand, a small χ SI means that a large decrement of static friction force due to the SI motion occurs.

Fig. 6
figure 6

Definitions of ΔF x_ini, ΔF x_SR, and ΔF x_SI used in Eqs. (12) and (13)

Full size image

Figure 7 shows the relationship between χ SR or χ SI and the factor μ k/μ s under different λ K and λ Fz . From the figure, it is seen that χ SR (or χ SI) monotonically increases (or decreases) as μ k/μ s increases. This indicates that when μ k has a relatively large value, a large effect of the tangential loading history on static friction force is observed. In contrast, in the case for μ k = 0, the tangential loading history dependence of static friction force is not observed. It is easily understood from Eq. (6); when μ k = 0, the value of l ieffective does not change during the tangential loading sequence. Thus, the value of static friction force does not depend on the type of tangential loading sequence. In addition, from Fig. 7, it was found that when the dispersion of the local tangential stiffness and local normal load has large values, there is a large tangential loading history dependence.

Fig. 7
figure 7

Relationships between a χSR and μ k/μ s and b χSI and μ k/μ s under different λ K and λ Fz ; F z  = 10 N, K = 1 N/µm, μ s = 1.0, μ k = 0.5, and N = 1000

Full size image

From Fig. 7, it was also found that a macroscopic static friction force depends not only on local static friction force but also on local kinetic friction force. As described in Eq. (3), the change in total tangential force, F x , includes local static friction force, f s, and also the local kinetic friction force, f k. Therefore, the optimization of kinetic friction force is one of the options for designing the macroscopic static friction. Thus, it was found that the development process of micro-slip that occurs prior to global slip, which characterizes the changes in N stick and N slip during tangential loading, is an important factor for determining the static friction force. In addition, this study newly presents the finding that static friction force can be adjusted by controlling surface topography focusing on the coherence of the distribution of threshold length.

The analytical model used in this study is based on the Amonton–Coulomb friction laws; thus, friction coefficients do not depend on normal load, and kinetic friction force is constant for the change in sliding speed. However, in the case of friction in polymers, the Amonton–Coulomb friction laws are not even broadly applicable. The friction coefficients depend on normal load, sliding speed, and other conditions [15, 16]. Therefore, the magnitude of the effect of the tangential loading history on static friction force will depend on a number of conditions, including sliding speed, normal load, temperature, and surface roughness.

Similar to the case of the effect of tangential loading history on static friction force, the effect of normal loading history on static friction force has been discussed [17–19]. The essence of the normal and tangential loading history dependence is the same; static friction force is characterized by the magnitude of the initial strain distribution, which affects the development process of micro-slip and also characterizes the macroscopic static friction force. Therefore, the control of the micro-slip propagation, focusing on the tangential or normal loading sequence, can design macroscopic static friction force. Finally, it is noted that, as presented in the previous research [20], the tangential loading history dependence of static friction force can be observed in another sliding system, in which a continuous sliding interface is considered instead of the split contact interface.

5 Conclusions

Through numerical analysis, tangential loading history dependence of static friction force was discussed, focusing on the sliding friction between an elastic slider with a split contact interface and a rigid flat surface. Consequently, it was found that the existence of the stop–restart (SR) motion works to increase static friction force compared to the static friction force under nonresidual surface strain conditions. In contrast, the SI motion reduces static friction force compared to that under no surface strain conditions. In addition, it was found that the coherence of the distribution of threshold length for the onset of transition from static to kinetic friction at each contact point characterizes the magnitude of the effect of tangential loading history on static friction force. Furthermore, the ratio of kinetic friction coefficient on static friction coefficient also characterizes the tangential loading history effect. Therefore, when kinetic friction coefficient has a relatively large value, a large tangential loading history effect is observed. Because the SR and SI motions are basic behaviors in many sliding systems, the effect of the tangential loading history on static friction force is an important consideration for improvements in the capabilities of systems that have sliding interfaces.