Effect of Buoyant Convection on the Spreading and Draining of Porous Media Gravity Currents along a Permeability Jump

Abstract

We investigate theoretically the impact of adding convective dissolution to the sharp interface problem of gravity current propagation along a sloping permeability jump. Three different dissolution modes are explored: constant dissolution, dissolution with simultaneous shutdown and dissolution with sequential shutdown. The last two modes are bookend opposites that make different assumptions about ambient mixing. For simultaneous (sequential) shutdown, different portions of the gravity current interface experience dissolution identically (differently). To gage the effectiveness of dissolution for trapping e.g., supercritical CO$_2$, we consider the evolution of storage efficiencies and examine the impact of changing the dissolution strength, the time, $t_1$, for the onset of shutdown and, for $t_1 < \infty$, the e-folding decay time, $t_2$, characterizing dissolution decay. We also highlight the phenomenon of intermediate run-out, a state where there is a balance between the fluid supplied to the gravity current vs. that lost by dissolution and basal draining. The state in question is transient because, for time $t>t_1$, shutdown decreases the rate of dissolution. The ensuing readjustment causes a remobilization of the previously-arrested gravity currents and their subsequent (though not indefinite) elongation. Our analysis concludes by studying unsteady sources, which provides keen insights into similarities and differences between simultaneous vs. sequential shutdown.

1 Introduction

Curbing the effects of global warming requires reducing carbon dioxide (CO$_2$) emissions. Geological sequestration of CO$_2$ emitted by stationary sources is an attractive alternative to atmospheric release (Szulczewski et al. 2012; Liyanage et al. 2019). Injection sites include depleted oil and gas reservoirs, empty coal seams and deep saline aquifers. Of the three, saline aquifers are the most voluminous (Huppert and Neufeld 2014). A challenge associated with geological sequestration is to arrest vertical migration. Leakage may occur through fissures, cap rock edges, or poorly-sealed boreholes. As the gravity current of CO$_2$ spreads by buoyancy, it samples the underside of the cap rock for leakage pathways. A variety of studies have been performed considering confined (Nordbotten and Celia 2006; Zhao and Ioannidis 2007) vs. unconfined layers (Pritchard 2007). In the latter case especially, the rate of leakage increases with the gravity current thickness. Leakage leads to lower overall storage efficiencies though details depend on formation geometry.

The other possibility is that injectate leakage is distributed. In the large Bond number limit, this problem has been investigated by, among others, Goda and Sato (2011), Sahu and Flynn (2015) and Bharath et al. (2020). Goda and Sato (2011) and Bharath et al. (2020) assume that high- and low-permeability layers are semi-infinite in vertical extent. Key to their analysis is to quantify the run-out length, defined as the terminal horizontal distance traveled by the gravity current. When run-out is achieved, the influx to the gravity current balances draining via leakage. Run-out lengths can also be defined when the depth of the low permeability layer is finite. Here, however, run-out is followed by a remobilization of the (primary) gravity current due to the formation and propagation of secondary gravity currents within the low permeability layer (Bharath and Flynn 2021). Here, we examine a complementary problem and instead make the high-permeability layer of finite thickness. This change does not alter draining but it is crucially important when one additionally considers convective dissolution. We thereby demonstrate that the variation of the convective dissolution rate with time, t, provides a second remobilization mechanism.

Convective dissolution was studied experimentally by MacMinn and Juanes (2013) in a sloping Hele Shaw cell with an impermeable upper boundary. They found that updip migration of the buoyant injectate stopped as a result of convective dissolution and the formation and propagation of dense fingers resulting from the mixing of the injectate and the ambient. Szulczewski et al. (2013) extended this work by categorizing different dissolution regimes of which they counted seven: early diffusion, fingering, shutdown/fingering, shutdown/slumping, shutdown/Taylor slumping, Taylor slumping, and finally late diffusion. In the fingering stage, the dissolution rate remains constant because fingers descend at constant speed. As the fingers strike the bottom boundary, a layer of contaminated fluid begins to accumulate. Eventually, the thickness of this layer is large enough to arrest convective dissolution.

Fig. 1

Time variation of the convective dissolution rate, $Q_d$; $Q_d$ is defined mathematically by (13)

Despite this complexity, convective dissolution can be parameterized according to Fig. 1 (MacMinn et al. 2011; Hidalgo et al. 2013). Here, $t^*_0$ signifies a non-dimensional delay time during which are established the hydrodynamic instabilities that feed finger growth. (We set $t_0^* = 0$ in much of the analysis to follow.) The constant dissolution regime characterized by the non-dimensional time $t^*_1$ corresponds to fingers falling at a constant velocity. When $t^* = t^*_0 + t^*_1$, dissolution slows because fingers make contact with an impermeable boundary. Fluid discharged by the fingers then ascends as a curtain, depressing the dissolution rate. The time $t^* = t^*_0 + t^*_1$ represents the onset of the so-called shutdown regime during which the dissolution rate decreases with an e-folding time $t^*_2$.

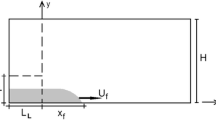
In light of the above, we will explore the interplay between injectate spreading, draining and dissolution. Our work simultaneously extends MacMinn and Juanes (2013) (spreading and dissolution, no draining) and Bharath et al. (2020) (spreading and draining, no dissolution). As depicted in Fig. 2 and consistent with Goda and Sato (2011), our analysis shall situate a (discrete) source along a sloping permeability jump. Here, and in contrast to e.g. MacMinn and Juanes (2013), we assume a dense rather than a buoyant injectate. This choice is made for mathematical convenience and also to render our analysis consistent with select seminal works on porous media gravity currents e.g. Huppert and Woods (1995), Vella and Huppert (2006) and Lyle et al. (2005). The orientation is immaterial, however, in the Boussinesq limit.

Calculations are for two dissolution modes, one local and the other global. In the global case, we assume that fluid containing dissolved injectate propagates with ease through the upper layer ambient, i.e., in the space above the up- and downdip gravity currents, concentration gradients are weak [c.f. Fig, 1 of Bolster (2014)]. Thus all points along the exposed upper surface of the gravity currents experience shutdown simultaneously. The dissolution mode in question is expected to be approximately correct when draining and/or dissolution is strong such that the up- and downdip gravity currents reach their respective terminal lengths in a time that is small compared to $t_1^*$ from Fig. 1—see e.g., the discussion of the large $t_1^*$/small injection time case presented in Sect. 4.2 below. At the opposite extreme, lateral motion of fluid containing dissolved injectate is supposed to be slow and different portions of the gravity current surface experience ambient fluid with different injectate concentrations. (Sequential) shutdown is therefore experienced at different times; regions proximal to the source shut down before distal regions (Hidalgo et al. 2013). Neither of the simultaneous or sequential descriptions is strictly correct. However, the predictions afforded by these limiting cases must bound the true solution. Where the bound is tight we enjoy good insights into the true nature of the flow.

Fig. 2

(Color online) Schematic showing the propagation of up- and downdip gravity currents along a sloping permeability jump where the source is situated at the origin. Also illustrated are dissolution and draining. Here, the vertical dimension of the up- and downdip gravity currents has been exaggerated for clarity

2 Mathematical Model

2.1 Problem definition and assumptions

We consider a two-layer porous medium with a permeability jump inclined at an angle $\theta$—see Fig. 2. The upper and lower layer permeabilities and porosities are, respectively, $(k_1,\phi _1)$ and $(k_2 \ll k_1,\phi _2 =\phi _1 = \phi )$. The rectilinear two-dimensional coordinate system is represented by (X, Z). Up- and downdip gravity currents are fed by a constant volume flux source located at the permeability jump. The evolution of the up- and downdip gravity currents is given by a balance between inflow from the constant flux source and outflow due to convective dissolution along the upper surface and draining along the lower surface.

We assume a deep lower layer; the upper layer is typically finite. The source fluid has a density, $\rho _s$, that is moderately larger than the ambient density, $\rho _0$. Inside the gravity currents (and also the fluid that drains from the gravity currents), we ignore spatial variations of density taking these to be either nonexistent or small w.r.t. to the density contrast between the gravity currents and the ambient. The gravity currents are assumed long so that a hydrostatic (sharp interface) analysis like that of Huppert and Woods (1995) applies. In this spirit, note that (i) draining of source fluid from the upper to the lower layer is likewise assumed to be driven by hydrostatic forces (Acton et al. 2001; Goda and Sato 2011), and, (ii) flows are evaluated in the large Bond number limit such that capillary effects may be ignored (Doster et al. 2013; Hidalgo et al. 2013). The source volume flux per unit width is $q_s$ and the source buoyancy flux per unit width is given by $F_s = q_s g'$. The reduced gravity is $g' = g(\rho _s-\rho _0)/\rho _0 \ll g$ in which g is gravitational acceleration.

2.2 Gravity Currents

Following the derivation presented in Bharath et al. (2020), we apply Darcy’s law and assume incompressibility. Accordingly, and for permeability jump angle, $\theta$,

$$\begin{aligned} u_c= -\frac{k_{1} \Delta \rho g}{\mu } \left( \frac{\partial {h}}{\partial {x}} \cos \theta - \sin \theta \right) \, , \end{aligned}$$

(1)

Here $u_c$ is the along-jump velocity component, $\Delta \rho = \rho _s - \rho _0$, $\mu$ is the dynamic viscosity and x is the spatial coordinate defined in Fig. 1. Equation (1) applies for $-x_{N_u} \le x \le x_{N_d}$ where $x_{N_u}$ and $x_{N_d}$, respectively, represent the gravity current nose positions up- vs. downdip. The spatio-temporal evolution equation for the gravity current thickness, h, is obtained by substituting (1) into the depth-averaged continuity equation, i.e.,

$$\begin{aligned} \phi \frac{\partial {h}}{\partial {t}} = \frac{k_{1} g'}{\nu } \frac{\partial {}}{\partial {x}}\left( h\frac{\partial {h}}{\partial {x}} \cos \theta -h \sin \theta \right) + w_{\mathrm{drain}} - q_d\, , \end{aligned}$$

(2)

where $\nu$ is the kinematic viscosity. Also $q_d\,(> 0)$ is the rate of convective dissolution and has units (m$^3$/s)/m$^2$ where the denominator corresponds to the upper surface area. (We will define $q_d$ more precisely later.) Meanwhile, $w_{\mathrm{drain}}\,(< 0)$ is the (hydrostatic) draining velocity, i.e., (Bharath et al. 2020)

$$\begin{aligned} \textit{w}_{\mathrm{drain}}=-\frac{k_{2} \Delta \rho g}{\mu } \left( 1 + \frac{h}{l} \cos \theta \right) \end{aligned}$$

(3)

(see Fig. 2). Combining (3) with an expression of mass balance gives

$$\begin{aligned} \displaystyle \phi \frac{\partial {l}}{\partial {t}} = - w_{\mathrm{drain}}= K \frac{k_{1} g'}{\nu } \left( 1 + \frac{h}{l} \cos \theta \right) \, , \end{aligned}$$

(4)

where $K = k_2/k_1$ is the permeability ratio.

2.3 Initial and Boundary Conditions

At $t=0$, the porous medium is fully saturated and $h = l = 0$. For $t>0$, (2) requires specification of an influx boundary condition such that the volume of fluid supplied to the gravity currents matches $q_s$. When $\theta = 0^\circ$, source fluid is divided equally between the up- and downdip directions. For $\theta > 0^\circ$, we denote the dimensionless volume fraction of the flow propagating downdip as $f_a$. The influx boundary conditions then read (Bharath et al. 2020)

$$\begin{aligned} \frac{k_{1} g'}{\nu } \left( h\frac{\partial {h}}{\partial {x}}\cos \theta -h \sin \theta \right) \Big \vert _{0^-}&= (1-f_a) q_s\,\,\,[\mathrm{updip}]\nonumber \\ \frac{k_{1} g'}{\nu } \left( h\frac{\partial {h}}{\partial {x}}\cos \theta -h \sin \theta \right) \Big \vert _{0^+}&= - f_a q_s\,\,\,[\mathrm{downdip}] \end{aligned}$$

(5)

Equation (5) is applied in conjunction with the following condition of height continuity:

$$\begin{aligned} \displaystyle h_{0^-}= h_{0^+} \end{aligned}$$

(6)

which allows us to solve for $f_a = f_a(t)$. The gravity current noses satisfy

$$\begin{aligned} h_{-x_{N_u}}=l_{-x_{N_u}}=0 \quad \text {and}\quad h_{x_{N_d}}=l_{x_{N_d}}=0 \end{aligned}$$

(7)

2.4 Non-dimensionalization

Similar to Goda and Sato (2011), we define the following space and time scales to non-dimensionalize the governing equations:

$$\begin{aligned} \Pi _x=\frac{q_s}{\phi \beta }\quad \hbox {and}\quad \Pi _t=\frac{q_s}{\phi \beta ^2} \end{aligned}$$

(8)

where $\beta ={k_{1} g'}/{\phi \nu }$. Thus do we define non-dimensional (starred) parameters, i.e.,

$$\begin{aligned} x^*=\frac{x}{\Pi _x}, \quad h^*=\frac{h}{\Pi _x}, \quad l^*=\frac{l}{\Pi _x}, \quad t^*=\frac{t}{\Pi _t} \end{aligned}$$

(9)

Accordingly, the evolution equations for h and l can be rewritten as

$$\begin{aligned} \frac{\partial {h^*}}{\partial {t^*}}=\frac{\partial {}}{\partial {x^*}} \left( h^*\frac{\partial {h^*}}{\partial {x^*}}\cos \theta -h^*\sin \theta \right) - K \left( 1 + \frac{h^*}{l^*} \cos \theta \right) -Q_d\, , \end{aligned}$$

(10)

and

$$\begin{aligned} \displaystyle \frac{\partial {l^*}}{\partial {t^*}} =K \left( 1 + \frac{h^*}{l^*} \cos \theta \right) \, , \end{aligned}$$

(11)

, respectively. Here, $Q_d$ specifies the non-dimensional dissolution rate, which we will define more carefully in the next paragraph. At $t^* = 0$, the initial condition is $h^*=l^*=0$. The dimensionless influx boundary conditions are

$$\begin{aligned} \displaystyle \left( h^*\frac{\partial {h^*}}{\partial {x^*}} \cos \theta -h^*\sin \theta \right) \Big \vert _{0^-}&= (1-f_a) \nonumber \\ \displaystyle \left( h^*\frac{\partial {h^*}}{\partial {x^*}} \cos \theta -h^*\sin \theta \right) \Big \vert _{0^+}&= - f_a \end{aligned}$$

(12)

Equations (12) are applied subject to $h^*_{0^-}= h^*_{0^+}$. Furthermore, and at the gravity current fronts, we require $h^*_{-x^*_{N_u}} = l^*_{-x^*_{N_u}} = 0$ and $h^*_{x^*_{N_d}} = l^*_{x^*_{N_d}} = 0$.

With reference to Fig. 1, and letting p denote the dissolution strength, $Q_d$ takes the following generic form (Szulczewski et al. 2013):

$$\begin{aligned} Q_d= 10^{-p} {\left\{ \begin{array}{ll} \displaystyle 0,&{} \quad 0< t^*<t^*_{0} \\ \displaystyle 1, &{}\quad t^*_{0}\le t^* <t^*_{0}+t^*_{1} \\ \displaystyle \mathrm{e}^{-(t^*-t^*_{1}-t^*_{0})/t^*_{2}},&{} \quad t^* \ge t^*_{0}+t^*_{1} \end{array}\right. } \end{aligned}$$

(13)

[c.f. Eq. (10) of Hidalgo et al. (2013)]. In section 3.1, we suppose that the upper layer is very deep such that dissolution, once it begins, never diminishes in intensity. Mathematically-speaking, we set $t^*_1 \rightarrow \infty$ in (13). Meanwhile, in Sect. 3.2, we assume very rapid horizontal mixing of the solute through the upper layer ambient such that the rate of dissolution is spatially uniform along the gravity current length. Here, $Q_d$ depends on time but does not depend on space, i.e., the onset of shutdown is the same everywhere along the length of the up- and downdip gravity currents. Finally, in Sect. 3.3, we explore the bookend opposite limit, i.e., one where the rate of horizontal mixing is slow such that significant spatial variations of the dissolution rate may arise. Mathematically-speaking, $Q_d$ from (13) is now made to be a function of $x^*$ as well as $t^*$ such that, with $t_0^* = 0$, dissolution initiates only when gravity current fluid first reaches the point in question. For example, if it takes 10 non-dimensional time units for the gravity current front to reach a horizontal position $\hat{x}^*$, the local dissolution rate (i.e., $Q_d$ measured at $\hat{x}^*$) is

$$\begin{aligned} Q_d(\hat{x}^*,t^*) =10^{-p}{\left\{ \begin{array}{ll} \displaystyle 0, &{}\quad 0< t^*< 10 \\ \displaystyle 1,&{} \quad 10 \le t^* < 10+t^*_{1} \\ \displaystyle \mathrm{e}^{-(t^*-t^*_{1}-10)/t^*_{2}},&{} \quad t^* \ge 10+t^*_{1} \end{array}\right. } \end{aligned}$$

(14)

Comparing (13) and (14), we realize that sequential dissolution can be modelled by making the term $t_0^*$ from (13) an increasing function of $x^*$ that depends on the speed of the gravity current front. An animation meant to further highlight the difference between simultaneous and sequential dissolution is included as part of the Supplementary Information.

3 Model Results

3.1 Constant Dissolution Rate

For later comparison with cases having $t_1^* < \infty$, it is helpful to generate “baseline” solutions having a constant dissolution rate. We solve the dimensionless governing Eqs. (11) and (13) numerically using a forward finite difference scheme with a grid size $\Delta x^* = 6 \times 10^{-2}$ and a time step $\Delta t^* = 9 \times 10^{-4}$. The source volume flux is assumed constant suggesting a continual supply of fluid to the gravity currents.

Fig. 3

Spatial-temporal evolution of the gravity currents and draining flow up to $t^* = 500$ for an inclined permeability jump with $\theta =20^{\circ }$. Values for p are as indicated

Fig. 4

Time series of the gravity current nose position (a, b), downdip volume fraction (c, d) and storage efficiency (e, f). Left: $\theta =5^{\circ }$; right: $\theta =15^{\circ }$

When the dissolution strength is vanishingly small such that the parameter p from (13) is indefinitely large, the gravity currents, both up- and downdip, travel comparatively long distances before becoming arrested at their respective run-out lengths—see Fig. 3. The figure exhibits snapshot images showing the temporal evolution for a case where $\theta =20^{\circ }$. For such a large value of $\theta$, there exists a pronounced asymmetry between the up- and downdip flows.

The significance of p is explored in Fig. 4. Figure 4a, b depicts for $\theta = 5^\circ$ and $\theta = 15^\circ$, respectively, the time evolution of the nose positions, $x_N^*$, of the up- and downdip gravity currents. Consistent with Fig. 3, gravity currents travel greater distances along the permeability jump as p is increased and dissolution is curtailed. Solutions exhibit the most sensitivity to p downdip for relatively large $\theta$. By contrast, dissolution has a weaker influence updip where gravity is often as or more important in arresting the flow. Considering the same range of p as in Fig. 4a–d show that $f_a$ increases sharply then later plateaus as run-out is approached.

To gauge the effectiveness of dissolution, we refer to the storage efficiency, $E^*_h$. Consistent with MacMinn et al. (2011), $E^*_h$ is defined as the volume ratio of the fluid discharged by the source that remains in the upper layer (whether dissolved or not) vs. the cumulative volume of fluid discharged by the source. In practical terms, the larger $E_h^*$, the greater the volume of injectate that can be securely sequestered. Mathematically-speaking, $E^*_h$ is expressed as follows:

$$\begin{aligned} E^*_h (t) = \frac{V_{\mathrm{retained}}(t)}{V_{\mathrm{injected}}(t)} = 1 - \frac{V_{\mathrm{drained}}(t)}{V_{\mathrm{injected}}(t)} \end{aligned}$$

(15)

Here $V_{\mathrm{retained}}$ is the net volume of discharged source fluid retained in the upper layer by advection and dissolution. Also, $V_{\mathrm{injected}} = \int _0^t q_s\,\mathrm{d}t$. Figure 4e, f show $E_h^*$ vs. time for different dissolution strengths. For small p, $E_h^*$ displays a decrease at early times after which it rebounds then plateaus as $t^* \rightarrow \infty$. The shape of the curves is explained as follows: at early times, the gravity current thicknesses remain modest and there is comparatively little draining. Over time, the thicknesses increase as does drainage into the lower layer and $E_h^*$ falls. Simultaneously, however, the gravity currents elongate thereby providing more surface area for dissolution. Dissolution then dominates and $E_h^*$ increases for sufficiently large $t^*$. In essence, thickness is punished by draining (which decreases $E_h^*$) whereas large lateral extents are punished by dissolution (which increases $E_h^*$). When p is large, by contrast, dissolution remains subordinate to draining even when the gravity currents have extended to long lengths. Therefore, and for $p \gtrsim 1.5$, $E_h^*$ is a monotone decreasing function of $t^*$. Finally, and in contrast to the panel pairs Fig. 4a–d, the storage efficiency is largely unaffected by $\theta$: as the jump angle increases, the downdip gravity current elongates but the updip gravity current shortens, i.e., the total surface area available for dissolution is comparable. Synthesizing these results, Fig. 5 shows a plot of gravity current run-out length, $L^*_N$, vs. p and $\theta$. Here $\theta$ in the range from $\theta =-20^{\circ }$ to $\theta =0^{\circ }$ ($\theta =0^{\circ }$ to $\theta =20^{\circ }$) shows run-out lengths measured updip (downdip). When $\theta =0^\circ$ and the permeability jump is horizontal, the run-out lengths up- vs. downdip are equal. Asymmetry arises for $\theta \ne 0^\circ$, however significant up- vs. downdip differences arise only for sufficiently large p. Dissolution is then weak and so differences between the up- and downdip flows are not masked by mass loss to the upper layer ambient. In the $p \rightarrow 0$ limit, by contrast, dissolution is strong and the (short) run-out lengths show a relative insensitivity to $\theta$.

Fig. 5

Line plot of the up-($\theta < 0$) and downdip ($\theta > 0$) run-out lengths, $L^*_N$ , as functions of the dissolution strength, p, and permeability jump angle, $\theta$ (measured in $\circ$)

3.2 Convective Dissolution with Simultaneous Shutdown

We now consider the case where $t^*_0 = 0$, $t^*_1$ is finite and, after a time $t^*_1$, the dissolution rate decreases in a spatially-uniform way. Figures 6a, c compare, for $t^*_2 = 50$, the temporal evolution of the gravity current nose for $\theta =5^{\circ }$ and $\theta =15^{\circ }$, respectively. When $t^*_1=0$, we implicitly assume an upper layer that is thin so that dissolution begins to slow immediately.¹ Conversely, large $t^*_1$ corresponds to an upper layer of large depth. Considering the downdip flow, curves of $x^*_N$ increase in a monotone fashion and later plateau provided $t^*_1$ is not small. For $t^*>t^*_1$, the front is remobilized and there appears a second regime of gravity current advance. In the long-time limit, all of the curves in Fig. 6a or in Fig. 6c approach the same limiting value. This coincidence is expected because p and $\theta$ are in all cases the same, i.e., $p=1$ and $\theta = 5^\circ$ or $15^\circ$. We refer to the plateau experienced at moderate (late) time as intermediate (terminal) run-out. In the former case, the sum of the rates of draining and of dissolution matches the influx to the gravity current.

Fig. 6

Gravity current nose positions for $p = 1$, $t^*_2 = 50$ and various $t^*_1$ a, b $\theta = 5^\circ$, c, d $\theta = 15^\circ$. The left- and right-hand side panels, respectively, consider simultaneous and sequential shutdown

Once $t^* > t^*_1$, some fraction of the fluid that would have dissolved into the upper layer instead accumulates in the gravity current whose height therefore increases leading to front remobilization (and additional draining). Although the surface area available for dissolution increases as the gravity current elongates, dissolution decreases overall—see Fig. 1. When, in the long-time limit, the gravity current stops for a second time, there is a balance between the rates of influx and draining. To better characterize the aforementioned flow asymmetries, we plot in Fig. 7a, c $f_a$ vs. $t^*$ for $\theta = 5^\circ$ and $15^\circ$, respectively. During re-mobilization, $f_a$ increases more rapidly with time than for $t^* < t^*_1$. As $t^* \rightarrow \infty$, $f_a$ approaches a constant, the precise value of which depends on $\theta$. Figure 8 shows the variation of $E_h^*$. At early times when draining is slight, much of the discharged source fluid is retained in the upper layer. As the gravity currents spread, $E_h^*$ decreases exponentially. When $t^*_1>0$, $E_h^*$ gradually plateaus as intermediate run-out is approached. There is now a fixed balance between drainage and dissolution (not yet diminished). Once $t^* = t^*_1$, this balance is disrupted so as to favour draining; correspondingly, $E_h^*$ falls. In the shutdown regime, larger values of $t^*_1$ lead to larger values of $E_h^*$. Note, however, that whatever the (finite) value of $t^*_1$, $E_h^* \rightarrow 0$ in the long time limit. Furthermore and consistent with Fig. 4e, f, there is little variation of the storage efficiency with $\theta$. Figure 9a illustrates, in the $t^*_1$-$\theta$ parameter space, a surface plot showing the non-dimensional time, $t^*_{95}$, to reach 95% of terminal run-out. For fixed $\theta$, Fig. 9a shows that $t^*_{95}$ increases with $t^*_1$: larger $t^*_1$ delays the onset of shutdown and extends the time spent in intermediate run-out.

Fig. 7

As in Fig. 6 but considering the downdip volume fraction, $f_a$

Fig. 8

As in Fig. 6 but considering the storage efficiency, $E_h^*$

Fig. 9

(Color online) Time, $t^*_{95}$, to reach 95% of terminal run-out vs. $t^*_1$ and $\theta$ (measured in degrees) for a simultaneous shutdown and b sequential shutdown

Till now, we have characterized the influence of $t^*_1$ all the while choosing $t^*_2 = 50$. In the Supplementary Information, we explore the effect of adjusting $t^*_2$.

3.3 Convective Dissolution with Sequential Shutdown

Similar to Fig. 6a–d show the up- and downdip advection but for the sequential shutdown case. In contrasting the panel pairs of Fig. 6a–d, similar behavior is observed with two exceptions. Firstly, and because dissolution stops more gradually, remobilization is more measured. Thus the kinks in the curves of Fig. 6b, d that arise when $t^* \simeq t^*_1$ ($t^*_1 = 0$ excepted) are less sharp. Secondly, and because remobilization is associated with the generation of new interfacial area directly below virgin ambient fluid, more convective dissolution will occur after intermediate run-out. Dissolution that occurs in the time interval $t^* > t_1^*$ is more modest than that which occurs for $t^* < t_1^*$. On the other hand, if $t^*_1$ is sufficiently large (e.g., $t^*_1 = 200$), dissolution that occurs for $t^* > t_1^*$ may be sufficient to again arrest the flow. Solution curves then show a “stop-start” pattern whereby the gravity current is remobilized multiple times over as new interfacial area is created, dissolution disrupts the balance between draining and advection, dissolution then slows and stops all in a cycle that is repeated approximately twice when $t^*_1 = 200$. The sequence just described is arrested only by the approach to terminal run-out, terminal run-out lengths being the same in Fig. 6b, d and a, c, respectively. However, because the overall dissolution rate declines more gradually in the former two figures, the time to reach this asymptotic state is correspondingly larger.

Similar to Fig. 7a–d show the time variation of $f_a$. Consistent with the comparison between the figure pairs Fig. 6a–d, we note from Fig. 7 that sequential shutdown is associated with a more gradual remobilization. Also, the stop-start signatures evident in Fig. 6b, d reappear in Fig. 7b, d: as expected, gravity current remobilization and arrest impact the fraction of source fluid flowing up- vs. downdip.

Similar to Fig. 8a–d show $E_h^*$ vs. time. Differences between the left- and right-hand side panels are now not as dramatic e.g., Fig. 8 does not exhibit evidence of stop-start behavior. Following intermediate run-out, the process of remobilizing then arresting the gravity current involves a trade-off between advection and dissolution. Because both processes retain injectate in the upper layer, the start-stop impact on $E_h^*$ is subdued. For $t^* \simeq t^*_1$ and excepting $t^*_1 = 0$, the storage efficiencies predicted in Fig. 8b, d decline less dramatically than do their counterparts from Fig. 8a, c: injectate retention in the upper layer is larger for sequential shutdown, which culminates in larger $E_h^*$ over the time interval considered.

Figure 9b shows the time to reach 95% of the terminal lengths. Consistent with our discussion of Fig. 6b, d, the time to reach terminal run-out is extended in the case of sequential shutdown, characterized as it is, for large $t^*_1$, by intermediate stages of arrested movement. To this end, $t^*_{95}$ values are much larger for $t^*_1=200$ where multiple starts and stops are encountered vs. $t^*_1 = 0$ where the advance of the gravity currents is more regular.

4 Unsteady Source

4.1 Problem Formulation

We have so far assumed a steady source , however, in industrial practice, there are many instances where the source is instead unsteady, e.g., with alternating periods of activity and inactivity. Here we explore the associated dynamics with an emphasis on the evolution (and disappearance) of the gravity currents post-injection, i.e., after the source has been “switched off.” We examine spreading, draining and dissolution for $t^* > t^*_{\mathrm{inj}}$ where $t^*_{\mathrm{inj}}$ is the non-dimensional time over which the source supplies fluid. When $t^* > t^*_{\mathrm{inj}}$, influx boundary conditions specified by (12) are modified so that, for all time, the equations read

$$\begin{aligned} \displaystyle \left( h^*\frac{\partial {h^*}}{\partial {x^*}} \cos \theta -h^*\sin \theta \right) \Big \vert _{0^-}&= \mathrm{H}(t^*_{\mathrm{inj}} - t^*) (1-f_a) \nonumber \\ \displaystyle \left( h^*\frac{\partial {h^*}}{\partial {x^*}} \cos \theta -h^*\sin \theta \right) \Big \vert _{0^+}&= - \mathrm{H}(t^*_{\mathrm{inj}} - t^*)f_a \end{aligned}$$

(16)

where $\mathrm{H}$ denotes the Heaviside step function. Figure 10 shows the nose position vs. time for simultaneous and sequential shutdown. We consider small $t^*_2$ (and also $t^*_1$) so as to better highlight the flow behavior in the period post-injection. Figure 10a, b are similar: for $t^* < t^*_{\mathrm{inj}}$, gravity currents advance quickly at first, then slow as intermediate run-out is approached. For $t^*_1 \le 45$, intermediate run-out is followed by remobilization. Once $t^* = t^*_{\mathrm{inj}} = 50$, however, the source is switched off. Although the front may travel some small additional distance downstream, there follows a period of rapid recession driven by basal draining. Assuming e.g., $t^*_1 = 0$ (simultaneous shutdown), no gravity current fluid remains in the upper layer for $t^* > t^*_f = 56.84$ where $t^*_f$ indicates the time required for the complete disappearance of injectate from the upper layer (except in dissolved form). By contrast, note that both $x_N^*$ curves collapse when $t_{\mathrm{inj}}^* < t_1^*\,\,(= 60\,\,\hbox {or}\,\,75)$. Here the gravity current begins to recede before the flow exits intermediate run-out.

Fig. 10

Gravity current nose positions for $t^*_{\mathrm{inj}} = 50$, $\theta = 0^\circ$, $p=1$, $t^*_2 = 10$ and various values of $t^*_1$. a Simultaneous shutdown and b sequential shutdown

The time interval between $t^*_{\mathrm{inj}}$ and the instant where $x_N^*$ is maximum is modest. This applies, especially for large $t^*_1$ where the maximum value of $x_N^*$ is likewise small. In a similar spirit, the time, $t^*_f - t^*_{\mathrm{inj}}$, required for gravity current fluid to disappear after the source is switched off is also small when $t^*_1$ is large.

Comparing Fig. 10a, b, remobilization evolves more slowly for sequential dissolution. Curves of $x^*_N$ start at lower maximum values than do the counterpart curves for simultaneous shutdown. By repeating the analysis leading to Fig. 10 for different $t^*_{\mathrm{inj}}$ (not shown), we find that discrepancies between sequential and simultaneous shutdown are more pronounced for smaller $t^*_{\mathrm{inj}}$. By contrast, when $t^*_{\mathrm{inj}}$ is large and terminal run-out is approached, gravity current recession occurs in a nearly identical manner. So as to further highlight similarities and differences between the two different shutdown regimes, Fig. 11 shows plots of $t^*_f - t^*_{\mathrm{inj}}$, which increase with $t_{\mathrm{inj}}^*$. This increasing behavior applies to both simultaneous and sequential dissolution but is slightly less prominent in the latter case: incomplete shutdown means that less time is needed for gravity current fluid to disappear from the upper layer. When $t^*_{\mathrm{inj}}$ comfortably exceeds $t^*_1$, a terminal run-out plateau is approached and differences between the left- and right-hand side panels decrease. The plots of Fig. 11 exhibit a second plateau where $t^*_1 \ge t^*_{\mathrm{inj}}$: with short injection times, complete drainage occurs before the onset of shutdown and so the details of shutdown become moot.

Fig. 11

Time, $t^*_f-t^*_{\mathrm{inj}}$, taken for gravity current fluid to completely disappear following the injection period as a function of $t^*_{\mathrm{inj}}$ for various $t^*_1$ and at constant $p=1$, $t^*_2=10$. a, c Simultaneous shutdown and b, d sequential shutdown. The top row of panels show the case of a horizontal permeability jump while the bottom row of panels show $\theta = 10^\circ$

Whereas Fig. 11a, b consider $\theta = 0^\circ$, Fig. 11c, d assume instead $\theta = 10^\circ$. Although strong qualitative similarities are evident in comparing Fig. 11a–d, we note that $t^*_f - t^*_{\mathrm{inj}}$ values are typically smaller when $\theta > 0^\circ$. In this case, a greater fraction of the source fluid is directed downdip. Once the source is switched off, it takes less time for this fluid to disappear from the upper layer. The plateaus from Fig. 11 are reproduced in Fig. 12, which shows plots of $x^*_{N\mathrm{max}}$, the maximum distance traversed by the nose. This distance is large when $t^*_1$ is small and shutdown occurs early on. Analogous to Fig. 11c, d, the last four panels of Fig. 12 show, for $\theta = 10^\circ$, the maximum extent of the gravity current down- ($x_{N\mathrm{max},d}^*$, panels c, d) vs. updip ($x_{N\mathrm{max},u}^*$, panels e, f). On the updip side, there exists a broad high-level plateau, particularly for simultaneous shutdown: the flow often becomes arrested well before $t^* = t^*_{\mathrm{inj}}$ due to gravity. No such impediment exists downdip and so the high-level plateau of Fig. 12c is smaller than that observed in either of Fig. 12a, e.

Fig. 12

Maximum along-jump distance traversed by the gravity current nose as a function of $t^*_1$ and $t^*_{\mathrm{inj}}$ for $p=1$, $t^*_2=10$. a, c, e Simultaneous shutdown, b, d, f sequential shutdown. The top row shows the case of a horizontal permeability jump while the bottom four panels consider $\theta = 10^\circ$

4.2 Solution Bounds

In Sect. 1, we noted that sequential and simultaneous shutdown are idealizations and that the true behavior must lie somewhere in between. With reference to the current unsteady problem, we identify those regions of the parameter space where the imposed bounds are tight vs. loose. Figure 13 shows the difference of $x^*_{N\mathrm{max}}$ values estimated from the left- and right-hand side panels of Fig. 12. From panel a, $\Delta x_{N\mathrm{max}}^*$ is small in two opposite limits: large $t^*_1$/small $t^*_{\mathrm{inj}}$ and small $t^*_1$/large $t^*_{\mathrm{inj}}$. In the former case, the source is switched off before the onset of shutdown. Consequently, the flow remains in a state of intermediate run-out and there is no difference between simultaneous vs. sequential dissolution. In the limit of small $t^*_1$/large $t^*_{\mathrm{inj}}$, dissolution begins to slow almost immediately and there is ample time to reach terminal run-out. In between the large $t^*_1$/small $t^*_{\mathrm{inj}}$ and small $t^*_1$/large $t^*_{\mathrm{inj}}$ limits, the flow lies between intermediate and terminal run-out and the two dissolution modes display differences one to the other owing to differences in the remobilization process. Similar to Fig. 13a–c respectively indicate, for $\theta = 10^\circ$, $x_{N\mathrm{max}}^*$ in the down- and updip directions. Downdip, the gravity current speed increases with $\theta$ so the trends of Fig. 13a are amplified. By comparison, we expect the aforementioned trends to be subdued when considering updip flow; Fig. 13c confirms this expectation.

Fig. 13

(Color online) Difference in the maximum nose position, $\Delta x_{N\mathrm{max}}^*$, between sequential and simultaneous shutdown for a $\theta = 0^\circ$ and $p=1$. The last two panels correspond to $\theta = 10^\circ$ and b downdip flow, $\Delta x_{N\mathrm{max},d}^*$, and c updip flow, $\Delta x_{N\mathrm{max},u}^*$

5 Conclusions

Herein, we superpose convective dissolution on the advancing front of a gravity current that propagates along the permeability jump between a high permeability upper layer and a low permeability lower layer. Our primary contribution is to add dissolution to a mathematical model that describes, in a sharp-interface, large Bond number limit, the evolution of a leaky gravity current. We consider dissolution rates that are constant vs. time-variable. In the latter case, Sect. 3.2 considers a “simultaneous shutdown” scenario where the dissolution rate is everywhere the same. Section 3.3 considers a “sequential shutdown” regime where different segments of the gravity current experience dissolution shutdown at different times. Neither scenario is a true representation of dissolution, however, they provide helpful limiting cases that bound the actual behavior. To this end, dissolution is parameterized with reference to variables $t^*_1$ and $t^*_2$ from Fig. 1.

We categorize the evolution of the gravity current shape (Fig. 3), nose position (Figs. 4 and 6), downdip flow fraction (Figs. 4 and 7) and storage efficiency (Figs. 4 and 8). Once the dissolution rate begins to fall, the balance between dissolution, draining and inflow is disrupted such that previously-arrested gravity current fronts may remobilize, at least temporarily. The stop-start motion just described is reminiscent of that described in Bharath et al. (2020). In that paper, the authors consider a lower, rather than an upper layer, of finite depth. A secondary gravity current is therefore generated once the draining fluid reaches the (impermeable) bottom boundary. This secondary gravity current “tugs” on the previously-arrested primary gravity current, causing it to resume its propagation, whereas the along-jump gravity current is arrested at most one time in the study of Bharath et al. (2020), sequential shutdown offers richer dynamical behavior, at least when $t^*_1$ is large, i.e., several intermediate stops of the gravity current front may occur.

When the source is unsteady, the gravity current rapidly recedes and ultimately disappears from the upper layer following an injection period, $t^*_{\mathrm{inj}}$. Further, the maximum nose distance, $x_{N\mathrm{max}}^*$ and the time, $t^*_f-t^*_{\mathrm{inj}}$, taken to fully drain following the injection period increase rapidly as $t^*_1$ is decreased. Comparing the domains where simultaneous and sequential shutdown yield comparable predictions, we observe such similarities in the opposing limits of large $t^*_1$/small $t^*_{\mathrm{inj}}$ and small $t^*_1$/large $t^*_{\mathrm{inj}}$.

In extending the present study, we wish to model the scenario of “inject low and let it rise” by examining, in the context of the inverted geometry of Fig. 1, cases where the source lies strictly above the permeability jump (Kumar et al. 2005; Bryant et al. 2008). The up- and downdip gravity currents would then be fed by a descending plume that may entrain external ambient fluid during its descent. Because the vertical distance of this descent will decrease as the gravity currents grow in height, the influx to the gravity current would then be time-variable even when the source is itself steady. Such considerations add an extra layer of dynamical complication whose resolution would prove informative.