Front velocity and structure of bottom gravity currents with a low volume of release propagating in a porous medium

Abstract

The paper reports results of large eddy simulations of lock exchange compositional gravity currents with a low volume of release advancing in a horizontal, long channel. The channel contains an array of spanwise-oriented square cylinders. The cylinders are uniformly distributed within the whole channel. The flow past the individual cylinders is resolved by the numerical simulation. The paper discusses how the structure and evolution of the current change with the main geometrical parameters of the flow (e.g., solid volume fraction, ratio between the initial height of the region containing lock fluid and the channel depth, ratio between the initial length and height of the region containing lock fluid) and the Reynolds number. Though in all cases with a sufficiently large solid volume fraction the current transitions to a drag-dominated regime, the value of the power law coefficient, α, describing the front position’s variation with time (x _f  ~ t ^α, where t is the time measured from the removal of the lock gate) is different between full depth cases and partial depth cases. The paper also discusses how large eddy simulation (LES) results compare with findings based on shallow-water equations. In particular, LES results show that the values of α are not always equal to values predicted by shallow water theory for the limiting cases where the current height is comparable, or much smaller, than the channel depth.

1 Introduction

In many practical applications, compositional and particulate gravity currents propagate through an array of obstacles. Important relevant classes of environmental applications include: (a) powder snow avalanches reaching a region containing arrays of retarding porous fences that are intended to decelerate the current, favor deposition of snow, reduce impact forces on buildings, and thus protect populated areas situated at the end of steep slopes on which avalanches can easily form [11]; (b) currents propagating in fully- or partially-vegetated channels (e.g., shallow vegetated regions of wetlands) where the nutrient uptake by the plants is affected by the passage of such currents [22, 26]; (c) particulate currents interacting with arrays of porous screens that are deployed to enhance sedimentation from the flow and thus to protect regions or hydraulics structures situated downstream of the screens against large accumulation of sediments [18]; and (d) gravity-current like flows propagating in wooded regions [10].

In such applications, the obstacles induce a relatively large amount of drag force that slows down the current and modifies its evolution compared to the widely studied case of currents propagating in environments with no obstacles. As discussed by Nepf [17] and Tanino et al. [22], the expression of the drag force is a function of the flow regime. If the Reynolds number defined with the characteristic length scale (e.g., diameter of the obstacle) and the surrounding velocity in the mean direction of propagation of the current is much larger than unity, then the drag force is proportional to the square of the flow speed (quadratic drag regime). If the same Reynolds number is much less than one, the drag force is expected to be proportional to the flow speed (linear drag regime). For sufficiently large values of the solid volume fraction associated with the obstacles in the domain, the drag force at the boundary over which the gravity current is propagating is expected to be much smaller than the total drag force induced by the obstacles in contact with the current. As a result, besides the slumping phase, one or multiple drag dominated regimes can be observed in the evolution of currents propagating in a porous medium [10, 22, 26]. In the drag dominated regimes, the main balance is between the buoyancy force and the drag force associated with the obstacles.

If the obstacles are fairly uniformly distributed in space, the region containing the obstacles can be considered a porous medium with a constant solid volume fraction, ϕ, defined as the ratio between the total volume of the obstacles and the volume of the region containing the obstacles. In many applications related to environmental problems, the obstacles can be approximated as two-dimensional (2-D) cylinders with a constant cross-section (e.g., circular or rectangular). The cylinders in the array are generally parallel, and their axes are oriented perpendicular to the main direction of propagation of the current. Supposing the diameter/width of the cylinder is D, then another important variable that determines how effective the cylinders are in decelerating the current is the frontal area of cylinders per unit volume, a. For square and circular cylinders, a is proportional to ϕ/D. The length scale characterizing the porous medium is 1/a.

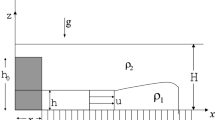
Vertical cylinders are a good approximation for vegetation and trees, while spanwise-oriented cylinders are a good approximation for porous fence elements used to decelerate powder-snow avalanches and turbidity currents. At a fundamental level, the role of the cylinders is to add drag. The drag force is mainly a function of the frontal area of the cylinders per unit volume, with the cylinders’ orientation and arrangement playing a secondary role [26]. Several fundamental studies were conducted for 2-D currents propagating in straight channels with a flat no-slip bottom in which the obstacles were an array of identical, uniformly-distributed cylinders. In most of the studies, the obstacles were distributed uniformly inside the channel [10, 12, 22], but studies of gravity currents propagating in channels where obstacles were present only over a limited region (e.g., porous layer) were also conducted, especially related to currents propagating in partially-vegetated channels [13, 27, 28]. Most of these experimental and theoretical studies were conducted for full depth (H _L  = H), lock exchange 2-D currents with a high volume of release (L _L /H ≫ 1) propagating in a straight channel of height H and initial area of release L _L *H _L , as shown in the sketch in Fig. 1. Though of particular relevance for practical applications in lakes and reservoirs, the case of (partial depth) lock-exchange currents with a low volume of release (L _L /H _L  = O(1)) received, comparatively, much less attention. Besides lock-exchange currents, the case of currents with a continuous release (e.g., constant flux currents) was also considered in the theoretical study of Hatcher et al. [10].

Fig. 1

Sketch of a lock-exchange flow with a low volume of release. In x–y cross-sections, the denser lock fluid occupies initially a rectangular region of length L _L and height H _L starting at the left end wall. The channel height is H ≥ H _L . Cylinders (not shown) are approximately uniformly distributed within the whole volume of the channel, with their axes parallel to the spanwise (z) direction. The gravity current forming after the lock release is shown in gray. Its front velocity is U _f . The front position, x _f , is measured from the vertical lock gate

Direct numerical simulation (DNS) and large eddy simulation (LES) offer an alternative way to laboratory experiments to investigate gravity current flows. Their advantage is that they provide the full velocity, density and vorticity flow fields (e.g., see [5, 9, 19]). In cases where the flow past the individual obstacles is resolved with sufficient mesh resolution, the only modeling assumptions are those associated with the turbulence model. In such simulations, there is no need to provide any empirical coefficients, nor to include additional terms in the governing equations to describe the flow inside the porous medium, as done in more classical approaches where the flow past the individual obstacles in not resolved [13, 14].

In a related study from our group [26], LES was used to study the structure and propagation of full depth compositional currents with a high volume of release (L _L /H _L  ≫ 1) in a channel containing an array of identically, uniformly-distributed, square cylinders. In the present study, we consider a similar set up, but we focus on lock-exchange compositional currents with a low volume of release (L _L  = O(H _L )). We consider both the case of full depth (H _L  = H) and partial depth (H _L  < H) currents (Fig. 1). We also discuss the asymptotic behavior of such currents for the limiting case of deep currents (h ≪ H, where h is the current height). The cylinders are distributed within the whole volume of the channel, their axes are aligned with the spanwise direction and are perpendicular to the direction of propagation of the current. Their cross section is square (cylinder’s edge length is D). We present results of a new set of numerical simulations, which allow us to understand how the main geometrical and flow parameters defining the lock-exchange flow (ϕ, L _L /H, H _L /H, L _L /H _L , Reynolds number) affect the structure of the current and the temporal variation of the front position during the different stages of its propagation. We compare LES simulation results with results based on shallow water theory and similitude analysis for limiting cases (e.g., for deep currents and for currents whose height is comparable to that of the channel). This allows assessing to what extent shallow water theory results (e.g., the power law constant describing the variation of the front position with time during the various drag-dominated regimes) are applicable to more complex cases in which the current height can change significantly during its evolution.

Section 2 discusses some relevant results obtained using shallow water theory related to the possible regimes in the evolution of 2-D gravity currents advancing in a porous medium. Section 3 describes the numerical model and relevant validation test cases. The simulation set up, boundary conditions and the main parameters of each test case are presented in Sect. 4. Section 5 discusses the effects of varying the solid volume fraction, the ratio between the initial height of the region containing lock fluid and the channel depth, the ratio between the initial length and height of the region containing lock fluid, and the Reynolds number on the structure of gravity currents advancing through an array of obstacles. The effects of the same geometrical and flow parameters on the temporal evolution of the front position are analyzed in Sect. 6. Section 7 summarizes the main findings.

2 Background

In the case of full depth currents with a high volume of release (L _L /H ≫ 1, H _L  = H) propagating in a channel with a sufficiently high ϕ, Yuksel Ozan et al. [26] have shown that the slumping phase, in which the front velocity U _f is constant and x _f  ~ t, is followed by a drag dominated regime. For sufficiently high Reynolds numbers, for which one can assume the drag coefficient of the cylinders, C _D , to be constant, shallow water theory and scaling analysis can be used to show that the current transitions first to a quadratic drag-dominated regime in which U _f  ~ t ^−1/3 and x _f  ~ t ^2/3. Then, as the current Reynolds number decreases sufficiently for viscous forces to become important, the current transitions to a linear drag-dominated regime in which C _D  ~ 1/Re _D , U _f  ~ t ^−1/2 and x _f  ~ t ^1/2 (see also [12, 22]). If the Reynolds number during the slumping phase is small enough such that Re _D  = O(1) or less, then the current can transition directly from the slumping phase to the linear drag-dominated regime. The start of the transition to the drag-dominated regime occurs at a time, t _c , that is of the order of (1 − ϕ)D/[C _D ϕ(g′H)^1/2] or H/[$\bar{C}_{D}$(g′H)^1/2], where g′ is the reduced gravity and $\bar{C}_{D}$ = C _D (1/D)ϕ/(1 − ϕ) controls the relative magnitude of the drag term associated with the obstacles present inside the porous medium.

One important result of the numerical simulations of Yuksel Ozan et al. [26] was to confirm the theoretical value of the power law coefficient in the temporal variation of the front position during the linear drag-dominated regime (α = 1/2, x _f  ~ t ^α). However, the same study showed that shallow water theory slightly underpredicts the power law coefficient (α = 3/4 in the simulations, α = 2/3 in the theoretical model) during the quadratic drag-dominated regime. This difference was attributed to mixing and entrainment processes, especially close to the front, which are not accounted for by the theoretical model.

Shallow water theory can also be used to identify the main phases of the evolution of lock-exchange 2-D currents with a small volume of release (L _L  = O(H) and area of release A(t) = L _L H _L  = constant) propagating in a porous medium for the particular case of deep currents, meaning currents for which h ≪ H and h ≫ D (Footnote 1). For such cases, the momentum equation has the form

$$(1 - \phi )\left( {\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + g'\frac{\partial h}{\partial x}} \right) = - \frac{{C_{D} \phi }}{D}u|u|$$

(1)

or

$$\left( {\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + g'\frac{\partial h}{\partial x}} \right) = - \bar{C}_{D} u|u|$$

(2)

where u(x,t) is the depth-averaged velocity, h(x,t) is the current height and $\bar{C}_{D}$ = (C _D /D)ϕ/(1 − ϕ). Neglecting entrainment, the depth-averaged continuity equation has the form

$$\frac{\partial h}{\partial t} + \frac{\partial }{\partial x}(hu) = 0$$

(3)

In the drag-dominated regime, the drag force induced by the obstacle is mainly balanced by the buoyancy force driving the flow. Equation (2) reduces to

$$g^{{\prime }} \frac{\partial h}{\partial x} = - \bar{C}_{D} u|u|$$

(4)

Using the scaling u ~ x/t, Eq. (4) reduces to:

$$g^{{\prime }} \frac{h}{x}\sim - \bar{C}_{D} \frac{{x^{2} }}{{t^{2} }}$$

Meanwhile, in the case of constant area of lock release, the continuity Eq. (3) reduces to

$$hut\sim hx\sim A$$

(5)

Combining the last two equations, one obtains:

$$x\sim \left( {\frac{{g^{{\prime }} At^{2} }}{{\bar{C}_{D} }}} \right)^{1/4}$$

(6)

In the quadratic drag-dominated regime, where C _D and $\bar{C}_{D}$ can be assumed constant, Eq. (6) implies that x _f  ~ t ^1/2 and U _f  ~ t ^−1/2. The transition to this drag-dominated regime occurs at a time, t _c , that is of the order of $(\bar{C}_{D}^{3} Ag')^{ - 1/2}$ [10]. In the linear drag-dominated regime, where C _D and $\bar{C}_{D}$ are proportional to 1/Re _D  ~ 1/u ~ t/x, Eq. (6) can be used to show that x _f  ~ t ^1/3 and U _f  ~ t ^−2/3.

One should also point out that the above theory applies also for currents for which H _L /H = 1 or H _L /H = O(1), at sufficiently large times after the release of the lock, when h ≪ H. ¹ For example, for a high Reynolds number current that starts as a full depth current (H _L /H = 1), or as a partial depth current for which H _L is not much smaller than H, the slumping phase can be followed by a quadratic drag-dominated regime in which U _f  ~ t ^−1/3 and x _f  ~ t ^2/3, similar to the case of full depth currents. Then, if Re _D is still much larger than one, the current can transition to a second quadratic drag-dominated regime in which U _f  ~ t ^−1/2 and x _f  ~ t ^1/2 once h ≪ H. At later times, the current will transition to the linear drag-dominated regime expected for currents with h ≪ H (x _f  ~ t ^1/3).

3 Numerical model

The Boussinesq approximation is employed to account for stratification effects in the Navier–Stokes solver used to perform the simulations. This assumes that the relative density difference between the lock and ambient fluids is relatively small. The viscous flow equations are solved together with a transport equation for the density in nondimensional form. Assuming the channel length scale is H ₀, a velocity scale can be defined with the reduced gravity, g′, as the buoyancy velocity $u_{b} = \sqrt {g^{{\prime }} H_{0} }$, where g′ = g(ρ _max − ρ _min)/ρ _max, g is the gravitational acceleration, ρ _max is the density of the lock fluid and ρ _min is the density of the ambient fluid. The nondimensional density is C = (ρ − ρ _min)/(ρ _max − ρ _min), where ρ is the dimensional density. The two parameters in the nondimensional governing equations are the Reynolds number, Re = u _b H ₀ /ν and the molecular Schmidt number, Sc = ν/κ, where ν is the molecular viscosity and κ is the molecular diffusivity. The time scale is H ₀ /u _b .

The governing equations are integrated on non-uniform Cartesian meshes. A semi-implicit iterative method [1, 3, 20] is used to advance the filtered Navier–Stokes equations in time. The pressure-poisson equation is solved by an algebraic multigrid method. All operators in the momentum and pressure equations are discretized using second-order central schemes. The algorithm is second order in time and discretely conserves the energy, which increases significantly the robustness of simulations performed at relatively high Reynolds numbers. The Quadratic Upwind Interpolation for Convective Kinematics scheme is used to discretize the convective term in the advection–diffusion equation solved for the nondimensional density. The subgrid-scale viscosity and the subgrid-scale diffusivity are calculated using the dynamic Smagorinsky model [21]. In such models, there is no need to specify any explicit stratification correction.

The code was validated for various types of simpler flows that are directly relevant for the configuration considered in the present study. Chang and Constantinescu [4] reported validation for constant density flow past a circular array of long, 2-D cylinders for arrangements and ϕ values that are similar to the ones considered in the present study. The validation included comparison with experimental data for the mean streamwise velocity and normal velocity fluctuations in the wake of the porous circular cylinder and dominant shedding frequency in the wake.

Relevant validation studies involving gravity currents include those of Ooi et al. [19] for currents with a high and a low volume of release propagating in an unobstructed channel. The predictions of the front velocity during the slumping phase as a function of the Reynolds number and of the ratio between the front and bore velocities were found to be in excellent agreement with experiments. The same was true for the distance from the lock gate at which the reflected bore catches the front and the values of the power law coefficients (α = 2/3 and α = 1/5) in the temporal evolution of the front position during the buoyancy-inertia and buoyancy-viscous regimes. Based on comparisons with experimental visualizations of the current evolution [8], the 3-D simulations were shown to accurately capture the general shape and structure of the head and tail regions of the current during its evolution.

Gonzalez-Juez et al. [7] found very good agreement between the predicted temporal time histories of the drag and lift forces induced by the interaction of a bottom propagating current with a high volume of release with an isolated, small, 2-D, spanwise-oriented, long cylinder situated close to the bottom surface and the experimentally measured forces. Tokyay and Constantinescu [24] considered the interaction of lock-exchange and constant-flux currents with a triangular, surface-mounted obstacle (dam). Based on comparison with video recordings from corresponding lock-exchange experiments, they found good agreement for the shape of the current during and after the front reached the obstacle, and for the temporal evolution of the current. Tokyay et al. [23, 25] studied lock currents propagating over an array of bottom-mounted obstacles (2-D dunes and square cylinders). Validation included comparison with experiment and theory for the temporal evolution of the front position during the different stages of the evolution of the current. Moreover, for currents propagating over a flat surface, the main characteristics of the velocity and turbulent kinetic energy vertical profiles predicted by simulations were found in good agreement with data obtained from experiments. The numerical simulations of Yuksel Ozan et al. [26] for gravity currents with a high volume of release propagating in a channel containing uniformly distributed, 2-D, rectangular cylinders showed good agreement with the experiments of Tanino et al. [22] in terms of the shape of the interface away from the front position (linear variation of the interface height with the distance from the lock gate for sufficiently high ϕ values) and the value of the power law coefficient corresponding to the temporal evolution of the front position during the linear drag-dominated regime.

The previous studies show that the present code can accurately predict gravity current flows and flow past isolated and large arrays of 2-D obstacles. In the aforementioned applications the mesh resolution inside the channel and around the obstacles was similar to the one used in the simulations performed in the present study, which are described next.

4 Test cases and simulation set up

The channel bottom was treated as a smooth no-slip surface. A shear-free, symmetry boundary condition was imposed at the top surface. No-slip boundary conditions were imposed on the surface of the cylinders. The cylinders were disposed in the x–y plane following a close-to-regular staggered pattern (see also [26]). The surface-normal density gradient was set to zero on all no-slip and free-slip boundaries. The flow was assumed to be periodic in the spanwise (z) direction. The flow was started from rest. The nondimensional density was set as C = 1 in the region containing initially (t = 0) lock fluid and C = 0 in the remaining of the computational domain.

The length scale, H ₀, was taken as the channel height corresponding to the simulations performed for full depth currents (H _L  = H). The molecular Schmidt number was equal to 6, which corresponds to cases when differences in density within the channel are mainly induced by differences in water temperature. Previous studies (e.g., [9]) have shown that variations in the value of the Schmidt number did not have a significant effect on the evolution and structure of the current as long as the Schmidt number was O(1) or larger.

Most of the simulations were performed with a Reynolds number Re = 150,000 (e.g., one can assume H ₀ ≈ 0.14 m, g ′ ≈ 0.1 m/s², u _b  ≈ 0.12 m/s, similar to the values used in the lab experiments reported by [10]) such that the current is expected to transition from the slumping phase to the quadratic drag-dominated regime. For applications related to exchange flow developing between zones with emerged and submerged vegetation due to temperature differences associated with different solar heating over the shaded and unshaded regions, Re = 150,000 roughly corresponds to marshes with an average depth H = 2–3 m. Previous studies reported differences of about 2 °C between the shaded and unshaded regions, which correspond to u _b  ≈ 0.05 m/s. Several simulations were performed with lower Reynolds numbers (Re = 100, 1000) to investigate the flow in the regime where the relative magnitude of the viscous processes become important and the flow eventually becomes fully controlled by viscous effects. In these lower Reynolds number simulations, the current is expected to transition from the slumping phase directly to the linear drag-dominated regime. The Reynolds number defined with the cylinder diameter, Re _D , was of the order of 10³–10⁴ in the higher Reynolds number simulations and less than 10² in the lower Reynolds number simulations (Re < 1.000).

As detailed in Table 1, simulations were performed with a range of solid volume fractions between 5 and 25%. Similar to the set up used in experiments, solid cylinders were disposed in a staggered, close to regular, pattern inside the channel. The main difference is that the cylinders were oriented parallel to the spanwise direction in the present simulations, while they are generally disposed vertically in experiments. This makes the present set up more directly relevant to applications in which arrays of porous screens are used to decelerate currents rather than to applications related to vegetated flows. Still, as the study of Yuksel Ozan et al. [26] showed, the orientation of the cylinders is not an essential parameter in predicting the global evolution and main features of the structure of gravity currents advancing in aquatic canopies, as long as the direction of the cylinders is perpendicular to that of the gravity current flow. The edge of the square cylinders in the array was varied between 0.035 and 0.07H ₀. For square cylinders, the frontal area of the cylinders is a = ϕ/D. The channel height was varied between H ₀ for full depth cases and 6H ₀ for deep cases. In most of the simulations, the initial region containing lock fluid was a square with H _L  = L _L  = H ₀ and the total length of the channel was 16H ₀.

Table 1 Main parameters of the simulations (α _q and α _l are the values of the power law coefficient describing the variation of x _f with time over the quadratic and linear drag-dominated regimes, respectively)

The number of grid points was of the order of 5000–8000 in the streamwise (x) direction and 400–1600 in the vertical (y) direction. The width of the computational domain was H ₀ and number of grid points in spanwise direction was equal to 64 in the 3-D simulations. This grid resolution was basically the same as the one used in the simulations reported by Yuksel Ozan et al. [26]. More details on the mesh refinement and preliminary simulations of flow past isolated cylinders are given in Yuksel Ozan et al. [26].

We already discussed the relevance of the Re = 150,000 simulations to applications related to thermally-driven exchange flow in vegetated channels. This Reynolds number is close to the upper limit of those considered in laboratory experiments of flow in vegetated channels [22, 28] and to the lower limit of those (10⁵ < Re < 10⁸) encountered in the field for powder-snow avalanches and turbidity currents encountering arrays of porous barriers [16, 18] or a woody region.

The ratio D/H = 0.035–0.07 is typical for experiments conducted in fairly small flumes of gravity currents advancing in a porous medium (e.g., [10, 22, 28]). The range of ϕ values corresponding to vegetated channels in the field is 0.01 to 45% [13, 28]. Typical ϕ values for 2-D porous fences containing horizontal cylinders used to decelerate snow avalanches are around 10–30%. Hatcher et al. [10] conducted lab experiments of full depth currents with a low volume of release with ϕ = 20% and D/H ≈ 0.04. For snow avalanches channeled in a valley and passing a wooded region, values of ϕ around 20–25% are common [10]. The nondimensional frontal area per unit volume, aH, varied between 1.4 and 3.5 in the present simulations, well within the range used in most laboratory experiments of gravity currents advancing in a porous medium [28].

In all the present simulations the current is expected to start its transition to the linear or quadratic drag-dominated regime a short time after the lock gate is removed. For example, assuming C _D during the quadratic drag-dominated regime is around 1, this gives t _c  ≈ 1 − 4t ₀ (t _c  ≈ 1.1–4.5 s) for most of the Re = 150,000 simulations. This value is similar to the estimate of t _c in the experiments performed by Hatcher et al. [10]. The simulations were run for more than 100t ₀. Thus, over most of the simulation time, the current evolves in one of the drag dominated regimes or transitions between two such regimes.

5 Structure of gravity current

Comparison of Figs. 2 and 3 allows studying the effect of varying the solid volume fraction, ϕ, on the structure of full depth gravity currents with Re = 150,000, as inferred from the x–y contour plots of the instantaneous nondimensional density, C, and nondimensional spanwise vorticity, ω _z (H/u _b ). The comparison in the bottom two frames of Figs. 2 and 3 is made when x _f /H ₀ ≈ 5 just after both currents finished their transition to the quadratic drag dominated regime. Additionally, Figs. 2 and 3 contain the nondimensional density contour plots at x _f /H ₀ ≈ 2 before the end of the transition to the quadratic drag regime and at x _f /H ₀ ≈ 7, way past the end of the transition. They are used to describe the temporal evolution of the current and to confirm some of the conclusions based on analysis of the structure of the current when x _f /H ₀ ≈ 5. In both simulations, the area of release is A = H ₀ *H ₀ and the spanwise width of the domain is identical. The ratio of the solid volume fractions in the two simulations is equal to 2.5, while that of the frontal areas of the cylinders per unit volume is equal to 1.25. So, the two simulations can be used to discuss together the effects of varying ϕ and a on the structure of the current.

Fig. 2

Distribution of instantaneous nondimensional density, C, (top frames) and nondimensional vorticity, ω _z (H ₀ /u _b ), (bottom frame for x _f /H ₀ = 5) within a Re = 150,000 bottom current propagating in a channel of depth H = H ₀ with ϕ = 5% containing cylinders with D/H ₀ = 0.035. The solid and dashed black lines show the C = 0.1 and C = 0.3 isocontours, respectively. The gray dashed line shows the initial position of the lock fluid (H _L  = H ₀, L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

Fig. 3

Distribution of instantaneous nondimensional density, C, (top frames) and nondimensional vorticity, ω _z (H ₀ /u _b ), (bottom frame for x _f /H ₀ = 5) within a Re = 150,000 bottom current propagating in a channel of depth H = H ₀ with ϕ = 12% containing cylinders with D/H ₀ = 0.07. The solid and dashed black lines show the C = 0.1 and C = 0.3 isocontours, respectively. The gray dashed line shows the initial position of the lock fluid (H _L  = H ₀ , L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

In both cases the average thickness of the interfacial layer over the tail of the gravity current is about the same past the end of the transition to the drag dominated regime. For the purpose of our analysis, the thickness of the interfacial layer is defined as the vertical distance between the C = 0.1 and C = 0.3 nondimensional density isocontour lines. On average, this layer becomes thinner as the back of the head region is approached. In the head region (4 < x/H ₀ < 5 for x _f /H ₀ = 5 and 5.8 < x/H ₀ < 7 for x _f /H ₀ = 7), the amount of mixed fluid is higher in the ϕ = 5% case. In both cases, the average thickness of the current in the tail region varies little with the streamwise position away from the head region after the end of the transition to the drag dominated regime (e.g., see concentration plots for x _f /H ₀ = 5 and x _f /H ₀ = 7 in Figs. 2, 3). The head and downstream part of the tail is characterized by large scale vortex shedding behind the cylinders and formation of energetic eddies generated by wake-to-cylinder interactions (e.g., see movie_1 that visualizes the evolution of the current in the ϕ = 5% case). This is expected, given the relatively high value of the Reynolds number in the two simulations. The average size of the eddies generated by the cylinders within the bottom current scales with the cylinder size (see vorticity contour plots in Figs. 2, 3). There is a clear decay of the energy of the large scale eddies in the upstream part of the tail (e.g., for x/H ₀ < 1.3 in the ϕ = 5% case and x/H ₀ < 1.5 in the ϕ = 12% case, as also seen from the corresponding local dissipation rate plots in Fig. 9a, b).

In all the present simulations with ϕ ≥ 5%, no large-scale Kelvin–Helmholtz billows are observed at the interface (e.g., see the 3-D interface visualized in Fig. 4). This is in contrast to what is observed for similar currents propagating in a channel with no obstacles, where strongly coherent Kelvin–Helmholtz billows extending over the whole width of the domain can be observed in the dissipative wake region (e.g., see Figs. 8, 9 in [19]). The main reason for this difference is that for sufficiently high ϕ, as the newly formed billows are broken by their interactions with the cylinders situated close to the front.

Fig. 4

Visualization of the 3D interface of a full depth, bottom propagating gravity current advancing in a channel containing an array of uniformly distributed cylinders (ϕ = 5%, D/H ₀ = 0.035). The interface is visualized using a nondimensional density isocontour surface (C = 0.1)

The interaction of the advancing heavier flow with the cylinders provides an important source for generation of large-scale disturbances of the separated shear layers and large eddies in the wakes of the cylinders situated inside head and tail regions of the current, as well as for regions of flow acceleration with a significant vertical velocity component, as heavier fluid is pushed in between two cylinders.

For example, the density contours in the two frames showing the head region in Fig. 5 show that several patches of higher density fluid are advected upwards in a region containing ambient fluid (e.g., see yellow arrow pointing toward patch situated around x/H ₀ = 4.65, y/H ₀ = 0.37 and red arrow pointing toward patch situated around x/H ₀ = 4.9, y/H ₀ = 0.05). This is possible because of the local amplification of the velocity induced by the contraction of the flow as it enters the space between two neighboring cylinders or because of the upward deflection of the incoming nearly horizontal flow by a cylinder. The mean direction of the velocity vector is not horizontal and sometimes the velocity vector has a significant positive (away from the bed) vertical velocity component, as is the case for the patch identified with the red arrow in Fig. 5. As a result, regions where the flow is unstably stratified (patches of heavier fluid are fully surrounded by ambient lighter fluid) form around the front. Together with the energetic eddies generated by the separated shear layers of the cylinders at the front, they are a main mechanism for mixing in the head region.

Fig. 5

Visualization of the structure of a gravity current with a low volume of release (ϕ = 5%; Re = 150,000, H _L  = H ₀ , L _L  = H ₀, D/H ₀ = 0.035) propagating through an array of obstacles inside the tail region (left frames) and the head region (right frames) when x _f /H ₀ = 4.92 (top frames) and x _f /H ₀ = 5.02. Velocity vectors are superimposed on contours of the instantaneous nondimensional density, C. Also shown with a solid and a dashed black line are the C = 0.1 and 0.3 isocontours, respectively. Results are shown in a z = constant plane

The eddies shed by the cylinders play also a very important role in mixing fluid inside the tail, at least over the downstream part of the tail where the separated shear layers are strongly coherent and large eddies are shed in the wake of the cylinders. As seen from the corresponding frames in Fig. 5, these eddies have a size that is of the order of the cylinder diameter and, as opposed to the case of uniform flow past an isolated cylinder, they do not move more or less parallel to the incoming flow direction. Rather once they form, they are deflected upwards or downwards as they approach upstream cylinders within the array. In some cases, some of the eddies shed by cylinders situated inside the interfacial layer (0.1 < C < 0.3) have enough positive or negative vertical momentum to advect patches of mixed fluid into the ambient fluid or into the heavier fluid (C > 0.3) situated inside the deeper part of the tail region. The black arrows in the frames showing the tail region in Fig. 5 point toward such an eddy that penetrates the deeper parts of the tail. The gray arrow in the same frames points toward an elongated streak of lower density fluid surrounded by higher density fluid from the tail. This streak formed as an eddy containing lower density fluid was advected downwards at an earlier time. That eddy was then stretched by eddies shed by the cylinders situated at lower heights. The elongated streak of lower density fluid is what is left of that eddy as mixing took place. Finally, the yellow arrows in the frames showing the tail region point towards a strongly energetic eddy shed in the wake of one of the cylinders situated slightly above the gravity current interface (C = 0.1) that is able to entrain streaks of higher density fluid from the interface region as it is advected in its vicinity. This is an important mechanism for mixing in the vicinity of the interface.

Comparisons of Figs. 2, 6 and 7 and of movie_1 and movie_2 allow investigating the effect of the relative depth of release, H _L /H, on the propagation of high Reynolds number currents (Re = 150,000) with identical areas of release. As the area of release is A = H ₀ *H ₀ in all three cases, comparison of the three simulations is equivalent to a study of the influence of the channel depth on the structure of the lock-exchange flow. As H _L /H decreases from 1 (Fig. 2 and movie_1) to less than 1 values (H _L /H = 0.33 in Fig. 6 and movie_2 and H _L /H = 0.17 in Fig. 7), the classification of the current also changes from a full depth current to a partial depth current (Fig. 8).

Fig. 6

Distribution of instantaneous nondimensional density, C, (top) and nondimensional vorticity, ω _z (H ₀ /u _b ), (bottom) within a Re = 150,000 bottom current propagating in a channel of depth H = 3H ₀ with ϕ = 5% containing cylinders with D/H ₀ = 0.035. The solid and dashed black lines show the C = 0.1 and C = 0.3 isocontours, respectively. The gray dashed line shows the initial position of the lock fluid (H _L  = H ₀ , L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

Fig. 7

Distribution of instantaneous nondimensional density, C, within a Re = 150,000 bottom current propagating in a channel of depth H = 6H ₀ with ϕ = 5% containing cylinders with D/H ₀ = 0.035. The solid and dashed black lines show the C = 0.1 and C = 0.3 isocontours, respectively. The gray dashed line shows the initial position of the lock fluid (H _L  = H ₀ , L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

Fig. 8

Distribution of instantaneous nondimensional density, C, (top) and nondimensional vorticity, ω _z (H ₀ /u _b ), (bottom) within a Re = 150,000 bottom current propagating in a channel of depth H = 3H ₀ with ϕ = 5% containing cylinders with D/H ₀ = 0.035. The solid and dashed black lines show the C = 0.1 and C = 0.3 isocontours, respectively. The gray dashed line shows the initial position of the lock fluid (H _L  = 0.5H ₀ , L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

Comparison of the vorticity fields in Figs. 2 and 6 (see also movie_1 and movie_2 for a comparison of the structure of the gravity current at other times and a visualization of the separated shear layers and large-scale eddies generated by the cylinders) shows that the increase of the channel depth has a fairly small effect on the strength of the separated shear layers and general characteristics of the eddies generated by the cylinders in the head region and the downstream part of the tail, away from the interface. For example, the coherence level of the eddies generated inside the head and downstream part of the tail is similar in the cases with H = H ₀ and H = 3H ₀, as inferred from comparison of the distributions of the absolute value of the local dissipation rate in these regions (see Fig. 9b, c). As the channel depth increases, the strength of the return flow decreases, as observed from the reduction in the coherence of the eddies contained in the flow above the current (e.g., compare vorticity contour plots in Figs. 2, 6 and corresponding local dissipation rate contour plots in Fig. 9b, c).

Fig. 9

Distribution of the absolute value of the nondimensional turbulent dissipation rate, |ε|, within a Re = 150,000 low volume of release current (H _L  = H ₀, L _L  = H ₀) propagating in a channel containing cylinders. a case with H = H ₀, ϕ = 5% and D/H ₀ = 0.035; b case with H = H ₀, ϕ = 12% and D/H ₀ = 0.07; c case with H = 3H ₀, ϕ = 5% and D/H ₀ = 0.035. The solid line shows the C = 0.1 and C = 0.3 isocontour

Away from the head region, the thickness of the interfacial layer decreases monotonically with increasing channel depth (e.g., by about 25% as H increases from H ₀ to 3H ₀; this estimate is based on the mean vertical distance between the C = 0.1 and C = 0.3 density contour lines in Figs. 2, 6). While in the full depth case the current height (e.g., as described by the C = 0.1 nondimensional density contour line) increases close to monotonically with increasing distance from the front, in the partial depth cases the height of the current is close to constant over the upstream part of the tail region. The amount of higher density fluid entrained into the ambient fluid region above the upstream part of the tail decreases with increasing channel height mostly because the average magnitude of the flow velocities inside the ambient fluid layer decreases with increasing channel height (e.g., compare the vorticity fields over the C = 0.1 isocontour line in Figs. 2, 6). The amount of mixed fluid inside the head region is fairly independent of the channel height. For example, the volume of mixed fluid with 0.01 < C < 0.99 inside the head region (4 < x/H ₀ < 5 for x _f /H ₀ = 5) differs by less than 3% in the cases with H = H ₀ (Fig. 2) and H = 3H ₀ (Fig. 6) when x _f /H ₀ = 5. Meanwhile, the difference is close to 40% when the same variable is evaluated over the tail region when x _f /H ₀ = 5.

The effect of varying the area of release is investigated in Figs. 6 and 8 for partial depth currents with Re = 150,000. Between the two simulations, H _L was reduced from H ₀ to 0.5H ₀. Because of the reduction in the volume of lock fluid, the height of the current in the simulation with H _L  = 0.5H ₀ is about half that of the current in the simulation with H _L  = H ₀. The same trend is observed for the height of the interfacial layer (region with 0.1 < C < 0.3) over the tail region. Interestingly, the vorticity magnitude levels around the cylinders situated inside the current and close to its front are comparable in the two simulations. In fact, the vorticity magnitude levels in the return flow, close to the front, are larger in the simulation with a lower H _L . This is also the main reason why the head shape is much more irregular and entrainment of higher density fluid from the head is significantly stronger in the simulation with H _L  = 0.5H ₀. In the latter case, some of the higher density fluid lost by the head region penetrates vertically up to distances from the bed that are more than 2 times the average thickness of the current in the tail region. These distances are only of the order of 1.5 times the average thickness of the current in the tail region in the simulation with H _L  = H ₀.

As already mentioned, the presence of cylinders in the channel has a large influence on entrainment of ambient fluid into the bottom current. Strong mixing occurs in the region situated close to the front and along the interfacial region. An approximate way to quantify mixing associated with entrainment in a flow that initially contains two unmixed regions is to estimate the variation with time of the volume containing fluid with a density falling between the initial densities of the ambient and lock fluids. After non-dimensionalizing with the initial volume of lock fluid, V ₀, the normalized volume containing mixed fluid is $V(x_{f} /H_{0} ) = \frac{1}{{V_{0} }}\int\limits_{\varOmega } {\gamma dV}$, in which Ω is the total volume of the channel, γ = 1 if 0.01 < C < 0.99 and γ = 0 otherwise, which defines mixed fluid as fluid for which the non-dimensional density differs from the initial values by at least 1%. Initially, the channel contains only unmixed fluid with C = 0 or C = 1, so V(0) = 0.

Results in Fig. 10a show that the volume of mixed fluid, V/V ₀, is fairly independent of ϕ before the start of the transition to the quadratic drag dominated regime. After the start of the transition to the drag dominating regime, the effect of increasing ϕ in the full depth, Re = 150,000 simulations is to decrease the volume of mixed fluid (e.g., by about 30% between cases with ϕ = 5 and 15% for x _f /H ₀ > 8). Interestingly, the rates of increase of V with x _f are fairly close in the three simulations after the end of the transition to the quadratic drag-dominated regime and before that start of the transition to the linear drag dominated regime.

Fig. 10

Variation of the normalized volume of mixed fluid (0.01 < C < 0.99), V/V ₀, as a function of the front position, x _f /H ₀, in the Re = 150,000 simulation. V ₀ is the initial volume of lock fluid. a effect of the solid volume fraction, ϕ, in the simulations with H = H _L  = H ₀ , L _L  = H ₀; b effect of the channel depth, H, in the simulations with ϕ = 5%, Re = 150,000, H _L  = H ₀, L _L  = H ₀; c effect of the channel depth, H, in the simulations with ϕ = 12%, Re = 150,000, H _L  = H ₀, L _L  = H ₀

The effect of increasing the channel depth, while maintaining the height of the initial volume of lock fluid, H _L , constant results in lowering the values of V/V ₀ for a given front position (Fig. 10b). This trend starts immediately after the lock gate is released and continues during the drag dominated regime. The decrease of V/V ₀ with x _f /H ₀ is sharper for low values of H _L /H (e.g., V/V ₀ decreases by about 15% as H _L /H decreases from 1 to 0.33 in the simulations withϕ = 5%). For partial depth currents with a relatively low H _L /H, the rate of decrease of V/V ₀ with decreasing H _L /H is much smaller (e.g., V/V ₀ decreases by about 4% as H _L /H decreases from 0.33 to 0.17 in the simulations with ϕ = 5%). The same trend is also observed in the simulations with ϕ = 12% (Fig. 10c), but the relative decrease in V/V ₀ with decreasing H _L /H is smaller than that observed in the ϕ = 5% simulations. For example, V/V ₀ decreases by about 9% as H _L /H decreases from 1 to 0.33 in the simulations with ϕ = 12%.

Until now only high Reynolds number currents that transition first to the quadratic drag-dominated regime were considered. To investigate the effect of the Reynolds number, the density and vorticity fields are also shown in Fig. 11 for a Re = 1000 current that transitions directly to the linear drag-dominated regime. So, when the structure of the two partial depth currents (H = 3H ₀, ϕ = 5%, H _L  = 0.5H ₀, L _L  = H ₀) is compared in Figs. 8 and 11, one current is in the quadratic drag regime, while the other is in the linear drag regime. As opposed to all previous cases, no well-defined separated shear layers form past the cylinders situated within the body of the Re = 1000 current (e.g., see vorticity contour plot in Fig. 11). This is true even for the cylinders situated close to the front. The vorticity is amplified close to the lateral sides of the cylinders in the region where the flow accelerates as it passes the cylinder. However, no large-scale eddies are shed in the wakes of these cylinders. The cylinder Reynolds number is too low for the cylinders’ wake to start shedding. Meanwhile, comparison of the density fields in Figs. 8 and 11 shows that for the same front position the amount of mixed fluid in the lower Reynolds number case is significantly higher, mainly because of the much larger molecular diffusion. This can be observed from comparison of the areas enclosed by the C = 0.1 isocontour line and by the maximum value of the nondimensional density inside the tail region, which is larger than 0.5 in the Re = 150,000 case and less than 0.35 in the Re = 1000 case. The interface is very smooth, the height of the current is monotonically increasing with the distance from the front and no Kelvin–Helmholtz billows are observed on the interface of the Re = 1000 current.

Fig. 11

Distribution of instantaneous nondimensional density, C, (top) and nondimensional vorticity, ω _z (H ₀ /u _b ), (bottom) within a Re = 1000 bottom current propagating in a channel of depth H = 3H ₀ with ϕ = 5% containing cylinders with D/H ₀ = 0.035. The solid line shows the C = 0.1 isocontour. The gray dashed line shows the initial position of the lock fluid (H _L  = 0.5H ₀, L _L  = H ₀). Only part of the computational domain is shown. Results are shown in a z = constant plane

6 Front velocity

The time histories of the front position in Fig. 12 show that the full depth currents in the Re = 150,000 simulations conducted with different solid volume fractions start their transition to the quadratic drag dominated regime around t = 3–5t ₀. While in the ϕ = 5% and ϕ = 12% cases, the power law coefficient describing the increase of the front position with time (x _f  ~ t ^α) is α = 3/5, for sufficiently large values of the solid volume fraction (e.g., for α = 25%) the coefficient increases to α = 2/3. The value predicted in the ϕ = 25% case (α = 2/3) is identical to the one predicted by theory for currents with a depth comparable to the channel depth (h = O(H)). For the other two cases with a smaller solid volume fraction, the predicted value of α (= 3/5) is in between the theoretical value predicted for currents in the quadratic regime with h = O(H) (α = 2/3) and for currents with h ≪ H (α = 1/2).

Fig. 12

Effect of the solid volume fraction on the temporal evolution of the front position, x _f /H ₀, in the simulations (Re = 150,000, H = H ₀ , H _L  = H ₀ , L _L  = H ₀) with ϕ = 5% (red line), ϕ = 12% (green line) and ϕ = 25% (blue line)

The current is slower in the ϕ = 25% case compared to the other cases. The ϕ = 25% case was run for a longer time (~400t ₀) compared to the other cases. Results in Fig. 12 show that around t = 150t ₀ the current transitions fairly rapidly to a second drag dominated regime. Examination of the vorticity fields confirmed the flow structure for t > 150t ₀ resembles that of a current in which inertial effects are relatively small. The power law coefficient is α = 1/3, in excellent agreement with the theoretical value expected for currents with h ≪ H during the linear drag dominated regime. So, for this case the current transitions fairly fast from a quadratic drag dominated regime expected for currents with h = O(H) to a linear drag dominated regime expected for currents with h ≪ H. This is not so surprising given that the average current height decreases monotonically with time so, at a certain time, the current should reach a stage in which h ≪ H. In the ϕ = 25% case, this happens around t = 150t ₀ when h/H ≈ 0.062.

The effect of decreasing the length of the initial area occupied by the lock fluid is to slightly decelerate the full depth current during the quadratic drag dominated regime, as seen from Fig. 13 where the ϕ = 5% Re = 150,000 simulations with L _L  = H ₀ and L _L  = 0.5H ₀ are compared. However, the value of α during this regime remains the same. The simulation with L _L  = 0.5H ₀ was run until t = 500t ₀. Similar to the ϕ = 25% case analyzed in Fig. 12, the current transitions to a linear drag dominated regime around t = 200t ₀. The value of α over the later regime is equal to 3/8, which is slightly larger than the value observed in the ϕ = 25% case and the theoretical value predicted for gravity currents with h ≪ H.

Fig. 13

Effect of initial length of lock region, L _L , on the temporal evolution of the front position, x _f /H ₀, in the simulations (ϕ = 5%, Re = 150,000, H = H ₀ , H _L  = H ₀) with L _L  = H ₀ (red line) and L _L  = 0.5H ₀ (dark blue line)

In the case of high Reynolds number currents, the effect of decreasing the ratio between the initial height of the release and the channel depth is to slightly modify the value of α during the quadratic drag dominated regime. Figure 14 compares results from four simulations conducted with ϕ = 5% and Re = 150,000. While in the full depth of release case α = 3/5, in the partial depth of release cases with H _L /H < 0.5 the value of α is 5/9. The latter value is much closer to the theoretical value of ½ expected for gravity currents with h ≪ H over the quadratic drag dominated regime. Results in Fig. 10 also show that the temporal evolutions of x _f , and thus the front velocity, are practically independent of the channel depth for H _L /H < 0.3 if all the other geometrical and flow parameters are kept constant.

Fig. 14

Effects of ratio between initial height of lock region and channel height, H _L /H, and of channel depth, H, on the temporal evolution of the front position, x _f /H ₀, in the simulations (ϕ = 5%, Re = 150,000, L _L  = H ₀) with H _L /H = 1, H = H ₀ (red line), H _L /H = 0.33, H = 3H ₀ (pink line), H _L /H = 0.17, H = 3H ₀ (purple line) and H _L /H = 0.17, H = 6H ₀ (orange line)

Results in Fig. 15 that compare two simulations conducted with Re = 150,000 and ϕ = 12% are consistent with those in Fig. 14. As H _L /H decreases from 1 to 0.33, the value of α during the quadratic drag dominated regime changes from 3/5 (full depth current) to 5/9 (partial depth current). So, it appears that the value of α for partial depth currents with moderate values of H _L /H is 5/9 independent of the channel solid volume fraction.

Fig. 15

Effect of channel depth, H, on the temporal evolution of the front position, x _f /H ₀, in the simulations (ϕ = 12%, Re = 150,000, H _L  = H ₀ , L _L  = H ₀) with H = H ₀ (green line) and H = 3H ₀ (brown line)

Figure 16 compares simulation results conducted with different Reynolds numbers for partial depth currents with H _L /H = 0.17. In all three simulations the initial area occupied by the lock fluid is the same. While the Re = 150,000 current transitions to a quadratic drag dominated regime with α = 5/9, the current in the other two simulations conducted with Re = 1000 and Re = 100 transitions to a linear drag dominated regime with α = 1.2. The transition to the linear regime takes place faster as the Reynolds number decreases. The fact that the currents with Re = 1000 and Re = 100 transition directly to a linear drag dominated regime is not surprising, as the cylinder Reynolds number is O(1) or lower for all the cylinders situated inside the current at all times during the evolution of the current. What is a little bit surprising is that the current transition to a linear regime in which the value of α is exactly equal to the theoretical value expected for currents with h = O(H). This is certainly the case during the initial stages of the evolution of the two currents. However, even at later times the temporal evolution of the front is still very well approximated by a power law with α = 1/2. One expects that eventually transition to a linear drag dominated regime corresponding to deep currents (α = 1/3) will take place.

Fig. 16

Effect of Reynolds on the temporal evolution of the front position, x _f /H ₀, in the simulations (ϕ = 5%, H = 3H ₀ , H _L  = 0.5H ₀ , L _L  = H ₀) with Re = 150,000 (orange line), Re = 1000 (light blue line) and Re = 100 (black line)

One should also mention that the low volume of release currents considered in the present study (ϕ > 5%) do start their transition to the drag-dominated regime before a buoyancy-inertia regime may be established (see discussion in Sect. 2), as is observed for currents propagating in a channel with no obstacles (ϕ = 0%). Cases with ϕ = 0% (e.g., see [19]) will be more relevant for currents propagating in channels with low solid volume fractions (ϕ < 1%), not considered in the present study, where transition to the drag dominated regime can start at much larger nondimensional times after the gate is released. Results obtained for both high and low Reynolds number currents by Ooi et al. [19] for full depth currents show a very different structure of the current, when compared with that of the currents in the present high solid volume fraction simulations. As already discussed, for high Reynolds number currents, no large-scale Kelvin–Helmholtz interfacial billows are observed in the present simulations (Fig. 4). This is in contrast to what is observed for currents with a low volume of release propagating in a channel with ϕ = 0% (see Figs. 8, 9 in [19] and Figs. 2, 3). As discussed in greater detail by Yuksel Ozan et al. [26] in the context of currents with a high volume of release with 0% < ϕ < 25%, this happens because the energetic eddies shed by the cylinders intensify vortex stretching and rapidly break the coherence of the interfacial Kelvin–Helmholtz billows. Even for low Reynolds number currents, the cylinders have a large influence on the structure of the current, as the bulk-shaped head observed in simulations with ϕ = 0% before the end of the transition to the viscous-buoyancy phase (see Fig. 10 in [19]) is not present in the corresponding simulations with high solid volume fractions.

The plots of the front position versus time for full depth currents (e.g., see Fig. 12) can also be used to estimate the penetration length of currents induced by thermally-driven, convective, shallow exchange in vegetated canopies developing in quiescent regions [2]. This allows estimating the penetration distance of the gravity current. For water quality applications, the (daily) flushing induced by the current influences the overall nutrient removal from the water by the roots and biofilms forming on the root surfaces. The exchange is generated by differences in the water temperature developing during the day [13]. These temperature differences are due to different solar heating between the shaded regions near the bank containing emerged vegetation, typically extending for couple of meters away from the bank, and the adjacent region containing mostly submerged vegetation. Another reason for the development of regions with different temperatures are differences in solar heating due to different concentrations of phytoplankton near and away from the edge of the pond/marsh that alter the penetration of solar radiation through the water column [6].

Typically, temperature differences of the order of 1–2 °C develop during the day [15] and persists for about 6 h each day before night cooling acts toward equalizing the water temperature inside the pond/marsh. For typical applications, the mean water depth in the pond/marsh can be assumed to be H = H ₀ = 3 m. This gives buoyancy velocities of the order of 0.05 m/s (Re ≈ 150,000) and a nondimensional time scale t ₀ = H ₀ /u _b  ≈ 60 s. The total length of the vegetated region may be of the order of tens to hundreds of meters in the field. Using results in Fig. 12 and the inferred value of the power law coefficient, α, over the quadratic drag-dominated regime, one can estimate the penetration length, L _p , as a function of time and ϕ. For example, after 6 h L _p  ≈ 17H ₀ = 51 m for ϕ = 5% and L _p  ≈ 12H ₀ = 36 m for ϕ = 25%. After 24 h, these values increase to 92 and 28H ₀ for ϕ = 5 and 25%, respectively. Moreover, using a simple volume conservation assumption, one can estimate the average height of the current as a function of time.

7 Summary and final discussion

Large eddy simulations were used to study the structure and evolution of lock-exchange compositional currents with a low volume of release propagating in a long horizontal channel of height H containing an array of identical obstacles placed is a staggered way. This geometrical set up mimics a porous medium of uniform solid volume fraction, ϕ. The area initially occupied by the lock fluid had a height H _L and a length, L _L . The simulations resolved the flow past the individual cylinders, which eliminated the need to include additional drag terms in the governing equations. The simulations revealed the critical role played by the large-scale energetic eddies shed by the cylinders situated sufficiently close to the front region in promoting mixing inside the current and at the interface between the current and the ambient flow for the high Reynolds number cases. The instantaneous flow fields from the simulations revealed that the effect of increasing the ratio between the channel depth and the initial height of the region containing lock fluid was to weaken the return flow around the advancing current, which in turn resulted in reduced mixing between the current and the surrounding fluid. In contrast, low Reynolds number currents that transition directly to the linear drag dominated regime are characterized by the absence of production of large-scale eddies resulting from the interaction of the current with the obstacles.

Numerical results showed that both full depth (H = H _L ) and partial depth (H _L  < H), high Reynolds number currents transition to a quadratic drag dominated regime in which the front position x _f is proportional to t ^α. While for full depth cases α = 3/5 for relatively small ϕ values and α = 2/3 for relatively high ϕ values, for partial depth cases with a sufficiently small H _L /H, simulations predicted α = 5/9. This shows that the theoretical value of α for currents with a depth h that is comparable to H (α = 2/3) is approached for full depth currents propagating in a channel with a sufficiently high ϕ. Moreover, the theoretical value (α = 1/2) for deep currents (h ≪ H) is approached by partial depth currents with 0.3 < H _L /H < 0.1. Meanwhile, low Reynolds number partial depth currents for which the cylinder Reynolds number is around unity or less than unity transition directly to a linear drag dominated regime with α = 1/2, which corresponds to the theoretical value predicted for currents with depth h comparable to H. Simulation results also showed that high Reynolds number full depth currents can transition from a quadratic regime with α close to the value expected for currents with a depth, h, comparable to H to a linear drag dominated regime with α = 1/3, which is the theoretical value expected for deep currents with h ≪ H. The main reason for the differences between the observed values of α and the theoretical values deduced based on shallow water theory is that theoretical solutions neglected entrainment.

Present low-volume of release simulations have also highlighted some important differences with the limiting case of full depth, high volume of release currents considered in a related study by Yuksel Ozan et al. [26]. In terms of the current structure, the most important difference is the shape of the interface away from the front. In the high volume of release cases, the height of the interface decays fairly monotonically and close to linearly with the distance from the lock gate position for ϕ > 5%. The height of the interface in the low volume of release cases is close to horizontal, mainly because the mean velocity is close to zero in these cases (e.g., no separated shear layers are visible over this region in Figs. 2, 3, 6). This is in contrast to what was observed for high volume of release cases (see Figs. 5, 6 in [26]) where the mean velocity is significant and strong separated shear layers are present at all streamwise locations in between the front and the lock gate. In terms of the front evolution, the most important difference is the change in the values of the power law coefficients corresponding to the linear and quadratic drag regimes between high volume of release cases (α = 1/2 and α = 3/4) and most of the low volume of release cases (see Table 1). Differences in the values of α are even observed between full depth cases with a high and, respectively, a low volume of release. Obviously, this has very important consequences in terms of predicting the position, front velocity and capacity of the current to induce large forces on the obstacles at large times after the flow started.

Future work will consider gravity currents advancing in a porous medium over a sloped channel bottom. Such cases are directly relevant especially for applications involving powder snow avalanches and salinity/turbidity currents propagating over the continental shelf that encounter a region containing natural (e.g., bottom vegetation) or artificial (man-made porous barriers) obstacles. The present simulations will serve as the limiting case (horizontal bottom) against which the changes in the evolution and structure of the current due to the increase in the bottom angle can be quantified.