1 Introduction

Pore size distribution (PSD) is known to profoundly influence the movement and distribution of fluids inside a porous medium as well as the transport and reaction of chemicals (Lala and El-Sayed 2017; Zhao et al. 2017). Some properties that are intimately linked to the PSD, e.g. capillary pressure curves, are used as inputs to reservoir simulation software (Rezaee 2015) and provide valuable information for management and decision making. Also, several methods used in enhanced oil recovery (EOR) are based on flooding with chemicals such as polymer solutions, foams or emulsions with the purpose of reducing the mobility ratio of displacing fluid to the displaced fluid (Wang et al. 2017). This results in reduction of viscous fingering and therefore in improved sweep efficiency in the reservoir (Sheng 2011). The PSD of the reservoir rock greatly affects the propagation of the fluid front and is often determinant to choose the most appropriate recovery technique. PSD is also extensively used to predict many processes of interest in soils (Zaffar and Lu 2015; Houston et al. 2017), e.g. biological dynamics (Monga et al. 2009) or decomposition of organic carbon (Juarez et al. 2013).

Despite the rapid progress in non-destructive imaging techniques such as X-ray computed tomography (Houston et al. 2017; Lindquist and Venkatarangan 2000; Burlion et al. 2006; Prodanovic et al. 2006, 2007; Wildenschild and Sheppard 2013; Viani et al. 2017), mercury intrusion porosimetry (MIP) is still at present the most widely used method to determine PSD (Giesche 2006; Zhou et al. 2017; Choi et al. 2017). Some of its advantages are the broad range of attainable pore sizes (\(\sim \) 3.5 nm to 300 \(\upmu \)m), the relatively short duration of the test (\(\sim \) 3 h) and the popularity of a well-established method that is recognized as the reference one. Diamond (2000) reviewed the conditions that must be met for MIP measurements to provide valid estimates of the PSD of porous solids. This author showed that this technique should be discarded in some cases due to indiscriminate filling of large and small pores once the pressure corresponding to the largest entrance or opening (threshold diameter) is reached. Also, MIP presents other serious drawbacks including toxicity of the employed fluid and low performance for unconsolidated porous media. Motivated by the preceding considerations, the IUPAC (International Union of Pure and Applied Chemistry) strongly emphasized the interest and the need to develop new effective and non-toxic porosimetry methods (Rouquerol et al. 2012). Furthermore, availability of MIP for the near future is threatened by the progressive mercury phase-out and the new international legislation that will be applicable following the ratification of the Minamata Convention on Mercury in October 2013 (United Nations 2013).

The theoretical basis of a porosimetry method based on the injection of yield stress fluids was first proposed by Ambari et al. (1990). These authors presented a procedure to derive the PSD from the measurement of the flow rate, Q, as a function of the pressure gradient, \(\nabla {P}\), when a yield stress fluid is injected through a bundle of parallel capillaries whose radii are distributed following a specific distribution (PSD). Only the simple case of a Bingham fluid (\({n} = 1\)) was investigated in this first work. The method was extended to the case of a bundle of randomly oriented capillaries by Chaplain et al. (1992). In a later work, Oukhlef et al. (2014) successfully performed analytical inversion of numerically generated (\({Q}, \nabla {P}\)) data for the flow of Bingham and Casson fluids through different bundles of capillaries. The mathematical determination of the PSD was achieved by using the partial derivatives of the continuous function resulting from polynomial regression of the experimental (\({Q}, \nabla {P}\)) data.

On the grounds of the preceding theoretical and numerical considerations, the basis of the yield stress fluids method (YSM) to obtain the PSD of a porous medium from laboratory experiments was presented by Rodríguez de Castro et al. (2014). YSM relies on considering the extra increment of Q when \(\nabla {P}\) is steeply increased, as a consequence of the pores of smaller and smaller radius that are newly incorporated to the flow. The critical behaviour of path opening during flow of a yield stress fluid in porous media was numerically and experimentally investigated by Chevalier and Talon (2015a, b). Also, Nash and Rees (2017) showed that the manner in which flow begins once the threshold pressure gradient is exceeded strongly depends on the channel size distribution of the porous media.

Recently, Rodríguez de Castro et al. (2016) performed a series of YSM experiments to characterize different porous media using a unique yield stress fluid in order to evaluate the influence of the type of porous media on the accuracy of the obtained PSD. These authors used an aqueous xanthan gum polymer solution as injected fluid and their results showed that YSM succeeded in providing representative PSDs for the tested media. YSM was presented as a potential alternative to MIP, based on the simplicity of the tests, their low cost as compared to MIP and X-ray microtomography devices, and the non-toxicity of the injected fluid. Moreover, YSM is versatile and can be used to characterize different types of porous media, e.g. unconsolidated porous media for which MIP and other currently used methods are not efficient. In the same work, Rodríguez de Castro et al. (2016) identified some of the critical questions regarding the experimental feasibility of the method, e.g. polymer adsorption, polymer retention and mechanical degradation of the polymer. Whereas no sign of important adsorption and mechanical degradation was reported, polymer retention, i.e. mechanical entrapment of the polymer macromolecules in the small pores, was shown to be important at the lowest flow rates due to the random orientation of the polymer molecules at these flow rates. An adapted experimental protocol was also proposed by the authors to minimize polymer retention.

Despite the recent progress, the robustness of YSM has still not been fully assessed. In particular, the sensitivity of the obtained PSDs with respect to errors in the determination of the shear-rheology parameters of the injected fluid is still unclear. Also, the capacity of xanthan gum solutions to approach the behaviour of a yield stress fluid depending on their polymer concentration must be further investigated. In order to accomplish this task, the sensitivity of YSM to errors in input rheological parameters is numerically evaluated in the present work and a set of YSM laboratory experiments using xanthan gum solutions with different polymer concentrations are presented and analysed.

2 Using YSM to Obtain the Pore Size Distribution

The procedure to obtain the PSD of the investigated porous material from the flow rate–pressure gradient raw data (\({Q}_{{i}},\nabla {P}_{{i}})\) measured during injection of a Herschel–Bulkley-type yield stress fluid was presented in detail by Rodríguez de Castro et al. (2014, 2016). The main aspects of this procedure are highlighted below.

Herschel–Bulkley’s law is often used to describe the rheological behaviour under shear of common yield stress fluids. This law can be written as:

$$\begin{aligned} \left\{ \begin{array}{ll} \tau =\tau _0 +{k} \dot{{\gamma }}^{{n}} &{}\quad \hbox {for } \tau >\tau _{0}\\ \dot{{\gamma }}=0&{}\quad \hbox {for } \tau \le \tau _{0} \end{array}\right. \end{aligned}$$
(1)

where \(\tau _0 \) is the yield stress, k is the consistency and n is the flow index. \(\tau _0 \), k and n are generally obtained by fitting the data obtained by measuring the shear rate \(\dot{{\gamma }}\) as a function of the applied shear stress \(\tau \) using a rheometer.

YSM assumes that the porous medium is homogeneous, isotropic and well represented by a bundle of parallel capillaries of various radii. For a set of (\({Q}_{{i}}, \nabla {P}_{{i}})\) data collected during a typical YSM experiment, each \(\nabla {P}_{{i}} \) defines a class of pores of representative radius \({r}_{{i}} =\alpha \frac{2\tau _0 }{\nabla {P}_{{i}} }\) (\({r}_1>{r}_2>\cdots >{r}_{{N}})\) where \(\alpha \) is a numerical factor greater than unity. The fundamental reason of \(\alpha \) being greater then unity is that for a given \(\nabla {P}_{i}\) the resulting \({Q}_{{i}}\) is generated in the pores whose radii are strictly larger than \(\frac{2\tau _0 }{\nabla {P}_{{i}}}\). In other words, \(\nabla {P}_{{i}}\) represents only the onset of the contribution to the flow of pores of radius \(\frac{2\tau _0 }{\nabla {P}_{{i}}}\). Details for the determination of the value of \(\alpha \) were provided by Rodríguez de Castro et al. (2014, 2016). In the routine used to calculate the number of pores \({n}_{{i}}\) of a targeted pore class \({r}_{{i}} ({i} = 1, {\ldots }, {N})\), and starting with \({n}_1 \), successive and increasing positive values are scanned until \({Q}_{\mathrm{s}} <\mathop {\sum }\nolimits _{{{g}}=1}^{{i}} {n}_{{g}} {q}\left( {\nabla {P}_{\mathrm{s}} ,{r}_{{g}} } \right) \) for a given s. The maximum value is then assigned to \({n}_{{i}} \). In the preceding inequality, \({q}\left( {\nabla {P},{r}} \right) \) is the flow rate of a Herschel–Bulkley fluid through a capillary of radius r as a function of \(\nabla {P}\) as given by Skelland (1967), and more recently by Chhabra and Richardson (2008).

Once \({n}_{{i}} \) (\({i} = 1, {\ldots }, {N}\)) have been calculated, the probability in terms of relative frequency \({p}\left( {{r}_{{i}} } \right) =\frac{{n}_{{i}} }{\mathop {\sum }\nolimits _{{j}=1}^{{N}} {n}_{{j}} }\hbox { for }i=1\cdots {N}\) and in terms of relative volume \({p}_{\mathrm{v}} \left( {{r}_{{i}} } \right) =\frac{{n}_{{i}} \pi {r}_{{i}}^2 }{\mathop {\sum }\nolimits _{{j}=1}^{{N}} {n}_{{j}} \pi {r}_{{j}}^2 }\hbox { for }i=1\cdots {N}\) are also obtained. It is highlighted that \({p}\left( {{r}_{{i}} } \right) \) are the fractions of the numbers of pores and \({p}_{\mathrm{v}} \left( {{r}_{{i}} } \right) \) are the fractions of the total pore volume in a given class. Also, it is recalled that the parallel bundle of capillaries model used in YSM assumes that all capillaries have equal length. The total flow rate Q as a function of the pressure gradient \(\nabla {P}\) corresponding to the obtained PSD is then calculated as follows:

$$\begin{aligned} {Q}\left( {\nabla {P}} \right) =\mathop {\sum }\limits _{{i}=1}^{{N}} {n}_{{i}} {q}\left( {\nabla {P},{r}_{{i}}} \right) \end{aligned}$$
(2)

Given that the actual rheology of xanthan gum solutions is described by Carreau’s model, one may argue that the corresponding \({q}\left( {\nabla {P},{r}} \right) \) should be computed and used in the inversion to obtain PSD. However, to the best of our knowledge, no simple closed-form expression correlating the volumetric flow rate to the pressure drop in capillaries has been reported in the literature for these fluids (Lopez et al. 2003; Lopez 2004; Balhoff et al. 2012). Only recently, Sochi (2015) presented an analytical solution for the flow of Carreau fluids through pipes, involving the solution of integral equations. The implementation of this analytical solution in YSM is not evident and should be specifically addressed in prospective studies.

YSM was used to characterize model porous media (Malvault 2013) and natural and synthetic porous media (Rodríguez de Castro et al. 2014, 2016) in previous studies, and the results were compared with MIP. As expected from the results of Chauveteau et al. (1996), the PSDs obtained by both methods did not coincide in all cases. The reasons for these discrepancies were discussed by Rodríguez de Castro et al. (2016). It is recalled that YSM is based on pressure drop measurements, so the characteristic pore dimension is related to the hydraulic diameter of the pores. In a different manner, the PSDs obtained by MIP are calculated from capillary pressure measurements, and the characteristic pore dimensions are related to the largest entrances or openings toward the pores (Roels et al. 2001; Giesche 2006). Consequently, YSM is expected to yield smaller pore sizes than MIP for a given porous medium. Also, the blind pores and the inter-connectedness between pores cannot be characterized by YSM.

It should be noted that YSM is based on the injection of an ideal yield stress fluid showing no thixotropy, no viscoelasticity and a well-defined yield stress. Among a number of candidate fluids, Rodríguez de Castro (2014) and Rodríguez de Castro et al. (2014, 2016) selected xanthan gum aqueous solutions due to their negligible thixotropy, their limited viscoelasticity (Jones and Walters 1989; Sorbie 1991), the stiffness of xanthan gum macromolecules and their flat monolayer adsorption on pore walls (Chauveteau 1982; Sorbie 1991; Dario et al. 2011).

Despite the above-mentioned advantages, the shear viscosity of xanthan gum polymer solutions at low shear rates is finite, as described by Carreau’s model (Carreau 1972), so strictly speaking xanthan gum solutions should be referred to as pseudo-yield stress. Indeed, due to the stiffness of the polymer molecule, xanthan semidilute aqueous solutions develop a high viscosity level at low shear rates and a very pronounced shear-thinning behaviour. Therefore, xanthan gum solutions have been reported to present an apparent yield stress (Withcomb and Macosko 1978; Carnali 1991; Song et al. 2006; Khodja 2008; Benmouffok-Benbelkacem et al. 2010), and previous works showed that the Herschel–Bulkley model described well the steady state shear flow of concentrated xanthan gum solutions (Rodríguez de Castro et al. 2014, 2016; Song et al. 2006). In this respect, there is much practical interest in considering concentrated xanthan gum solution as yield stress fluids in many applications.

For a fluid flowing through a capillary, assuming fully developed flow, the momentum balance under equilibrium state leads to a linear dependence of the shear stress on the radial coordinate r for a given pressure gradient:

$$\begin{aligned} \tau =\frac{\nabla {Pr}}{2} \end{aligned}$$
(3)

Xanthan gum concentrated solutions exhibit high viscosities at low shear stresses (lower Newtonian plateau), shear-thinning behaviour at intermediate shear stresses and a low viscosity plateau at high shear stresses (upper Newtonian plateau) (Rodríguez de Castro et al. 2014, 2016). According to Eq. (3), the fluid is subjected to higher shear stresses in the larger pores. Therefore, concentrated xanthan gum solutions flowing through a porous medium at a constant pressure gradient \(\nabla {P}\) will be subjected to low shear stresses, that lie within the lower Newtonian plateau, in the small pores (high viscosity) while being subjected to higher shear stresses, outside this plateau, in the large pores. This is schematically represented in Fig. 1, where shear viscosity is plotted as a function of \(\nabla {P}\) for pores with different sizes \(({r}_{1}> {r}_{2}> {\cdots } > {r}_{7})\). From this figure, it can be deduced that the flow rate in all pores is negligible for \(\nabla {P}<\nabla P_1 \) (due to high viscosity values), while the fluid flows through all pores with low viscosity for \(\nabla {P}>\nabla P_3 \). For intermediate values of pressure gradient, e.g. \(\nabla {P}_2 \), the shear viscosity of the fluid is highly dependent on the pore size, which is similar to the case of an ideal yield stress fluid. Consequently, the success of xanthan gum polymer solutions as injected fluids in YSM tests will depend on their ability to exhibit high levels of viscosity at low values of \(\nabla {P}\) and a strong decrease in viscosity at intermediate values of \(\nabla {P}\).

Shear viscosity versus shear stress relationships are known to be strongly dependent on polymer concentration \({C}_{\mathrm{p}}\). For this reason, xanthan solutions with different polymer concentrations will be used in the following section to characterize the same porous material. This is expected to provide further insight into the choice of the \({C}_{\mathrm{p}}\) of the injection fluid.

Fig. 1
figure 1

Schematic representation of shear viscosity versus pressure gradient for the flow of xanthan gum-type polymer solutions through pores with different radii \(({r}_{1}> {r}_{2}>{\cdots } > {r}_{7})\). Negligible flow through all pores is generated for \(\varvec{\nabla } \mathbf{P}<\varvec{\nabla } \mathbf{P}_1\). Fluid flows with low viscosity through pores with \({r} >{r}_{3}\) for \(\varvec{\nabla } \mathbf{P}=\varvec{\nabla } \mathbf{P}_2 \) and through all pores for \(\varvec{\nabla } \mathbf{P}>\varvec{\nabla } {\varvec{P}}_3\)

Full size image

3 Materials and Methods

The robustness of YSM will be first tested in the case of numerically generated experiments. An ideal Herschel–Bulkley fluid with known values of \(\tau _0 , {k}\) and n will be numerically injected through a bundle of capillaries with known PSD so as to generate (\({Q}, \nabla {P}\)) data. Then, the YSM will be used to obtain the PSD from these (\({Q}, \nabla {P}\)) and a sensitivity analysis of the obtained PSD to errors in the rheological parameters will be performed. Also, a set of YSM laboratory experiments using xanthan gum solutions with different polymer concentrations are presented in order to assess the capacity of these fluids to approach the behaviour of a yield stress fluid.

3.1 Sensitivity Analysis of the Obtained PSD Versus \(\varvec{\tau }_0 \), \(\mathbf{k}\) and \(\mathbf{n}\)

Following the procedure presented by Rodríguez de Castro et al. (2014), a Herschel–Bulkley fluid with \(\tau _0 = 10\) Pa, \({k} = 1\hbox { Pa}\hbox { s}^{{n}}\) and \({n} = 0.60\) was numerically injected through a bundle of 1,000,000 capillaries whose radii are distributed according to the following bimodal probability density function: \({p}\left( {r} \right) =\frac{\omega _1}{\sqrt{2\pi \sigma _1^2 }}\hbox {e}^{-\frac{\left( {{r}-{m}_1} \right) ^{2}}{2\sigma _1^2 }}+\frac{\omega _2 }{\sqrt{2\pi \sigma _2^2}}\hbox {e}^{-\frac{\left( {{r}-{m}_2} \right) ^{2}}{2\sigma _2^2 }}\), which is a weighted sum of two normal laws with means \({m}_1 = 12~\upmu \hbox {m}\) and \({m}_2 = 24~\upmu \hbox {m}\), standard deviations, \(\sigma _1 = 3~\upmu \hbox {m}\) and \(\sigma _2 =6~\upmu \hbox {m}\), and weights \(\omega _1 = 2/3\) and \(\omega _2 = 1/3\). 50 different pressure gradients (N50) given by \(\nabla {P}_{{i}} =\frac{2\tau _0 }{{r}_{{i}} }\) with \({i} = (1, \ldots , {N}), {r}_{{i}} ={r}_{\max } -\frac{\left( {{r}_{\max } -{r}_{\min }} \right) }{\left( {{N}-1} \right) }\left( {{i}-1} \right) \), \({r}_{\min } ={m}_1 -3\sigma _1 \), \({r}_{\max } ={m}_2 +3\sigma _2 \) were imposed and the resulting flow rates were calculated using Eq. (2). The obtained \(({Q}_{{i}}, \nabla {P}_{{i}})\) data are provided in Fig. 2.

Fig. 2
figure 2

\(({Q}_{{i}}, \nabla {P}_{{i}})\) data corresponding to the numerical injection of a Herschel–Bulkley fluid with \(\tau _0 = 10\hbox { Pa}, {k} = 1\hbox { Pa s}^{n}\) and \({n} = 0.60\) through a bundle of 1,000,000 capillaries whose radii are distributed according to the original p(r). The upper axis represents the radii of the pores joining the flow at each \(\nabla {P}\) (smaller pores at higher \(\nabla {P}\))

Full size image

Then, YSM was applied to the \(({Q}_{{i}},\nabla {P}_{{i}})\) data using the correct values of \(\tau _0 \), k and n to calculate the PSD. The same \(({Q}_{{i}}, \nabla {P}_{{i}})\) data were also exploited with YSM using overestimated or underestimated values of \(\tau _0 \), k and n in order to assess the sensitivity of the obtained PSD on these input parameters. In other words, the (\({Q}_{{i}},\nabla {P}_{{i}})\) data deduced from the original set of rheological inputs were used to obtain the PSD assuming a different set of rheological inputs. In each test, only one of the three rheological inputs (\(\tau _0 \), k or n) contained an error, while correct values were used for the other two parameters. Erroneous yield stresses \(\tilde{\tau }_{0}\) with values \(0.7\tau _0 \), \(0.9\tau _0 \), \(1.1\tau _0 \) and \(1.3\tau _0 \) were tested. Likewise, erroneous consistencies \(\tilde{{k}}\) with values 1.1k, 0.9k, 1.3k and 0.7k, and erroneous flow indexes \(\tilde{{n}}\) with values 0.95n, 0.983n, 1.017n and 1.05n were used to exploit the \(({Q}_{{i}}, \nabla {P}_{{i}})\) data.

3.2 Experimental Setup and Procedure

In the present experiments, the injected fluids were xanthan gum solutions obtained by dissolving a certain amount of xanthan gum powder (Cargill 2013) in de-ionized and filtered water containing 400 ppm of \(\hbox {NaN}_{3}\) as a bactericide. Four solutions with polymer concentrations of 4000, 5000, 6000 and 7000 ppm were prepared at \(\hbox {pH} = 7\) using an overhead stirrer with blade impeller. The detailed procedure for preparing the xanthan gum solutions was described by Rodríguez de Castro (2014). During their preparation, the xanthan powders were progressively added to the water while stirring. Once all the powder was added, the solution was kept under moderate stirring (500 rpm) for a time period of 12–24 h depending on \({C}_{\mathrm{p}}\). After that, the fluid was stored at a temperature of \(4\,^{\circ } \hbox {C}\pm 1\) for 12 h and then degassed using a vacuum pump.

The experimental setup was the same as the one used by Rodríguez de Castro et al. (2014). In these experiments, each polymer solution was injected through a cylindrical core of Aerolith\(^\circledR \)10 (PALL Corporation, USA). The samples were cylindrical with a length of \({L} = 10\hbox { cm}\) and a diameter of \({D} = 5\hbox { cm}\). The two extremities of the cores were in contact with aluminium injector plates. Surfaces in contact with the porous medium were Teflon coated to prevent any ion exchange between the metal and the core. The lateral surface of the porous medium was coated with a non-wetting epoxy resin and then wrapped with epoxy-coated fibreglass to insure liquid imperviousness and mechanical strength. A differential pressure sensor (Rosemount 2009) was installed to measure the evolution of the pressure drop \(\Delta {P}\) between the inlet and the outlet of the porous media, and the corresponding pressure gradient was calculated as \(\nabla {P}=\frac{\Delta {P}}{{L}}\). The fluid was injected through the porous media at a controlled flow rate using a syringe pump (Harvard Apparatus 2012) and collected at the outlet using a vessel. Prior to saturation with xanthan gum solutions, the porous medium was saturated with degassed de-ionized and filtered water. Moreover, and to avoid bubble gas formation inside the porous medium, the polymer solution was also degassed under moderate vacuum.

A set of \({N}+1\, ({Q}_{{i}}\), \(\Delta {P}_{{i}})\) raw data were collected during each experiment, with \(N+1\) ranging from 39 to 53. The imposed flow rate during the injection of the solutions was steeply decreased, and the corresponding pressure drops were measured at the steady state using the pressure sensor. The time allowed for each measurement was optimized in order to minimize the possible polymer retention in the porous medium. The range of imposed flow rates was the same for all investigated polymer concentrations, covering from 2000 ml/h to 0.05 ml/h. The flow rates were slightly greater for the 4000 ppm solution since its lower viscosity generated lower pressure drops which were close to the limit of the working range of the pressure sensor. The relative standard deviation of the pressure drop measurements was 8% for \({Q}< 1\hbox { ml/h}\), 1% for \(1\hbox { ml/h}< {Q} < 150\hbox { ml/h}\) and 0.5% for \({Q} > 150\hbox { ml/h}\). The temperature of the lab was kept constant at \(20\,^{\circ }\hbox {C} \pm 0.1\) during all the experiments.

From these \(({Q}_{{i}}, \Delta {P}_{{i}})\) raw data, the procedure described in Sect. 2 was used to obtain the PSD of the investigated porous medium. An analogous sample of the same porous medium was also analysed by MIP using a mercury porosimeter (Micromeritics 2008). Only an intrusion cycle was performed in the MIP test.

3.3 Fluid Properties

Xanthan gum is a naturally non-toxic polysaccharide, commonly used as rheology modifier (Garcia-Ochoa et al. 2000; Abidin et al. 2012) especially in manufacturing food grade products (Palaniraj and Jayaraman 2011), as well as in polymer flooding technics for EOR (Jones and Walters 1989; Abidin et al. 2012). The chemical composition, structure and other physicochemical properties of xanthan gum macromolecules can be consulted elsewhere (Song et al. 2006; Garcia-Ochoa et al. 2000). In solution state, an isolated xanthan macromolecule is semirigid, with a contour length of typically 1 \(\upmu \hbox {m}\), a transverse size of approximately 2 nm (Rodd et al. 2000; Mongruel and Cloitre 2003; Iijima et al. 2007) and is usually modelled as a rod-like macromolecule (Chauveteau 1982; Milas and Rinaudo 1983; Carnali 1991; Lopez et al. 2003).

The shear rheology of the xanthan solutions used in the present experiments was characterized by means of a stress-controlled rheometer (ARG2 from TA Instruments) equipped with cone-plate geometry. All rheological measurements were taken at \(20\,^{\circ }\hbox {C}\) by applying shear stresses linearly sampled from 0 to a maximum value producing a shear rate of approximately \(1000\hbox { s}^{-1}\), which covered the range of shear rate experienced by the fluid in the porous medium (Rodríguez de Castro 2014).

The \(\tau \left( \dot{{\gamma }} \right) \) data were fitted to a Herschel–Bulkley law following the same procedure as Rodríguez de Castro et al. (2014, 2016). The measured rheograms and corresponding fits are displayed together in Fig. 3a. The same data were also plotted in terms of viscosity versus shear rate as shown in Fig. 3b. From Fig. 2, it is deduced that when polymer concentration is high, the viscosity at the lowest shear rates seems to diverge (within the considered shear rates interval) attaining very high values before drastically decreasing with increasing shear rates, thus approaching Herschel–Bulkley model. Therefore, the behaviour of the tested xanthan gum solutions is closer to that of an ideal yield stress fluid as \({C}_{\mathrm{p}}\) is increased. Consequently, the PSDs obtained by YSM are expected to be more accurate in the case of xanthan gum solutions with high values of \({C}_{\mathrm{p}}\). The values of \(\tau _0 \), k and n obtained from fitting the rheograms to a Herschel–Bulkley law are represented as a function of \({C}_{\mathrm{p}}\) in Fig. 4. It is observed that whereas \(\tau _0 \) and k are strongly dependent on \({C}_{\mathrm{p}}\), n is almost constant within the explored range of \({C}_{\mathrm{p}}\).

The uncertainty in the experimentally measured values of \(\tau _0\), k and n was also assessed for comparison with the results of numerical experiments presented in Sect. 3.1. For all the tested values of \({C}_{\mathrm{p}}\), the uncertainties corresponding to a 95% confidence interval were close to \(\pm ~4\%\) for \(\tau _0 \), \(\pm ~20\%\) for k and \(\pm ~4\%\) for n. This uncertainty was determined through evaluation of the goodness of fit of the measured rheogram to the reconstructed one (Herschel–Bulkley model with the obtained parameters).

Fig. 3
figure 3

a Rheograms for different polymer concentrations of the injected fluid. The symbols represent experimental data, and dashed lines represent the fitted curves using the Herschel–Bulkley model. b Effective viscosity versus shear rate. The symbols represent experimental data joined by continuous segments

Full size image
Fig. 4
figure 4

a Yield stress \(\tau _0 \), b consistency k and c flow index n for each \({C}_{\mathrm{p}}\) value

Full size image
Fig. 5
figure 5

PSDs obtained through application of YSM to the numerically generated \(({Q}_{{i}}\), \(\nabla {P}_{{i}})\) data using erroneous input values of a \(\tau _0\), b k and c n. Black symbols represent the PSD obtained using the correct values of \(\tau _0 \), k and n as inputs. Blue, red, green and purple symbols represent the PSDs obtained using erroneous values of \(\tau _0 \), k and n

Full size image
Fig. 6
figure 6

PSDs calculated using overestimated values of n for original PSDs with different standard deviations. Red symbols represent the calculated PSD using \(\hat{\mathbf{n}}= 1.033{ n}\). Black symbols represent the original PSDs, which are normal distributions with an average radius of 24 \(\upmu \hbox {m}\) and standard deviations of a 1 \(\upmu \hbox {m}\), b 2 \(\upmu \hbox {m}\) and c 3 \(\upmu \hbox {m}\), respectively

Full size image

4 Results

4.1 Numerical Experiments

As can be seen in Fig. 5, the PSDs obtained using the correct values of \(\tau _0 \), k and n are in good agreement with the original PSD. However, Fig. 5a shows that the errors in the values of the yield stress generate horizontal shifting of the obtained PSDs with respect to the original one. This shift is directed toward large pores in the case of overestimated \(\tau _0\) and toward small pores in the case of underestimated \(\tau _0\). However, the form of the PSD is conserved in all cases. From Fig. 5b, it can be deduced that errors in the value of k do not entail significant changes in the obtained PSDs. Nonetheless, it should be noted that even though no significant change in the probabilities \({p}({r}_{{i}})\) of each pore size class \({r}_{{i}}\) was observed, the calculated number of pores \({n}_{{i}}\) with each radius did change. Indeed, no change is detected in terms of probability due to normalization with the total number of pores \(({p}({r}_{{i}}) = {n}_{{i}}/\mathop {\sum }\nolimits _{{j}} {n}_{{j}} )\). This means that underestimation of k is compensated by a lesser number of pores, while overestimation of k is compensated by a greater number of pores.

Figure 5c shows that, unlike the previous cases, errors in n have a strong effect on the obtained PSDs, deforming it especially in the small pores region. This is explained by the fact that overestimation of n \((\hat{{n}}> {n})\) means underestimating the shear-thinning behaviour of the fluid. This leads to the underestimation of the contribution of large pores to the total flow rate at high flow rates, which is compensated by a greater number of small pores joining the flow at high pressure gradients. This results in an increasing shift of the calculated PSD with respect to the original PSD as the considered pore size decreases. Analogously, underestimation of n (\(\hat{{n}}< {n}\)) results in underestimation of the number of small pores as a result of the overestimated contribution of large pores to total flow rate at high pressure gradients. It should be noted that MIP presents an analogous drawback, but the largest pores are mainly concerned in this case. Indeed, large pores are not detected by MIP as this method is only sensitive to the largest openings toward pore bodies (Roels et al. 2001; Giesche 2006).

The sensitivity of the PSDs obtained by YSM to errors in n is strongly dependent on the dispersion of the pore sizes. This is shown in Fig. 6, in which overestimated values of n (\(\hat{{n}}= 1.033{ n}\)) are tested for Gaussian PSD with different standard deviations. It was observed that the more the PSD is dispersed, the more the YSM method is vulnerable to errors in n. Indeed, only moderate effects were reported for narrow PSDs. It is worth mentioning that even though the errors in the rheological parameters \(\tau _0 \), k and n may shift or deform the obtained PSD, this does not generate significant deviations of \(\alpha \) with respect to the case in which there is no error (\(\alpha \) very close to 1.07 in all cases).

4.2 Laboratory Experiments

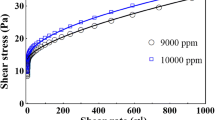
Figure 7 summarizes the experimental results obtained for all polymer concentrations \({C}_{\mathrm{p}}\) showing that, as expected, the more the solution is concentrated, the more the pressure loss is important for a given flow rate. It is recalled here that \(\Delta \)P is linked to \(\tau \) and likewise Q is linked to \(\dot{{\gamma }}\). Therefore, the \(\tau (\dot{{\gamma }})\) plot is similar to the \(\Delta {P}\) (Q) plot. Also, it is remarked that a threshold pressure exists in the case of yield stress fluids, below which there is no flow. However, there is not such a threshold pressure for real fluids with apparent yield stress. Instead, there is a pressure gradient below which the flow rate is negligible.

Fig. 7
figure 7

\(({Q}_{{i}}\), \(\Delta {P}_{{i}})\) raw data obtained from injection of xanthan gum solutions with different polymer concentrations through analogous samples of A10 sintered silicate

Full size image

The method presented in Sect. 2 was applied to the \(({Q}_{{i}}\), \(\Delta {P}_{{i}})\) raw data shown in Fig. 7. It is remarked that similar values of \(\alpha \) were obtained following the procedure presented by Rodríguez de Castro et al. (2016) for all tested polymer concentrations (\(\alpha \) is comprised between 1.2 and 1.4). The resulting PSDs expressed in terms of relative volume \({p}_{\mathrm{v}} \left( {{r}_{{i}} } \right) \) of pore classes of representative radii \({r}_{{i}} \) are displayed in Fig. 8, together with the PSD deduced from MIP for comparison. It is observed that even if the obtained PSDs are quite similar in all cases, the more the polymer concentration is high, the larger is the pore size corresponding to the peak of the PSD and the lesser is the deviation of the obtained PSD from that of MIP. As explained before, more reliable PSDs are expected for higher concentrations due to the closer approximation to a yield stress fluid behaviour. It is also remarked that the PSD obtained by YSM for \({C}_{\mathrm{p}} = 7000\hbox { ppm}\) is close to the one obtained by MIP for this material even if, strictly speaking, the quality of a PSD should not be assessed from its agreement with MIP.

Fig. 8
figure 8

Comparison between the PSD obtained with MIP (black symbols) and the PSDs obtained with YSM using different values of \({C}_{\mathrm{p}}\) (blue, red, green and purple symbols)

Full size image

5 Discussion

In Sect. 4.1, it was shown that the accuracy of PSD is mainly sensitive to errors in n, while the effects of the errors in \(\tau _0\) and k are much weaker. A potential solution to reduce the effects of errors in the determination of the value of n consists in the use of Bingham fluids, for which \({n} = 1\). Bingham model (Bingham 1916) can be written as:

$$\begin{aligned} \left\{ \begin{array}{ll} \tau =\tau _0 +{k}\dot{{\gamma }}&{}\quad \hbox {for }\tau > \tau _0 \\ \dot{{\gamma }}=0&{}\quad \hbox {for }\tau \le \tau _0 \end{array}\right. \end{aligned}$$
(4)

As can be observed in the preceding equation, only \(\tau _0\) and k are involved in the case of Bingham fluids, so the sensitivity of YSM to errors in n is expected to be lower when using this type of yield stress fluids. However, it is noted that most yield stress fluids present a certain degree of shear-thinning behaviour, so finding a real Bingham fluid can be challenging. Some examples of Bingham fluids can be found in the works of Bingham (1916) and Bernardiner and Protopapas (1994).

Despite the advantages of its simplicity, the classical bundle of capillaries model, which is also frequently used to exploit data coming from capillary pressure measurements in MIP, can be considered as a drawback of YSM. For a better description of the actual topology of the pore space, some improvements have been proposed in the literature and were reviewed by Malvault et al. (2017). In their recent work, Malvault et al. (2017) simulated the flow yield stress fluids through improved bundle of capillaries models to evaluate the effects of non-circularity of the cross section and its axial variation. These authors showed that a non-circularity only had a moderate influence on the flow rate versus pressure drop relationship. In contrast, the latter authors observed that the onset pressure gradient obtained in capillaries with varying cross section was increased with respect to capillaries having a constant cross section equal to the minimum constriction of the pores with axial variation. The inclusion of this effect in YSM is expected to result in higher accuracy of the PSDs obtained from laboratory experiments and must be the scope of future work.

Given that the uncertainty on the experimental determination of n was estimated to be ± 4% (95% confidence interval), one may argue that the PSD obtained from laboratory experiments might be deformed in the same manner as shown in Fig. 5c for numerical experiments. However, it should be noted that the PSD of the A10 sintered silicates investigated here was quite narrow and had only one peak. Therefore, the sensitivity of the PSDs obtained with YSM to errors in n is expected to be lower than in the case of the numerical tests for the reasons presented in Sect. 4.1. In order to go further, flow indexes \(\tilde{{n}}\) with values of 1.05n and 0.95n (where n is the flow index obtained through fitting of the rheograms as explained in Sect. 3.3) were also used to exploit the \(\left( {{Q}_{{i}} ,\Delta {P}_{{i}} } \right) \) raw data presented in Fig. 7. The resulting PSDs are displayed in Fig. 9, showing only slight differences when n is increased or decreased by 5%, especially for the highest values of \({C}_{\mathrm{p}}\).

Fig. 9
figure 9

PSDs obtained with YSM for a \({C}_{\mathrm{p}} = 4000\hbox { ppm}\), b \({C}_{\mathrm{p}} = 5000\hbox { ppm}\), c \({C}_{\mathrm{p}} = 6000\hbox { ppm}\) and d \({C}_{\mathrm{p}} = 7000\hbox { ppm}\) using different values \(\tilde{{n}}\) of the flow index: \(\tilde{{n}} = {n}\), \(\tilde{{n}}=1.05{ n}\) and \(\tilde{{n}} = 0.95\hbox { n}\), with n being the flow index obtained through fitting of the rheograms for each fluid

Full size image

6 Summary and Conclusions

In this work, the robustness of YSM method was investigated in order to evaluate its experimental feasibility in the case of real laboratory experiments. In particular, the sensitivity of the obtained PSDs to the use of pseudo-yield stress fluids and errors in the rheological inputs of the method was analysed. Also, the effects of polymer concentration on the expected accuracy of the PSD were assessed.

Differences between ideal and pseudo-yield stress fluids as aqueous xanthan gum solutions were discussed in terms of their shear viscosity dependence on shear rate. It was concluded that concentrated polymer solutions emulate better the yield stress fluid behaviour due to their high viscosity values at low shear rates. Given that the shear rate to which the fluid is subjected decreases with decreasing pore size, the high viscosity levels at low shear rates presented by concentrated solutions lead to negligible flow rates in the small pores, behaving similarly to a yield stress fluid.

A set of laboratory experiments was carried out in order to characterize the PSD of a synthetic porous medium with YSM using xanthan gum solutions with different polymer concentrations, \({C}_{\mathrm{p}}\), and the results were compared to the PSDs obtained by MIP. As expected, better agreement between both methods was observed for the highest values of \({C}_{\mathrm{p}}\).

Numerical experiments were performed to evaluate the sensitivity of the PSDs obtained by YSM to the input rheological parameters. The results of these experiments showed that the accuracy of PSD is mainly sensitive to errors in the flow index, n, while the effects of the errors in the yield stress, \(\tau _0 \), and consistency, k, are moderate. The effects of errors in n were also observed to be weaker in the case of narrow PSDs with only one peak, as the one experimentally characterized in the present laboratory experiments. A potential solution was proposed, consisting in the use of Bingham fluids with only \(\tau _0 \) and k as rheological inputs.

The results of the present work permitted to gain further insight into the choice of the injection fluid, the robustness of YSM and its efficacy as an alternative non-toxic porosimetry method.