Non-linear viscoelasticity and temporal behavior of typical yield stress fluids: Carbopol, Xanthan and Ketchup

Abstract

The viscoelastic properties of yield stress fluids are difficult to measure outside the linear viscoelastic regime, in particular above their yield stress. These properties are investigated for several common yield stress fluids using inertio-elastic oscillations. From this coupling between the instrument’s inertia and the viscoelasticity of the materials, the complete simple shear rheology can be determined, including viscoelasticity under flow. Findings show that the tested materials have an almost constant elasticity below and above the yield stress, even for applied stresses several times larger than the yield stress. Moreover, the temporal behavior of the materials is unambiguously determined. Concentrated Xanthan is shown to be thixotropic, while Ketchup mainly shows retarded viscoelasticity. Carbopol does not show long-term temporal dependance but apparently exhibits fracturation.

Introduction

Yield stress fluids are materials that can behave both like liquids and solids, depending on the applied stress. On the one hand, when the applied stress is low enough, these materials behave like soft elastic solids while, for large enough stresses, they flow like liquids. This kind of behavior is very interesting from an industrial point of view as the solid behavior corresponds to the products stability and durability while the liquid behavior allows the application of processes such as sterilization or mixing. In the latter situations, as the material flows, it behaves as a fluid which may have elastic properties. As a consequence, since elasticity influences strongly flow characteristics such as the existence and extension of secondary flows, the promotion or quenching of instabilities, it will control in a large part the material behavior in the process.

So, not only the yield stress and shear thinning properties but also the viscoelasticity of yield stress fluids may play an important role in their industrial processing as it directly influences the design, efficiency and properties of those processes. However, the determination of the viscoelastic properties of those materials in both solid and fluid regimes is no simple task as it corresponds to determining their complete non-linear viscoelastic properties. The central problem, as explained in detail by Yao et al. (2008) is that most rheometrical methods (such as the Large Amplitude Oscillation) designed to determine these non-linear properties are ad-hoc extensions of linear methods, whose relevance is, at best, questionable. Besides, the most appropriate method, consisting of small amplitude oscillation around a flow rarely work in our case, precisely because of the irreversible flow that occurs as soon as the yield stress is overcome. Consequently, non-linear viscoelastic data for yield stress fluids are rare.

Recently however, a method has been proposed that can be used for this task. Indeed, the determination of the linear viscoelastic properties of materials using controlled stress oscillations generates apparatus inertia effects which must be closely analysed to obtain the true material properties (Krieger 1990; Franck 1992). These effects can be thought of as an experimental limitation or as a useful tool for the characterization of materials (e.g. Struik 1967; Roscoe 1969; Zolzer and Eicke 1993). Baravian and Quemada (1998) devised a method called “inertio-elastic oscillations” that allows to determine the non-linear behavior of complex fluids in the solid regime. More recently, Baravian et al. (2007) compared this method with dynamical oscillations experiments. The inertio-elastic method appeared to be the more reliable method because of the resonance effect generated in the oscillations measurements. Finally, Yao et al. (2008) compared several rheometrical methods used to determine the non-linear viscoelastic behavior of fibrin gels. They showed that the method using inertio-elastic oscillations not only allows to determine the appropriate material properties, but is also the most straightforward and accurate method. Interestingly Yao et al. (2008) also underline that the oscillations occur in sufficiently short time spans so that the measurements can be made before structural changes occur.

In the present work, using the above strong foundations, we investigate the non-linear viscoelastic properties and the temporal behavior of several common yield stress fluids (Carbopol 940 at 0.3%, Xanthan at 2% and Ketchup). Our aim is to show that very simple creep experiments can provide an extensive characterization of the simple shear rheology of these complex materials. By applying successive creeps, the viscoelastic behavior of the material as well as its temporal dependence can be described both below and above yield. First, we present the modelling of the interaction between the viscoelasticity and the apparatus inertia used to analyse the experimental data. Then, we expose the experimental system and the measurement methods. Finally, we present and discuss the results.

Theory

Coupling between the instrumental inertia and the fluid’s viscoelasticity

The equation of motion of the mobile part of the rheometer can be expressed as (Krieger 1990):

$$\label{eq0} I\cdot{\ddot D}=\Gamma_{app}-\Gamma_{felt} $$

(1)

I is the moment of inertia of the mobile part, D its angular displacement. Γ _app and Γ _felt are respectively, the torque applied by the rheometer and the torque felt by the materials.

By assuming that shear is homogeneous in the gap, Eq. 1 can be written as:

$$\label{eq1} \alpha \cdot {\ddot \gamma}= \sigma_{app}-\sigma_{felt} $$

(2)

with $\alpha=I\frac{F_{\sigma}}{F_{\gamma}}$ where γ is the deformation, σ _app and σ _felt are respectively the shear stress applied by the rheometer and the shear stress felt by the material. The parameter α is the inertia parameter and involves not only the moment of inertia of the mobile part, but also the shear stress and the shear rate geometrical factors F _σ and F _γ of the used geometry.

Locally linear viscoelastic model

Figure 1 shows an example of the evolution of the measured strain for two successive creep measurements. These curves are taken in the middle of a rheometrical procedure that will be described in part (Fig. 5). At this moment of the experiment, the applied stresses is about twice the yield stress.

Fig. 1

Strain response for two successive creeps at 44 Pa and 48 Pa for the Carbopol solution (0.3%). Both stresses are about twice the yield stress

As already discussed by Baravian et al. (2007) and Yao et al. (2008), the strain oscillations of Fig. 1 are of small amplitude relative to the total strain experienced by the material. Those perturbations are actually small enough to be well described by a linear approximation of the complete constitutive equation. So, the behavior of the material can be described using this method as long as this locally linear approximation is valid. This supposes that the actual changes in shear stress are close to quasi static. Experimentally, if the shear stress steps are too large, a locally linear model does not describe the data well. Thus it is simply a matter of designing the experiment so that this condition is satisfied.

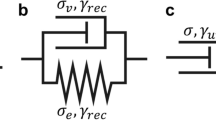
Finally, we choose to describe the materials by a Jeffrey model (see Fig. 2), as it is the simplest model able to describe the behavior of a viscoelastic material which may be dominated either by its elastic or viscous behavior. This model has two viscoelastic characteristic times η ₁/G and η ₂/G with η ₁/G ≪ η ₂/G:

$$\label{eq2} \eta_{2}(\sigma)G(\sigma)\dot{\gamma}{\kern-1pt} +{\kern-1pt}\eta_{1}(\sigma) \eta_{2}(\sigma) \ddot{\gamma}{\kern-1pt}={\kern-2pt}\left(\eta_{1}(\sigma){\kern-1.5pt}+{\kern-1.5pt}\eta_{2}(\sigma)\right)\dot{\sigma}{\kern-1.5pt}+{\kern-1.5pt}G(\sigma) \sigma $$

(3)

Fig. 2

Diagram of the Jeffrey model

Equations of motion

The coupling between instrumental inertia (Eq. 2) and the fluid’s viscoelasticity described by the Jeffrey model (Eq. 3), allows one to obtain the following motion equation of the material:

$$ \begin{array}{lll}\label{eq3} &&{\kern-6pt} \underbrace{\alpha\left[\left(\eta_{1}+\eta_{2}\right)\dot{\ddot{\gamma}}+G\ddot{\gamma}\right]}_{inertia}+\, \eta_{2}G\dot{\gamma}+\eta_{1}\eta_{2}\ddot{\gamma}\\ &&{\kern6pt} =\left(\eta_{1}+\eta_{2}\right)\dot{\sigma}_{app}+G\sigma_{app} \end{array} $$

(4)

The Eq. 4 is composed by an inertia term, involving not only the inertia parameter, but also the viscoelastic parameters. Once the form of the applied shear stress is defined for a given experiment, Eq. 4 can be solved, giving an analytical solution.

Analytical solution for successions of creep experiments

Creep experiments consists of sudden changes in the applied torque. A schematic representation of a creep is plotted on Fig. 3.

Fig. 3

Creep of the nth step

Thus, Eq. 4 is solved with:

$$\label{eq4} \sigma_{app}(t)=\sigma_{n-1}+\Delta\sigma_{n}.h(t) $$

(5)

where Δσ _n  = σ _n  − σ _n − 1; where σ _n and σ _n − 1 are respectively the shear stress applied at the n ^th and (n − 1)^th creep steps; h(t) is the Heaviside distribution function.

The solution is:

$$\begin{array}{lll}\label{eq5} \gamma_{n}(t)&=& \sigma_{n-1}\left[-\frac{2\lambda}{B\eta_{2}}+\frac{t}{\eta_{2}}\right.\\&&+\left.e^{-\lambda t}\left(\frac{2\lambda}{B\eta_{2}}cos(\omega t)+\frac{\lambda^{2}-\omega^{2}}{B\eta_{2}\omega}sin(\omega t)\right)\right] \\ &&+\, \Delta\sigma_{n}\left[-\beta+\frac{t}{\eta_{2}}\right.\\&&+\left.e^{-\lambda t}\left(\beta cos(\omega t)+\frac{\lambda}{\omega}\left(\beta-\frac{1}{\lambda \eta_{2}}\right)sin(\omega t)\right)\right] \\ &&+\, \dot{\gamma}_{n-1}\left[\frac{2\lambda}{B}+e^{-At}\left(\frac{2\lambda}{B}cos(\omega t)\right.\right.\\&&+\left.\left.\left(\frac{1}{\omega}-\frac{2\lambda^{2}}{\omega B}\right)sin(\omega t)\right)\right] \end{array} $$

(6)

with: $\beta=\frac{1}{B}\left(\frac{2\lambda}{\eta_{2}}-\frac{1}{\alpha}\right)$, $B=\frac{\eta_{2}G}{\alpha(\eta_{1}+\eta_{2})}$, $\lambda=\frac{\alpha G+\eta_{1}\eta_{2}}{2\alpha (\eta_{1}+\eta_{2})}$ et $\omega=\sqrt{\frac{\eta_{2}G}{\alpha (\eta_{1}+\eta_{2})}-\lambda^{2}}$ for:

$$G\geq\frac{2\eta_{2}^{2}}{\alpha}\left(1+\frac{\eta_{1}}{2\eta_{2}}+\sqrt{1+\frac{\eta_{1}}{\eta_{2}}}\right).$$

In general, a creep experiment leads to inertio-elastic oscillations at short times, when the elasticity is sufficient (Zolzer and Eicke 1993; Baravian and Quemada 1998; Baravian et al. 2007). It is the case for all materials studied here. Fitting this model to the temporal strain data gives the three viscoelastic material properties η ₁, η ₂ and G as a function of the applied stress.

Experimental system and materials

Materials

Three typical yield stress materials are studied: Ketchup, Carbopol 0.3% and Xanthan 2%.

The Ketchup solution is an industrial product (Vitahiour), mainly made of tomato puree (see Iseki et al. 2001). The Carbopol gel (Carbopol 940 provided by BF Goodrich) was prepared at 0.3%, using magnetic agitation, in demineralized water. It was progressively neutralized at pH = 7 with NaOH solution (during 1-h agitation). The prepared solution was kept at rest at room temperature for 4 days. For details about Carbopol solutions structures and properties, see e.g. Piau (2007). The Xanthan (a natural polysaccharide) used in this study, was obtained from Skw Biosystems. The powder was diluted to 20 g/l (2%), in salted demineralized water with 0.1 mol/l of NaCl. The solution was prepared using magnetic agitation, and was heated at 80°C during 1 h. In order to hydrate and cool the polymer, the prepared solution was kept at rest at room temperature for more than 12 h prior to conducting the rheological measurements, see Song et al. (2006). To avoid degradation of both Carbopol and Xanthan solutions (development of bacteria), a few drops per liter of Formaldehyde (37%) solution were added.

All measurements are taken at 20°C.

Measurement techniques

The viscoelastic properties of the materials were measured using a controlled stress rheometer (AR 1000) and a six-blade vane geometry with an external cylinder (R _e  = 24 mm). The vane is used to reduce the wall effects (slip) (see e.g. Sherwood and Meeten 1991) and requires a specific calibration procedure to determine the shear rate and shear stress average geometric factors (respectively F _σ and F _γ ). The procedure, described in detail in Baravian et al. (2002) gives an equivalent radius of R _i  = 10.4 mm and an equivalent height of H = 44.7 mm. The inertia of the rotating part of the rheometer (shaft + geometry) was measured using the build in procedure of the rheometer.¹

Rheological methods and procedures

The materials we intend to study call for specific precautions as they can be time dependent. In other words, they generically show memory effects such as thixotropic, aging or retarded viscoelastic behaviours. However, if rheological properties are to be determined univocally they should not depend on the (eventually unknown) material shear history. Thus a prerequisite to determine the material properties is to obtain at least one steady state, steady state which will reset the material memory and set a “zero” time. A steady state, for a given material and rheological experiment, is defined as a state for which not only the macroscopic (shear stress and shear rate) fields are constant, but also all the internal viscoelastic and structural variables. Thus, the only way of verifying that a steady state has been achieved is to check directly the absence of influence of previous shear history, that is to perform the same experiment several times and look whether or not the results are identical.

Procedure

Steady state and reversibility test

Before applying any rheometrical procedure, a steady state test is carried out on the material under study. This determines how a steady state can be obtained, and also allows to check how reversible the material actually is. Indeed, physical, chemical or biological phenomena (evaporation, settling, coalescence, ripening, bacterial growth) always affect the material in amounts that need to be quantified.

To this end, four identical creeps were applied (see Fig. 4a), each creep lasting for 1 min. This test was performed with applied stresses both above and below the yield stress. The first creep is used to reset the memory of the material. If it is long enough so that a steady state is obtained, the three next creep steps should give identical results. This is indeed the case (see an example in Fig. 4b as for each material, the viscosity between the first and the third creep changes by 20% at most for one sample, a value which we set as our arbitrary limit for reversibility. This criterion is a balance between the irreversible evolution of the material and the already very large time it takes to perform the experiments.

Fig. 4

a Reversibility test: three creeps applied for one sample of material. b Response of three identical creeps applied for one sample of Ketchup for σ ≺ σ _y and σ ≻ σ _y

Since all three creeps are identical (within our criterion), this means that the material properties are indeed independent of the material history, and thus that the initial creep was applied for a sufficiently long time so that a proper steady state was found.

Also, as the results are reproducible over the complete duration of the experiment, we consider that the samples of the materials used here were reversible, for experiments lasting no more than 1 h (Fig. 4b).

Reference state

Prior to any measurement, the material shear history is reset. For this, the procedure to obtain the steady state as determined above is first applied to the material, which is then allowed to rest during 5 min, while the material’s structure may reconstitute itself. This time corresponds to a time for which the materials have recovered most of their elastic modulus (data not shown). The reference state corresponds to the state of the material at the end of this rest period (Fig. 4a). We begin the rheometry procedure starting from this state.

Rheometry procedure

Successions of creep steps are used starting from the above reference state. The duration of each creep is 1 min. The first creep is applied starting from rest. For the next creep step, the stress is abruptly changed (4 Pa for Carbopol and Ketchup, and 2 Pa for Xanthan) without stopping the vane rotation. The succession of creep experiments is applied in ramp-up (rise) and ramp-down (descent), to evaluate the temporal dependence of the material (Fig. 5).

Fig. 5

Procedure of characterisation

Determination of the materials’ properties

Viscoelastic properties

The viscoelastic parameters (G, η ₁, η ₂) (which depend only on the stress) are determined by fitting the theoretical curve Eq. 6 to the experimental measurements (Fig. 6) during the two first seconds for each creep, which is longer than the time necessary for the oscillations to dissipate. For time scales smaller than 2 s, the material internal structure has not changed, while, for longer times, retarded viscoelasticity and/or thixotropic effects can occur.

Fig. 6

Creep experiment for a Carbopol 0.3% at 48Pa applied stress. This is the same curve as in Fig. 1. Adjustment of Eq. 6: G = 433,2Pa, η ₁ = 1.7Pa.s, η ₂ = 4143Pa.s

Also, the usual steady state viscosity is determined at the end of each creep by calculating the ratio of the applied stress to the measured shear rate, averaged over a few seconds. To differentiate between the viscosity calculated from the Jeffrey model (η ₂) and this usual viscosity, we call the latter the “long-time viscosity” ($\eta_{long-time}=\sigma/\dot{\gamma}$).

Yield stress estimations

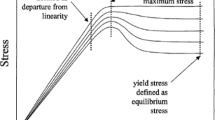
There are many definitions of the yield stress depending on the community of the writer, on the type of material studied and even on the performed experiments (stress versus strain-controlled experiments). Some even doubt its very existence (see eg. Barnes 1999). While we have no intention of refuelling this long-lived debate (see eg. Piau 2007), we recently showed that the concept of yield stress seems ill defined as it depends strongly on the shear step duration, even for non thixotropic materials (Caton and Baravian 2008). As a consequence, we will use down to earth definitions of the yield stress. In the following, the yield stress corresponds to the apparent viscosity divergence. It is simply the stress above which we can detect apparent flow, the important words being here “detect” and “apparent”.

For stresses lower than the yield stress, the material behaves like an elastic solid which means that a Kelvin–Voigt model is sufficient to describe this viscoelastic behavior. For stresses larger than the yield stress, since the material flows, the Kelvin–Voigt model cannot be fitted to the data anymore and it is necessary to use a Jeffrey model to describe its viscoelastic behavior. We define the “short time yield stress” as the stress at which the fit using the Jeffrey model is visually better than the one using the Kelvin–Voigt model.

A “long-time yield stress” was also estimated. It corresponds to the stress for which the long-time viscosity η _{long − time} becomes non-measurable. This instrumental detection limit with the used geometry occurs when the shear rate is smaller than $\dot{\gamma}_{limit}=10^{-6} s^{-1}$, which gives a limit of $\eta_{limit}=10^{6} Pa.s$. In practice, the long-time yield stress is the stress at which the measured viscosity becomes larger than this apparatus limit. The difference between the short-time and long-time yield stresses is represented by the gray zone in Figs. 8, 9 and 10.

Finally, it is clear that in both cases the definition is not absolute, as it depends on the quality of the instrument used for the experiments, on the duration of the measurement, and on the definition of yield stress we choose.

Results and discussion

Prior to describing non-linear visoelastic results, we compare the linear viscoelastic behavior deduced from creep experiments to that obtained from oscillations in the linear regime. This comparison is shown for Carbopol 0.075% only, data extracted from our previous article on a similar topic (Baravian et al. 2007).

Linear viscoelasticity of Carbopol 0.075%

In Baravian et al. (2007), we compared the inertio-elastic technique to standard oscillations measurements analysed either using the rheometer software, or by fitting the complete analytical solution for forced oscillations to the experimental data (see Baravian et al. (2007) for details). We plot in Fig. 7 an alternative way of displaying those data. We show the usual G’ G” data, the circles representing G’, while the squares represent G”. The big symbols represent the standard analysis implemented in the AR1000 rheometer, while the small symbols are the values calculated from the fit of the strain data of the oscillations. The lines correspond to G’ and G” values calculated from the values of η ₁, eta ₂ and G obtained from the fit of the creep steps. The first observation is that there is a good agreement between the three methods on two decades of frequency. A more detailed look at the graph shows that the standard method gives unreliable results at high frequency while the linear behavior deduced by fitting the complete solution for either oscillations or creep steps are almost identical. Finally, it also shows that the two modes of the Jeffrey’s model are sufficient to describe the material on two decades of frequency.

Fig. 7

G’ (circles) and G” (squares) as a function of applied frequency. Big symbols correspond to the standard analysis of the oscillations using TA instrument software, small symbols to the fit of the full waveform of the oscillations and the lines to the calculus from the rheological parameters deduced from creep experiments

We will now present the results obtained in the non-linear regime from the analysis of the creep experiments for the three materials (Carbopol, Xanthan and Ketchup). As ramp-up followed by ramp-down creeps were performed, not only the steady-state properties, but also the quantitative temporal behavior of the materials will be described.

Carbopol 0.3%

As the careful reader will have already noticed on Figs. 1 and 6, the elasticity of yields stress fluids does not disappear above the yield stress. On those graphs, while the applied stress is more than twice the yield stress, the elastic modulus is clearly not zero as oscillations are observed at the beginning of creep (σ _n  = 48Pa, σ _n − 1 = 44Pa), even though the material was already flowing during the previous creep (the tool is not stopped between the successing creeps). We will now expose in detail the results for each material, starting with the Carbopol solution.

Neutralized Carbopol solutions are considered to be “model” yield stress fluids. As such, their flow curves have been extensively studied in relation with the Yield Stress Controversy embodied in the papers by Barnes (1999) and Piau (2007). Given our definitions, the short-time yield and long-time yield stress for Carbopol (Fig. 8c) are respectively 26 Pa and 16 Pa, which is a quite large difference (approximately 40%). This difference is almost identical to the one found when varying the duration of the creep steps in Caton and Baravian (2008), confirming the dependence of the yield stress evaluation on the experiment duration.

Fig. 8

Successing creep in rise and descent for Carbopol 0.3%: a Elastic modulus G, b Elastic dissipation η ₁, c Viscosity η ₂ and η _{long − time} obtained at the end of creep

When the applied stress is larger than 60 Pa (more than twice the apparent yield stress), we observe a typical shear thinning fluid behavior, the viscosity η ₂ decreasing by almost three orders of magnitude while the stress increases by 40 Pa. Interestingly, the short-term and the long-term viscosity are perfectly superimposed in this whole region, and are exactly the same in the ramp up or ramp down experiments. This shows clearly that this material bears no temporal dependence of its material properties in this region. In other words, it shows no thixotropy nor retarded viscoelasticity which explains partly why it is so commonly used in the industry. As soon as the applied stress is large enough the material loses any memory of previous shear history and behaves like a pure viscoelastic fluid.

The region between the yield stress and 60 Pa is very interesting also. It shows a plateau with the long-term viscosity being the same on rise and descent, while the short term ramp up shows a significant difference. As the apparent viscosity seems to increase with time as stress is increased (ramp up), this cannot be explained by a thixotropic behavior. As there is no difference between the short and long time viscosities, this can neither be explained by retarded viscoelasticity. This behavior maybe due to shear localisation or fracturation at ramp up. For ramp down, as the material was already flowing it does not need to be fractured. This is consistent with the behavior observed for Carbopol by Bertola et al. (2003). This shows that the quantity of embedded information in the creep experiments is quite remarkable and fairly easy to interpret.

Finally, the elastic modulus of the Carbopol solution under study is quite large at 250Pa i.e. roughly ten times the yield stress. As suggested above, Fig. 8a shows that the elasticity modulus G remains constant even under a stress much more important than the yield stress. The elasticity, far from disappearing when the material starts to flow, stays remarkably constant. This constancy may be traced down to its microscopic origin, suggesting that this material is build up from elastic microscopic objects as has been shown independently by Piau (2007). At the same time, Fig. 8b shows that the elastic dissipation η ₁ is almost constant and even increases a little for strong stresses which is also compatible with the above microscopic description. However those results are incompatible with the usual vision of structured fluids as made of networks that are progressively broken down by shear as the total elasticity of the system should decrease with increasing stress. It asks for more detailed investigations of the shear induced solid-liquid transition for this material.

Xanthan 2%

Since Xanthan is a natural product, it is very widely used in the food industry as a thickener. In the research community it is also used as a model material because of its birefringent properties. Although dilute solutions are known to be shear thinning, the concentrated suspension studied here clearly exhibits a yield stress comprised between 8 Pa (long-term) and 13 Pa (short-time), once more a 40% difference. Like the Carbopol, the behavior of Xanthan close to the yield stress is quite complex, but does not seem to show a plateau, i.e. shear localization or fracturation phenomena, in agreement with Song et al. (2006). Xanthan is also a very shear thinning fluid as the viscosity decreases by three orders of magnitude while the stress increases by only 40 Pa.

Figure 9c shows that, unlike Carbopol, the different viscosity curves are not superimposed, which means that this material is time dependent. Indeed, for a given stress, the viscosity at short times η ₂ is larger than the viscosity at long times η _{long − time} in rise, and the viscosity at short times η ₂ is smaller than the viscosity at long times η _{long − time} in descent. Further, viscosities at long time respectively at the rise and the descent tend to the same value. This clearly indicates a thixotropic character of the Xanthan solution, the viscosity at the begining of the step being higher (smaller) than the long time viscosity for rise (descent) experiments. The creep lasting for a minute, we can deduce that the thixotropy time is smaller than this, probably of a few tens of seconds. This behavior could be analysed in detail by using the creep curves, but is outside the scope of this article. Concerning its viscoelastic properties, Fig. 9a shows, once more, that the elasticity modulus G remains constant even under a stress much more important than the yield stress, Fig. 9b shows that the elastic dissipation η ₁ is almost constant and increases a little for increasing stresses. This suggests again that this material is made of fairly large blobs that slowly deform and/or orient under stress.

Fig. 9

Successing creep in rise and descent for Xanthan 0.2%: a Elastic modulus G, b Elastic dissipation η ₁, c Viscosity η ₂ and η _{long − time} obtained at the end of creep

Ketchup

Ketchup is a very interesting material as it is very often used to demonstrate the interplay between yield stress and thixotropy effects.

Figure 10c shows clearly that Ketchup does have a yield stress, albeit quite small as we found that it lies between 4 and 9 Pa (long-time and short-time, respectively). Unlike the two previous materials, its behavior close to the yield stress is straightforward and uncomplicated. It is also a shear thinning material, as its viscosity decreases by two orders of magnitude while the stress increases by 60 Pa.

Fig. 10

Successing creep in rise and descent for Ketchup: a Elastic modulus G, b Elastic dissipation η ₁, c Viscosity η ₂ and η _{long − time} obtained at the end of creep

Its temporal behavior is quite different from the two situations encountered previously. Indeed, the viscosity at short times η ₂ in rise is the same as in descent. Similarly, the viscosity at long times η ₂ in rise is the same as in descent. Thus, the Ketchup used in this study is not thixotropic.

However, it is clear in Fig. 10c that the viscosity at short times η ₂ is always smaller than viscosity at long times η _{long − time} in both rise and descent. This can be interpreted as a retarded (slow) viscoelastic behavior. Its time scale is much larger than the viscoelastic characteristic time (t ≻ η ₂/G) accessible with the Jeffrey model. This effect of retarded viscoelasticity will always lead to an underestimation of the viscosity η ₂ both for rise and descent experiments.

Finally, Fig. 10a and b shows respectively that the elasticity modulus G and the elastic dissipation η ₁ change little even under a stress much more important than the yield stress. Again this suggests that the material is a suspension of soft objects which are not destroyed by the shear applied in the present experiments.

Conclusions

First, the simple shear viscoelastic properties of three different yield stress materials were determined using the creep mode of control stress rheometers and an appropriate modelling of the interaction between the viscoelasticity of the material and the rheometer’s inertia. The first result of this study is that the elastic modulus and the elastic dissipation of those yield stress fluids stay almost constant for applied stresses up to several times larger than the yield stress. Recent results show that other materials do not show the same behavior. For instance, AOT lamellar phases show a decrease of their elasticity as the stress is increased through the yield stress (Auffret et al. 2009). This suggests that the measured elasticity is intimately related to the (visco)elasticity of the suspended objects.

The second main result is that this method allows to determine a yield stress which is reasonable while showing clearly that such a concept is not absolute, but experiment dependent.

Finally, another asset of this method is that the viscoelastic determination is almost instantaneous as only a few oscillations are needed, which usually amount to 1 s. Thus, this method allows in a straightforward fashion to observe directly the temporal behavior of those materials by comparing the measured viscosities at (at least) two different times. So, it allows to discriminate between thixotropic, retarded viscoelastic and inhomogeneous (fracturing) behaviors.

As such, it appears to be a tool of choice to study yield stress materials, and to investigate in detail the shear-induced solid liquid transition.