1 Introduction

Pore size distribution influences the distribution of fluids and capillary pressures inside a porous medium, its permeability, particles retention, solute dispersion, etc. As a consequence of the interest in PSD of porous media, engineers and researchers have developed techniques for its determination, each of them having particular advantages and drawbacks. For example, recent advances provide improved spatial and temporal resolution for microtomography (Lindquist and Venkatarangan 2000; Burlion et al. 2006; Prodanovic et al. 2006, 2007; Wildenschild and Sheppard 2013). At present, multiphase flow and displacement can be quantified with this non-destructive technique, regardless of whether the images contain two or more phases. However, several obstacles have not yet been overcome, among which are resolution (\({\sim } 1\,\upmu \hbox {m}\)) and reliable segmentation of the images. Moreover, acquisition and image construction times are still too long and some materials cannot be characterized. Other methods are convenient to obtain PSD of macroporous materials (\({>}50\,\hbox {nm}\)), but they are often time-consuming and require meticulous preparation as in water-desorption calorimetry (Rouquerol et al. 2012).

Nowadays, mercury porosimetry is the most widespread technique to determine pore size distribution of porous media (Giesche 2006). Some of its advantages are the broad range of attainable pore sizes (\({\sim } 3.5\,\hbox {nm}\)–\(300\,\upmu \hbox {m}\)), the relatively short duration of the test (\({\sim } 3\,\hbox {h}\)) and the popularity of a well-established method that is recognized as the reference one. However, this technique presents several drawbacks including toxicity of the employed fluid and low performance for unconsolidated porous media. Furthermore, the new international legislation that will be applicable following the ratification of the Minamata Convention on Mercury in October 2013 is intended to ban or severely restrict the use of mercury porosimetry. For that reason, the IUPAC (International Union of Pure and Applied Chemistry) recently appealed to the international scientific community (Rouquerol et al. 2012) emphasizing the interest and the need to develop new effective and non-toxic porosimetry methods.

The most likely outcome of the decline of mercury porosimetry is that 3D microtomography becomes the dominant technique to obtain PSD. However, there is an absence of alternatives during the years ahead until microtomography reaches full development in terms of resolution and cost. In this context, the objective of the present work is to answer the following question: Is it possible to develop a simple, efficient and non-toxic method to characterize porous media in terms of their pore size distribution?

To answer this question, the starting point is the work of Ambari et al. (1990), who proposed the theoretical basis of a new data analyzing method to derive the PSD from the flow rate Q measurements as a function of the pressure gradient \(\nabla {P}\) when a yield stress fluid is injected through a bundle of parallel capillaries whose radii are distributed following a specific distribution (PSD). On the grounds of these theoretical considerations, the basis of the yield stress fluids method (YSM) to obtain the PSD of a porous medium from laboratory experiments was recently presented by Rodríguez de Castro (2014) and Rodríguez de Castro et al. (2014). It relies on considering the extra increment of Q when \(\nabla {\textit{P}}\) is steeply increased, as a consequence of the pores of smaller and smaller radius that are newly incorporated to the flow. In these works, Herschel–Bulkley law was used to describe the rheological behavior under shear of yield stress fluids. This law can be written as:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \tau = \tau _{0} +k\dot{\gamma }^{n} &{}\hbox { for }\tau \ge \tau _{0} \\ {\dot{\gamma }} = 0 &{}\hbox { for }\tau \le \tau _{0} \\ \end{array} \right. \end{aligned}$$
(1)

where k is the consistency and n is the flow index. \(\tau _0 \), k and n are generally obtained by fitting the data obtained by measuring the shear rate \(\dot{\gamma }\) as a function of the applied shear stress \(\tau \) using a rheometer.

For a set of \(\left( {Q_i ,\nabla \textit{P}_i } \right) \) data collected during a typical YSM experiment, each \(\nabla \textit{P}_i \) defines a class of pores of representative radius \(r_i =\alpha \frac{2\tau _0 }{\nabla \textit{P}_i }\) where \(\alpha \) is a numerical factor greater than unity \((r_1>r_2>\cdots >r_N )\). The fundamental reason of this is that for a given \(\nabla \textit{P}_i \) the resulting \(Q_i \)is due to the pores whose radii are strictly larger than \(\frac{2\tau _0 }{\nabla P_i }\). In other words, \(\nabla \textit{P}_i \) represents only the onset of contribution to the flow of pores of radius \(\frac{2\tau _0 }{\nabla P_i }\). In the routine used to calculate the number of pores of a targeted pore class \(n_i (i = 1, {\ldots }, N)\), and starting with \(n_1 \), successive and increasing positive values are scanned until \(Q_\mathrm{s} <\sum _{g=1}^i n_{\mathrm{g}} q\left( {\nabla \textit{P}_\mathrm{s} ,r} \right) \) for a given s. The maximum value is then assigned to \(n_i \). In the preceding inequality, \(q\left( {\nabla \textit{P},r} \right) \) is the flow rate of a Herschel–Bulkley fluid through a capillary of radius r as a function of \(\nabla \textit{P}\) as given by Skelland (1967). In the scanning procedure to calculate each \(n_i \), and as large pores contribute significantly to the total flow rate, the scanning should be more refined when the considered pore radius is large. The step used in the scanning procedure is:

$$\begin{aligned} \hbox {Step}_i =\frac{\zeta q\left( {\nabla \textit{P}_{N+1} ,r_N } \right) }{q\left( {\nabla \textit{P}_{N+1} ,r_i } \right) } \end{aligned}$$
(2)

where \(\zeta \) is an index that determines the refinement of scanning. Equation (2) expresses that the minimum contribution to the overall flow for a given pore size \(r_i \) at the highest pressure gradient \(\nabla \textit{P}_{N+1} \) is the same for all \(r_i \).

Moreover, a filtering step is necessary. Indeed, all the pore classes \(r_j \) for which the number of pores \(n_j\) is bounded only by the highest couple of experimental data \(\left( {Q_{N+1} ,\nabla P_{N+1} } \right) \) are excluded. The reason is that these pore classes are bounded by \(\left( {Q_{N+1} ,\nabla \textit{P}_{N+1} } \right) \) solely because no further flow rates or pressure gradients have been imposed during the experiments, so no meaningful information on the number of these pores can be obtained. Consequently:

$$\begin{aligned}&\hbox {If}\qquad \quad Q_{N+1} >\mathop \sum \limits _{g=1}^{s-1} n_g q\left( {\nabla \textit{P}_{N+1} ,r_g } \right) \nonumber \\&\hbox {and}\qquad \quad Q_{N+1} =\mathop \sum \limits _{g=1}^s n_g q\left( {\nabla \textit{P}_{N+1} ,r_g } \right) \nonumber \\&\qquad \quad \hbox { then }n_\mathrm{s}\hbox { is unknown} \end{aligned}$$
(3)

Once \(n_i (i = 1, {\ldots }, N)\) have been calculated, the probability in terms of relative frequency \(p\left( {r_{\mathrm{i}}} \right) =\frac{n_{i} }{\mathop \sum \nolimits _{{j}=1}^{N} n_{j} }\hbox { for } i=1\cdots N\) and in terms of relative volume \(p_\mathrm{v} \left( {r_i } \right) =\frac{n_i \pi r_i^2 }{\mathop \sum \nolimits _{j=1}^N n_j \pi r_j^2 }\hbox { for }i=1\cdots N\) are also obtained. The total flow rate Q as a function of the pressure gradient \(\nabla \textit{P}\) corresponding to the obtained PSD is then calculated as follows:

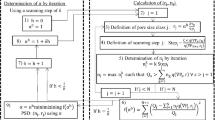
$$\begin{aligned} Q\left( {\nabla \textit{P}} \right) =\mathop \sum \limits _{i=1}^N n_i q\left( {\nabla \textit{P},r_i } \right) \end{aligned}$$
(4)

To determine the suitable value of \(\alpha \), named \(\alpha ^{*}\), successive increasing values will be used to calculate the PSD, from \(\alpha = 1\) to \(\alpha = \)2 and using a step of \({\delta }\). \(\alpha ^{*}\) is the value of \(\alpha \) that minimizes the least squares relative difference between calculated (through Eq. 4) and experimental \(\left( {Q_i ,\nabla \textit{P}_i } \right) \) data. This new criterion to select \(\alpha ^{*}\) replaces the one previously presented by Rodríguez de Castro et al. (2014). The algorithm used to calculate the PSD using YSM is schematized in Fig.  1.

Fig. 1
figure 1

Algorithm used for the calculation of PSD using YSM

Full size image

YSM was used to characterize model porous media in previous studies (Malvault 2013). In the present paper, YSM is applied to exploit data coming from laboratory experiments with natural and synthetic porous media and the resulting PSDs are compared with those provided by mercury porosimetry. The results are also compared with the average pore radius estimator obtained by Kozeny (1927) from combination of Hagen–Poiseuille law and Darcy’s law (Darcy 1856) using a bundle-of-capillaries model. Indeed, permeability K may be linked to porosity \(\varepsilon \) and average pore radius \(\bar{r}\) through:

$$\begin{aligned} K=\frac{{\varepsilon }\bar{r}^{2}}{8} \end{aligned}$$
(5)

where \(\bar{r}\) is the radius of the capillaries of a bundle of identical cylindrical capillaries having the same porosity and permeability as the analyzed porous medium.

It should be noted that the PSDs obtained with different methods do not give the same pore characteristic sizes. Chauveteau et al. (1996) studied the relationships between 3 characteristic pore dimensions for sandstones and sand packs. These dimensions were: the minimum throat diameter \(d_\mathrm{min}\) (diameter of the narrowest throat), the hydrodynamic pore diameter \(d_\mathrm{h}\) and the MIP diameter \(d_\mathrm{Hg}\). \(d_\mathrm{h}\) is defined as the diameter of a cylindrical capillary having the same length than the considered stream line and giving the same pressure drop for the same flow rate. \(d_\mathrm{Hg}\) is calculated from the pressure required to invade 50 % of pore volume with mercury. Each of these characteristic diameters is relevant to describe different phenomena, and the experiments needed to quantify them are therefore different. Chauveteau and co-workers concluded that \(d_\mathrm{h}\) is approximately \(2d_\mathrm{min}\) in sharp-edged geometries. They also found that \(d_\mathrm{Hg}\) is greater than \(d_\mathrm{h}\). We should remark that, as YSM is linked to \(d_\mathrm{h}\), YSM is expected to yield smaller pore sizes than \(d_\mathrm{Hg}\) obtained using MIP.

The performances that are sought with the yield stress fluids porosimetry method (YSM) are diverse. Obviously, the first requisite is the non-toxicity of the fluids in contrast to mercury. In addition, we seek a simple and inexpensive method which allows rapid characterization of a large spectrum of porous media without need of any sophisticated equipment. Moreover, the method should be applicable to both consolidated and unconsolidated porous media.

Other important goals of the present work are to identify and assess the most critical questions regarding the experimental feasibility of the method, determine its strengths and weaknesses, and propose ways to improve its performance. In this respect, some issues linked to interactions of complex fluids with porous media are evaluated.

2 Experimental: YSM Tests with Different Types of Porous Media

2.1 Materials

In the present experiments, the injected fluids were xanthan gum solutions prepared by dissolving an amount of purified xanthan gum powder (Arlès agroalimentaire 2013) in deionized and filtered water containing 400 ppm of \(\hbox {NaN}_{3}\) using an overhead stirrer. Xanthan gum is a commonly used viscosifier (Garcia-Ochoa et al. 2000; Abidin et al. 2012), especially in manufacturing food grade products (Palaniraj and Jayaraman 2011), as well as in polymer flooding technics for “Enhanced Oil Recovery” (Jones and Walters 1989; Abidin et al. 2012). Its chemical composition, structure and other physicochemical properties can be referred to, for example, Song et al. (2006). In solution state, an isolated xanthan macromolecule is more or less rigid, with a contour length of typically \(1\,\upmu \hbox {m}\) and a transverse size of approximately 2 nm (Rodd et al. 2000; Mongruel and Cloitre 2003; Iijima et al. 2007), and is usually modelled as a rod-like macromolecule (Chauveteau 1982; Milas and Rinaudo 1983; Carnali 1991; López et al. 2003).

Xanthan gum solutions are one of the main examples of inelastic, shear-thinning fluids in contrast to linear flexible polymers as polyacrylamide (Jones and Walters 1989; Sorbie 1991a) which are highly viscoelastic. Due to the stiffness of its molecule, xanthan semidilute aqueous solutions develop a high viscosity level and a very pronounced shear-thinning behavior. Therefore, xanthan gum solutions have been reported to present an apparent yield stress (Song et al. 2006; Carnali 1991; Withcomb and Macosko 1978; Khodja 2008; Benmouffok-Benbelkacem et al. 2010) even if strictly speaking, they should be referred to as pseudo-yield stress fluids. The Herschel–Bulkley model has been proved to describe the steady-state shear flow of concentrated xanthan gum solutions (Song et al. 2006). In porous media, other arising phenomena such as xanthan adsorption on pore walls were studied by several authors (Chauveteau 1982; Sorbie 1991a; Dario et al. 2011), emphasizing that petrophysical properties are only weakly affected in contrast to polyacrylamide. However, xanthan gum may induce a depleted layer close to pore walls with a lesser concentration in that region. It produces an apparent wall slip which leads to a reduced average viscosity in the pores (Chauveteau 1982; Sorbie 1991b). The size of that depleted layer has been reported to be of typically 300 nm in dilute regime (Chauveteau 1982; Sorbie 1991a).

In the present study, two solutions with polymer concentration \((C_\mathrm{p})\) of 7000 ppm were prepared at pH 7:

  • \(\hbox {Solution 1:} C_\mathrm{p} = 7000\hbox { ppm, in pure water.}\)

  • \(\hbox {Solution 2:} C_\mathrm{p} = 7000\hbox { ppm, in 5 g/L NaCl brine.}\)

In the present study, it was assumed that the injected solutions have no effect on the porous morphology. The exact procedure for preparing the xanthan gum solutions was described by Rodríguez de Castro (2014).

In these experiments, 5 cylindrical samples of different porous media were investigated. These materials are listed in Table 1, giving their measured macroscopic porosities and permeabilities, their lengths L and their diameters D. Solution 1 was injected only in Sample 1, while Solution 2 was injected in Samples 2 to 5.

Table 1 Measured porosities, permeabilities and dimensions of the investigated porous media
Full size table

The effective rheology of xanthan solutions was characterized by means of stress-controlled rheometers (TA Instruments 2006; Anton Paar 2012) equipped with cone-plate or double-gap geometry. All rheological measurements were performed at \(18{^{\circ }}\hbox {C}\) by applying shear stresses linearly sampled from 0 to a maximum value producing a shear rate of approximately \(1000\hbox { s}^{-1}\). The obtained rheograms were then fitted to a Herschel–Bulkley law giving \(\tau _0 , k\) and n as listed in Table 2.

Table 2 Herschel–Bulkley parameters for Solutions 1 and 2
Full size table

2.2 Experimental Setup and Procedure

In the case of Sample 1, the experimental setup is similar to the one presented by Rodríguez de Castro et al. (2014), in which the porous medium was coated with resins and fiberglass to insure liquid imperviousness and mechanical strength. However, Samples 2–5 were mounted in a Hassler core holder. In particular, each sample was inserted into a Viton sleeve and two metallic grids were put at both ends of the core so as to prevent detachment of grains. After that, the Viton sleeve containing the core and the grids was mounted in the core holder and confined with pressurized brine (5 g/L NaCl) surrounding the sleeve in order to avoid lateral leaks. The confinement pressure was 20 bars. Moreover, a robust piston pump was used (Composites & Technologies 2001) to inject the yield stress fluid because of the high pressures required in these low permeable media and metallic tubing installed for safety reasons. Once the sample was mounted and confined, it was outgassed using a vacuum pump. Then, when a strong vacuum was reached, the core holder was connected to a graduated burette containing degassed brine (5 g/L NaCl, prepared with filtered water) at a pressure of 5 bar so as to saturate the sample and then determine its porosity. The brine-saturated porous medium was then kept at rest during approximately 12 h. After that, the permeability to brine was measured.

After saturation of Samples 2–5 with brine and before their saturation with xanthan gum solution, a dispersion test was performed in order to characterize the dispersion of the injection front through these porous media. This test consisted in injecting a tracer (brine with different NaCl concentration) through each porous medium and measuring the evolution of the effluent density. At the initial time, the media were fully saturated with 5 g/L brine. Then, 20 g/L brine was injected at a flow rate corresponding to a Péclet number (as defined by Sheng 2011) Pe = 1 so as to guarantee homogeneous fluid penetration. During this injection, the density of the effluent was continuously measured with a density meter until the density of the injected brine was retrieved. At that time, the 5 g/L brine was injected and the density of the effluent was measured.

The next stage consisted in saturating the sample with xanthan solution. During this stage, the density meter was also connected to the outlet of the porous medium to measure the density of the outgoing fluid. A fraction collector was installed downstream of the density meter in order to collect samples for subsequent measurements with a rheometer. In this xanthan saturation step, 3 pore volumes of xanthan gum solution were injected at a flow rate corresponding to Pe = 2000 followed by a pore volume at the highest flow rate to be imposed during the experiments (1000 mL/h). The core holder was placed vertically during saturation, and the xanthan solution was injected from the bottom. Once saturated with xanthan solution, the porous medium was kept at rest for 12 h.

Then, the \(Q\left( {\nabla \textit{P}} \right) \) measurements were taken in horizontal position. The imposed flow rate was decreased from its upper to its lower limit through \(N+1\) steps (\(N+1\) ranging from 37 to 40), and the corresponding pressure drops were measured at the steady state using a pressure sensor (Rosemount 2009). It was decided to impose the same range of flow rates in all experiments except for Sample 1, for which higher flow rates were considered due to its greater diameter. This range of flow rates was from 1000 to 0.01 mL/h, the largest technically achievable with our equipment. The time allowed for each measurement was optimized in order to minimize the duration of the experiment, hence reducing the possible polymer retention in the porous media while attaining equilibrium pressures. The relative standard deviation of the pressure drop measurements was 8 % for \(Q < 1\hbox {mL/h}, 1\,\%\) for \(1\,\hbox {mL/h }< Q < 150\,\hbox {mL/h}\) and 0.5 % for \(Q > 150\,\hbox {mL/h}\). The temperature of the laboratory was kept constant at \(T = 18\,{^{\circ }}\hbox {C}\pm 1\) during all the experiments.

Analogous samples of the porous media used in the YSM experiments were analyzed by MIP. A mercury porosimeter (Micromeritics 2008) was used to perform these experiments, and only an intrusion cycle was carried out.

2.3 Complementary Measurements

Several complementary measurements were conducted during the saturation of the porous samples with xanthan gum solution. The goal of these additional tests was to provide evidence of the importance of polymer retention, mechanical degradation and adsorption of the molecules in the porous media. Firstly, the BTCs (breakthrough curves) resulting from dispersion tests with brines were compared to those coming from the injection of xanthan solutions. By doing so, and ignoring the possible plugging in the very small pores, comparison of such BTCs may give information about polymer adsorption and other possible phenomena. In addition to the density, the viscosity of the effluent was also measured during saturation of the cores with xanthan solution and after the YSM test. This was done by sampling the effluents and using a controlled-stress rheometer (Anton Paar 2012).

3 Results

3.1 Xanthan Saturation Stage

3.1.1 Dispersion Tests in the Porous Media

The BTCs corresponding to Samples 2–5 are presented in Fig. 2 in terms of relative density difference (see the caption).

Fig. 2
figure 2

Density evolution of the effluent as a function of the number of pore volumes of tracer injected through the core. The flow rate corresponds to Pe = 1. D is the density of the effluent, \(D_{F}\) is the density of the influent brine, and \(D_{0}\) is the density of the brine with which the porous medium is originally saturated. Error bars represent \(\pm 3\sigma \) with \(\sigma \) being the standard deviation

Full size image
Fig. 3
figure 3

Density evolution of the effluent using 2 g/L NaCl brine and xanthan Solution 2 as injected fluids. The samples were initially saturated with 5 g/L brine. Standard deviation relative density measures was 0.015 for brine and 0.05 for Solution 2

Full size image

When the convection–diffusion equation is solved for a semi-infinite medium, the ratio of density differences as in Fig. 2 is roughly given by a complementary error function (Ogata and Banks 1961; Sheng 2011):

$$\begin{aligned} \frac{D-D_0 }{D_{ F} -D_0 }\approx \frac{1}{2}\hbox {erfc}\left( {\frac{L-\vartheta t}{2\sqrt{\psi t}}} \right) \end{aligned}$$
(6)

where \(\vartheta \) is the average interstitial velocity, \(\vartheta =Q/\left( {\varepsilon A} \right) \), and \(\psi \) is the longitudinal dispersion coefficient.

The data presented in Fig. 1 were fitted to the complementary error function given by Eq. (6) with \(t=( {\hbox {injected volume}}/Q\), thus obtaining \(\psi \) for each experiment (Sample 2: \(1.0 \times 10^{-7}\hbox { m}^{2}\); Sample 3: \(3.8 \times 10^{-8}\hbox { m}^{2}\); Sample 4: \(1.1 \times 10^{-7}\hbox { m}^{2}\); Sample 5: \(1.0 \times 10^{-6}\hbox { m}^{2})\). As can be deduced from these results, Sample 5 (Berea Sandstone) is the most dispersive medium, which may be the consequence of a PSD presenting a larger spread (Perkins and Johnston 1963; Carbonell 1979). Also, it can be seen that \(\left( {D-D_0 } \right) /\left( {D_{F} -D_0 } \right) = 0.5\) when one pore volume of tracer has been injected in the sample (Sheng 2011). However, this occurs untimely as the visited pore volume does not match the effective pore volume.

3.1.2 Analysis of Polymer Adsorption: Effluent Density Measurements During Saturation with Xanthan Gum Solution

As explained before, similar experiments were performed on Samples 2, 3 and 5 initially saturated with 5 g/L brine, by injecting xanthan gum solution. It is noticed that the density of the effluent attained a stable plateau in all cases (Fig. 3). Pore blocking or formation of a multilayer would lead to an effluent concentration lower than that of the injected fluid, so \(\left( {D-D_0 } \right) /\left( {D_{F} -D_0 } \right) \) would remain lower than 1 for a long period of time in the case of continuous retention or pore blocking, without reaching the final plateau. Therefore, we can conclude that no continuous retention or filtration and no multilayer adsorption of polymer on pore walls occurred in the present experiments.

3.1.3 Analysis of Mechanical Degradation: Effluent Viscosity Measurements During Saturation with Xanthan Gum Solution

The viscosity of each effluent sample was measured at low (\(1\,\hbox {s}^{-1})\) and high \((100\hbox { s}^{-1})\) shear rates. As an example, the results for Sample 5 are presented in Fig. 4. It is noticed that, in contrast to density, a rapid increase in viscosity occurred only when more than one pore volume was injected since, whereas density was proportional to concentration, viscosity followed a power law of \(C_\mathrm{p} \), and the increase in viscosity was more pronounced at the last stage of polymer effluence. We also observe that the attained plateau value was almost equal to the viscosity of the influent solution, meaning that no significant mechanical degradation occurred inside the porous media.

Fig. 4
figure 4

Effluent viscosity evolution (black circles) as a function of the injected volume of Solution 2 through Sample 5. Red lines represent the viscosity of Solution 2 before injection. Viscosity is measured at a \(\dot{\gamma }= 1\hbox {s}^{-1}\) and b \(\dot{\gamma } = 100\hbox { s}^{-1}\). The relative standard deviation of viscosity measurements was 1.5 %

Full size image
Fig. 5
figure 5

PSDs obtained with YSM

Full size image

3.2 PSD Obtained with YSM

YSM was applied to the \((Q_i, \nabla \textit{P}_i )\) raw data resulting from the laboratory experiments presented in Sect. 3. The corresponding PSDs expressed in terms of relative volume of pore classes of representative radii \(r_i , p_\mathrm{v} \left( {r_i } \right) \), are displayed in Fig. 5. Also, the corresponding \(\alpha ^{*}\) and the average pore radius predicted by Eq. (5) are presented in the same figure. It is remarked that, apart from Sample 2, these PSDs are coherently arranged with respect to such average pore radius. Indeed, the order of these samples according to the peak or the mean of the obtained PSDs is the same as their order according to the mentioned average radius (apart from Sample 2). Therefore, it can be concluded that YSM provided representative PSDs of the analyzed porous media. Moreover, the value of \(\alpha ^{*}\) was found to be almost the same for all experiments (1.2 and 1.3), so \(\alpha ^{*}\) was not porous medium-dependent.

3.3 Comparison of YSM with MIP

It is known that PSD is an elusive characteristic of porous media whose definition depends on the method used for its determination. Therefore, a comparison between YSM and MIP is presented here with the purpose of highlighting the key differences that could explain any possible discrepancies and facilitate data interpretation.

3.3.1 Comparison in Terms of PSD

As mentioned above, analogous samples of the porous media used in the YSM experiments were analyzed by MIP, recalling that the PSDs obtained by MIP are mainly sensitive to the radii of the largest entrances or openings toward the pores. All the MIP PSDs were obtained through application of Washburn equation taking a contact angle \(\theta = 140{^{\circ }}\), which is a commonly used value (Giesche 2006). Also, the characteristic size of pore classes in MIP is \(r_i =-2\sigma \cos \theta /P_i \) (\(P_i\) being the applied pressures to mercury and \(\sigma \) being the surface tension of the mercury–air couple), whereas they are defined as \(r_i =\alpha ^{*}2\tau _0 /\nabla \textit{P}_i \) in YSM. Consequently, a preliminary step when comparing PSDs of both methods consists in calculating the equivalent probabilities for the same pore size classes.

Figure 6 shows the PSDs obtained from MIP and YSM for the 5 samples analyzed here and for the same pore classes. As expected, YSM yielded smaller pores than MIP. Also, the distributions obtained by both methods were observed to have a similar shape (except for Sample 2). The average pore radii \(\bar{r}\) were calculated using Eq. (5) and compared with the average radius obtained by MIP and YSM, showing that YSM average radius is always closer to \(\bar{r}\) than MIP average radius. Indeed, there is very good accordance between YSM average radius and \(\bar{r}\) for Samples 1, 3 and 4. The agreement was found to be worse for Sample 2 and Sample 5. These observations are based only on a limited number of experiments, and more experimental data are needed to deduce a correlation between the two parameters. It is also observed that the correlation between MIP average radius and \(\bar{r}\) is better than between YSM average radius and \(\bar{r}\). However, if Sample 2 is excluded, the correlation with YSM is better. Also, it should be noted that the measures of \(Q\left( {\nabla \textit{P}} \right) \), and consequently the obtained PSD, may be affected by clay swelling in the case of Sample 5. Moreover, it was observed that the PSD of Sample 5 did not present a larger spread than the PSDs of the other samples even though the longitudinal dispersion coefficient was higher as presented in Sect. 3.1.1.

MIP can be used to analyze a wide range of pore sizes. It is also true for YSM, provided that a yield stress fluid with appropriately small elements (particles, polymer molecules, droplets, etc.) is used. The pressure P to be imposed for the analysis of a given pore radius \(r_i\) with MIP is given by \(=-\frac{2\sigma \cos \theta }{r_i }\approx \frac{0.74\,\hbox { N m}^{-1}}{r_i }\). The pressure needed to characterize pores of radius \(r_i \) with YSM is \(P=( {2\tau _0 L})/r_i \) (with \(\tau _0 = 10\,\hbox { Pa}\) and \(L = 0.05\) m). Consequently, the required pressures at the laboratory scale are of the same order of magnitude for both methods.

Fig. 6
figure 6

PSDs obtained with YSM compared with those obtained with MIP. The average radius defined by Eq. (5) is also presented (dashed line)

Full size image

3.3.2 Comparison in Terms of Capillary Pressure Curves

Essentially, in MIP, the primarily measured quantity is the capillary pressure curve \(P_\mathrm{c} \left( S \right) \) obtained by displacing a wetting fluid (air) with a non-wetting fluid (mercury) for different imposed pressures as a function of the non-wetting phase saturation S. Moreover, capillary pressure controls the fluids distribution in a reservoir and affects oil recovery in petroleum industry, and its measurement may be the major issue for some applications. In this section, the YSM results will be treated to obtain capillary pressure curves for comparison with the ones directly obtained by MIP.

In YSM, \(P_\mathrm{c} \left( S \right) \) curve is calculated from the PSD by associating a \(P_\mathrm{c} \) with each pore size class through Eq. (7) and the saturation is calculated through the cumulated volume probability for each pore size class (Eq. 8):

$$\begin{aligned} P_{\mathrm{c}_i}= & {} -\frac{2\sigma \cos \theta }{r_i } \end{aligned}$$
(7)
$$\begin{aligned} S\left( {P_{\mathrm{c}_i}}\right)= & {} \mathop \sum \limits _{\forall \,r_i \ge -\frac{2\sigma \cos \theta }{r_i }} p_\mathrm{v} \left( {r_i } \right) \end{aligned}$$
(8)

\(\theta \) is assumed to be \(140{^{\circ }}\) and \(\sigma = 0.485\,\hbox {Nm}^{-1}\) at \(25\,{^{\circ }}\hbox {C}\).

However, the pore size classes \(r_i \) calculated by YSM are intimately linked to pore throats as the method is based on the measure of \(\nabla \textit{P}\) as a function of Q. Therefore, by using Eq. (7) to obtain \(P_\mathrm{c} \), it is implicitly assumed that the whole volume of a pore will be saturated only when the applied pressure is high enough to penetrate the pore throat (of hydrodynamic diameter \(d_\mathrm{h }{\sim } \, r_i )\). As a consequence, the capillary pressure coming from YSM will be overestimated unless \(r_i\) are transformed before being used as input in Eq. (7). This transformation must ensure that the corrected \(r_i \) are representative of the saturation process with a non-wetting liquid, i.e., \(r_i{\sim }\, d_\mathrm{Hg}\).

Fig. 7
figure 7

Capillary pressure PSDs deduced from YSM compared to the PSDs obtained using MIP

Full size image
Fig. 8
figure 8

\(P_\mathrm{c}\) as a function of mercury saturation measured with MIP compared with \(P_\mathrm{c}(S)\) calculated from the capillary pressure PSDs deduced from YSM

Full size image

A first simple approach to achieve that objective is addressed here. Let us begin by assuming that the pressure drop along a percolating path is located exclusively in its narrowest throat, i.e., \(r_i {\sim } \, d_\mathrm{h}{\sim } d_\mathrm{min}\). In this case, \(n_i \) delivered by YSM represent the number of percolating paths whose narrowest throat has a radius \(r_i \). The total number of percolating paths is \(\sum _i n_i \). It should be noted that the volume of the throats is not representative of the whole volume of the percolating paths, so \(\sum _i n\pi r_i ^{2}<\varepsilon \pi R^{2}\) with R being the radius of the sample. Let us assume now that all percolating paths have the same volume, which is completely contained in “pore bodies” of length L and volume \(\varepsilon L\pi R^{2}/\sum _i n_i \). Therefore, the radius of the “pore bodies” will be \(r_\mathrm{body} =\sqrt{\varepsilon R^{2}/\sum _i n_i }\). A percolating path whose pore body radius is \(r_\mathrm{body} \) and whose minimum throat has a radius \(r_i \) will be saturated with a non-wetting fluid at pressures ranging from \(-2\sigma \cos \theta /r_\mathrm{body} \) to \(-2\sigma \cos \theta /r_i \). As a first approximation, we consider that a percolating path will be saturated with non-wetting fluid when the applied pressure is \(-2\sigma \cos \theta /\left[ {\left( {r_\mathrm{body} +r_i } \right) /2} \right] \). Consequently, the PSD obtained with YSM can be transformed into its equivalent “capillary pressure PSD” through the next expressions:

$$\begin{aligned} \tilde{r}_i= & {} \frac{r_\mathrm{body} +r_i }{2} \end{aligned}$$
(9)
$$\begin{aligned} \widetilde{p\left( {r_i } \right) }= & {} \frac{n_i }{\sum _i n_i } \end{aligned}$$
(10)

where \(\tilde{r}_i \) is the “capillary-pressure-equivalent” pore radius class and \(\widetilde{p\left( {r_i } \right) }\) its equivalent frequency.

The “capillary pressure PSDs” corresponding to the experiments performed in Sect. 3 and the resulting \(P_\mathrm{c} \left( S \right) \) curves are presented in Figs. 7 and 8 together with the MIP results. Good agreement is found between both methods, especially for natural media (Samples 3–5). It is remarked that for all these materials there is a critical value of \(P_\mathrm{c} \) above which S increases abruptly. This critical value is well predicted by YSM. Besides, while in MIP capillary pressure curves a further increase in \(P_\mathrm{c} \) is needed to attain the highest saturations after the plateau, this is not the case for YSM. In fact, these high capillary pressures are due to the smallest pores, which are not scanned with YSM. The reason is that their analysis with YSM would require the imposition of very high pressures and flow rates which were not possible with the used equipment. It should be noted that mercury porosimeters contain a number of pressure sensors adapted to the several orders of magnitude of pressure imposed during a test.

Further information can be obtained through interpretation of the PSDs obtained by YSM. Indeed,\(\sum _i n_i \) is the total number of percolating paths and \(\bar{r} =\sum _i n_i r_i /\sum _i n_i \) is the average throat radius. Therefore, \(r_\mathrm{body} /\bar{r}\) can be used as an estimator of the pore-to-throat size ratio (listed in Table 3).

Our assumptions will be more realistic in the case of high pore-to- throat size ratios because we have supposed that all the volume is contained in the bodies and all the pressure drop is produced by the throats. In effect, better agreement between MIP and YSM was found when the pore-to-throat size ratio was high (Samples 3–5). Nevertheless, this is only a simple interpretation leading to encouraging results, so further research will be required so as to provide reliable relationships.

Table 3 Pore-to-throat size ratio calculated using YSM
Full size table

We must highlight that the use of MIP as a reference method when PSDs are devoted to calculate \(P_\mathrm{c} \left( S \right) \) is justified, because \(P_\mathrm{c} \left( S \right) \) is directly measured with this technique. However, MIP should not be considered as the reference method for the calculation of PSD in all applications, even if it is often the case simply by tradition or because it is a routine technique, as stated by Lassen et al. (2008).

4 Discussion, Interpretation and Recommendations

As shown in Fig. 3, the plot of the BTCs of brine and xanthan solution as injected fluids does not coincide and the observed delay of the polymer is usually attributed to cumulative effects of polymer adsorption, depleted layer and inaccessible pore volume (see Sheng 2011; Sorbie 1991b for details). However, in the case of Sample 3, it is the BTC corresponding to brine which is delayed with respect to xanthan solution, probably due to inaccessible pore volume (as when the size of the polymer macromolecules is of the same order as the mean pore radius plus a contribution of the depleted layer close to pore wall). These effects may hide adsorption and precipitate the polymer BTC. In contrast, for Samples 2 and 5, the BTCs of xanthan solution are delayed with respect to those of brine, clearly evidencing the existence of polymer adsorption as reported in the literature for HPAM solutions flowing through sandstones (Mungan 1969; Wei et al. 2014). In any case, it is expected that even if polymer adsorption occurs, xanthan gum macromolecules should be flattened onto the pore wall with negligible modification of the petrophysical characteristics of the porous medium, in contrast to HPAM and other flexible polymers (Chauveteau 1982; Sorbie 1991a).

Fig. 9
figure 9

a Rheogram of Solution 2 before injection through Sample 5 compared to the rheogram of the effluent after saturation. b Rheogram of the effluent before \(Q\left( {\nabla \textit{P}} \right) \) measurements compared to the rheograms of the successive effluent fractions collected during flushing stage (after \(Q\left( {\nabla \textit{P}} \right) \) measurements). The relative standard deviation of shear rate measurements was 1.5 %

Full size image

Xanthan gum solutions flowing through porous media may experience retention and adsorption and are subjected to elongation as xanthan macromolecules pass continuously from pore bodies to pore throats. At low shear rates, xanthan gum molecules are not oriented in the direction of flow, so retention is more likely to occur under these conditions. Nevertheless, when the shear stress is increased, the macromolecules are oriented in the direction of the flow and retention is expected to be very weak. Increasing further the flow rate, the macromolecules undergo significant elongation rates and may break. Fortunately, in the present case, xanthan macromolecules are too stiff to be broken and their mechanical degradation should be negligible. Moreover, the effluent viscosity after saturation with xanthan solution was found to be similar to that of the inflowing xanthan solution as shown in Fig. 9a). These are additional arguments allowing us to consider that both polymer adsorption and mechanical degradation are not significant.

However, a completely different situation arises once the whole \(Q\left( {\nabla \textit{P}} \right) \) measurements sequence is performed. Indeed, during the \(Q\left( {\nabla \textit{P}} \right) \) measurements that are exploited with YSM, the flow rate is decreased from 1000 to 0.01 mL/h through \(N+1\) steps and one may wonder whether the rheology of the outgoing fluid is still similar to that of the injected solution. In order to answer that question, 1.4 pore volumes of xanthan solution were injected through Sample 5 at the highest flow rate (1000 mL/h) after the \(Q\left( {\nabla \textit{P}} \right) \) measurements and the effluent was regularly sampled. The corresponding rheograms were experimentally determined, and the obtained results are gathered in Fig. 9b). In this figure, we also report the rheogram of the effluent xanthan solution just after the saturation step. As it is observed, the outgoing xanthan solutions were clearly less viscous after the \(Q\left( {\nabla \textit{P}} \right) \) measurements. Such a difference cannot be explained by mechanical degradation, since no loss of viscosity was noticed after saturation stage (in good agreement with Argillier et al. 2013). Besides, it was noticed that the viscosity of the effluent increased by flushing at a high flow rate. In fact, the second fraction was found to be slightly more viscous than the fluid before injection suggesting that the retained molecules were swept when flushing, leading to an increase in the concentration of the effluent and therefore its viscosity. Finally, the viscosity of the third fraction was closer to the original viscosity. Therefore, it can be concluded from this experiment that the origin of the viscosity drop was polymer retention at low flow rates and that the initial viscosity was recovered after flushing at high flow rates. Similar experiments were conducted with Samples 2, 3 and 4, leading to analogous results.

5 Summary and Conclusions

The new YSM data analyzing method to characterize PSD of porous media was recently presented, in a context of international consensus on the need to develop alternatives to toxic mercury porosimetry. It is based on flow experiments of yield stress fluids through porous media. In this work, a series of experiments were carried out with the same fluid and different porous media in order to study the influence of the type of porous medium on the obtained PSD. The PSDs were found to be coherently arranged with respect to the average radius from Eq. (5). These results are encouraging as YSM succeeded in providing representative PSDs for the tested samples. However, further experiments would be necessary to confirm these observations for a larger number of samples.

We also studied the importance of polymer adsorption, polymer retention and mechanical degradation by means of density and viscosity measurements of the ingoing and outgoing fluids in the porous media. Whereas no sign of important adsorption and mechanical degradation was observed, polymer retention was shown to be important at the lowest flow rates due to the random orientation of the polymer molecules at these flow rates.

In this work, YSM was compared to MIP. The PSDs obtained by these methods do not coincide in all cases as expected, and the main reasons for such discrepancies have been presented. Due to its industrial interest, \(P_\mathrm{c} \left( S \right) \) curves corresponding to each method were obtained through a simple procedure. Evidently, MIP is the more appropriated method to obtain \(P_\mathrm{c} \left( S \right) \) curves because they are directly measured during the tests. Nevertheless, a right definition of the correspondence between the pore dimensions characterized by each technique may lead to good estimations of \(P_\mathrm{c} \left( S \right) \) curves using the other methods. It is worth insisting on the fact that a broader definition of PSD is essential. PSD must be conceived as a set of application-oriented probability functions, each of them being pertinent only for a particular use.

Definitely, YSM experiments are very simple. Only the measure of \(Q\left( {\nabla \textit{P}} \right) \) is required to characterize PSD, which is a routine task in most petrophysics laboratories. As a consequence, the operators do not need any specific training and the experiments can be easily assembled. Besides, it is inexpensive because no special equipment is necessary as is the case for other porosimetry techniques (mercury porosimetry, microtomography). In fact, this advantage is not negligible if we take into account the prohibitive prices of an X-ray microscope and a mercury porosimeter. Furthermore, YSM is non-toxic, versatile and can be used to characterize different types of porous media. For instance, YSM may be useful to characterize unconsolidated porous media for which MIP and other currently used methods are not efficient.

YSM also presents some drawbacks that should be specifically addressed in future works. In particular, the assumption that the injected solutions have no effect on the porous morphology must be validated. Also, polymer retention poses a concern regarding the characterization of small pores, so additional stages such as intermediate flushing should be investigated. Given that these drawbacks arise from fluid–solid interactions, they might be mitigated by adapting the experimental procedures and the choice of the injected yield stress fluid. Another limitation of YSM is that \(P_\mathrm{c} \left( S \right) \) curves are not directly measured (in contrast to MIP), so relationships between the PSDs obtained by YSM and the corresponding \(P_\mathrm{c} \left( S \right) \) curves need further study.

In summary, it can be concluded that the starting point of a broad exploratory work on the experimental feasibility of a new data analyzing method to characterize pore size distributions based on the injection of yield stress fluids has been presented. Numerous aspects of such a method have been discussed and its trickiest points have been identified, raising some yet unresolved issues. However, YSM has a big potential as a porosimetry method, not only to calculate PSDs related to permeability, but also to obtain \(P_\mathrm{c} \left( S \right) \) curves if a right relationship between the determined pore dimensions is used.