1 Introduction

The natural convection occurs due to buoyancy difference in a fluid. The well-known buoyancy force in fluids is the thermal expansion of the fluid. This effect has been extensively studied in the literature (Ingham and Pop 2005). There are also cases in which the natural convection is due to mass transfer in binary fluids. The migration of heavy molecules in a fluid could induce a buoyancy force in the fluid and result in a natural convection flow, which is known as double-diffusive convection. The simultaneous presence of concentration gradients and thermal differences in an enclosure could result in opposing or aided convective flows that in most case are very complicated in nature. The natural convective heat transfer of double-diffusive fluids inside porous media has been studied in many of previous publications, for example the study of Costa (2004), Varol et al. (2008), Chamkha and Al-Mudhaf (2008), Mahdy et al. (2010), Chamkha et al. (2010, 2011), Subhashini et al. (2011), Abdou and Chamkha (2012), Ravikumar et al. (2013) and Mallikarjuna et al. (2014). However, there are engineering applications in which the fluid consists of three phases with distinct densities and mass diffusive coefficients, for example the migration of moisture and natural gas through the air in soil or grains. The dispersion of chemical contaminants through water in saturated soil or dispersion of carbon dioxide and carbon monoxide through the air in natural convection in a fibrous media or filter.

Despite the many practical engineering applications of triple-diffusive natural convection heat and mass transfer in enclosures, the available studies in the literature are very limited. Rudraiah and Vortmeyer (1982), Poulikakos (1985), Kantur and Tsibulin (2004), Rionero (2012, 2013, 2014, 2015), Bulgarkova (2012), Capone and De Luca (2012) and Chand (2012, 2013) have addressed different aspects of the onset of instability in triple-diffusive convection in porous media. Khan et al. (2013, 2015) and Khan and Pop (2013) have analyzed the boundary layer heat and mass transfer of a three- component solution over a flat plate embedded in a porous media.

The present study aims to analyze the aided flow of triple-diffusive natural convective heat and mass transfer in an enclosure filled with a porous medium.

2 Basic Equations

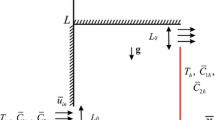
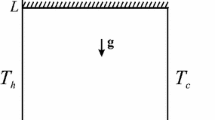
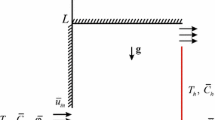
We consider the steady triple-diffusive convective flow in a square cavity filled with a fluid-saturated porous medium. A schematic geometry of the problem under investigation is shown in Fig. 1, where \(\bar{{x}}\) and \(\bar{{y}}\) are the Cartesian coordinates measured along the lower wall and along the vertical wall of the cavity, respectively, and L is the size of the cavity. The cavity is assumed to be impermeable, and the left vertical wall is maintained at the constant temperature \(T_h \) and concentrations \(C_{1h} \) and \(C_{2h} \), while the right wall is maintained at the constant temperature \(T_c \) and concentrations \(C_{1c} \) and \(C_{2c} \), respectively. The horizontal walls are adiabatic \(\left( {{\partial T}/{\partial \bar{{y}}}=0} \right) \) and impermeable \(\left( {{\partial C_1 }/{\partial \bar{{y}}}=0\; \hbox {and} \;{\partial C_2 }/{\partial \bar{{y}}}=0} \right) \).

Fig. 1
figure 1

Schematic diagram of coordinate system and physical model

Full size image

Following Rionero (2013), we also assume that two different chemical components (“salts”) \(S_m \) (\(m=1,2\)) have dissolved in the fluid-saturated porous medium, which have concentrations \(C_m \) (\(m=1,2\)), respectively, and that the equation of state is

$$\begin{aligned} \rho =\rho _0 \left[ {1-\beta _T \left( {T-T_0 } \right) -\beta _1 \left( {C_1 -C_{1C} } \right) -\beta _2 \left( {C_2 -C_{2C} } \right) } \right] , \end{aligned}$$
(1)

where \(\rho _0 \) is a reference density and the constants \(\beta _T ,\;\beta _1 \) and \(\beta _2 \) denote the coefficient of thermal expansion and solute \(S_m \) expansion coefficients, respectively (\(m=1,2\)), which are defined by

$$\begin{aligned} \beta _T =- \frac{1}{\rho } \left( {\frac{\partial \rho }{\partial T}} \right) _p ,\quad \beta _1 =- \frac{1}{\rho } \left( {\frac{\partial \rho }{\partial C_1 }} \right) _p ,\quad \beta _2 =- \frac{1}{\rho } \left( {\frac{\partial \rho }{\partial C_2 }} \right) _P . \end{aligned}$$
(2)

Combining Darcy’s law

$$\begin{aligned} \frac{\mu }{K} {\bar{\mathbf{v}}}=- \nabla \bar{{p}}\;+\;\rho \mathbf{g} , \end{aligned}$$
(3)

with (thermal) energy and continuity equations together with the Boussinesq approximation (1), we obtain the following fundamental vectorial equations in dimensional form governing the isochoric motions

$$\begin{aligned}&\displaystyle \nabla \cdot {\bar{\mathbf{v}}}=0, \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \frac{\mu }{K} {\bar{\mathbf{v}}}=- \nabla \bar{{p}}\;+\rho _0 \left[ {1-\beta _T \left( {T-T_0 } \right) -\beta _{ 1} \left( {C_1 -C_C } \right) -\beta _{_2 } \left( {C_2 -C_C } \right) } \right] \mathbf{g}, \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle {\bar{\mathbf{v}}}\;\cdot \nabla T=\alpha _m \nabla ^{2}T, \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle \frac{1}{\varepsilon }{\bar{\mathbf{v}}}\;\cdot \nabla C_1 =D_1 \nabla ^{2}C_1 , \end{aligned}$$
(7)
$$\begin{aligned}&\displaystyle \frac{1}{\varepsilon }{\bar{\mathbf{v}}}\;\cdot \nabla C_2 =D_2 \nabla ^{2}C_2 , \end{aligned}$$
(8)

where \({\bar{{\mathbf{v}}}}\) is the velocity vector, \(\bar{{p}}\) is the pressure field, \(\mu \) is the dynamic viscosity, K is the permeability, g is the gravity vector, \(\alpha _m \) is the thermal diffusivity of the porous medium and \(D_m \;(m=1,2)\) are the mass diffusivity of the salts \(S_m \).

Eliminating the pressure \(\bar{{p}}\) from Eq. (5), the following governing equations for the proposed model are valid in Cartesian coordinates \(\bar{{x}}\) and \(\bar{{y}}\)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{{u}}}{\partial \bar{{x}}}+\frac{\partial \bar{{v}}}{\partial \bar{{y}}}=0, \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \frac{\partial \bar{{u}}}{\partial \bar{{y}}}\;-\;\frac{\partial \bar{{v}}}{\partial \bar{{x}}}=- \frac{g K}{\mu } \left( {\beta _T \frac{\partial T}{\partial \bar{{x}}}\;+\;\beta _1 \frac{\partial C_1 }{\partial \bar{{x}}}\;+\;\beta _2 \frac{\partial C_2 }{\partial \bar{{x}}}} \right) \end{aligned}$$
(10)
$$\begin{aligned}&\displaystyle \bar{{u}}\frac{\partial T}{\partial \bar{{x}}}+\bar{{v}}\frac{\partial T}{\partial \bar{{y}}}=\alpha _m \left( {\frac{\partial ^{2}T}{\partial \bar{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \bar{{y}}^{2}}} \right) , \end{aligned}$$
(11)
$$\begin{aligned}&\displaystyle \frac{1}{\varepsilon }\left( {\bar{{u}}\frac{\partial C_1 }{\partial \bar{{x}}}+\bar{{v}}\frac{\partial C_1 }{\partial \bar{{y}}}} \right) = D_1 \left( {\frac{\partial ^{2}C_1 }{\partial \bar{{x}}^{2}}+\frac{\partial ^{2}C_1 }{\partial \bar{{y}}^{2}}} \right) , \end{aligned}$$
(12)
$$\begin{aligned}&\displaystyle \frac{1}{\varepsilon }\left( {\bar{{u}}\frac{\partial C_2 }{\partial \bar{{x}}}+\bar{{v}}\frac{\partial C_2 }{\partial \bar{{y}}}} \right) = D_2 \left( {\frac{\partial ^{2}C_2 }{\partial \bar{{x}}^{2}}+\frac{\partial ^{2}C_2 }{\partial \bar{{y}}^{2}}} \right) , \end{aligned}$$
(13)

Further, we introduce the following dimensionless variables

(14)

where \(T_0 ={\left( {T_h +T_c } \right) }/2\) is the mean temperature of heated and cooled vertical walls of the cavity, \(\Delta T=T_h -T_c ,\; \Delta C_1 =C_{1h} -C_{1c} \) and \(\Delta C_2 =C_{2h} -C_{2c} \).

Further, we introduce the dimensionless stream function \(\psi \) defined by

$$\begin{aligned} u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}, \end{aligned}$$
(15)

such that the continuity Eq. (9) is automatically satisfied. We are then left with the following five equations,

$$\begin{aligned}&\displaystyle \frac{\partial ^{2}\psi }{\partial x^{2}}+\frac{\partial ^{2}\psi }{\partial y^{2}}=-Ra\left( {\frac{\partial \theta }{\partial x}+Nc_1 \frac{\partial \phi _1 }{\partial x}+Nc_2 \frac{\partial \phi _2 }{\partial x}} \right) , \end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle \frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}=\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}, \end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle Le_1 \left( {\frac{\partial \psi }{\partial y}\frac{\partial \phi _1 }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \phi _1 }{\partial y}} \right) =\frac{\partial ^{2}\phi _1 }{\partial x^{2}}+\frac{\partial ^{2}\phi _1 }{\partial y^{2}}, \end{aligned}$$
(18)
$$\begin{aligned}&\displaystyle Le_2 \left( {\frac{\partial \psi }{\partial y}\frac{\partial \phi _2 }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \phi _2 }{\partial y}} \right) =\frac{\partial ^{2}\phi _2 }{\partial x^{2}}+\frac{\partial ^{2}\phi _2 }{\partial y^{2}}, \end{aligned}$$
(19)

with the boundary conditions

$$\begin{aligned}&\psi =0,\quad \theta =0.5,\quad \phi _1 =1,\quad \phi _2 =1\quad \hbox {on}\quad x=-0.5 \nonumber \\&\psi =0,\quad \theta =- 0.5,\quad \phi _1 =0,\quad \phi _2 =0 \quad \hbox {on}\quad x=0.5 \\&\psi =0,\quad \frac{\partial \theta }{\partial y}=0,\quad \frac{\partial \phi _1 }{\partial y}=0,\quad \frac{\partial \phi _2 }{\partial y}=0\quad \hbox {on}\quad y=0\; \hbox {and}\; y=1,\nonumber \end{aligned}$$
(20)

where Ra is the Rayleigh number for the porous medium, \(Nc_1 \) and \(Nc_2 \) are the buoyancy parameters for the salts 1 and 2, and \(Le_1 \) and \(Le_2 \) are the Lewis numbers for the salts 1 and 2, which are defined

$$\begin{aligned} Ra=\frac{gK\beta _T \Delta TL}{\nu \alpha _m },\quad Nc_1 =\frac{\beta _1 \Delta C_1 }{\beta _T \Delta T},\quad Nc_2 =\frac{\beta _2 \Delta C_2 }{\beta _T \Delta T},\quad Le_1 =\frac{\alpha _m }{\varepsilon D_1 },\quad Le_2 =\frac{\alpha _m }{\varepsilon D_2 },\nonumber \\ \end{aligned}$$
(21)

The physical quantities of practical interest are the local Nusselt number Nu and the local Sherwood numbers \(Sh_1 \) and \(Sh_2 \) for salts 1 and 2, respectively, which are defined as

$$\begin{aligned}&Nu=\frac{L}{\Delta T}\left( {- \frac{\partial T}{\partial \bar{{x}}}} \right) _{\bar{{x}}=-0.5} ,\quad Sh_1 =\frac{L}{\Delta C_1 }\left( {-\frac{\partial C_1 }{\partial \bar{{x}}}} \right) _{\bar{{x}}=-0.5} ,\nonumber \\&Sh_2 =\frac{L}{\Delta C_2 }\left( {-\frac{\partial C_2 }{\partial \bar{{x}}}} \right) _{\bar{{x}}=-0.5}. \end{aligned}$$
(22)

Substituting (14) into (22), we obtain

$$\begin{aligned} Nu=\left( {-\frac{\partial \theta }{\partial x}} \right) _{x=-0.5} ,\quad Sh_1 =\left( {-\frac{\partial \phi _1 }{\partial x}} \right) _{x=-0.5} ,\quad Sh_2 =\left( {-\frac{\partial \phi _2 }{\partial x}} \right) _{x=-0.5} . \end{aligned}$$
(23)

Also, of interest are the average Nusselt number \(\overline{Nu} \) and average Sherwood numbers \(\overline{Sh_1 } \) and \(\overline{Sh_2 } \), which are given by

$$\begin{aligned} \overline{Nu} = \int \limits _0^1 Nu \hbox {d}y ,\quad Sh_1 =\;\int \limits _0^1 {Sh_1 } \hbox {d}y,\quad \overline{Sh_2 } =\int \limits _0^1 {Sh_2 } \hbox {d}y. \end{aligned}$$
(24)

3 Numerical Method

The non-dimensional governing equations, represented by Eqs. (19)–(21), and subject to the boundary conditions, Eq. (20), were written in weak form and solved numerically utilizing Galerkin finite element method (Reddy 1993). Invoking basis set \(\left\{ {\xi _k } \right\} _{k=1}^N \), the stream function (\(\psi \) ), the temperature, the concentration for phase 1, and the concentration for phase 2 were expanded as,

$$\begin{aligned} \psi\approx & {} \sum _{k=1}^N {\psi _k \xi _k \left( {x,y} \right) , }\quad \theta \approx \sum _{k=1}^N {\theta _k \xi _k \left( {x,y} \right) , \quad \phi _1 \approx \sum _{k=1}^N {\phi _1{_k } \xi _k \left( {x,y} \right) , } }\nonumber \\ \phi _2\approx & {} \sum _{k=1}^N {\phi _{{2}_{k}} \xi _k \left( {x,y} \right) , } \end{aligned}$$
(25)

for \(-0.5<x<0.5\) and \(0<y<1\). For all four variables, the basis function is the same, and hence, the total number of nodes for all variables is N. Employing the Galerkin finite element method on Eqs. (16)–(19) at nodes of internal domain \(\varOmega \), the nonlinear residual equations are, respectively, derived as,

$$\begin{aligned} R_i^1= & {} \sum _{k=1}^N {\psi _k \int _\Omega {\left[ {\frac{\partial \xi _i }{\partial x}\frac{\partial \xi _k }{\partial x}+\frac{\partial \xi _i }{\partial y}\frac{\partial \xi _k }{\partial y}} \right] \hbox {d}x\hbox {d}y} } -Ra\left( {\sum _{k=1}^N {\theta _{_k } } \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } \right) \nonumber \\&-Ra.Nc_1 \left( {\sum _{k=1}^N {\phi _{{1}_{k}} } \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } \right) - Ra.Nc_2 \left( {\sum _{k=1}^N {\phi _{{2}_{k}} } \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } \right) ,\quad \end{aligned}$$
(26)
$$\begin{aligned} R_i^2= & {} \left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\theta _{_k } \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&-\left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\theta _{_k } \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&+\sum _{k=1}^N {\theta _{_k } } \int _\Omega {\left( {\frac{\partial \xi _i }{\partial x}\frac{\partial \xi _k }{\partial x}+\frac{\partial \xi _i }{\partial y}\frac{\partial \xi _k }{\partial y}} \right) ,} \end{aligned}$$
(27)
$$\begin{aligned} R_i^3= & {} Le_1 \left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\phi _{1_{k} }\int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&-Le_1 \left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\phi _{1_{k }} \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&+\sum _{k=1}^N {\phi _{1_{k }} } \int _\Omega {\left( {\frac{\partial \xi _i }{\partial x}\frac{\partial \xi _k }{\partial x}+\frac{\partial \xi _i }{\partial y}\frac{\partial \xi _k }{\partial y}} \right) } , \end{aligned}$$
(28)

and

$$\begin{aligned} R_i^4= & {} Le_2 \left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\phi _{2_{k }} \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&-Le_2 \left( {\sum _{k=1}^N {\psi _k \int _\Omega {\frac{\partial \xi _k }{\partial x}\xi _i \hbox {d}x\hbox {d}y} } } \right) \left( {\sum _{k=1}^N {\phi _{2_{k }} \int _\Omega {\frac{\partial \xi _k }{\partial y}\xi _i \hbox {d}x\hbox {d}y} } } \right) \nonumber \\&+\sum _{k=1}^N {\phi _{2_{k }} } \int _\Omega {\left( {\frac{\partial \xi _i }{\partial x}\frac{\partial \xi _k }{\partial x}+\frac{\partial \xi _i }{\partial y}\frac{\partial \xi _k }{\partial y}} \right) } . \end{aligned}$$
(29)

In the above residual equations, \(R_{i}\), the bi-quadratic functions with three-point Gaussian quadrature were utilized to evaluate the integrals. Moreover, the Newton–Raphson method is employed to solve the nonlinear residual equations, Eqs. (26)–(29), for the coefficients of the expansions in Eq. (25). The details of the solution procedure have been discussed in the literature (Reddy 1993; Basak et al. 2006a, b) and have not been repeated here for the sake of brevity. It should be noted that the model incorporates Darcy’s law and the Lewis numbers which could be large about order of 10. Therefore, the flow behavior next to the walls is very important. Hence, the discretized equations were implemented on the non-uniform grid. In the non-uniform grid, the grid points are symmetrically clustered near the walls in both x and y directions with the aspect ratio of 1.05. The obtained system of equations was solved iteratively. The iteration process commenced from the initial guess of zero for stream function and 0.5 for the temperature and concentrations and repeated until the residuals for the stream functions, temperature and concentrations become lower than \(10^{-7}\). For parametric analysis of the problem, the parameter of study was smoothly increased and the obtained steady state solution in each step was utilized as an initial guess for the next solution in order to reduce the time of calculations. For example, for analysis of the effect of the increase in Rayleigh number on the solution, the problem was solved for Ra = 25 and converged. Then, the obtained solution was utilized as an initial guess for Ra = 50 and the iteration process commenced until the equations converge. The solution procedure, in the form of an in-house computational fluid dynamics (CFD) code, has been validated successfully against the results available in the literature.

3.1 Code Validation

In the case of a pure fluid when \(Nc_1 =Nc_2 =0\), a comparison between the results of the present study and the previous studies is performed in Table 1. Table 1 shows very good agreement between the results of the present study and those reported in the literature.

Table 1 Comparison of the average Nusselt number of the hot wall
Full size table

In addition, Costa (2004) has analyzed the double-diffusive natural convection in parallelogrammic enclosures filled with fluid-saturated porous media. Considering parallelogrammic enclosures with the inclination angle of zero, the geometry of the study of Costa (2004) reduces to the geometry of the present study, and assuming \(Nc_{2}=Le_{2}=0\) the present study reduces to the problem of double-diffusive natural convection. Hence, in this case the results of the present study are validated against the results of Costa (2004) in Table 2. As seen, the results are in very good agreement.

Table 2 Comparison of the average Nusselt number for the case of double-diffusive natural convection in a square cavity when \(Le_{1}=0.8\) and \(Nc_{1}=2\)
Full size table

3.2 Grid Check

A non-uniform structured \(100\times 100\) mesh, expanding with a symmetric distribution from the walls toward the center of the cavity with the element ratio of 1.05, is selected after some experimental execution of the results. Table 2 shows the evaluated values of the Nusselt numbers for mixture and the Sherwood numbers for phases 1 and 2. The results are reported for different grid sizes and two values of Rayleigh numbers (\(Ra=50\) and \(Ra=100\)) and three values of Lewis number phase 1 (\(Le_{1}=0.1\), 1.0 and 10) when \(Le_{2}=0.8\), \(Nc_{1}=2.0\) and \(Nc_{2}=2.0\). Table 3 shows that the grid size of \(100\times 100\) provides sufficient accuracy for the calculations. The results were also repeated for higher grid sizes, and consistence results were found. Hence, the grid size of \(100\times 100\) was utilized for the calculations.

Table 3 The evaluated values of Nu, \(Sh_{1}\) and \(Sh_{2}\) for different grid sizes when \(Le_{2}=0.8\), \(Nc_{1}=2.0\) and \(Nc_{2}=2.0\)
Full size table

4 Results and Discussion

The non-dimensional parameters in the present study are the \(Le_{1}\), \(Le_{2}\), \(Nc_{1}\), \(Nc_{2}\) and Ra. The Rayleigh number for the natural convection in the porous medium is considered in the practical range of \(\hbox {Ra}<100\). The Lewis number for gas mixtures is less than unity (i.e., Lewis number of the moisture air is about 0.8) and for some liquid mixtures is higher than unity. Hence, the Lewis number is considered in the range of 0.1–10. In the study of Costa (2004), the buoyancy ratio parameters are adopted in range of 0–5. Here, the range of buoyancy ratio parameters, \(Nc_{1}\) and \(Nc_{2}\), is adopted between 0 and 10.

Figures 2 and 3 show the contours of the isotherms, concentration of phase 1 and the streamlines for \(Ra=25\) and \(Ra=100\), respectively. The results of these figures are reported for fixed value of \(Le_{1}=Le_{2}=0.8\), \(Nc_{1}=Nc_{2}=2.0\). As the values of Lewis number and the buoyancy ratio parameters for two phases are equal, the contours of concentration for both phases of 1 and 2 are identical in this case. Comparison between the results of Figs. 2 and 3 shows that the increase in the Rayleigh number increases the velocity of the flow in the vicinity of the walls, and hence, the isotherms and isoconcentrations are closer to the walls for the case of Ra = 100. In the case of Ra = 100, the heat and mass transfer in the core of the cavity is almost vertical due to diffusion.

Fig. 2
figure 2

The isotherms, isoconcentrations and the streamlines for \(Le_{1} = Le_{2} = 0.8\), \(Nc_{1} = Nc_{2} = 2.0\) and \(Ra = 25\). a Isotherms (\(\theta \)). b Isoconcentrations (\(\phi _1\)). c Streamlines (\(\psi )\)

Full size image
Fig. 3
figure 3

The isotherms, isoconcentration and the streamlines for \(Le_{1} = Le_{2} = 0.8\), \(Nc_{1} = Nc_{2} = 2.0\) and \(Ra=100\). a Isotherms (\(\theta \)). b Isoconcentrations (\(\phi _1\)). c Streamlines (\(\psi \))

Full size image

Figure 4 shows the isotherms, streamlines and isoconcentrations for phases of 1 and 2 for the case of \(Le_{1}=0.8\), \(Le_{2}=10.0\), \(Nc_{1}=2.0\), \(Nc_{2}=10.0\) and \(Ra=100\). Indeed, the increase in \(Le_{2}\) tends to decrease the thickness of the concentration boundary layer, formed near the walls. The increase in \(Nc_{2}\) also tends to increase the induced buoyancy effects due to mass transfer. The \(Nc_{2}\) higher than unity indicates that the buoyancy effects due to mass transfer of phase 2 are strong and comparable with the thermal buoyancy effects. Hence, the migration of phase 2 in the vicinity of the vertical walls strongly influences the streamlines and the effect of mass transfer of phase 2 is the dominant effect in the cavity. In contrast with streamlines of Fig. 2c, which almost follow the isotherm patterns, the streamlines of Fig. 3b are under the influence of the concentration of phase 2. The mass transfer of phase 2 in the middle of the cavity is diffusive dominant and in vertical direction.

Fig. 4
figure 4

The isotherms, streamlines and isoconcentrations for \(Le_{1} = 0.8\), \(Le_{2} = 10.0\), \(Nc_{1} = 2.0\), \(Nc_{2} = 10.0\) and \(Ra = 100\). a Isotherms (\(\theta \)). b Streamlines (\(\psi \)). c Isoconcentrations (\(\phi _1\)). d Isoconcentrations (\(\phi _2\))

Full size image

Comparison between the results of this figure and Fig. 2 indicates that the isotherms and isoconcentrations of phase 1 are compacted in the bottom left and top right corners of the cavity. This is because of the increase in the velocity of the fluid near the vertical walls because of the induced strong buoyancy forces of phase 2. Almost entire of the top of the cavity is hot and high concentration of phase 1, and entire of the bottom of the cavity is cold and low concentration of phase 1. Hence, the temperature and concentration boundary layers next to the vertical walls almost follow the patterns of the streamlines, induced by the phase 1.

Figures 5, 6 and 7 show the average Nusselt number for mixture (fluid), the average Sherwood number for phase 1 and the average Nusselt number for phase 2, respectively. The parameters of interest, i.e., Nu, \(Sh_{1}\) and \(Sh_{2}\), are plotted as a function of Lewis number for phase 1 (\(Le_{1})\) and for various values of the Lewis number for phase 2 (\(Le_{2})\). Figure 5 shows that for very small values of \(Le_{1}\), the Nusselt number increases and then starts to decrease monotonically. Hence, for small values of \(Le_{1}\) (about 0.1) there are maximum values for Nusselt number. The increase in \(Le_{1}\) tends to reduce the thickness of the concentration boundary layer next to the wall. Figure 7 also shows a peak for the mass transfer of phase 2 at the surface (\(Sh_{2})\) about \(Le_{1}=0.1\) for small value of \(Le_{2}\,(Le_{2}=1\), \(Le_{2}=2.0\)). However, for large value of \(Le_{2}\), i.e., \(Le_{2}=10.0\), the observed peak is very smooth and shifts to values of \(Le_{1}\approx 2\). These figures also depict that the increase in \(Le_{1}\) or \(Le_{2}\) reduces the Nusselt number. As shown in Fig. 4, for large values of Lewis number, the thickness of the formed boundary layer of concentration over the vertical walls decreases.

Fig. 5
figure 5

The variation of average Nusselt number as a function of \(Le_{1}\) for various values of \(Le_{2}\)

Full size image
Fig. 6
figure 6

The variation of average Sherwood number for phase 1 as a function of \(Le_{1}\) for various values of \(Le_{2}\)

Full size image
Fig. 7
figure 7

The variation of average Sherwood number for phase 2 as a function of \(Le_{1}\) for various values of \(Le_{2}\)

Full size image

For very large values of Lewis numbers, the concentration gradient over the vertical walls is a very narrow region next to the walls, in which the induced buoyancy effect due to concentration gradient is very strong. In the mentioned narrow regions, the flow would move fast toward the top (for hot and high concentration) and toward bottom (for cold and low concentration) walls. The strong flow near the vertical walls will carry a significant amount of the volume fraction of the corresponding phase and a lower amount of the other phase from the area adjacent to vertical walls and move it toward the horizontal top and bottom walls.

It should be noticed that in the regions next to walls, where the flow is fast, Darcy’s forces are also very large and tend to reduce the velocities at the edge of the boundary layers instantly. Hence, the rest of the cavity is almost stratified. In the stratified regions, the mass transfer is mostly limited to the diffusive mechanism. Indeed, as the Lewis numbers increases, the induced buoyancy forces, due to mass transfer effects, are strong, but the effective regions are very limited. When the Lewis number decreases, the thickness of the boundary layer increases, and hence, the buoyancy force due to mass transfer could be distributed in a larger area; as a result, the induced velocities in the cavity are smooth. When the Lewis number significantly decreases, the affective region of the buoyancy induced force due to mass transfer reaches the core of the cavity. Increasing the Lewis number beyond this point would reduce the induced mass transfer buoyancy force in the entire cavity, and consequently, it would reduce the flow velocities, the Sherwood and Nusselt numbers, which this is the reason for the observed maximum Sherwood and Nusselt peaks in Figs. 5 and 7.

Figures 6 and 7 show that the increase in the Lewis number for phase 1 would increase the Sherwood for phase 1 (\(Sh_{1})\), and similarly the increase in \(Le_{2}\) increases \(Sh_{2}\). As mentioned, the increase in Le decreases the thickness of the concentration boundary layer over the vertical walls for the corresponding phase, which results in the augmentation of the concentration slope (Sherwood number) of the corresponding phase at the vertical walls. The effect of variation of Lewis number for a phase is complicated on the other phase. Figure 7 shows some peaks for \(Sh_{2}\) by the variation of the \(Le_{1}\). The reason for these peaks is similar to those for Nusselt number in Fig. 5.

Figures 8, 9 and  10 show the average Nusselt number for the mixture, the average Sherwood number for phase 1 and the average Sherwood number for phase 2, respectively. These figures depict the effect of the buoyancy ratio parameters (\(Nc_{1}\) and \(Nc_{2})\) as a function of the Lewis number for phase 1 (\(Le_{1})\) on the heat and mass transfer in the cavity. These figures also in agreement with the previous figures depict the maximum peaks for the average Nusselt number and the average Sherwood number for phase 2.

Fig. 8
figure 8

The variation of average Nusselt number as a function of \(Le_{1}\) for different values of the buoyancy ratio parameters of \(Nc_{1}\) and \(Nc_{2}\)

Full size image
Fig. 9
figure 9

The variation of average Sherwood number for phase 1 as a function of \(Le_{1}\) for different values of the buoyancy ratio parameters of \(Nc_{1}\) and \(Nc_{2}\)

Full size image
Fig. 10
figure 10

The variation of average Sherwood number for phase 2 as a function of \(Le_{1}\) for different values of the buoyancy ratio parameters of \(Nc_{1}\) and \(Nc_{2}\)

Full size image

Figure 8 shows that the increase in buoyancy ratio parameters increases the average Nusselt number. Indeed, the induced buoyancy force due to mass transfer is a function of the Lewis number and the corresponding buoyancy ratio parameter. The Lewis number dictates the affecting area of the buoyancy force and the corresponding buoyancy ratio parameter dictates the strength of the induced buoyancy force. For each phase, the variation of these sets of parameters (i.e., Le and Nc) would directly affect the flow and then the heat transfer rate from the surface. However, the variation of these parameters (Le and its corresponding Nc) would indirectly affect the other phase through the effect on the streamlines. Hence, the green dash line indicates that the raise of \(Nc_{2}\) increases the average Nusselt number; however, this increase is almost independent of the Lewis number for phase 1 (\(Le_{1})\). The blue dash-dot line indicates that the raise of \(Nc_{1}\) also increases average Nusselt number, but the observed increase is a decreasing function of the \(Le_{1}\). Comparison between the dashed line (green line for \(Nc_{1}=0.1\) and \(Nc_{2}=1.0\)) and the dash-dot line (blue line for \(Nc_{1}=1.0\) and \(Nc_{2}=0.1\)) in Fig. 8 indicates that the effective region of phase 1 is wide when the \(Le_{1}\) is very small, and hence, the increase in \(Nc_{1}\) from 0.1 to 1.0 induces high and smoother buoyancy forces, and consequently, it results in higher values of average Nusselt number compared to the same increase in the amount of \(Nc_{2}\). The same conclusion as Fig. 8 is also true for Fig. 10 as the second phase would also follow the induced flow patterns as the temperature distribution in the cavity. Figures 8, 9 and 10 show that the increase in \(Le_{1}\) raises the average mass transfer for its corresponding phase (average Sherwood number for phase 1). The raise of \(Nc_{1}\) or \(Nc_{2}\) would boost the heat and mass transfer from the surface due to the enhancement in the buoyancy forces.

Figures 11 and 12 show the effect of buoyancy ratios (\(Nc_{1})\) and (\(Nc_{2})\) on the average Nusselt number and the average Sherwood number of phase 1, when \(Le_{1}=Le_{2}=0.8\). Figures 11 and 12 in agreement with Figs. 8, 9 and 10 show that the increase in the buoyancy ratio parameters increases the heat and mass transfer from the surface. These figures indicate that the increase in the average Nusselt and Sherwood numbers is almost a linear function of the buoyancy ratios. As the Lewis number for both phases is considered equal (\(Le_{1}=Le_{2}=0.8\)), the obtained Sherwood numbers for both phases would be the same, and hence, the figure of \(Sh_{2}\) is not depicted here for the sake of brevity.

Fig. 11
figure 11

The variation of average Nusselt number as a function of \(Le_{1}\) for different values of the buoyancy ratio parameters of \(Nc_{1}\) and \(Nc_{2}\)

Full size image
Fig. 12
figure 12

The variation of average Sherwood number for phase 1 as a function of \(Le_{1}\) for different values of the buoyancy ratio parameters of \(Nc_{1}\) and \(Nc_{2}\)

Full size image

Figures 13, 14 and  15 show the average Nusselt number for the mixture, the average Sherwood number for phase 1 and the average Sherwood number for phase 2, respectively. These figures depict the effect of the Rayleigh number as a function of the \(Le_{1}\) on the heat and mass transfer in the cavity. These figures illustrate that the increase in the Rayleigh number boosts the heat and mass transfer from the surfaces. The increase in Rayleigh number almost linearly shifts the Nusselt number curves upwards. When Lewis number is about unity, the thickness of the concentration boundary layer is about the thickness of the temperature boundary layer over the vertical and horizontal walls, and hence, the behaviors of the temperature distribution in the cavity are very similar to the concentration distribution for this phase. Thus, in Fig. 15, in which \(Le_{2}=0.8\) (about unity) the pattern and the order of magnitude of Nusselt and Sherwood numbers (Nu and \(Sh_{2})\) are very similar. This is because of the fact that the variation of \(Le_{1}\) indirectly and through the streamlines affects Nu and \(Sh_{2}\).

Fig. 13
figure 13

The variation of average Nusselt number as a function of \(Le_{1}\) for different values of the Rayleigh number

Full size image
Fig. 14
figure 14

The variation of average Sherwood number for phase 1 as a function of \(Le_{1}\) for different values of the Rayleigh number

Full size image
Fig. 15
figure 15

The variation of average Sherwood number for phase 2 as a function of \(Le_{1}\) for different values of the Rayleigh number

Full size image

For very small values of Rayleigh number, the induced buoyancy forces due to heat and mass transfer are small, and hence, the variation of Lewis or buoyancy ratio only shows smooth effects on the heat and mass transfer parameters (i.e., Nu and Sh). The raise of the Rayleigh number boosts the effect of Nc and Le and induces large buoyancy forces. As a result, the increase in Rayleigh number increases the effect of the variation of Lewis number on the mass transfer from the walls (see Fig. 14).

Fig. 16
figure 16

The variation of average Nusselt number as a function of Rayleigh number for different values of Lewis number of phase 2

Full size image
Fig. 17
figure 17

The variation of average Sherwood number for phase 1 as a function of Rayleigh number for different values of Lewis number of phase 2

Full size image
Fig. 18
figure 18

The variation of average Sherwood number for phase 2 as a function of Rayleigh number for different values of Lewis number of phase 2

Full size image

Figures 16, 17 and 18 show the average Nusselt number for the mixture, the average Sherwood number for phase 1 and the average Sherwood number for phase 2, respectively, as a function of Rayleigh number and various values of \(Le_{2}\). These figures also depict that the average Nusselt number and average Sherwood number for phase 1 are a raising function of the Rayleigh number but a decreasing function of \(Le_{2}\). The variation of Rayleigh number and Lewis number (\(Le_{2})\) in Fig. 18 interestingly shows when the \(Le_{2}\) is very small (\(Le_{2}=0.1\)), and the raise of Rayleigh number does not affect the mass transfer from the wall. For large values of Rayleigh number, the increase in Rayleigh number significantly increases the mass transfer from the wall (\(Sh_{2})\). The large values of \(Le_{2}\) result in a very narrow boundary layer of concentration for phase 2 and large gradients of the concentration for phase 2. The buoyancy forces are also strong in the mentioned narrow region. Hence, in this case, any increase in the Rayleigh number significantly boosts the mass transfer for phase 2. In contrast, when the \(Le_{2}\) is very small, the concentration gradients, and the corresponding buoyancy forces are very low and the increase in Rayleigh number could only show very smooth effects on \(Sh_{2}\).

5 Conclusion

Triple-diffusive natural convection flow, heat and mass transfer of a mixture in a square porous cavity is theoretically analyzed. The governing partial differential equations were transformed into a non-dimensional form. The non-dimensional governing equations are a function of Rayleigh number, Lewis numbers for phases 1 and 2, and the buoyancy ratios for phases 1 and 2. The governing equations were solved using a finite element code. The effect of the non-dimensional parameters on the flow, temperature and concentrations was studied. The main outcomes of the present study can be summarized as follows:

  1. (1)

    When the Lewis number of a phase is about 0.1, there is a maximum value for the heat transfer and mass transfer of the other phase due to strong mass transfer buoyancy forces.

  2. (2)

    The increase in Lewis number increases the mass transfer of the corresponding phase from the wall, but it could reduce or raise the mass transfer of the other phase, depending on the Lewis number of the second phase.

  3. (3)

    The increase in the buoyancy ratio parameters and the Rayleigh number boosts the mass transfer buoyancy forces and increases the heat and mass transfer.

  4. (4)

    When the Lewis number for a phase is small, the augmentation of Rayleigh number cannot induce a significant boost on the mass transfer of the corresponding phase.

In the present study, as a first study, we focused on the aided mass transfer of the phases. The future studies can focus on the opposing mass transfer on the triple-convective heat transfer. In addition, it was found that the mass transfer of a phase could significantly affect the heat transfer of the mixture as well as the mass transfer of the other phase; hence, one of the phases could be employed as a controlling phase for control of heat and mass transfer in the system.