1 Introduction

Convective flow in cavities filled with porous media is a topic of fundamental heat transfer in many analyses and has received considerable attention over the last few decades. This interest is due to its wide range of applications, for example, high-performance insulation for buildings, chemical catalytic reactors, packed sphere beds, grain storage, float glass production, air-conditioning in rooms, cooling of electronic devices, and such geophysical problems as frost heave (Kaviany 1999; Nield and Bejan 2013; Saleh and Hashim 2013).

It has been shown by Mohamad (1995) that natural convection in open cavities has received much attention due to the importance of such geometry in solar thermal receiver systems, fire research, electronic cooling devises, energy-saving household refrigerators, etc. Further, Bilgen and Oztop (2005) pointed out that partially open cavities are encountered in various engineering systems, uncovered flat plate solar collectors having rows of vertical strips, in buildings, etc. In these situations, the flow may be substantially affected by the flow at the openings. The spread and growth of the combustion products in a room, for example, are substantially governed by the location and size of the doors and windows (Abib and Jaluria 1988).

It is well established (see De Groot and Mazur 1984) that a multicomponent system under non-isothermal condition is subject to mass transfer related to coupled-transport phenomena. This has strong practical importance in many situations since the flow dynamics and convective patterns in mixtures are more complex than those of one-component fluids due to the interplay between advection and mixing, solute diffusion (see Davarzani et al. 2010). There are many important processes in nature and technology where thermal diffusion plays a crucial role. It has various technical applications, such as isotope separation in liquid and gaseous mixtures (see Rabinovich 1981), polymer solutions and colloidal dispersions (see Wiegand 2004), study of compositional variation in hydrocarbon reservoirs (see Firoozabadi 1991), and coating of metallic items. It also affects component separation in oil wells, solidifying metallic alloys, volcanic lava, and in the Earth Mantle (see Ilya 2006).

The double-diffusive convection in a porous cavity has been studied by several researchers. Goyeau et al. (1996) considered the double-diffusive natural convection in a porous cavity using Darcy-Brinkman formulation. Karimi-Fard et al. (1997) investigated the non-Darcian effects on double-diffusive natural convection within a porous square cavity filled with a porous media. At the same time, Nithiarasu et al. (1997) considered the double-diffusive natural convection in a fluid-saturated porous cavity with a freely convecting wall. Bennacer et al. (2001) considered the problem of the double-diffusive natural convection in a vertical enclosure filled with anisotropic porous medium. The problem of double-diffusive convection in inclined triangular porous enclosures with sinusoidal variation of boundary conditions was discussed numerically by Mansour et al. (2011). Finally, we mention the paper by Rashad et al. (2014) (who has studied the effects of chemical reaction and thermal radiation on unsteady double-diffusive convection in a square enclosure filled with a porous medium with sinusoidal boundary conditions on the bottom wall).

It is already well known that ultrahigh-performance cooling is one of the most vital needs of many industrial technologies. However, inherently low thermal conductivity is a primary limitation in developing energy-efficient heat transfer fluids that are required for ultrahigh-performance cooling. Because of the increasing necessity of the modern technology, including chemical processes, microelectronics, biotechnology, etc., it is very important to obtain new type of fluids, having improved heat transfer characteristics. In order to enhance the thermal characteristics of the fluids, one can form mixtures by adding ultrafine solid particles (metallic, nonmetallic or polymeric) to the fluid. Nanofluids technology, a new interdisciplinary field of great importance, where nanoscience, nanotechnology, and thermal engineering meet, has largely developed over the past several decades. Nanofluids are new types of fluids containing small fractions of nanoparticles, usually smaller than 100 nm, which are uniformly and stable suspended in a liquid. The thermal behavior of nanofluids provides a basis for heat transfer intensification, in industrial sectors including power generation, thermal therapy for cancer treatment, chemical sectors, ventilation, refrigeration, etc. It is also mentioned in the book by Schaefer (2010) that from the top ten advances in materials science, at least five are directly related to nanoscience, such as materials science, information processing, biotechnology, chemistry, and medicine. In biological systems, nanosized structures play an important role from proteins to deoxyribonucleic acid carrying the genetic code, ribonucleic acid.

Buongiorno (2006) developed a non-homogeneous equilibrium model by considering the effect of the Brownian diffusion and thermophoresis that are important slip mechanisms in nanofluid. This model has been widely used by many researchers to study the free convection boundary layer flow past a vertical flat plate embedded in a porous medium filled by nanofluids (Nield and Kuznetsov 2011; Kuznetsov and Nield 2011) or flow and heat transfer over a stretching/shrinking surface (Khan and Pop 2010; Bachok et al. 2011), etc.

In the present study, we investigate the double-diffusive mixed convection in a porous open cavity filled with a nanofluid using the mathematical nanofluid model proposed by Buongiorno (2006). The Darcy model is used in the porous layer. It should be mentioned that many researchers focused their studies on effects of aspect ratios on the double-diffusive natural convection in enclosures. Chamkha and Al-Naser (2001) studied the unsteady laminar double-diffusive convective flow in an inclined rectangular enclosure filled with a uniform porous medium. Costa (2004a) studied the double-diffusive natural convections in parallelogrammic enclosures, and emphasis was given to the situation that the porous media in the enclosure were saturated with moist air. The same author (Costa 2004b) also pointed out that the combinations of different aspect ratios and inclination angles can lead to considerably high heat and mass transfer rates in the enclosure. Further, we mention that Jeng et al. (2009) performed the experimental and numerical studies of the transient natural convection due to mass transfer in the inclined enclosures at different inclination angles. The Rayleigh number Ra ranged from \(1.126\times 10^{8}\) to \(1.157\times 10^{11}\) and the angle of inclination \(\varphi \) varied from 30 to \(90^{\circ }\); the aspects ratio of the enclosure \(A\) was changed from 0.6 to 1.

2 Basic Equations

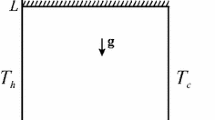
Figure 1 shows the considered double-diffusive mixed convection flow, heat and mass transfer in a porous open cavity filled with a water based nanofluid. It is assumed that nanoparticles are suspended in the nanofluid using either surfactant or surface charge technology. This prevents nanoparticles from agglomeration and deposition on the porous matrix (see Nield and Kuznetsov 2011; Kuznetsov and Nield 2011). The porous medium is assumed to be homogeneous and isotropic, and the local thermal equilibrium is valid. The flow in the cavity is considered to be steady, laminar, and incompressible. The domain of interest is a square cavity of size \(L\) with an inlet of size \(0.2\cdot L\) in the bottom part of the left vertical wall and an outlet of the same size in the upper part of the right vertical wall. The heat source of high temperature \(T_h \) and a contaminant source of high concentration \(\overline{{C}}_h \) are considered on the right vertical wall. The rest of the walls of the cavity are assumed to be adiabatic and impermeable. In addition, the incoming nanofluid through the inlet with nanoparticle volume fraction \(\overline{{\varphi }}_{\mathrm{in}} \) is at a uniform horizontal velocity \(\overline{{u}}_{\mathrm{in}} \left( {\overline{{v}}_{\mathrm{in}} =0} \right) \) at the constant ambient temperature \(T_{\mathrm{in}} \) and concentration \(\overline{{C}}_{\mathrm{in}} \).

Fig. 1
figure 1

Physical model and coordinate system

Full size image

It should be noted that we investigate in this paper the interaction between base fluid, nanoparticles, and porous structure when the base fluid of nanofluid is a binary fluid such as salty water. The outcome is that we are studying a sort of triple-diffusion problem in a porous structure involving heat, the nanoparticles and the contaminant. As suggested by one Reviewer, there should be a net throughflow through the cavity, so that there will be an extra contribution to the nanoparticle flux (see Jaimala and Singh 2014; Nield and Kuznetsov 2015). Thus, the basic equations for the flow, heat transfer, contaminant and nanoparticles transport can be written in the following form (see Jaimala and Singh 2014, and Nield and Kuznetsov 2015).

$$\begin{aligned}&\nabla \cdot \mathbf{V}=0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\rho _{_{f0}}}{\varepsilon }\frac{\partial \mathbf{V}}{\partial t}=-\nabla p-\frac{\mu }{K}\mathbf{V}+\left[ {\overline{{\varphi }}\rho _p +\left( {1-\overline{{\varphi }}} \right) \left\{ {\rho _{_{f0}} \left( {1-\beta _T \left( {T-T_{\mathrm{in}} } \right) -\beta _C \left( {\overline{{C}}-\overline{{C}}_{\mathrm{in}} } \right) } \right) } \right\} } \right] \mathbf{g} \end{aligned}$$
(2)
$$\begin{aligned}&\left( {\rho C_p } \right) _m \frac{\partial T}{\partial t}\;+\left( {\rho C_p } \right) _f \left( {\mathbf{V}\cdot \nabla } \right) T =\nabla \left( {k_m \nabla T} \right) +\varepsilon \left( {\rho C_p } \right) _p \Bigg [ D_B \nabla \overline{{\varphi }}\cdot \nabla T\nonumber \\&\left. +\left( {{D_T }/{T_c }} \right) \nabla T\cdot \nabla T- \frac{\left( {\overline{{\varphi }}-\overline{{\varphi }}_{\mathrm{in}} } \right) }{\varepsilon }\mathbf{V}\cdot \nabla T \right] +\;\left( {\rho C_p } \right) _m \nabla \left( {D_{T C} \nabla \overline{{C}}} \right) \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \overline{{C}}}{\partial t}+\frac{1}{\varepsilon }\left( {\mathbf{V}\cdot \nabla } \right) \overline{{C}}=\nabla \left[ {D_{Sm} \nabla \overline{{C}}+D_{CT} \nabla T} \right] \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial \overline{{\varphi }}}{\partial t}+\frac{1}{\varepsilon }\left( {\mathbf{V}\cdot \nabla } \right) \overline{{\varphi }}=\nabla \left[ {D_B \nabla \overline{{\varphi }}+\left( {{D_T }/{T_c }} \right) \nabla T} \right] \end{aligned}$$
(5)

where \(\mathbf{V}\) is the Darcy velocity vector, \(T\) is the fluid temperature, \(\overline{{C}}\) is the contaminant concentration, \(\overline{{\varphi }}\) is the nanoparticle volume fraction, \(t\) is the time, \(p\) is the fluid pressure, g is the gravity vector, \(\varepsilon \) is the porosity of the porous medium, \(K\) is the permeability of the porous medium, \(\rho _{f0} \) is the reference density of the fluid, \(\mu \) is the viscosity of the fluid, \(\beta _T \) is the thermal expansion coefficient, \(\beta _C \) is the contaminant expansion coefficient, \(\rho _p \) is the nanoparticle mass density, \(\left( {\rho {{C}}_p } \right) _f \) is the volume heat capacity of the fluid, \(\left( {\rho {C}_p } \right) _m \) is the effective volume heat capacity of the porous medium, \(k_m \) is the effective thermal conductivity of the porous medium, \(\left( {\rho {{C}}_p } \right) _p \) is the effective volume heat capacity of the nanoparticle material, \(D_B \) is the Brownian diffusion coefficient, \(D_T \) is the thermophoretic diffusion coefficient, \(D_{TC} \) is the diffusivity of Dufour type, \(D_{Sm} \) is the contaminant diffusivity for the porous medium, and \(D_{CT} \) is the diffusivity of Soret type. It should be mentioned that we have neglected here the term \(k_d \nabla T\), where \(k_d\) is the enhancement in the thermal conductivity due to the thermal dispersion (see Khanafer et al. 2003 and Nakayama 1995). This is because we have used the model proposed by Buongiorno (2006), and Nield and Kuznetsov (2015). But, in the future work, we will take into account this phenomenon in order to evaluate this mechanism in comparison with other ones.

The flow is assumed to be slow so that an advective term and a Forchheimer quadratic drag term do not appear in the momentum equation. It is assumed also that the contaminant does not affect the transport of the nanoparticles. In keeping with the Boussinesq approximation and an assumption that the nanoparticle concentration is dilute, and with a suitable choice for the reference pressure, we can linearize the momentum equation and write Eq. (2) as

$$\begin{aligned} 0=-\nabla p-\frac{\mu }{K}\mathbf{V}+\left[ {\overline{{\varphi }}\left( {\rho _p -\rho _{{_{f0}}} } \right) +\rho _{{_{f0}}} \left( {1-\left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) \left\{ { \beta _T \left( {T-T_{\mathrm{in}} } \right) + \beta _C \left( {\overline{{C}}-\overline{{C}}_{\mathrm{in}} } \right) } \right\} } \right) } \right] \mathbf{g} \end{aligned}$$
(6)

Equations (1), (3)–(6) for the steady problem under consideration can be written in dimensional coordinates \(\overline{{x}},\overline{{y}}\) as follows

$$\begin{aligned}&\frac{\partial \overline{{u}}}{\partial \overline{{x}}}+\frac{\partial \overline{{v}}}{\partial \overline{{y}}}=0 \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\partial p}{\partial \overline{{x}}}=-\frac{\mu }{K}\overline{{u}} \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\partial p}{\partial \overline{{y}}}=-\frac{\mu }{K}\overline{{v}}-\left[ {\overline{{\varphi }}\left( {\rho _p -\rho _{_{f0}} } \right) +\rho _{_{f0}} \left( {1-\left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) \left\{ { \beta _T \left( {T-T_{\mathrm{in}} } \right) + \beta _C \left( {\overline{{C}}-\overline{{C}}_{\mathrm{in}} } \right) } \right\} } \right) } \right] g \end{aligned}$$
(9)
$$\begin{aligned}&\overline{{u}}\frac{\partial T}{\partial \overline{{x}}}+\overline{{v}}\frac{\partial T}{\partial \overline{{y}}}=\alpha _m \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) +\delta \left\{ {D_B \left( {\frac{\partial \overline{{\varphi }}}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{x}}}+\frac{\partial \overline{{\varphi }}}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{y}}}} \right) } \right. \nonumber \\&\quad \left. {-\frac{\left( {\overline{{\varphi }}-\overline{{\varphi }}_{\mathrm{in}} } \right) }{\varepsilon }\left( {\overline{{u}}\frac{\partial T}{\partial \overline{{x}}}+\overline{{v}}\frac{\partial T}{\partial \overline{{y}}}} \right) +\frac{D_T }{T_c }\left[ {\left( {\frac{\partial T}{\partial \overline{{x}}}} \right) ^{2}+\left( {\frac{\partial T}{\partial \overline{{y}}}} \right) ^{2}} \right] } \right\} +\sigma D_{T C} \left( {\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(10)
$$\begin{aligned}&\frac{1}{\varepsilon }\left( {\overline{{u}}\frac{\partial \overline{{C}}}{\partial \overline{{x}}}+\overline{{v}}\frac{\partial \overline{{C}}}{\partial \overline{{y}}}} \right) =D_{Sm} \left( {\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{y}}^{2}}} \right) +D_{CT} \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(11)
$$\begin{aligned}&\frac{1}{\varepsilon }\left( {\overline{{u}}\frac{\partial \overline{{\varphi }}}{\partial \overline{{x}}}+\overline{{v}}\frac{\partial \overline{{\varphi }}}{\partial \overline{{y}}}} \right) =D_B \left( {\frac{\partial ^{2}\overline{{\varphi }}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{\varphi }}}{\partial \overline{{y}}^{2}}} \right) +\frac{D_T }{T_{\mathrm{in}} }\left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(12)

where \( \overline{{u}},\overline{{v}}\) are the velocity components along \(\overline{{x}},\overline{{y}}\) directions, respectively.

One can introduce a stream function \(\overline{{\psi }}\) defined by

$$\begin{aligned} \overline{{u}}=\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}},\quad v=- \frac{\partial \overline{{\psi }}}{\partial \overline{{x}}} \end{aligned}$$
(13)

so that Eq. (7) is satisfied identically. We are then left with the following equations

$$\begin{aligned}&\frac{\partial ^{2}\overline{{\psi }}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{\psi }}}{\partial \overline{{y}}^{2}}=\frac{\rho _p -\rho _{{_{f0}}} }{\mu }Kg\frac{\partial \overline{{\varphi }}}{\partial \overline{{x}}}-\frac{\rho _{{_{f0}}} g\beta _T \left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) K}{\mu }\frac{\partial T}{\partial \overline{{x}}}-\frac{\rho _{_{f0}} g\beta _C \left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) K}{\mu }\frac{\partial \overline{{C}}}{\partial \overline{{x}}} \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{x}}}-\frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{y}}}=\alpha _m \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) +\delta \left\{ {D_B \left( {\frac{\partial \overline{{\varphi }}}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{x}}}+\frac{\partial \overline{{\varphi }}}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{y}}}} \right) } \right. \nonumber \\&\quad \left. {-\frac{\left( {\overline{{\varphi }}\;-\;\overline{{\varphi }}_{\mathrm{in}} } \right) }{\varepsilon }\left( {\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial T}{\partial \overline{{x}}}-\frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial T}{\partial \overline{{y}}}} \right) +\frac{D_T }{T_c }\left[ {\left( {\frac{\partial T}{\partial \overline{{x}}}} \right) ^{2}+\left( {\frac{\partial T}{\partial \overline{{y}}}} \right) ^{2}} \right] } \right\} \nonumber \\&\quad +\sigma D_{T C} \left( {\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(15)
$$\begin{aligned}&\frac{1}{\varepsilon }\left( {\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial \overline{{C}}}{\partial \overline{{x}}}- \frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial \overline{{C}}}{\partial \overline{{y}}}} \right) =D_{Sm} \left( {\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{C}}}{\partial \overline{{y}}^{2}}} \right) +D_{CT} \left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(16)
$$\begin{aligned}&\frac{1}{\varepsilon }\left( {\frac{\partial \overline{{\psi }}}{\partial \overline{{y}}}\frac{\partial \overline{{\varphi }}}{\partial \overline{{x}}}- \frac{\partial \overline{{\psi }}}{\partial \overline{{x}}}\frac{\partial \overline{{\varphi }}}{\partial \overline{{y}}}} \right) =D_B \left( {\frac{\partial ^{2}\overline{{\varphi }}}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}\overline{{\varphi }}}{\partial \overline{{y}}^{2}}} \right) +\frac{D_T }{T_{\mathrm{in}} }\left( {\frac{\partial ^{2}T}{\partial \overline{{x}}^{2}}+\frac{\partial ^{2}T}{\partial \overline{{y}}^{2}}} \right) \end{aligned}$$
(17)

Introducing the following dimensionless variables

$$\begin{aligned} x= & {} {\overline{{x}}}/L,\quad y={\overline{{y}}}/L,\quad \psi ={\overline{{\psi }}}/{\alpha _m },\quad \theta ={\left( {T-T_{\mathrm{in}} } \right) }/{\left( {T_h -T_{\mathrm{in}} } \right) },\quad \nonumber \\ C= & {} {\left( {\overline{{C}}-\overline{{C}}_{\mathrm{in}} } \right) }/{\left( {\overline{{C}}_h -\overline{{C}}_{\mathrm{in}} } \right) },\quad \varphi ={\overline{{\varphi }}}/{\overline{{\varphi }}_{\mathrm{in}} } \end{aligned}$$
(18)

and substituting (18) into Eqs. (14)–(17), we obtain

$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial x^{2}}\;+\;\frac{\partial ^{2}\psi }{\partial 2^{2}}=-{\textit{Ra}} \left( {\frac{\partial \theta }{\partial x}\;+\;{\textit{Nc}} \frac{\partial C}{\partial x}\;-\;{\textit{Nr}}\frac{\partial \varphi }{\partial x}} \right) \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}=\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}+{\textit{Nb}}\left( {\frac{\partial \varphi }{\partial x}\frac{\partial \theta }{\partial x}+\frac{\partial \varphi }{\partial y}\frac{\partial \theta }{\partial y}} \right) \nonumber \\&\quad +\left( {1-\;\varphi } \right) {\textit{Nb}}\cdot {\textit{Ln}}\left( {\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}} \right) +{\textit{Nt}}\left[ {\left( {\frac{\partial \theta }{\partial x}} \right) ^{2}\!+\!\left( {\frac{\partial \theta }{\partial y}} \right) ^{2}} \right] +{\textit{Nd}}\left( {\frac{\partial ^{2}C}{\partial x^{2}}\!+\!\frac{\partial ^{2}C}{\partial y^{2}}} \right) \end{aligned}$$
(20)
$$\begin{aligned}&\frac{\partial \psi }{\partial y}\frac{\partial C}{\partial x}- \frac{\partial \psi }{\partial x}\frac{\partial C}{\partial y}=\frac{1}{{\textit{Le}}}\left( {\frac{\partial ^{2}C}{\partial x^{2}}+\frac{\partial ^{2}C}{\partial y^{2}}} \right) +\frac{{\textit{Ld}}}{{\textit{Le}}}\left( {\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}} \right) \end{aligned}$$
(21)
$$\begin{aligned}&\frac{\partial \psi }{\partial y}\frac{\partial \varphi }{\partial x}- \frac{\partial \psi }{\partial x}\frac{\partial \varphi }{\partial y}=\frac{1}{{\textit{Ln}}}\left( {\frac{\partial ^{2}\varphi }{\partial x^{2}}+\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) +\frac{{\textit{Nt}}}{{\textit{Ln}}\cdot {\textit{Nb}}}\left( {\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}} \right) \end{aligned}$$
(22)

The corresponding boundary conditions for these equations are as follows (see Kuznetsov and Nield 2013)

$$\begin{aligned} \psi= & {} {\textit{Re}}\cdot \textit{Pr} \cdot 0.2,\quad \frac{\partial \theta }{\partial x}=0,\quad \frac{\partial C}{\partial x}=0,\quad \frac{\partial \varphi }{\partial x}=0\quad \hbox {on}\quad x=0,\quad 0.2\le y<1 \nonumber \\ \psi= & {} {\textit{Re}}\cdot \textit{Pr} \cdot y,\quad \theta =0,\quad C=0,\quad \varphi =1\quad \hbox {on}\quad x=0,\quad 0<y<0.2 \nonumber \\ \psi= & {} 0,\quad \theta =1,\quad C=1,\quad {\textit{Nb}}\frac{\partial \varphi }{\partial x}+{\textit{Nt}}\frac{\partial \theta }{\partial x}=0\quad \hbox {on}\quad x=1,\quad 0<y\le 0.8\nonumber \\ \frac{\partial \psi }{\partial x}= & {} 0,\quad \frac{\partial \theta }{\partial x}=0,\quad \frac{\partial C}{\partial x}=0,\quad \frac{\partial \varphi }{\partial x}=0\quad \hbox {on}\quad x=1,\quad 0.8<y<1 \nonumber \\ \psi= & {} 0,\quad \frac{\partial \theta }{\partial y}=0,\quad \frac{\partial C}{\partial y}=0,\quad \frac{\partial \varphi }{\partial y}=0\quad \hbox {on}\quad y=0 \nonumber \\ \psi= & {} {\textit{Re}}\cdot \textit{Pr} \cdot 0.2,\quad \frac{\partial \theta }{\partial y}=0,\quad \frac{\partial C}{\partial y}=0,\quad \frac{\partial \varphi }{\partial y}=0\quad \hbox {on}\quad y=1 \end{aligned}$$
(23)

Here Re is the Reynolds number, Pr is the Prandtl number for the porous medium,Ra is the Rayleigh number for the porous media, Nr is the nanofluid buoyancy ratio, Nc is the regular double-diffusive buoyancy ratio, Nb is the Brownian motion parameter, Nt is the thermophoresis parameter, Nd is the modified Dufour parameter, Le is the usual Lewis number, Ld is the Dufour-contaminant Lewis number, and Ln is the nanofluid Lewis number, which are defined as

$$\begin{aligned} {\textit{Re}}= & {} \frac{\rho _{{_{f0}}} \overline{{u}}_{\mathrm{in}} L}{\mu },\quad \Pr =\frac{\mu }{\rho _{{_{f0}}} \alpha _m },\quad {\textit{Ra}}=\frac{\left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) gK\rho _{{_{f0}}} \beta _T \left( {T_h -T_{\mathrm{in}} } \right) L}{\alpha _m \mu },\quad \nonumber \\ {\textit{Nr}}= & {} \frac{\left( {\rho _p -\rho _{{_{f0}}} } \right) \overline{{\varphi }}_{\mathrm{in}} }{ \rho _{{_{f0}}} \beta _T \left( {T_h -T_{\mathrm{in}} } \right) \left( {1-\overline{{\varphi }}_{\mathrm{in}} } \right) }, \nonumber \\ {\textit{Nc}}= & {} \frac{\beta _C \left( {\overline{{C}}_h -\overline{{C}}_{\mathrm{in}} } \right) }{\beta _T \left( {T_h -T_{\mathrm{in}} } \right) },\quad {\textit{Ln}}=\frac{\alpha _m }{\varepsilon D_B },\quad {\textit{Nb}}=\frac{ \delta D_B \overline{{\varphi }}_{\mathrm{in}} }{\alpha _m },\quad {\textit{Nt}}=\frac{\delta D_T \left( {T_h -T_{\mathrm{in}} } \right) }{\alpha _m T_{\mathrm{in}} },\nonumber \\ {\textit{Nd}}= & {} \frac{\sigma D_{TC} \left( {\overline{{C}}_h -\overline{{C}}_{\mathrm{in}} } \right) }{\alpha _m \left( {T_h -T_{\mathrm{in}} } \right) },\nonumber \\ {\textit{Le}}= & {} \frac{\alpha _m }{\varepsilon D_{Sm} },\quad {\textit{Ld}}=\frac{D_{CT} \left( {T_h -T_{\mathrm{in}} } \right) }{D_{Sm} \left( {\overline{{C}}_h -\overline{{C}}_{\mathrm{in}} } \right) } \end{aligned}$$
(24)

The physical quantities of interest are the local Nusselt Nu and Sherwood \({\textit{Sh}},{\textit{Sh}}_\varphi \) numbers along the right vertical wall, which are defined as

$$\begin{aligned} {\textit{Nu}}=-\left( {\frac{\partial \theta }{\partial x}} \right) _{x=1} ,\quad {\textit{Sh}}=-\left( {\frac{\partial C}{\partial x}} \right) _{x=1} ,\quad {\textit{Sh}}_\varphi =-\left( {\frac{\partial \varphi }{\partial x}} \right) _{x=1} \end{aligned}$$
(25)

and the average Nusselt \(\overline{{\textit{Nu}}} \) and Sherwood \(\overline{{\textit{Sh}}} \hbox {, }\overline{{\textit{Sh}}_\varphi } \) numbers, which are given by

$$\begin{aligned} \overline{{\textit{Nu}}} =\frac{1}{0.8}\int _0^{0.8} {{\textit{Nu}}}\, \hbox {d}y,\quad \overline{{\textit{Sh}}} =\frac{1}{0.8}\int _0^{0.8} {{\textit{Sh}}} \,\hbox {d}y,\quad \overline{{\textit{Sh}}_\varphi } =\frac{1}{0.8}\int _0^{0.8} {{\textit{Sh}}_\varphi } \hbox {d}y \end{aligned}$$
(26)

3 Numerical Method

The partial differential equations (19)–(22) with corresponding boundary conditions (23) were solved using the finite difference method with the second-order central differencing schemes (see Aleshkova and Sheremet 2010; Sheremet and Trifonova 2013; Sheremet et al. 2014; Sheremet and Pop 2014). The solution for the corresponding linear algebraic equations was obtained through the successive under relaxation method. Optimum value of the relaxation parameter was chosen on the basis of computing experiments. The computation is terminated when the residuals for the stream function get bellow \(10^{-7}\).

For the purpose of obtaining grid independent solution, a grid sensitivity analysis was performed by preparing the solution for steady-state double-diffusive mixed convection in a square porous cavity filled with a Cu–water nanofluid at \({\textit{Re}}=100, Pr=0.2, {\textit{Ra}}=100\), \({\textit{Nc}}={\textit{Nr}}={\textit{Nb}}={\textit{Nt}}= {\textit{Nd}}=0.1\), \({\textit{Le}}={\textit{Ld}}= {\textit{Ln}}=1.0, \upvarepsilon =~0.9\), solid matrix of the porous medium is the aluminum foam. Four cases of non-uniform grid are tested: a grid of \(100\times 100\) points \(\left( {\Delta x_{\mathrm{min} } =\Delta y_{\min } =0.00087} \right. \) and \(\left. {\Delta x_{\max } =\Delta y_{\max } =0.038} \right) \), a grid of 150\(\times \)150 points \(\left( {\Delta x_{\min } =\Delta y_{\min } =0.00022} \right. \) and \(\left. {\Delta x_{\max } =\Delta y_{\max } =0.033} \right) \), a grid of \(200\times 200\) points \(\left( {\Delta x_{\min } =\Delta y_{\min } =0.00019} \right. \) and \(\left. {\Delta x_{\max } =\Delta y_{\max } =0.024} \right) \), and a grid of \(250\times 250\) points \(\left( {\Delta x_{\min } =\Delta y_{\min } =0.00015} \right. \) and \(\left. {\Delta x_{\max } =\Delta y_{\max } =0.0194} \right) \). Table 1 shows an effect of the mesh on the average Nusselt number of the right vertical wall.

Table 1 Variations of the average Nusselt and contaminant Sherwood numbers with the non-uniform grid
Full size table

On the basis of the conducted verifications, the non-uniform grid of \(200\times 200\) points has been selected for the following analysis.

The numerical methodology was coded in C++, and to check its validity, a comparison with selective data from the published literature was carried out. The performance of the double-diffusive convection was tested against the results of Goyeau et al. (1996) and Bourich et al. (2004) for steady-state double-diffusive natural convection in a porous cavity differentially heated and salted. Table 2 shows the values of the average Nusselt and Sherwood numbers computed for various Rayleigh and Lewis numbers at \({\textit{Nc}}=0\) in comparison with data of Goyeau et al. (1996) and Bourich et al. (2004).

Table 2 Comparison of the average Nusselt and Sherwood numbers
Full size table

It can be seen in Table 2 that the present mathematical model and numerical method are in good agreement with the earlier results for double-diffusive natural convection in a porous cavity. The performance of natural convection in a porous enclosure part of the model was tested earlier (see Sheremet et al. 2014; Sheremet and Pop 2014).

4 Results and Discussion

Numerical investigation of the boundary value problem (19)–(23) has been carried out at the following values of key parameters: Reynolds number \(({\textit{Re}}=10{-}100)\), Prandtl number \((Pr=0.2)\), Rayleigh number \(({\textit{Ra}}=50{-}500)\), usual Lewis number \(({\textit{Le}}=1{-}50)\), Dufour-contaminant Lewis number \(({\textit{Ld}}=1{-}50)\), nanofluid Lewis number \(({\textit{Ln}}=1{-}50)\), nanofluid buoyancy ratio \(({\textit{Nr}}=0.1{-}0.4)\), regular double-diffusive buoyancy ratio \(({\textit{Nc}}=0.1{-}0.4)\), Brownian motion parameter \(({\textit{Nb}}=0.1{-}0.4)\), the thermophoresis parameter \(({\textit{Nt}}=0.1{-}0.4)\), modified Dufour parameter \(({\textit{Nd}}=0.1{-}0.4)\). Particular efforts have been focused on the effects of these key parameters on the fluid flow, heat and mass transfer characteristics.

Figure 2 presents the effect of the Reynolds number on isolines of stream function, temperature, contaminant concentration and nanoparticles volume fraction at \({\textit{Ra}} =50, {\textit{Le}}= {\textit{Ld}}={\textit{Ln}}=1.0\), \({\textit{Nr}}={\textit{Nc}}={\textit{Nb}}={\textit{Nt}}={\textit{Nd}}=0.1\).

Fig. 2
figure 2

Streamlines \(\psi \) , isotherms \(\theta \), isoconcentrations of contaminant \(C\), and nanoparticles volume fraction \(\upvarphi \) at \({{\textit{Ra}}}=50\), \({{\textit{Le}}}={{\textit{Ld}}}= {{\textit{Ln}}}=1.0\), \({{\textit{Nr}}}={{\textit{Nc}}}={{\textit{Nb}}}={{\textit{Nt}}}= {{\textit{Nd}}}=0.1:{\textit{Re}}=10-a\), \({\textit{Re}}=50- b\), \({\textit{Re}}=100 - c\), \({\textit{Re}}=500 - d\)

Full size image

It should be noted that an increase in the Reynolds number is related to an increase in the inlet velocity \(\overline{{u}}_{\mathrm{in}} \). Regardless of Re in the domain of interest, one can find a forced flow due to a presence of inlet and outlet and a single circulation flow due to the effect of the temperature and concentration differences between the right vertical wall and the fluid inside the cavity. Therefore, the considered modes are defined by the interaction of the forced flow and natural convection circulation. The presence of external forced flow leads to cooling of the domain of interest with a reduction in the contaminant concentration. Distributions of low temperature and concentration wave from the inlet to outlet characterize the momentum transport in the same direction. An increase in the inlet velocity \(( {\textit{Re}}\le 100)\) leads to an intensification of forced flow along the bottom wall and as a result the convective single circulation in the central part of the cavity. The latter is caused by an intensification of flow along interface between these flows. For high values of Re, the intensive forced flow is characterized by widening of the forced fluid tube. In case of \({\textit{Re}}=500\) (Fig. 2d), the forced flow is a prevailing flow inside the cavity. Therefore, it is possible to conclude that for \({\textit{Re}}<100\), we have the natural convection mode, for \(100\le {\textit{Re}}<300\), we have the mixed convection regime and for high values of the Reynolds number, we have the forced convection regime. It is worse noting that in case of the forced convection regime, the single circulation flow has small sizes or is absent. The average temperature and contaminant concentration inside the cavity are fully defined by the inlet conditions and confined the essential variations of \(\uptheta \) and \(C\) close to the right vertical wall.

Distributions of nanoparticles volume fraction are essentially non-homogeneous. An increase in the inlet velocity leads to homogenization of nanoparticles distribution inside the cavity. It should be noted that homogenization of nanoparticles distribution in case of the intensive circulation has been noticed early in the case of natural convection inside the three- and two-dimensional domains (see Sheremet et al. 2014; Sheremet and Pop 2014).

In Fig. 3, streamlines, isotherms, contaminant isoconcentrations, and nanoparticles isoconcentrations are presented for different values of the Rayleigh number at \({\textit{Re}}=100, {\textit{Le}}={\textit{Ld}}={\textit{Ln}}=1.0\), \({\textit{Nr}}={\textit{Nc}}= {\textit{Nb}}={\textit{Nt}}={\textit{Nd}}=0.1\). Study of the Rayleigh number effect on the mixed convection processes within a porous medium is very important. For small values of the Rayleigh number \(({\textit{Ra}}=50)\), the forced convection is a prevailing heat transfer mode with heat and mass conduction regime. The latter is clearly presented in the temperature and concentration fields close to the right vertical wall. The isotherms and isoconcentrations are parallel to each other close to this wall. The flow inside the cavity is characterized only by external forced flow without any recirculation. At the same time, a penetration of the cold temperature and low contaminant concentration for this regime is more essential in comparison with other one. An increase in the Rayleigh number to the value \({\textit{Ra}}=50\) (Fig. 2c) leads to a formation of the single recirculation in the central part of the cavity that distorts the forced flow and reduces the penetration of the low temperature and contaminant concentration into the cavity. Further increase in Ra leads to a formation of central convective vortex of high intensity that essentially confines external forced flow. Distributions of nanoparticles characterize the developed hydrodynamic and temperature field.

Fig. 3
figure 3

Streamlines \(\psi \), isotherms \(\theta \), isoconcentrations of contaminant \(C\), and nanoparticles volume fraction \(\varphi \) at \({\textit{Re}}=100\), \({\textit{Le}}={\textit{Ld}}= {\textit{Ln}}=1.0\), \({\textit{Nr}}={\textit{Nc}}={\textit{Nb}}={\textit{Nt}}= {\textit{Nd}}=0.1\):\({\textit{Ra}}=10 -a\), \({\textit{Ra}}=100 - b\), \({\textit{Ra}}=500 - c\), \({\textit{Ra}}=1000 - d\)

Full size image

The effect of the Reynolds and Rayleigh numbers on the average Nusselt and contaminant Sherwood numbers at right vertical wall for \({\textit{Le}}={\textit{Ld}}={\textit{Ln}}=1.0\), \({\textit{Nr}}={\textit{Nc}}= {\textit{Nb}}={\textit{Nt}}={\textit{Nd}}=0.1\) is presented in Fig. 4. Taking into account boundary conditions for the nanoparticles volume fraction (23) dependences of \(\overline{{\textit{Sh}}_\varphi } \) are similar to Fig. 4a.

Fig. 4
figure 4

Variation of the average Nusselt (a) and Sherwood (b) numbers at right vertical wall with different Reynolds and Rayleigh numbers for \({\textit{Le}}={\textit{Ld}}={\textit{Ln}}=1.0\), \({\textit{Nr}}={\textit{Nc}}={\textit{Nb}}={\textit{Nt}}={\textit{Nd}}=0.1\)

Full size image

s

An increase in Re from 10 to 500 leads to an essential increase in \(\left| {\overline{{\textit{Nu}}} } \right| \) and \(\left| {\overline{{\textit{Sh}}} } \right| \) due to the heat and contaminant removal from the vertical wall. An increase in the Rayleigh number also leads to an increase in \(\left| {\overline{{\textit{Nu}}} } \right| \) with non-monotonic changes of \(\left| {\overline{{\textit{Sh}}} } \right| \). It should be noted that an increase in the Rayleigh number from 100 to 400, one can find a reduction in \(\left| {\overline{{\textit{Sh}}} } \right| \) and the following increase in Ra leads to an increase in \(\left| {\overline{{\textit{Sh}}} } \right| \). Such behavior can be explained by thermo diffusion effect.

Figure 5 shows an effect of the usual Lewis number on the average Nusselt and contaminant Sherwood numbers. An increase in Le leads to an essential intensification of convective mass transfer and attenuation of convective heat transfer, namely \(\left| {\overline{{\textit{Sh}}} } \right| \) increases while \(\left| {\overline{{\textit{Nu}}} } \right| \) and \(\left| {\overline{{\textit{Sh}}_\varphi } } \right| \) decrease (e.g., an increase in Le from 1.0 to 10.0 at \({\textit{Ra}} =~50, {\textit{Re}}=100.0\) leads to both a reduction in \(\left| {\overline{{\textit{Nu}}} } \right| \) up to 42 % and an increment in \(\left| {\overline{{\textit{Sh}}} } \right| \) in 30 times).

Fig. 5
figure 5

Variation of the average Nusselt (a) and Sherwood (b) numbers at right vertical wall with different Reynolds and usual Lewis numbers for \({\textit{Ra}}=50, {\textit{Ld}}={\textit{Ln}}=1.0, {\textit{Nr}}={\textit{Nc}}={\textit{Nb}}={\textit{Nt}}={\textit{Nd}}=0.1\)

Full size image

The effects of the Brownian motion and thermophoresis parameters on the average Nusselt and contaminant Sherwood numbers are presented in Figs. 6 and 7. An increase in the Brownian motion parameter leads to an insignificant decrease in \(\left| {\overline{{\textit{Nu}}} } \right| \) and an inessential increase in \(\left| {\overline{{\textit{Sh}}} } \right| \) (see Fig. 6). At the same time, an increase in the thermophoresis parameter from 0.1 to 0.4 leads to insignificant nonlinear changes of \(\left| {\overline{{\textit{Nu}}} } \right| \), namely for \({\textit{Re}}<90\), one can find an inessential reduction in convective heat transfer, for \(100<{\textit{Re}}<200\) one can find an inessential intensification of convective heat transfer and for \({\textit{Re}}>300\), we have also an attenuation of convective heat transfer. Changes of the average contaminant Sherwood numbers with Nt are nonlinear. An increase in Nt leads to an insignificant intensification of convective mass transfer for \({\textit{Re}}<90\), a reduction in \(\left| {\overline{{\textit{Sh}}} } \right| \) for \(90<{\textit{Re}}<500\) and also intensification of convective mass transfer for \({\textit{Re}}>500\).

Fig. 6
figure 6

Variation of the average Nusselt (a) and Sherwood (b) numbers at right vertical wall with different Reynolds and Brownian motion parameter for \({\textit{Ra}}=50, {\textit{Le}}= {\textit{Ld}}={\textit{Ln}}=1.0,{\textit{Nr}}={\textit{Nc}}={\textit{Nt}}= {\textit{Nd}}=0.1\)

Full size image
Fig. 7
figure 7

Variation of the average Nusselt (a) and Sherwood (b) numbers at right vertical wall with different Reynolds and thermophoresis parameter for \({\textit{Ra}}=50, {\textit{Le}}= {\textit{Ld}}={\textit{Ln}}=1.0, {\textit{Nr}}={\textit{Nc}}={\textit{Nb}}= {\textit{Nd}}=0.1\)

Full size image

5 Conclusions

Double-diffusive mixed convection in a porous cavity with one isothermal vertical wall filled with a nanofluid has been numerically studied. Particular efforts have been focused on the effects of the Rayleigh, Reynolds and usual Lewis numbers, Brownian motion and thermophoresis parameters on flow field, temperature, contaminant and nanoparticles volume fraction distributions, and average Nusselt and Sherwood numbers. It has been found that the average Nusselt number at hot vertical wall is an increasing function of the Rayleigh and Reynolds numbers and a decreasing function of the usual Lewis number. While the average Sherwood number at this vertical wall is an increasing function of the usual Lewis. Effects of the Rayleigh and Reynolds numbers on \(\left| {\overline{{\textit{Sh}}} } \right| \) and the thermophoresis parameter on the average Nusselt and Sherwood numbers are non-monotonic. It has been shown that in the present porous problem, the Richardson number \({\textit{Ri}}={{\textit{Gr}}}/{{\textit{Re}}^{2}}\) does not define the prevailing of the forced or natural convection modes. For example, at \({\textit{Ra}}=500\) and \({\textit{Re}}=100\) (Fig. 3c), we have the natural convection regime with essential central circulation while \({\textit{Ri}}=0.25<1\).