A unified approach to reliability and edge fault tolerance of cube-based interconnection networks under three hypotheses

Abstract

The topological structures of the interconnection networks of some parallel and distributed systems are designed as n-dimensional hypercube $Q_n$ or n-dimensional folded hypercube $FQ_n$ with $N=2^n$ processors. For integers $0\le k\le {n-1}$, let $\mathcal {P}_1^k$, $\mathcal {P}_2^k$ and $\mathcal {P}_3^k$ be the property of having at least k neighbors for each processor, containing at least $2^k$ processors and admitting average neighbors at least k, respectively. $\mathcal {P}$-conditional edge-connectivity of G, $\lambda (\mathcal {P},G)$, is the minimum cardinality of faulty edge-cut, whose malfunction divides this network into several components, with each component satisfying the property of $\mathcal {P}$. For each integer $0\le k\le {n-1}$, and $1\le i\le 3$, this paper offers a unified method to investigate the $\mathcal {P}_i^k$-conditional edge-connectivity of $Q_n$ and $FQ_n$. Exact value of $\mathcal {P}_i^k$-conditional edge-connectivity of $Q_n$, $\lambda (\mathcal {P}_i^k,Q_n)$, is $(n-k)2^k$, and that of $\mathcal {P}_i^k$-conditional edge-connectivity of $FQ_n$, $\lambda (\mathcal {P}_i^k,FQ_n)$, is $(n-k+1)2^k$. Our method generalizes the result of Guo and Guo in [The Journal of Supercomputing, 2014, 68:1235-1240] and the previous other results.

1 Introduction

With the onset of digital age, big data based on massively parallel distribute processing systems greatly facilitates our lives. To deal with the problem of processing and storage of ever-increasing volume of massive data, various topological structures of interconnection networks of parallel and distributed system are designed and extensively investigated. The performance of a parallel and distributed system is not only related to properties of each single processor, but also highly relied on the topological structures and their parameters of the interconnection networks. The topological interconnection network of parallel and distributed system is usually modeled as a graph G(V, E), where the vertices (nodes) and edges (links) represent processors and communicative links between them. If no confusion caused, the terms graphs and networks are replaceable each other.

Both hypercube and folded hypercube (one of the most famous variants, which was first proposed by El-Amawy and Latifi in 1991 [6]) share some attractive topological properties, such as regularity, highly symmetric property, vertex transitivity, lower diameter, easy scalability and high reliability [3, 6, 24]. They are applied to underlying topological structures of most potential interconnection networks of parallel and distributed system, such as ATM switches [19, 20], 3D Fold-Noc network [8] and PM2I networks [15].

Definition 1

An n-dimensional hypercube $Q_{n}$ is an undirected graph with $|V(Q_n) |=2^n$ and $|E(Q_n) |=n2^{n-1}$. Each vertex can be represented by an n-bit binary string in $\{x_{n} x_{n-1}\cdots x_{2} x_{1}:x_{i}\in \{0,1\}, 1\le i\le n\}$. There is an edge between the vertex $x=x_n x_{n-1}\cdots x_{2} x_{1}$ and $y=y_{n} y_{n-1}\cdots y_{2} y_{1}$ if and only if their binary string representations differ in only one bit position.

Definition 2

[6] An edge between vertex $x=x_{n} x_{n-1}\cdots x_{2} x_{1}$ and $y=y_{n} y_{n-1}\cdots y_{2} y_{1}$ of $Q_n$, (x, y), is a complementary edge if and only if the bits of x and y are complements of each other, that is, $y_i=\overline{x_i}$ for each $i=1,2,\dots ,n$. The n-dimensional folded hypercube, denoted by $FQ_n$, is an undirected graph obtained from $Q_n$ by adding all complementary edges. $\overline{M_n}$ is edge set containing all complementary edges of $FQ_n$.

Because of coagulation and robustness of local networks, all processors and links incident to the same processor cannot malfunction simultaneously. Although the classical Menger’s theorem about connectivity or edge-connectivity (defined as the minimum number of vertices or edges whose removal from G results in a disconnected graph) lays a cornerstone for evaluating the reliability and fault tolerance of a static interconnection networks, once coagulation and robustness are enhanced dynamically, that is, when the size of faulty-free sets varies, Menger’s theorem no longer offers a more accurate parameter for the reliability of a large-scale parallel and distributed processing systems [3, 7, 9, 10, 12, 18, 23,24,25]. In 1983, Harary generalized the Menger’s theorem of connectivity in both vertex and edge version by introducing the notion of conditional connectivity and theoretically enriched the theory of connectedness of networks [12]. Instead of focusing on the vertex version [4, 14, 16, 22], this paper mainly studies the conditional edge-connectivity of a connected graph G, which is defined as follows.

Definition 3

Let $\mathcal {P}$ be a property of a graph $G=(V,E)$. The edge subset $F\subset E(G)$ is defined as a $\mathcal {P}$-connected edge-cut of G, if any, G–F is disconnected, and each component of G–F satisfies the condition $\mathcal {P}$. $\lambda (\mathcal {P},G)$, $\mathcal {P}$-conditional edge-connectivity of G, is defined as the minimum cardinality $\mathcal {P}$-conditional edge-cuts F of G.

Based on the different properties and the faulty-free set, various kinds of $\mathcal {P}$-conditional edge-connectivity are studied. Let

$\mathcal {P}_1^k=\{$having the minimum degree $\delta \ge k\}$,

$\mathcal {P}_2^k=\{$containing at least $2^k$ vertices$\}$,

and $\mathcal {P}_3^k=\{$satisfying the average degree at least $k\}$.

Then $\lambda(\mathcal {P}_1^k, G)$, $\lambda(\mathcal {P}_2^k, G)$ and $\lambda(\mathcal {P}_3^k, G)$ are the $k$-super edge-connectivity $\lambda_\delta^k(G)$ [1, 11], $2^k$-extra edge-connectivity $\lambda_{2^k}(G))$ [2, 9], and $k$-average degree edge-connectivity $\overline{\lambda}^k(G)$, respectively. As a $k$-super edge-connectivity of $G$, $\lambda(\mathcal {P}_1^k, G)=\lambda_{\delta}^{k}(G)$ is the minimum cardinality of all the $k$-super edge-cut of $G$ [10, 18]. While given a positive integer $k$, if $\mathcal {P}=\mathcal {P}_2^k$, it gives the $2^k$-extra edge-connectivity of $G$, $\lambda_{2^k}(G)$, which was first introduced by F$\grave{a}$brega and Foil in [9]. If $F$ is a $\mathcal {P}_{2}^{k}$-conditional edge-cut, $F$ is also called a $2^k$-extra edge-cut. $\lambda(\mathcal {P}_2^k, G)=\lambda_{2^k}(G)$ is the minimum cardinality of the $2^k$-extra edge-cuts of $G$. Similarly, $\lambda(\mathcal {P}_3^k, G)=\overline{\lambda}^k(G)$ is the minimum cardinality of tht $k$-average degree edge-cuts of $G$.

In recent years, the exact values of $\lambda (\mathcal {P}_i^k, Q_n)$ and $\lambda (\mathcal {P}_i^k, FQ_n)$ of cube-based interconnection networks were widely investigated. The focus of these results is either on $Q_n$ and $FQ_n$ for some special $k\le 4$ under some $\mathcal {P}_i^k$-conditional constrain for a fixed i [3, 11, 25] or on some special cube-based graphs for some fixed i and general $0\le k\le {n-1}$ [17]. For above special cases, the related results are summarized in Table 1. However, seldom do the researchers pay their attentions to investigating $\lambda (\mathcal {P}_i^k, Q_n)$ and $\lambda (\mathcal {P}_i^k, FQ_n)$ for each nonnegative integer $0\le k\le {n-1}$ and $1\le i\le n$.

For each nonnegative integer $0\le k\le {n-1}$, $n\ge 1$ and $1\le i\le 3$, this paper mainly finds a unified approach to explore the $\mathcal {P}_i^k$-conditional edge-connectivity of $Q_n$ and $FQ_n$, or rather, the minimum cardinality of faulty edge-cut of $Q_n$ and $FQ_n$, whose malfunction divides network into several components, with each resulting component satisfying the property of $\mathcal {P}_i^k$, respectively. The exact values of them are equal to the minimum number of edges to delete such that the remaining one connected subgraph is induced by $2^k$ vertices and the other is also connected, respectively. Our main results are reflected in the last two lines of Table 1, and marked in bold. Before giving the proof of our main results, we show some preliminaries.

Table 1 Previous known results and our results on $\lambda (\mathcal {P}_i^k,G)$ of the cube-based G

2 Preliminaries

By the definitions of $Q_n$ and $FQ_n$, the vertex set $V(Q_n)$ and $V(FQ_n)$ is denoted by $X_n X_{n-1}\cdots X_2 X_1=\{x_n x_{n-1}\cdots x_2 x_1:x_i\in \{0,1\},i=1,2,\ldots ,n\}$. For further simplification, let $X^n$ denote $X_n X_{n-1}\cdots X_2 X_1$, $x^n$ denote $x_n x_{n-1}\cdots x_2 x_1$, and the same is true for the following. Let $0 X^{n-1}$ and $1 X^{n-1}$ be the vertex subsets $\{0 x^{n-1}:x_i\in \{0,1\},i=1,2,\ldots ,n-1\}$ and $\{1x^{n-1}:x_i\in \{0,1\},i=1,2,\ldots ,n-1\}$. Let $D_0$ and $D_1$ be induced subgraphs $Q_n[0 X^{n-1}]$ and $Q_n[1 X^{n-1}]$. They are both $(n-1)$-dimensional hypercube and $E(D_0)$, $E(D_1)$ and $M_n$ is a decomposition of $E(Q_n)$. we can express $Q_n$ as $D_0\bigoplus D_1$. Similarly, we write $z^{n-k} X^k$ for the vertex $\{ z^{n-k} X^k:X_i\in \{0,1\},i=1,2,\ldots ,k,z_j$ is fixed, for $j=k+1,k+2,\ldots ,n\}$. Inductively, the subgraph $Q_n[z^{n-k} X^k]$ is a k-dimensional subcube in $Q_n$ induced by $z^{n-k} X^k$. Since $FQ_n$ can be obtained from $Q_n$ by adding complementary edges $\overline{M_n}$, $E(D_0)$, $E(D_1)$, $M_n$ and $\overline{M_n}$ be a decomposition of $E(FQ_n)$. We express $FQ_n$ as $D_0\overline{\bigoplus } D_1$. A vertex in $0X^{n-1}$ has exactly one neighbor in $1X^{n-1}$ in $Q_n$, but have two neighbors in $FQ_n$.

After deeply mining the properties of the three definitions of the above $\mathcal {P}_{i}^{k}$-conditional edge-connectivity of G, one can see that the optimal $\mathcal {P}_{i}^{k}$-conditional edge-cut is reached if and only if there are just two components left after removing such edge-cuts from G. Thus, it is necessary to introduce the following two important functions $\xi _m(G)$ and $ex_m(G)$.

Given a vertex set $X\subset V(G)$, we denote G[X] the subgraph of G induced by X. For two vertex sets X and $\overline{X}$, we denote $[X, \overline{X}]$ the edge subset of G with one end in X and the other end in $\overline{X}$. Let $\xi _m(G)=min\{|[X, \overline{X}]|:X\subset V(G)$,$|X|=m\le \lfloor |V(G)|/2\rfloor$, both G[X] and $G[\overline{X}]$ are connected$\}$, where $|[X, \overline{X}]|$ is the number of elements of $[X, \overline{X}]$. In other words, $\xi _m(G)$ is the minimum number of edges to delete such that the remaining one connected subgraph is induced by m vertices and the other is also connected, where $m\le \lfloor |V(G)|/2\rfloor$. For a d-regular graph, it follows that $\xi _m(G)=dm-ex_{m}(G)$, where $ex_m(G)$ is the twice of the maximum number edges of the subgraph of G induced by m vertices.

For convenience, the vertex $x^n$ of n-dimensional hypercube and n-dimensional folded hypercube also can be represented by decimal number $\sum _{i=1}^{n} x_{i} 2^{i-1}$ in this paper. For instance, $x^{5}=x_{5}x_{4}x_{3}x_{2}x_{1}=01011$ can be disassembled into $1\times 2^{0}+1\times 2^{1}+0\times 2^{2}+1\times 2^{3} +0\times 2^{4}=1+2+8=11$. A positive integer m can be decomposed into $\sum _{i=0}^{s} 2^{t_{i}}$, where $t_{0}=\lfloor log _{2} m\rfloor$, $t_{i}=\lfloor log _{2}(m-\sum _{i=0}^{i-1} 2^{t_i})\rfloor$ for $i\ge 1$ and $t_i > t_{i+1} \geq 0$. Let $S_m$ be the set $\{0, 1, 2,\ldots ,m-1\}$ under decimal representation and $L_m^n$ the corresponding set represented by their n-binary strings. Let ${\overline{L_m^n}}$ be the complement set of $V(Q_n)\setminus L_m^n$. Obviously, by the definition of $Q_n$, both of $L_m^n$ and $\overline{L_m^n}$ are the subset of $V(Q_n)$. Both $Q_n[L_m^n]$ and $Q_n[\overline{L_m^n}]$ are the subgraphs induced by $L_m^n$ and $\overline{L_m^n}$, respectively. Since $Q_n$ is n-regular, in [13] and [18], exact values of $\xi _m(Q_n)$ and $ex_m(Q_n)$ had been given.

Lemma 1

[13, 18] For a positive integer m, $m=\sum _{i=0}^{s} 2^{t_i} \le 2^{n}$, $\xi _m(Q_n)=nm-ex_m(Q_n)$, where $ex_m(Q_n)=2|E(Q_n[L_m^n])|=\sum _{i=0}^{s}t_{i}2^{t_i}+\sum _{i=0}^{s}2i2^{t_{i}}$.

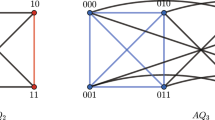
For example, assume that $m=5$ and $n=4$. We have $S_5=\{0,1,2,3,4\}$, then $L_{5}^{4}=\{0000,0001,0010,0011,0100\}$, and hence $[L_5^4,\overline{L_5^4}]$ is the minimum edge-cut of $Q_4$ when deleting many edges and resulting in one connected subgraph having five vertices and the other being also connected. Since $5=2^{2}+2^{0}$, we have $t_0=2$, $t_1=0$ and $s=1$. By Lemma 1, we can obtain that

$$ \begin{aligned} ex_{5} (Q_{4} ) &= 2\left| {E\left( {Q_{4} [L_{5}^{4} ]} \right)} \right| \\ & = \sum\limits_{{i = 0}}^{1} {t_{i} } 2^{{t_{i} }} + \sum\limits_{{i = 0}}^{1} 2 i2^{{t_{i} }} \\ & = t_{0} \times 2^{{t_{0} }} + t_{1} \times 2^{{t_{0} }} + 2 \times 0 \times 2^{{t_{0} }} + 2 \times 1 \times 2^{{t_{1} }} \\ & = 2 \times 2^{2} + 0 \times 2^{0} + 2 \times 0 \times 2^{2} + 2 \times 1 \times 2^{0} \\ & = 10. \\ \end{aligned} $$

By the definition of $\xi _5(Q_{4})=min\{|[X, \overline{X}]|:X\subset V(Q_{4})$, $|X|=5\le \lfloor |V(Q_{4})|/2\rfloor$, both $Q_{4}[X]$ and $Q_{4}[\overline{X}]$ are connected$\}$, we have

$$ \begin{aligned} \xi _{5} (Q_{4} ) &= \left| {[L_{5}^{4} ,\overline{{L_{5}^{4} }} ]} \right| \\ & = nm - ex_{m} (Q_{n} ) \\ & = 4 \times 5 - 10 \\ & = 10. \\ \end{aligned} $$

Furthermore, if $S^{'}=\{0000,0001,0010,0100,1000\}$ and $S^{''}=\{0000,0010,0011,0100,0101\}$, then $[S^{'},\overline{S^{'}}]$ and $[S^{''},\overline{S^{''}}]$ are edge-cuts of $Q_n$ with $|[S^{'},\overline{S^{'}}]|=12>10$, $|[S^{''},\overline{S^{''}}]|=12>10$. But $[S^{'},\overline{S^{'}}]$ and $[S^{''},\overline{S^{''}}]$ are not minimum number of edges to delete when the remaining one connected subgraph is induced by five vertices and the other is also connected. $[L_{5}^{4}, \overline{L_{5}^{4}}]$ in $Q_4$, $[S^{'},\overline{S^{'}}]$ and $[S^{''},\overline{S^{''}}]$ are represented in imaginary lines in Fig. 1.

Fig. 1

$[L_{5}^{4}, \overline{L_{5}^{4}}]$ in $Q_4$ (imaginary lines in left one), $[S^{'},\overline{S^{'}}]$ and $[S^{''},\overline{S^{''}}]$ (imaginary lines in right two)

Obviously, by the definition of $FQ_n$, both $L_m^n$ and $\overline{L_m^n}$ are also the subset of $V(FQ_n)$. Both $FQ_n[L_m^n]$ and $FQ_n[\overline{L_m^n}]$ are the subgraphs induced by $L_m^n$ and $\overline{L_m^n}$, respectively. From the following lemma, one can obtain that $ex_m(Q_n)=ex_m(FQ_n)$ for each $m\le 2^{n-1}$.

Lemma 2

[21, 24] For a positive integer $m=\sum _{i=0}^{s} 2^{t_i} \le 2^{n}$, $\xi _m(FQ_n)=(n+1)m-ex_m(FQ_n)$, where

$$ \begin{aligned} ex_{m} (FQ_{n} ) &= 2|E\left( {FQ_{n} [L_{m}^{n} ]} \right)| \\ & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{{i = 0}}^{s} {t_{i} } 2^{{t_{i} }} + \sum\limits_{{i = 0}}^{s} 2 i2^{{t_{i} }} } \hfill & {if{\text{ }}1 \le m \le 2^{{n - 1}} } \hfill \\ {\sum\limits_{{i = 0}}^{s} {t_{i} } 2^{{t_{i} }} + \sum\limits_{{i = 0}}^{s} 2 (i + 1)2^{{t_{i} }} - 2^{n} } \hfill & {if{\text{ }}m > 2^{{n - 1}} .} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

Thus, for $m=5$ and $n=4$, $ex_5(FQ_4)=ex_5(Q_4)=10$ and $\xi_5(FQ_4)=(4+1)\times 5-10=15$. If $S^{'''}=\{0000,0001,0011,0100,1000\}$ and $S^{''''}=\{0000,0010,0011,0100,0101\}$, then $[S^{'''},\overline{S^{'''}}]$ and $[S^{''''},\overline{S^{''''}}]$ are edge-cuts of $FQ_4$ with $\lvert [S^{'''},\overline{S^{'''}}]\rvert =17>15$, $\lvert [S^{''''},\overline{S^{''''}}]\rvert =16>15$. But $[S^{'''},\overline{S^{'''}}]$ and $[S^{''''},\overline{S^{''''}}]$ are not the minimum number of edges to delete when deleting some edges of $FQ_4$ and resulting in one connected subgraph having 5 vertices and the other being also connected. $[L_{5}^{4}, \overline{L_{5}^{4}}]$ in $FQ_4$, $[S^{'''},\overline{S^{'''}}]$ and $[S^{''''},\overline{S^{''''}}]$ are represented by imaginary lines in Fig. 2.

Fig. 2

$[L_{5}^{4}, \overline{L_{5}^{4}}]$ in $FQ_4$ (imaginary lines in left one), $[S^{'''},\overline{S^{'''}}]$ and $[S^{''''},\overline{S^{''''}}]$ with one component 5 vertices (imaginary lines in right two)

Note that for each $m\le 2^{n-1}$, the subgraph $Q_n[L_m^n]$ is isomorphic to $FQ_n[L_m^n]$. The subgraphs $Q_n[L_m^n]$, $Q_n[\overline{L_m^n}]$, $FQ_n[L_m^n]$ and $FQ_n[\overline{L_m^n}]$ are connected. They are the components which can be separated from $Q_n$ and $FQ_n$ by deleting the edge-cuts $[L_m^n,\overline{L_m^n}]$ in $Q_n$ and $FQ_n$ for each $m\le 2^n$.

3 The bounds of $\mathcal {P}_{i}^{k}$-conditional edge-connectivity of $FQ_{n}$ and $Q_{n}$

A unified method for the bounds of $\mathcal {P}_{i}^{k}$-conditional edge-connectivity of $FQ_{n}$ and $Q_{n}$ under three hypotheses can be illustrated. First, we show the upper bounds.

Lemma 3

For each integer $0\le k\le {n-1}$, and $1\le i\le 3$, $n\ge 1$, $\lambda (\mathcal {P}_i^{k},Q_n)\le \xi _{2^k}(Q_n)=(n-k)2^k$; $\lambda (\mathcal {P}_i^{k},FQ_n)\le \xi _{2^k}(FQ_n)=(n-k+1)2^k$.

Proof

For $Q_n$, it is sufficient to show that there exists a $\mathcal {P}_i^k$-conditional edge-cut of the size $2^k(n-k)$ in $Q_n$ for each $0\le k\le n-1$ and $1\le i\le 3$. On the one hand, the size of the edge-cut $[L_{2^k}^n, \overline{L_{2^k}^n}]$ is $\xi _{2^k}(Q_n)=(n-k)2^k$ for each $0\le k\le n-1$. $Q_n[L_{2^k}^n]=Q_n[0^{n-k-1}0X^k]$ is isomorphic to k-dimensional subcube $Q_k$, and $Q_k$ is k-regular and $|\overline{L_{2^k}^n}|=2^n-2^k=2^{n-1}+2^{n-2}+\cdots +2^{k+1}+2^k$. $Q_n[\overline{L_{2^k}^n}]=Q_n[0^{n-k-1}1X^k\cup 0^{n-k-2}1X^{k+1}\cup \cdots \cup 01X^{n-2}\cup 1X^{n-1}]$. $Q_n[L_{2^{k}}^n]$ is k-regular, with $|L_{2^k}^n|=2^k$. So both minimum-degree and average-degree of $Q_n[L_{2^k}^n]$ are at least k. As $Q_n[\overline{L_{2^k}^n}]$ has minimum degree k, its average degree is also at least k. This is because that for each subgraph $Q_n[0^{n-s-1}1X^s]$ is vertex disjoint for each $k\le s\le {n-1}$. It is isomorphic to $Q_s$ and is s-regular for each $k\le s\le {n-1}$. There exists at least one edge between the vertex in different $Q_n[0^{n-s-1}1X^s]$. So $Q_n[\overline{L_{2^k}^n}]$ is connected. $|L_{2^k}^n|=2^k\ge 2^k, |\overline{L_{2^k}^n}|=2^n-2^k\ge 2^k$. Based on the above facts, removing the edge-cut $[L_{2^k}, \overline{L_{2^k}^n}]$ from $Q_n$ results in exactly two components $Q_n[L_{2^k}^n]$ and $Q_n[\overline{L_{2^k}^n}]$. Both $Q_n[L_{2^{k}}^n]$ and $Q_n[\overline{L_{2^k}^n}]$ satisfy the properties $\mathcal {P}_1^k$, $\mathcal {P}_2^k$ and $\mathcal {P}_3^k$. Thus, in $Q_n$, $[L_{2^k}^n, \overline{L_{2^k}^n}]$ is a $\mathcal {P}_i^k$-conditional edge-cut in $Q_n$ for each positive $0\le k\le {n-1}$ and $1\le i\le 3$.

Similarly, because $Q_n[L_{2^k}^n]=FQ_n[L_{2^k}^n]$ and $E(Q_n[\overline{L_{2^k}^n}])\subset E(FQ_n[\overline{L_{2^k}^n}])$ for each $k\le n-1$, in $FQ_n$, $[L_{2^k}^n, \overline{L_{2^k}^n}]$ is also a $\mathcal {P}_i^k$-conditional edge-cut. As $2|E(Q_n[L_{2^k}^n])|=k2^k$ and $FQ_n$ is $(n+1)$-regular, $|[L_{2^k}^n, \overline{L_{2^k}^n}]|=(n+1)2^k-k2^k=\xi _{2^k}(FQ_n)$ for each positive $0\le k\le {n-1}$ and $1\le i\le 3$.

All in all, by the minimality of $\lambda (\mathcal {P}_i^k,Q_n)$ and $\lambda (\mathcal {P}_i^k,FQ_n)$, the results $\lambda (\mathcal {P}_i^k,Q_n)\le (n-k)2^k=\xi _{2^k}(Q_n)$ and $\lambda (\mathcal {P}_i^k,Q_n)\le (n+1-k)2^k=(n-k+1)2^k=\xi _{2^k}(FQ_n)$ hold. $\square$

The lower bounds of $\mathcal {P}_{i}^{k}$-conditional edge-connectivity of $FQ_{n}$ and $Q_{n}$ under three hypotheses can be shown as follows.

Lemma 4

For each $0\le c\le {n-2}$, $2^c\le h\le 2^{n-1}$, then $\xi _h(Q_n)\ge \xi _{2^c}(Q_n)=(n-c)2^c$; $\xi _h(FQ_n)\ge \xi _{2^c}(FQ_n)=(n-c+1)2^c$.

Proof

By Lemmas 1 and 2, $ex_{2^c}(Q_n)=ex_{2^c}(FQ_n)=c2^c$. For any $d=c,c+1,\cdots ,n-2$,

$$ \begin{aligned} ex_{{2^{{d + 1}} }} & (Q_{n} ) - ex_{{2^{d} }} (Q_{n} ) \\ & = ex_{{2^{{d + 1}} }} (FQ_{n} ) - ex_{{2^{d} }} (FQ_{n} ) \\ & = (d + 1)2^{{d + 1}} - d2^{d} \\ & = (d + 2)2^{d}. \\ \end{aligned} $$

So,

$$ \begin{aligned} \xi _{{2^{{d + 1}} }} & (Q_{n} ) - \xi _{{2^{d} }} (Q_{n} ) \\ & = n2^{{d + 1}} - ex_{{2^{{d + 1}} }} (Q_{n} ) - [n2^{d} - ex_{{2^{d} }} (Q_{n} )] \\ & = n2^{d} - (d + 2)2^{d} \\ & = (n - d - 2)2^{d} \\ & \ge 0. \\ \end{aligned} $$

The equality of the last inequality above holds if and only if $n=d+2$.

Similarly,

$$ \begin{aligned} \xi _{{2^{{d + 1}} }} & (FQ_{n} ) - \xi _{{2^{d} }} (FQ_{n} ) \\ & = (n + 1)2^{{d + 1}} - ex_{{2^{{d + 1}} }} (FQ_{n} ) - [(n + 1)2^{d} - ex_{{2^{d} }} (FQ_{n} )] \\ & = (n + 1)2^{d} - (d + 2)2^{d} \\ & = (n - d - 1)2^{d} \\ & \ge 2^{d} \\ & > 0. \\ \end{aligned} $$

On the other hand, $h=2^d+m_0<2^{d+1}$, let $h=\sum _{i=0}^{s} 2^{t_i}$, $t_0=2^d$, $m_0=h-2^d$, then $m_{0}=\sum _{i=1}^{s} 2^{t_{i}}=\sum _{i=0}^{s-1} 2^{t_{i+1}}<2^{k}\le 2^{n-2}$. Since $h\le 2^{n-1}$, $ex_h(Q_n)=ex_h(Q_{n-2})$,

$$ \begin{aligned} \xi _{h} (Q_{n} ) & - \xi _{{2^{d} }} (Q_{n} ) \\ & = nh - ex_{m} (Q_{n} ) - [n2^{d} - ex_{{2^{d} }} (Q_{n} )] \\ & = n\sum\limits_{{i = 0}}^{s} {2^{{t_{i} }} } - \sum\limits_{{i = 0}}^{s} {t_{i} } 2^{{t_{i} }} - \sum\limits_{{i = 0}}^{s} 2 i2^{{t_{i} }} - n2^{d} \\ & = n\sum\limits_{{i = 0}}^{{s - 1}} {2^{{t_{{i + 1}} }} } - \sum\limits_{{i = 0}}^{{s - 1}} {t_{{i + 1}} } 2^{{t_{{i + 1}} }} - \sum\limits_{{i = 0}}^{{s - 1}} 2 (i + 1)2^{{t_{{i + 1}} }} \\ & = (n - 2)(h - 2^{d} ) - \sum\limits_{{i = 0}}^{{s - 1}} {t_{{i + 1}} } 2^{{t_{{i + 1}} }} - \sum\limits_{{i = 0}}^{{s - 1}} 2 i2^{{t_{{i + 1}} }} \\ & = (n - 2)m_{0} - ex_{{m_{0} }} (Q_{n} ) \\ & = (n - 2)m_{0} - ex_{{m_{0} }} (Q_{{n - 2}} ) \\ & = \xi _{{m_{0} }} (Q_{{n - 2}} ) \\ & \ge 0. \\ \end{aligned} $$

Similarly, $h=2^d+m_0<2^{d+1}$, in $FQ_n$,

$$ \begin{aligned} \xi _{h} & (FQ_{n} ) - \xi _{{2^{d} }} (FQ_{n} ) \\ & = (n + 1)h - ex_{{m_{0} }} (FQ_{n} ) - (n + 1)2^{d} - ex_{{2^{d} }} (FQ_{n} ) \\ & = (n + 1 - 2)m_{0} - ex_{{m_{0} }} (FQ_{n} ) \\ & = (n - 1)m_{0} - ex_{{m_{0} }} (FQ_{n} ) \\ & = (n - 1)m_{0} - ex_{{m_{0} }} (Q_{{n - 1}} ) \\ & = \xi _{{m_{0} }} (Q_{{n - 1}} ) \\ & \ge 0. \\ \end{aligned} $$

The above results hold because $m_0\le 2^{n-1}$, $ex_{m_0}(FQ_n)=ex_{m_0}(Q_{n-1})$ by Lemmas 1 and 2. The last inequality holds because of the connectedness of $Q_{n-1}$. The proof is done. $\square$

Lemma 5

[5] For $A \subseteq V(Q_{n})$, let $Q_n[A]$ be the induced subgraph of A with average d, then $|A|\ge 2^d$.

Lemma 6

For any nonnegative integer $0\le k\le {n-1}$ and $1\le i\le 3$, $n\ge 1$, $\lambda (\mathcal {P}_{i}^{k},Q_n)\ge \xi _{2^k}(Q_n)=(n-k)2^k$; $\lambda (\mathcal {P}_{i}^{k},FQ_n)\ge \xi _{2^k}(FQ_n)=(n-k+1)2^k$.

Proof

For any integer $0\le k \le {n-1}$, $1\le i\le 3$, let F be any $\mathcal {P}_i^k$-conditional edge-cut of $Q_n$. Removal this edge-cut F from $Q_n$ results in p components $C_1, C_2,\ldots ,C_{p}$, $p\ge 2$. By the definition of $\lambda (\mathcal {P}_i^k, Q_n)$, each component should satisfy the property of $\mathcal {P}_{i}^{k}$.

Let $C^*$ be the minimum component among them. If the minimum degree of $C^*$ is at least k, then so is the average degree of $C^*$. By Lemma 5, $C^*$ contains at least $2^k$ vertices; then, one can have $|F|\ge |[V(C^{*}), \overline{V(C^{*})}]|\ge \xi _{|V(C^{*})|}(Q_{n}) \ge \xi _{2^{k}}(Q_{n})=(n-k) 2^{k}$. So the result $\lambda (\mathcal {P}_{i}^{k}, Q_{n}) \ge (n-k) 2^{k}$ holds.

As for any $m\le 2^{n-1}$, $ex_{m}(Q_{n})=2|E(Q_{n}[L_{m}^{n}])|=2|E(F Q_{n}[L_{m}^{n}])|=ex_{m}(FQ_{n})$. Similarly, let $C_0^*$ be the minimum component of $FQ_n$ after deleting any minimum $\mathcal {P}_i^k$-conditional edge-cut F, then $|F|\ge |[V(C_{0}^{*}), \overline{V(C_{0}^{*})}]|\ge \xi _{2^{k}}(F Q_{n})=(n-k+1) 2^{k}$. So for any $1\le i \le 3$, $0\le k \le {n-1}$, the result $\lambda (\mathcal {P}_{i}^{k}, F Q_{n}) \ge \xi _{2^{k}}(F Q_{n})=(n-k+1) 2^{k}$ also holds. The proof is finished. $\square$

4 The proof of main theorem for $\mathcal {P}_i^k$-conditional edge-connectivity of $FQ_n$ and $Q_n$

Theorem 1

For any nonnegative integer $0\le k\le {n-1}$ and $1\le i\le 3$, $n\ge 1$, $\lambda (\mathcal {P}_{i}^{k},Q_n)=\xi _{2^k}(Q_n)=(n-k)2^k$; $\lambda (\mathcal {P}_{i}^{k},FQ_n)=\xi _{2^k}(FQ_n)=(n-k+1)2^k$.

Proof

On the one hand, by the definition of $\lambda (\mathcal {P}_i^k, Q_n)$ and $\lambda (\mathcal {P}_i^k, FQ_n)$, for $0\le k\le {n-1}$, $1\le i\le 3$ and $n\ge 1$, and their minimality, Lemma 3 offers a $\mathcal {P}_{i}^{k}$-conditional edge-cut of $Q_n$ and $FQ_n$, $|[L_{2^k}^n, \overline{L_{2^k}^n}]|$, with $\xi _{2^{k}}(Q_{n})=|[L_{2^k}^n, \overline{L_{2^k}^n}]|=(n-k)2^k$ and $\xi _{2^{k}}(FQ_{n})=|[L_{2^k}^n, \overline{L_{2^k}^n}]|=(n-k+1)2^k$, respectively. So $\lambda (\mathcal {P}_i^{k},Q_n)\le \xi _{2^k}(Q_n)=(n-k)2^k$; $\lambda (\mathcal {P}_i^{k},FQ_n)\le \xi _{2^k}(FQ_n)=(n-k+1)2^k$.

On the other hand, by Lemma 6, for any $\mathcal {P}_{i}^{k}$-conditional edge-cut of $Q_n$ and $FQ_n$, $|F|\ge \xi _{2^{k}}(Q_{n})=(n-k)2^{k}$ in $Q_n$ and $|F|\ge \xi _{2^{k}}(F Q_{n})=(n-k+1) 2^{k}$ in $FQ_n$, respectively.

Combining Lemmas 3 and 6, the value $\xi _{2^k}(Q_n)=(n-k)2^k$ offers both upper and lower bound for $\mathcal {P}_i^k$-conditional edge-connectivity of $Q_n$, $\lambda (\mathcal {P}_i^k, Q_n)$ , and so does $\xi _{2^k}(FQ_n)=(n-k+1)2^k$ for the $\mathcal {P}_i^k$-conditional edge-connectivity of $\lambda (\mathcal {P}_i^k, FQ_n)$ of $FQ_n$. The proof of main theorem is completed. $\square$

5 Application

The n-dimensional hypercube $Q_n$ and folded hypercube $FQ_n$ are applied to underlying topological structures of most potential interconnection networks of parallel and distributed system, such as ATM switches, 3D Fold-Noc networks and PM2I networks. Our unified method of the robustness of hypercube and folded hypercube is based on these systems in the presence of failing links. Based on our main result, we give some exact values for $\lambda (\mathcal {P}_i^k,Q_n)$ and $\lambda (\mathcal {P}_i^k,FQ_n)$ when $0\le k\le 10$ in Table 2. Moreover, the visual images of both $\lambda (\mathcal {P}_{i}^{k},Q_n)$ and $\lambda (\mathcal {P}_{i}^{k},FQ_n)$ are shown in Fig. 3, for cases $n=11$ and $n=12$.

Table 2 Some exact values of $\lambda (\mathcal {P}_i^k,Q_n)$ and $\lambda (\mathcal {P}_i^k,FQ_n)$

Fig. 3

The plots of $\lambda(\mathscr{P}_i^k,Q_n)$ and $\lambda(\mathscr{P}_i^k,FQ_n)$ for $0\leq k\leq n-1$ and $11\leq n\leq 12$

Fig. 4

Edge-disjoint paths in two subgraphs of $Q_4$ and $FQ_4$

For $0\le k\le {n-1}$, let $\mathcal {P}_1^k$, $\mathcal {P}_2^k$ and $\mathcal {P}_3^k$ be the property of having at least k neighbors for each processor, containing at least $2^k$ processors and admitting average neighbors at least k, respectively. For the n-dimensional hypercubes and folded hypercubes networks with $N=2^n$ processors, we can find the minimum cardinality $(n-k)2^k$ and $(n-k+1)2^k$ of edge subsets of $Q_n$ and $FQ_n$, respectively, whose removal disconnects the network with each component satisfying the property of $\mathcal {P}_i^k$, where $1\le i\le 3$. In other words, similar to Menger’s theorem, we want to find edge-disjoint paths to connect any two subnetworks satisfying the property $\mathcal {P}_{i}^{k}$ in $Q_n$, the maximum number of such edge-disjoint paths in $Q_n$ is $(n-k)2^k$. For $FQ_n$ , such numerical value is $(n-k+1)2^k$.

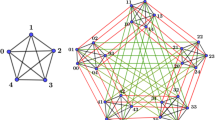
In order to make this issue more intuitive, we take some examples. For $n=4$, $k=2$ and $k=3$, under above three conditions, there are 8 edge-disjoint paths of $Q_4$ marked by dotted lines of different thicknesses in the first two picture in Fig. 4. For $n=4$ and $k=1$, under above three conditions, there are also 8 edge-disjoint paths of $FQ_4$ marked by dotted lines of different thicknesses in the last picture of Fig. 4. Our results enriched the theory of reliability and edge fault tolerance of cube-based interconnection networks.