Introduction

Atomic radius is an important periodic concept in chemical and physical sciences. Atomic radius plays an important role in describing various chemical and physical characteristics of the elements and predicts their reactivity behaviour. It has a pivotal role to describe lanthanide/actinide contraction, ionization energy, electron affinity, and strength of the chemical bond [1,2,3,4]. It is a well-known fact that an atom cannot be considered as a rigid sphere; hence, size of an atom depends upon the external forces acting upon it. Atoms do not have an independent existence except noble gases. Based upon the types of chemical bonding, the atomic radii are classified into various categories, i.e. ionic (interaction between ions), covalent (if atoms are covalently bonded), metallic (interaction between metals), van der Waals (interaction between non-bonded atoms), and absolute radius (based on free atom definition).

Various attempts have been made by many researchers to measure the atomic size for a long time and have suggested numerous scales. There were many experimental procedures that were carried out to get more accurate results. Meyer determined the atomic radii experimentally [5] followed by X-ray structure determination by Bragg [6] and studies by Pauling [7]. The theoretical prediction of atomic radii began with Slater [8]. A lot of theoretical scales have been suggested to determine the size of an atom [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Clementi et al. [10] suggested a double-zeta basis set for calculating atomic radii. They used the HF method with a minimum STO type data set without including relativistic effect. Pyykkӧ and Atsumi [25] suggested a self-consistent system of additive covalent radii while Chakraborty et al. [3] determined the absolute radii based on the conjoint action of two periodic properties, i.e. effective nuclear charge and ionization energy. Alvarez [4] reported van der Waals radii based on a statistical analysis using the Cambridge Structural Database (CSD). Rahm et al. [2] have reported atomic radii (van der Waals) in terms of average distance from the nucleus, where the electron density decreases to 0.001 electrons per Bohr3. Recently Rahm et al. [2] have reported atomic radii (Van der waals) in terms of average distance from the nucleus, where the electron density decreases to 0.001 electrons per Bohr3. Szarek and Grochala [30] has suggested a scale of the most probable radii which can be defined as the square root of polarizability (α) and hardness (η). In a previous work, Tandon et al. [31, 32] defined atomic radii in terms of nucleophilicity index and electrophilicity index. Very recently Prasanna et al. [33] did a non-relativistic study and used various DFT methods to evaluate theoretical radii. A good number of theoretical scales have been suggested to determine the size of an atom as of now [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. However, due to the presence of several scales, it has become very difficult to find the appropriate one. There is no study which provides a clear description on which atomic radius scale is the most consistent of all. In order to eliminate this perplexity, we have provided an analysis for these radii and discussion on some of the well-known scales of radii in the present work. We have compared the different scales of radii by using them to calculate atomic properties (electronegativity, chemical hardness, polarizability) and finding out the best probable radii based on its performance to compute atomic and molecular parameters.

Method of computation

Since there are a lot of scales of atomic radii, there is a mystification as to which is the best one. Hence, this work is carried out to explain the best possible one and ‘why’. For the comparison of atomic data, we have used absolute radii from Chakraborty et al. rC [3], covalent radii from Pyykkӧ and Atsumi rPA [25], van der Waal radii from Alvarez rA [4], radii given by Clementi et al. rCL [10], and van der Waal radii from Rahm et al. rR [2] for calculating some atomic properties, i.e. electronegativity, hardness, and polarizability. All types of radii are important and they are used to define the reactivity and stability of chemical species. Since all of these properties are size dependent, hence, we have performed their theoretical computation and then compared with existing experimental counterparts. The results assist in explaining which radius performs the best and which can be suitable in particular situations. For every set, radii change; however, other quantities are taken common so that the effect of radius change could be studied.

Electronegativity

Electronegativity is an old concept which is used in chemistry to correlate reactivity and other physico-chemical properties of atoms and molecules. Electronegativity (χ) is an important tool in describing the distribution and rearrangement of electronic charge in molecules [34, 35]. Electronegativity is not a physically observable property and hence it cannot be directly measured as per quantum mechanics. Electronegativity was first defined by Pauling in terms of ‘the power of an atom in a molecule to attract the electrons towards it’ [36]. Since then, numerous scales have been suggested by theoretical chemists to measure it [37,38,39,40,41,42,43]. In the present study, we have used the electrostatic approach, given by Allred and Rochow [39], to calculate electronegativity which is expressed as

$$\chi =0.359\frac{{Z}_{\mathrm{eff}}}{{r}^{2}}+0.744$$
(1)

Here Zeff represents effective nuclear and r is atomic radii. We have calculated electronegativity of elements by using Eq. (1) by using various scales of radii, i.e. rR [2], rC [3], rA [4], rCL [10], rPA [25]. Here Zeff [21] is considered as a constant input as it is the same for a particular atom in all the calculations where atomic radius is a variable parameter. Computed electronegativity is compared with experimental scale [44].

Hardness

Hardness (η) is defined as the hindrance in the distortion of the electron cloud of atoms, ions, or molecules [45]. It is useful in explaining various chemical properties [46]. The concept was first introduced by Mulliken [47]. A large number of scales have been suggested to measure hardness [48,49,50,51,52,53]. Here we have calculated atomic hardness by using Ghosh et al.’s [51] formula, which is expressed as

$$\eta =\frac{1}{2r}$$
(2)

Here η refers to hardness and r is taken from different works, i.e. rR [2], rC [3], rA [4], rCL [10], rPA [25]. The calculated hardnesses are compared with the hardness scale of Pearson [49].

Polarizability

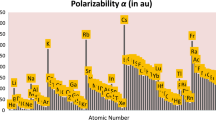
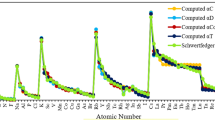
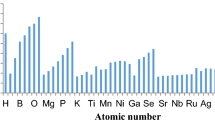
Polarizability (α) is defined as the linear response of an electronic charge distribution of an atom or a molecule with respect to an external applied electric field [54, 55]. Polarizability is a reactivity descriptor used to understand covalent as well as non-covalent interactions. Various scales of polarizability have been suggested time to time [15, 56,57,58,59,60,61,62]. We have calculated atomic polarizability on the basis of ansatz given by Szarek and Grochala [30], i.e.

$$\alpha =\frac{{r}^{2}}{\eta }$$
(3)

Here r refers to atomic radii and η represents atomic hardness. Here hardness is taken from reference [51] for all the sets while radii is taken from various sources rC [3], rA [4], rPA [25], rR [2], and rCL [10]. The computed polarizabilities are compared with experimental scale of polarizability [61].

Internuclear bond distances of diatomic molecules

There are some fundamental conceptual descriptors which are based on electronegativity and atomic radii such as internuclear distance, bond energies, and bond polarities [63]. In the present paper, we have calculated internuclear bond distances of some diatomic molecules, since internuclear bond distance is a size-dependent real-world descriptor and it would serve as a validity test for different scales of atomic radii. Ray et al. [64] have suggested an ansatz to calculate the internuclear bond distance by using electronegativity equalization principle [65,66,67,68] and zero-order approximation [69], which is based upon the simple bond charge model [70,71,72,73]. It is expressed as:

$${R}_{\mathrm{XY} }= \left({r}_{\mathrm{X}}+{r}_{\mathrm{Y}}\right)-\left[\frac{{r}_{\mathrm{X}}{r}_{\mathrm{Y} }{\left({\chi }_{\mathrm{X}}^\frac{1}{2} - {\chi }_{\mathrm{Y}}^\frac{1}{2}\right)}^{2}}{{\chi }_{\mathrm{X}}{r}_{\mathrm{X}} + {\chi }_{\mathrm{Y}}{r}_{\mathrm{Y}}}\right]$$
(4)

Here RXY represents internuclear bond distance for atoms X and Y, rX and rY defines the covalent radius of atoms X and Y while χX and χY denote the electronegativities of atoms X and Y. To check the performance of different radii such as rC [3], rA [4], rPA [25], rR [2], and rCL [10], we have used Eq. (4) to calculate the internuclear bond distance of some heteronuclear atomic molecules. Here we have used published electronegativity [44] for each radius set. The computed intermolecular distances are compared with the spectroscopic values [74] as shown in Table 1.

Table 1 Computed internuclear distance (RXY) of a number of diatomic molecules vis-à-vis their spectroscopic internuclear distances (RSpect) [74]
Full size table

Result and discussion

In the present work, we have compared five different types of atomic radii. By using Eq. (1), we have calculated electronegativities by using radii from rC [3], rA [4], rPA [25], rR [2], and rCL [10] and then compared them with a reliable scale of electronegativity given by Allen [44], as shown in Fig. S1. From the comparative graph, it can be seen that all the electronegativities are close to each other and show a good correlation (R2 > 0.75). R2 of rPA [25] shows a better correlation than others. The covalent radii of Pyykkö and Atsumi [25] were calculated on the basis of additive rule of the atomic radius for the calculation of bond length. Hence, it depends upon orbital hybridization. It is a well-known fact that the cationic radius of an element are shorter than its covalent radius, while the anionic radius are longer than covalent radius, which indicates that the effective radius of an atom depends on its electronegativity relative to that of the atom to which it is bonded. This is the reason we have obtained a good correlation with respect to rPA [25]. It is observed that electronegativity of Al is less than that of Ga for all types of radii we have used, and this is due to the reason of poor nuclear shielding by the d-electrons present in Ga. Next, the values of Fr and Ra are higher than Cs and Ba respectively for rC [3], due to relativistic contraction and stabilization of the 7s orbital [61]. The first member of the group in p-block elements should have the highest value of electronegativity than rest of the elements. This trend is shown by electronegativities computed using rC [3], rCL [10], and rPA [25] (refer Table S1). Due to relativistic effect, Hg and Au show chemical inertness. Relativistic effects have a strong influence on physico-chemical properties of heavier elements [75,76,77]. For example, in the case of Hg (5d10 6s2), due to relativistic stabilization of the 6s2 subshell, its first ionization energy is highest in its respective period [78]. This shows the inert nature of Hg. Also, Au (5d10 6s1) shows inert behaviour but less than Hg due to less stabilized 6s1 subshell as compared to Hg. This inert behaviour of Au and Hg is shown by our computed values by using rR [2], rC [3], and rCL [10]. It can be seen from Fig. S2 that R2 of rCL [10] shows a poor correlation. This may be due to the reason that Clementi et al. [10] have used a non-relativistic approach to calculate atomic radii and that is why for heavy elements, i.e. Z > 20, the radii do not fit well.

By using Eq. (2), we have calculated atomic hardness by employing rR [2], rC [3], rA [4], rCL [10], and rPA [25]. To check the performance of different types of atomic radii, we have compared the computed atomic hardness with Pearson’s scale of hardness as shown in Fig. S2. From this comparative study, it can be seen that computed atomic hardness based on rC [3] shows a good correlation (R2 = 0.859) than others. The computed atomic hardness based on rC [3] also defines the inert nature of Hg and Au perfectly; Hg has the highest value of hardness in its period followed by Au. Also in the case of Pb, the 6p21/2 shell is stabilized and hence its first ionization energy becomes higher than Tl (6s2 6p11/2) and Bi (6s2 6p21/2 6p13/2). As a result, the hardness value of Pb should also be greater than that of Tl and Bi. This behaviour is reflected in the computed hardness values based on rC [3] while computed hardnesses based on other radii violate this effect (see Table S2). This demonstrates the reliability of rC.

Next we have also calculated polarizability of elements by using Eq. (3) and then compared the computed data with experimental counterparts as shown in Fig. S3. It can be seen that computed hardness based on rC [3] has the highest value of regression coefficient (R2 = 0.940) among all others. Here also absolute radii, i.e. rC [3], perform very well. Also, the lowest value of polarizability for Hg and Au in the respective period is demonstrated through the values of rR [2], rC [3], and rCL [10] (refer Table S3).

We have calculated intermolecular bond length of some diatomic molecules by using Eq. (4). The calculated internuclear bond distances of some diatomic molecules vis-à-vis their experimental counterparts [74] are presented in Table 1. Here R1XY, R2XY, R3XY, R4XY, and R5XY represent the bond lengths of molecules while R21, R22, R23, R24, and R25 represent the regression coefficients with respect to rR [2], rC [3], rA [4], rCL [10], and rPA [25]. From Table 1, it can be seen that the value of regression coefficient (R2) is above 0.9 in almost every set of atomic radii, which gives a good correlation with the published value. However, in the case of rC [3]-based values, almost every set gives a correlation coefficient (R2) equal to 0.999.

Thus, we observe that absolute radius demonstrates a good agreement in calculating reactivity descriptors (as mentioned above) in contrast to other radii. This is perhaps due to the reason that absolute radius is a free atom property; unlike covalent radii, which is non-transferable and an in situ property. Also, it depends on the potency of bond and scope of covalency. The radii derived by Rahm et al. are related to the density of a free and neutral atom but these radii are not directly related with radial wave function, they are different from the most probable radii. From the results, we examined that all the radii which we have used for comparison are quite effective in explaining various descriptors but the one which shows a good correlation with almost all the descriptors is absolute radii. It is assumed that relativistic effects have a great influence on atomic size.

Conclusion

In the present work, we have compared different sets of atomic radii in terms of on their applicability in calculating some size-dependent atomic properties, i.e. electronegativity, chemical hardness, polarizability, and a real-world descriptor, i.e. intermolecular bond distance. Since all these properties are size dependent, hence, the efficacy of each set of radii has been examined by correlating the computed data with existing scales which give a measure of the reliability of different radii scale. It is concluded that all the radii perform well in calculating these atomic properties and show a good correlation with existing scales; however, absolute radii seem to be minutely more reliable. In a significant number of cases, the theoretically calculated atomic properties in terms of the absolute radii are quantitatively close to their published values. Hence, it is apparent that absolute radius may act well in understanding atomic and molecular behaviours and explaining the causes behind prevalent and possible phenomenon in comparison to other scales. Other radii such as covalent and ionic are also useful in the predictions; however, it is difficult to get each and every detail using these radii as they are nature specific. While when we employ absolute radii, as it is a free atom property, it can better analyze and explain the subject of concern. We therefore do not suggest that other radii are less useful but absolute radii can be a bit more advantageous while studying and comparing a wide variety of systems whether metallic, ionic, covalent, or any other.