1 Introduction

Conceptual Density Functional Theory (CDFT) helps to define various reactivity parameters such as chemical hardness [1], electronegativity [2], chemical potential [3], etc. Global hardness can be conceptualized as the hindrance in the distortion of the electron cloud of a chemical species, i.e., atoms, ions or molecules [4]. It can help in explaining many chemical properties like solubility of molecules, chemical reactivity and complex stability [5]. The term chemical hardness was first introduced by Mulliken in his seminal work [6]. He suggested that the “Hard” and “Soft” character of different chemical species can be understood during an acid–base reaction. Following this proposition, Pearson [7, 8] and Klopman [9, 10] tried to classify this property. Pearson [7, 8] presented a qualitative categorization for different chemical species and termed it as Hard-Soft Acid–Base (HSAB) Principle. According to this principle, “soft acid prefers to react with soft base and hard acid prefers to react with hard base". As per Pearson [11],

$$ \chi = - \mu = \left( {\frac{\partial E}{{\partial N}}} \right)_{\nu (r)} $$
(1)
$$ \eta = \frac{1}{2}\left[ {\frac{{\partial^{2} E}}{{\partial N^{2} }}} \right]{}_{\nu (r)} = \frac{1}{2}\left[ {\frac{\partial \mu }{{\partial N}}} \right]{}_{\nu (r)} $$
(2)

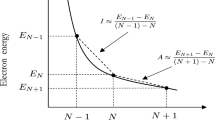
He also suggested a new relationship based on finite differences method, i.e.,

$$ \eta = \left( {\frac{I - A}{2}} \right) $$
(3)

where I is ionization potential, and A is electron affinity. Successively, Pearson [12], defined these terms using Koopmans theorem, i.e.,

$$ I = - \in_{HOMO} andA = - \in_{LUMO} $$
(4)

Accordingly the relationship for evaluating hardness in terms of Self-Consistent Field Theory is written as,

$$ \eta = - \left( {\frac{{ \in_{HOMO} - \in_{LUMO} }}{2}} \right) $$
(5)

By using this approximation, Pearson [13] evaluated hardness of 63 elements of the periodic table. Tozer and De Proft [14], proposed a model to calculate chemical hardness. According to this method, orbital energies obtained from DFT are used to calculate chemical hardness. For this purpose, Koopman’s theorem requires a simple correction,

$$ \eta = \left( {\frac{{ \in_{HOMO} + \in_{LUMO} }}{2}} \right) + I $$
(6)
$$ {\text{or}}\quad \eta = - \chi + I $$
(7)

According to Eq. (7), chemical hardness can be defined as a difference between electronegativity and ionization potential. The theoretical basis for the hard-soft acid-base character was found in ‘Conceptual Density Functional Theory’ [15] (CDFT). This theory has added two principles in the list of fundamental laws of nature, i.e., Maximum Hardness Principle [16] (MHP) and Minimum Polarizability Principle [17] (MPP). Pearson formulated MHP which states that “there seems to be a rule of nature that molecules arrange themselves to be as hard as possible. Both MHP and MPP can help to predict the most stable isomer and are consistent with the Bent’s rule as suggested by Noorizadeh [18]. Thus, the importance of hardness as a descriptor is transparent from the literature.

Recently Kaya et al. [19] proposed a new scale for the calculation molecular hardness, which is given as:

$$ \eta_{M} = \frac{{2\sum\limits_{i = 1}^{N} {\frac{{b_{i} }}{{a_{i} }} + q_{M} } }}{{\sum\limits_{i = 1}^{N} {\frac{1}{{a_{i} }}} }} $$
(8)

Here ƞM and qM denote the molecular hardness and charge of molecule; ai and bi parameters are defined as:

$$ a_{i} = \frac{IE + EA}{2} $$
(9)
$$ b_{i} = \frac{IE - EA}{2} $$
(10)

Here IE and EA denote ionization energy and electron affinity. Cardenas et al. [20] defined the benchmark value of atomic hardness from the energies of isoelectronic Series. The main objective of the present study is to obtain a new model which provides reasonable values for chemical hardness of atoms and molecules. It is an important reactivity descriptor and is widely used in chemistry but due to lack of its universal values, there is still scope of improvement. Various attempts have been made to measure hardness for a long time, and numerous scales have been suggested to measure it. However, it is observed that the best measurement scale for hardness has not been proposed until now. Reed [21] has pointed out that the evaluation of global hardness by using finite difference approximation method contains mathematical inconsistency. So, there is sufficient scope of suggesting empirical method for evaluation of global hardness of atoms. It is important to note that the suggested model is comparatively simple and makes it possible to determine and explain chemical reactivity in terms of atomic indices. New relations and related principles are taken into consideration which leads to the development of more reliable model and provides results superior than the previous ones.

2 Method of computation

The quantitative definition of electrophilicity was proposed by Parr et al. [22]. As per Parr and his co-workers,

$$ \omega = \frac{{\mu^{2} }}{2\eta } = \frac{{\chi^{2} }}{2\eta } $$
(11)
$$ {\text{or}}\quad \eta = \frac{{\chi^{2} }}{2\omega } $$
(12)

According to Chattaraj and Maiti [23], electrophilicity index is inversely related to the nucleophilicity index,

$$ \omega = \frac{1}{N} $$
(13)

In 1946, Gordy [24] proposed electrostatic potential felt by one of valence electrons in an atom as its electronegativity.

$$ \chi = \frac{{Z_{eff} \times e}}{r} $$
(14)

In Eq. (14), Zeff refers to the effective nuclear charge, e is the electronic charge and r represents the covalent radius of an atom.

On substituting Eq. (13) and (14) in Eq. (12), we obtain a new model for the atomic hardness which is expressed by Eq. (15):

$$ \eta = \frac{N}{2}\left( {\frac{{Z_{eff} \times e}}{r}} \right)^{2} $$
(15)

Thus, Eq. (15) is used for the evaluation of atomic hardness (ƞ).The new model is based on three important descriptors, i.e., nucleophilicity index (N), effective nuclear charge (Zeff) and absolute radius (r) of atoms. Atomic hardness has been computed for 103 elements of the periodic table by performing regression analysis. Hardness acts as a dependent variable while the other three descriptors are independent variables. The data for computation are taken from the work of Tandon et al. [25] for Nucleophilicity index, Ghosh and Biswas for effective nuclear charge [26], and Chakraborty et al. for absolute radius [27]. We have used absolute radius in this work as it is a true size descriptor of atomic property. The computation is performed in atomic unit (au).

Recently Parr and Ayers [28], have described higher order global softness and global hardness. Their study justified that local hardness is equal to global hardness at every point in space; it proves that chemical hardness is also equilibrated like electronegativity. In 1986, Yang et al. [29] defined molecular softness post which Datta [30] suggested Hardness Equalization Principle (HEP) for the calculation of molecular hardness by using the geometric mean principle. According to this principle, ‘The hardness gets equalized during molecule formation’ and it is expressed as the geometric mean of the chemical hardness of the corresponding isolated atoms in the molecule’. It is represented as,

$$ \eta_{GM} = \left( {\prod\limits_{K = 1}^{P} {\eta_{K} } } \right)^{\frac{1}{P}} $$
(16)

In Eq. (16), P refers to the total number of atoms in a molecule, ƞK is the hardness of the Kth atom where K = 1, 2, 3,...,P. The validity of hardness equalization principle is also suggested by Ghosh et al. [31]. Relying upon this principle (HEP), we have calculated molecular hardness for some alkali halides (inorganic ionic crystal) and compared them with the reported values [32]. The relationship of molecular hardness with lattice energy is studied for the selected ionic crystals.

3 Application of hardness in determining reactivity and stability of compounds

In the present study, the newly evaluated hardness is used to develop a QSPR (Quantitative Structure–Property Relationship) model to study the dependence of hardness on lattice energy. QSPR is applied to build up mathematical as well as computational models which find a statistically important relationship between different molecular properties [33,34,35]. This technique allows prediction of molecular properties for a variety of known and unknown compounds by employing statistical procedures and optimizing novel lead molecules. DFT dominates QSPR since a last few years. The absolute hardness describes the reactivity and stability of chemical species [5]. HSAB Principle and MHP based on chemical hardness favor this. The chemical compounds which are hard, have low polarizabilities and stable electron distributions are more stable as compared to soft compound having high polarizabilities. This concept is known as the Maximum Hardness Principle. Lattice energy is defined as the energy which is required to convert an ionic solid into its constituent ions (gaseous form). It is also a measure of stabilities of ionic compounds. Hence it is considered that there should be an appreciable correlation between lattice energies and chemical hardness values of ionic compounds. Pearson noticed that there is a considerable correlation between chemical hardness and cohesive energy which defines the stability and reactivity of compounds. Recently Kaya et al. [32], proposed a new scale for the calculation of lattice energy of inorganic ionic crystal based on chemical hardness. We have studied the effect of change in hardness on lattice energy of some diatomic ionic crystal. The lattice energy data (U) are taken from [36], which is an experimental value. In order to construct a QSPR model, linear regression analysis is employed in our study. Here, lattice energy (U) is expressed as a linear function of the independent variable such as molecular hardness.

$$ U = a\left( \eta \right) + b $$
(17)

Here ‘a’ and ‘b’ are determined for the selected alkali metal halides. The effectiveness of the proposed model is accomplished by estimating the coefficient of determination (R2). The computed ‘hardness dependent’ lattice energy values are correlated with the experimental lattice energy value to confirm the persistence of the model (as shown in Table 2).

4 Result and discussion

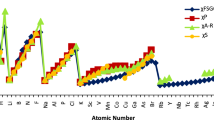
In the present work, we have suggested an ansatz for calculating the atomic hardness. The computed atomic hardness values for 103 elements in atomic unit (au) are shown in the form of a periodic chart in Table 1. To check the periodicity of newly evaluated data, we have plotted global hardness as a function of atomic number in Fig. 1. It can be seen from Table 1 and Fig. 1 that the computed hardness of 103 elements exhibits the periodic behavior. It can be observed from Fig. 1 that the value of hardness is the maximum for noble gases. It is a rule of nature that high hardness means less deformability. It is well known that noble gases show the least deformability or less polarization due to stable electronic configuration. Further, from Table 1, it can be seen that the magnitude of hardness of all transition and lanthanide elements is small. This fact indicates soft nature of these elements. The high reactivity of Cs and Fr in their respective group can be well explained by their small values of hardness in the particular group. Our computed hardness data of some particular elements (N, O, F, P, S and Cl) follows an expected pattern, viz. N (0.215) < O (0.222) < F (0.293) < P (0.402) < S (0.461) < Cl (0.769), in accordance with the literature [37].

Table 1 Periodic chart of computed atomic hardness (ƞ) values for 103 elements (approximated to 3rd decimal place)
Full size table
Fig. 1
figure 1

Plot of hardness (ƞ, in au) as a function of atomic number (H and He atom are excluded from the figure due to their considerably high hardness values)

Full size image

According to the theory of relativity, the mass of an electron increases as its speed approaches the speed of light. The relative velocity (v) of an electron of an element holds the relation \(v\propto Z\), where Z is an atomic number. In case of lighter elements, as the velocities of electrons are not very high, the effects of relativity can be neglected. However for the heavier elements (mainly the sixth and seventh period elements with Z > 50), these effects become significant [38,39,40]. Relativistic effects have a strong impact on the chemical and physical properties of heavy elements and their compounds. The consequences of relativistic effect can be seen in the form of lanthanide and actinide contraction, liquidity of mercury at room temperature, yellow color of gold and extreme contraction of chemical bond lengths [38, 39]. A look at our hardness data in Table 1 shows the presence of such relativistic effects in the form of lanthanide and actinide contraction. The hardnesses of lanthanides and actinides increase very slowly with an increase in their atomic numbers. It is also observed that the first ionization energy of Hg is higher than most other metals of the sixth period due to the relativistic stabilization of the 6 s subshell [41]. This indicates inertness of Hg. It is noted that our computed value of hardness for Hg (0.295 au) is also the highest among the sixth period signifying its inertness. The presence of Hg in liquid state is also probably a consequence of relativity as it leads to a stable filled 6s2 shell. Similarly Au (0.230 au) is also a noble element, trivalent and yellow in color owing to these effects [38] which is in accordance with our computed hardness values.

Spin orbit coupling is also one of the relativistic effects. It is a relativistic interaction of orbital angular momentum and spin angular momentum of an individual particle, such as electron [38]. For heavy atoms (particularly sixth and seventh period elements), spin orbit coupling is large. Due to this spin orbit coupling, the heavy elements and their compounds show anomalous behavior as compared to the other elements in their respective group, for instance, the spin–orbit splitting between 6p1/2 and 6p3/2 is quite large for sixth period elements. Specifically in case of Pb, 6p21/2 shell becomes completely filled causing the metal to be semi-inert. It has been reported that the computed dissociation energy of Pb2 is almost half of that of Sn2 or the non-relativistic value [42]. Further, due to stabilized 6p21/2 shell of Pb, its first ionization energy also becomes higher than Tl (6s2 6p11/2) and Bi (6s2 6p21/2 6p13/2) [41]. As a consequence, the hardness value of Pb should also be greater than Tl and Bi. However, in the present calculation, it is noted that the hardness of Pb (0.081 au) is less than that of Bi (0.083 au). A study on the clusters of group V shows that Bi clusters exhibit anomalies due to very large spin–orbit [43]. Next, the value of Pb (0.081 au) should be below but closer to Sn (0.130), but it is seen that there is a considerable gap between the two. In general, it is observed that the computed hardness of Pb and Bi do not follow the properties of molecules and clusters containing Pb and Bi. All these discrepancies in the expected behavior are due to the lack of inclusion of spin–orbit coupling in our proposed model.

Next in order to check the validity and soundness of our newly evaluated data we have done a comparative study of our present work atomic data with atomic hardness of Pearson [44], Robles and Bartolotti [45] and Cardenas et al. [20]. It can be observed from Fig. 2 that our newly evaluated data show a good correlation with the different existing hardness scales evidencing its reliability. Calculated molecular hardness has been compared with reported [32] values (see Table 2) for the same set of molecules as illustrated in Fig. 3. This analysis has been done to check the effectiveness of our model and computed data. As reflected from Fig. 3, a good correlation exists between the computed and reported sets. Thus, our computed hardness nicely follows the HEP.

Fig. 2
figure 2

Comparison of computed atomic hardness with that of Pearson’s [44], Robles and Bartolotti’s [45] Cardenas et al. [20] hardness (in au)

Full size image
Table 2 Chemical hardness (ƞ) and lattice energy (U) of alkali halides
Full size table
Fig. 3
figure 3

Comparison of computed molecular hardness (ƞ) of some inorganic ionic crystals (alkali halides) vis-á-vis reported molecular hardness [32] (in au)

Full size image

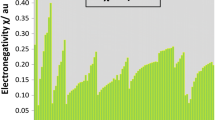
As proposed by Szarek and Grochala [46], polarizability is inversely related to hardness. Recently Tandon et al. [47] also proposed a new scale of calculating atomic polarizability based on this assumption. Thus, we have tried to compare our hardness scale with that of inverse polarizability scale of Tandon et al. [47]. As illustrated by Fig. 4, our proposed hardness scale shows a good correlation with that of Tandon et al. scale of polarizability, i.e., inverse relationship between hardness and polarizability. Atoms having high hardness value show low polarizability and vice versa.

Fig. 4
figure 4

Comparative plot of computed atomic hardness (ƞ) values vis-à-vis inverse of atomic polarizability (α) values [47] (in au)

Full size image

It can be understood that the molecule having the highest value of the hardness (ƞ) has high lattice energy (U) value. Lattice energy is an important descriptor which defines the reactivity and stability of ionic compounds. Initially, we calculated the atomic hardness by using Eq. (15) and then by using HEP, viz. Equation (16), we have calculated molecular hardness. We have examined the dependence of lattice energy of ionic crystals on molecular hardness by constructing a QSPR model. A linear Eq. (17) is constructed to determine the lattice energy, for which the obtained value of ‘a’ and ‘b’ are as follows:

$$ U = 3.794\eta + 0.127 $$
(18)

The value of lattice energy obtained by this model is compared with the experimental value of lattice energy (U) evaluated from Born-Haber-Fajans thermochemical cycle [36]. It provides very close results to the experimentally obtained values which are listed in Table 2. The reliability of the proposed model can be checked by the value of regression coefficient (R2 = 0.867). Although several theoretical methods have been proposed to calculate the lattice energies of inorganic ionic solids, this is a simple method to calculate lattice energy by using hardness. Our results and comparisons with other theoretical models establish that the new model is very much helpful for achieving nearly accurate calculations of lattice energies for inorganic ionic crystals without the need of ab initio methods or any other complex calculations.

Furthermore this model, Eq. (15) is very useful for the prediction of lattice energies of ionic compounds such as metal oxides, metal sulfides and the obtained lattice energies are very close to the experimental value. This equation is useful in calculating lattice energies of ionic compounds with energies less than 5000 kJ/mol.

5 Conclusion

In the present report, we have suggested an ansatz for the computation of atomic hardness of 103 elements of the periodic table. It provides reasonable values for atoms and follows periodicity trends across the periods and down the groups. The reliability of hardness model has been established by correlating with existing scales of hardness. The present scale also satisfies the Hardness Equalization Principle very well. Our suggested ansatz of chemical hardness also shows a good correlation with lattice energy and polarizability and explains the reactivity and stability of compounds. A QSPR model is constructed for alkali metal halides using hardness as a predictor to evaluate their lattice energy. An excellent analogy is found between predicted and observed lattice energies. The high value of coefficients of determination establishes efficiency of the proposed model. Thus, it is believed that our new model is significant for determining and elucidating several physicochemical properties and related phenomenon.

The proposed model can be further extended to compute atomic hardness beyond Lr based on the availability of data for the descriptors used for the computation. For super-heavy elements, the direct relativistic effect is known to be large for the outmost s and p1/2 valence electrons. It is believed that the 7 s orbital of Cn (Z = 112) will undergo 25% contraction as a result of relativistic stabilization [48]. Accordingly, it is expected that Cn will be harder than the lighter members of its group. Inert-pair effect increases as we move downwards in a group. This effect is found to be most dominant for the last element of a group. Thus, if the model is extended, it is believed that the inert-pair effect pointed out for Pb will also be dramatically reflected for Fl (Z = 114). It is suggested that due to inert-pair effect, the 7p21/2 shell of Fl becomes so inert that it is predicted to be an inert gas rather than a very reactive metal [49]. This fact also indicates toward a higher value of hardness for Fl. Although these are some possibilities, the effect of relativity on the valence orbitals of super-heavy elements is highly pronounced, and they may lead to an exceptional behavior with regards to atomic property trends, including hardness, as compared to their lighter counterparts.