Estimation of time-varying autoregressive stochastic volatility models with stable innovations

Abstract

A new time-varying autoregressive stochastic volatility model with $\alpha$-stable innovations (TVAR$\alpha$SV) is proposed. This new model for time series data combines a time-varying autoregressive component and a stochastic scaling as known from stochastic volatility models with $\alpha$-stable distributed noise. Hence, the model can cover extreme events better than classical stochastic volatility models. Furthermore, we develop a Gibbs sampling procedure for the estimation of the model parameters. The procedure is based on the estimation strategy by Kim et al. (Rev Econ Stud 65(3): 361–393, 1998) for classical stochastic volatility models, however, the estimation procedure requires a deliberate approximation of $\alpha$-stable distributions by finite mixtures of normal distributions and the application of a simulation smoother for linear Gaussian state space models. A simulation study for the new estimation procedure illustrates the appealing accuracy. Finally, we apply the model to electricity spot price data.

1 Introduction

Stochastic volatility (SV) models are widely used in financial econometrics and have been extensively studied over many years. These models date back into the 1980s, cf. Hull and White (1987). Properties were discussed, e.g., in Taylor (1994), Shephard (1996) and Ghysels et al. (1996). The papers by Jacquier et al. (1994) and Kim et al. (1998) proposed Bayesian estimation algorithms. The key feature of the SV models is the stochastic scaling of the innovations, so that periods of higher and lower volatility are accurately captured. Usually Gaussian or Student-t innovations were used in the literature. Whereas these distributions seem to be sufficient for many situations of classical financial markets, they can not handle extreme price changes (spikes) which can be observed, e.g., on electricity markets, where extreme values result from the lack of efficient storage possibilities and a sudden imbalance of supply and demand. Hence, for modeling such phenomenons, distributions with heavy tails, as $\alpha$-stable distributions, seem to be more appropriate. As a generalization of normal distributions, the $\alpha$-stable distributions also provide the possibility to account for skewness in the empirical data.

The novel idea of this paper is to combine a time-varying autoregressive component and a stochastic scaling as known from stochastic volatility models with $\alpha$-stably distributed noise. We will abbreviate this model by TVAR$\alpha$SV. Note that we use the notion stochastic volatility for our model due to its similarity to the classical SV models although for the non-degenerated $\alpha$-stable distributions the variance as the second centered moment does not exist. Our model is related to Primiceri (2005) who generalized the autoregressive model to a time-varying structural vector autoregression model, where the time variation derives both from the coefficients and the covariance matrix of the multivariate Gaussian innovations. Casarin (2004), Lombardi and Calzolari (2009) and Vankov et al. (2019) also worked with SV-like models with $\alpha$-stable innovations, however, they did not include an autoregressive structure in the observation equation.

Our primary goal is the development of an estimation procedure for the TVAR$\alpha$SV model parameters. The challenge for the use of $\alpha$-stable distributions is that their moments of order greater than or equal to $\alpha$ do not exist, for $\alpha \ne 2$, and their density function cannot be described in closed form. For this reason, maximum likelihood or moment-based estimation procedures are not applicable. In order to estimate parameters of similar models with $\alpha$-stable distributions, mainly approximate Bayesian computation (Martin et al. 2019; Vankov et al. 2019), likelihood-free Bayesian inference (Peters et al. 2012) or indirect inference methods (Calzolari et al. 2014; Lombardi and Calzolari 2009) were used in the existing literature. Our new proposed estimation procedure for the TVAR$\alpha$SV model parameters, and in general for the class of SV-like models with $\alpha$-stable distributions, is also carried out in a Bayesian framework, leading to a Markov chain Monte Carlo algorithm (Brooks et al. 2011). The core idea is the approximation of intractable innovation distributions by finite mixtures of normal distributions and the application of a simulation smoother for linear Gaussian state space models. This approach was developed by Shephard (1994), De Jong and Shephard (1995) and Kim et al. (1998). Since we have to approximate $\alpha$-stable densities, we will use not only classical minimum distance mixture approximations but also additionally employ specific component distributions, which we will call tail components, to improve the approximation of the tails of the $\alpha$-stable distributions.

Benth et al. (2014) and Müller and Seibert (2019) have dealt with modeling electricity prices. They have shown that long-term non-stationarities, i.e. significant price level deviations from the mean price after removing seasonalities and short-term effects, are present in the data. Benth et al. (2014) take this into account by using a Lévy process in addition to the CARMA(2,1) (continuous-time autoregressive moving average) model from García et al. (2011). Indeed, prices show some autoregressive behavior due to the fact that the circumstances leading to higher or lower prices, e.g., weather or power plant failures, usually last for more than one day. The current structural change in energy supply, mainly due to the expansion of renewable energies, requires additional flexibility of the model. Our application of the TVAR$\alpha$SV model to electricity spot price data in Sect. 5 shows that such structural breaks can be modeled well with time-varying parameters. For this reason, classical autoregressive models or autoregressive-moving-average models with constant parameters seem not to be sufficiently flexible. Therefore, describing electricity prices requires an autoregressive model which accounts for time-variation in the parameters and allows for extreme price changes as well.

The paper is organized as follows. In Sect. 2 we introduce the TVAR$\alpha$SV model. A suitable estimation method of the TVAR$\alpha$SV model is presented in Sect. 3. We investigate the quality of the proposed estimation algorithm in a simulation study in Sect. 4. In Sect. 5 we apply the estimation procedure of the TVAR$\alpha$SV model to electricity spot price data.

Regarding notation, we use lower case letters to denote random variables, whereas capital letters are used for their realizations. Also, we shall use $x_{1:n}$ to denote the set $\{x_1,\dots ,x_n\}$. The notation $p(\cdot )$ is used to denote a generic probability density. In case of continuous distributions the reference measure is the Lebesgue measure, whereas the counting measure is used for distributions with discrete support.

2 The time-varying autoregressive stochastic volatility model with stable innovations (TVAR$\alpha$SV)

Following the representation of Samorodnitsky and Taqqu (1994), a random variable x is said to have an $\alpha$-stable distribution, i.e. $x\sim {\mathcal {S}}(\alpha , \beta , \gamma , \delta )$, with $\alpha \in (0,2]$, $\beta \in [-1,1]$, $\gamma >0$ and $\delta \in {\mathbb {R}}$, if it has the characteristic function

$$\begin{aligned} \mathrm {E}\exp (iux)= {\left\{ \begin{array}{ll} \exp \Big (-\gamma ^\alpha |u|^\alpha [1-i\beta (\text {sign}\ u)\tan \frac{\pi \alpha }{2}]+i\delta u\Big ), &{} \text {for}\ \alpha \ne 1\\ \exp \Big (-\gamma |u|[1+i\beta \frac{2}{\pi }(\text {sign}\ u)\log |u|]+i\delta u\Big ), &{} \text {for}\ \alpha =1\\ \end{array}\right. }. \end{aligned}$$

(1)

The characteristic parameter $\alpha$ describes the tail thickness. The other three parameters $\beta$, $\gamma$, and $\delta$ are called skewness parameter, scale parameter, and location parameter, respectively. For $\alpha \ne 2$ an $\alpha$-stable random variable is symmetric about $\delta$ if and only if $\beta =0$. Moreover, for $\alpha \ne 2$ an $\alpha$-stable distribution is right-skewed if $\beta >0$ and left-skewed if $\beta <0$.

The probability densities of $\alpha$-stable random variables exist and are continuous; however, with a few exceptions, they are not known in closed form. The most famous exception is the normal distribution, ${\mathcal {N}}\left( \mu ,\sigma ^2\right) ={\mathcal {S}}(2,\beta ,\frac{\sigma }{\sqrt{2}},\mu )$, with arbitrary $\beta$, since for $\alpha =2$ it follows that $\tan \left( \frac{\pi \alpha }{2}\right) =0$ in the characteristic function (1). For $\alpha \ne 2$, $\alpha$-stable distributions have infinite variance and when $\alpha \le 1$, they have an infinite mean as well.

A proof of the following property is presented in (Samorodnitsky and Taqqu 1994, Property 1.2.2 and 1.2.3 on page 11): Let $x\sim {\mathcal {S}}(\alpha ,\beta ,\gamma ,\delta )$, c be a real constant and a be a real non-zero constant. Then

$$\begin{aligned} ax+c\sim {\left\{ \begin{array}{ll} {\mathcal {S}}(\alpha ,(\text {sign}\ a)\beta ,|a|\gamma ,a\delta +c), &{} \text {for}\ \alpha \ne 1\\ {\mathcal {S}}(\alpha ,(\text {sign}\ a)\beta ,|a|\gamma ,a\delta -\frac{2}{\pi }a(\log |a|)\gamma \beta +c), &{} \text {for}\ \alpha =1 \end{array}\right. }. \end{aligned}$$

(2)

In the following, we introduce the time-varying autoregressive stochastic volatility model with $\alpha$-stable innovations and discuss some important properties.

Definition 1

(TVAR$\alpha$SV) A process $\{y_t\}_{t \in {\mathbb {N}}_0}$ is called time-varying autoregressive stochastic volatility process with $\alpha$-stable innovations, if and only if it satisfies for every $t \in {\mathbb {N}}$ the equation

$$\begin{aligned} y_t&=\phi _t y_{t-1}+e^{\frac{h_t}{2}}\varepsilon _t,&\varepsilon _t&\sim {\mathcal {S}}(\alpha ,\beta ,1,0), \end{aligned}$$

(3)

such that the dynamic of the time-varying autoregressive coefficient $\phi _{t}\in {\mathbb {R}}$ and the time-varying scale parameter $h_{t}\in {\mathbb {R}}$ is determined by the equations

$$\begin{aligned} \phi _t&=\phi _{t-1}+\sigma _{\phi }\xi _{t,\phi },&\xi _{t,\phi }&\sim {\mathcal {N}}(0,1), \end{aligned}$$

(4)

$$\begin{aligned} h_t&=h_{t-1}+\sigma _{h}\xi _{t,h},&\xi _{t,h}&\sim {\mathcal {N}}(0,1), \end{aligned}$$

(5)

where all innovations $\varepsilon _t$, $\xi _{t,\phi }$ and $\xi _{t,h}$ are mutually independent. The standard deviations $\sigma _{\phi }$ and $\sigma _{h}$ are assumed to be positive real numbers.

The essential feature of this model is that both heteroskedasticity and structural changes can be captured. As in the prominent stochastic volatility models the noise $\varepsilon _t$ is stochastically scaled via the time-varying parameter $h_t$. In particular, in view of (2) the conditional distribution of $y_t$, conditioned on $y_{t-1}$, $\phi _t$, $h_t$, $\alpha$ and $\beta$, is given by

$$\begin{aligned}&y_t | y_{t-1},\phi _t,h_t,\alpha ,\beta \nonumber \\&\quad \sim {\left\{ \begin{array}{ll}{\mathcal {S}}\left( \alpha ,\beta ,e^{\frac{h_t}{2}},\phi _t y_{t-1}\right) ,&{}\alpha \ne 1\\ {\mathcal {S}}\left( \alpha ,\beta ,e^{\frac{h_t}{2}},\phi _t y_{t-1}-\frac{\beta h_t}{\pi }e^{\frac{h_t}{2}}\right) ,&{}\alpha =1 \end{array}\right. },\nonumber \\ \end{aligned}$$

(6)

so that extreme observations can be modeled. Furthermore, we can describe data with asymmetric heavy tails. For identifiability reasons we set the scale and the location parameter of the $\alpha$-stable distribution in (3) equal to 1 and 0, respectively. Replacing the distribution of $\varepsilon _t$ by $\mathcal {S}(\alpha ,\beta ,\gamma ,0)$, where $\gamma >0$, or by $\mathcal {S}(\alpha ,\beta ,1,\delta )$ (or by the combination of both) would cause an identifiability problem: In the first case define the random variables $h_t^*{:}{=}h_t + \log \gamma ^2$. Together with $\varepsilon _t^*\sim \mathcal {S}(\alpha ,\beta ,1,0)$ this leads to a TVAR$\alpha$SV process which is equivalent to the TVAR$\alpha$SV process where $h_t$ and $\varepsilon _t \sim \mathcal {S}(\alpha ,\beta ,\gamma ,0)$ is used. In the latter case exploit the recursive definition $y_t^*{:}{=}y_t + \phi _t (y_{t-1}^*- y_{t-1}) - e^{h_t/2} \delta$.

Again, together with $\varepsilon _t^*\sim \mathcal {S}(\alpha ,\beta ,1,0)$ this leads to a TVAR$\alpha$SV process which is equivalent to the TVAR$\alpha$SV process where $y_t$ and $\varepsilon _t \sim \mathcal {S}(\alpha ,\beta ,1,\delta )$ is used. For the remaining parameters it is not straightforward to check identifiability. However, from our simulation studies, with randomly drawn starting parameters from reasonably chosen intervals but posterior mean estimates close to the true values, there is evidence that we are not facing any identifiability problem here.

3 An estimation procedure of the TVAR$\alpha$SV model

3.1 General description

In this section we develop a Gibbs sampling procedure for estimating the unknown parameters $\phi _{1:T},h_{1:T}$, $\sigma _\phi ^2$, $\sigma _h^2$, $\alpha$, $\beta$ given data $y_{0:T}$ of the TVAR$\alpha$SV model. When deriving full conditional distributions we mostly suppress all parameters and variables from which the parameter to update is independent from, for notational convenience. We estimate $\phi _{1:T}$ and $h_{1:T}$ using the simulation smoother of De Jong and Shephard (1995). Since this simulation smoother appears, dependent on the situation at hand, in many different forms, we briefly summarize the corresponding formulas required for our analysis in the Appendix. The simulation smoother requires to approximate the TVAR$\alpha$SV model by a linear Gaussian state space model.

Therefore an important step in our estimation approach is the approximation of $\alpha$-stable distributions ${\mathcal {S}}(\alpha ,\beta ,1,0)$ by finite mixtures of normal distributions. Obviously, a standard minimum distance approach to determine the weights and parameters of the component distributions will not lead to satisfying results since it only approximates the center of the distribution accurately. The tails which play an important role for our model are hardly taken into account. Therefore, we use mixture components which are designed specifically to approximate the tails of the $\alpha$-stable distribution by fitting corresponding extreme quantiles. We call these components tails components. For the choice of the tail components see Sect. 3.2.

Since the parameters $\alpha$ and $\beta$ are updated in each iteration of the Gibbs sampler, the $\alpha$-stable distribution we have to approximate changes in each iteration. To shorten the computation time, we decided to compute the parameters of the mixture approximations, i.e. weights, means and variances of the components, before starting the algorithm. To this end we discretize the parameter space of the parameters $\alpha$ and $\beta$ by defining the set

$$\begin{aligned}&{\mathfrak {P}}=\big \{(\alpha ,\beta ) \,\, \big | \,\, \alpha \in \{1.1,1.105,1.110,\dots ,2\},\\&\quad \beta \in \{-1,-0.995,-0.990,\dots ,1\}\big \}. \end{aligned}$$

In this discretized parameter space, the range of $\alpha$ is [1.1, 2], since our developed estimation algorithm in its execution in Sects. 4 and 5 at no time sampled values for $\alpha$ smaller than 1.1. For this reason, we have so far only calculated the parameters for the approximations for $\alpha$ greater than or equal to 1.1 (of course, it is straightforward to calculate parameters for the approximations also for $\alpha$ smaller than 1.1). The parameters of the mixture approximations for these combinations of $\alpha$ and $\beta$ are stored in a file and can be used for different runs of the Gibbs sampler and different data analyses as well. Of course the accuracy of the discretization can be chosen arbitrarily. However, in our simulation study it turns out that we obtain accurate results using this discretization.

3.2 Estimation of $\phi _{1:T}$

For estimation of the autoregressive parameter $\phi _t$ we use the state space model given by the equations (3) and (4), whereby we approximate the distribution of the random variable $\varepsilon _t$ for fixed $\alpha$ and $\beta$, which we write as $(\varepsilon _t|\alpha ,\beta )$, by a seven-component mixture of normal distributions:

$$\begin{aligned} p(\varepsilon _t|\alpha ,\beta )\approx \sum _{i=1}^7 \Pr (\tau _t=i|\alpha ,\beta )\cdot p(u_t|\tau _t=i,\alpha ,\beta ), \end{aligned}$$

(7)

where $u_t|\tau _t=i,\alpha ,\beta$, for $i=1,\dots ,7$, denote normally distributed random variables with mean $\mu (\tau _t,\alpha ,\beta )$ and variance $\sigma ^2(\tau _t,\alpha ,\beta )$ and $\Pr (\tau _t=i|\alpha ,\beta )$ denote the mixture weights. Depending on the $\alpha$-stable parameters $\alpha$ and $\beta$ let $\tau _t\in \{1,\dots ,7\}$ indicate the component which occurs at time t. Thus the mixture weight $\Pr (\tau _t=i|\alpha ,\beta )$ is the prior density of $\tau _t$ and reflects the probability that the ith component occurs at time t. Furthermore, we suppose that all normal random variables

$$\begin{aligned} \big \{u_t|\tau _t,\alpha ,\beta \ \big | \ t=1,\dots ,T,\ \tau _t=1,\dots ,7,\ (\alpha ,\beta ) \in {\mathfrak {P}}\big \} \end{aligned}$$

are independent. For every combination $(\alpha ,\beta ) \in {\mathfrak {P}}$ the weights and the parameters of the normally distributed components are determined in two steps.

First, we only care about the tail components, which are the sixth and the seventh component. In order to cover the tails of the $\alpha$-stable distribution $(\varepsilon _t|\alpha ,\beta )$ we use the mean and the variance of the sixth component $(u_t|\tau _t=6,\alpha ,\beta )$ such that both the $5\times 10^{-7}$-quantile and $1-5\times 10^{-7}$-quantile of the sixth component and the $\alpha$-stable distribution coincide. We use $\Pr (\tau _t=6|\alpha ,\beta )=0.0009$, and the mean $\mu (\tau _t,\alpha ,\beta )$ is chosen as the midpoint between the two quantiles. Let $q_{\varepsilon _t}(\cdot )$ be the quantile function of the $\alpha$-stable random variable $\varepsilon _t|\alpha ,\beta$ and let $q(\cdot )$ be the quantile function of a standard normal variable. Then the required variance can be calculated by

$$\begin{aligned} \sigma ^2(\tau _t=6,\alpha ,\beta )=\left( \frac{q_{\varepsilon _t}(1-5\times 10^{-7})-q_{\varepsilon _t}(5\times 10^{-7})}{2\cdot q\left( \frac{5\times 10^{-7}}{\Pr (\tau _t=6|\alpha ,\beta )}\right) }\right) ^2. \end{aligned}$$

Then we repeat the same procedure for the seventh component with weight $\Pr (\tau _t=7|\alpha ,\beta )=0.0001$ and for the $5\times 10^{-10}$-quantile and the $1-5\times 10^{-10}$-quantile. In our simulation studies we found using two tail components to be sufficient to achieve accurate estimation results in our setup. Of course, in other situations it might be advantageous to add more tail components to cover the tails of the $\alpha$-stable distribution even more accurately.

Second, the weights and the parameters of the five remaining components are estimated using a minimum distance approach (see Titterington et al. 1985, Section 4.5). Let $f_{\mathcal {S}}(\,\cdot \,|\alpha ,\beta ,1,0)$ be the density function of the $\alpha$-stable random variable $\varepsilon _t|\alpha ,\beta$. As support for the minimum distance estimation we choose ${\mathcal {X}}=\{q_{\varepsilon _t}(x)\ |\ x\in \{0.002,0.006,0.01,\dots ,0.998\}\}$ and the $L_2$-norm as distance function. To this end, we have to find a solution for the optimization problem

$$\begin{aligned}&\min _{\psi \in \Psi } \sum _{x\in {\mathcal {X}}}\left[ f_{\mathcal {S}}(x|\alpha ,\beta ,1,0)-\sum _{i=1}^7 \frac{\Pr (\tau _t=i|\alpha ,\beta )}{\sqrt{2\pi \sigma ^2(\tau _t=i,\alpha ,\beta )}}\right. \\&\left. \quad \exp \left( -\frac{(x-\mu (\tau _t=i,\alpha ,\beta ))^2}{2\sigma ^2(\tau _t=i,\alpha ,\beta )}\right) \right] ^2 \end{aligned}$$

with parameter space

$$\begin{aligned} \begin{aligned} \Psi =&\left\{ \quad \left\{ \Pr (\tau _t|\alpha ,\beta ),\mu (\tau _t,\alpha ,\beta ),\sigma ^2(\tau _t,\alpha ,\beta )\right\} _{\tau _t=1}^5\ \Bigg | \right. \\&\ 0\le \Pr (\tau _t|\alpha ,\beta )\le 1,\mu (\tau _t,\alpha ,\beta )\in {\mathbb {R}},\\&\quad \sigma ^2(\tau _t,\alpha ,\beta )\in {\mathbb {R}}^{+}\ \text {for}\ \tau _t=1,\dots ,5\ \text {and}\ \\&\left. \quad \sum _{i=1}^5 \Pr (\tau _t=i|\alpha ,\beta )=0.999 \right\} . \end{aligned} \end{aligned}$$

We have implemented this optimization problem in MATLAB (2020) using the function fmincon with the stopping criterion that the $L_2$-norm must be less than 0.02. For a more detailed examination of the approximation quality using the $L_2$-norm as well as the Hellinger distance we refer to Sect. A of the Appendix.

Hence we can simulate $\phi _{1:T}$ from $p(\phi _{1:T}|y_{0:T},h_{1:T},\sigma _{\phi }^2,\tau _{1:T},\alpha ,\beta )$ by using the simulation smoother with respect to the linear Gaussian state space model

$$\begin{aligned} y_t&=e^{\frac{h_t}{2}}\mu (\tau _t,\alpha ,\beta )+\phi _t y_{t-1}+e^{\frac{h_t}{2}}\left( \sigma ^2(\tau _t,\alpha ,\beta )\right) ^{\frac{1}{2}}{\tilde{u}}_t,\nonumber \\&\quad {\tilde{u}}_t \sim {\mathcal {N}}(0,1), \end{aligned}$$

(8)

$$\begin{aligned} \phi _t&=\phi _{t-1}+\sigma _{\phi }\xi _{t,\phi },\xi _{t,\phi }\sim {\mathcal {N}}(0,1), \end{aligned}$$

(9)

using the centered and standardized version ${\tilde{u}}_{1:T}$ of $u_{1:T}$. The application of the simulation smoother requires an initial value $\phi _0$. We use a constant improper prior, $p(\phi _0)=1$, so that we can draw samples of $\phi _0$ from the posterior distribution ${\mathcal {N}}(\phi _1,\sigma _\phi ^2)$, where we use $\phi _1$ from the last iteration of the Gibbs sampler (or its starting value at the beginning: this could be any reasonable fixed hyperparameter or a randomly drawn value depending of the specific situation at hand, cf. the simulation study in Sect. 4).

3.3 Estimation of $h_{1:T}$

For estimation of the scale parameter $h_t$ we transform equation (8) which leads to the state space model

$$\begin{aligned}&\log \left( y_t-\phi _t y_{t-1}\right) ^2=h_t+\log \left( u_t^2\right) ,\nonumber \\&\quad u_t|\tau _t,\alpha ,\beta \sim {\mathcal {N}}\left( \mu (\tau _t,\alpha ,\beta ),\sigma ^2(\tau _t,\alpha ,\beta )\right) , \end{aligned}$$

(10)

$$\begin{aligned}&h_t=h_{t-1}+\sigma _{h}\xi _{t,h},\quad \xi _{t,h} \sim {\mathcal {N}}(0,1). \end{aligned}$$

(11)

For fixed t, $\alpha$ and $\beta$ there are seven different normally distributed random variables $u_t$ indicated by $\tau _t$. Since equations (10) and (11) define a non-Gaussian state space model, we approximate the distribution of the random variable $\log \left( u_t^2\right)$ for fixed $\tau _t$, $\alpha$ and $\beta$ again by a seven-component mixture of normal distributions, similar to Shephard (1994), where the transformation of a standard normal distribution was approximated:

$$\begin{aligned}&p\left( \log \left( u_t^2\right) \Big | \tau _t,\alpha ,\beta \right) \nonumber \\&\quad \approx \sum _{j=1}^7 \Pr (\omega _t=j|\tau _t,\alpha ,\beta )\cdot p(v_t|\omega _t=j,\tau _t,\alpha ,\beta ). \end{aligned}$$

(12)

Here $v_t|\omega _t=j,\tau _t,\alpha ,\beta$, for $j=1,\ldots ,7,\ t=1,\dots ,T, \tau _t=1,\dots ,7,\ (\alpha ,\beta ) \in {\mathfrak {P}}$, are independent and normally distributed with mean $\mu (\omega _t,\tau _t,\alpha ,\beta )$ and variance $\sigma ^2(\omega _t,\tau _t,\alpha ,\beta )$ and $\Pr (\omega _t=j|\tau _t,\alpha ,\beta )$ denote the mixture weights. For $t=1,\dots ,T$ the variables $\omega _t$ define independently distributed integer valued random variables with prior $\Pr (\omega _t|\tau _t,\alpha ,\beta )$. Using again the described minimum distance approach in Sect. 3.2 with the same distance function and stopping criteria we estimate the weights and the parameters of the normal distributions appearing in equation (12) for each possible combination $(\alpha ,\beta ,\tau _t) \in {\mathfrak {P}} \times \{ 1,\ldots ,7 \}$. As support for the minimum distance approach the $0.002,0.006,0.01,\dots ,0.998$-quantiles of the distribution of $\log \left( u_t^2\right)$ are also used.

By defining $y_t^*=\log \left( y_t-\phi _t y_{t-1}\right) ^2$ we finally obtain the linear Gaussian state space model

$$\begin{aligned} y_t^*&=\mu (\omega _t,\tau _t,\alpha ,\beta )+h_t+\left( \sigma ^2(\omega _t,\tau _t,\alpha ,\beta )\right) ^{\frac{1}{2}} {\tilde{v}}_t,\nonumber \\&\quad {\tilde{v}}_t\sim {\mathcal {N}}(0,1), \end{aligned}$$

(13)

$$\begin{aligned} h_t&=h_{t-1}+\sigma _{h}\xi _{t,h},\xi _{t,h} \sim {\mathcal {N}}(0,1). \end{aligned}$$

(14)

The application of the simulation smoother to the equations (13) and (14) provides samples from $p(h_{1:T}|y_{0:T},\phi _{1:T},\sigma _h^2,\omega _{1:T},\tau _{1:T},\alpha ,\beta )$, where we assume a constant improper prior, $p(h_0)=1$, so that we can draw samples of $h_0$ from the posterior distribution ${\mathcal {N}}(h_1,\sigma _h^2)$, where we use $h_1$ from the last iteration of the Gibbs sampler (or its starting value at the beginning: this could be any reasonable fixed hyperparameter or a randomly drawn value depending of the specific situation at hand, cf. the simulation study in Sect. 4).

3.4 Estimation of the parameters $\tau _{1:T}$, $\omega _{1:T}$, $\sigma _\phi ^2$, $\sigma _h^2$, $\alpha$ and $\beta$

The unknown mixture indices $\tau _{1:T}$ and $\omega _{1:T}$, the variances $\sigma _\phi ^2$ and $\sigma _h^2$ and the parameters of the $\alpha$-stable distribution $\alpha$ and $\beta$ must also be updated in every iteration of the Gibbs sampler, whereby the general estimation procedure is specified here and technical details leading to the conditional distributions can be found in the Appendix.

Since the mixture indices $\tau _{1:T}$ (resp. $\omega _{1:T}$) are conditionally independent, we can draw $\tau _t$ (resp. $\omega _t$) separately. For this purpose we evaluate, for $\tau _t,\omega _t=1,\dots ,7$, the following densities

$$\begin{aligned}&p(\tau _{t}|y_{0:T},\phi _{1:T},h_{1:T},\alpha ,\beta )\\&\quad \propto p(y_{t}|y_{t-1},\phi _{t},h_{t},\tau _{t},\alpha ,\beta )\cdot \Pr (\tau _{t}|\alpha ,\beta ) \end{aligned}$$

and

$$\begin{aligned}&p(\omega _t|y_{0:T},\phi _{1:T},h_{1:T},\tau _{1:T},\alpha ,\beta )\\&\quad \propto p(y_t^*|h_t,\omega _t,\tau _t,\alpha ,\beta )\cdot \Pr (\omega _t|\tau _t,\alpha ,\beta ), \end{aligned}$$

where $y_t$ and $y_t^*$ conditioned on the chosen mixture components are normally distributed according to equation (8) and (13). After standardizing these probabilities we can draw $\tau _t\in \{1,\dots ,7\}$ and $\omega _t\in \{1,\dots ,7\}$.

We assume that the prior distributions for $\sigma _{\phi }^2$ and $\sigma _h^2$ are the inverse gamma distributions ${{\mathcal {I}}}{{\mathcal {G}}}(s_{\phi },r_{\phi })$ and ${{\mathcal {I}}}{{\mathcal {G}}}(s_h,r_h)$, where $s_{\phi },s_h>0$ are the shape parameters and $r_{\phi },r_h>0$ the scale parameters. Due to the use of conjugate priors, one obtains the following inverse-gamma distributions as posterior distributions:

$$\begin{aligned}&\sigma _{\phi }^2|\phi _{1:T}\sim {{\mathcal {I}}}{{\mathcal {G}}}\left( s_\phi +\frac{T-1}{2}\ ,\ r_\phi +\frac{1}{2}\sum _{j=2}^T(\phi _{j}-\phi _{j-1})^2\right) ,\\&\sigma _h^2|h_{1:T}\sim {{\mathcal {I}}}{{\mathcal {G}}}\left( s_h+\frac{T-1}{2}\ ,r_h+\frac{1}{2}\sum _{j=2}^T\left( h_j-h_{j-1}\right) ^2\right) . \end{aligned}$$

It turned out that the accuracy of the estimation of $\sigma _\phi ^2$ (resp. $\sigma _h^2$) can be further improved, when we scale always the new sample of $\sigma _\phi ^2$ (resp. $\sigma _h^2$) in such a way that the estimated residuals ${\hat{\xi }}_{1:T,\phi }$ (resp. ${\hat{\xi }}_{1:T,h}$) are standardized, cf. equation (4) and (5).

For the estimation of $\alpha$ and $\beta$ the original observation equation (3) can be used without a mixture approximation of the $\alpha$-stable distributions. We choose flat priors for $\alpha$ and $\beta$, i.e. $p(\alpha )=\frac{1}{2}\mathbb {1}_{(0,2]}(\alpha )$ and $p(\beta )=\frac{1}{2}\mathbb {1}_{[-1,1]}(\beta )$. Hence $\alpha$ and $\beta$ can be drawn from the posterior density

$$\begin{aligned}&p(\alpha ,\beta |y_{0:T},\phi _{1:T},h_{1:T})\\&\quad \propto \prod _{t=1}^T p(y_{t}|y_{t-1},\phi _{t},h_{t},\alpha ,\beta )\cdot p(\alpha )\cdot p(\beta ), \end{aligned}$$

where the observation $y_t$ is distributed according to (6). Since we can not directly draw samples from the posterior distribution of $\alpha$ and $\beta$, we perform one step of the random walk Metropolis-Hastings algorithm in every iteration of the Gibbs sampler. Therefore we draw a proposal of $\alpha$ and $\beta$ from a two-dimensional normal distribution with covariance matrix $\Sigma$ to be chosen by the user. If the new proposed value is rejected, we retain the last sample of $\alpha$ and $\beta$. Finally, the drawn samples of $\alpha$ and $\beta$ must be rounded to the nearest values in the discretized parameter space ${\mathfrak {P}}$. It should not remain unmentioned that there are of course also alternative approaches to generate candidates for $\alpha$ and $\beta$.

3.5 Gibbs sampling procedure

In this subsection we design a suitable Gibbs sampling procedure where all unknown parameters are drawn from the corresponding full conditional distribution.

The Gibbs sampler starts with the estimation of the scale parameters $h_{1:T}$ where the distribution of $\log \left( u_t^2\right)$ is approximated by a finite mixture of normal distributions (cf. Sect. 3.3). Next we update the variance $\sigma _h^2$ and the $\alpha$-stable parameters $\alpha$ and $\beta$.

We point out that sampling $\phi _{1:T}$ can be performed using equation (8) so that we do not require the approximation of $\log \left( u_t^2\right)$; hence, the parameters $\omega _{1:T}$ are not involved here. The same holds for sampling $\tau _{1:T}$. As a consequence, the parameters $\phi _{1:T},\sigma _{\phi }^2,\tau _{1:T}$ and $\omega _{1:T}$ need to be simulated in one common block of the Gibbs sampling algorithm. It is therefore advantageous to draw from the joint distribution of $\phi _{1:T}$, $\sigma _\phi ^2$ and $\tau _{1:T}$ and then from the conditional distribution of $\omega _{1:T}$ given $\phi _{1:T}$, $\sigma _\phi ^2$ and $\tau _{1:T}$, using

$$\begin{aligned}&p(\phi _{1:T},\sigma _{\phi }^2,\tau _{1:T},\omega _{1:T})=p(\omega _{1:T}|\phi _{1:T},\sigma _{\phi }^2,\tau _{1:T})\\&\quad \cdot p(\phi _{1:T},\sigma _{\phi }^2,\tau _{1:T}). \end{aligned}$$

Due to the dependence structure of our model it is crucial for a fast convergence of the sampler to update $\phi _{1:T}$, $\sigma _\phi ^2$ and $\tau _{1:T}$ in one block. Since it seems impossible to draw all these parameters from one single high-dimensional distribution, we employ again a Gibbs sampler to draw from the joint distribution $\phi _{1:T}$, $\sigma _\phi ^2$ and $\tau _{1:T}$ conditional on all other parameters. After this inner Gibbs sampler has been executed in one iteration of the overall Gibbs sampler, a sample of $\phi _{1:T}$, $\sigma _\phi ^2$ and $\tau _{1:T}$ is randomly selected, with the first draws discarded as burn-in period. Thus a suitable Gibbs sampling procedure is given as follows:

• (I) Simulate ${\varvec{h}}_{{\varvec{1:T}}}\$ from $p(h_{1:T}|y_{0:T},\phi _{1:T},\sigma _h^2,\omega _{1:T},\tau _{1:T},\alpha ,\beta )$.

• (II) Simulate ${\varvec{\sigma }}_{{\varvec{h}}}^{{\varvec{2}}}\$ from $p(\sigma _h^2|h_{1:T})$.

• (III) Simulate ${\varvec{\alpha }}$, ${\varvec{\beta }}\$ from $p(\alpha ,\beta |y_{0:T},\phi _{1:T},h_{1:T})$.

• (IV) Simulate ${\varvec{\phi }}_{{\varvec{1:T}}}$, ${\varvec{\sigma }}_{\varvec{\phi }}^{\varvec{2}}$, ${\varvec{\tau }}_{{\varvec{1:T}}}$, ${\varvec{\omega }}_{{\varvec{1:T}}}$.

  • (1) Simulate ${\varvec{\phi }}_{{\varvec{1:T}}}$, ${\varvec{\sigma }}_{\varvec{\phi }}^{\varvec{2}}$, ${\varvec{\tau }}_{{\varvec{1:T}}}\$ using Gibbs sampling.

    • (i) Simulate ${\varvec{\tau }}_{{\varvec{1:T}}}\$ from $p(\tau _{1:T}|y_{0:T},\phi _{1:T},h_{1:T},\alpha ,\beta )$.

    • (ii) Simulate ${\varvec{\phi }}_{{\varvec{1:T}}}\$ from $p(\phi _{1:T}|y_{0:T},h_{1:T},\sigma _\phi ^2,\tau _{1:T},\alpha ,\beta )$.

    • (iii) Simulate ${\varvec{\sigma }}_{\varvec{\phi }}^{\varvec{2}}\$ from $p(\sigma _\phi ^2|\phi _{1:T})$.

  • (2) Simulate ${\varvec{\omega }}_{{\varvec{1:T}}}\ |\ {\varvec{\phi }}_{{\varvec{1:T}}}$, ${\varvec{\sigma }}_{\varvec{\phi }}^{\varvec{2}}$, ${\varvec{\tau }}_{{\varvec{1:T}}}\$ from $p(\omega _{1:T}|y_{0:T},\phi _{1:T},h_{1:T},\tau _{1:T},\alpha ,\beta )$.

The precise algorithm is outlined in Algorithm 1, which we have completely implemented in R (R Core Team 2020). Similarly to Del Negro and Primiceri (2015) it is possible to add a Metropolis-Hastings step for sampling $\phi _{1:T}$ and $h_{1:T}$ in order to remove the mixture approximation error. However, this is practically not desirable here due to the enormous additional computing time (an estimated doubling of the computing time) caused by the $\alpha$-stable density functions. Furthermore, Del Negro and Primiceri (2015) conclude that the results of the original and the extended algorithm are indistinguishable and the mixture approximation error is negligible.

4 Simulation study

For assessing the accuracy of the proposed estimation procedure described in Sect. 3 we investigate 1000 data sets each consisting of $Y_{0:2500}$, $\phi _{1:2500}$ and $h_{1:2500}$ ($T=2500$) of the TVAR$\alpha$SV model according to Definition 1 with $\sigma _\phi ^2=0.00058$, $\sigma _h^2=0.011$, $\phi _0=0.5$, $h_0=2.5$, $\alpha =1.73$, $\beta =-0.14$ and $y_0 \sim {\mathcal {S}}(\alpha ,\beta ,e^{h_0/2},0)$. These parameters were set equal to those found in the application of the TVAR$\alpha$SV model to electricity spot price data, cf. Sect. 5.

The behavior of the observed realization from the TVAR$\alpha$SV process depends crucially on the range of the autoregressive parameters $\phi _{1:T}$. If these leave the interval $(-1,1)$ substantially long and/or significantly this usually leads to an explosion of the observable time series $Y_{0:T}$ (even if the process returns to the initial level again later). Since we do not observe such an extreme behavior for electricity spot price data, we focus here in assessing the quality of our Bayesian inference procedure for realizations from the TVAR$\alpha$SV process, where $\phi _t$ takes on only values in the interval $(-1,1)$. In Sect. D of the Appendix we investigate additionally TVAR$\alpha$SV processes, where $\phi _t$ takes values outside the interval $(-1,1)$, too.

Since in most cases in practice one has a priori no information about the range of $\phi _t$, our estimation procedure here does not use this knowledge, that $\phi _t$, for all $t=1,\dots ,T$, takes on only values in the interval (-1,1), and we apply Algorithm 1 unchanged for the 1000 simulated time series. On the other hand, the systematic consideration of TVAR$\alpha$SV processes with underlying $|\phi _t|<1$, for all $t=1,\dots ,T$, corresponds to introducing an indicator function to the prior of $\phi _{1:T}$. Hence, also the posterior of $\phi _{1:T}$ must reflect this specification. For this reason, assuming that this additional knowledge about the prior of $\phi _{1:T}$ is available, we have applied an adapted version of Algorithm 1 to the same 1000 simulated time series, which is presented in Sect. E of the Appendix. At the end, the question about the truncated posterior boils down to which prior information the practitioner wants to use. If one is convinced that the data set at hand is based on a truncated vector $\phi _{1:T}$, one must use the second version of the Gibbs sampler (cf. Sect. E of the Appendix), which includes a resampling step for $\phi _{1:T}$. If one does not want to put such a prior information on $\phi _{1:T}$, Algorithm 1 is appropriate.

Table 1 Results of the simulation study using 6000 iterations after a burn-in period of 4000 iterations

Table 2 Results of the simulation study using 6000 iterations after a burn-in period of 4000 iterations

For the estimation of $\alpha$ and $\beta$ we use a normal proposal density with a diagonal matrix with 0.001 on the main diagonal as covariance matrix $\Sigma$. Moreover, we choose $s_h=r_h=s_\phi =r_\phi =0.001$ such that we obtain quite noninformative priors. As starting values we use for each data set randomly drawn values from uniform distributions: ${\sigma _\phi ^2}^{(0)}\sim {\mathcal {U}}[0.00001,0.1]$, $\phi _{1}^{(0)}=\phi _{2}^{(0)}=\dots =\phi _{T}^{(0)}\sim {\mathcal {U}}[0.1,0.9]$, $\alpha ^{(0)}\sim {\mathcal {U}}[1.4,1.9]$, ${\sigma _h^2}^{(0)}\sim {\mathcal {U}}[0.00001,0.1]$, $h_1^{(0)}\sim {\mathcal {U}}[-2,7]$, $\beta ^{(0)}\sim {\mathcal {U}}[-0.6,0.6]$. The boundaries of the uniform distributions were determined according to the following considerations: Looking at the observations of the simulation study, it can be checked a priori whether or not the signs of the first observations are systematically alternating and whether or not there are explosive periods, which leads in our case to fixing the underlying interval of the uniform distribution for the starting values of $\phi _{1:T}$ to [0.1, 0.9]. If the time series initially shows values with alternating signs we recommend to choose negative initial values of $\phi _{1:T}$ instead. From degenerated submodels we can also guess the magnitude of the other parameters. For instance, assuming one constant value for $\phi _{1:T}$ and one constant value h for $h_{1:T}$, and $\alpha =2$, one can estimate the magnitude of h by fitting the degenerated submodel to the truncated time series, where the truncation is used to exclude extreme observations caused by the $\alpha$-stable distribution. Moreover, from recent publications using $\alpha$-stable processes for modelling electricity prices (cf. Müller and Seibert 2019) we learn that even for daily peak prices the parameter $\alpha$ is usually greater then 1.4, so that the interval given above seems to be a reasonable choice for the starting values of $\alpha$. Assuming a quite smooth behavior of $\phi _{1:T}$ and $h_{1:T}$ the chosen intervals for $\sigma _\phi ^2$ and $\sigma _h^2$ have a very large right boundary in view of the two-sigma rule. We avoid values of $\beta$ close to 1 or $-1$, since those values would imply an extreme behavior of the noise process $\varepsilon _{1:T}$. Next we need to initialize the mixture indices $\tau _{1:T}^{(0)}$ and $\omega _{1:T}^{(0)}$. First, the mixture indices $\tau _{1:T}^{(0)}$ are independently drawn from $\{1,\dots ,7\}$ according to the probabilities $\Pr (\tau _t|\alpha ^{(0)},\beta ^{(0)})$. Afterwards, we independently draw the mixture indices $\omega _{1:T}^{(0)}$ from $\{1,\dots ,7\}$ according to the prior probabilities $\Pr (\omega _t|\tau _t^{(0)},\alpha ^{(0)},\beta ^{(0)})$.

The Gibbs sampler in Sect. 3.5 was carried out through 10000 iterations for each of the 1000 time series. Furthermore, the inner Gibbs sampler for the simulation of $\tau _{1:T}$, $\phi _{1:T}$ and $\sigma _\phi ^2$ was carried out through 50 iterations. We kept the last 6000 draws for inference. To measure the accuracy of the posterior mean estimates of $\phi _{1:T}$ we calculated 1000 root mean square errors (RMSEs) of the form $(\sum _{t=1}^{2500} ({\hat{\phi }}_t -\phi _t)^2/2500)^{1/2}$ and 1000 average biases of the form $\sum _{t=1}^{2500} ({\hat{\phi }}_t -\phi _t)/2500$ where ${\hat{\phi }}_t$ denotes the posterior mean estimate of $\phi _t$ (analogously for $h_{1:T}$). The results are summarized in Table 1 and Table 2.

On average the RMSEs of $\phi _{1:T}$ is quite concentrated around 0.09, which is remarkably accurate given the range of $|\phi _t|< 1$ for the simulated parameters. Similarly, the average RMSE of $h_{1:T}$ can be considered satisfactory, as the magnitude of $h_{1:T}$ is not limited and the simulated paths of $h_{1:T}$ range from -14.45 to 20.46. In view of $\sigma _h^2\approx 19\cdot \sigma _\phi ^2$ and the correspondingly higher range of $h_t$ also $h_t$ is estimated quite accurately on average. From Table 2 it is easy to see that all parameters $\sigma _\phi ^2$, $\sigma _h^2$, $\alpha$ and $\beta$ are estimated very precisely.

Additionally, we plotted estimation and convergence results of one simulation for illustrative purpose in Fig. 1. This figure supports that all parameters including the time-varying parameters $\phi _t$ and $h_t$ are estimated very accurately. The 95% credibility corridors cover almost all true values. Moreover, from the last four plots of Fig. 1 it is obvious that the chains converge very quickly to the area around the true values and that the mixing behavior of the chains is very satisfying.

Finally we note that running the Algorithm in Sect. 3.5 with 10000 iterations for one data set of length 2500 takes about 28 hours on an Intel Core i7-3635QM (2.40 GHz) processor.

Fig. 1

Application of the estimation procedure presented in Sect. 3. The time series $Y_{0:2500}$ was generated according to Definition 1 (first row). In the second and third row the smooth dashed line constitutes the posterior mean of the 6000 used Gibbs sampling estimations and the solid line constitutes the true values of $\phi _{1:2500}$ and $h_{1:2500}$. The $95\%$ confidence bound is plotted gray. In the fourth and fifth row the solid (resp. horizontal dashed) line corresponds to the estimated (resp. true) values of $\sigma _\phi$, $\sigma _h$, $\alpha$ and $\beta$

5 Application of the TVAR$\alpha$SV model to electricity spot price data

5.1 Description of the electricity spot prices

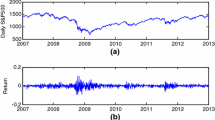
We consider the daily base prices for power traded at the European Power Exchange (EPEX SPOT SE). The base price is the average of the hourly market prices of one day. The price index for the German and Austrian market is called the Physical Electricity Index (Phelix). The data are available from EEX (European Energy Exchange) and cover the period from July 1, 2002 to November 18, 2017. Hence, our data set has length 5620 and is shown in the first row of Fig. 2. We summarize some key features of daily electricity spot prices in the following list, without any intention to be exhaustive in our presentation. We refer to Klüppelberg, Meyer-Brandis and Schmidt (2010), where the stylized facts of electricity spot prices are presented in detail.

• (i) Seasonality The plot of the empirical autocorrelation function demonstrates seasonal behavior in weekly cycles (see Fig. 8 in the Appendix). Moreover, a seasonal behavior in yearly cycles can be observed (cf. Sect. F in the Appendix).

• (ii) Spikes, Skewness, Non-Gaussianity The electricity spot prices exhibit large spikes (see Fig. 2) and skewness which cannot be modeled by a Gaussian distribution.

• (iii) Mean reversion After attaining extreme spikes, electricity spot prices are mean reverting. The price index does not jump directly from the extreme value to the trend, but decreases step by step.

• (iv) Heteroscedasticity A rolling window analysis of the Phelix Day Base prices shows that the standard deviation significantly changes over time (see Fig. 3).

According to the argumentation in Sect. 2 the TVAR$\alpha$SV model covers the stylized facts (ii), (iii) and (iv) and, hence, seems to be appropriate for modeling these data after accounting for (i) by removing seasonal effects.

Fig. 2

Daily EEX Phelix Base electricity price index from July 1, 2002 to November 18, 2017 and deseasonalized and trend adjusted data ${\hat{Y}}_t$ (cf. Sect. F of the Appendix)

Fig. 3

Estimated standard deviations of the deseasonalized Phelix Day Base prices using a rolling window of size 101

5.2 Estimation results

After estimation and elimination of trend and (weekly and yearly) seasonal components, cf. Sect. F in the Appendix, we applied our estimation procedure for the TVAR$\alpha$SV model (Algorithm 1) to the deseasonalized and trend adjusted electricity spot prices ${\hat{Y}}_t$, which are shown in the second row of Fig. 2. The Gibbs sampler in Sect. 3.5 was carried out through 10000 iterations, with the last 6000 draws being kept for inference. Furthermore, the inner Gibbs sampler for the simulation of $\tau _{1:T}$, $\phi _{1:T}$ and $\sigma _\phi ^2$ was carried out for 50 iterations each. We suppose the same prior hyperparameters as in the simulation study of Sect. 4 and ${\sigma _\phi ^2}^{(0)}=0.01$, $\phi _{1:T}^{(0)}=0.6$, $\alpha ^{(0)}=1.5$, ${\sigma _h^2}^{(0)}=0.01$, $h_1^{(0)}=0$, $\beta ^{(0)}=0.25$ as starting values. The results are shown in Table 3 and Fig. 4.

The marginal posterior distributions of $\sigma _\phi ^2$ and $\sigma _h^2$ support our assumption of time-varying parameters $\phi _t$ and $h_t$. The stability parameter $\alpha$ has a posterior mean of about 1.733 with a small standard deviation of 0.021, which indicates clearly that the distribution of the innovations $\varepsilon _t$ has heavier tails than the Gaussian distribution. From the estimate of $\beta$ we learn that the innovations are slightly negatively skewed. Figure 4 shows that there is evidence of a significant autoregressive structure in the electricity spot price data. Furthermore, rises of the scale parameter $h_t$ coincide with periods of higher fluctuations of $\hat{Y}_t$. Investigating extreme values of the data set, the extreme spikes are created by large values of the innovations, but not by high values of the time-varying scale parameter $h_t$.

Table 3 Means and standard deviations of the marginal posterior distributions using 6000 iterations after a burn-in period of 4000 iterations

Fig. 4

Application of the estimation procedure presented in Sect. 3 to the Phelix Day Base price ${\hat{Y}}_t$ after removing the trend and the seasonal component. In the first and second row the solid line constitutes the posterior mean of the 6000 used Gibbs sampling estimations of $\phi _{1:T}$ and $h_{1:T}$. The $95\%$ confidence bound is plotted in gray

5.3 Model verification

In this subsection we briefly check whether some basic model assumptions are satisfied in our empirical data analysis. In particular, we look at the assumptions of normality, homoscedasticity and serial independence of $\xi _{t,\phi }$ and $\xi _{t,h}$ appearing in equations (4) and (5). To this end, we check the null of normality of the series using Jarque-Bera tests (Jarque and Bera 1980), the null of residual homoscedasticity using ARCH tests (Engle 1982), and the null of independence of the series by Ljung-Box tests (Ljung and Box 1978). In each of the 6000 iterations after the burn-in period, we first derived estimates $\hat{\xi }_{t,\phi }$ and $\hat{\xi }_{t,h}$ using the estimates of $\phi _{1:T}$, $h_{1:T}$, $\sigma _{\phi }^2$ and $\sigma _{h}^2$, and then calculated all corresponding statistics. Each line of Table 4 evaluates the 6000 values of the test statistics by reporting the percentage which leads to a rejection of the null on the levels of $2.5\%$, $5\%$, and $10\%$. The table indicates that the model assumptions under investigation are satisfied.

These results are also strongly supported by Fig. 5: It shows the the autocorrelation and quantile plots for the estimated residuals ${\hat{\xi }}_{2:T,\phi }$ and ${\hat{\xi }}_{2:T,h}$ of one randomly chosen iteration in the Gibbs sampling estimation. The plots shown in Fig. 5 are a further indication that the assumption of normality and serial independence of $\xi _{t,\phi }$ and $\xi _{t,h}$ have been met.

Table 4 Test results for the 6000 iterations after a burn-in period of 4000 iterations

6 Conclusion and outlook

Motivated by the stylized facts of electricity spot prices, we introduced the time-varying autoregressive stochastic volatility model with $\alpha$-stable innovations $\big ($TVAR$\alpha$SV$\big )$. The novel idea is to combine a time-varying autoregressive component and a stochastic scaling as known from stochastic volatility models with stably distributed noise. Furthermore, we developed a Gibbs sampling procedure for the estimation of the model parameters. A key step of this estimation procedure is the approximation of $\alpha$-stable densities and transformed mixture components by finite mixtures of normal distributions, which enable the application of the simulation smoother of De Jong and Shephard (1995). In a simulation study we showed that the algorithm provides very accurate estimates. In an empirical application the TVAR$\alpha$SV model was fitted to the daily base prices of PHELIX. We observed that the spikes in the data are associated to the $\alpha$-stable innovations, whereas the time-varying scaling parameter accounts for periods of larger fluctuations.

Fig. 5

Empirical autocorrelation functions for the estimated residuals ${\hat{\xi }}_{t,\phi }$ (first row left) and ${\hat{\xi }}_{t,h}$ (first row right). QQ-plots of the estimated residuals ${\hat{\xi }}_{t,\phi }$ and ${\hat{\xi }}_{t,h}$ against standard normal distributions can be seen in the second row

It is work in progress to extend the TVAR$\alpha$SV model in the way that it is able to discover a (classical or inverse) leverage effect, as it has been discussed, e.g., in Benth and Vos (2013) or Kristoufek (2014). However, there is evidence that the leverage (or inverse leverage) effect is quite limited in Germany (cf. Erdogdu 2016), so that this extension seems to be irrelevant for the data analyzed here. Nevertheless, adapting our model in that direction is an interesting challenge, since we use stable distributions, where introducing a leverage effect is not as straightforward as in the Gaussian case: Due to the lack of finite second moments, a correlation in its original sense does not exist for stable distributions. Instead, various modified notions of “covariance” have been proposed in the literature (see, e.g., Samorodnitsky and Taqqu 1994). In particular, the correlation structure of a multivariate stable distribution is usually determined by the spectral measure. Besides the theoretical efforts of incorporating a leverage effect into our model, also the estimation of the extended model including the spectral measure (cf. Pivato and Seco 2003) seems to be a new challenge which we defer to a future paper.

Appendices

Appendix

A Investigation of the approximation accuracy of $\alpha$-stable distributions by finite mixtures of normal distributions

In our estimation procedure, the approximations of $\alpha$-stable distributions as well as of their squared and logarithmized normally distributed components by finite mixtures of normal distributions are a key step for successful parameter estimation (cf. Sects. 3.2 and 3.3). For this reason, the approximation accuracy will be examined in this section. We used the $L_2$-norm as distance function for both approximations with a corresponding stopping criteria and the $0.002,0.006,0.01,\dots ,0.998$-quantiles of the respective approximated distribution as support. In addition to the $L_2$-norm, the mean absolute percentage error (MAPE) and the continuous form of the Hellinger distance is evaluated on the support used for the optimization in order to quantify the similarity between the true distribution and its approximation: Let $f_{\mathcal {S}}(\,\cdot \,)$ be the density function of the $\alpha$-stable random variable $\varepsilon _t|\alpha ,\beta$ and $f_{\mathcal {A}}(\,\cdot \,)$ the density function of the approximation defined in equation (7). Using the $0.002,0.006,0.01,\dots ,0.998$-quantiles of the distribution of $\varepsilon _t|\alpha ,\beta$ as support points ${\mathcal {X}}=\{x_1,x_2,x_3,\dots ,x_{250}\}$, the MAPE is defined by $\frac{1}{|{\mathcal {X}}|}\sum _{x\in {\mathcal {X}}}\left| f_{\mathcal {S}}(x)-f_{\mathcal {A}}(x)\right| /\left| f_{\mathcal {S}}(x)\right|$. With the trapezoidal rule, the continuous form of the Hellinger distance can be approximated by

$$\begin{aligned} \begin{aligned}&\left( \frac{1}{2}\int _{{\mathbb {R}}}\left( \sqrt{f_{\mathcal {S}}(x)}-\sqrt{f_{\mathcal {A}}(x)}\right) ^2\, \mathrm {d}x\right) ^{\frac{1}{2}}\approx \left( \frac{1}{4}\sum _{k=2}^{250}(x_k - x_{k-1})\right. \\&\quad \left. \quad \left( \left( \sqrt{f_{\mathcal {S}}(x_{k-1})}-\sqrt{f_{\mathcal {A}}(x_{k-1})}\right) ^2+\left( \sqrt{f_{\mathcal {S}}(x_{k})}-\sqrt{f_{\mathcal {A}}(x_{k})}\right) ^2\right) \right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

An advantage of considering Hellinger distances is that they only take on distance values between 0 and 1, and their interpretability: The closer the distance value is to 0, the more the two probability distributions match. This evaluation of the mentioned distance functions was also performed equivalently for the approximation to the distribution of the random variables $\left( \log \left( u_t^2\right) \Big |\tau _t,\alpha ,\beta \right)$ in Sect. 3.3. The results are shown in Table 5.

Table 5 Evaluated distance functions for the approximations to the distributions of the random variables $(\varepsilon _t|\alpha ,\beta )$ and $\left( \log \left( u_t^2\right) \Big |\tau _t,\alpha ,\beta \right)$ for $(\alpha ,\beta ,\tau _t) \in {\mathfrak {P}} \times \{ 1,\ldots ,7 \}$

Table 6 Parameters of the mixture approximation for $\alpha =1.73$ and $\beta =-0.14$

The evaluated distance functions reveal an appealing accuracy for both approximations, which is additionally supported by the successful parameter estimation in the simulation study in Sect. 4. The two components created for the approximation of the tails provide additional certainty about the approximation quality at the tails of the $\alpha$-stable distributions, since these two components are constructed in such a way that they correspond to the alpha-stable distribution in the $5\times 10^{-7}$ (resp. $5\times 10^{-10}$) and $1-5\times 10^{-7}$-quantile (resp. $1-5\times 10^{-10}$-quantile).

For illustration, the parameters of the mixture approximation for the $\alpha$-stable distribution with $\alpha =1.73$ and $\beta =-0.14$, for which the Hellinger distance is equal to 0.0143, can be found in Table 6.

B Computation of conditional distributions

1.1 B.1 Estimation of $\tau _{1:T}$

Since the mixture indices $\tau _{1:T}$ are conditionally independent, we can draw $\tau _t$ from

$$\begin{aligned}&p(\tau _{t}|y_{0:T},\phi _{1:T},h_{1:T},\alpha ,\beta )\\&\quad =p(\tau _{t}|y_{t},y_{t-1},\phi _{t},h_{t},\alpha ,\beta )\\&\quad \propto p(y_{t}|y_{t-1},\phi _{t},h_{t},\tau _{t},\alpha ,\beta )\cdot p(y_{t-1},\phi _{t},h_{t},\tau _{t},\alpha ,\beta )\\&\quad \propto p(y_{t}|y_{t-1},\phi _{t},h_{t},\tau _{t},\alpha ,\beta )\cdot \Pr (\tau _{t}|\alpha ,\beta ), \end{aligned}$$

where the last proportionality follows from the fact that the mixture index $\tau _t$ for the approximation of $\varepsilon _t$ does not depend on the product $\phi _ty_{t-1}$ and the scale parameter $h_t$ in the observation equation (3). Since $y_t$ conditioned on the chosen mixture component is normally distributed according to equation (8), the likelihood is given by

$$\begin{aligned} r_{i,t}^\tau&{:}{=}p(y_{t}|y_{t-1},\phi _{t},h_{t},\tau _{t}=i,\alpha ,\beta )\\&=\, \left( 2\pi e^{h_t}\sigma ^2(\tau _t=i,\alpha ,\beta )\right) ^{-\frac{1}{2}}\\&\qquad \exp \left( -\frac{\left( y_t-e^{\frac{h_t}{2}}\mu (\tau _t=i,\alpha ,\beta )-\phi _t y_{t-1}\right) ^2}{2e^{h_t}\sigma ^2(\tau _t=i,\alpha ,\beta )}\right) , \end{aligned}$$

for $i=1,\dots ,7$ and $t=1,\dots ,T$. Therefore we draw $\tau _t$ from $\{1,\dots ,7\}$ according to the posterior probabilities

$$\begin{aligned}&p(\tau _t=i|y_{0:T},\phi _{1:T},h_{1:T},\alpha ,\beta )\nonumber \\&\quad =\frac{r_{i,t}^\tau \cdot \Pr (\tau _{t}=i|\alpha ,\beta )}{\sum _{j=1}^7r_{j,t}^\tau \cdot \Pr (\tau _{t}=j|\alpha ,\beta )},\quad i=1,\dots ,7. \end{aligned}$$

(A1)

1.2 B.2 Estimation of $\omega _{1:T}$

We have to draw $\omega _{t}$ in each iteration of the Gibbs sampler from

$$\begin{aligned}&p(\omega _t|y_{0:T},\phi _{1:T},h_{1:T},\tau _{1:T},\alpha ,\beta )\\&\quad =p(\omega _t|y_t,y_{t-1},\phi _{t},h_{t},\tau _{t},\alpha ,\beta )\\&\quad \propto p(y_t^*|h_t,\omega _t,\tau _t,\alpha ,\beta )\cdot p(h_t,\omega _t,\tau _t,\alpha ,\beta )\\&\quad \propto p(y_t^*|h_t,\omega _t,\tau _t,\alpha ,\beta )\cdot \Pr (\omega _t|\tau _t,\alpha ,\beta ), \end{aligned}$$

where $y_t^*$ is normally distributed, cf. equation (13). In order to update $\omega _t$ we calculate the value of the conditional distribution

$$\begin{aligned} r_{i,t}^\omega&{:}{=}\ p(y_t^*|h_t,\omega _t=i,\tau _t,\alpha ,\beta )\\&=\,\left( 2\pi \sigma ^2(\omega _t=i,\tau _t,\alpha ,\beta )\right) ^{-\frac{1}{2}}\\&\quad \exp \left( -\frac{\left( y_t^*-\mu (\omega _t=i,\tau _t,\alpha ,\beta )-h_t\right) ^2}{2\sigma ^2(\omega _t=i,\tau _t,\alpha ,\beta )}\right) \end{aligned}$$

for $i=1,\dots ,7$ and then we draw $\omega _t\in \{1,\dots ,7\}$ according to the posterior probabilities

$$\begin{aligned}&p(\omega _t=i|y_{0:T},\phi _{1:T},h_{1:T},\tau _{1:T},\alpha ,\beta )\nonumber \\&\quad =\frac{r_{i,t}^\omega \cdot \Pr (\omega _t=i|\tau _t,\alpha ,\beta )}{\sum _{j=1}^7 r_{j,t}^\omega \cdot \Pr (\omega _t=j|\tau _t,\alpha ,\beta )}. \end{aligned}$$

(A2)

1.3 B.3 Estimation of $\sigma _\phi ^2$ and $\sigma _h^2$

We assume that the prior distribution for $\sigma _{\phi }^2$ is the inverse gamma distribution ${{\mathcal {I}}}{{\mathcal {G}}}(s_{\phi },r_{\phi })$ with density $r_{\phi }^{s_{\phi }} x^{-s_{\phi }-1} \exp (-r_{\phi }/x) / \Gamma (s_{\phi }), \,\,x>0$, where $s_{\phi }>0$ is the shape parameter and $r_{\phi }>0$ the scale parameter. From the state equation (4) we derive

$$\begin{aligned}&p\left( \phi _{1:T}\Big |\sigma _{\phi }^2\right) \,\, = \,\, \prod _{j=2}^T p\left( \phi _j\Big |\phi _{j-1},\sigma _{\phi }^2\right) \,\,\\&\propto \,\, \sigma _{\phi }^{-(T-1)}\exp \left( -\frac{\sum _{j=2}^T(\phi _j -\phi _{j-1})^2}{2\sigma _{\phi }^2}\right) \end{aligned}$$

so that

$$\begin{aligned}&p\left( \sigma _{\phi }^2\Big |\phi _{1:T}\right) \,\, \propto \,\,\left( \sigma _{\phi }^2\right) ^{-\left( s_\phi +\frac{T-1}{2}\right) -1}\\&\quad \exp \left( -\frac{r_\phi +\frac{1}{2}\sum _{j=2}^T(\phi _{j}-\phi _{j-1})^2}{\sigma _{\phi }^2}\right) . \end{aligned}$$

Hence we can simulate $\sigma _\phi ^2$ from the posterior distribution

$$\begin{aligned}&\sigma _{\phi }^2|\phi _{1:T}\\&\quad \sim {{\mathcal {I}}}{{\mathcal {G}}} \left( s_\phi +\frac{T-1}{2}\ ,\ r_\phi +\frac{1}{2}\sum _{j=2}^T(\phi _{j}-\phi _{j-1})^2\right) . \end{aligned}$$

It turned out that the accuracy of the estimation of $\sigma _\phi ^2$ can be further improved, when we scale always the new sample of $\sigma _\phi ^2$ in such a way that the estimated residuals ${\hat{\xi }}_{1:T,\phi }$ are standardized. An analogous procedure was also chosen for the estimation of $\sigma _h^2$.

1.4 B.4 Estimation of $\alpha$ and $\beta$

We choose flat priors for $\alpha$ and $\beta$, i.e. $p(\alpha )=\frac{1}{2}\mathbb {1}_{(0,2]}(\alpha )$ and $p(\beta )=\frac{1}{2}\mathbb {1}_{[-1,1]}(\beta )$. For the estimation of $\alpha$ and $\beta$ the original observation equation (3) can be used without a mixture approximation of the stable distributions. We draw $\alpha$ and $\beta$ from the posterior density

$$\begin{aligned}&p(\alpha ,\beta |y_{0:T},\phi _{1:T},h_{1:T})\\&\quad \propto p(y_{0:T}|\phi _{1:T},h_{1:T},\alpha ,\beta )\cdot p(\alpha )\cdot p(\beta )\\&\quad =\prod _{t=1}^T p(y_{t}|y_{t-1},\phi _{t},h_{t},\alpha ,\beta )\cdot p(\alpha )\cdot p(\beta ), \end{aligned}$$

where the observation $y_t$ is distributed according to equation (6). As described in Sect. 3.4, we perform one step of the random walk Metropolis-Hastings algorithm in every iteration of the Gibbs sampler, i.e. we draw a proposal of $\alpha$ and $\beta$ from a two-dimensional normal distribution with covariance matrix $\Sigma$ to be chosen by the user, and accept the proposal with probability

$$\begin{aligned} \min \left\{ \frac{\prod _{t=1}^T f_{\mathcal {S}}\Big (y_t|\alpha ^{new},\beta ^{new},e^{\frac{h_t}{2}},\mu _{\alpha ^{new},\beta ^{new}}\Big )\cdot \mathbb {1}_{(0,2]}(\alpha ^{new})\cdot \mathbb {1}_{[-1,1]}(\beta ^{new})}{\prod _{t=1}^T f_{\mathcal {S}}\Big (y_t|\alpha ^{old},\beta ^{old},e^{\frac{h_t}{2}},\mu _{\alpha ^{old},\beta ^{old}}\Big )}\ ,\ 1\right\} , \end{aligned}$$

(A3)

where

$$\begin{aligned} \mu _{\alpha ,\beta }= {\left\{ \begin{array}{ll} \phi _t y_{t-1},&{} \alpha \ne 1\\ \phi _t y_{t-1}-\frac{\beta h_t}{\pi }e^{\frac{h_t}{2}},&{} \alpha =1 \end{array}\right. }. \end{aligned}$$

If the new proposed value is rejected, we retain the last sample of $\alpha$ and $\beta$. Finally, the drawn samples of $\alpha$ and $\beta$ must be rounded to the nearest values in the discretized parameter space ${\mathfrak {P}}$.

C Formulas of the simulation smoother in our analysis

We briefly summarize here the formulas of the simulation smoother by De Jong and Shephard (1995) in the form required for our analysis. We consider the linear Gaussian state space model defined by the equations

$$\begin{aligned} y_t&= c_t + z_t x_t + g_t \varepsilon _t,&\varepsilon _t&\sim {\mathcal {N}}(0,1), \end{aligned}$$

$$\begin{aligned} x_t&= d_t + s_t x_{t-1} + h_t \xi _t,\!\!\!\!\!\!&\xi _t&\sim {\mathcal {N}}(0,1), \end{aligned}$$

where the innovations $\varepsilon _t$ and $\xi _t$ are mutually independent for $t=1,\dots ,T$. The parameter vector $\theta =(c_{1:T},z_{1:T},g_{1:T},d_{1:T},s_{1:T},h_{1:T})$ is assumed to be known. The simulation smoother provides a sample from the distribution $p(\varepsilon _{1:T}|y_{1:T},\theta )$.

It can be shown that ${\tilde{\varepsilon }}_t$ in Algorithm 2 is a sample from $p(\varepsilon _t|\varepsilon _{t+1:T},y_{1:T},\theta )$. Since

$$\begin{aligned} p(\varepsilon _{1:T}|y_{1:T},\theta )=\prod _{t=1}^T p(\varepsilon _t|\varepsilon _{t+1:T},y_{1:T},\theta ) \end{aligned}$$

this implies directly that ${\tilde{\varepsilon }}_{1:T}$ is a sample from $p(\varepsilon _{1:T}|y_{1:T},\theta )$.

D TVAR$\alpha$SV processes with $|\phi _t|\ge 1$

In the simulation study of Sect. 4, we have only investigated TVAR$\alpha$SV processes where the process of the autoregressive parameter $\phi _t$ moves exclusively in the interval $(-1,1)$. In this section also the TVAR$\alpha$SV processes are analyzed, for which $\phi _t$ takes values outside the interval $(-1,1)$ too. These processes were simulated with the same parameters as in the simulation study of Sect. 4. When analyzing these time series, it is noticeable that if the absolute value of $\phi _t$ is greater than 1 over a certain period of time, the time series very quickly reaches extreme values that are not caused by the $\alpha$-stable innovations. If this behavior occurs, one can differentiate between the two scenarios that the time series either returns to values of the initial magnitude or continues to increase (or decrease) within the time period under consideration.

Figure 6 shows the first scenario where the underlying Gaussian random walk of $\phi _t$ causes an extremely strong decrease and subsequent increase of the observable time series $Y_{0:2500}$ in a certain time period. In this time frame, $\phi _t$ is estimated very accurately by the posterior mean, whereas the posterior mean of $h_t$ differs clearly from the true values. This can be explained by the fact that in this situation in the observation equation (3), due to the achieved order of magnitude of the last observations $y_{t-1}$, the stochastically scaled innovations are negligible in contrast to the autoregressive part.

Fig. 6

Application of the estimation procedure presented in Sect. 3. The time series $Y_{0:2500}$ was generated according to Definition 1 (first row). In the second and third row the smooth dashed line constitutes the posterior mean of the 6000 used Gibbs sampling estimations and the solid line constitutes the true values of $\phi _{1:2500}$ and $h_{1:2500}$. The $95\%$ confidence bound is plotted gray. In the fourth and fifth row the solid (resp. horizontal dashed) line corresponds to the estimated (resp. true) values of $\sigma _\phi$, $\sigma _h$, $\alpha$ and $\beta$

Fig. 7

The time series $Y_{0:2500}$ and the underlying $\alpha$-stable innovations $\varepsilon _{1:2500}$ were generated according to Definition 1

The second scenario, in which the observable time series $Y_{0:2500}$ does not return to the initial magnitude, is illustrated in Fig. 7. The last line in this figure also clarifies that this development is not caused by the $\alpha$-stable innovations $\varepsilon _{1:2500}$. According to our experience for the reason already mentioned above, $h_t$ cannot be estimated at the end of this time series at all and endangers the overall stability of the estimation algorithm, which is why the estimation procedure was not applied to this TVAR$\alpha$SV realization.

E Simulation study with additional prior knowledge of $\phi _{1:T}$

In the simulation study of Sect. 4, we truncated the prior of $\phi _{1:T}$ by systematically selecting only TVAR$\alpha$SV processes with $|\phi _t|<1$, for $t=1,\dots ,T$, which actually requires a reflection in the posterior of $\phi _{1:T}$. In this section we assume that this information about the prior of $\phi _{1:T}$ is available and take the changed posterior into account by resampling $\phi _{1:T}$. This means that Algorithm 1 changes in the way that now in each iteration of the Gibbs sampler the vector ${\tilde{\phi }}^{(j)}_{1:T}$ is sampled repeatably using the same simulation smoother until $|{\tilde{\phi }}^{(j)}_t|<1$, for $t=1,\dots ,T$, is achieved. We applied this adjusted Gibbs sampler to the same 1000 simulated time series from Sect. 4, using the same random starting values and hyperparameters. Furthermore, resampling of $\phi _{1:T}$ was only used after 3500 iterations so that the algorithm can conduct more flexible moves in a certain part of the burn-in phase. In a next step we performed the identical evaluation of the estimation results as in Sect. 4, which is summarized in Table 7 and Table 8. When comparing these tables with Table 1 and Table 2 in Sect. 4, one can see that the estimation results do not differ essentially.

Table 7 Results of the simulation study with resampled $\phi _{1:T}$ using 6000 iterations after a burn-in period of 4000 iterations

Table 8 Results of the simulation study with resampled $\phi _{1:T}$ using 6000 iterations after a burn-in period of 4000 iterations

F Estimation and elimination of trend and seasonal components

When we plot the daily EEX Phelix Base electricity price index, we observe a slowly changing local trend component, cf. Fig. 2. Moreover, considering the empirical autocorrelation function, cf. Fig. 8, we see that the data contain a weekly seasonal component. To estimate and eliminate the trend and seasonal component we apply a method based on moving average estimation; see Brockwell and Davis (1991).

Fig. 8

Empirical autocorrelation function for the Phelix Day Base prices

Fig. 9

Estimation of trend and seasonal components according to the approach described in Sect. 1. Day 0 reflects Monday

We assume that the data $x_t$ are the sum of a trend component $m_t$, a weekly seasonal component $s_t$ and a TVAR$\alpha$SV process $y_t$ which is scaled by a yearly periodical component $\zeta _t^*$:

$$\begin{aligned} x_t = m_t+s_t+\zeta _t^*y_t, \end{aligned}$$

where $\mathrm {E}y_t=0$, $s_{t+7}=s_t$, for $t=0,\dots ,T$, $\sum _{j=0}^6s_j=0$. The exact form and meaning of $\zeta _t^*$ is explained later. First, we estimate the trend $m_t$ using a moving average with a window of length 161, that is ${\hat{m}}_t= \sum _{j=-80}^{80}x_{t+j}/161$, where $x_{-j}=x_0$ and $x_{T+j}=x_T$ for $j=1,\dots ,80$. Second, we compute the weekly seasonal component $s_t$ by calculating $w_k = \frac{1}{w}\sum _{j=0}^{w-1}(x_{k+7j}-{\hat{m}}_{k+7j})$ for $k=0,\dots ,6$, where $w=\frac{T}{7}$ is the number of weeks covered by the data, and then setting

$$\begin{aligned} {\hat{s}}_t = {\left\{ \begin{array}{ll} w_t - \frac{1}{7}\sum _{j=0}^6 w_j, &{} \text {for} \ t=0,\dots ,6\\ {\hat{s}}_{t-7}, &{} \text {for} \ t>6 \end{array}\right. }. \end{aligned}$$

As in Brockwell and Davis (1991), Section 1.4 (Method S2) we finally reestimate the trend component ${\hat{m}}_t$ from the deseasonalized data $x_t-{\hat{s}}_t$. For removing a seasonal pattern in the scaling, we first define

$$\begin{aligned} \zeta _t{:}{=}{\left\{ \begin{array}{ll} -\cos \left( \frac{2\pi t}{366}\right) , &{} \text {if }t\text { lies in a leap year}\\ -\cos \left( \frac{2\pi t}{365}\right) , &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

Due to the extreme spikes the commonly used variance estimate is very sensitive. Hence, we work here with the modulus, i.e. we assume a linear regression of the form

$$\begin{aligned} |x_t-{\hat{m}}_t-{\hat{s}}_t|=\mu +\beta \zeta _t + \kappa _t. \end{aligned}$$

The parameter $\mu$ reflects the mean level of the scaling, and $\beta$ is the amplitude of the cosine oscillation modeled by $\zeta _t$. The random variables $\kappa _t$ reflect the noise in the regression equation. As estimates we obtain ${\hat{\mu }}=6.753$ with a standard error of 0.117 and ${\hat{\beta }}=1.537$ with a standard error of 0.166 which clearly indicates the presence of a yearly seasonal scaling factor. To keep the magnitude of values in the original data set, we do not divide $x_t-{\hat{m}}_t-{\hat{s}}_t$ by ${\hat{\mu }}+{\hat{\beta }} \zeta _t$, but by $\zeta _t^*= 1+({\hat{\beta }}/{\hat{\mu }}) \zeta _t$, i.e.

$$\begin{aligned} {\hat{y}}_t = \frac{x_t - {\hat{m}}_t - {\hat{s}}_t}{1+\frac{{\hat{\beta }}}{{\hat{\mu }}}\zeta _t}, \quad t=0,\dots ,T. \end{aligned}$$

The results of the described method are shown in Fig. 9.