1 Introduction

Analyzing solar activity is important since variations in the Sun’s behavior affect both the Earth and the interplanetary environment (Pulkkinen 2007). Short-term solar activity variations, known as “space weather”, can be manifested through fluctuations in solar radiation and the magnetic field (Schwenn 2006). Furthermore, the occurrence of energetic phenomena, such as coronal mass ejections and solar flares (Kahler 1992; Howard 2014; Temmer 2021), can also trigger severe disturbances in the near-Earth space environment (Ansor, Hamidi, and Shariff 2019; Syed Zafar et al. 2021). Specifically, inclement space weather can adversely affect air travel or spaceflight and interfere with radars, satellites, the electricity grid, and high-frequency communications (Schrijver et al. 2015; Krausmann et al. 2016).

Meanwhile, the “space climate” also involves significant long-term solar activity changes spanning from decades to millennia (Solanki et al. 2004; Versteegh 2005; Usoskin 2023). It can be seen that these slower variations display 11-year solar cycles (Muñoz-Jaramillo and Vaquero 2019; Jayalekshmi, Pant, and Prince 2022; Clette et al. 2023; Usoskin 2023), which are involved, for example, in the variability of solar irradiance (Solanki and Krivova 2003; Chatzistergos et al. 2020; Kopp 2021) and magnetic flux (Usoskin et al. 2002). These fluctuations can also influence the atmosphere’s upper layers (causing warming), affect how many cosmic rays reach the Earth (Usoskin et al. 2021), and cause changes in the magnetosphere, which in turn influence the Earth’s geomagnetic activity (Mursula, Zieger, and Vilppola 2003). The current space climate context presents a scenario where the observed solar activity level has decreased from high solar activity in the mid-20th century to weak solar activity in the previous Solar Cycle 24 (Usoskin 2023). In this sense, it is worth mentioning that some authors (Feynman and Ruzmaikin 2011; Karak 2023) have proposed that we are currently at a minimum phase of the centennial solar cycle, as originally determined by Gleissberg (1939, 1945).

Predicting solar-cycle evolution is particularly relevant as it enables us to forecast how the Sun’s activity may affect the Earth. As these cycles determine the likelihood of extreme solar events like flares and coronal mass ejections, a society as dependent on technology as ours must pay attention to the Sun’s behavior in order to mitigate its impact.

With more than 400 years of systematically recorded data available, the sunspot record is the longest-lived extant dataset of direct solar observations (Clette et al. 2014; Vaquero et al. 2016; Arlt and Vaquero 2022; Clette et al. 2023). The so-called sunspot number (\(\mathrm{S}_{\mathrm{N}}\)) is thus widely used for describing future solar activity across a variety of scientific fields, including climate change, solar physics and spaceflight mission planning (Bothmer and Daglis 2007; Haigh 2007; Muñoz-Jaramillo and Vaquero 2019). This has drawn increasing scholarly and public attention to predicting solar activity via the \(\mathrm{S}_{\mathrm{N}}\) (Petrovay 2020; Overbye 2021).

Recently, significant research has been performed on this topic, with works offering various predictions for the maximum peak amplitude of \(\mathrm{S}_{\mathrm{N}}\) in the present solar cycle (Solar Cycle 25) (Nandy 2021). Various techniques have been used to make these predictions (Petrovay 2020). One approach uses physical methods to predict \(\mathrm{S}_{\mathrm{N}}\). In this sense, Guo, Jiang, and Wang (2021) predicted a maximum \(\mathrm{S}_{\mathrm{N}}\) amplitude of 126 for Solar Cycle 25 (above that of Solar Cycle 24, which peaked at 116.4) based on a solar dynamo model. Statistical methods have also been used for sunspot prediction. This way, Aparicio, Carrasco, and Vaquero (2023), utilizing the slope of the inflection point during the cycle’s ascending part, predicted a maximum \(\mathrm{S}_{\mathrm{N}}\) of 131 ± 32 for Solar Cycle 25. Other researchers have used nonlinear modeling to make predictions. Employing the Kalman filter to calculate solar cycles under consideration of a nonlinear system of equations that modeled a dynamo system, Kitiashvili (2020) estimated a maximum \(\mathrm{S}_{\mathrm{N}}\) of 50 ± 15 in 2024 – 2025. Techniques based on spectral analysis have also been used to predict the \(\mathrm{S}_{\mathrm{N}}\). Taking the annual sum of time series (from 1874 to 2013) of sunspot group areas, Javaraiah (2015) employed fast Fourier transform (FFT), the maximum entropy method, and Morlet wavelet analysis, producing a maximum \(\mathrm{S}_{\mathrm{N}}\) amplitude prediction for Solar Cycle 25 of 50 ± 10. Several researchers have drawn on precursor methods to forecast the maximum \(\mathrm{S}_{\mathrm{N}}\) amplitude for Solar Cycle 25. For instance, considering the previous cycle’s peak and asymmetry as well as geomagnetic indices as precursors, Lu et al. (2022) predicted an \(\mathrm{S}_{\mathrm{N}}\) peak value of 145.3 in October 2024. For their part, Asikainen and Mantere (2022) drew on solar magnetism periodicity in Hale cycles and the peak geomagnetic aa* index as a precursor to predict an \(\mathrm{S}_{\mathrm{N}}\) maximum of 171 ± 23 in May 2024.

One of the most successful and robust precursor methods for predicting the maximum \(\mathrm{S}_{\mathrm{N}}\) amplitude is probably the so-called polar precursor method, which considers the polar magnetic field as a precursor parameter for solar activity (Nandy 2021). The Sun’s polar magnetic field plays a crucial role in solar activity dynamics and is fundamental to our understanding of our star’s magnetic behavior (Muñoz-Jaramillo et al. 2012). This field undergoes a cyclical reversal approximately every 11 years, coinciding with the solar cycle. During this cycle, the fields weaken, reverse polarity, and then strengthen again, a phenomenon that is intricately linked to the generation and evolution of sunspots as well as the overall solar activity (Tobias 2023). On the other hand, a measure of the strength of the polar magnetic field over a specific area is the so-called polar flux. Thus, the polar flux quantifies the total magnetic field passing through an area near the Sun’s poles. In this sense, it is essentially the product of the polar magnetic field and the area over which this field extends. Therefore, the polar flux is directly dependent on the strength of the polar magnetic field. Likewise, the polar flux can also be obtained from the so-called polar faculae, as shown in Muñoz-Jaramillo et al. (2012), since their formation is directly related to the Sun’s magnetic field. In particular, the polar precursor technique exploits the notion that the amplitude of a solar cycle is likely proportional to the poloidal field’s amplitude (or that of the polar flux) near the cycle’s start. However, Kumar et al. (2021) used the polar field (and the proxy) data four years after the polar field reversal to predict an \(\mathrm{S}_{\mathrm{N}}\) peak for Cycle 25 of 120 ± 25 (in addition to forecast an \(\mathrm{S}_{\mathrm{N}}\) maximum of 126 ± 3 using the usual prediction of the polar precursor at cycle minimum). Subsequently, Kumar, Biswas, and Karak (2022) predicted a peak in Cycle 25 of 137 ± 23, exploiting the fact that the polar solar field’s growth rate correlates highly with the next cycle’s amplitude and growth rate. Similarly, Biswas, Karak, and Kumar (2023) explored the reliability and robustness of using the polar field rise rate as a precursor for an early prediction of solar cycle. After that, Javaraiah (2023) predicted 125 ± 7 as the maximum \(\mathrm{S}_{\mathrm{N}}\) amplitude for Solar Cycle 25, using the polar magnetic field as a precursor and considering the fact that the main and secondary peaks of a solar cycle maximum (Gnevyshev peaks) correlate. Recently, Upton and Hathaway (2023) predicted an \(\mathrm{S}_{\mathrm{N}}\) peak for Solar Cycle 25 of 134 ± 8, occurring in the fall of 2024. These authors used geomagnetic activity levels and the Sun’s polar magnetic field configuration—particularly the polar fields and axial dipole moment at cycle minimum—as predictors.

Lastly, methods using machine learning (ML) have also been applied to sunspot prediction in past works. For example, Moustafa and Khodairy (2023) employed a hybrid model comprising Long Short-Term Memory (LSTM) and AutoRegressive Integrated Moving Average (ARIMA) algorithms to predict Solar Cycle 25’s \(\mathrm{S}_{\mathrm{N}}\) peak, arriving at 137.04 in September 2024. Meanwhile, through a deep learning (DL) approach, Su et al. (2023) estimated 133.9 in February 2024, while Prasad et al. (2023) predicted 136.9 in April 2023 based on an LSTM model. Finally, Peguero and Carrasco (2023) also employed an LSTM model to forecast the maximum amplitude of Solar Cycle 25, concluding that it would be a new minimum of the Gleissberg cycle.

As the previous research outlined above shows, and as highlighted in Nandy’s (2021) review, substantial disparity exists in the prediction results concerning Solar Cycle’s peak \(\mathrm{S}_{\mathrm{N}}\) value and its timing, even when using the same method. This inconsistency reflects the inherent challenges in grasping the finer details of our star’s behavior. To be specific, the mentioned 11-year period emerges clearly in the \(\mathrm{S}_{\mathrm{N}}\) series, remaining almost constant throughout. However, there are changes in the solar dynamo’s behavior within the different cycles, producing amplitude variations. Consequently, reliably predicting how the \(\mathrm{S}_{\mathrm{N}}\) will evolve—not just in the current cycle, but also generally in future cycles—is still a challenge. Hereby, we should note that the prediction techniques outlined above have certain limitations. For instance, not all statistical models account for the underpinning physical processes that produce sunspot cycles, often leading to inaccurate predictions (Nandy 2021). Meanwhile, the absence of detailed and accurate data on the solar system’s initial conditions and parameters can diminish the effectiveness of physical or precursor models (Upton and Hathaway 2018). Finally, \(\mathrm{S}_{\mathrm{N}}\) prediction models that rely solely on ML approaches are unable to consider the fundamental solar physics driving sunspot generation (Camporeale 2019), limiting their applicability. Based on the discrepancies and limitations described above, there is an urgent need to deepen the research in this field by developing techniques that enable highly accurate solar activity forecasting (Asensio Ramos et al. 2023).

Seeking to overcome the limitations of single estimation models, we here combine several methods based on currently available data (up to September 2023) to develop an innovative technique for \(\mathrm{S}_{\mathrm{N}}\) prediction. Specifically, we consider a precursor parameter of solar activity, namely the polar fluxes of the northern and southern hemispheres (a proxy of the polar magnetic field), conduct a spectral analysis of the time series under consideration (to identify periodicities that can be used to lag the series, thereby producing new attributes that can serve as predictors in our prediction model), and lastly apply multivariate ML algorithms (where the dependent variable is \(\mathrm{S}_{\mathrm{N}}\) and the independent variables are the two series of the northern and southern polar fluxes, respectively, subjected to spectral analysis). The purpose of this approach is to create a method that incorporates all the strengths of the abovementioned techniques, thereby gathering the benefits from three distinct approaches under a single umbrella. We expect this method to offer substantially better predictions for solar cycles, thereby improving on the findings of prior work that solely used a univariate ML approach without precursor parameters (Rodríguez, Rodríguez-Rodríguez, and Woo 2022), ultimately offering a deeper understanding of the solar dynamo’s long-term behavior.

Our focus lies, in particular, on forecasting the remainder of Solar Cycle 25 and Solar Cycle 26 using that innovative method. The outline of this article is as follows: the data and methodology used in this work are explained in Section 2. We present the results obtained along with our discussion in Section 3. Section 4 is dedicated to showing the main conclusions derived from this work.

2 Methodology

2.1 Data Description

The sunspot number data for this work were taken from the values of the \(\mathrm{S}_{\mathrm{N}}\) (version 2) index available on the website of the World Data Center SILSO (Clette and Lefèvre 2016) belonging to the Royal Observatory of Belgium (ROB) in Brussels: www.sidc.be/silso/datafiles.

To predict the \(\mathrm{S}_{\mathrm{N}}\) via the multivariate ML algorithms of the final proposed model, we consider two time series corresponding to the northern and southern polar fluxes. These hemispheric solar flux series, recognized as precursor parameters of solar activity, are used as the predictors (independent variables) of our dependent variable (\(\mathrm{S}_{\mathrm{N}}\)). The polar flux series corresponding to both hemispheres were extracted from Muñoz-Jaramillo et al. (2012).Footnote 1

2.2 Data Processing

Firstly, it should be noted that data from the above-mentioned site, corresponding to the polar fluxes, are annual. Therefore, a linear interpolation of the data of these series is carried out to obtain monthly estimated values (this work attempts a long-term forecast of solar cycle evolution, in terms of the 13-month smoothed \(\mathrm{S}_{\mathrm{N}}\) values). Next, we estimate a 13-month centered running average for the time series considered, where all elements of the averages have the same weight (1), except for the first and last elements, whose weight is 0.5 (as we have considered a 13-month centered running average, for each series, neither the first six months nor the last six months have smoothed averages). By adhering to this convention, we ensure that the results can be easily compared and contrasted across different investigations, promoting collaboration and knowledge advancement in this area. Moreover, by processing the data using such an average, along with the avoidance of a model too complex, we avert potential overfitting in the ML algorithms. Overfitting is possible when a model fits the training phase data too well and cannot correctly generalized to new data that were not incorporated during the training (this can be due, among other things, to the presence of noise in the training data).

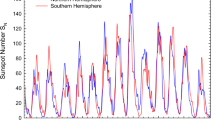
In Figure 1 (bottom), the considered times series corresponding to the polar fluxes from both hemispheres can be observed, after applying the 13-month running average. The 13-month smoothed \(\mathrm{S}_{\mathrm{N}}\) is also shown at the top of Figure 1. Table 1 displays date ranges for each series, in addition to the number of records of each, after the 13-month running average has been applied. It is worth mentioning that the original annual data for both polar flux series are published each year in different months for each hemisphere (September for the Northern Hemisphere and March for the Southern Hemisphere). This fact implies that although the same number of records is available for both series (1393), there will be a different number of predicted values for the polar flux in each hemisphere up to the stipulated common time horizon (January 2038), as shown below.

Figure 1
figure 1

\(\mathrm{S}_{\mathrm{N}}\) times series (top) and considered time series corresponding to the northern and southern polar fluxes (bottom) after applying the 13-month running average for the same range of dates.

Full size image
Table 1 Period and number of records for each considered series (after the 13-month running average has been applied).
Full size table

2.3 Time Series Fourier Transform Analysis

As mentioned above, Fourier-transform-based spectral analysis permits the extraction of certain characteristics of a given time series, which enhances predictive ML algorithms’ performance (Koç and Koç 2022). Hence, we apply FFT to all 13-month smoothed data series (including the dependent variable \(\mathrm{S}_{\mathrm{N}}\)), seeking to identify suitable periodicities with which these series can be lagged (by a number of positions equal to these periods or multiples thereof) as frequently as possible for as long as the series have data. This produces lagged series, which in turn offer new predictors or attributes that can be incorporated into the input dataset for the predictive ML algorithms. This approach is based on the idea that for time series containing certain identifiable periods, their behavior at instants lagged by a time equivalent to those periods—or multiples thereof—can offer useful information for estimating these series’ behavior in the future. We conduct this analysis for all series, because when forecasting \(\mathrm{S}_{\mathrm{N}}\) (target), the multivariate ML algorithm uses as predictors (inputs) not only the \(\mathrm{S}_{\mathrm{N}}\) series itself, lagged in line with its periodicities, but also the polar flux series already forecasted until the time horizon for which the \(\mathrm{S}_{\mathrm{N}}\) prediction is to be made. Thus, in order to previously carry out such polar flux series predictions, a univariate ML forecast will be performed for each polar flux series, wherein the predictors are, in turn, the series lagged according to their periodicities. Figure 2 displays the periodograms for the series considered here, indicating the different peaks that represent the various identified periodicities. Table 2 presents the main periodicities’ values alongside the number of positions they represent regarding these series’ displacement.

Figure 2
figure 2

Periodograms of the sunspot number (top panel), and the northern (bottom-left panel) and southern (bottom-right panel) polar fluxes.

Full size image
Table 2 Main periodicities of the considered time series (obtained from their respective periodograms) and number of positions to be lagged that these periods represent.
Full size table

2.4 ML Algorithm Implementation, Selection, and Application

The different ML models employed in our \(\mathrm{S}_{\mathrm{N}}\) prediction approach are implemented in Python (scikit-learn library). We select linear regression (LR), random forest (RF), support vector machines (SVM) and Gaussian processes (GP) as these provide a set of diverse strategies that permit us to perform multivariate analysis on time series data that have cyclical as well as nonlinear patterns, i.e., the \(\mathrm{S}_{\mathrm{N}}\) and the two polar flux series. Moreover, these algorithms are well known for their capability for modeling sequential data. A more detailed description of these algorithms can be found in Shmueli and Lichtendahl (2016) for LR, Vapnik (2013) for SVM, Oshiro, Perez, and Baranauskas (2012) for RF, and Seeger (2004) for GP. The root mean square error (RMSE) estimated in the test phase is used to assess the goodness of fit of each algorithm. Then, we select the algorithm with the best performance to predict the polar flux series and \(\mathrm{S}_{\mathrm{N}}\).

Notably, the series’ predictive time horizon is January 2038. In this sense, the prediction period for the \(\mathrm{S}_{\mathrm{N}}\) will be from June 2023 to January 2038 (176 records), that of the northern polar flux will be from October 2023 to January 2038 (172 records), and that of the southern polar flux will be from April 2023 to January 2038 (178 records). This way, the number of records reserved for the test phase in each case is assumed to be identical to the number of records to be predicted from known data up until January 2038: 176 for the \(\mathrm{S}_{\mathrm{N}}\), 172 for the northern polar flux and 178 for the southern polar flux. We dedicate the remaining data in each series (not used for the test phase) to training and validation, using a \(n\)-split expanding window cross-validation in the training/validation phase to adjust the hyperparameters. The number of splits is selected in order to provide a balance between the amount of data used for training and the robustness of the validation, ensuring that the model is evaluated on different data segments to improve its generalization. Therefore, \(n\) will be different for the \(\mathrm{S}_{\mathrm{N}}\) series (\(n=5\)) and for the northern and southern polar fluxes (\(n=3\)). The validation window is assumed to consist of a number of records (\(v\)) equal to that in the testing phase and the training dataset of each split/iteration consists of a number of records of round [\(i/n\cdot (T-v)\)] (where \(i\) is the number of split/iteration—from 1 to \(n\)—and \(T\) is the total number of records reserved for training and validation). Table 3 shows the initialization parameters for the different ML algorithms. It should be noted that the choice of these parameters responds to the call for a balance between performance, accuracy, and computational complexity.

Table 3 Initialization parameters for the different ML algorithms employed.
Full size table

3 Results and Discussion

3.1 Multivariate Prediction Model Construction

To begin with, we perform a univariate prediction of the two polar flux time series until January 2038. We hereby assume the series themselves as the predictors of each, lagged by the number of positions equal to their periodicities, as outlined previously. Thus, each prediction is an ultimately autoregressive/multivariate problem (although we only consider the time series data). To this end, we draw on the four abovementioned ML algorithms, i.e., RF, LR, GP and SVM. Table 4 presents the RMSE values for each algorithm in the test phase of the respective prediction models constructed for the two polar flux series (for each series, the lowest RMSE value from among the four algorithms is highlighted in bold). Furthermore, the above-mentioned number of records considered for the test phase in each case is also provided (which is different for each hemisphere, since the number of records for the test phase has been assumed to be the same as the number of values to be predicted in each series until January 2038, and as discussed above at the end of section ‘Data processing’, the latter number differs for each hemisphere). It clearly emerges that for the northern polar flux series, the RF technique makes the best prediction based on RMSE, while the southern polar flux series is most reliably predicted by SVM.

Table 4 RMSE values (in units of \(10^{21}\) Mx) for four algorithms considered for the test phases of each prediction model for both polar flux series.
Full size table

It should be noted that although the data type of the two series is the same, factors related to the specific behavior of each series, as well as to the particular characteristics of the ML model considered, may cause the lower RMSE to be obtained with a different algorithm in each case. In this sense, RF models perform better when trying to capture particularly nonlinear and complex interactions in the data, as well as more abrupt fluctuations in the series (Breiman 2001), as is the case with the northern polar flux series (see cycles between 1950 and 1970). Nevertheless, SVM models are more effective in series where the behavior of the data is more stable and less subject to strong fluctuations (Cristianini and Shawe-Taylor 2000), as is the case for the southern polar flux series.

Figures 3 and 4 show a comparison between predicted and observed values for the test phases of both the northern polar flux (172 records, from June 2009 to September 2023, using the RF algorithm) and the southern polar flux (178 records, from June 2008 to March 2023, using the SVM algorithm), respectively.

Figure 3
figure 3

Observed data compared with predicted data for the northern polar flux univariate prediction model’s testing phase (172 records) using the RF algorithm.

Full size image
Figure 4
figure 4

Observed data compared with predicted data for the southern polar flux univariate prediction model’s testing phase (178 records) using the SVM algorithm.

Full size image

As can be seen in Figures 3 and 4, the prediction for the test phases of both the northern and southern polar flux series is consistent with the observed data, as indicated by the RMSE values obtained for both cases: \(9.7\cdot 10^{20}\text{ Mx}\) and \(8.3\cdot 10^{20}\text{ Mx}\), respectively.

Therefore, Figure 5 presents the prediction curves (until January 2038) for the two polar flux series, each obtained with the algorithm that produced the lowest RMSE value. Observed data are blue for the Northern Hemisphere and red for the Southern Hemisphere. Predictions are light blue for the Northern Hemisphere and pink for the Southern Hemisphere.

Figure 5
figure 5

Prediction curves for the two considered polar flux series until January 2038.

Full size image

Lastly, we construct the multivariate model for predicting the \(\mathrm{S}_{\mathrm{N}}\) (until January 2038) using the four considered algorithms (RF, LR, GP and SVM). As predictors, we assume both the \(\mathrm{S}_{\mathrm{N}}\) series itself, lagged by various numbers of positions according to periodicity (Table 2), and the two polar flux precursor series, as predicted until January 2038. Table 5 presents the RMSE values obtained during the testing phase (176 records) for the four algorithms. As shown in Table 5, the lowest RMSE for the test phase (10.04) is produced by the RF algorithm; hence, we consider this algorithm for the multivariate prediction of \(\mathrm{S}_{\mathrm{N}}\).

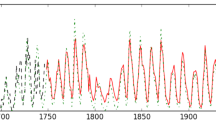
Table 5 RSME values obtained in the test phase by the four algorithms considered to build the multivariate model to predict the \(\mathrm{S}_{\mathrm{N}}\) series.
Full size table

Figure 6 presents a comparison between the observed values and our predictions for the testing phase (red line) (from October 2008 to May 2023) based on RF.

Figure 6
figure 6

Observed data compared with predicted data for the \(\mathrm{S}_{\mathrm{N}}\) multivariate prediction model’s testing phase (176 records) using the RF algorithm.

Full size image

The curves are in good agreement in terms of the cyclic behavior of the series and, in particular, throughout the entire Solar Cycle 24. The model hereby offers a good fit regarding the \(\mathrm{S}_{\mathrm{N}}\) values and the maxima’s occurrence dates. For Solar Cycle 24, the observed and predicted maxima are 116.4 and 118.3 ± 10.0, respectively, both of which occurred in April 2014.

Figure 7 compares the modeled and observed data in a training phase time slot based on RF (only since 1970—as it is merely a sample to illustrate the goodness of fit of the model in the training phase—and up to September 2008, where the data reserved for the test phase begins). There is excellent agreement, as shown by the RMSE for this phase of 2.02.

Figure 7
figure 7

Example comparison between observed data and modeled data for a training phase time slot of the \(\mathrm{S}_{\mathrm{N}}\) multivariate prediction model (since 1970 and up to September 2008) using RF.

Full size image

3.2 Predicting Activity for Solar Cycles 25 and 26

Figure 8 provides the final multivariate prediction (grey line, top panel) of the \(\mathrm{S}_{\mathrm{N}}\) series until January 2038 (176 records), alongside the previously made predictions for the two selected polar flux series (light blue and pink lines, bottom panel).

Figure 8
figure 8

Final multivariate prediction of the \(\mathrm{S}_{\mathrm{N}}\) series (grey line, top panel) until January 2038, as well as the previously made predictions of the selected two polar flux series (light blue and pink lines, bottom panel).

Full size image

The model predicts a maximum \(\mathrm{S}_{\mathrm{N}}\) of 131.4 ± 10.0 (in July 2024) for Solar Cycle 25 and 121.2 ± 10.0 (in September 2034) for Solar Cycle 26. The \(\mathrm{S}_{\mathrm{N}}\) values obtained in both solar cycles are significantly below the average of the maximum amplitudes considering Solar Cycles 1 – 24, which is ∼ 180. In this sense, we note that the observations made during Solar Cycle 25 so far hints that this cycle will be below average within the lowest 25th percentile (Carrasco and Vaquero 2023; Ridley 2023). Furthermore, although there have been some predictions regarding the maximum amplitude of Cycle 25 that forecasted that this cycle will be a strong cycle (Han and Yin 2019; McIntosh et al. 2020; McIntosh, Leamon, and Egeland 2023), our prediction for Cycle 25 is in agreement with most of the predictions covered in Nandy (2021). Meanwhile, the predicted maximum of Solar Cycle 26 is slightly lower than that of the preceding Solar Cycle 25 and is similar to the maximum amplitude observed in Solar Cycle 24 (116.4). This would imply that Solar Cycles 24, 25, and 26 belong to a minimum in the centennial Gleissberg cycle. As an example, this was the case for Cycles 12, 13, and 14 in the final years of the 19th century and near the beginning of the 20th century. Notably, the average maximum amplitude for Solar Cycles 12 – 14 was 126.0, whereas based on our results it would be 123.0 for Solar Cycles 24 – 26. Moreover, our findings point to the same direction as those obtained by Feynman and Ruzmaikin (2012, 2014) and Karak (2023), who contended that Solar Cycles 23 and 24 could belong to a minimum of the Gleissberg cycle. In addition, the predicted dates for the two \(\mathrm{S}_{\mathrm{N}}\) maxima for Solar Cycle 25 and 26 (July 2024 and September 2034, respectively) are similar to those obtained for the two polar flux polarity reversals for Solar Cycles 25 and 26 (April 2024 and August 2034, respectively). In this regard, it is worth mentioning that our prediction for the next polar flux reversal for Cycle 25 (April 2024) would be in agreement with the latest data provided by the Wilcox Solar Observatory (WSO), since signs of such a polar flux reversal have already been observed.

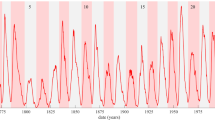
On the other hand, there is a well-known relationship between the absolute value of the difference between the polar fluxes of both hemispheres at a minimum of the \(\mathrm{S}_{\mathrm{N}}\) and the maximum of the \(\mathrm{S}_{\mathrm{N}}\) of the subsequent cycle (Upton and Hathaway 2023). In this sense, it is worth mentioning that the polar field at the \(\mathrm{S}_{\mathrm{N}}\) cycle minima exclusively impacts the magnitude of the subsequent \(\mathrm{S}_{\mathrm{N}}\) cycle (Karak and Nandy 2012; Nandy 2021). Figure 9 shows the \(\mathrm{S}_{\mathrm{N}}\) peak values of Solar Cycles 15 to 24 as a function of the absolute value of the difference between the polar fluxes of both hemispheres at the minimum \(\mathrm{S}_{\mathrm{N}}\) preceding each cycle.

Figure 9
figure 9

\(\mathrm{S}_{\mathrm{N}}\) peak values of Cycles 15 to 24 as a function of the absolute value of the difference between polar fluxes of both hemispheres at the minimum \(\mathrm{S}_{\mathrm{N}}\) preceding each cycle.

Full size image

The values in Figure 9 can be fitted by a linear regression line with the equation \(y=3\cdot 10^{-21} x+87.933\) (with a correlation coefficient \(r=0.7\) and a \(p\text{-value}=0.025\)), being \(x\) the absolute value of the difference between polar fluxes of both hemispheres at the minimum \(\mathrm{S}_{\mathrm{N}}\) preceding each cycle and \(y\) the maximum amplitudes of the \(\mathrm{S}_{\mathrm{N}}\) cycles. Therefore, if we apply such an equation to predict the \(\mathrm{S}_{\mathrm{N}}\) maxima for Solar Cycles 25 and 26, we obtain maximum amplitudes of 142.3 for Solar Cycle 25 (with an absolute value of the difference between the polar fluxes at the preceding \(\mathrm{S}_{\mathrm{N}}\) minimum of \(1.81 \cdot 10^{22}\text{ Mx}\), which is already known from observed data) and 126.9 for Solar Cycle 26 (with an absolute value of the difference between polar fluxes at the preceding \(\mathrm{S}_{\mathrm{N}}\) minimum of \(1.29 \cdot 10^{22}\text{ Mx}\), which, in this case, is obtained from the univariate predictions previously carried out for both polar fluxes). Taking into account that the RMSE obtained when calculating the regression line is 34.22, the \(\mathrm{S}_{\mathrm{N}}\) peak values estimated using this method for Solar Cycles 25 and 26 closely align (within the margin of error) with those predicted with the multivariate ML prediction (131.4 ± 10.0 and 121.2 ± 10.0, respectively). Therefore, it is noteworthy to point out that we obtain similar predictions for the \(\mathrm{S}_{\mathrm{N}}\) maximum amplitudes of Solar Cycles 25 and 26 using two different approaches.

4 Conclusions

This work has proposed a novel and innovative technique for solar cycle prediction, specifically the \(\mathrm{S}_{\mathrm{N}}\), employing multivariate ML techniques, considering both hemispheres’ polar fluxes as precursor parameters, and subjecting the considered time series to spectral analysis via FFT.

The RF algorithm yielded the lowest RMSE in the testing phase (10.0) and was therefore used in the final multivariate ML prediction of \(\mathrm{S}_{\mathrm{N}}\). We thus present our predictive results for the \(\mathrm{S}_{\mathrm{N}}\) of Solar Cycles 25 and 26, namely maxima of 131.4 (in July 2024) and 121.2 (in September 2034), respectively. Our results suggest that Cycle 25 will have a below-average maximum, while Cycle 26 will have a lower maximum than the preceding cycle. This could indicate that we are at present in the minimum of a centennial Gleissberg cycle.

The predicted dates for \(\mathrm{S}_{\mathrm{N}}\) maxima in Solar Cycles 25 and 26 (July 2024 and September 2034, respectively) are similar to those obtained for the next two polar flux polarity reversals for Solar Cycles 25 and 26 (April 2024 and August 2034, respectively).

Moreover, the \(\mathrm{S}_{\mathrm{N}}\) peak values for Cycles 25 and 26 have also been estimated using the equation of the linear regression resulting from the known relationship between the absolute value of the difference between the polar fluxes of both hemispheres at an \(\mathrm{S}_{\mathrm{N}}\) minimum and the \(\mathrm{S}_{\mathrm{N}}\) maximum of the subsequent cycle, resulting in values of 142.3 ± 34.2 and 126.9 ± 34.2, respectively. Hence, it is noteworthy that, using two different approaches, we produce similar predictions for the \(\mathrm{S}_{\mathrm{N}}\) maximum amplitudes of Solar Cycles 25 and 26.

Finally, we would like to draw an analogy between the evolution of weather prediction and solar cycle prediction. Over the last century, theoretical meteorologists have focused their efforts on weather prediction using the physical equations of meteorological models, achieving truly astonishing results (Fleming 2016). However, recently, exceptional advances have been made in weather prediction using machine learning techniques, driven by observed or quasi-observed data (Lam et al. 2023). Similarly, solar physicists have made notable strides in recent decades in the theoretical modeling of the solar dynamo based on magnetohydrodynamic equations for predicting the solar cycle (Choudhuri 2015). Nevertheless, we firmly believe that the time has definitively come for machine learning techniques to predict the solar cycle, driven by observed or quasi-observed data. This approach proves to be a crucial milestone, and this work is a compelling example of it.