1 Introduction

Several studies have shown that solar activity has an important influence on space weather and Earth (Foukal et al. 2006; Soon et al. 2011), in particular, as it relates to climate change (Ineson et al. 2011; Zhao, Xu, and Wang 2011). Each solar cycle (SC) has a different distribution of extreme solar activity, and therefore space weather (Le et al., 2013, 2014), which can impact communication, power transmission, and the aerospace environment (Sushanta 2016). Hence, the study and prediction of solar activity have become of great importance in recent decades, especially as related to the development of accurate, predictive forecasting tools for determining the size, shape, and timing of an SC.

Techniques for predicting and forecasting solar activity include: i) regression analysis (Thompson 1988; Hathaway, Wilson, and Reichmann 1994; Wilson and Hathaway, 2006a, 2006b), ii) correlative analysis using multiple indicators of solar activity (e.g., sunspot number, sunspot area, 10.7-cm radio flux, geomagnetic activity, etc.) (Hathaway, Wilson, and Reichmann 1999; Hathaway and Wilson 2002; Cameron and Schussler 2008), iii) comparative analysis with similar cycles (Wang and Han 1997; Han and Wang 1999; Wang et al. 2008), and iv) the rate of rise in sunspot number (SSN) (Wilson, 1990a, 1990b, 1990c; Han 2000; Karak and Choudhuri 2010; Du and Wang 2012; Yin and Han 2018). As applied to the past three SCs (i.e. SC22 – 24), these techniques have given a broad range of sunspot maximum amplitudes (RM), ranging from 38 to 210 for SC22, from 40 to 220 for SC23, and from 42 to 185 for SC24 (Li, Yun, and Gu 2001; Pesnell 2012). The ratios for which the relative errors (predictions with respect to the observed RM) were within ± 10% are only 21%, 14%, and 26% for SC22 – 24, while those for which the relative errors were ± 20% are only 35%, 27%, and 35%, respectively, for the three SCs separately (Han, Yin, and Wang 2018). Hence, an accurate prediction for the size of an SC remains a difficult task at present (Miao et al. 2015).

As related to the RM of the upcoming SC25, we have collected some 35 individual predictions published between 2004 and 2017, the smallest being about \(50 \pm 15\), based on the V1.0 series of SSN, equivalent to about \(80 \pm 24\), based on the revised V2.0 series of SSN (Clette, Svalgaard, and Vaquero 2014), available online at http://sidc.oma.be/silo/datafiles . We note that 12 of the 35 predictions have \(\mbox{RM} <150\), 19 of the 35 predictions have RM between 150 and 200, and only 4 of the 35 predictions have \(\mbox{RM} >200\). Of the 35 predictions, 15 predict the epoch of occurrence for RM. Of these, three predict the epoch of occurrence for RM between 2020 and 2030, two in 2022, six in 2023, and four in 2024. Of the 35 predictions five predict the epoch of sunspot minimum. Of these, one suggests the onset of SC25 to begin in late 2019, three in mid-2020, and one sometime between 2019 and 2020. Based on the variation of the number of spotless days relative to the epoch of sunspot minimum, Wilson (2015, 2017) suggests that SC25 onset will occur in 2020 or later.

In this article, we give predictions for the expected size and occurrences of sunspot minimum and maximum for SC25 using a particular regression method. Previously, Han (2000) used the method to study the relationship between the rising rate of monthly sunspot number (SSN) in the initial phase of a solar cycle and the following RM for SC23. Later, Han, Yin, and Wang (2018) used the method to simulate predictions for SC22 – 24. In particular, the method generates a monthly series of SSN, which based on the rate of change in SSN during the descending phase of an SC can be used to predict the epochs of minimum and maximum for the following SC (and its size).

2 Vondrak Smoothing Series of SSN

In the studies of SSN prediction, the 13-month smoothed SSN series (denoted as SSN-13mS) is commonly used because to the monthly mean SSN series (denoted as SSN-mon) has relatively large fluctuations. SSN-13mS lags SSN-mon by six months. In order to use the observed SSN data as early as possible, we employ the Vondrak smoothing method (Vondrak 1977) to generate a new smoothed SSN series (SSN-VS), which is of the same length as the SSN-mon series. The Vondrak smoothing method minimizes the value \(Q = F + \lambda^{2}S\), where \(F\) expresses the fidelity of the graduated values, \(S\) is the smoothness of the graduated curve, and \(\lambda^{2}\) is an arbitrary constant that defines the degree of graduation. We employ the smoothing factor \(\varepsilon = 1/ \lambda^{2}\), where \(\varepsilon \) has values between zero and infinity noting that smaller values of \(\varepsilon \) yield a smoother curve. The chief advantage of the method is that the pre-defined fitting function is not required and that the filter values at the two ends of the data series can be calculated (Zheng, Zhong, and Ding 2005; Yin and Han 2018).

We aim that the generated series SSN-VS matches as closely as possible the SSN-13mS for the trend of the rising and declining phase. Using various values of \(\varepsilon \), we find that the value \(\varepsilon = 0.01\) provides the best fit. Figure 1 compares the SSN-mon (the V2.0 series) and SSN-VS series for the years 1749 – 2017. Figure 2 compares SSN-13mS and SSN-VS for the years 1933 – 2017, spanning SC17 – 24. Clearly, SSN-VS is smoother than SSN-13mS and the resultant RM values are slightly smaller than the RM values based on SSN-13mS. In this article, we will examine the relationship between the SSN changing rates in the declining phase (denoted bd) and selected parameters of the present and following solar cycles described using SSN-13mS. We note that the SSN-VS series reduces the large fluctuations found in the SSN-13mS series and that the bd determined using the SSN-VS series might provide a better representation of the variation trend during the late stages of a solar cycle.

Figure 1
figure 1

The SSN-mon, SSN-13mS, and SSN-VS series from 1749 to 2017.

Full size image
Figure 2
figure 2

The SSN-13mS and SSN-VS from 1933 to 2017.

Full size image

3 Predictions of Some Parameters for SC25

Previously, Yoshida and Yamagishi (2010) found that the monthly smoothed SSN values in the last few years of a solar cycle (the descending phase of a solar cycle) correlate with the RM value of the following SC, with the best correlation obtained after the SSN has dropped below about 50 (based on the V1.0 SSN series). In our analysis (using SSN-VS), we also find this to be true, not just for RM of the following cycle but also for other parameters, as well. In particular, we find that when SSN-VS drops below about 70, using the next 20 months of SSN allows us to determine a slope (bd) that strongly correlates with the following RM (\(r >0.99\), statistically significant at the 99.9% level of confidence).

In order to facilitate the following discussion, we define some parameters related to the solar cycle and show them in a schematic diagram in Figure 3. In the figure, \(i\) is the serial number of the SC, LCMin is the elapsed time between the minima of two consecutive cycles, LCMax is the time between the RM for two consecutive cycles, Ld is the duration of the declining phase, and Lr is the duration of the rising phase of an SC. The parameters of the past 24 SCs in the SSN-13mS series are listed in Table 1. In the table, the abbreviation ‘my’ is for year of minimum and ‘mm’ is for month of minimum, ‘My’ is for year of maximum and ‘Mm’ is for month of maximum, respectively. The analysis shows that the bd of SC\(i\) has a significant correlation with the main parameters of SC(\(i+1\)). Before attempting a prediction of the main parameters for SC25, we will first perform simulated predictions for SC18 – 24 and compare them with their observed values to evaluate the effectiveness of our method. Then we will make predictions of the main parameters for SC25.

Figure 3
figure 3

Schematic diagram of some parameters of the solar cycle.

Full size image
Table 1 Data and relevant parameters of each SC used in the work.
Full size table

In Table 1, the maxima and minima of a few of the SCs are found to be slightly different from those given by Hathaway (2015). Namely, using the SSN V1.0 series, Hathaway (2015) determined that SC22 has \(\mbox{RM} = 158.5\) in July 1989. Using the SSN V2.0, we determine \(\mbox{RM} = 212.5\) in November 1989 for SC22. Likewise, for SC23, Hathaway determined \(\mbox{RM} = 120.7\) in April 2000, while we determine \(\mbox{RM} = 180.3\) in November 2001. For SC16, Hathaway (2015) identified August 1923 (5.6) as minimum, while we determine July 1923 (9.4) to be minimum. For SC21, he identified March 1976 (12.2) as minimum, while we determine the minimum to be June 1976 (17.9). Lastly, he identified May 1996 (8.0) as minimum for SC23, while we determine minimum to be August 1996 (11.2). The numbers between parenthesis are the smoothed monthly sunspot numbers.

3.1 Prediction for the Beginning of SC25

The linear regression analysis shows that the bd value of SC\(i\) correlates with the LCMin value between SC\(i\) and SC(\(i+1\)). Hence, we can use the known bd value of SC\(i\) to predict the LCMin value and thereby estimate the occurrence of the minimum between SC\(i\) and SC(\(i+1\)). For the past seven cycles, we determine the linear regression equations (given below as Equations 1 – 7) for the LCMin values between SC\(i\) and SC(\(i+1\)). The inferred linear correlation coefficient \(r\) for each of these inferred regressions is 0.568, 0.578, 0.594, 0.562, 0.570, 0.582, and 0.576, respectively. Although the inferred regressions can explain only about one-third of the variance in LCMin, statistical testing shows that the inferred regressions are statistically important at the 99% level of confidence. The linear regression equations are:

$$\begin{aligned} \mbox{LCMin}_{17/18} =& (14.60 + 1.539~ \mbox{bd}_{17}) \pm 1.11, \end{aligned}$$
(1)
$$\begin{aligned} \mbox{LCMin}_{18/19} =& (14.63 + 1.560~ \mbox{bd}_{1 8}) \pm 1.08, \end{aligned}$$
(2)
$$\begin{aligned} \mbox{LCMin}_{19/20} =& (14.55 + 1.519~ \mbox{bd}_{1 9} ) \pm 1.04, \end{aligned}$$
(3)
$$\begin{aligned} \mbox{LCMin}_{20/21} =& (14.26 + 1.419~ \mbox{bd}_{20} ) \pm 1.05, \end{aligned}$$
(4)
$$\begin{aligned} \mbox{LCMin}_{21/22} =& (14.26 + 1.417~ \mbox{bd}_{21} ) \pm 1.02, \end{aligned}$$
(5)
$$\begin{aligned} \mbox{LCMin}_{2 2 /2 3} =& (14.20 + 1.389~ \mbox{bd}_{2 2} ) \pm 0.99, \end{aligned}$$
(6)
$$\begin{aligned} \mbox{LCMin}_{2 3 /2 4} =& (14.19 + 1.403~ \mbox{bd}_{2 3} ) \pm 0.99. \end{aligned}$$
(7)

Using the bd values listed in Table 1 for the past seven cycles, we determine simulated predictions for LCMin (i.e. PLCMin) for each SC. Shown in Table 2 are the LCMin, PLCMin, DLCMin (i.e. the difference PLCMin–LCMin) and DLCMinP (i.e. the relative error DLCMin/LCMin) for the seven SCs. The results show that there is close agreement between the observed and predicted values with small relative errors, suggesting that the technique is promising to estimate the onset of a following cycle. Based on SC1 – 23, we infer the regression equation to be

$$ \mbox{LCMin}_{24/25} = (14.36 + 1.464~\mbox{bd}_{24}) \pm 0.98, $$
(8)

where 14.36 represents the y-axis intercept, 1.464 is the inferred slope, and 0.98 is the inferred standard deviation about the regression line. The inferred regression is found to be statistically important at the 99.5% level of confidence.

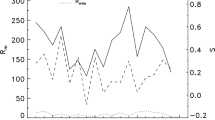
Table 2 Simulated predictions of LCMin for SC18 – SC24 using bd.
Full size table

Figure 4 displays the scatterplot of LCMin versus bd for SC1 – 23, where the horizontal and vertical bars are the median values of LCMin (11.246) and bd (2.347), respectively, and the inferred regression line. Also shown are the bd value for SC24 (shown as an arrow along the horizontal axis) and the results of Fisher’s exact test for the observed \(2 \times 2\) contingency table, indicating that the probability of obtaining the observed result is \(P = 2.7\%\). The probability of obtaining the observed result, or one more suggestive of the departure from independence, is slightly larger, being \(P = 3.0\%\). Because the known value of bd for SC24 is −2.818 (based on the regression analysis of the 20 months spanning September 2015 to May 2017), we predict that the \(\pm 1\) standard deviation prediction interval for LCMin24 and LCMin25 is \(10.23 \pm 0.98\) years, inferring a minimum for SC25 about \(2019.188 \pm 0.98\) years (i.e. \((2008.958 + 10.23) \pm 0.98\)). Unless SC25 is a statistical outlier, its expected LCMin should be \({<}\,11.246\) years (i.e. it should be located in the lower-left quadrant of Figure 4).

Figure 4
figure 4

Scatter plots and regression line of bd and LCMin.

Full size image

3.2 Prediction for the Maximum Amplitude of SC25

For the past SCs, we note that RM for SC(\(i+1\)) correlates strongly with the preceding bd for SC\(i\). Before making a prediction of RM for SC25, we will first make simulated predictions for the past seven SCs, as we did in the previous section. The results of the linear regression analysis for SC18 – 24 is the following:

$$\begin{aligned} \mbox{RM}_{18} =& ( -41.80 - 95.236~ \mbox{bd}_{17} ) \pm 39.4, \end{aligned}$$
(9)
$$\begin{aligned} \mbox{RM}_{19} =& ( -44.01 - 96.653~ \mbox{bd}_{18} ) \pm 38.3, \end{aligned}$$
(10)
$$\begin{aligned} \mbox{RM}_{20} =& ( -56.92 - 103.176~ \mbox{bd}_{19} ) \pm 38.0, \end{aligned}$$
(11)
$$\begin{aligned} \mbox{RM}_{21} =& ( -52.71 - 101.716~ \mbox{bd}_{20} ) \pm 37.1, \end{aligned}$$
(12)
$$\begin{aligned} \mbox{RM}_{22} =& ( -25.29 - 91.796~ \mbox{bd}_{21} ) \pm 42.6, \end{aligned}$$
(13)
$$\begin{aligned} \mbox{RM}_{23} =& ( -15.93 - 86.980~ \mbox{bd}_{2 2} ) \pm 42.1, \end{aligned}$$
(14)
$$\begin{aligned} \mbox{RM}_{24} =& ( -16.05 - 86.846~ \mbox{bd}_{2 3} ) \pm 41.1. \end{aligned}$$
(15)

The inferred linear correlation coefficients are −0.770, −0.777, −0.809, −0.808, −0.732, −0.726, and −0.725, respectively, and all are statistically important within a 99.9% level of confidence.

Table 3 gives the simulated predictions in comparison to the observed values of RM, where PRM is the predicted RM, DRM is the difference between the predicted and observed RM (i.e. PRM–RM) and DRMP is the relative error expressed as a percentage (i.e. 100 × DRM/RM). We note that DRM for SC21 measures −100.89 (\(\mbox{DRMP} = -43.3\%\)), very different in comparison to the other cycles, suggesting that the bd value for SC20 (used to predict RM for SC21) is a statistical outlier. Indeed, SC20 displayed large fluctuations during its declining phase, in contrast to the usual gradual decline seen for most SCs. We believe that this inherent fluctuating behavior during the declining phase of SC20 accounts for the large PRM and DRMP seen in SC21. Hence, when large fluctuations are encountered during the late stages of an SC, predictions of RM for the following SC will be less reliable (i.e. DRMP will be considerably larger).

Table 3 Simulated predictions for RM for SC18 – SC24 using bd.
Full size table

Based on SC1 – 23 bd values (Table 1), we infer the regression equation relating RM for SC(\(i+1\)) to bd for SC\(i\) to be

$$ \mbox{RM}_{25} = (-22.25 - 89.084~\mbox{bd}_{24}) \pm 40.5. $$
(16)

The inferred regression equation has a linear correlation coefficient \(r = -0.738\) and is found to be statistically important within a 99.9% level of confidence.

Figure 5 shows the scatterplot of RM for SC(\(i+1\)) versus bd for SC\(i\), the inferred regression line and the results of Fisher’s exact test for the observed \(2 \times 2\) contingency table (determined by the medians, −2.347 and 186.2), indicating that the probability of obtaining this contingency table is \(P = 0.89\%\). Using \(\mbox{bd} = -2.818\) for SC24, we infer from the linear regression that RM for SC25 will be about \(228.8 \pm 40.5\) units of sunspot number (the \(\pm 1\) prediction interval) and very probably \({\geq}\, 186.2\) (based on the observed \(2 \times 2\) contingency table).

Figure 5
figure 5

Scatter plots and regression line of bd(\(i\)) and RM(\(i+1\)).

Full size image

3.3 Prediction for the Maximum Epoch of SC25

For the past SCs, we note that LCMax for SC(\(i+1\)) also correlates with bd for SC\(i\). As previously, before predicting the occurrence of RM for SC25, we first show the results of the linear regression analysis for the past seven SCs, given as follows:

$$\begin{aligned} \mbox{LCMax}_{17/18} =& (18.28 + 3.256~ \mbox{bd}_{17} ) \pm 1.82, \end{aligned}$$
(17)
$$\begin{aligned} \mbox{LCMax}_{18/19} =& (18.26 + 3.245~ \mbox{bd}_{18} ) \pm 1.76, \end{aligned}$$
(18)
$$\begin{aligned} \mbox{LCMax}_{19/20} =& (17.45 + 2.836~ \mbox{bd}_{19} ) \pm 1.79, \end{aligned}$$
(19)
$$\begin{aligned} \mbox{LCMax}_{20/21} =& (17.11 + 2.717~ \mbox{bd}_{20} ) \pm 1.76, \end{aligned}$$
(20)
$$\begin{aligned} \mbox{LCMax}_{21/22} =& (16.81 + 2.610~ \mbox{bd}_{21} ) \pm 1.73, \end{aligned}$$
(21)
$$\begin{aligned} \mbox{LCMax}_{22 /23} =& (16.58 + 2.491~ \mbox{bd}_{22} ) \pm 1.69, \end{aligned}$$
(22)
$$\begin{aligned} \mbox{LCMax}_{23/ 24} =& (16.60 + 2.473~ \mbox{bd}_{23} ) \pm 1.67. \end{aligned}$$
(23)

The inferred regressions have linear correlation coefficients equal to 0.666, 0.669, 0.628, 0.612, 0.601, 0.601, and 0.593, respectively, and all are found to be statistically important within a 99.5% level of confidence.

Table 4 presents the simulated predictions for the past seven SCs, where PLCMax is the predicted LCMax, DLCMax is the difference between the predicted and observed LCMax (i.e. PLCMax–LCMax), and DLCMaxP is the relative error in percentage (i.e. 100 × DLCMax/LCMax). From SC1 – 23, we determine the inferred linear regression to be

$$ \mbox{LCMax}_{24/25} = (16.68 + 2.50~\mbox{bd}_{24}) \pm 1.64. $$
(24)
Table 4 Simulated predictions of LCMax for SC18 – SC24 using bd.
Full size table

Figure 6 shows the scatterplot of LCMAX for SC(\(i+1\)) versus bd for SC\(i\), the inferred regression and the results of Fisher’s exact test for the observed \(2 \times 2\) contingency table (\(P = 2.7\%\)). Being, \(\mbox{bd} = -2.818\) for SC24, we have \(\mbox{PLCMax} = (9.63 \pm 1.64)\) years for SC25 (i.e. the \(\pm 1\) prediction interval). Hence, we estimate RM occurrence for SC25 to be about \((2023.918 \pm 1.64)\) years (i.e. \((2014.288 + 9.63) \pm 1.64\)), probably before 2025.121 (February 2025), based on the \(2 \times 2\) contingency table.

Figure 6
figure 6

Scatter plot and regression line of bd and LCMax.

Full size image

4 Conclusion and Discussion

This study has shown that major characteristics of the immediately following SC (e.g. the epochs of sunspot minimum and maximum and the RM) can be determined based on the behavior characteristics late in the declining phase of the preceding SC. The variation of solar activity over an SC is very complex, involving a variety of components of varying timescales (Le and Wang 2003). Although a solar cycle is generally described using SSN (i.e. SSN-13mS), Hathaway (2015) note that each SC actually starts well before its minimum smoothed SSN occurrence and ends well after the following cycle minimum smoothed SSN occurrence (cf. Jiang et al. 2016), with consecutive cycles overlapping typically by 1 – 3 years. Likewise, long ago, Waldmeier (1935) showed that the maximum amplitude of a cycle is related to the time it takes to reach that maximum amplitude, denoted here as Lr.

Figure 7 displays the scatterplot of Lr for SC(\(i+1\)) versus bd for SC\(i\). The format of the figure follows that of our previous figures. Using \(\mbox{bd} = -2.818\) from SC24, we note that the Lr for SC25 should be about \(3.4 \pm 0.82\) years (from the inferred regression equation) and probably \({<}\,4.081\) years (based on the \(2\times2\) contingency table). The inferred regression equation is

$$ \mbox{Lr}_{25} = (7.50 + 1.453~\mbox{bd}_{24}) \pm 0.82. $$
(25)
Figure 7
figure 7

Scatter plot and regression line of bd(\(i\)) and Lr(\(i+1\)).

Full size image

The linear correlation coefficient is \(r = 0.640\), meaning the inferred regression can explain about 41% of the variation in Lr, and the regression is inferred to be statistically important within a 99.9% level of confidence. The results of Fisher’s exact test of the observed \(2 \times 2\) contingency table is \(P = 0.27\%\). Hence, once we know when SC25 minimum occurs, we can use Equation 25 to determine when we should expect SC25 maximum (i.e. RM) to occur.

Figure 8 shows the scatterplot of LCMax for SC\(i\) versus Ld for SC\(i\), where Ld is the length of the descent from maximum amplitude for SC\(i\) to minimum amplitude for SC(\(i+1\)). Again, the format of the figure follows that of the previous figures. The inferred regression equation is

$$ \mbox{LCMax}_{24/25} = (1.51 + 1.408~\mbox{Ld}_{24}) \pm 0.97. $$
(26)

The linear correlation coefficient is \(r = 0.881\), meaning that the inferred regression can explain about 78% of the variation in LCMax, and the regression is inferred to be statistically important within a 99.9% level of confidence. The results of Fisher’s exact test of the observed \(2 \times 2\) contingency table is \(P = 0.95\%\). Hence, again, once we know when the SC25 minimum occurs, we will then know Ld for SC24 and can then use Equation 26 to determine when we should expect SC25 maximum to occur.

Figure 8
figure 8

Scatter plot and regression line of Ld and LCMax.

Full size image

Figure 9 shows the scatterplot of RM for SC\(i\) versus Lr for SC\(i\). The inferred regression equation is

$$ \mbox{RM}_{25} = (345.0 - 38.25~\mbox{Lr}_{25}) \pm 38.8. $$
(27)

The inferred regression has a linear correlation coefficient \(r = -0.753\) that is statistically important within a 99.9% level of confidence. The observed \(2 \times 2\) contingency table has a probability of occurring by chance of only \(P = 0.16\%\). Hence, there is a very strong correlation between the length of the rise and the maximum amplitude of an SC, as previously noted by many investigators (e.g. Waldmeier 1935; Kiepenheuer 1953; Karak and Choudhuri 2010; Hathaway 2015; Wilson 2015; and many others).

Figure 9
figure 9

Scatter plot and regression line of Lr and RM.

Full size image

4.1 Discussion of RM Prediction of SC25

As previously noted, using \(\mbox{bd} = -2.818\) for SC24, we have predicted: 1) \(\mbox{RM} = 228.8 \pm 40.5\) and 2) \(\mbox{Lr} = (3.40 \pm 0.82)\) years for SC25. Now, these are \(\pm 1\) standard deviation prediction intervals. This means that there is a 68.3% probability that SC25 will have both an RM and Lr within the stated ranges, or an 84.3% probability that SC25 will have \(\mbox{RM} \geq 188.3\) and \(\mbox{Lr} \geq 2.58\) years (the same probabilities are found for \(\mbox{RM} <269.3\) and \(\mbox{Lr} <4.22\) years). In comparison with SC24, the predicted values for SC25 suggest that it will be both larger than SC24 and have a faster rise (\(\mbox{RM} = 116.4\) and \(\mbox{Lr} = 5.33\) years for SC24). Because SC25 is an odd-numbered SC, the predictions we give for SC25 are in line with those expected from the even–odd effect (i.e. the Gnevyshev-Ohl rule (Gnevyshev and Ohl 1948)); namely, the odd-following cycle usually is larger in amplitude compared to the preceding even cycle. We do note, however, that of the 11 even–odd cycle pairs (see Table 1), 3 do not adhere to the inferred preferential behavior, including Cycle pairs 4 and 5, 8 and 9, and 22 and 23. In fact, SC5 is 153.3 units of sunspot number smaller than was seen in SC4.

From Table 1, we note that there have been 11 cycles that have \(\mbox{RM} \geq 188.3\), all of these cycles have Lr between 2.92 and 4.58 years, within an average to about (\(3.48 \pm0.44\)) years. This suggests that, assuming \(\mbox{RM} \geq 188.3\) for SC25, we should expect \(\mbox{Lr} <3.92\) years, suggesting that it will rise fast. Once SC25 gets under way, we hope that its rising rate will provide a better prediction of its RM (Han, Yin, and Wang 2018; Yin and Han 2018).

4.2 Discussion of the Prediction of the RM Epoch of SC25

As previously noted, using \(\mbox{bd} = -2.818\) for SC24, we also have predicted \(\mbox{LCMax} = (9.63 \pm 1.64)\) years for SC25, inferring that its maximum epoch should be about \((2023.918 \pm 1.64)\) years, or about December \(2023 \pm 20\) months. Solar activity is extremely low at present and has been so for some time. The rapid decrease in monthly SSN began in late 2017 with a smoothed monthly SSN decreasing below 10 in March 2018. Monthly values of SSN for the first three months of 2019 have been 7.8, 0.8, and 9.5, respectively, and smoothed monthly SSN have continued to decrease, being 7.1, 6.7, and 6.6 for July – September 2018. Many solar observers are now suggesting that the minimum between SC24 and 25 will be an extended minimum, much like that experienced between SC23 and 24 (Russell, Luhmann, and Jian 2010). If true, then both the predicted epochs of the minimum and the maximum SSN for SC25 will occur later.

At present (April 2019), the decline phase of SC24 has extended 5 years, with an inferred \(\mbox{LCMax} \geq (8.55 \pm 0.82)\) years for SC25 (see Figure 8). With each passing month, the value of LCMax for SC25 will increase to a higher value. Should Ld for SC24 be 6 years, \(\mbox{LCMax} \geq (9.96 \pm 0.82)\) years, indicating the epoch of maximum for SC25 probably in late 2024 to early 2025. It is important to note that Ld has almost always been longer than Lr. There have been only three exceptions, all early cycles, including SC1, 5, and 7. For all other SCs, \(\mbox{Ld} >\mbox{Lr}\), with the difference in length averaging to about \((36 \pm 16)\) months. The smallest observed difference is 8 months (SC16). Therefore, the epoch of minimum for SC25, likely, will be late 2019 or later.

In conclusion, our results based on SC24 having \(\mbox{bd} = -2.818\) and presuming that SC25 is not a statistical outlier, are as follows: i) sunspot minimum occurrence about \((2019.188 \pm 0.98)\) years (i.e. before February 2020), ii) sunspot maximum occurrence about \((2023.918 \pm 1.64)\) years (i.e. before July 2025), and iii) a maximum amplitude about (\(228.8 \pm 40.5\)) units of sunspot number (i.e. \({\geq}\, 188.3\)).