Stacked 1D Convolutional LSTM (sConvLSTM1D) Model for Effective Prediction of Sunspot Time Series

Abstract

A multi-layer, deep-learning (DL) architecture consisting of stacked Convolutional Long Short Term Memory (sConvLSTM1D) layers is proposed to forecast the sunspot number (SSN) more effectively. The proposed model with optimized hyper-parameters performs efficiently on four kinds of sunspot data with different frequencies of time that are yearly, monthly, daily, and 13-month smoothed provided by the World Data Center-Sunspot Index and Long Term Solar Observation (WDC-SILSO), the Royal Observatory of Belgium (SILSO World Data Center). The model was contrasted with other traditional DL models on different performance metrics, namely root-mean-square error (RMSE), mean-absolute error (MAE), mean-absolute-percentage error (MAPE), and mean-absolute-scaled error (MASE). A non-parametric statistical test has also been carried out to confirm the model’s effectiveness. The prediction of the highest yearly mean of total sunspot number (SSN) in Solar Cycle 25 (SC25) has also been performed. The proposed sConvLSTM1D model suggests that the solar cycle exhibits the characteristics of a weak cycle. However, it is anticipated to be stronger than the preceding Solar Cycle 24 (SC24). The year of peak sunspot number will be 2024, as per the prediction, with the peak value of yearly mean sunspot number as 140.84, which is 24.3% higher than the peak value of the yearly mean of total sunspot number, which was 113.3 in the Solar Cycle 24 in the year 2014.

1 Introduction

Sunspots are the observable dark areas that emerge on the surface of the Sun due to relatively lower temperatures in that specific region than the other regions. Since 1610, astronomers have observed the solar surface with the help of telescopes and recorded the occurrence and appearance of sunspots (Vokhmyanin, Arlt, and Zolotova, 2020). As per the study of Marques, Leal-Júnior, and Kumar (2023), variances caused by sunspot activity in space are a significant factor in determining the architecture and design of spacecraft. The radiation hazard that is observed in space has a significant source, which is known as cosmic rays. The flux of these cosmic rays is anti-correlated with the solar cycle (Pesnell, 2008). Therefore, accurate prediction of sunspot numbers along with their peaks and resulting solar cycle is quite essential to perform various developments in astronomy. In this study, the performance of some traditional deep-learning (DL) models has been analyzed and compared with the proposed model with the primary objective of reducing the error in the prediction of sunspot numbers. As per the study of Benson et al. (2020), sunspot-activity forecasts for the upcoming solar cycle have been classified as a multi-step univariate time-series technique. Therefore, the concept of time series has been utilized along with DL technologies to design a model that can foretell the number of SSNs appearing on the surface of the Sun with less error.

Chattopadhyay, Jhajharia, and Chattopadhyay (2011) explained that the prediction based on periodicity present in time-series data of sunspot numbers is known as the numeric method, while the prediction based on geophysical parameters and methodologies related to it is known as the precursor method. In most of the studies, the data of the sunspot number has been taken from the SILSO centre of SIDC, Belgium since it has the data for an extended period, which is helpful in prediction using deep-learning approaches. Büyükşahin and Ertekin (2019) proposed a hybrid model of ANN and ARIMA and performed a comparative analysis of their suggested model’s efficacy with the individual model’s performances. In contrast, Pala and Atici (2019) introduced deep-learning techniques as a solution to this problem, forecasted the total monthly mean of sunspot numbers using the LSTM method, and showed that deep-learning models outperform the statistical models. The difference in the previously stated works is that the former utilized the monthly average of sunspot numbers while the latter analyzed the results on the annual data. Apart from this, Büyükşahin and Ertekin (2019) also used Empirical Mode Decomposition to fragment data into Intrinsic Mode Functions (IMFs) and then executed their proposed models. Pala and Atici (2019) utilized two stacking layers of LSTM for their study, while Elgamal (2020) utilized deep and stacked LSTM to predict SC25.

Compared to the above works, Lee (2020) proposed a novel model with a hybrid of LSTM and EMD suggesting it as a better alternative for modeling the sunspot time series because of its cyclic nature. In this study, ensemble EMD has been utilized to obtain the IMFs. Unlike the above-mentioned strategies, Panigrahi et al. (2021) introduced a combination of machine-learning algorithms and statistical methods. In this research, SVM has been utilized alongside ARIMA and Exponential Smoothing with error, trend, and seasonality combined, known as ETS, where seasonality means repeating patterns over a fixed time interval. In contrast to this work regarding methodology, Arfianti et al. (2021) utilized deep-learning techniques namely GRU and LSTM individually for forecasting and summarized that GRU outperformed LSTM in their experiments. Similarly, Prasad et al. (2022) experimented with stacked LSTM to forecast the Solar Cycle 25 based on 13-month smoothed observations of sunspot numbers and compared their work with the proposed model of Wang 2021. They concluded that the performance improved significantly.

Apart from the studies mentioned above, Hasoon and Al-Hashimi (2022) proposed three models, namely RNN, DNN, and a hybrid of DNN and LSTM, and concluded that the hybrid model has higher detection performance than the individual models. From a comparison point of view, an elaborate study was carried out by Dang et al. (2022) where methodologies not associated with deep learning, namely Prophet, Exponential Smoothing, and SARIMA, were compared with approaches associated with deep learning, namely Transformer, GRU, Informer, and LSTM where the Informer model outperformed all other models. Then, an ensemble of all models was also built based on mean, median, error, regression, and XGBoost, and it was deduced that an ensemble of deep-learning algorithms based on XGBoost is better than all other experimented combinations.

Another study by Ramadevi and Bingi (2022) suggested that a Nonlinear Autoregressive Network (NAR), a neural network, performs better on 13-month smoothed observations of sunspot numbers. The NAR neural network is a neural network of feed-forward orientation with input and output layers along hidden layers. Specific activation functions “purelin” and “tansig” have been utilized to achieve optimal results. Nghiem et al. (2022) proposed a model that is a hybrid of CNN and LSTM along with Bayesian optimization and compared its performance with six state-of-the-art models, including four approaches of the DL methodology that are Informer, GRU, Transformer, and LSTM along with two models not associated with deep learning namely Prophet and SARIMA, and summarized that the CNN-Bayes LSTM model performed more effectively than these six models.

Kumar, Sunil, and Yadav (2023) also proposed a hybrid model, combining a statistical model with a deep-learning model. In their research, the $\beta$ SARMA and LSTM models were combined to predict yearly sunspot numbers, and the performance was compared with other traditional models such as ARIMA, LSTM, and MLP along with an ensemble of ARIMA and ANN, and the proposed model was found to be good in most of the cases. In most studies, the monthly mean of total SSN has been utilized. Some of the researchers such as Chattopadhyay, Jhajharia, and Chattopadhyay (2011), Büyükşahin and Ertekin (2019), Elgamal (2020), and Panigrahi et al. (2021) utilized the annual average of total sunspot numbers as well. A few researchers also performed forecasts over 13-month smoothed observations of sunspot numbers such as Prasad et al. (2022) and Ramadevi and Bingi (2022).

While comparing the performance measures, it was found that Elgamal (2020) used RMSPE and MAPE along with RMSE, while Panigrahi et al. (2021) used MASE and MAE along with RMSE. Hasoon and Al-Hashimi (2022) used MSE and MAE to measure the effectiveness of their proposed deep-learning models. Dang et al. (2022) used RMSE and MAE measures to compare the effectiveness of deep-learning techniques, methodologies other than deep-learning techniques and their ensemble models. From the above, most researchers have utilized RMSE as a standard metric to measure the effectiveness of the proposed models.

From the study of the previous works, it is clear that the effective prediction of SSNs is essential, and researchers have made efforts to improve the efficacy of the forecasting model. DL models perform well in the prediction of SSN, but errors still exist in the prediction of SSN, so there is still scope for improvement for the DL models. In this study, a novel stacked model based on ConvLSTM1D is proposed to improve the prediction of SSN, which is validated on different performance measures and datasets. In comparison to earlier studies where researchers utilized a maximum of two sunspot datasets with two different frequencies of time, we have utilized four kinds of sunspot data with four different frequencies of time that are daily, yearly, monthly, and 13-month smoothed for better evaluation of the proposed prediction model. This study evaluates the proposed model based on RMSE, MASE, MAE, and MAPE for better comparison. The proposed model is compared with traditional deep-learning models based on non-parametric statistical tests to validate its efficacy. In contrast to the earlier studies where researchers utilized a statistical approach, machine-learning models, vanilla LSTM, GRU, hybrid models, ensemble DL models, or stacked LSTM model, we have utilized a novel stacked ConvLSTM1D DL model for the predictions, which resulted in effective predictions over all four variants of the data. Finally, the proposed model is utilized for a more precise prediction of SC25, along with its peak and trough. The rest of the article contains the Methodology in Section 2, Data Analysis and Experimental Setup in Section 3, Results and Analysis in Section 4, and Conclusions in Section 5.

2 Methodology

This study includes basic DL approaches, namely LSTM, CNN, GRU, RNN, and BiLSTM, for the comparison purpose, while the proposed model is a two-layer stacked architecture of ConvLSTM1D with a repeat-vector layer embedded in between the ConvLSTM1D layers followed by dropout and fully connected layers.

2.1 Mathematical Background

This section consists of fundamental mathematical aspects of the dataset and different basic models.

2.1.1 Mathematical Principles Related to the Dataset

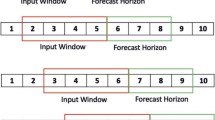
The time-series univariate dataset is denoted as “D” consisting of finite data points d1, d2, d3, and so on, with time as the variable. $\mathrm{X_{Data}}$ and $\mathrm{Y_{Data}}$ are the lags as training features and target features, respectively. $\mathrm{X_{Data}}$ is trifurcated into their corresponding set of $\mathrm{X_{train}}$, $\mathrm{X_{validation}}$, and $\mathrm{X_{test}}$. $\mathrm{Y_{Data}}$ is trifurcated into the set of $\mathrm{Y_{train}}$, $\mathrm{Y_{validation}}$, and $\mathrm{Y_{test}}$. Furthermore, the $Input Sequence$ is a combination of both $\mathrm{X_{train}}$ and $\mathrm{Y_{train}}$ for the training of the models, which is utilized to feed the DL models.

2.1.2 Mathematical Principles Related to LSTM

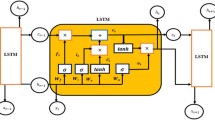
LSTM was initially proposed by Hochreiter and Schmidhuber (1997) in the field of neuro-computing. LSTM is a DL model specifically linked with RNN, which can address the vanishing or exploding gradient issue. LSTM can divulge the temporal dynamic behavior associated with the time series (Bai et al., 2019). The memory cell has three gates: forget, input, and output gate. Of these three gates, the forget gate is crucial since it is the decision-making gate that decides whether information from the preceding time step needs to be carried forward or forgotten. The other two gates are the input and output gate, which regulate the input’s activation flow in the memory unit’s direction and the information stream from the memory unit to the output. The LSTM architecture is depicted in Figure 1. LSTM models are designed to work with sequential data consisting of one-dimensional vectors over time and can forecast the future sequence (Zhang et al., 2019):

$$ i_{t} = \sigma (\mathbf{W}_{\mathrm{i}}\cdot[h_{t-1},x_{ t}]+b_{\mathrm{i}}), $$

(1)

$$ f_{t}=\sigma (\mathbf{W}_{\mathrm{f}}\cdot[h_{t-1},x_{t}]+b_{ \mathrm{f}}), $$

(2)

$$ o_{t}=\sigma (\mathbf{W}_{\mathrm{o}}\cdot[h_{t-1},x_{t}]+b_{ \mathrm{o}}). $$

(3)

Figure 1

Schematic architecture of LSTM cell.

Equation 1, Equation 2, and Equation 3 represent the equations for input, forget, and output gate, respectively, where $x_{t}$ denotes the input at the current time step $t$ and $\mathbf{W}_{\mathrm{f}}$, $\mathbf{W}_{\mathrm{o}}$, and $\mathbf{W}_{\mathrm{i}}$ are the weight matrices for forget, output, and input gates. Apart from these, $b_{\mathrm{f}}$, $b_{\mathrm{o}}$, and $b_{\mathrm{i}}$ are the bias terms for the respective gates. $\sigma$ and tanh represent sigmoid and hyperbolic tangent activation functions, respectively:

$$\begin{aligned} c_{t}&=f_{t} c_{t-1}+i_{t} g_{t}, \end{aligned}$$

(4)

$$\begin{aligned} g_{t}&=\tanh (\mathbf{W}_{g} [h_{t-1},x_{t}]+b_{g}), \end{aligned}$$

(5)

$$\begin{aligned} h_{t}&=o_{t} \tanh (c_{t}). \end{aligned}$$

(6)

Equation 4, Equation 5, and Equation 6 represent the equations for memory cell, candidate memory, and hidden state, respectively, where $h_{t-1}$ and $c_{t-1}$ denote hidden state and memory state at the previous time step $(t-1)$.

2.1.3 Mathematical Principles Related to ConvLSTM1D

The ConvLSTM1D arrangement is an adaptation of LSTM. Changes are made to the architecture of LSTM to produce the ConvLSTM1D, which is presented in Figure 2. Based on the equations of LSTM, the main equations for ConvLSTM1D are expressed in the following manner:

$$ i_{t} = \sigma (\mathit{Conv1D}(\mathbf{W}_{\mathrm{i}}, \mathcal{X}) + \mathit{Conv1D}(\mathbf{U}_{ \mathrm{i}}, \mathbf{H}) + b_{\mathrm{i}}). $$

(7)

Equation 7 represents the input gate and $\mathbf{W}_{\mathrm{i}}$ and $b_{i}$, the learnable parameters indicating the weight and bias associated with the input gate applied to input tensor $\mathcal{X}$ at the current time step, whereas $\mathbf{U}_{i}$ represents the weight matrix associated with the input gate applied to the hidden state $\mathbf{H}$ from the preceding time step.

$$ f_{t} = \sigma (\mathit{Conv1D}(\mathbf{W}_{\mathrm{f}}, \mathcal{X}) + \mathit{Conv1D}(\mathbf{U}_{ \mathrm{f}}, \mathbf{H}) + b_{\mathrm{f}}). $$

(8)

Equation 8 represents the forget gate where $\sigma$ represents the sigmoid activation function operating over the learnable parameters $\mathbf{W}_{\mathrm{f}}$, $b_{\mathrm{f}}$, and $\mathbf{U}_{\mathrm{f}}$ associated with the forget gate.

$$ o_{t} = \sigma (\mathit{Conv1D}(\mathbf{W}_{\mathrm{o}}, \mathcal{X}) +\mathit{Conv1D}(\mathbf{U}_{ \mathrm{o}}, \mathbf{H}) + b_{\mathrm{o}}). $$

(9)

Figure 2

Schematic architecture of Convolutional LSTM cell.

Similarly, Equation 9 represents the output state $o_{t}$ as a sigmoid function with learnable parameters $\mathbf{W}_{\mathrm{o}}$, $b_{\mathrm{o}}$, and $\mathbf{U}_{\mathrm{o}}$ associated with the output state.

$$ \widetilde {\boldsymbol{C}}= \tanh (\mathit{Conv1D}(\mathbf{W}_{\mathrm{c}}, \mathcal{X}) + \mathit{Conv1D}(\mathbf{U}_{\mathrm{c}}, \mathbf{H}) + b_{\mathrm{c}}). $$

(10)

Equation 10 represents the candidate cell state, which is the information that can be potentially added to the cell state in the current time step where the learnable parameters $\mathbf{W}_{\mathrm{c}}$, $b_{\mathrm{c}}$, and $\mathbf{U}_{\mathrm{c}}$ are associated with the candidate state. In this equation, tanh, represents the hyperbolic tangent activation function, which squashes the value between −1 and +1.

$$ \boldsymbol{C}= f_{t}\boldsymbol{C} + i_{t}\widetilde {\boldsymbol{C}}, $$

(11)

$$ H= o_{t} \tanh (\boldsymbol{C}). $$

(12)

Equations 11 and 12 represent the revised state of the cell stated denoted as $\boldsymbol{C}$ and the hidden state $\mathbf{H}$, respectively.

The proposed model in this study utilizes the ConvLSTM1D layer similar to the models mentioned in the study of Shi et al. (2015), Cantillo-Luna et al. (2023), and Shi et al. (2022) but it is different from their models as it is using two layers of ConvLSTM1D stacked over each other with a layer of RepeatVector embedded between them. Apart from these, the ConvLSTM1D layer utilized in our study uses a “swish” activation function with 32 units in the first layer and 16 units in the second layer. A dropout layer has been attached at the end, followed by a dense layer.

2.2 Proposed Model Framework

The proposed model takes the sequential input at the first layer. Then, there is a ConvLSTM1D layer with 32 units, a “swish” activation function and a kernel size equal to 12 followed by a RepeatVector layer with repetition factor two, which is placed after flattening the output tensor obtained from the previous ConvLSTM1D layer. After the RepeatVector layer, another ConvLSTM1D layer is placed with 16 units, a “swish” activation function, and a kernel size equal to 12. The “swish” activation function has been utilized for the design of the model since it has been observed that for DL models a “swish” activation function outperforms “relu” and other similar activation functions (Ramachandran, Zoph, and Le, 2017; Szandała, 2021). The output tensor received from this layer is again flattened and passed through a dropout layer with a 10% dropout rate, and ultimately, a fully connected layer is positioned at the final stage. The model is used with a RMSProp optimizer because, based on empirical evidence, RMSProp has demonstrated effectiveness and practicality as an optimization technique for DNN (Goodfellow, Bengio, and Courville, 2016). The illustration of the proposed model is presented in Figure 3. The proposed model framework depicts the flow of the experiment. The steps of the model framework are explained in Algorithm 1, and the corresponding steps are illustrated in Figure 4. Input data are taken as univariate data concerning time. As a part of data pre-processing, missing-value imputation is performed. Then, data standardization is performed with the help of Equation 13 where $\mu$ represents the average and $\sigma$ the standard deviation of the dataset

$$ d_{\mathrm{new}}=(d_{\mathrm{i}}-\mu )/\sigma , \; \forall \; d_{ \mathrm{i}} \in \boldsymbol{D}. $$

(13)

Figure 3

Schematic Diagram of the Proposed Model.

Algorithm 1

The Proposed sConvLSTM1D Model Framework.

Figure 4

Proposed sConvLSTM1D model working framework for sunspot-number time-series prediction.

After this, time-series data are generated using the given dataset and a fixed value of lookback is obtained after trial and error for an optimized value of the lag. Then, the dataset is bifurcated into training and test sets, along with further partitioning of the training dataset into training and validation sets.

The proposed framework has been utilized for analyzing the effectiveness of the proposed sConvLSTM1D model with the optimized hyper-parameters. Hyper-parameter optimization for the proposed sConvLSTM1D model has been carried out using trial and error. The detailed layout of the proposed framework is presented in Figure 4.

2.3 Model-Performance Measures

This study utilizes five performance metrics: RMSE, MAE, MAPE, $R^{2}$, and MASE. The selection of performance measures is based on a literature survey. The most frequently used performance metric has been taken for better comparison and evaluation of the performance and effectiveness of the proposed model. These performance metrics have been compared for the traditional models, state-of-the-art models, and the proposed sConvLSTM1D model.

These measures depict the deviation of the predicted result from the actual values from different aspects. Before utilizing these performance metrics, the concept of residual-error is of utmost importance, which is the difference between $y$ and $\hat{y}$, where $y$ is the actual value of SSN and $\hat{y}$ is the predicted value of SSN in the context of these experiments. The equations related to the RMSE are represented in Equation 14, where $m$ is the number of samples along with $y_{j}$ and $\widehat{y_{j}}$ are the $j$th actual and predicted values, respectively,

$$ RMSE=\sqrt{\frac{1}{m}\sum _{j=1}^{m}\left (y_{j}-\widehat{y_{j}} \right )^{2}}. $$

(14)

Equation 15 refers to the formula of Mean Absolute error, which is the simplest measure for performance evaluation. In this equation, “D” represents the complete dataset,

$$ MAE=\sum _{j=1}^{D}|\left (y_{j}-\widehat{y_{j}} \right )|. $$

(15)

Equation 16 defines the mean absolute scaled error, where $e_{i}$ signifies residual error, also known as forecast error, $n$ is the seasonal period, and $T$ corresponds to the number of data points contained within the time-series data and the summation part in the denominator is the mean absolute error,

$$ MASE= mean\left ( \frac{\left |e_{i}\right |}{\frac{1}{T-n}\sum _{t=n+1}^{T} \left |Y_{t}-Y_{t}\__{n} \right | } \right ). $$

(16)

MAPE is a data-independent performance measure used to calculate the fractional error. The related formula is presented in Equation 17, where $\epsilon$ is a small positive arbitrary number chosen to prevent undefined outcomes in cases where $y_{j}$ equals zero and other symbols have their meanings as mentioned above,

$$ MAPE=\frac{1}{m}\sum _{j=1}^{m-1} \frac{\left |\widehat{y_{j}}-y_{j}\right |}{max(\epsilon ,y_{j})}. $$

(17)

3 Data Analysis and Experimental Setup

3.1 Data

Data have been obtained from the SIDC, Royal Observatory, Belgium (SILSO World Data Center) website in four variants described in Table 1. The “Total Features” characteristic corresponds to the total number of features present in the raw data, which includes other related descriptions along with actual observations of sunspot numbers such as fractional year, standard deviation, definitive indicator, number of observations utilized to compute the value, etc., whereas “Feature for Analysis” represents the actual number of SSN utilized for the processing. Further, statistical descriptions of all four variants of the sunspot data are explained in Table 2.

Table 1 Descriptions of four variants of sunspot data (SILSO World Data Center).

Table 2 Statistical data description of four variants of sunspot data.

The additive-seasonal decomposition for all four dataset variants is depicted in Figure 5, where the original data are split into the three components: trend, seasonality, and noise. Although the decomposition has been performed on the complete dataset for all four variants, the seasonal decomposition depicted in Figure 5 is for a slice of data for a specific duration for visualization. From Figure 5, it can be deduced that the data follow the cyclic trend with seasonality within each cycle and some associated noise, except for the yearly data, which lack seasonality and noise. A study by Chattopadhyay, Jhajharia, and Chattopadhyay (2011) propounds that the SSN data are stationary concerning time owing to the sinusoidal decaying nature of ACF.

Figure 5

Additive decomposition of sunspot data with different frequencies.

3.2 Experimental Setup

This section presents the analysis of experiments performed utilizing five basic deep-learning models and the proposed model.

3.2.1 Data Pre-processing

Data pre-processing has been performed over each variant of the dataset to obtain cleaned data for time-series analysis. During the data-pre-processing phase, the feature corresponding to the sunspot data from each variant of the dataset is obtained separately and missing values are replaced with the average of previous and next observations. Then, data standardization is performed using z-score normalization. Time-series data have been created out of univariate data using a lag of 11 as it was found on the experimental basis that the data with a lag of 11 performs better than lags of 1, 6, 22, 66, and 132 using trial and error. It was also suggested by Chattopadhyay, Jhajharia, and Chattopadhyay (2011) in their study that the highest autocorrelation coefficient occurs at lags of 11, which was supported by our experimental results. Then, the dataset is trifurcated into training, validation, and a test set in the ratio of 81%, 9%, and 10%, respectively.

3.2.2 Hyper-parameter Setting of Traditional and Proposed Model

The proposed model has been contrasted with five DL models, namely RNN, CNN, GRU, LSTM, and BiLSTM, with their hyper-parameters described in Table 3 for evaluating the efficiency of the proposed model over basic DL models. The batch size is fixed at 66, and the “adam” optimizer has been utilized for all basic models. Patience is set to 20, and each model is trained for 250 epochs with early stopping criteria enabled based on validation loss, min_delta equal to 0, and loss being calculated over “mean squared error”.

Table 3 Hyper-parameter description of deep-learning models.

The software and hardware specifications utilized for carrying out all the experiments related to this study are as follows:

• Software Specification: All the analyses conducted in the study were performed on a Windows 11 Home Operating System in the Python programming language version 3.10.9, which is highly performing and open source. The environment has been created using jupyter version 3.5.3. Tensorflow has been utilized with version 2.11.0 for developing the models and performing the experiments.

• Hardware Specification: All experiments reported here used a PC with i3-1115G4 processor (11th Gen Intel^® Core™), 3.00 GHz CPU, and 8 GB of RAM.

4 Results and Analysis

The observations made while executing DL and the proposed models are presented here. First, the training of the different models was verified using the graphs of the training loss of the models concerning the number of epochs. The evaluation of the efficacy of different DL models on the monthly mean of total SSN was analyzed using the box plot presented in Figure 6, where each box contains 24 iterated results of specific performance metrics obtained from 24 independent iterations. The graph shows that the mean value of measures obtained for the proposed sConvLSTM1D model is better than others for all four measures utilized for evaluation.

Figure 6

Performance measures of traditional and proposed DL models over the monthly mean of total SSN.

The performances of GRU and BiLSTM are comparatively less efficient with a mean of RMSE of 19.75 and 19.71, respectively, as depicted in Figure 6b. The performance of DL models concerning the proposed model is depicted in Figure 7 for 13-month smoothed SSN data, which validates that the proposed model outperforms the traditional approaches with the second most efficient performance observed using CNN. The proposed model’s mean of RMSE reached 5.69, as illustrated in Figure 7b.

Figure 7

Performance measures of traditional and proposed deep-learning models over the 13-month smoothed SSN.

The plot of actual vs. predicted for different models on monthly mean SSN is depicted in Figure 8, illustrating the pattern-capturing capacity of all the models. The scatter plot depicts the relation between actual and predicted values along with the trend line, which is almost at a $45^{\circ}$ angle with the value of $R^{2}$, showing that the proposed model has a better $R^{2}$-value, which is nearer to unity. The spread of the data points along the linear trend line is less for the proposed model, characterizing its unbiased prediction nature. The scatter plot of actual vs. predicted for monthly average of SSN is depicted in Figure 9. The predicted values concerning the actual values are depicted in Figure 10, which shows almost coinciding lines representing efficient predictions for all models.

Figure 8

Actual vs. predicted values of monthly mean of total SSN.

Figure 9

Actual vs. predicted values of monthly mean of total SSN.

Figure 10

Actual vs. predicted values of 13-month smoothed SSN.

The representation of the predicted values corresponding to actual values for the test data slice of 13-month smoothed sunspot data is in Figure 11, which shows that the data points are highly aligned with the linear-trend line with a high value of $R^{2}$ illustrating less error for this variant of data among all four variants of the data. For this variant of SSN data, the value of $R^{2}$ is the highest for the proposed model among all six models. From Figure 12, it can be observed that despite the similar performance of the CNN model with the proposed model, the standard deviation of the proposed model is small, illustrating the consistency of the model, and the proposed model is more effective from other traditional models as per three performance metrics except for the CNN model. It is more suitable than the other traditional models based on RMSE, as depicted in Figure 12b. The better performance of CNN is due to the more significant number of samples available for training while performing analysis over daily SSN data. However, Wibawa et al. (2022) already observed that CNN is more suitable for time-series predictions. Scatter plots with the corresponding value of $R^{2}$ are illustrated in Figure 13 for the best predictions of each model out of 24 iterations, which shows that the proposed model has better $R^{2}$; that is 0.9377, while the CNN model has $R^{2}$-value equal to 0.9277, which is similar but lower than the proposed model. The GRU model has the worst performance due to being most scattered along the linear-trend line, representing high variance. Figure 14 depicts the trend capturing capacity of all models for daily SSN. The comparative view of all models based on the fourth variant of SSN data with yearly frequency over the four different performance metrics is depicted in Figure 15 where it can be observed that despite the smaller number of available samples for SSN data at yearly frequency, the proposed model is performing far better than all other traditional models. The mean of RMSE reached 14.55, as depicted in Figure 15b. The summarized version of the comparative performance measures over all four variants of SSN data is represented in Table 4. Apart from this, the error measures obtained in the literature have also been included in Table 5 for a comparative analysis of the efficiency of different models from the literature and the proposed model. Figure 16 and Fig 17 represent the actual vs. predicted line and scatter plots of all models respectively. The dotted line in Figure 18 is the forecast plot of SC25 utilizing the proposed model. The Figure 19 to Figure 26 presents the training and validation loss of all the models on all four variants of the SSN data.

Figure 11

Actual vs. predicted values of 13-month smoothed SSN.

Figure 12

Performance measures of traditional and proposed deep-learning models over the daily SSN.

Figure 13

Actual vs. predicted values of daily SSN.

Figure 14

Actual vs. predicted values of daily SSN.

Figure 15

Performance measures of traditional and proposed DL models over the yearly mean of total SSN.

Figure 16

Actual vs. predicted values of yearly mean of total SSN.

Figure 17

Actual vs. predicted values of yearly mean total SSN.

Table 4 Performance comparison of different models over different performance measures (Bold value represents the best performance in the respective section for each error measure).

Table 5 Comparative analysis of different state-of-the-art models with the proposed model (Bold value represents the best performance in the respective section for each error measure).

4.1 Non-parametric Statistical Test

Average ranks have been obtained by implementing the Friedman test over all four variants of data over every evaluation parameter. The Friedman test has been carried out in Table 4 with the ranking of different datasets over different performance measures as all are independent. The final results of the Friedman test, along with Holm’s adjustment and unadjusted p-value, can be seen in Table 6 (Demšar, 2006).

Table 6 Average Friedman rankings of the algorithms.

From Table 6, it is deduced that the proposed sConvLSTM1D model has the best ranking with 1.1875. The unadjusted p-value obtained for CNN is insufficient to disprove the null hypothesis. Hence, Holm’s is utilized to adjust the p-value. After applying Holm’s, the value reached 0.05, sufficient to disprove the null hypothesis, proving the proposed model’s effectiveness over the traditional models. The Friedman statistic exhibits a distribution that conforms to a ${\chi}^{2}$-distribution with five degrees of freedom, which is 61.1. The p-values, depicted in Table 6, are derived by employing post-facto methods on the outcomes of the Friedman procedure.

Based on the Friedman ranking of the proposed model (sConvLSTM1D) concerning other traditional deep-learning models depicted in Table 6 and comparative analysis of performance measures with state-of-the-art models illustrated in Table 5, it can be deduced that the sConvLSTM1D model has more accurate predictions.

4.2 Predition of Solar Cycle 25

As per the study of Pesnell and Schatten (2018), the anticipated peak of SC25 is 2025.2 ±1.5 year, while Pala and Atici (2019) predicted that the SC25 will reach its peak in 2023.2 ±1.1 year with a maximum of 167.3. A forecast of SC25 has also been made by Upton and Hathaway (2018) using the Advective Flux Transport model, noting the resemblance of the pattern of the SC25 with that of the SC24 and establishing it as the smallest cycle in the previous century. We partially agree with the statement as it is also a weak solar cycle, but in our study, it has been observed that SC25 will be slightly stronger than SC24. As per our iterated one-step-ahead forecast from the static model over the yearly mean of total SSN, it has been observed that the peak value of SSN in SC25 will be 140.8 in 2024, whereas the span of the present cycle will be up to the year 2030 with a minimum value of 16.1. Considering the minimum value of the yearly average of total SSN, which was 3.6 observed in 2019, this cycle will also be 11 years. Similarly, dynamo-based forecasting carried out by Labonville, Charbonneau, and Lemerle (2019) suggests that SC25 would be weaker than the preceding cycle with a short duration and a peak in the first half of 2025. Similar to our prediction, Li et al. (2018) also forecast that SC25 will be of higher intensity than SC24 in terms of amplitude and reach its peak in October 2024 with an anticipated value of 168.5 ±16.3. SC25 has also been predicted by Kakad, Kakad, and Ramesh (2017) based on Shannon Entropy estimates, suggesting a 63 ±11.3 peak for the smoothed SSN. Utilizing an optimized LSTM model, Zhu et al. (2023) predicted that SC25 will reach its peak in January 2025 with a maximum value of 213, while Han and Yin (2019) predicted that the maximum value of sunspots will reach approximately 228.8 ±40.5 at 2023.9 ±1.6 year. Another study on the prediction of SC25 by Zhu, Zhu, and He (2022) anticipates the peak of SSN in July 2025 ±two months with a SSN peak amplitude 143.6 ±8.7 using LSTM with $F_{10.7}$. According to the study of Okoh et al. (2018) using hybrid regression and a neural-network method for the SC25, the peak of SSN will be 122.1 ±18.2 in January 2025 ±six months. Another prediction comes from Du (2022) based on the rising rate of the solar cycle, which means the growth rate of solar activity in the early phase of the solar cycle. Du (2022) predicted that the SC25 will peak with an SSN value of 135.5 ±33.2 in December 2024. A summary version of the comparative analysis of the peak of SSN for SC25 is presented in Table 7.

Table 7 Comparison of peak of SSN for SC25 and its corresponding time.

5 Conclusions

In this work, an attempt is made to improve the prediction of SC25 by reducing the error while testing the model using a novel stacked model made up of ConvLSTM1D layers with an embedded layer of a “repeat vector” within it, followed by dropout and a fully connected layer. The model’s effectiveness is validated on the four variants of the SSN data obtained from the SILSO, Royal Observatory, Belgium, with the four different frequencies of sampling of the SSN on the solar surface and different statistical characteristics. Friedman ranking has been carried out as a non-parametric statistical test to assess the effectiveness of the proposed sConvLSTM1D model with five traditional models namely LSTM, GRU, CNN, RNN, and BiLSTM, which resulted in the rejection of the null hypothesis for all other models suggesting the better performance of the proposed model. This ensures that the proposed model composed of stacked ConvLSTM1D layers provides more accurate predictions than the traditional deep-learning models. After validating the efficacy of the model, the forecast for the ongoing SC25 has been carried out with the prediction of the peak value of SSN to be reached as 140.8 and 2024 as the year in which the peak is achieved. Apart from this comparative analysis of the peak and timing for SC25, a literature search has been carried out to find the differences and resemblances in the predictions. Observing the forecast, it is also deduced that SC25 is a weak cycle based on the temporal duration and amplitude, and it will last up to 2030. The future scope for improving the SSN prediction model includes improvement to overcome the problem of residuals present in it. Furthermore, the forecasting model can also be adjusted with different orientations and numbers of layers for better performance and to reduce the error. The decomposition of the dataset can also be utilized for separate training and prediction of different components of the dataset.

Appendix: Loss Plots of Different Models for Different Datasets

Figure 18

Forecast of SC25 based on the proposed stacked ConvLSTM1D model over yearly mean of sunspot number.

Figure 19

Training loss of all models on the yearly mean of SSN.

Figure 20

Validation loss of all models on the yearly mean of SSN.

Figure 21

Training loss of all models on the monthly mean of total SSN.

Figure 22

Validation loss of all models on the monthly mean of total SSN.

Figure 23

Training loss of all models on the 13-month smooth of total SSN.

Figure 24

Validation loss of all models on the 13-month smooth of total SSN.

Figure 25

Training loss of all models on the daily SSN.

Figure 26

Validation loss of all models on the daily SSN.