Reconstruction of the North–South Solar Asymmetry with a Kuramoto Model

Abstract

This paper applies a Kuramoto model of coupled oscillators to investigate the north–south (N–S) solar asymmetry and properties of meridional circulation. We focus our study on the asymmetry of the 11-year phase, which is slight but persistent: only two changes of sign (around 1928 and 1968) are observed in the past century. We present a model of two non-linear coupled oscillators that links the hemispheric phase asymmetry of sunspots with the asymmetry of the meridional flow. We use a Kuramoto model with evolving frequencies and constant symmetric coupling to show how asymmetry in meridional circulation could produce a persistent phase lead of one solar hemisphere over the other. We associate the natural frequencies of the two oscillators with the velocities of the meridional flow cells in the northern and southern hemispheres. We assume the respective circulations to be independent and estimate the value of the relevant cross-equatorial coupling by the coupling coefficient in the Kuramoto model. We find that a persistent N–S asymmetry of sunspots and the change of the leading hemisphere could indeed both be the result of the evolving frequencies of meridional circulation; the necessary asymmetry of the meridional flow may be small; and the cross-equatorial coupling has an intermediate range value. Possible applications of these results in solar dynamo models are discussed.

1 Introduction

The dynamo theory faces the challenge of explaining the existence and observed evolution of the solar magnetic field (Charbonneau 2014). One of the peculiar properties of the solar magnetic field is the observed hemispheric asymmetry, which does not directly follow from the solar dynamo equations. It is believed to be closely related to the meridional circulation, which is also responsible for the long-term changes of the solar cycle (Lopes et al. 2014; Hathaway 2015).

Recent research in the solar north–south (N–S) asymmetry may be divided into two main directions: studies of the amplitude asymmetry, and studies of the phase asymmetry (Hathaway 2015). Different aspects of the amplitude of the N–S asymmetry are widely investigated (Newton and Milsom 1955; Vizoso and Ballester 1990; Carbonell, Oliver, and Ballester 1993; Knaack, Stenflo, and Berdyugina 2004; Ballester, Oliver, and Carbonell 2005; Temmer et al. 2006; Carbonell et al. 2007, Badalyan, Obridko, and Sykora 2008; Norton and Gallagher 2010; Sýkora and Rybák 2010; Badalyan 2011; Badalyan and Obridko 2011; Muraközy and Ludmány 2012; Svalgaard and Kamide 2013; Zou et al. 2014; Lopes and Silva 2015; Nagovitsyn and Kuleshova 2015), and first attempts are made to understand the role of asymmetry in the flux transport dynamo models (Belucz and Dikpati 2013; Shetye, Tripathi, and Dikpati 2015). Three ranges of periodicities greater than 1 year are found in the amplitude asymmetry: short periods of about 1 – 4 years (e.g. Badalyan, Obridko, and Sykora 2008; Knaack, Stenflo, and Berdyugina 2004, Badalyan and Obridko 2011), a medium range of about one to three solar cycles (e.g. Carbonell, Oliver, and Ballester 1993), and long-term periodicities of about 100 years (Li, Gao, and Zhan 2009). It is found that the short- and mid-term periodicities in the amplitude asymmetry indices are similar but not exactly equal to that of the initial series in both hemispheres (Carbonell, Oliver, and Ballester 1993; Knaack, Stenflo, and Berdyugina 2004; Badalyan, Obridko, and Sykora 2008; Sýkora and Rybák 2010; Badalyan and Obridko 2011; Lopes and Silva 2015). The characteristic time of the long-term variation is difficult to establish because the data sets are short, but the estimated values are similar to the length of the Gleissberg cycle (Li, Gao, and Zhan 2009; Muraközy and Ludmány 2012, Zou et al. 2014).

The N–S asymmetry changes its sign during each solar cycle (e.g. Temmer et al. 2006). The lead of one hemisphere is replaced by the lead of the other during one solar cycle. For example, during the rise of Solar Cycle 24, the northern hemisphere was dominating and the excess of the southern hemisphere is observed during the declining phase (Chowdhury, Choudhary, and Gosain 2013). A similar change of the leading hemisphere was detected for Solar Cycles 12 – 15, 21 – 23, and the opposite change in Cycles 17 – 18 (see Temmer et al. 2006; Hathaway 2015 as a review). A close look at the N–S asymmetry reveals that although the two hemispheres are “generally in phase” (Hathaway and Wilson 2004), there is a slight phase difference between them that may reach 1.5 years in some solar cycles. In the past decade the evolution of the hemispheric phase difference was investigated (Zolotova and Ponyavin, 2006, 2007; Donner and Thiel 2007; Zolotova et al., 2009, 2010; Deng et al., 2011, 2013; McIntosh et al. 2013). Muraközy and Ludmány (2012) find no significant relation between the amplitude and the phase of the hemispheric asymmetry, and these two measures are now considered as independent characteristics.

In the present article we follow Donner and Thiel (2007) and characterize the N–S asymmetry by the hemispheric phase difference of the 11-year signal of daily sunspot areas. Although Donner and Thiel (2007) considered a period of 10.75 years, they checked that the evolution of the phase difference was stable in a wide range of periods associated with the length of the solar cycle. Statistical investigations reveal no significant correlation between the asymmetry and the length of the solar cycle (Carbonell, Oliver, and Ballester 1993; Norton and Gallagher 2010).

The persistence of phase-leading in one of the Sun’s hemispheres over time spans on the order of four solar cycles has been shown (Zolotova et al. 2010; McIntosh et al. 2013; Norton, Charbonneau, and Passos 2014). During the past century, for which reliable daily data are available, there are only two changes in the leading hemisphere (near 1928 and 1968). These dates are close to the moment of the N–S asymmetry change obtained by Li, Gao, and Zhan (2009) and Deng et al. (2013). This persistence argues against a stochastic phenomenon (Zolotova et al. 2010; Norton, Charbonneau, and Passos 2014). Zolotova et al. (2010) pushed their analysis back by some three centuries and suggested that these phase reversals in leading hemisphere are quasi-periodic, with a period close to eight solar cycles, i.e. that of the Gleissberg cycle also observed in the long-term evolution of the amplitude asymmetry (Li, Gao, and Zhan 2009; Muraközy and Ludmány 2012; Zou et al. 2014). Lopes et al. (2014) showed that a combination of low-order dynamo models (LODM) with inverse methods has significant potential to help in understanding the N–S asymmetry and its origin. Several authors have suggested that the origin of the N–S asymmetry of sunspots, including the persistent lead of one hemisphere, may be related to the asymmetry of the meridional flow (McIntosh et al. 2013; Norton, Charbonneau, and Passos 2014; Virtanen and Mursula 2014).

Meridional circulation is believed to be a large-scale plasma flow whose surface component transports the residual field toward the poles; this contributes to the polarity reversals. Inversions of heliospheric measurements have indicated that there are at least two cells overlying each other in each hemisphere. The deep-seated equatorward component of the meridional circulation is responsible for the migration of dynamo waves over the course of a solar dynamo cycle (Passos, Charbonneau, and Miesch 2015). Both poleward and equatorward flows show significant hemispheric asymmetry (Rightmire-Upton, Hathaway, and Kosak 2012, Zhao et al. 2013), which is believed to be related to the N–S asymmetry of the solar magnetic field and sunspot distribution (Norton, Charbonneau, and Passos 2014). Recent research in the flux transport dynamo models is focused on reproducing irregularities of solar dynamics such as the change of the solar cycle (Lopes et al. 2014) and the N–S asymmetry (Belucz and Dikpati 2013; Shetye, Tripathi, and Dikpati 2015). An important parameter essential for this modeling is the cross-equatorial coupling, which connects solar hemispheres (Norton and Gallagher 2010; Svalgaard and Kamide 2013). In the present article we apply the Kuramoto model and reconstruct the optimum value of the cross-equatorial coupling from the evolution of the phase difference between solar hemispheres.

The Kuramoto model is usually applied for direct modeling of synchronization phenomena in systems with a large number of oscillators (see Strogatz 2000, for a review). The model depends on the natural frequencies of the oscillators, which are usually chosen to be constant or randomly distributed (e.g. Hong and Strogatz 2011). Partial or total synchronization is studied depending on a coupling coefficient, which is initially considered to contribute symmetrically to all equations. Recent developments of the Kuramoto model led to certain modifications of the classical model, including non-constant frequencies (Hong and Strogatz 2011), for instance, stochastic components in the coupling coefficients, stochastic components in the equations themselves, couplings that evolve with time (e.g. Leander, Lenhart, and Protopopescu 2015), or low-dimensional (rather than high-dimensional) systems with constant parameters (e.g. Maistrenko et al. 2010; Kuznetsov and Sedova 2014).

Blanter et al. (2016) considered a model of two coupled oscillators with constant natural frequencies and evolving coupling to reproduce the evolution of the solar cycle period. In the present article, we use the same model with two evolving frequencies and constant symmetric cross-equatorial coupling in an attempt to reproduce changes in the leading hemisphere. We associate the natural frequencies of the oscillators with the velocities of the meridional flow cells in the northern and southern solar hemispheres. Following conclusions of previous studies (e.g. Temmer et al. 2006; Norton and Gallagher 2010), we assume the natural frequencies of the two cells to be independent, and the circulation in the two hemispheres to be connected by a cross-equatorial coupling.

Blanter et al. (2016) used an inversion to reconstruct the evolution of the phases of the poloidal and toroidal components of the solar magnetic field. In the present article we also consider an inverse problem; we attempt to estimate the hemispheric asymmetry of the meridional flow that is required to reproduce the observed phase evolution of sunspot areas in the northern and southern hemispheres. The inverse approach has recently become a major tool that allows one to reconstruct properties of the meridional circulation through magnetic field observations and dynamo modeling (e.g. Zhao et al. 2013; Lopes et al. 2014; Passos, Charbonneau, and Miesch 2015).

In Section 2 we present the data (sunspot areas) and calculate the phases of the 11-year solar cycles in the northern and southern hemispheres, respectively, over the time span of 1875 – 2015. The evolution of the phase difference and instantaneous solar cycle period is determined through the evolution of these hemispheric phases. In Section 3 we solve an inverse problem in the frame of the Kuramoto model with two oscillators. Natural frequencies of two coupled oscillators are estimated from the hemispheric phases determined in Section 2. We estimate the asymmetry of reconstructed natural frequencies and the value of the optimum coupling relevant to the model with two independent cells. Simple model examples are used for illustration and comparison. Finally, we discuss the results and draw some conclusions in Section 4.

2 Hemispheric Phases of Sunspot Areas

In the present article, we consider the N–S asymmetry of sunspot areas in terms of the phase difference and investigate how its long-term evolution may be reconstructed by a Kuramoto model with two non-linear coupled oscillators.

2.1 Data

We consider the daily sunspot areas from the Greenwich–USAF/NOAA sunspot data from 1874 to 2015 for the northern (NH) and southern (SH) solar hemispheres, which are available through http://solarscience.msfc.nasa.gov/greenwch/daily_area.txt . A 1-year sliding averaging is performed before applying any further analysis to avoid contamination of the 11-year phase by high-frequency components. We also considered 2- and 4-year sliding windows, but the resulting phase is close to the 1-year sliding averaging (see Appendix).

2.2 Change of Leading Hemisphere

We consider the evolution of the phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ of the 11 yr signal in the daily Greenwich–USAF/NOAA sunspot total areas relevant in the northern and southern hemispheres, respectively. The frequency of the Fourier transform is taken to be $\Omega = 2\pi/ \Theta$, with $\Theta= 11~\mbox{yr}$, which is the approximate period of the solar Schwabe cycle, and phases are estimated in an 11 yr long centered sliding window $\Theta$ in the following way:

$$\Phi_{f} ( t ) = - \arctan \biggl( \frac{B_{f}}{A_{f}} \biggr), $$

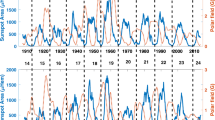
where

$$A_{f} ( t ) + iB_{f} ( t ) = \int_{t - \Theta /2}^{t + \Theta/2} f ( \tau ) \bigl( \cos ( \Omega\tau ) + i\sin ( \Omega\tau ) \bigr)\,\mathrm{d}\tau, $$

$f$ being a given function integrated over time $\tau$. Time $t$ is counted from 1850. The phases of both hemispheres drift by some 3 radians between 1900 and 2000 (Figure 1a), implying that the Schwabe cycle does not have constant 11 yr periodicity. This simple calculation applied to the Greenwich–USAF/NOAA time series of sunspot areas immediately confirms the two changes in the leading hemisphere, one in 1927 and the other in 1964 (Figure 1b). The change in phase difference between the two hemispheres that took place in 1964 during Solar Cycle 20 is particularly strong (Figures 1b). Altogether, the hemispheric phase difference $\Delta\Phi= \Phi_{\mathrm{NH}} - \Phi_{\mathrm{SH}}$ ranges over an amplitude over about 1 radian. Our aim in this article is to reproduce the evolution of the hemispheric phase difference with a Kuramoto model through the solution of an inverse problem. As seen in more detail in the following section, the method takes variations in the main ${\sim}\,11~\mbox{yr}$ period fully into account.

Figure 1

Evolution of the 11 yr phases (a) and their difference (b) for sunspot areas in the northern (blue) and southern (red) hemispheres.

2.3 Instantaneous Period of the Solar Cycle

The length of the solar cycle period may be estimated from the evolution of hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$. Figure 1a shows a clear common trend in the evolution of the two hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$. This trend originates in the variability of the length of the solar cycle, which is different from the 11 yr period that corresponds to the standard frequency $\Omega$. The instant frequencies of the solar cycle in both hemispheres may be retrieved from the evolution of phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$:

$$ \begin{aligned} \nu_{\mathrm{NH}} ( t ) &= \Omega+ \dot{ \Phi}_{\mathrm{NH}} (t), \\ \nu_{\mathrm{SH}} ( t ) &= \Omega+ \dot{\Phi}_{\mathrm{SH}} (t). \end{aligned} $$

(1)

In order to reduce the daily variability of the instantaneous frequencies $\nu_{\mathrm{NH}} ( t )$ and $\nu_{\mathrm{SH}} ( t )$, the derivatives $\dot{\Phi}_{\mathrm{NH}} ( t )$ and $\dot{\Phi}_{\mathrm{SH}} ( t )$ of the phases should be averaged over a centered interval $T$. The evolution of instantaneous frequencies $\nu_{\mathrm{NH}} ( t )$ and $\nu _{\mathrm{SH}} ( t )$, for $T = \Theta= 11~\mbox{yr}$ is shown in Figure 2a; it is quite similar for both hemispheres, except in the 1960s. Figure 2b shows the evolution of the combined instantaneous period

$$ P ( t ) = \frac{4\pi}{ \langle\nu_{\mathrm{NH}} \rangle _{T} + \langle\nu_{\mathrm{SH}} \rangle_{T}}, $$

(2)

which is similar to the evolution of the instantaneous period of sunspot activity used in Blanter et al. (2016), and the same obtained through a cubic spline interpolation of the lengths of the actual solar cycles (in that case, the length of individual solar cycles is determined as the distance between two consecutive minima; see Blanter et al. 2016, for details of the method). The difference between the two instantaneous period curves of Figure 2b in the beginning (1880s) is due to an edge effect of the interpolation method (Blanter et al. 2016).

Figure 2

Solar cycle evolution. (a) Evolution of the hemispheric instant frequencies for $T = 11~\mbox{yr}$ of sunspot areas in the northern (blue) and southern (red) hemispheres. The dashed line indicates the frequency $\Omega$ that corresponds to the 11 yr period. (b) Evolution of the instantaneous period of sunspot activity estimated as the combined instantaneous period of both hemispheres (blue) and as a spline interpolation of the distances between two consecutive minima of individual solar cycles (red).

3 Kuramoto Model and Inverse Problem Solution

In this section we solve an inverse problem in the frame of a Kuramoto model with two oscillators of the form:

$$ \begin{aligned} \dot{\theta}_{1} ( t ) &= \omega_{1} (t) + \frac{\kappa}{2}\sin \bigl( \theta_{2}(t) - \theta_{1}(t) \bigr), \\ \dot{\theta}_{2} ( t ) &= \omega_{2} ( t ) + \frac{\kappa}{2}\sin \bigl(\theta_{1}(t) - \theta_{2} (t) \bigr). \end{aligned} $$

(3)

Parameters of the model are estimated from the hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ computed above. In order to reduce the transition interval, we take initial conditions to be equal to the first values of hemispheric phases $\theta_{1} ( 0 ) = \Phi_{\mathrm{NH}} ( t_{0} )$; $\theta_{2} ( 0 ) = \Phi_{\mathrm{SH}} ( t_{0} )$. Two synthetic series $X_{1} ( t ) = \sin ( \theta_{1} ( t ) )$ and $X_{2} ( t ) = \sin ( \theta_{2} ( t ) )$ are then generated by a Kuramoto model with these parameters. Phases $\varphi_{1} ( t )$ and $\varphi_{2} ( t )$ of the 11 yr signal in the synthetic series $X_{1} ( t )$ and $X_{2} ( t )$ are finally compared with hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$. The distance between the reconstructed and the original phase differences is a measure of the quality of the Kuramoto model reconstruction (KMR). Another measure of a successful reconstruction is the distance between the reconstructed and original combined instantaneous periods.

3.1 Choice of Parameters

In the Kuramoto model given by Equation (3), there are three free parameters: the frequencies $\omega_{1}$, $\omega_{2}$, and the coupling $\kappa$. Blanter et al. (2014, 2016) considered the frequencies $\omega_{1}$ and $\omega_{2}$ to be constant and symmetrical with respect to the solar cycle frequency $\Omega$ and the coupling $\kappa= \kappa ( t )$ (symmetrical or non-symmetrical) to evolve with time, derived from the evolution of the phase difference and instantaneous period. In the present article, we reconstruct the Kuramoto parameters from the evolution of hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$. Thus, we consider a model with non-zero constant coupling $\kappa$ and evolving frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ based on Equation (3).

In order to estimate frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$, we replace phases $\theta_{1}$ and $\theta_{2}$ in Equation (3) by the observed phases $\Phi _{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ shown in Figure 1. The frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ are expressed through phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ and their difference $\Delta\Phi ( t ) = \Phi_{\mathrm{NH}} ( t ) - \Phi_{\mathrm{SH}} ( t )$ as follows:

$$ \left \{ \textstyle\begin{array}{l} \omega_{1} (t) = \Omega+\dot{\Phi}_{\mathrm{NH}} ( t ) + \frac{\kappa}{2}\sin ( \Delta\Phi(t)), \\ \omega_{2} (t) = \Omega+ \dot{\Phi}_{\mathrm{SH}} ( t ) -\frac{\kappa}{2}\sin ( \Delta\Phi(t)). \end{array}\displaystyle \right . $$

(4)

The coupling coefficient $\kappa$ may be arbitrary, but its value should not be too close to zero to avoid instability of the reconstruction with respect to the initial conditions (see Section 3.7). We show later (Section 3.7) that the quality of the reconstruction does not depend on the coupling $\kappa$.

Hemispheric phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ are estimated with respect to oscillations with frequency $\Omega$, which is also a hidden parameter of our inverse problem. We assume $\Omega= 2\pi/ \Theta$, with $\Theta= 11~\mbox{yr}$, and we show in Section 3.7 that the quality of the reconstruction is stable with respect to $\Omega$ when the relevant period $\Theta= 2\pi/ \Omega$ is close enough to 11 years.

3.2 Synthetic Series and Their Phases

We introduce the frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ determined by Equation (4) into Equation (3) to compute the phases $\theta_{1} ( t )$ and $\theta_{2} ( t )$, and then determine the two synthetic series $X_{1} ( t ) = \sin ( \theta_{1} ( t ) )$ and $X_{2} ( t ) = \sin ( \theta_{2} ( t ) )$.

Phases $\varphi_{1} ( t )$ and $\varphi_{2} ( t )$ of the 11 yr Fourier components estimated from series $X_{1} ( t )$ and $X_{2} ( t )$ as described in Section 2.2 are considered as the reconstruction of phases $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$, respectively. The evolution of the phase difference $\Delta\varphi ( t ) = \varphi_{1} ( t ) - \varphi_{2} ( t )$ and the combined instantaneous period

$$ p ( t ) = \frac{2\pi}{\Omega+ \langle\frac{ ( \dot{\varphi}_{1} + \dot{\varphi}_{2} )}{2} \rangle_{T}} $$

(5)

are compared with $\Delta\Phi ( t )$ and $P ( t )$, respectively.

3.3 Quality of the Kuramoto Model Reconstruction

In order to estimate the closeness of an observed series $F ( t )$ to its Kuramoto reconstruction $f ( t )$ obtained through a given Kuramoto model, we calculate the relative residual $r_{0}$ by normalizing the $L_{2}$-difference between the two series to the variance of the observed series (the mean value $\langle F \rangle$ and integrals are taken over the whole time span of the reconstructed series):

$$ r_{0} ( f ) = \frac{\int ( F ( t ) - f (t))^{2}\,\mathrm{d}t}{\int ( F ( t ) - \langle F \rangle )^{2}\,\mathrm{d}t}. $$

(6)

The relative residual relevant to the representation of $F ( t )$ by its mean value $f ( t ) = \langle F \rangle$ is $r_{0} ( f ) = 1$, therefore the smaller $r_{0} < 1$, the more successful the reconstruction.

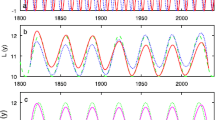
Figure 3 shows how the phase evolution and change of leading hemisphere (Figure 3a) are reproduced in the Kuramoto model with parameters $\Omega= 2\pi/ 11~\mbox{yr}$ and $\kappa= 0.2$ (Figure 3b). The phase difference $\Delta \Phi ( t )$ is successfully reconstructed by the phase difference $\Delta\varphi ( t )$ with a relative residual $r_{0} ( \Delta\varphi ) = 0.11$ (Figure 3c). The combined instantaneous period $P ( t )$ is even more successfully reconstructed by the combined instantaneous period $p ( t )$ given by Equation (5) with a relative residual $r_{0} ( p ) = 0.06$ (Figure 3d).

Figure 3

Solar cycle evolution. Left: Evolution of the hemispheric phases for sunspot areas (a) and corresponding KMR (b) for the northern (blue) and southern (green) hemispheres. Right: Evolution of phase difference (c) and combined instantaneous period (d) for sunspot areas (blue) and corresponding KMR (red). The base frequency $\Omega$ corresponds to the 11 yr period. Coupling is $\kappa= 0.2$, $T = 11~\mbox{yr}$.

3.4 KMR Frequencies and Coupling

The reconstruction of natural frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ depends on the coupling parameter $\kappa$. Stronger coupling leads to higher values of the long-term frequency variations $\omega_{i} ( t )$ and suppresses their short-term oscillations (compare examples relevant to $\kappa= 0.2$, 1, and 5 in Figure 4a, b, and c). When the coupling is strong enough, the change in leading hemisphere is clearly reflected in the evolution of frequencies (Figure 4c). We note that when the coupling is weak, the frequencies in both hemispheres have the same sign (Figures 4a, b). Negative frequencies may be interpreted as rotation in the opposite direction.

Figure 4

Frequencies in the Kuramoto model. Evolution of frequencies $\omega_{1}(t)$ (blue) and $\omega_{2}(t)$ (red) in the Kuramoto model with $\Omega= 2\pi/ 11~\mbox{yr}$ and coupling $\kappa= 0.2$ (a), $\kappa= 1$ (b), and $\kappa = 5$ (c). The dashed line indicates the base frequency $\Omega$. (d) Evolution of the period length relevant to the mean frequency $\omega$ (red) and combined instantaneous period $P$ (blue) estimated for $T = \Theta= 11~\mbox{yr}$.

The mean frequency $\omega ( t ) = ( \omega_{1} ( t ) + \omega_{2} ( t ) ) / 2$ is determined by phases $\Phi_{\mathrm{NH}} ( t )$, $\Phi_{\mathrm{SH}} ( t )$ according to Equation (4), thus

$$ \omega ( t ) = \Omega+ \frac{\dot{\Phi}_{\mathrm{NH}} ( t ) + \dot{\Phi}_{\mathrm{SH}} ( t )}{2}. $$

(7)

It does not depend on coupling and represents the evolution of the combined instantaneous frequency $\nu ( t ) = ( \nu_{\mathrm{NH}} ( t ) + \nu_{\mathrm{SH}} ( t ) ) / 2$ (see Equation (1)). We note that the equality $\omega ( t ) = \nu ( t )$ appears as a consequence of the symmetrical coupling in Equation (4).

Figure 4d compares the evolution of $2\pi/ \omega$ with the combined instantaneous period $P$ estimated by Equation (2) for $T = \Theta= 11~\mbox{yr}$. The latter gives a smoother version of the former.

The evolution of natural frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ in the case of weak coupling follows the evolution of the solar cycle instantaneous frequencies $\nu_{\mathrm{NH}} ( t )$ and $\nu_{\mathrm{SH}} ( t )$ in the northern and southern hemispheres, respectively. In the case of strong coupling, the evolution of frequencies $\omega_{i} ( t )$ follows the evolution of the phase difference $\Delta\Phi$. These properties of frequencies $\omega _{i} ( t )$ directly follow from Equation (4): in the case of weak coupling, we can neglect the last term in Equation (4) and the frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ are determined by the solar cycle hemispheric frequencies $\nu_{\mathrm{NH}} ( t )$ and $\nu_{\mathrm{SH}} ( t )$ according to Equation (1):

$$\omega_{1} ( t ) \sim\nu_{\mathrm{NH}} ( t ), \quad \quad \omega _{2} ( t ) \sim\nu_{\mathrm{SH}} ( t ). $$

In the case of strong coupling, the last term of Equation (4) determines the evolution of frequencies:

$$\omega_{1} ( t ) \sim\frac{\kappa}{2}\sin \bigl( \Delta\Phi ( t ) \bigr),\quad \quad \omega_{2} ( t ) \sim- \frac{\kappa}{ 2}\sin \bigl( \Delta\Phi ( t ) \bigr). $$

3.5 Asymmetry and Coupling

Figures 4a – c show that the difference between hemispheric natural frequencies $\omega_{i} ( t )$ increases with coupling. We introduce a measure of asymmetry,

$$ A = \frac{\int ( \omega_{1} ( t ) - \omega_{2} ( t ) )^{2}\,\mathrm{d}t}{\int ( \omega_{1} ( t ) + \omega_{2} ( t ) )^{2}\,\mathrm{d}t}. $$

(8)

Figure 5a shows that the quality of the KMR does not depend on coupling when the initial conditions in Equation (3) correspond to those of the data. However, when the initial conditions are remote from the first data point, we obtain larger relative residuals because of the weak convergence in the domain of weak coupling. The asymmetry grows with coupling (Figure 5b), and the absolute value of the correlation between natural frequencies $\omega_{i} ( t )$ and the phase difference $\Delta \Phi$ increases (Figure 5c). In contrast, the correlations of the periods $p_{i} = 2\pi/ \omega_{i}$ with the corresponding instantaneous periods, $P_{\mathrm{NH}} = 2\pi/ \nu_{\mathrm{NH}}$ and $P_{\mathrm{SH}} = 2\pi/ \nu_{\mathrm{SH}}$ respectively, decrease and tend to zero (horizontal dashed line) for strong coupling (Figure 5d).

Figure 5

KMR features depending on coupling. (a) Quality of the reconstruction of the phase difference (blue) and combined instantaneous period (red). Initial conditions are $\theta_{i} ( 0 ) = \Phi_{i} ( t_{0} )$ (solid line) and $\theta_{i} (0) = 0$ (dotted line). (b) Hemispheric asymmetry $A$; (c) correlation between frequencies $\omega$ in the NH (blue) and SH (red) and $\Delta\Phi$; (d) correlation between the inverse frequencies $2\pi/ \omega_{i}$ and the combined instantaneous period of the solar cycle $P$. Only the quality of the reconstruction (a) depends significantly on the initial conditions. The horizontal dashed lines (c, d) indicate the zero level.

3.6 Optimum Coupling

In the case of weak coupling, both natural frequencies $\omega_{i} ( t )$ correlate with the solar cycle combined instantaneous frequency $\nu ( t ) = 2\pi/ P ( t )$ (Figure 5d). This implies a strong positive correlation $C ( \omega_{1},\omega_{2} )$ between the two hemispheric frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ (Figure 6). For high values of coupling, $\omega_{1} ( t )$ correlates and $\omega_{2} ( t )$ anticorrelates with the phase difference $\Delta\Phi ( t )$ (Figure 5c). This implies a highly negative correlation $C ( \omega_{1},\omega_{2} )$, as seen in Figure 6. When $\kappa= \kappa_{0} = 0.55$, the correlation between natural frequencies is zero, frequencies are orthogonal, and the connection between the northern and southern hemispheres is fairly well represented by the coupling in Equation (3). We call the coupling $\kappa_{0}$ corresponding to the orthogonal frequencies $\omega_{1} ( t )$ and $\omega_{2} ( t )$ the “optimum coupling” of the reconstruction (see also Appendix).

Figure 6

Correlation between hemispheric frequencies $C(\omega_{1},\omega_{2})$ depending on coupling $\kappa$. Orthogonal frequencies correspond to the zero correlation (horizontal dotted line) and a value of the coupling equal to 0.55 (vertical dashed line).

3.7 Variability of the Reconstruction Quality

Figure 5a shows that when coupling is weak, the quality of the KMR of the phase difference depends on initial conditions. The best quality is achieved when $\theta ( 0 ) = \Delta\Phi ( t_{0} )$. In contrast to $r_{0} ( \Delta\varphi )$, the quality of the reconstruction of the mean period $r_{0} ( p )$ and asymmetry $A$ do not depend on initial conditions. As already pointed out, the influence of initial conditions increases as couplings become weaker.

The instantaneous frequencies $\Phi_{\mathrm{NH}} ( t )$ and $\Phi_{\mathrm{SH}} ( t )$ are retrieved when the base frequency $\Omega$ of the solar cycle is taken to be 11 years (see Section 2). Consequently, the reconstruction qualities $r_{0} ( \Delta\varphi )$ and $r_{0} ( p )$ may depend on $\Theta= 2\pi/ \Omega$. We note that our estimates of instantaneous frequencies, based on the derivatives of phases in Equation (1), are correct only for $\Theta$ chosen close to the mean value of the solar cycle period. When $\Theta$ is between 10 and 12 years, the relative residuals remain small: $r_{0} ( \Delta\varphi ) = 0.12 \pm0.03$ and $r_{0} ( p ) = 0.1 \pm0.05$. These relative residuals are similar to the typical values obtained in their Kuramoto reconstructions by Blanter et al. (2014, 2016). Both relative residuals reach their minima when $\Theta= 2\pi/ \Omega= 10.75~\mbox{yr}$, which is the mean value of the solar cycle in the time span under consideration (1875 – 2015).

3.8 Variability of Optimum Coupling and Asymmetry: Two Simulations

In order to interpret the variability of optimum coupling $\kappa_{0}$ and asymmetry $A$, we now perform two direct simulations of the Kuramoto model given by Equation (3). We take natural frequencies $\omega _{1} ( t ) = \omega_{m1} ( t )$ and $\omega_{2} ( t ) = \omega_{m2} ( t )$ that oscillate around $\Omega_{m} = 2\pi/ 11~\mbox{yr}$:

$$ \begin{aligned} \omega_{m1} ( t ) &= \Omega_{m} + a\sin \biggl(\frac{\Omega_{m}}{8}t - \frac{\pi}{4} \biggr) + b\sin \biggl( \Omega_{m}t -\frac{\pi}{2} \biggr), \\ \omega_{m2} ( t ) &= \Omega_{m} + a\sin \biggl( \frac{\Omega_{m}}{8}t + \frac{\pi}{4} \biggr) + b\sin ( \Omega_{m}t ). \end{aligned} $$

(9)

The first oscillatory term reflects the Gleissberg cycle and the second term corresponds to the Schwabe cycle. Both cycles are to be expected in the evolution of the meridional flow (Jiang et al. 2014; Hathaway and Upton 2014). The coupling is taken to be $\kappa= \kappa_{m} = 0.48$, and two series $X_{m1} ( t ) = \sin ( \theta_{m1} ( t ) )$ and $X_{m2} ( t ) = \sin ( \theta_{m2} ( t ) )$ are simulated by Equation (3) with frequencies from Equation (9). Figure 7 shows the evolution of the phase difference $\theta_{m} ( t ) = \theta_{m1} ( t ) - \theta_{m2} ( t )$ in comparison with the solar phase difference $\Delta\Phi$ for two pairs of parameters $( a,b )$: $(0.15,0.1)$ and $( 0.1,0.05 )$. Equation (8) determines the relevant values of asymmetry $A = A_{m}$, which are equal to 0.023 and 0.01, respectively.

Figure 7

Evolution of the phase difference between solar hemispheres $\Delta\Phi$ (red) in comparison with the phase difference $\theta_{m}$ of two Kuramoto model simulations with parameters $a=0.15$, $b=0.1$, (blue) and $a=0.1$, $b=0.05$ (green).

Now for any value of the coupling parameter $\kappa$ and the base frequency $\Omega$, we can perform an inversion using the two phase series $\theta_{m1} ( t )$ and $\theta_{m2} ( t )$ to reconstruct natural frequencies $\omega_{i} ( t )$ through Equation (4) and the asymmetry $A$ through Equation (8). The optimum coupling $\kappa_{0}$ is estimated according to Section 3.6. The optimum coupling $\kappa_{0}$ and the relevant asymmetry $A_{0}$ are compared with coupling $\kappa_{m}$ and asymmetry $A_{m}$.

By varying the base frequency $\Omega$, we find that the optimum coupling reaches its minimum value for $\Omega= \Omega_{0}$, where $2\pi/ \Omega_{0} = 10.75$ (Figure 8, left) and the asymmetry relevant to the optimum coupling $\kappa_{0}$ has a flat minimum for $\Theta= 2\pi/ \Omega$ between 10.6 and 10.85 yr (Figure 8, right). Comparison with model series shows that both the optimum coupling and asymmetry are overestimated with respect to the original values (dashed lines). The minimum values of the optimum coupling and asymmetry in the model reconstructions correspond to $\Omega= \Omega_{0}$. They extend to slightly lower periods (higher frequencies) with respect to the value $\Omega= \Omega_{m}$ used in the simulation. We can consider values $\kappa_{0}$, $A_{0}$, and $\Omega_{0}$ as estimates of $\kappa_{m}$, $A_{m}$, and $\Omega_{m}$, respectively, and we are led to conclude that all these estimates are somewhat too large. Thus, when the evolution of natural frequencies is given by Equation (9), the Kuramoto model allows us to estimate only upper bounds of optimum coupling, asymmetry, and base frequency.

Figure 8

Reconstruction of optimum coupling (left) and hemispheric asymmetry $A$ (right) depending on the base frequency $\Omega$ of the KMR. Sunspot areas (red) are compared with two Kuramoto model simulations with parameters $a=0.15$, $b=0.1$ (blue) and $a=0.1$, $b=0.05$ (green). Horizontal dashed lines show the values of coupling (left) and asymmetry (right) used in the simulations.

4 Discussion

Solutions of the full magnetohydrodynamical (MHD) equations that would account for solar activity are extremely difficult to obtain (Charbonneau 2010). Several researchers have turned to LODM, such as kinematic mean-field models obtained by a simplification and truncation of the original MHD equations. Various properties of the solar cycle have been retrieved based on these non-linear oscillators (Lopes et al. 2014; Nagy and Petrovay 2013; Passos and Lopes, 2008, 2011; Mininni, Gomez, and Mindlin, 2000, 2001), and an important connection between features of the solar cycle and meridional circulation has been put forward (e.g. Lopes and Passos 2009; Karak 2010; Hathaway and Rightmire 2010; Karak and Choudhuri 2011; Nandy, Muñoz Jaramillo, and Martens 2011; Belucz and Dikpati 2013; Shetye, Tripathi, and Dikpati 2015). The nature of the relationship between the northern and southern hemispheres is a subject of great importance and is hotly debated in connection with solar dynamo modeling. The evolution of the N–S amplitude asymmetry gives evidence of a weak coupling between the hemispheres (Norton and Gallagher 2010; Svalgaard and Kamide 2013) and tends to be simulated by the differences in the meridional circulation (Belucz and Dikpati 2013; Shetye, Tripathi, and Dikpati 2015). The phase asymmetry between hemispheres is not yet modeled, and we make a first step in this direction with the present article.

We have introduced the idea of hemispheric meridional-flow circulation into a Kuramoto model through variable natural frequencies of the two coupled oscillators, and obtained that the phase asymmetry may indeed be induced by a relatively small asymmetry of the meridional circulation in the two hemispheres. We estimated the value of cross-equatorial coupling relevant to the independent frequencies of the northern and southern meridional flow circulations. This coupling value is estimated to be about $0.55 \pm0.05$ and cannot be considered as a strong coupling in agreement with Norton and Gallagher (2010), because it does not induce a complete synchronization of the hemispheric circulation, and natural frequencies remain sensitive to the high-frequency and QBO components (see Appendix). On the other hand, the evolution of natural frequencies is not completely determined by high-frequency oscillations, as is expected in the case of weak coupling (Figure 4a), and the long-term evolution relevant to the Gleissberg cycle is evident, in agreement with previous findings (Zolotova et al., 2009, 2010; Li, Gao, and Zhan 2009; Muraközy and Ludmány 2012). Consequently, we may consider the cross-equatorial coupling as intermediate, and therefore its value is essential for the mutual evolution of solar hemispheres.

We explain the origin of the change in hemispheric phase lead by the variations in meridional flow frequencies. In terms of the Kuramoto model with two oscillators, we have two possible causes of this change: variations in natural frequencies of the oscillators, and variations in their coupling. We note, however, that the change in leading hemisphere is relevant to the zero value of the phase difference, and therefore the coupling coefficient enters Equation (3) with zero factor $\sin ( \theta )$. This means that the coupling variation cannot be crucial during the change in hemispheric lead, and the only candidate inducing this change is the change in natural frequencies. We have to accept, however, that our assumption of constant coupling in Equation (3) is a pure simplification, and in real life, coupling may vary as well as the natural frequencies.

The inverse technique is a powerful method to estimate several characteristics of deep solar dynamo processes that cannot be observed or measured at the solar surface. It is widely applied in helioseismology (e.g. Turck-Chièze and Couvidat 2011; Rightmire-Upton, Hathaway, and Kosak 2012; Schad, Timmer, and Roth 2012; Zhao et al. 2013; Hathaway and Upton 2014; Brun et al. 2015) as a way to estimate properties of the meridional circulation. However, each type of inversion has its limitations and uncertainties (see Schad et al. 2015 for a review). In the present Kuramoto model we use the inverse method to estimate the cross-equatorial coupling, but comparison with simple model examples (Section 3.8) shows that our estimates may be higher than the original values and that this difference is sensitive to the variation of natural frequencies. From considering the sensitivity of coupling to the change in natural frequencies (see model examples at Figures 7 and 8), we suggest that the estimate of the cross-equatorial coupling and the meridional circulation asymmetry may be affected by centennial and decadal cycles (Gleissberg and Schwabe cycles) as well as by quasi-biennial oscillations (see Appendix). However, this sensitivity is lower than 10% of the estimated value.

In the Kuramoto model, which we present in this article, the phase difference between hemispheres is not produced by variations in coupling, but stems from the evolution of the frequencies attributed to the meridional flow. We consider the N–S asymmetry as the result of the asymmetry of the hemispheric frequencies; the Kuramoto model provides a way to connect the asymmetry of meridional circulation with cross-equatorial coupling. We note that the whole interval of low coupling values ($\kappa< 0.1$) shows the same N–S asymmetry (Figure 5b) and that the optimum coupling ($\kappa_{0} = 0.55$) is strong enough to produce visible variations in the asymmetry. Recent measurements of meridional flow (Jiang et al. 2014; Hathaway and Upton 2014) could provide an estimate of this asymmetry, but unfortunately, the length of the records is too short (shorter than two solar cycles) and the variability of observations is too large to allow a proper comparison with the Kuramoto model results in which all values are averaged over 11 yr windows.

5 Conclusions

Our main conclusion is that a persistent N–S asymmetry of sunspot phases does not require high values of the meridional flow dissymmetry (2% is sufficient). Our second conclusion is that the change in the leading hemisphere may be produced by a slow evolution of natural frequencies similar to that found in the Gleissberg cycle. High coupling values lead to a strong positive correlation between the hemispheric phase difference and natural frequencies (Figure 5c) and a weak correlation of the natural frequencies with the solar cycle instantaneous frequency (Figure 5d). We have found that the optimum coupling obtained in the model is weak enough for us to claim that the evolution of frequencies of the meridional flow correlates with the evolution of the solar cycle frequency, in agreement with observations (Hathaway and Upton 2014) and other modeling (Hazra, Karak, and Choudhuri 2014). Both conclusions support the expectation that the long-term evolution of the velocity of the solar meridional flow can eventually be reconstructed from the N–S asymmetry of the solar activity.

Appendix

It is well known that the solar activity spectrum contains frequencies outside the 11 yr band of periods. These frequencies may contaminate the 11 yr phase. In the main text we apply a Kuramoto model to 1 yr preliminary averaged data. This averaging reduces oscillations with periods below 1 year. However, so-called quasi-biennial oscillations with periods from 2 to 4 years may still affect the 11 yr phase evolution. We perform our analysis on 2 yr and 4 yr preliminary averaged data. Figure 9 (top) shows the cumulative energy of periods between 2 and 4 years in the 11 yr sliding window normalized to the energy of the 11 yr component. The relative energy reaches 0.15 after 1 yr preliminary averaging of data, but after 4 yr averaging, its maximum is equal to 0.06. The evolution of the phase difference $\Delta\Phi$ between the northern and southern hemispheres is presented in the bottom panel of Figure 9, and we see the same profile independent of the preliminary averaging. We can see the contamination of the 11 yr phase by high-frequency oscillations of the solar activity as high-frequency variations of the natural frequencies (Figure 10). These oscillations are smoothed by 4 yr preliminary averaging, and the long-term evolution of natural frequencies remains the same. The estimate of the optimum coupling relevant to the 4 yr preliminary averaging is slightly higher: $\kappa_{0} = 0.59$ instead of 0.55 relevant to the 1 yr preliminary averaging used in the main text (Figure 11).

Figure 9

Influence of preliminary averaging on the 11 yr phase evolution. Top: Relative energy of periods between 2 and 4 years; bottom: evolution of 11 yr phase difference between the north and south hemispheres estimated in the 11 yr sliding window. The sliding window of preliminary averaging is 1 yr (blue), 2 yr (red), and 4 yr (yellow).

Figure 10

Contamination of natural frequencies by quasi-biennial oscillations. Evolution of natural frequencies of the northern (blue) and southern (red) hemispheres after 1 yr (top) and 4 yr (bottom) preliminary averaging. The coupling coefficient is $\kappa= 0.55$.

Figure 11

Contamination of the optimum coupling by quasi-biennial oscillations. The correlation between natural frequencies after 1 yr (blue) and 4 yr (red) preliminary averaging. The horizontal dashed line corresponds to a zero correlation; the vertical dashed lines correspond to the optimum coupling.