Oscillator Models of the Solar Cycle

Abstract

This article reviews some of the leading results obtained in solar dynamo physics by using temporal oscillator models as a tool to interpret observational data and dynamo model predictions. We discuss how solar observational data such as the sunspot number is used to infer the leading quantities responsible for the solar variability during the last few centuries. Moreover, we discuss the advantages and difficulties of using inversion methods (or backward methods) over forward methods to interpret the solar dynamo data. We argue that this approach could help us to have a better insight about the leading physical processes responsible for solar dynamo, in a similar manner as helioseismology has helped to achieve a better insight on the thermodynamic structure and flow dynamics in the Sun’s interior.

1 Introduction

The number of dark spots in the Sun’s surface has been counted in a systematic way since Rudolf Wolf introduced the concept, in the first half of the nineteenth century. More than any other solar observable, the sunspot number is considered the strongest signature of the 22-year magnetic cycle. Moreover, since the sunspot number is the longest time series from all solar observables (Owens 2013), it makes it the preferred proxy to study the variability and irregularity of the solar magnetic cycle.

In the Sun’s interior the large scale magnetic field is generated by a magnetohydrodynamic dynamo that converts part of the kinetic energy of the plasma motions into magnetic energy. Polarity reversals occur every 11 years approximately, as it can be observed directly in the Sun’s dipolar field, and taking a full 22-years to complete a magnetic cycle. In fact during each magnetic cycle, the Sun experiences two periods of maximum magnetic activity, during which magnetic flux tubes created in the tachocline layer, rise to the Sun’s surface by the action of buoyancy, emerging as sunspots pairs (Parker 1955). The polarity switch is also observed in the change of polarity alignment of these bipolar active regions.

Although we know that the solar dynamo resides within the convection zone, we still don’t have a complete picture where all the physical mechanisms operate (Charbonneau 2013). There is a strong consensus that the physical mechanism behind the production of the large scale toroidal field component, the so called Ω-effect, is located in the tachocline, a shear layer created by differential rotation and located at the base of the convection zone. The major source of uncertainty is the location of the α-effect, the physical mechanism responsible to convert toroidal into poloidal field and close the system. In truth, this effect could be in fact a collection of several physical mechanisms that operate at different places and with different efficiencies. Some examples are the Babcock-Leighton mechanism that operates in the solar surface and converts the product of decaying active regions into poloidal field, or the action of the turbulent magnetic helicity that takes place in the bulk of the convection zone. One of the main questions that is still being debated is the quantification of the importance and relative contribution of each component to the operation of the solar dynamo. Because different authors choose to give the leading role to one or another α source term, there is vast number of dynamo models. Most of these are two dimensional models (usually referred as 2.5D because they include two spatial coordinates plus time) and are constructed using the mean-field theory framework proposed by Steenbeck and Krause (1966). Despite some short-comes, fruit of the approximations and formulation used, this type of models running in the kinematic regime, i.e. with prescribed large scale flows, has been very popular within the solar community because they can explain many of the observable features of the solar cycle. A detailed discussion on solar dynamo models, stellar magnetism and corresponding references to the vast literature on this subject can be found in the reviews by Charbonneau (2010) and Miesch and Toomre (2009).

Another way of tackling the solar dynamo problem is by producing 3D magnetohydrodynamic (MHD) simulations of the solar convection zone. These computer intensive simulations solve the full set of the MHD equations (usually under the inelastic approximation) and are fully dynamical in every resolved scale, i.e. they take into consideration the interactions between flow and field and vice-versa—unlike the kinematic regime usually used in mean field models, where only the flow influences the field. Recently these simulations have started to show stable large scale dynamo behaviour and they are starting to emerge as virtual laboratories for understanding in detail some of the mechanisms behind the dynamo (Ghizaru et al. 2010; Brown et al. 2011; Käpylä et al. 2012; Passos and Charbonneau 2014).

On the other end of the modelling spectrum, we can find oscillator models, that use simplified parameterizations of the main physical mechanisms that participate in the dynamo process. Although in the Sun’s interior the magnetic field generated by the dynamo has a very rich and complex structure, as a consequence of the structure of the magnetohydrodynamic differential equations, some of its main properties can be understood by analyzing low order differential equations obtained by simplification and truncation of their original MHD counterparts. Then, several properties of the cycle that can be extracted by studying these non-linear oscillator models, as is usually done in non-linear dynamics. These models have a solid connection to dynamical systems and are, from the physics point of view the most simple. This does not mean that they are the easiest to understand because the reduction in the number of dimensions can sometimes be difficult to interpret (viz. introduction section of Wilmot-Smith et al. 2005). These low order dynamo models (LODM), as they are some times called, allow for fast computation and long integration times (thousands of years) when compared to their 2.5D and 3D counterparts. They can be thought as a first order approximation to study the impact of certain physical mechanisms in the dynamo solution, or some of the properties of the dynamo itself as a dynamical system.

The variability exhibited by the sunspot number time series, inspired researchers to look for chaotic regimes in the equations that describe the dynamo. For a complete review on this subject consult Spiegel (2009); Weiss (2010) and references therein. Some of the first applications of LODM were done in this context (e.g. Ruzmaikin 1981; Weiss and Cattaneo 1984; Tobias et al. 1995). These authors found solutions with cyclic behaviour and variable amplitude, including extended periods of low amplitude reminiscent of the grand minima behaviour we see in the Sun. The downside of these initial works was the fact that although the proposed model equations made sense from a mathematical point of view, the physics realism they attained was small. These low order models, with higher or lower degrees of physical complexity, can be used in many areas and several of their results have been validated by 2.5D spatially distributed mean field models, which grants them a certain degree of robustness. This happens specially in LODM whose formulation is directly derived from MHD or mean-field theory equations. Some examples of the results obtained with LODM that have been validated by more complex mean field models are: the study of the parameter space, variability and transitions to chaos in dynamo solutions (Beer et al. 1998; Wilmot-Smith et al. 2005; Charbonneau et al. 2005; Hiremath 2006); the role of Lorentz force feedback on the meridional flow (Rempel 2006; Passos et al. 2012); and the influence of stochastic fluctuations in the meridional circulation and in the α-effect (Charbonneau and Dikpati 2000; Mininni et al. 2001; Mininni and Gómez 2002; Lopes and Passos 2009). Some models even include time delays that embody the spatial segregation and communication between the location of source layers of the α- and Ω-effects. These have been applied to a more general stellar context by Wilmot-Smith et al. (2006) and recently, Hazra et al. (2014); Passos et al. (2014) showed that one of this type of time delay LODM that incorporates two different α source terms working in parallel, can explain how the Sun can enter and exit in a self-consistently way from a grand minimum episode. A couple of LODM even ventured in the “dangerous” field of predictions. For example Hiremath (2008) combined his LODM with an autoregressive model in order to forecast the amplitude of future solar cycles.

In this article we show how can one of these LODM be used as a tool to study the properties of the solar magnetic cycle. For this purpose we use the international sunspot number time series during the past 23 solar magnetic cycles. Nevertheless, the main focus of this work is to present a strategy inspired by helioseismology, were an inversion methodology is used to infer variations of some of the LODM parameters over time. Since these parameters are related to the physical mechanisms that regulate the solar dynamo, this should in principle, allow for a first order reconstruction of the main dynamo parameters over the last centuries. In a similar manner to helioseismology, the comparison between model solutions and data can be done by means of a forward method in which solar observational data is directly compared with the theoretical predictions, or by means of a backward method in which the data is used to infer the behaviour of leading physical quantities of the theoretical model. Naturally, it is necessary to develop an inversion technique or methodology that allows to reconstruct the quantities that have changed during the evolution of solar dynamo. This type of studies is well suited to explore several aspects of the solar and stellar dynamo theory. This can be done by: (i) building a tool to study the dynamo regimes operating in stars; (ii) establishing an inversion methodology to infer the leading quantities responsible for the dynamics and variability of the solar cycle over time; (iii) comparing the dynamo numerical simulations with the observational data; (iv) use this tool as a toy model to test global properties of the solar dynamo.

Here we particularly focus in discussing the three last items of this list, with special attention on the development of an inversion method applied here to the sunspot number time series. This is used to infer some of the dynamics of the solar dynamo back-in-time. In principle this should allow us to determine the variation profiles of the quantities that drive the evolution of the magnetic cycle during the last few centuries.

In Sect. 2, we present a non-linear oscillator derived from the equations of a solar dynamo that is best suited to represent the sunspot number. In Sect. 3, we discuss how the non-linear oscillator analogue can be used to invert some of the leading quantities related with solar dynamo. In Sect. 4 is discussed how solar observational data is use to infer properties of the solar magnetic cycle. In Sect. 5 we present a discussion about how the low order dynamo model can be used to test the basic properties of modern axisymmetric models and numerical simulations, as well to infer some leading properties of such dynamo models. In Sect. 6, we discuss the outlook for the Sun and other stars.

2 A LODM for the Evolution of the Large Scale Magnetic Field

The basic equations describing the dynamo action in the interior of a star are obtained from the magnetic-hydrodynamic induction, and the Navier-Stokes equations augmented by a Lorentz force (Moffatt 1978). Under the usual kinematic approximation the dynamo problem consists in finding a flow field with a velocity U that has the necessary properties capable of maintaining the magnetic field, B against Ohmic dissipation (Charbonneau 2010).

For a star like the Sun such dynamo models should be able to reproduce well-known observational features such as: cyclic magnetic polarity reversals with a period of 22 years, equatorward migration of B during the cycle (dynamo wave), the π/2 phase lag between poloidal and toroidal components of B, the antisymmetric parity across the equator, predominantly negative/positive magnetic helicity in the Northern/Southern hemisphere, as well as many of the empirical correlations found in the sunspot records, like the Waldmeier Rule—anti-correlation between cycle duration and amplitude; the Gnevyshev-Ohl Rule—alternation of higher-than-average and lower-than-average cycle amplitude and Grand Minima episodes (like the Maunder Minimum)—epochs of very low surface magnetic activity that span over several cycles. Given the amount of complex features that a solar dynamo model has to reproduce, the task at hand is far from simple.

The vast majority of dynamo models currently proposed to explain the evolution of the solar magnetic cycle (kinematic mean-field models) became very popular with the advance of helioseismology inversions and the inclusion of the differential rotation profile. In the kinematic regime approximation, the flow field U is prescribed and only the magnetic induction equation is used to determine the evolution of B. Generally, the large scale magnetic field, the one responsible for most of the features observed in the Sun is modelled as the interaction of field and flow where two source terms (Ω and α) naturally emerge from mean-field theory (e.g., Moffatt 1978; Krause and Raedler 1980; Cardoso and Lopes 2012). From the mean-field electrodynamics, the induction equation reads

$$ \frac{\partial \mathbf {B} }{\partial t} =\nabla\times (\mathbf {U}\times \mathbf {B} +\alpha \mathbf {B}-\eta\nabla \times \mathbf {B} ), $$

(1)

where U is the large-scale mean flow, and η is the total magnetic diffusivity (including the turbulent diffusivity and the molecular diffusivity). Currently, as inferred from helioseismology, U can be interpreted as a large-scale flow with at least two major flow components, the differential rotation throughout the solar interior, and the meridional circulation in the upper layers of the solar convection (Howe 2009).

Given all the points above, and based on their popularity among the community, we start our study by considering a reference model based in the kinematic mean-field flux transport framework. Although the results obtained here are based on this specific type of model, most of the analysis method used, as well the conclusions reached, can easily be extended to other models. As usual, under the simplification of axi-symmetry the large-scale magnetic field B can be conveniently expressed as the sum of toroidal and poloidal components, that in spherical polar coordinates (r,θ,ϕ) can be written as

$$ \mathbf {B}(r,\theta,t)=\nabla\times\bigl(A_p(r,\theta,t) \mathbf {e}_\phi\bigr) +B_\phi (r,\theta,t) \mathbf {e}_\phi. $$

(2)

Similarly, the large-scale flow field U as probed by helioseismology can be expressed as the sum of an axisymmetric azimuthal (differential rotation) and poloidal (meridional flow) components:

$$ \mathbf {U}(r,\theta)=\mathbf {u}_p(r,\theta) + \tilde{r} \varOmega(r, \theta) \mathbf {e}_\phi $$

(3)

where $\tilde{r}=r\sin{\theta}$, Ω in the angular velocity and u _p is the velocity of the meridional flow. Accordingly, such decomposition of B (that satisfy the induction equation (1)) and U leads to the following set of equations:

$$\begin{aligned} \frac{\partial A_p}{\partial t} =&\eta \bigl(\nabla^2-\tilde {r}^{-2} \bigr) A_p -\tilde{r}^{-1}\mathbf {u}_p\cdot\nabla( \tilde{r}A_p)+\alpha B_\phi \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial B_\phi}{\partial t} =&\eta \bigl(\nabla^2-\tilde {r}^{-2} \bigr)B_\phi -\tilde{r} \mathbf {u}_p\cdot\nabla\bigl( \tilde{r}^{-1} B_\phi\bigr) + \tilde {r} \bigl[\nabla \times(A_p \mathbf {e}_\phi) \bigr]\cdot\nabla\varOmega - \varGamma(B_\phi) B_\phi \end{aligned}$$

(5)

where η is the magnetic diffusivity and α is the source term of A _p (the mechanism to convert toroidal to poloidal field). Moreover, following the suggestions of Pontieri et al. (2003) we also considered that the toroidal field can be removed from the layers where it is produced by magnetic buoyancy and obeying $\varGamma\sim\gamma B_{\phi}^{2}/8\pi\rho$, where γ is a constant related to the removal rate and ρ is the plasma density.

2.1 A van der Pol-Duffing Oscillator for the Solar Cycle

As the Sun’s magnetic field changes sign from one solar cycle to the next it is a plausible idea to attribute alternating signs in odd/even cycles also to other solar activity indicators such as the sunspot number (SSN). The resulting time series displays cyclic variations around zero in the manner of an oscillator. This suggests an oscillator as the simplest mathematical model of the observed SSN series. As, however, the profile of sunspot cycles is known to be markedly asymmetric (a steep rise in 3–4 years from minimum to maximum, followed by a more gradual decline to minimum in ∼7 years), a simple linear oscillator would be clearly a very poor representation of the sunspot cycle. A damped linear oscillator

$$ \ddot{x} = -\omega^2x-\mu\dot{x} $$

(6)

will, on the other hand, naturally result on asymmetric profiles similar to what is observed. The obvious problem that the oscillation will ultimately decay due to the damping could be remedied somewhat artificially by applying a periodic forcing or by reinitializing the model at each minimum. A much more natural way to counteract the damping, however, is the introduction of non-linearities into the equation—indeed, such non-linearities are naturally expected to be present in any physical system, see below. As long as the non-linearity is relatively weak, the parameters ω ² and μ can be expanded into Taylor series according to x. Due to the requirement of symmetry (i.e. the behaviour of the oscillators should be invariant to a sign change in x) only terms of even degree will arise in the Taylor series. To leading order, then, we can substitute

$$ \omega^2 \rightarrow\omega^2-\lambda x^2\qquad \mu\rightarrow\mu\bigl(\xi x^2 - 1\bigr) $$

(7)

into (6) resulting in

$$ \ddot{x} = -\omega^2x-\mu\bigl(\xi x^2 - 1\bigr)\dot{x} +\lambda x^3 $$

(8)

In the particular case when λ=0 (i.e. the non-linearity affects the damping only) and the other parameters are positive, the system described by (8) is known as a van der Pol oscillator. The alternative case when non-linearity affects the directional force/frequency only, i.e. ξ=0, μ<0 and λ≠0, in turn, represents a Duffing oscillator. Due to their simplicity and universal nature these two systems are among those most extensively studied in non-linear dynamics. It is straightforward to see that the oscillator is non-decaying, i.e. the origin is repeller, whenever μ>0 (negative damping) in the case of a van der Pol oscillator and/or ω ²>0 and λ>0 in a Duffing oscillator. When a non-linearity is present in both parameters (i.e. λ and ξ are both non-zero) a combined van der Pol-Duffing oscillator results.

The van der Pol–Duffing oscillator, however, is more than just a good heuristic model of the solar cycle. In fact, an oscillator equation of this general form can be derived by a truncation of the dynamo equations. As noted before, we are especially interested in capturing the temporal dynamics associated with the large scale magnetic field. In order to construct a low order model aimed at capturing this dynamics, we follow the procedures described in Passos and Lopes (2008b, 2011).

It has been suggested by Mininni et al. (2000, 2001) and Pontieri et al. (2003) that a dimensional truncation of the dynamo equations (4) and (5) is an effective method to reduce the system’s dimensions and capture phenomena just on that scale. Following that ansatz, gradient and Laplacian operators are approximated by a typical length scale of the system l ₀ (e.g. convection zone length or width of the tachocline), leading to $\nabla\sim l_{o}^{-1}$ and $\nabla^{2}\sim l_{o}^{-2}$. Analogously this can be interpreted as a collapse of all spatial dimensions, leaving only the temporal behaviour. In terms of dynamical systems, we are projecting a higher dimensional space into a single temporal plane. After grouping terms in B _ϕ and A _p (now functions only dependent of the time) we get

$$\begin{aligned} \frac{d B_\phi}{d t} =& c_{1} B_\phi+ c_{2}A_p - c_{3} B_\phi^3 \end{aligned}$$

(9)

$$\begin{aligned} \frac{d A_p}{d t} =& c_{1} A_p + \alpha\,B_\phi \end{aligned}$$

(10)

where we have defined the structural coefficients, c _n , as

$$\begin{aligned} c_{1} =&\eta \biggl(\frac{1}{l_0^2} - \frac{1}{\bar{r}^2} \biggr) - \frac{v_p}{l_0} \end{aligned}$$

(11)

$$\begin{aligned} c_{2} =& \frac{\bar{r} \varOmega}{l_0^2} \end{aligned}$$

(12)

$$\begin{aligned} c_{3} =& \frac{\gamma}{8 \pi\rho} \end{aligned}$$

(13)

We now concentrate in creating an expression for the time evolution of B _ϕ since it is the field component directly associated with the productions of sunspots. We derive expression (9) in order to the time, and substitute (10) in it to take away the A _p dependence yielding

$$ \frac{d^2 B_\phi}{d t^2} + \omega^2 B_\phi+ \mu\bigl(3 \xi B_\phi^2 - 1\bigr)\frac{\partial B_\phi}{\partial t} - \lambda B_\phi^3 = 0, $$

(14)

where $\omega^{2}=c_{1}^{2} - c_{2} \alpha$, μ=2c ₁, ξ=c ₃/2c ₁ and λ=c ₁ c ₃ are model parameters that depend directly on the structural coefficients. The name used to describe c _n comes from the fact that these coefficients contain all the background physical structure (rotation, meridional circulation, diffusivity, etc.) in which the magnetic field evolves.

This oscillator (14) is a van der Pol-Duffing oscillator and it appears associated with many types of physical phenomena that imply auto-regulated systems. This equation is a quite general result which B should satisfy. In this case, unlike in the classical van der Pol-Duffing oscillator, the parameters are interconnected by a set of relations that link the present oscillation model with the original set of dynamo equations (4)–(5). This interdependency between parameters will eventually constrain the solution’s space. As in the classical case, ω controls the frequency of the oscillations or the period of the solar magnetic cycle, μ controls the asymmetry (or non-linearity) between the rising and falling parts of the cycle and ξ affects directly the amplitude. The λ parameter, related to buoyancy loss mechanism sets the overall amplitude peak amplitude of the solution. Figure 1 shows the solution of (14) in a time vs. amplitude diagram (left) and in a {B _ϕ ,dB _ϕ /dt} phase space. From this figure we find that this dynamo solution, under suitable parametrization (viz. next section) is a self-regulated system that rapidly relaxes to a stable 22-year oscillation. In the phase space the solution tend to a limit cycle or attractor. A complete (clockwise) turn in the phase space corresponds to a complete solar magnetic cycle.

Fig. 1

Left panel represents the time evolution of B _ϕ (t) obtained from equation (14) with parameters c ₁=0.08, c ₂=−0.09, c ₃=0.001, α ₀=1. In the right we have a (B _ϕ ,dB _ϕ /dt) phase space representation of the solution. The blue arrows indicate the direction of increasing time and the red dot the initial value used. Also indicated in this panel are the regions corresponding to the maxima and minima of the cycle. Adapted from Passos and Lopes (2011)

2.2 A Semi-classical Analysis Method Using a Non-linear Oscillator

In order to estimate values for the coefficients in (14), Mininni et al. (2000) and Passos and Lopes (2008b) fitted this oscillator model either to a long period of the solar activity (several solar cycles) or to each magnetic cycle individually. We shall return to this point in subsequent sections. A more general approach to the problem of finding the parameter combinations with which the classical van der Pol-Duffing oscillator returns solar-like solutions was taken by Nagy and Petrovay (2013). The authors mapped the parameter space of the oscillator by adding stochastic noise to its parameters using different methods. The objective was to constrain the parameter regime where this non-linear model shows the observed attributes of the sunspot cycle, the most important requirement being the presence of the Waldmeier effect (Waldmeier 1935) according to the definition of Cameron and Schüssler (2008).

Noise was introduced either as an Ornstein–Uhlenbeck process (Gillespie 1996) or as a piecewise constant function keeping a constant value for the interval of the correlation time. The effect of this noise was assumed to be either additive or multiplicative. The amplitudes and correlation times of the noise defined the phase space. The attributes of the oscillator model were first examined in the case of the van der Pol oscillator (no Duffing cubic term) with perturbation either in the non-linearity parameter, ξ or the damping parameter, μ, as shown in the equations below:

$$\begin{aligned} \ddot{x} =&-\omega_0^2x-\mu(t) \bigl[\xi_0 x^2-1 \bigr]\dot{x} \end{aligned}$$

(15)

$$\begin{aligned} \ddot{x} =&-\omega_0^2x-\mu_0\bigl[ \xi(t) x^2-1 \bigr]\dot{x}. \end{aligned}$$

(16)

The constant parameters, ω ₀, μ ₀ and ξ ₀ used were taken from the fitted values listed by Mininni et al. (2000). Note that in this simple case, variations in these parameters were assumed to be independent from each other, whereas in reality they are interrelated (cf. (14)). The results show that the model presents solar-like solutions when a multiplicative noise is applied to the non-linearity parameter, as in (16). An example of a time series produced by this type of oscillator is shown in Fig. 2.

Fig. 2

Bottom panel: a 600 year long time series resulting from a stochastically perturbed van der Pol oscillator stochastically perturbed in one of its parameters (non-linearity ξ(t)). SSN values were defined as x ²(t). The noise applied (piecewise constant in this case) is shown in the top panel

As a next step towards a fully general study, let us consider the case where both ξ and μ are simultaneously perturbed and the Duffing term −λx ³ is also kept in the oscillator equation (8). Noise is applied to μ but it also affects ξ as the values of ξ and μ are assumed to be related as

$$\begin{aligned} \xi(t)=\frac{C_{\xi}}{\mu(t)} \quad \mbox{and} \quad \lambda (t)=C_{\lambda}\frac{\mu(t)}{2}, \end{aligned}$$

(17)

(Passos and Lopes 2008b); here, C _ξ and C _λ are constants.

A mapping of the parameter space shows that in this case solar-like solutions are more readily reproduced compared to the case when only one parameter was assumed to vary (see Fig. 3). This finding is in line with the information derived from the LODM developed in the previous section. An ongoing study shows that the corresponding time dependence in the Duffing parameter, as predicted by the LODM, has a significant effect on the character of the solution.

Fig. 3

Bottom panel: a 600 year long time series resulting from a van der Pol–Duffing oscillator stochastically perturbed in two of its parameters, ξ and μ. SSN values were here defined as x ^3/2(t), following Bracewell (1988). The noise applied is shown in the top and middle panels. The Duffing parameter was here given a constant value λ ₀=5×10⁻⁵

We note that additive noise was first applied to one parameter (ξ) of a van der Pol oscillator by Mininni et al. (2000, 2001) but the focus of that work was on reproducing cycle to cycle fluctuations, without considering the Waldmeier effect. This model was further analysed by Pontieri et al. (2003) (and references therein) who studied the behavior of the Hurst exponent of this system and concluded that this type of fluctuations implies that the stochastic process which underlies the solar cycle is not simply Brownian. This means that long-range time correlations could probably exist, opening the way to the possibility of forecasts on time scales comparable to the cycle period. An attempt to introduce the effects of such non-Gaussian noise statistics into the LODM was made by Vecchio and Carbone (2008) who suggest that this may contribute to cyclic variations of solar activity on time scales shorter than 11 years.

3 Coupling a LODM with Observational Data—Inversions

In the previous example a perturbation method was studied in order to find solar like solutions for this non-linear oscillator. Another way of thinking is to pair the oscillator directly to some solar observable and try to constraint its parameters. As mentioned in the introduction we choose the international sunspot number, SSN and we use it to build a proxy of the toroidal magnetic component. Since the SSN is usually taken to be proportional to the toroidal field magnetic energy that erupts at the solar surface ($\propto B_{\phi}^{2}$) (Tobias et al. 1995), this makes it ideal for compare with solutions of the LODM. Taking this in consideration, Mininni et al. (2000); Passos and Lopes (2008b) have built a toroidal field proxy based on the sunspot number by following the procedure proposed by Polygiannakis and Moussas (1996), i.e. $B_{\phi}\approx\pm\sqrt{\mathit{SSN}}$. Details about the construction of the toroidal proxy (see Fig. 4) can be found in Mininni et al. (2001); Passos and Lopes (2008b) and Passos (2012).

Fig. 4

Black dashed line represents the built proxy for the toroidal field. B _ϕ is obtained by calculating $\sqrt{\mathit{SSN}}$, changing the sign of alternate cycles (represented in gray), and smoothing it down using an FFT low pass filter of 6 months. The vertical thin dotted lines represent solar cycle minima

3.1 The Averaged Behaviour of the Solar Dynamo Attractor

The solution obtained for (14) presented in Fig. 1 shows that the solar cycle is a self-regulated system that tends to a stable solution defined by an attractor (limit cycle). If we allow for the different physical processes responsible for the solar dynamo and embedded in the structural coefficients ((11), (12) and (13)), i.e. the differential rotation, the meridional circulation flow, the α mechanism, and the magnetic diffusion, to change slowly from cycle to cycle then we start to observe deviations from the equilibrium state. If deviations from this sort of dynamical balance occur, such that if one of these processes changes due to an external cause, the other mechanisms also change to compensate this variation and ensure that the solar cycle finds a new equilibrium.

To test this idea of an equilibrium limit cycle, we fit the LODM parameters to the {B _ϕ ,dB _ϕ /dt} phase space of the built toroidal proxy (see Fig. 5).

Fig. 5

Phase-space diagram for the toroidal proxy B _ϕ (t): The crosses correspond to local area averaged values found by dividing the data into 32 temporal intervals. The red dashed curve is a fit to the crosses. The continuous black curves correspond to a fit to all data points (not grouped in intervals). For the red curve we have that μ=0.1645, ω=0.3523, ξ=0.0147 and λ=0.0005. Figure adapted from Passos and Lopes (2008a)

If one of the parameter’s variation is very large the system can be dramatically affected, leading to a quite distinct evolution path like the ones found during the solar grand minima. We will develop this subject in a subsequent section.

3.2 Matching of Solutions to Observable Characteristics of the Solar Cycle

Solutions with fluctuation similar to those we see on the solar cycle are easily set by variations in the μ parameter (and the physical processes associated with it). By definition the structural coefficient that regulates this parameter (c ₁) also has an important role in the other parameters (ω, ξ and λ). In the LODM equation (14) the μ and μξ quantities regulate the strength and the non-linearity of the damping. Moreover, an occasional variation on μ, like a perturbation on the meridional flow amplitude, v _p (see structural coefficient (11)) will affect all sets of parameters leading to the solar dynamo (14) to find a new equilibrium, which will translate into the solar magnetic cycle observable like the sunspots number, showing an irregular behaviour.

The well-known relation discover by Max Waldmeier (Wolf and Brunner 1935), that the time that the sunspot number takes to rise from minimum to maximum is inversely proportional to the cycle amplitude in naturally captured by the LODM assuming discrete variations in μ. Notice that the Waldmeier effect occurs as a consequence of the limit cycle becoming increasingly sharp as μ increases, i.e., the sunspot number amplitude increases as the cycle’s rising times gets shorter.

4 How to Infer Properties of the Solar Magnetic Cycle

From the physical point of view, based on observations, we know that in the Sun some of the physical background structures that are taken as constant in our standard dynamo solution aren’t so. In order to test that specific changes of the background state lead to the observed changes in the amplitude of the solar cycle, the following strategy was devised. At a first approximation we assume that the structural coefficients can change only discretely in time, more specifically from cycle to cycle while the magnetic field is allowed to evolve continuously. The idea is that changing coefficients will generate theoretical solutions with different amplitudes, periods and eigen-shapes at different times and by comparing these different solution pieces with the observed variations in the solar magnetic field, we are able to infer information about the physical mechanisms associated with the coefficients.

To do this we compare our theoretical solution with a proxy built from the International monthly averaged SSN since 1750 to the present. As mentioned before we assume that $B_{\phi}\propto\sqrt{\mathit{SSN}}$. The proxy data is separated into individual cycles and fitted using (14), considering that the buoyancy properties of the system are immutable, i.e. c ₃ is constant throughout the time series. This means that when we fit the LODM to solar cycle N, we will retrieve the set of c _nN coefficients that best describe that cycle. This allows to probe how these coefficients vary from cycle to cycle and consequently how the physical mechanisms associated with them evolve in time (Lopes and Passos 2009; Passos 2012). Equation (14) is afterwards solved by changing the parameters to their fit value, at every solar minimum using a stepwise function (similar to that presented in Fig. 7 for c ₁). Figures 7 and 6 highlight this procedure. The fact that such a simplified dynamo model can get this degree of resemblance with the observed data just by controlling one or two parameters is an indication that it captures the most important physical processes occurring in the Sun.

Fig. 6

(A) Theoretical solution (red) obtained by fitting it the proxy at each individual cycle. (B) Direct comparison of the model behavior (red) and observed solar cycle amplitude (black). In panel (B) we just plot the squared of panel (B) and this also amplifies the differences between both curves. Adapted from Passos (2012)

4.1 Meridional Circulation Reconstruction

The simple procedure previously described allows to reconstruct the behavior of solar parameters back in time. Using an improved fitting methodology, Passos (2012) obtained with this model the reconstruction of the variation levels of the solar meridional circulation for every solar (sunspot) cycle over the last 250 years. One must notice that in this specific LODM the amplitude of the cycle depends directly on the amplitude of the meridional flow during the previous cycle. It is completely possible to imagine that other models that consider a different theoretical setup might return a different behaviour.

Looking at (11), we can see that the coefficient c ₁ depends on two physical parameters, the magnetic diffusivity, η, and the amplitude of the meridional circulation, v _p . The magnetic diffusivity of the system is a property tightly connected with turbulent convection and is generally believed to change only in time scales of the order of stellar evolution. This leaves variations in v _p as the only plausible explanation for the variation observed from cycle to cycle. Therefore, by looking at the evolution of c ₁ we can effectively assume that we are looking at the variation in the strength of meridional circulation. The results obtained are presented in Fig. 7.

Fig. 7

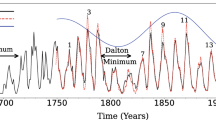
Reconstruction of the meridional circulation profile represented by c ₁ (black line) compared to smoothed the sunspot number (gray). Adapted from Passos (2012)

Although this result is in itself interesting, a more important concept came from this study. When Passos and Lopes (2008b) presented their results for the first time, they introduced the idea that coherent long term variations (of the order of the cycle period) in the strength of the meridional circulation could provide an explanation for the variability observed in the solar cycle (see Fig. 8). This result was also a posteriori numerically validated using a 2.5D flux transport model (Lopes and Passos 2009; Karak 2010). Only a couple of years later, Hathaway and Rightmire (2010) presented meridional circulation measurements spanning over the last solar cycle. Their measurements confirmed that the amplitude of this plasma flow changes considerably from cycle to cycle.

Fig. 8

Comparison between the observed solar cycle amplitude (top), a sunspot reconstruction using the Surya Dynamo Code (middle) and the LODM results (bottom). In these simulations were only considered variations in the meridional flow amplitude every 2 sunspot cycles (1 magnetic cycle). Adapted from Passos and Lopes (2008b); Lopes and Passos (2009) and Passos (2010)

Recently two other groups have tested this idea with their 2.5D dynamo models finding additional features based in this effect, cf. Karak (2010), Karak and Choudhuri (2011) and Nandy et al. (2011). For example it was found that the instant at which the change in the meridional flow takes place, has an influence in the duration of the following solar cycle. This was used as an explanation for the abnormally long duration of the last minimum. Just for reference, the numbering of solar cycles only started after 1750 with solar cycle 1 beginning in 1755. At this moment we are in the rising phase of solar cycle 24.

4.2 Explaining Solar Grand Minima

4.2.1 Variations in the Meridional Flow

Solar grand minima correspond to extended periods (a few decades) where very low or no solar activity occurs. During theses periods no sunspots (or very few) are observed in the solar photosphere and it is believed that other solar phenomena also exhibit low levels of activity. The most famous grand minimum that has been registered is the Maunder Minimum which occurred between the years of 1645 and 1715 (Eddy 1976).

A possible explanation for the origin of these quiescent episodes was put forward by Passos and Lopes (2011). Using a LODM, they showed that a steep decrease in the meridional flow amplitude can lead to grand minima episodes like the Maunder minimum (see Figs. 9 and 10). This effect presents the same visual characteristics as the observed data, namely a rapid decrease of magnetic intensity and a gradual recovery into normal activity (see Fig. 9) after the meridional circulation amplitude returns to its normal values. A similar result was later obtained by Karak (2010), again using a more complex 2.5D numerical flux transport model. Nevertheless the reasons that could lead to a decrease of the meridional flow amplitude were not explored. This served as a motivation to study the behavior of this LODM in the non-kinematic regime, explained in Sect. 5.2.

Fig. 9

Top panel represents the sunspot measurements where the Maunder Minimum period is highlighted by the red arrow. In the bottom we show the response of the LODM (magnetic energy in arbitrary units) to a decrease in the strength of the meridional flow exemplified by the green dashed line. Adapted from Passos and Lopes (2011)

Fig. 10

The phase-space diagram for B(t) corresponds to the value obtained from the sunspot number temporal series as in Fig. 9. Adapted from Passos and Lopes (2011) and Passos (2010)

4.2.2 Fluctuations in the α Effect

Some examples mentioned in the introduction, hint that fluctuations in the α mechanism can also trigger grand minima. We focus on a specific example now, the LODM developed by Hazra et al. (2014). In this work the authors used a time-delay LODM similar to that presented in Wilmot-Smith et al. (2006) but expanded with the addition of a second α effect. This model incorporates two of these mechanisms, one that mimics the surface Babcock-Leighton mechanism (BL), and another one analogous to the classical mean-field (MF) α-effect that operates in the bulk of the convection zone. This set up captures the idea that the BL mechanism should only act on strong magnetic fields that reach the surface, and that weak magnetic fields that diffuse through the convection zone should feel the influence of the MF α. The authors subject these two effects to different levels of fluctuations and find that in certain parameter regimes, the solution of the system shows the same characteristics as a grand minimum. These results were also validated by implementing a similar set up into a 2.5D mean-field flux transport dynamo model (Passos et al. 2014). Again this shows the usefulness of low order models to probe ideas before their implementation into more complex models.

4.3 Solar Cycle Predictability

For the near future, perhaps one of most interesting applications of this LODM is its use in the predictability of future solar cycles amplitudes. The first step towards this objective is presented in Passos (2012). The authors studied the correlations between the LODM fitted structural coefficients and cycle’s characteristics (amplitude, period and rising time). They found very useful relationships between these quantities measured for cycle N and the amplitude of cycle N+1. These relationships were put to the test by predicting the amplitude of current solar cycle 24 (see Fig. 11).

Fig. 11

Observed values (white squares) and predicted values black circles with gray error bars for the cycle amplitude. The red circle is the predicted amplitude for solar cycle 24 based on this methodology. Adapted from Passos (2012)

5 LODM as Probe of Numerical Dynamo Models

In recent years there have been strong developments of different types of dynamo models to compute the evolution of the solar magnetic activity and to explore some of the causes of magnetic variability. Two classes of models have been quite successful, the kinematic dynamo models and, more recently, the global magnetohydrodynamical models. Both types of dynamo models have a quite distinct approach to the dynamo theory, the first one resolves the induction magnetic equation for a prescribed velocity field (which is consistent with helioseismology), and the second one obtains global magnetohydrodynamical simulations of the solar convection zone. Many of these models are able to reproduce some of the many observational features of the solar magnetic cycle. Nevertheless, it remains quite a difficult task to successfully identify which are the leading physical processes in current dynamo models that actually drive the dynamo in the solar interior. The usual method to test these dynamo models is to compare their theoretical predictions with the different sets of data, including the sunspot numbers, however, in many cases the conclusions obtained are very limited, as different physical mechanisms lead to very identical predictions. This problem also arises in the comparison between different dynamo models, including different types of numerical simulations.

A possible solution to this problem is to use inverted quantities (obtained form observational data) to test the quality of the different solar dynamo model, rather than making direct comparison of data. For those of you familiarized with helioseismology, there is a good analogue: it is the equivalent to compare the inverted sound speed profile (obtained from observational data) with the sound speed profile predicted by solar models (backward approach), rather than compare predicted frequencies with observational frequencies (forward approach). The former method to test physical models is more insightful than the latter one. At the present level of our understanding of the solar dynamo theory, as a community we could gain a more profound understanding of the mechanisms behind the solar magnetic variability, if we start developing some backward methods to analyse solar observational data and test dynamo models.

5.1 Using a LODM in the Kinematic Regime

Using the meridional velocity inverted from the sunspot number time series (cf. Fig. 7), Lopes and Passos (2009) showed that most of the long term variability of the sunspot number could be explained as being driven by the meridional velocity decadal variations, assuming that the evolution of the solar magnetic field is well described by an axisymmetric kinematic dynamo model.

Figure 8 shows a reconstructed sunspot times series that has been obtained using the meridional velocity v _p inverted from the sunspot observational time series, and Fig. 12 shows the phase space of a standard axisymmetric kinematic dynamo model (with the same v _p for all cycles) (e.g., Choudhuri et al. 1995) and a solar dynamo model where the v _p changes from cycle to cycle as inverted from the sunspot times series (Lopes and Passos 2009). It is quite encouraging to find that such class of dynamo models for which the v _p changes overtime successfully reproduced the main features found in the observational data.

Fig. 12

The phase-space diagram for B(t) of a kinematic dynamo model (using the Surya’s kinematic model): (A) a standard kinematic dynamo model (v _p is constant); (B) a variable kinematic dynamo model in which the v _p for each magnetic cycle corresponds to the value obtained from the sunspot number temporal series. Both simulations correspond to 130-year time series. The small variability present in the left panel is due to the stabilization of the numerical solution. Figure adapted from Lopes and Passos (2009)

Moreover, in their article Lopes and Passos (2009) tested two different methods of implementing the velocity variation for each magnetic cycle, namely, by considering that amplitude variations in v _p that take place at sunspot minima or at sunspot maxima. All the time series show a few characteristics that are consistent with the observed sunspot records. In particular, all the simulations show the existence of low amplitudes on the sunspot number time series between 1800 and 1840 and between 1870 and 1900. The simulation that best reproduces the solar data corresponds to the model SSNrec[3] (see Fig. 8), in which was implemented a smoothed v _p variation profile between consecutive cycles and taking place at the solar maximum. This clearly highlights the potential of such methodology.

Here, we discuss the same methodology as the one used in the previous section, but instead of applying it to observational sunspot number records, it is used to reconstruct the sunspot time series. The results obtained clearly show that the present kinematic dynamo models can reproduce in some detail the observed variability of the solar magnetic cycle. The fact that for one of the sunspot models—model SSNrec[3], it presents a strong level of correlation with the observational time series, lead us to believe that the main idea behind this backward approach is correct and it is very likely that the inverted v _p variation is probably very close to the v _p variation that happens in the real Sun. Clearly, under the assumed theoretical framework the meridional circulation is the leading quantity responsible for the magnetic variability found in the sunspot number time series and current solar dynamo models are able to reproduce such variability to a certain degree.

5.2 Using a LODM in the Non-kinematic Regime

So far, the vast majority of the LODM applications presented here followed the traditional assumption that the solar dynamo can be correctly modeled in the kinematic regime, where only the plasma flows influence the production of magnetic field, and not the other way around. This kinematic approximation is used in the vast majority of the present 2.5D spatially resolved dynamo models.

In the last couple of years though, evidence started to appear supporting the claim that this kinematic regime might be overlooking important physical mechanisms for the evolution of the dynamo. The idea that the meridional flow strength can change over time and affect the solar cycle amplitude coupled with the measurements of Hathaway and Rightmire (2010) and Basu and Antia (2010) indicate that the observed variation in this flow is highly correlated with the levels of magnetic activity. This leads to the fundamental question: “Is the flow driving the field or is the field driving the flow?”.

The first clues are starting to appear from 3D MHD simulations of solar convection. The recent analysis of the output of one of the large-eddy global MHD simulations of the solar convection zone done by Passos et al. (2012) shows interesting clues. These simulations solve the full set of MHD equations in the inelastic regime, in a broad, thermally-forced stratified plasma spherical shell mimicking the SCZ and are fully dynamical on all spatiotemporally-resolved scales. This means that a two way interaction between field and flow is always present during the simulation. The analysis shows that the interaction between the toroidal magnetic field and the meridional flow in the base of the convection zone indicates that the magnetic field is indeed acting on the equatorward deep section of this flow, accelerating it. This observed relationship runs contrary to the usually assumed kinematic approximation.

In order to check if this non-kinematic regime has any impact in the long term dynamics of the solar dynamo, Passos et al. (2012) implemented a term that accounts for the Lorentz force feedback in a LODM similar to the one presented here. This allows to fully isolate the global aspects of the dynamical interactions between the meridional flow and magnetic field in a simplified way.

They assumed that the large-scale meridional circulation, v _p , is divided into a “kinematic” constant part, v ₀ (due to angular momentum distribution) and a time dependent part, v(t), that encompasses the Lorentz feedback of the magnetic field. Therefore they redefine v _p as v _p (t)=v ₀+v(t) where the time dependent part evolves according to

$$ \frac{\textrm{d} v(t)}{\textrm{d} t} = a\, B_\phi A_p - b\, v(t). $$

(18)

The first term is a magnetic non-linearity representing the Lorentz force and the second is a “Newtonian drag” that mimics the natural resistance of the flow to an outside kinematic perturbation. Under these conditions the Lorentz force associated with the cyclic large-scale magnetic field acts as a perturbation on the otherwise dominant kinematic meridional flow. This idea was not new and it was used before in the context of magnetically-mediated variations of differential rotation in mean-field dynamo models (Tobias 1996; Moss and Brooke 2000; Bushby 2006). The modified LODM equation they end up defining are

$$\begin{aligned} \frac{\textrm{d} B_\phi}{\textrm{d} t} =& \biggl(c_{1} -\frac{v_p(t)}{\ell_0} \biggr)B_\phi + c_{2} A_p - c_{3} B_\phi^3, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\textrm{d} A_p}{\textrm{d} t} =& \biggl(c_{1} -\frac{v_p(t)}{\ell_0} \biggr) A_p + \alpha B_\phi, \end{aligned}$$

(20)

where c ₁, is defined as $c_{1}=\frac{\eta}{\ell_{0}^{2}}-\frac{\eta }{R_{\odot}^{2}}$ and takes the role of magnetic diffusivity, while the other coefficients remain the same.

While the values used for the structural coefficients, are mean values extracted from the works presented in the previous in sections, the parameters associated with the meridional flow evolution, a, b and v ₀ deserved now the attention. These parameters have an important role in the evolution of the solution space. The behavior observed in the solutions range from fixed-amplitude oscillations closely resembling kinematic solutions, multiperiodic solutions, and even chaotic solutions. This is easier to visualize in Fig. 13 where are presented analogs of classical bifurcation diagrams by plotting successive peak values of cycle amplitudes, for solutions with fixed (a,v ₀) combinations but spanning through values of b. Transitions to chaos through bifurcations are also observed when holding b fixed and varying a instead.

Fig. 13

Bifurcation maps for maximum amplitude of the toroidal field (equivalent to solar cycle maximum) obtained by varying b between 10⁻⁴ and 1 for different a and v ₀. (A) Single period regime, v ₀=−0.1, a=0.01; (B) appearance of period doubling, v ₀=−0.1, a=0.1 and (C) shows signatures of chaotic regimes with multiple attractors and windows, obtained with v ₀=−0.13, a=0.05. Adapted from Passos et al. (2012)

The authors expanded the methodology used and applied stochastic fluctuations to parameter a, the one that controls the influence of the Lorentz force. As a result, and depending on the range of fluctuations, they observed that the short term stochastic kicks in the Lorentz force amplitude create long term modulations in the amplitude of the cycles (hundreds of years) and even episodes where the field decays to near zero values, analog to the previously mentioned grand minima. The duration and frequency of these long quiescent phases, where the magnetic field decays to very low values, is determined by the level of fluctuations of a and the value of b. The stronger this drag term b is, the shorter the minima are and the higher the level of fluctuation of a, the more common these intermittency episodes become. Figure 14 shows a section of a solution that spanned for 40000 years and that presents all the behaviors described before.

Fig. 14

Simulation result fluctuating a∈[0.01,0.03], b=0.05 and v ₀=−0.11. All other model parameters are the same as in the reference solution. Panel (A) shows a section of the simulation where the long term modulation can be seen. In black is $B_{\phi}^{2}(t)$, red $A_{p}^{2}(t)$ and blue a scaled version of the meridional flow, in this case 5v _p (t). In panel (B) the same quantities but this time zooming in into a grand minimum (off phase) period. Adapted from Passos et al. (2012)

In this specific example they used 100 % fluctuation in a and maintaining all the other parameters constant. In the parameter space used to produce this figure, the solution without stochastic forcing is well behaved in the sense that it presents a single period regime. Therefore, the fluctuations observed in this solution are a direct consequence of the stochastic forcing of the Lorentz force and not from a chaotic regime of the solution’s space.

To understand how the grand minima episodes arise they resort to visualizing one of these episodes with phase space diagrams of {B _ϕ ,A _p ,v _p }. This allows to see how these quantities vary in relation to each other and try to understand the chain of events that trigger a grand minimum.

The standard solution for the LODM without stochastic forcing, i.e. with a fixed at the mean value of the random number distribution used, is the limit cycle attractor, i.e., a closed trajectory in the {B _ϕ ,A _p } phase space. This curve is represented as a black dashed trajectory in the panels of Fig. 15. The gray points in this figure are the stochastic forced solution values sampled at 1 year interval. These points scatter around the attractor representing the variations in amplitude of the solution. Occasionally the trajectories defined by these points collapse to the center of the phase space (the point {0,0,v ₀} is also another natural attractor of the system) indicating a decrease in amplitude of the cycle, i.e. a grand minimum. The colored trajectory evolving in time from purple to red represents one of those grand minimum. This happens when the solution is at a critical distance from the limit cycle attractor and gets a random kick further away from it. This kick makes the field grow rapidly. In turn, since the amplitude of the field grows fast, the Lorentz force will induce a similar growth in v(t) eventually making v _p change sign. When this occurs, v _p behaves as a sink term quenching the field growth very efficiently. This behavior is seen in the two bottom panels of Fig. 15 where v _p decays to its imposed “kinematic” value v ₀ after the fields decay. After this collapse of v _p to v ₀ it starts behaving has a source term again and the cyclic activity proceeds.

Fig. 15

Phase spaces of the solution with stochastic fluctuations. The gray dots represent 1 year intervals between t=35000 and t=40000. The colored line shows the trajectory of a grand minima (starting from purple, t=27300 and ending in red, t=27400. The black dashed line represents the unperturbed solution with a=0.02. Adapted from Passos et al. (2012)

One clear advantage of low order models emerges from this example. Currently 3D MHD simulations of solar convection spanning a thousand years take a couple of months to run in high efficiency computational clusters or in supercomputers. Longer simulations are at the moment prohibitive not only for the amount of time they take but also for the huge amount of data they generate. Statistical studies on grand minima originated by the kind of magnetic back-reaction described here, require long integration times where many thousands of cycles need to be simulated. The LODM calculations can be done in a few minutes or hours in any current desktop.

The grand minima mechanism presented in this section is now being studied by looking at the data available from 3D simulations. Some effects are easier to find when you know what to look for.

6 Outlook for the Sun and Stars

So far we have shown that low order dynamo models (for which the approximation must be carefully chosen to keep the relevant physics within) could lead the way to explore some features of the solar magnetic activity including the long-term variability. The study of the phase diagram $\{B_{\phi}(r),\dot{B}_{\phi}(t)\}$ clearly shows that on a scale of a few centuries the solar magnetic cycle shows evidence for a van der Pool attractor—put in evidence by the mean solar magnetic cycle, although on a time-scale of a few solar magnetic cycles the phase space trajectory changes dramatically. In some cases the trajectory collapses completely for several magnetic cycles as in the periods of grand minima. This gives us an indication about the existence of a well defined self regulated system under all this observed magnetic variability, for which we still need to identify the leading physical mechanisms driving the solar dynamo to extreme activity scenarios like periods of grand minima. Actually, the fact that a well-defined averaged van der Pool limit curve exists for all the sunspot records, can be used to test different solar dynamo models, including numerical simulations, against observational data or between different dynamo models.

Moreover, the fact that such well-defined attractor exists in the phase space, and several dynamo models are able to qualitatively reproduce the solar variability (as observed in the phase space $\{B_{\phi}(r),\dot{B}_{\phi}(t)\}$ gives us hope that in the near future we will be able to make quite reliable short term predictions of the solar magnetic cycle variability, at least within certain time intervals of solar magnetic activity. A significant contribution can be done by the utilization of more accurate sunspot time series in which many of the historical inaccuracies were corrected (Lefevre and Clette 2014).

In the future, similar inversion techniques could be developed, namely to study the possible asymmetry between the North and South Hemispheres using the sunspot areas, either by treating each of the sunspot areas as two distinct times series or by attempting two-dimension inversions of sunspot butterfly diagrams. In the former case, recently Lopes et al. (2014) have analysed these long-term sunspot areas time series and found that turbulent convection and solar granulation are responsible by the stochastic nature of the sunspot area variations. In the last case, we could learn about the evolution of the solar magnetic cycle in the tachocline during the last two and a half centuries. Moreover, most of the inversion methods used for the sunspot number can be easily extended to other solar magnetic cycles proxies such as TSI, H _α and Magnetograms.

The oscillator models, as a first order dynamo model are particularly suitable to study the magnetic activity in other stars. A good proxy of magnetic activity in stars in the chromospheric variations of Ca II H and K emission lines. Baliunas et al. (1995) have found many F2 and M2 stars which seem to have cyclic magnetic cycle activity, as observed in the Sun (cf. Fig. 16). In some of these stars the observational time series covers several cycles of activity. In particular, it will be interesting to identify how the dynamo operating in these stars differs from the solar case.

Fig. 16

Magnetic activity signature expressed by the variation of the intensity of the Ca II emission line (S-index) for two solar like stars. Adapted from Baliunas et al. (1995)

More recently, the CoROT and Kepler space missions have observed photometric variability associated with solar-like activity in a very large number of main sequence and sub-giant stars. While the time coverage is too short to derive cycle periods for stars very close to the Sun, the overall level of activity and its dependence on various stellar parameters can be studied on a large statistical sample (Basri et al. 2010; McQuillan et al. 2012). Nevertheless, with so many stars with quite distinct masses and radius, it is reasonable to expect that we will find quite different type of dynamos and regimes of stellar magnetic cycle. Actually, we think it is likely to find a magnetic diversity identical to the one found in the acoustic oscillation spectra measured for the more than 500 sun-like stars already discovered (Chaplin et al. 2014), some of which have already shown evidence of a magnetic cycle activity. García et al. (2010) have obtained a proxy of the starspots number for the star HD49933 from amplitudes and frequencies of the acoustic modes of vibration. As in the non-linear oscillator models the activity level is determined by the structural parameters which in turn depends on the dynamo model. These studies potentially offer a simple theoretical scheme against which to test the observational findings.