Option pricing under non-normality: a comparative analysis

Abstract

This paper carries out a comparative analysis of the calibration and performance of a variety of options pricing models. These include Black and Scholes (J Polit Econ 81:637–659, 1973), the Gram–Charlier (GC) approach of Backus et al. (1997), the stochastic volatility (HS) model of Heston (Rev Financ Stud 6:327–343, 1993), the closed-form GARCH process of Heston and Nandi (Rev Financ Stud 13:585–625, 2000) and a variety of Lévy processes including the Variance Gamma (VG), Normal Inverse Gaussian (NIG), and, CGMY and Kou (Manag Sci 48:1086–1101, 2002) jump-diffusion models. Unlike most studies of option pricing, we compare these models using a common point-in-time data which reflects the perspective of a new investor who wishes to choose between models using only the most minimal recent data set. For each of these models, we also examine the accuracy of delta and delta-gamma approximations to the valuation of both individual options and an illustrative option portfolio.

1 Introduction

The Geometric Brownian Motion (GBM) process of Black and Scholes (BS 1973) provides a very tractable and in some respects very attractive basis for option pricing. However, these benefits come at a price. One problem is that GBM specifies that geometric asset returns are normally distributed, and this goes against a great deal of evidence showing that most asset returns are skewed and have higher than normal kurtosis. Evidence of this can be found in Alles and Murray (2010) amongst host of others. Asset returns may also experience jumps as for example recently found by Chan et al. (2007) in the case of the Thai Baht exchange. A second problem is the assumption that volatility is constant, which contradicts a vast literature suggesting that volatilities are themselves volatile. A recent example of this in an international context can be found in Arora et al. (2009).

These weaknesses have spawned a number of alternatives to the Black–Scholes approach to option pricing such as the constant elasticity variance model, empirically tested by Chen et al. (2009). Another is the Gram–Charlier (GC) approach of Backus et al. (1997), but this model is still restrictive in so far as it, like BS, still assumes a constant volatility. A third, the stochastic volatility (HS) model of Heston (1993), allows the volatility to follow a Cox–Ingersoll–Ross (CIR process 1985) stochastic process, and a fourth is the closed-form GARCH process of Heston and Nandi (2000). All of these models allow for skewness and excess kurtosis, but they all exclude the presence of jumps in asset returns. If we wish to obtain jumps, on the other hand, we can use models of Lévy processes. Such models include the pure jump Lévy processes—such as the Variance Gamma (VG), Normal Inverse Gaussian (NIG) and CGMY models—that model asset prices as a continuous-time (and non-diffusive) process of small jumps, and the jump-diffusion models such as that of Kou (2002). All these Lévy process allow for both skewness and excess kurtosis in asset returns. This list of models, though far from exhaustive, is nonetheless representative of the range of alternative approaches that have been proposed to remedy the limitations of BS.

Most studies of option price performance consider only one or a very limited number of approaches, and typically do so using time-series approaches involving long spans of historical data. This paper, by contrast, is the first in its kind in which BS, Gram–Charlier, stochastic volatility, GARCH and Lévy models are jointly estimated and their performance assessed on a common data set. Our approach is also distinctive in that it uses point-in-time data—basically traded options data from a single week. Our proposal is to investigate which model provides the best calibration subject to a potential new investor’s willingness to use only the most recent minimum market information without having to make detailed time-series analyses.

The paper is structured as follows. Section 2 provides a short description of the models and discusses how they address skewness and kurtosis. It also sets out the risk-neutral dynamics required for pricing options. Section 3 deals with the models’ calibration. Section 4 discusses the models’ pricing performance and Sect. 5 discuss their skew-smirk patterns. Section 6 then examines the models’ Greek-based (Δ; Г) approximations and Sect. 7 address their use in portfolio approximations of option prices. Section 8 briefly discusses the models’ risk-neutral densities which determine their pricing. Section 9 concludes.

2 The models and their dynamics

Our starting point is Black and Scholes (1973), who assume that asset prices S _t follow a Geometric Brownian Motion (GBM) process:

$$ \frac{{dS_{t} }}{{S_{t} }} = \mu dt + \sigma \sqrt {dt} Z_{t} $$

(1)

where μ is the drift rate, σ the volatility and Z _t is a standard normal random process. The option can be priced using the equivalent risk-neutral pricing measure in which we replace μ in Eq. 1 with the risk-free rate $r - \tfrac{1}{2}\sigma^{2}$ to obtain the famous Black–Scholes (BS) price formula for a vanilla European call option with strike K and maturity T on a stock of current value S _t :

$$ c_{BS} = S_{t} \Upphi (d) - Ke^{ - rT} \Upphi \left( {d - \sigma \sqrt T } \right) $$

(2)

where $\Upphi ( \cdot )$ is the standard normal distribution function and

$$ d = \frac{{\ln \left( {S_{t} /K} \right) + \left( {r + \sigma^{2} /2} \right)T}}{\sigma \sqrt T } $$

A major limitation of the BS model and of the underlying GBM process on which it is based is that it fails to allow for skewness and excess kurtosis in the underlying process (see e.g., Hull and White 1988; or Jondeau et al. 2007; Sapp 2009). This leads to the smile skew effect in BS option prices and also leads to the BS model often undervaluing out-of-the-money (OTM) options.

We now consider a number of models that can handle skewness and/or excess kurtosis.

2.1 The Gram–Charlier model

The first of these is the Gram–Charlier (GC) model introduced in Backus et al. (1997). It involves an extension of the BS density that allows for skewness and excess kurtosis:

$$ f(x) = \phi (x) - \varsigma_{1T} \frac{1}{3}\phi^{3} (x) + \varsigma_{2T} \frac{1}{4}\phi^{4} (x) $$

(3)

where the superscripts on ϕ indicate the order of derivative of the BS density f(x), $\varsigma_{1T} = \tfrac{{\varsigma_{11} }}{\sqrt T }$ and $\varsigma_{2T} = \tfrac{{\varsigma_{21} }}{\sqrt T }$ are the skewness and kurtosis on a horizon of T, and ς₁₁ and ς₂₁ are the per unit skewness and kurtosis. Backus et al. (1997) show that with this density the call price can be written as the following straightforward generalization of the BS formula (2):

$$ \begin{aligned} c_{GC} & \cong S_{t} \Upphi (d) - Ke^{ - rT} \Upphi \left( {d - \sigma \sqrt T } \right) \\ & \quad + S_{t} \Upphi (d)\sigma \left[ {\frac{{\varsigma_{11} }}{3!}\left( {2\sigma \sqrt T - d} \right) - \frac{{\tfrac{{\varsigma_{21} }}{\sqrt T }}}{4!}\left( {1 - d^{2} + 3d\sigma \sqrt T - 3T\sigma^{2} } \right)} \right] \\ \end{aligned} $$

(4)

2.2 The Heston stochastic volatility model

The stochastic volatility model (SV) of Heston (1993) assumes a diffusion process for the stock price given by:¹

$$ \frac{{dS_{t} }}{{S_{t} }} = \mu dt + \sqrt \upsilon_{t} \sqrt {dt} Z_{t} $$

(5)

and a Cox–Ingersoll–Ross (CIR 1985) process for the volatility υ _t given by:

$$ d\upsilon_{t} = \kappa \left[ {\upsilon - \upsilon_{t} } \right]dt + \xi \sqrt {\upsilon_{t} } \sqrt {dt} W_{t} $$

(6)

where υ is the long-run mean volatility, κ is the volatility mean-reversion parameter, ξ is the volatility of volatility and W _t is a standard normal random variable with correlation ρ against Z _t .

The SV model has a flexible distributional structure in which the correlation (ρ) between volatility and asset returns serves to control the level of asymmetry (and hence incorporates skewness) and the volatility of volatility coefficient (ξ) serves to control the level of kurtosis. The risk-neutral specification is

$$ d\upsilon_{t} = \kappa^{*} \left[ {\upsilon^{*} - \upsilon_{t} } \right]dt + \xi \sqrt {\upsilon_{t} } \sqrt {dt} dW_{t} $$

(7)

where $\kappa^{*} = \kappa + \lambda$ and $\xi^{*} = \tfrac{\kappa \xi }{\kappa + \lambda }$, where λ is the market price of volatility risk.

This model has the following closed-form solution for the call price:

$$ c_{SV} = S_{t} \left( {\frac{1}{2} + \frac{1}{\pi }\int\limits_{0}^{\infty } {\text{Re} \left[ {\frac{{K^{ - iz} f_{1} }}{iz}} \right]dz} } \right) - Ke^{{ - r\left( {T - t} \right)}} \left( {\frac{1}{2} + \frac{1}{\pi }\int\limits_{0}^{\infty } {\text{Re} \left[ {\frac{{K^{ - iz} f_{2} }}{iz}} \right]dz} } \right) $$

(8)

where ${\text{Real}}[ \cdot ]$ refers to the real part of the expression in $[ \cdot ]$ and $f_{j} = \exp \left\{ {C_{j} + D_{j} \upsilon + izx} \right\}$ with

$$ \begin{aligned} & x = x_{t} = \log (S_{t} ) \\ & \upsilon = \upsilon_{t} \\ & C_{j} = irz\left( {T - t} \right) + \frac{\kappa \upsilon }{{\xi^{2} }}\left\{ {\left( {b_{j} - i\rho \xi z + d_{j} } \right)\left( {T - t} \right) - 2\ln \left[ {\frac{{1 - g_{j} e^{{d_{j} \left( {T - t} \right)}} }}{{1 - g_{j} }}} \right]} \right\} \\ & D_{j} = \frac{{b_{j} - iz\rho \xi + d_{j} }}{{\xi^{2} }}\left[ {\frac{{1 - e^{{d_{j} \left( {T - t} \right)}} }}{{1 - g_{j} e^{{d_{j} \left( {T - t} \right)}} }}} \right] \\ & g_{j} = \frac{{b_{j} - iz\rho \xi + d_{j} }}{{b_{j} - iz\rho \xi - d_{j} }} \\ & d_{j} = \sqrt {\left( {iz\rho \xi - b_{j} } \right)^{2} - \left( {2iu_{j} z - z^{2} } \right)\xi^{2} } \\ & u_{1} = \frac{1}{2} \\ & u_{2} = - \frac{1}{2} \\ & b_{1} = \kappa + \lambda - \rho \xi \\ & b_{2} = \kappa + \lambda \\ \end{aligned} $$

2.3 The Heston–Nandi GARCH model

Heston and Nandi (2000) provide a closed form pricing formula for a European option, where the underlying follows the non-linear GARCH process:

$$ \begin{aligned} & \log \left( {\frac{{S_{t + 1} }}{{S_{t} }}} \right) = r + \lambda \sigma_{t}^{2} + \sigma_{t + 1} z_{t + 1} ;\quad z_{t + 1} \sim N(0,1) \\ & \sigma_{t + 1}^{2} = \omega + \alpha \left( {z_{t} - \theta \sigma_{t} } \right)^{2} + \beta \sigma_{t}^{2} \\ \end{aligned} $$

(9)

where $\beta + \alpha \theta^{2} < 1$ is necessary for the volatility σ _t to be mean-reverting. In this model θ determines skewness and α determines kurtosis, and the risk-neutral characterization of Eq. 9 may be obtained by plugging $\lambda = - \tfrac{1}{2}$ and replacing θ with $\theta^{*} = \theta + \lambda + \tfrac{1}{2}$. This model has a moment-generating function of the form:

$$ f(z) = S_{t}^{z} \exp \left\{ {A\left( {t;t + T,z} \right) + B\left( {t;t + T,z} \right)\sigma_{t + 1}^{2} } \right\} $$

(10)

where $A(t;t + T,z)$ and $B(t;t + T,z)$ are given by the recursive relations:

$$ A\left( {t;t + T,z} \right) = A\left( {t + 1;t + T,z} \right) + zr + B\left( {t + 1;t + T,z} \right)\omega - \frac{1}{2}\ln \left( {1 - 2\alpha B\left( {t + 1;t + T,z} \right)} \right) $$

(11)

$$ B\left( {t;t + T,z} \right) = z\left( {\lambda + \theta } \right) - \frac{1}{2}\theta^{2} + \beta B\left( {t + 1;t + T,z} \right) + \frac{{\tfrac{1}{2}\left( {z - \theta } \right)^{2} }}{{1 - 2\alpha B\left( {t + 1;t + T,z} \right)}} $$

(12)

Heston and Nandi then show that the closed-form GARCH (CFG, for short) call price can be obtained as:

$$ c_{GARCH} = S_{t} \left( {\frac{1}{2} + \frac{1}{\pi }\int\limits_{0}^{\infty } {\text{Re} \left[ {\frac{{K^{ - iz} f^{*} \left( {iz + 1} \right)}}{{izf^{*} \left( 1 \right)}}} \right]dz} } \right) - Ke^{{ - r\left( {T - t} \right)}} \left( {\frac{1}{2} + \frac{1}{\pi }\int\limits_{0}^{\infty } {\text{Re} \left[ {\frac{{K^{ - iz} f^{*} \left( {iz} \right)}}{iz}} \right]dz} } \right) $$

(13)

where $f^{*}$ is the risk-neutral version of f and $f^{*} (1) = E_{t}^{Q} \left[ {S_{t} } \right] = e^{r(T - t)} S_{t}$. See Christoffersen (2003).

2.4 Pure jump Lévy models

The remaining models we consider are Lévy models. Unlike the previous processes considered, not all Lévy processes have closed form solutions. Consequently, Lévy processes and derivatives on them should conveniently be analyzed and priced via their characteristic functions. Following Carr and Madan (1999), we can price the option using:

$$ C_{T} (k) = \frac{{e^{ - \alpha k} }}{\pi }\int\limits_{0}^{\infty } {e^{ - iuk} } \psi_{T} (u)du $$

(14)

where α is dampening factor that ensures that C _T (k) is integrable for all values of the log strike k, and $\psi_{T} (u)$ is an expression involving the risk-neutral characteristic function of the model for which prices are computed, viz.:

$$ \psi_{T} (u) = \frac{{e^{ - rT} \Upphi_{T} \left( {u - \left( {\alpha + 1} \right)i} \right)}}{{\alpha^{2} + \alpha - u^{2} - i\left( {2\alpha + 1} \right)u}} $$

(15)

The option price (14) can then be estimated using a FFT routine as described (e.g., Fusai and Roncoroni 2008).

The general characteristic function for a Lévy process governing the random variable $X_{{\left( {t_{2} - t_{1} } \right)}} = \ln \left( {\tfrac{{S_{{t_{2} }} }}{{S_{{t_{1} }} }}} \right)$ is given by:

$$ E\left[ {e^{{isX_{{\left( {t_{2} - t_{1} } \right)}} }} } \right] = \exp \left\{ {\left( {t_{2} - t_{1} } \right)\left[ {ias - \frac{1}{2}s^{2} b^{2} } \right] + \int\limits_{{\Re \backslash \left\{ 0 \right\}}} {\left[ {e^{isx} - 1 - isx{\rm I}_{{\left\{ { - 1,1} \right\}}} (x)\nu (dx)} \right]} } \right\} $$

(16)

where t ₁ can naturally be zero. The scalars $a,b \in \Re$ and the measure ν satisfies $\nu (\{ 0\} ) = 0$ and $\int_{{\Re \backslash \{ 0\} }} {\left( {\left| x \right|^{2} \wedge 1} \right)} \,\nu (dx) < \infty$, where this latter property helps us extract a square integrable martingale process in the limit.²

In this subsection we consider three models of the pure jump family of Lévy models, which assume that all possible movements in stock price are caused by the frequent arrival of jumps (see Geman 2002 for further details).

Our first case is the variance gamma (VG) process which involves the following Lévy measure for $\nu ( \cdot )$:

$$ \nu_{VG} (dx) = \frac{1}{\gamma \left| x \right|}\exp \left( {\frac{x\theta }{{\sigma^{2} }} - \frac{\left| x \right|}{\sigma }\sqrt {\frac{2}{\gamma } + \frac{{\theta^{2} }}{{\sigma^{2} }}} } \right)dx $$

(17)

When integrated for jumps of all possible sizes equation, Eq. 17 implies that the total jump rate is infinite, i.e., $\int_{0}^{\infty } {\nu_{vg} } (dx) = \infty$. However for any ε > 0, we have $\int_{\varepsilon }^{\infty } {\nu_{vg} } (dx) < \infty$, implying that jumps exceeding any threshold ε > 0 are finite and arrive in compound Poisson fashion. This Lévy measure is then used in Eq. 16 with a = b = 0 to yield the following closed-form characteristic function for X _t :

$$ \Upphi_{{X_{t} }}^{(VG)} (s) = \left( {\frac{1}{{1 - is\theta \gamma + \tfrac{1}{2}s^{2} \sigma^{2} \gamma }}} \right)^{{\frac{t}{\gamma }}} $$

(18)

For the VG pure jump Lévy model the skewness and kurtosis in log returns over an interval of length one are given respectively by:

$$ \frac{{\theta \gamma \left( {3\sigma^{2} + 2\gamma \sigma^{2} } \right)}}{{\left( {\sigma^{2} + \gamma \theta^{2} } \right)^{\frac{3}{2}} }} $$

(19a)

$$ 3\left( {1 + 2\gamma - \frac{{\gamma \sigma^{4} }}{{\left( {\sigma^{2} + \sigma \theta^{2} } \right)^{2} }}} \right) $$

(19b)

We can then price the VG call option using the risk-neutral (or mean-corrected) version of the characteristic function (16) suggested by Carr and Madan (1999):

$$ \Upphi_{{X_{t} }}^{(VG;rn)} (s) = \exp \left\{ {i\left[ {r + \frac{1}{\gamma }\ln \left( {1 - \theta \gamma - \frac{1}{2}\sigma^{2} \gamma } \right)} \right]st - \frac{t}{\gamma }\ln \left( {1 - is\theta \gamma + \frac{1}{2}s^{2} \sigma^{2} \gamma } \right)} \right\} $$

(20)

A second pure jump model is the CGMY model proposed by Carr et al. (2002). The Lévy measure of the CGMY model is given by:

$$ \nu_{CGMY} (dx) = \left\{ {\begin{array}{*{20}c} {C\frac{{e^{ - Mx} }}{{x^{1 + Y} }}dx} \hfill & {{\text{if}}\; \, x > 0} \hfill \\ {C\frac{{e^{ - Gx} }}{{\left| x \right|^{1 + Y} }}dx} \hfill & {{\text{if}}\; \, x < 0} \hfill \\ \end{array} } \right. $$

(21)

for positive constants C, G, M and Y < 2. Applying Eq. 16, this Lévy measure leads to the closed-form characteristic function:

$$ \Upphi_{{X_{t} }}^{(CGMY)} (s) = \exp \left\{ {Ct\Upgamma \left( { - Y} \right)\left( {\left( {M - is} \right)^{Y} - M^{Y} + \left( {G + is} \right)^{Y} - G^{Y} } \right)} \right\} $$

(22)

The skewness and kurtosis in log-returns on an interval of length 1 are then given by:

$$ \frac{{C\left( {M^{Y - 3} - G^{Y - 3} } \right)\Upgamma \left( {3 - Y} \right)}}{{\left( {C\left( {M^{Y - 2} + G^{Y - 2} } \right)\Upgamma \left( {2 - Y} \right)} \right)^{{\tfrac{3}{2}}} }} $$

(23a)

$$ 3 + \frac{{C\left( {G^{Y - 4} + M^{Y - 4} } \right)\Upgamma \left( {4 - Y} \right)}}{{\left( {C\left( {M^{Y - 2} + G^{Y - 2} } \right)\Upgamma \left( {2 - Y} \right)} \right)^{2} }} $$

(23b)

This model’s risk-neutral characteristic function is given by:

$$ \Upphi_{{X_{t} }}^{(CGMY;rn)} (s) = \exp \left\{ \begin{aligned} & i\left( {r - C\Upgamma \left( { - Y} \right)\left( {\left( {M - 1} \right)^{Y} - M^{Y} + \left( {G + 1} \right)^{Y} - G^{Y} } \right)} \right)st \hfill \\ & \quad + Ct\Upgamma \left( { - Y} \right)\left( {\left( {M - is} \right)^{Y} - M^{Y} + \left( {G + is} \right)^{Y} + G^{Y} } \right) \hfill \\ \end{aligned} \right\} $$

(24)

The third model we consider in the pure jump category is the Normal Inverse Gaussian (NIG). The Lévy measure of a $NIG(\alpha ,\beta ,\delta )$ process is given by:

$$ \nu_{NIG} (dx) = \frac{\delta \alpha }{\pi \left| x \right|}e^{\beta x} K_{1} \left( {\alpha \left| x \right|} \right)dx $$

(25)

where K ₁ is a modified Bessel function of the third kind with index 1. Plugging this Lévy measure into Eq. 16, with a = b = 0 yields the closed-form characteristic function:

$$ \Upphi_{{X_{t} }}^{(NIG)} (s) = \exp \left\{ { - \delta t\left( {\sqrt {\alpha^{2} - \left( {\beta + is} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right)} \right\} $$

(26)

For the NIG model, the skewness and kurtosis in log returns over an interval of length 1 are:

$$ \frac{3\beta }{{\alpha \delta^{{ - \tfrac{1}{2}}} \left( {\alpha^{2} - \beta^{2} } \right)^{{ - \tfrac{1}{4}}} }} $$

(27a)

$$ 3\left( {1 + \frac{{\alpha^{2} + 4\beta^{2} }}{{\delta \alpha^{2} \sqrt {\alpha^{2} - \beta^{2} } }}} \right) $$

(27b)

We then obtain the risk-neutral form of the characteristic function (26) by mean-correction:

$$ \Upphi_{{X_{t} }}^{(NIG;rn)} (s) = \exp \left\{ {i\left( \begin{array}{l} r + \delta \left( {\sqrt {\alpha^{2} - \left( {\beta + 1} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right)st \hfill \\ - \delta \left( {\sqrt {\alpha^{2} - \left( {\beta + is} \right)^{2} } - \sqrt {\alpha^{2} - \beta^{2} } } \right) \hfill \\ \end{array} \right)} \right\} $$

(28)

2.5 A jump-diffusion model

Our last model is the jump-diffusion model of Kou (2002). In contrast to other models such as those considered by Psychoyios et al. (2010), this model assumes that, in addition to drifted diffusion, the log-return process has occasional jumps that follow a double exponential distribution DE(p,η ₁, η ₂), where p is the probability of an upward jump and η ₁ and η ₂ govern the decay of the tails for the distribution of negative and positive jump sizes respectively. The Lévy measure for this process is given by:

$$ \nu_{JD} (dx) = \left[ {p\lambda \eta_{1} e^{{ - \eta_{1} x}} I_{x < 0} + \left( {1 - p} \right)\lambda \eta_{2} e^{{ - \eta_{2} \left| x \right|}} I_{x > 0} } \right]dx $$

(29)

where $\int_{ - \infty }^{\infty } {\nu_{JD} } (dx) < \infty$. Applying this Lévy measure to Eq. 16 then provides the closed form characteristic function:

$$ \Upphi_{{X_{t} }}^{(JD)} (s) = \exp \left\{ {t\left( {ias - \frac{1}{2}b^{2} s^{2} + is\lambda \left[ {\frac{{p\eta_{1} }}{{\eta_{1} + is}} + \frac{{\left( {1 - p} \right)\eta_{2} }}{{\eta_{2} + is}} - 1} \right]} \right)} \right\} $$

(30)

The skewness in this model is not explicitly characterized, but Kou suggests that the tails (and, by implication, kurtosis) become more pronounced with the increase of either the jump size expectation (1/η _j ) or the jump rate (λ). The risk-neutral characteristic function for this process is then:

$$ \Upphi_{{X_{t} }}^{(JD;rn)} (s) = \exp \left\{ \begin{aligned} & i\left( {r - \frac{1}{2}b^{2} - \lambda \left[ {\frac{{p\eta_{1} }}{{\eta_{1} + 1}} + \frac{{\left( {1 - p} \right)\eta_{2} }}{{\eta_{2} + 1}} - 1} \right]} \right)st \hfill \\ & - \frac{1}{2}b^{2} s^{2} t + is\lambda t\left[ {\frac{{p\eta_{1} }}{{\eta_{1} + is}} + \frac{{\left( {1 - p} \right)\eta_{2} }}{{\eta_{2} + is}} - 1} \right] \hfill \\ \end{aligned} \right\} $$

(31)

2.6 Summary of models

In sum, we consider eight models: Black–Scholes (BS), Gram–Charlier (GC), Heston’s stochastic volatility model (SV), the Heston–Nandi closed-form GARCH model (CFG), the three pure-jump models (VG, CGMY and NIG) and the Kou jump-diffusion (JD) model.

3 Data and calibration

We consider options on the S&P500 index traded on Wednesday 23rd January 2008, a day on which there was 178 options traded in the market. This day was chosen on a random basis.³ We begin by cleaning the data following the standard cleaning criteria set by Bakshi et al. (1997). The models are then calibrated using NonLinear Least Squares, minimizing the RMSE defined as:⁴

$$ RMSE = \frac{1}{mean\,price}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {C_{i}^{market} - C_{i}^{model} } \right)}^{2} } $$

(32)

Table 1 reports the calibrated parameters for all the models. All parameters have the expected signs and are significant (by the ratio of each parameter estimate to its SE) except for the kurtosis term (ς₂₁) in the GC model and the ω term in the CFG model. Even so, all models provide reasonable ‘fits’ to the data and, except some parameters of the CFG model, the calibrations seem broadly consistent with others’ findings.

Table 1 Model calibrations

4 Pricing performance

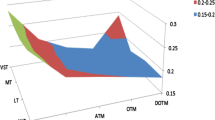
Figure 1 shows plots of the models’ RMSEs against moneyness. For the most part, it is hard to distinguish among the models’ performance as judged by this criterion. However, we see that the SV is a consistently good performer across both moneyness and maturity. We also see that the CFG model’s performance improves with the length of the maturity, and this model is unambiguously the best performer for the longer maturities in Fig. 1c.

Fig. 1

Models’ in-sample pricing performance for options traded on S&P500 index on January 23, 2008. a Options with 0–60 days to maturity (dtm). b Options with 60–120 days to maturity (dtm). c Options with over 120 days to maturity (dtm)

5 Smile-skew patterns

Figures 2 and 3 give the models smile-skew patterns, i.e., plots of the models’ implied volatilities against moneyness. The BS plot is flat, as of course is well known, but we also get nearly flat plots for the CFG model as well. By contrast, we get pronounced smile-type patterns for the short-maturity GC and Lévy models and for the long-maturity SV model, and pronounced smirks for the short-maturity SV models and the long-maturity GC and Lévy models.

Fig. 2

Smile-skew patterns exhibited by pricing models calibrated to S&P500 index options traded on January 23, 2008: short maturities

Fig. 3

Smile-skew patterns exhibited by pricing models calibrated to S&P500 index options traded on January 23, 2008: long maturities

These results suggest that the SV and Lévy models can accommodate the smile-skew patterns found in the data, but the BS model cannot and the CFG model might have difficultly doing so.

6 Greek-based approximations to option prices

We turn now to consider approximations to option prices using the options’ deltas and gammas. These are often highly convenient (e.g., for mapping purposes, see Dowd 2005, chapter 12 and for portfolio approximation, of which more below), but can sometimes be inaccurate, especially in the face of large fluctuations in the underlying. This inaccuracy arises partly because the delta and gamma themselves often inadequately reflect the full non-linearity of option prices and partly because estimates of the deltas and gammas, themselves, are often inaccurate.

One reason for this latter inaccuracy is that these methods often use inaccurate ‘one point’ approximations for a generic underlying asset price S that is (hopefully) ‘close’ to the current price S _t :

$$ C^{model} (S) \approx C^{model} (S_{t} ) + \delta^{model} (S - S_{t} ) $$

(33)

$$ C^{model} (S) \approx C^{model} (S_{t} ) + \delta^{model} (S - S_{t} ) + \frac{1}{2}\gamma^{model} (S - S_{t} )^{2} $$

(34)

(see e.g., Christoffersen 2003 or Dowd 2005). For any generic underlying asset price the option price is then approximated using the same delta and gamma, which are calculated once (only for the current value of the underlying) no matter how much the underlying asset price deviates. Of course, this approximation presupposes that the underlying price remains ‘close’ enough to the value it took when the delta and gamma were estimated. This may (sometimes) be reasonable but it is highly questionable in the context of jumpy Lévy models or stochastic volatility processes.

Another reason for inaccurate delta and gamma estimates is that amongst the models we are considering, closed-form formulas only exist for the BS and GC models. In the case of the other models, we need to estimate Greeks using numerical methods, and these are subject to potential inaccuracies of their own due to factors such as perturbation errors.

The typical method used is the finite difference technique, which is popular because it can be applied to estimate all the Greeks reasonably quickly (see Duffy 2006). Suppose C ^model(S), for a particular model, is the price of a European option with strike K and time to maturity T, when the price of the underlying is S. As is well-known, the finite difference method gives us the following approximation for the option delta for that particular model:

$$ \delta^{model} = \frac{\partial C}{\partial S} = \frac{{C^{model} (S + dS) - C^{model} (S)}}{dS} $$

(35)

where dS is a small perturbation to the price of the underlying. Similarly, to obtain the gamma, the sensitivity of delta, we need to obtain two values of delta. Let δ₁ be the δ as defined in Eq. 35 and δ₂ be some value close to it:

$$ \delta_{2} = \frac{\partial C}{\partial S} = \frac{{C^{model} (S + 2dS) - C^{model} (S + dS)}}{dS} $$

(36)

Then the finite difference method gives us the following approximation for the option’s gamma:

$$ \gamma^{model} = \frac{{\partial^{2} \delta }}{{\partial S^{2} }} = \frac{{\delta^{2} - \delta^{1} }}{dS} \, = \frac{{C^{model} (S + 2dS) - 2C^{model} (S + dS) + C^{model} (S)}}{{(dS)^{2} }} $$

(37)

However, the finite difference estimates of these parameters are extremely sensitive to the perturbation size dS: the Greek surfaces are unstable and the ranges over which the method works vary across different Greeks and different models. Furthermore, to our knowledge there is no working rule to choose a perturbation that works for all models.

Given this, it is possible to obtain ‘respectable’ surfaces. To illustrate, Fig. 4 plots the Delta surfaces for all the models under consideration, where all are based on the finite difference approach with the perturbation size (which is common to all models) found by trial and error. We see that the delta changes dramatically when the option is close to ATM, converges to zero for OTM options and to one for ITM options. Figure 5 plots the comparable surfaces for the gamma. For a short maturity option the gamma changes dramatically when the option is close to ATM, and converges to zero both for ITM and OTM options. These plots are broadly similar across most models, but one might notice that those for the SV and CFG models are somewhat different from those of the others.

Fig. 4

Delta surfaces of pricing models. Note: The right-hand side shows a slice corresponding to an option with 16 DTM and strike of 1,550

Fig. 5

Gamma surfaces of pricing models. Note: The right-hand side shows a slice corresponding to an option with 16 DTM and strike of 1,550

7 Greek-based approximations to option portfolio values

We now consider a portfolio similar to one used in Britten-Jones and Schaefer (1999). This portfolio is constructed from our data set subject to the proviso that, while the call options in the portfolio are traded in the market, the put option is priced using put-call parity. The option portfolio is described in Table 2.

Table 2 Illustrative option portfolio constructed using options traded on January 23, 2008

However, whilst Britten-Jones and Schaefer (1999) and Christoffersen (2003) only considered the valuation of similar portfolio under the BS model, we wish to examine portfolio valuation under all 8 of our models.

Now assume a risk-management horizon of five trading days (seven calendar days), which corresponds to the sampling interval for our weekly data. As in Christoffersen (2003) we consider the complete pay-off profile of the portfolio, under all considered models, for different future values of the underlying asset prices S _t+5. Let P _t and P(S _t+5) denote the portfolio value today and at the end of five trading days respectively. We have:

$$ P_{t} = m_{1} put + m_{2} call_{1} + m_{3} call_{2} $$

(38)

$$ P^{\delta } \left( {S_{t + 5} } \right) = P_{t} + \delta^{p} \left( {S_{t + 5} - S_{t} } \right) $$

(39)

$$ P^{\delta \gamma } \left( {S_{t + 5} } \right) = P_{t} + \delta^{p} \left( {S_{t + 5} - S_{t} } \right) + \frac{1}{2}\gamma^{p} \left( {S_{t + 5} - S_{t} } \right)^{2} $$

(40)

Here δ^p and γ^p are model-dependent portfolio hedge factors defined as:

$$ \delta^{p} = m_{1} \delta_{put}^{m} + m_{2} \delta_{{call_{1} }}^{m} + m_{3} \delta_{{call_{2} }}^{m} $$

(41)

$$ \gamma^{p} = m_{1} \gamma_{put}^{m} + m_{2} \gamma_{{call_{1} }}^{m} + m_{3} \gamma_{{call_{2} }}^{m} $$

(42)

where the superscript m is any number between 1 and 8 representing each of the 8 different models considered. m ₁ is the number of puts and m ₂ and m ₃ are the number of calls respectively in the portfolio.

The true value of the option portfolio is then obtained through full-valuation using model-based option prices:

$$ \begin{aligned} P^{exact} \left( {S_{t + 5} } \right) & = m_{1} \times put^{m} \left( {K = 1200,\;T = 23 - 7} \right) \\ & \quad + m_{2} \times call_{1}^{m} \left( {K = 1200,\;T = 23 - 7} \right) \\ & \quad + m_{3} \times call_{2}^{m} \left( {K = 1550,\;T = 23 - 7} \right) \\ \end{aligned} $$

(43)

The accuracy of these approximations is evident in the valuation plots shown in Fig. 6. The most pronounced feature of these plots is the way the Greek-based approximations for all models diverge away from the full valuations when there are large swings in the underlying asset price. However, for relatively small asset price movements, the Greeks-based valuations are accurate for all models. We also see that there are differences between the delta and delta-gamma approximations, though the magnitude of these differences varies a little across the models, being least for the JD model and greatest for the GC model.

Fig. 6

Portfolio valuation: full valuations versus Greek approximations. Note: Current asset price is 1,338.6

We also see that, in general, valuations based on the delta approximation are a little more accurate than those based on the delta-gamma approximation in the face of upward asset price movements, and slightly less accurate in the face of downward asset price movements. Thus, on average, the more sophisticated delta-gamma approximation is no more accurate than the simpler delta approximation.

The corresponding approximation errors are shown in Fig. 7 and these show some notable differences between the models. We see that the worst model is the BS and the second-worst is the JD model. We also note that both stochastic volatility (SV) and GARCH(CFG) models perform quite well for both increasing and decreasing asset prices.

Fig. 7

Approximation errors of Greek-based valuations increasing (left) and decreasing (right) asset prices. a Delta approximations. b Delta–Gamma approximations. Note: Current asset price is 1,338.6

8 Risk-neutral densities

Finally, Fig. 8 shows the risk-neutral densities obtained by inverting risk neutral characteristic functions. We see some notable differences in the shapes of these densities, and perhaps the most notable differences are in their tails: the SV model gives the widest tails and the CFG the narrowest.

Fig. 8

Risk-neutral densities of pricing models calibrated on traded options on January 23, 2008. a Models without jump. b Pure jump and jump-diffusion model

9 Conclusion

The inability of the Black-Scholes option pricing model to incorporate skewness and excess kurtosis has led to the development of a series of alternative models over the years. This study compares the overall performance of a wide range of models—including Gram–Charlier, stochastic volatility, GARCH and Lévy models, as well as BS—using a common data set. We find a number of notable differences between the models and we find that the BS and Gram–Charlier models often perform less accurately than the GARCH, stochastic volatility and Lévy models. Of these the stochastic volatility model performs robustly well and the Lévy models often perform well too.

We have also shown that satisfactory estimates of these models’ hedge ratio deltas and gammas can be obtained using traditional finite difference methods, and that these can be used to value portfolios of options. In this respect, our study extends the earlier work of Britten-Jones and Schaefer (1999), who only considered such problems in the context of Black–Scholes. We find that regardless of the model used, delta and delta-gamma approaches can yield inaccurate approximations of option portfolio values, especially in the face of large swings in the price of the underlying. These findings suggest that delta and delta-gamma approximations can be very misleading and reinforce the need for full-valuation methods instead. They also remind us that even the most (otherwise) sophisticated models can be very inaccurate during times of financial market turbulence.

This study can be extended in a number of ways. First, the stochastic volatility and GARCH models can be combined with Lévy processes, in which normal innovations are replaced with Lévy innovations. Such a combination would combine the complementary strengths of both approaches and also benefit from closed-form solutions resulting in quick calibrations. Second, to date there are no systematic comparisons of option risk measures (such as VaR or Expected Shortfall) based on all eight models. It would be useful to compare these on common data sets encompassing both stable and turbulent market conditions. Finally, it would be useful to examine the performance of different numerical schemes to calculate the Greeks. Quick and accurate calculation of these would help in hedging and risk-managing the options involved.